倒易点阵介绍
倒易点阵概念

倒易点阵概念
倒易点阵是一种用于描述晶体结构中原子排列和晶格常数的强大数学工具。
在倒易点阵中,一系列点表示晶格中原子位置的倒易矢量,这些点对应着晶体结构中的原子位置。
通过这些倒易点阵,我们可以计算出晶格常数、原子间距以及晶格结构中的对称性和对称元素。
倒易点阵的概念在晶体学和材料科学中具有极其重要的意义。
首先,它可以帮助我们深入理解晶体的结构和性质。
通过倒易点阵,我们可以直观地观察到原子在晶体中的排列和分布,从而更好地理解晶体的构造和形成机制。
此外,倒易点阵还可以帮助我们预测和解释晶体的物理和化学性质。
通过对倒易点阵的分析,我们可以推断出晶体的力学、光学、电学等性质,为材料科学的研究和应用提供重要依据。
此外,倒易点阵还可以用于计算晶体结构中的对称性和对称元素。
对称性是晶体学中的一个核心概念,它涉及到晶体的几何结构和物理性质。
通过对称性分析,我们可以了解晶体的稳定性和各向异性等特点,从而更好地理解晶体的性质和应
用。
倒易点阵是一种强大的工具,可以帮助我们理解和描述晶体的结构和性质。
它是晶体学和材料科学领域的重要概念之一,对于研究晶体的物理和化学性质、探索新的材料和设计具有广泛应用价值。
倒易点阵

*
* * * * * a r*001 * * * * * * *c * β * *
*
*
202 * * r*001 * *
a* = r*200 = 1/d200 = 2/(a.cos[β-90])= 2/(a.sinβ) b* = r*002 = 1/d002 = 2/b c* = r*001 = 1/d001 = 1/(c.cos[β-90])= 1/(c.sinβ) *
5、对于面心型,指数同为偶数或奇数的晶面才出现; 、对于面心型,指数同为偶数或奇数的晶面才出现; (111) (220)
(200)
(三)、倒易点阵小结 )、倒易点阵小结
1、均为无限的周期点阵, 、均为无限的周期点阵, 2、正点阵的晶面对应于倒易点阵的阵点(除有公因子指数外); 、正点阵的晶面对应于倒易点阵的阵点(除有公因子指数外); 3、晶系不变,为11种中心对称的劳厄点群; 种中心对称的劳厄点群; 、晶系不变, 种中心对称的劳厄点群 4、P->P*, C->C*, I->F*, F->I*,即对复合单胞出现倒易点阵系统消光, 、 ,即对复合单胞出现倒易点阵系统消光, 立方系指数表见下表
r∗ r∗ r r r∗ r∗ r rhkl ⋅ AB = (ha + kb + lc ) (b / k − a / h) = 1 − 1 = 0 r∗ r c ∴ rhkl ⊥ AB r r∗ 同理可证: 同理可证: rhkl ⊥ AC C r b r∗ rhkl ⊥ BC B
∴
性质一证明 r r r r O A = a / h OB = b / k
1/ a2 cos γ * G* = ab 0
cos γ * ab 1/ b2 0
倒易点阵介绍

n O
光程差 On Am OA S OA S0 OA ( S S0 )
相应的位向差为
2
2
( S S0 )
OA
其中p、q、r是整数 因为S0是入射线方向单位矢量, S是衍射线方向为单 位矢量,因此S- S0是矢量,则:(S S0 ) * *
2
1/
A
O
S0 /
5 、以S0端点O点为原点,作
倒易空间,某倒易点(代表
某倒易矢量与hkl面网)的 端点如果在反射球面上, 说明该g*=S, 满足Bragg’s Law。某倒易点的端点如果
P
S/
S S0 g
2
不在反射球面上, 说明不
满足Bragg’s Law,可以直
1/
A
O
S0 /
25
概念回顾
以A为圆心,1/λ 为半径所做的球称为反 射球,这是因为只有在这个球面上的倒 易点所对应的晶面才能产生衍射。有时 也称此球为干涉球, Ewald球。 围绕O点转动倒易晶格,使每个倒易点 形成的球称为倒易球 以O为圆心,2/λ 为半径的球称为极限球。
26
大倒易球半径为
g=1/d≤ 2/:
hkl
即 d hkl
2
S/的晶面不Fra bibliotek1/
2 C S0/
g
O
Direction of direct beam
可能发生衍射
Sphere of reflection
极限球
Limiting sphere
关于点阵、倒易点阵及Ewald球的思考
(1) 晶体结构是客观存在,点阵是一个数学抽象。 晶体点阵是将晶体内部结构在三维空间周期平移这 一客观事实的抽象,有严格的物理意义。 (2) 倒易点阵是晶体点阵的倒易,不是客观实在, 没有特定的物理意义,纯粹为数学模型和工具。 (3) Ewald球本身无实在物理意义,仅为数学工具。 但由于倒易点阵和反射球的相互关系非常完善地描 述了X射线和电子在晶体中的衍射,故成为研究晶 体衍射有力手段。
倒易点阵

倒易点阵的应用—解释X射线及电子衍射
• 劳厄方程
当相邻原子的散射X射线光程差等于 入射X射线波长整数倍时发生衍射。
a(cosα-cosα0) = Hλ
一维原子列的衍射示意图
倒易点阵的应用—解释X射线及电子衍射
• 劳厄方程
设空间点阵的三个平移向量为a ,b和c,入射的X射线与它们的交角分别为α0,β0和γ0。 衍射方向与它们的交角分别为α,β和γ 。根据上述讨论可知,衍射角α,β和γ在x, y, z三个轴上应满足以下条件:
单晶体电子衍射花样标定
• 确定零层倒易截面上各ghkl矢量端点(倒易阵点)的指数,定出零层倒易截面的 法向(即晶带轴[uvw]),并确定样品的点阵类型、物相及位向。 (1)测量靠近中心斑点的几个衍射斑点至中心斑点距离R1、R2、R3、R4…及 R1与R2、R1与R3等衍射斑点之间的夹角。 (2) 计算R12∶R22∶R32∶…=N1∶N2∶N3∶… 其中N = h2 + k2 + l2
故
于是,它们的点乘 根据倒易基矢定义式,显然有
和
都为0。
倒易点阵的应用—解释X射线及电子衍射
• „ 劳厄的一个科学假设
1911年埃瓦尔德在索末菲的指导下在慕尼黑大学从事博士论文研究,劳厄在 与他的讨论中了解到晶格的平移周期与X射线的波长属于同一量级,因此想到 在二维光栅的两个衍射方程组中再加一个类似的方程,就可以描述X射线在三 维晶体中的衍射。 在此假设的指导下,Knipping和Friedrich在1912年4月开始用CuSO4 后来 用闪锌矿(立方ZnS)进行实验,很快就得到X射线衍射的证据。这不但证明 了X射线的波动性,还确定了晶体的三维周期性。
a*、b*、c*
即倒易基矢
倒易点阵名词解释

倒易点阵名
倒易点阵是由被称为倒易点的点所构成的一种点阵,它也是描述晶体结构的一种几何方法,它和空间点阵具有倒易关系。
倒易点阵中的一倒易点对应着空间点阵中一组晶面间距相等的点格平面。
倒易点阵的概念在晶体结构和固体物理学中都有十分重要的作用。
到目前为止,大多数教程都是在密勒指数或晶面指数无关的情况下来定义倒易点阵概念的。
由于晶面指数的概念出现得很早,有一些老的晶体学和固体物理学教程中甚至没有提到倒易点阵这个概念。
在目前流行的固体物理学教科书中,对倒易点阵均有叙述,而且处处应用。
但是,倒易点阵概念的引入比较生硬,对倒易点阵与晶面指数的关系交待得不够清楚。
晶体学基础-倒易点阵
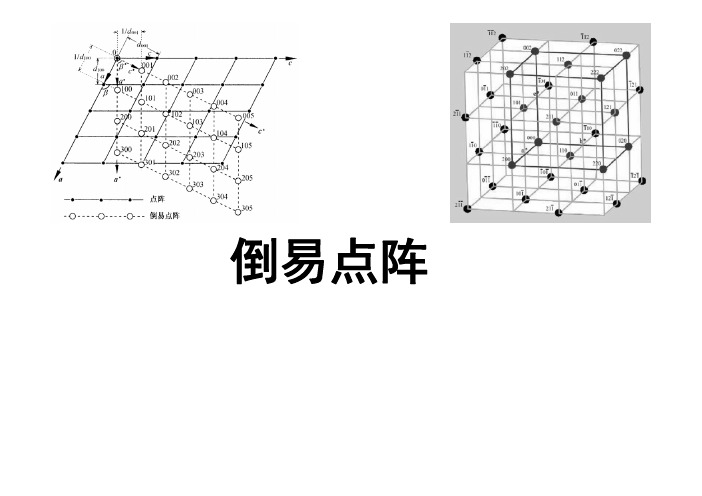
倒易点阵晶体学中最关心通常是晶体取向,即晶面的法线方向。
倒易点阵是在晶体点阵的基础上按一定对应关系建立起来的空间几何图形(倒易空间),是晶体点阵的另一种表达形式。
将晶体点阵空间称为正空间。
倒易空间中的结点称为倒易点。
部分。
a a * = b把正点阵基矢与倒易点阵基矢的关系代入,得正点阵与倒易点阵的关系•O 点到(hkl)晶面的垂直距离就是晶面间距d hkl 。
倒数关系(大小)●d hkl =h a H H H1=•确定倒易矢量H ,就确定了正点阵晶面。
S hkl P 及Q ⊥•倒易矢量[hkl]的大小(模)就是其正点阵中相邻平行(hkl)晶面间距的倒数。
(倒—Reciprocal)进行矢量相乘并且展开。
a H hkl •在倒易点阵中,从原点指向阵点[坐标hkl ]的倒易矢量H hkl = ha* +kb* +lc*•H hkl 必和正点阵的(hkl )面垂直,•即倒易点阵的阵点方向[hkl ]*和正点阵的(hkl )面垂直:[hkl ]*⊥(hkl )。
CBAx y z(010)(100)(001)a例:由单斜点阵导出其倒易点阵•单斜点阵:b轴垂直于a和c轴。
左图图面为(010)面。
•从作图可以看出,正点阵和其对应的倒易点阵同属一种晶系。
把上面三个式子写成矩阵形式:•同理,可按下式求出与方向指数为[uvw]的方向相垂直的面的面指数(hkl):•例如,对立方系而言,a*●a* = b* ●b* = c*●c *=1/a2;a*●b* = b* ●c* = c*●a *=0;•u:v:w=h:k:l。
所以(hkl)面的法线指数和面指数同名,即为[hkl]。
倒易点阵 晶体结构

倒易点阵晶体结构倒易点阵晶体结构倒易点阵晶体结构是一种特殊的晶体结构,它具有许多独特的性质和应用。
本文将介绍倒易点阵晶体结构的基本概念、性质和应用。
一、基本概念倒易点阵是指在晶体中原子或分子排列的方式。
晶体是由周期性排列的原子或分子组成的固体,而倒易点阵则是晶体中原子或分子排列的镜像。
倒易点阵具有高度的对称性和周期性,其结构可以用倒易点群来描述。
二、性质1. 高度的对称性:倒易点阵具有高度的对称性,这是由于晶体中原子或分子的周期性排列所决定的。
倒易点阵的对称性可以通过倒易点群来描述,倒易点群是一组对称操作,包括旋转、镜像和反演等操作。
2. 布拉格定律:倒易点阵的周期性排列使得它们能够散射入射的电磁波。
布拉格定律描述了散射波与倒易点阵的相互作用。
根据布拉格定律,散射波的波矢量与倒易点阵的倒格矢量之间满足关系式:2π/λ = |G|,其中λ是散射波的波长,G是倒格矢量的模长。
3. 能带结构:倒易点阵的周期性排列使得它们具有能带结构。
能带结构是描述固体中电子能量与动量关系的理论。
倒易点阵的能带结构对于材料的电子输运和光学性质具有重要影响。
三、应用倒易点阵晶体结构在许多领域都有重要的应用,以下列举几个典型的应用:1. 光学器件:倒易点阵晶体结构具有特殊的光学性质,可用于制造光学器件。
例如,倒易点阵光纤具有高度的光学导引性能,可用于制造光纤通信设备。
2. 光子晶体:倒易点阵晶体结构可以形成光子禁带,即在某一频率范围内禁止光的传播。
光子晶体具有重要的光学性质,可用于制造光学滤波器、光学调制器等光学器件。
3. 电子器件:倒易点阵晶体结构对于电子输运具有重要的影响,可用于制造电子器件。
例如,倒易点阵晶体管具有优良的电子输运性能,可用于制造高频放大器和微波器件。
4. 气体吸附:倒易点阵晶体结构具有大的表面积和孔隙度,可用于吸附气体。
倒易点阵材料可以用作气体传感器、催化剂和分离膜等。
四、总结倒易点阵晶体结构是一种特殊的晶体结构,具有高度的对称性和周期性。
倒易点阵介绍重点

8
衍射条件
设:入射线波长为λ ,入 射线方向为单位矢量S0, 衍射线方向为单位矢量S, 那么在S方向有衍射线的 条件是:在与S方向相垂 直的波阵面上,晶体中各 原子散射线的位向相同。 先计算原点O和任一原子 A的散射线在与S方向的 位向差。
g
1
m
θ
hkl
A
θ θ
S 2 (S-S0) (HKL) S0
n O
光程差 On Am OA S OA S0 OA ( S S0 )
相应的位向差为
2
2
( S S0 )
OA
其中p、q、r是整数 因为S0是入射线方向单位矢量, S是衍射线方向为单 位矢量,因此S- S0是矢量,则:(S S0 ) * *
6
1. 倒易矢量 ghkl 垂直于正点阵中相应的 [hkl] 晶面,或 平行于它的法向Nhkl 2.倒易点阵中的一个点代表的是正点阵中的一组晶面
ghkl=h a*+k b*+lc* 表明:
7
晶带定理
在正点阵中,同时平行于某一晶 向[uvw]的一组晶面构成一个晶带, 而这一晶向称为这一晶带的晶带 轴。 图示为正空间中晶体的[uvw]晶带 图中晶面(h1k1l1)、(h2k2l2)、 (h3k3l3)的法向N1、N2、N3和倒 易矢量gh1k1l1、gh2k2l2、gh3k3l3的方 向相同. 晶带定理:因为各倒易矢量都和 其晶带轴r=[uvw]垂直,固有 ghkl•r=0 ,即 hu+kv+lw=0, 这就 是晶带定理。
(S-S0)/λ= 2sinθ )/λ=ghkl=1/d
2dsinθ =λ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
倒易点阵
❖ 倒易点阵概念及定义 ❖ 倒易点阵的物理意义 ❖ 倒易点阵的应用是一个假想的点阵.
❖ 将空间点阵(真点阵或实点阵)经过倒易变换,就 得到倒易点阵,倒易点阵的外形也是点阵,但其 结点对应真点阵的晶面,倒易点阵的空间称为倒 易空间。
❖ 1860年法国结晶学家布拉菲提出并作为空间点 阵理论的一部分,但缺乏实际应用。
24
25
点阵中单胞的体积:V=a·(b×c)=b·(a×c) =c·(a×b)
5
倒易点阵基矢与正点阵基矢的关系
(仅当正交晶系)
6
倒易点阵的性质
1. 正倒点阵异名基矢点乘为0;
a*·b= a*·c=b*·a=b*·c=c*·b=0
同名基矢点乘为1。
a*·a=b*·b=c*·c=1.
2. 在倒易点阵中,由原点O*指向任意坐标为hkl的阵点
的。即倒易矢量ghkl是与相应指数的晶向[hkl] 平行的。
7
ghkl=h a*+k b*+lc* 表明:
❖ 1平.倒行易于矢它量的法gh向kl垂N直hkl于正点阵中相应的 [hkl]晶面,或 ❖ 2.倒易点阵中的一个点代表的是正点阵中的一组晶面
8
晶带定理
❖ 在正点阵中,同时平行于某一晶 向[uvw]的一组晶面构成一个晶带, 而这一晶向称为这一晶带的晶带 轴。
向平行于(hkl)晶面的法线,则有K‘ –K= G,即为布拉格方程 14
的矢量形式。
倒易点阵的应用
倒易点阵使许多晶体几何学问题的解决变得简易。例如单胞体 积,晶面间距、晶面夹角的计算以及晶带定理的推导等等。以 下是倒易点阵的应用。 1°由倒易点阵的基本性质可得: a*=1/d100,b*=1/d010,c*=1/d100 (a*=G100=1/d100) 在晶体点阵S 中,点之间或点阵平面之间的距离用Å 作单位, 因此,a*、b*、c*的单位为Å-1。在用图解法解决实际问题时, 用相对标度值表示相对大小即可。
ghkl(倒易矢量)为:ghkl=h a*+k b*+lc* 式中hkl为正点阵中的 晶面指数
3. 倒易矢量的长度等于正点阵中相应晶面间距的倒数,即
ghkl=1/dhkl 4. 对正交点阵,有 a*∥a,b*∥b,c*∥c,
a*=1/a,b*=1/b,c*=1/c,
5. 只有在立方点阵中,晶面法线和同指数的晶向是重合(平行)
❖ 图示为正空间中晶体的[uvw]晶带
❖ 图中晶面(h1k1l1)、(h2k2l2)、 (h3k3l3)的法向N1、N2、N3和倒 易矢量gh1k1l1、gh2k2l2、gh3k3l3的方 向相同.
❖ 晶带定理:因为各倒易矢量都和
其晶带轴r=[uvw]垂直,固有
ghkl•r=0 ,即 hu+kv+lw=0, 这就
18
倒易点阵的应用
19
倒易点阵的应用
4°晶带轴 按定义,指数为(h1、k1、l1)和(h2、k2、l2)两晶面的 晶带轴即为这两个晶面的交线方向,若含此交线平行于某一 (正)矢量,puvw p=ua+vb+wc 所求晶带轴即求出[uvw]三数即可。 (h1、k1、l1)和(h2、k2、l2)晶面的法线是平行Gh1k1l1 和Gh2k2l2
于是它们的点乘为0 20
倒易点阵的应用
根据倒易基矢定义式,显然有:
为了便于记忆,一般写成如下形式:
21
倒易点阵的应用
证明
22
倒易点阵的应用
23
1 黄昆原(著).韩汝琦(改编).固体物理学[M].北京:高等教育出版社,1988 2 王莉.WANG Li 正点阵与倒易点阵中的对应关系[期刊论文]-唐山师范学院学报 2004(5) 3 陈难先.CHEN Nan-xian 倒易点阵与晶面指数的关系[期刊论文]-大学物理 2011(2) 4 申成.SHEN Cheng 二维晶体的衍射及其倒易点阵的物理内容[期刊论文]-长沙电 力学院学报(自然科学版)2005,20(4) 5 付宝连 广义倒易定理及其应用[期刊论文]-应用数学和力学2002,23(2)
中,AO*与AG 的夹角为θ,则ΔAO*G 满足布拉格方程,即此时电 子束波长λ,晶面间距dhkl 及取向关系θhkl之间可用直角三角形表
示出来:即AO* = 2/λ, ∠O*AG =θ , O*G = 1/d,沿AO*方向入射
的电子束照射在O 点处的晶体,一部份电子束透射过去,一部份 使晶面间距为dhkl 的(hkl)面发生衍射,在OG 方向产生衍射束。 若入射波卡量用K 表示,衍射波矢量用K表示,含O*G=G,其方
于其倒易矢量长度的一半。
12
Ewald 图解
入射线
θ
B
1
反射方向 P
反射线
g
2θ
θ (hkl)
A
θO
反射球
Ewald 作图法
以一晶体为中心(O 点), 以1/λ为半径,在空间画一 个球,这个球即为爱瓦尔 德球
如图令电子束沿直径AO*的方向入射,经过晶体O
点亦到达O*点,取O*G 的长度为1/dhkl,若直角三角形ΔAO*G
9
是晶带定理。
倒易点阵的物理意义
在研究晶体对X射线或对电子束的衍射效应时, 某晶面{hkl}能否产生衍射的重要条件就是该晶 面相对于入射束的取向以及晶面间距d(hkl)满足: d(hkl)sin=n ,即著名的布拉格方程,其中-入 射角,-波长。各晶面的散射波干涉加强的条 件是,波程差为波长的整数倍。这是满足衍射 的必要条件,但不是充分条件。
10
倒易点阵的物理意义
❖ 为了从几何学上形象的确定衍射条件,人们就找到一个新的 点阵(倒易点阵),使其与正点阵(实际点阵)相对应。
❖ 对应的条件:新点阵中的每一个结点都对应着正点阵的一定 晶面,该结点既反映该晶面的取向也反映该晶面的面间距。
❖ 具体条件: ❖ a正. 点新阵点中阵{中hk原l}面点的O到法任线意方结向点。P(hkl) (倒易点)的矢量正好沿 ❖ b. 新点阵中原点O到任意结点P(hkl)的距离等于正点阵中{hkl}
❖ 1921年德国物理学家埃瓦尔德把倒易点阵引入
衍射领域。此后,倒易点阵成了研究各种衍射
问题的重要工具。
3
倒易点阵定义
❖ 倒易点阵的定义 ❖ 倒易点阵的性质 ❖ 晶带定理
4
倒易点阵的定义
倒易点阵的基本矢量垂直于正点阵异名矢量构成的平 面。 用a、b、c表示晶体点阵(正点阵)的基本矢量;用 a*、b * 、c *表示倒易点阵的基本平移矢量,则倒易 点阵与正点阵的基本对应关系为:
15
倒易点阵的应用
2°晶面间距公式 ( hkl )晶面的间距dhkl为: dhkl=1/IGhklI (dhkl )-2 =G2hkl =ha*+ kb*+ lc* 2
16
倒易点阵的应用
17
倒易点阵的应用
3°晶面之间的夹角ϕ ,(h1、k1、l1)晶面与(h2、k2、l2) 晶面之间的夹角ϕ (也即这两个晶面的法线之间的夹角ϕ 即为 Gh1、k1、l1 与Gh2、k2、l2 晶面之间的夹角),故
面的面间距的倒数。
❖ 将实际晶体中一切可能的的{hkl}面所对应的倒易点都画出来, 由这些倒易点组成的点阵称为倒易点阵。
11
倒易点阵的物理意义
爱瓦尔德球(反射球)(P.P.Ewald) ❖ Ewald 图解是衍射条件的几何表达式。 ❖ sinθ =λ/2d ❖ 令d= λ /ghkl (此时比例系数用X射线的波长) ❖ 则sinθ = ghkl /2 ❖ 即某衍射面( hkl)所对应的布拉格角的正弦等
