地球物理正演方法
地球物理正反演理论综述
KL201
KL2
KL204
气藏顶部
E
气藏底部
相干数据体平面断层解释
KL203 KL205 KL201 KL2 KL204
下第三系白云岩段顶面构造图
相干数据体技术
T6沿层相干切片
阿拉尔断裂 ш号断层
Ⅶ号断层
沿层相干数据解释切片
ⅤⅢ号断 层
ⅩⅢ号断层
•80年代，随着计算机工作
站的发展：
数字处理技术从二维向三维迅速发 展，可以清晰地看清地下结构的图 像，从而完成了从受地质学驱使到驱 动地质学发展的循环。
地球物理学家通过使用地球物理的 数据采集技术、数字处理技术和可视 化技术看清三维地下地质构造。
地震勘探历程图
N
层面可视化成果图
相干体发现的曲流河
河道砂体地震正演模型
充填相
地震剖面上河道的反映
充填相
主河道
地质解释结果 LN 65
河道间沉积
N
决口扇
N
三角洲前缘朵叶
ISNOTU砂体平面分布
FUSION 频谱分解 – 油气对频谱的选择性吸收
10HZ 20HZ
不同等频地震剖面 10, 20 30, 40 Hz
30HZ
40HZ
•反演问题
波阻抗反演技术
孔隙度分布
S7-12
Y110-7 Y110
Y138
Y143-14
随机反演的七个结果
Training Phase
Seismic Attributes
波动方程
射线追踪
绕射方法
单炮记录
法线入射
垂直入射
射线成像
模拟不同河道砂叠合 地质模型与地震响应的关系
地球物理中的有限单元法
地球物理算法技术（论文）地球物理中的有限单元法院系:地球物理与信息技术院姓名:刘雅宁学号:2010120053任课老师:张贵宾地球物理中的有限单元法一、有限单元法的介绍在地球物理理论计算中，存在着两类基本问题：正问题和反问题。
给定场源的分布，求解场值的大小，这是正问题，或者称为正演问题。
地球物理正演的数值计算方法，种类很多，最常用的有：有限差分法和有限单元法。
有限单元法是50年代首先在弹性力学中发展起来的方法。
主要优点是，适用于物性参数复杂分布的区域，但计算量大。
随着计算机技术的发展，有限单元法在解决各个工程领域的许多数学物理问题中，得到了广泛的应用，称为一种高效、通用的计算方法。
地球物理中的一些边值问题，也采用了有限单元法，解决了许多从前无法计算的地球物理问题。
有限单元法解决数学物理边值问题的基本思路和过程如下：1、给出地球物理边值问题中的偏微分方程和边界条件（及初始条件）。
这一点看起来似乎容易，但做起来并不容易，特别是边界条件的给定。
只有对地球物理方法的原理和问题有深入的理解，才能给边值问题中的偏微分方程和边界条件以正确的描述。
2、将地球物理边值问题转变为有限元方程。
实现这种转变的主要数学工具是变分法，用变分法得到的有限元法方程称为泛函极值问题。
3、用优先单元法解决泛函极值问题其步骤大致如下：把研究区域剖分成有限个小单元，在每个单元上，把函数简化成线性函数、二次函数或高次函数，这称为单元上函数的插值。
用简化后的函数计算每个单元上的泛函。
各单元之间，通过单元间节点上的函数值相互联系起来。
对各单元的泛函求和，获得整个区域上的泛函。
这样，有限单元法将连续函数的泛函，离散成各单元节点上函数值得泛函。
根据泛函取极值的条件，得到各节点的函数值应满足的线性代数方程组。
解代数方程组，得到各节点的函数值。
有限单元法的主要优点是，适用于物性复杂分布的地球物理问题，而且，其解题过程也比较规范化。
这些优点是有限单元法在地球物理中获得广泛的应用。
地球物理正演方法
计算速度快 微分方程法，适于模拟复 边界刻化好 杂的地质情况
涉及较复杂的数学推导，仅需在异常区求 出未知场，经济，易于处理三维模拟问题
快速离散傅里叶变换法 拟谱法（伪、虚）谱法
F域计算
用离散傅立叶变换求空间导数，可在 大空间网格上得到精确波场值
射线追踪法 易刻化运动学特性
一、有限差分法
基本原理：差分原理。即，用各离散点上函数的差商来 近似替代该点的偏导数（微商），把要解的边值问题转 化为一组相应的差分方程。然后，解出差分方程组 (线 性代数方程组)在各离散点上的函数值，便得到边值问 题的数值解。
2、将势场u展成某种简单函数和系数的线性组合 假定，单元内势可用线性(一阶)方程表示，有 V=a+bx+cy 沿三角元边缘势V可以由相应两角点势值线性内插而 来，如果两个三角元共用一条边，则位势在跨单元时 保持连续。 为求各系数，设三个顶点上势为V1，V2，V3
用Cramer准则解线性方程组，求得系数a,b,c的表达式。代回原方程可 得三角元内任一点位势的一阶近似式
其一般只对基本方程中的空间微分算子作逼近，而与时 间微分有关的计算仍然多采用有限差分法。 基本原理：变分原理或最小势能原理
认为：对与势场能量有关的泛函极小化等效于直接解 相应的场的方程
对Laplace方程
势场能量表达式
***满足Laplace方程的势场，同时也是满足势场能量 F(u)取极小的场。
有限差分法采用了直接解方程的办法，有限元法采用了F(u)极小化逼近势场
位场：在场源外区域满足拉普拉斯方程的物理场称为，如 重力场、磁场和稳定电流场
波场：在场源外区域满足波动方程或扩散方程的物理场， 如电磁场、弹性波场
求解正 演问题
电法正反演方法和软件使用介绍
结果评估与改进
对计算结果进行评估和改进，以提高正反演的准 确性和稳定性。
THANKS
感谢您的观看
04
正演方法和反演方法各有优缺点，在实际应用中需要结合使用，相互 验证和补充。
02
电法正演方法详解
线性正演方法
线性正演方法是一种基于线性偏微分方程的数值模拟方法，通过将地下介质视为线性体，将地下电场 分布表示为各向异性或各向同性介质中电流分布的线性组合。这种方法适用于简单地质结构和均匀介 质条件，计算速度快，但精度相对较低。
非线性反演方法的优点是能够处理非线性问题和复杂结构的情况，具有更高的反演精度和可靠性。但是， 它计算量大、速度慢，需要更多的计算资源和时间。
反演方法的优缺点
线性反演方法的优点是计算简单、速度快，适用于大规模数据反演。但是，它对初始模型和 噪声敏感，容易陷入局部最优解，无法处理非均匀介质和复杂结构的情况。
参数选择
根据实际情况选择合适的参数，如网格大小、迭 代次数等，以保证计算结果的准确性和稳定性。
3
结果后处理
对计算结果进行后处理，如数据可视化、结果分 析等，以便更好地理解和应用结果。
误差分析和质量控制
误差来源分析
分析计算结果的误差来源，如数据采集误差、模 型误差等，以便采取相应的措施减小误差。
质量控制方法
04
电法正反演软件介
绍
主要电法正反演软件
FDEM Pro
一款功能强大的电法正反演软 件，适用于多种电法勘探方法
。
EIDORS
专门用于电法图像处理和反演 的软件，具有图像增强、正演 模拟等功能。
Elest
地球物理正反演理论(正演部分)
正演理论方法
正演理论方法
•地震波场正演数值计算
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
正演理论方法
•算例演示’s Principle
Diffractions
正演理论方法
Huygen’s Principle
Diffractions
正演理论方法
•地震波与岩石物性
•岩石性质与地震波速度 •与岩石性质关系
正演理论方法
•地震波与岩石物性
•岩石性质与地震波速度 •与孔隙度关系
正演理论方法
Diffractions
正演理论方法
Huygen’s Principle
Diffractions
正演理论方法
Huygen’s Principle
Diffractions
正演理论方法
Huygen’s Principle
Diffractions
正演理论方法
Huygen’s Principle
Diffractions
•速度和密度资料的获取 •地震子波的选取
正演理论方法
正演理论方法
•一维模型计算（人工合成地震记录）
•计算合成地震记录
正演理论方法
正演理论方法
正演理论方法
•一维模型计算（人工合成地震记录）
•考虑透过系数合成地震记录（自学） •考虑多次波和透过系数合成地震记录（自学）
正演理论方法
•波动方程克希霍夫积分解
地球物理新方法
等效源指在一定的误差范围内，有多种可能的场源分布与观测场相对应，其中与观测场对应的场源又非真正场源的场。
13、等效源的特点。
一，把各种繁杂的胃肠转换，变成一个简单的正演计算，计算过程简单，便于统一处理。二，不丢掉边部测点，条件好的情况下，可适当外推。三，对地形起伏较大的观测面，作位场转化的效果仍较好。四，位场转换特别是向下延拓只限于一定范围内而非整个空间。
15、地震波正演用处：一，对波场特征进行理论研究。二，指导野外数据采集工作设计。三，作为地震资料处理中心比可少的环节。四，帮助资料解释。
16、高斯射线系计算波长时分几步分别是什么内容。
三步。一，做射线追踪，通常做法是将程函方程化为介质中射线轨迹的微分方程组，然后用龙格-库塔法求足够密的射线轨迹；二，做动力学射线追踪，沿射线球高斯射线数的解，即对多条射线求解微分方程得到p和q的值；三，对检波点附近的高斯射线束的贡献进行加权叠加，求得波长值。
三，面元法，用一组相互平行的平面去分割任意形体，每个截面用一个多边形去代替该形体在界面内的形状；影响精度的因素为各多边形吻合该形体各截面的程度以及所用数值积分法。
四，表面积分法：用一系列多边形水平面的组合来近似全表面，精度取决于多边形水平对该形体外表面的吻合程度。
4、表面法的具体步骤。
表面积分法是用一系列多边形水平面来逼近任意形体的全部表面形态。首先计算边数为Nj的第j个多边形的积分制，为此建立新坐标系，使该多边形平面在新坐标下能视为水平面，求得新坐标系中的三个轴向磁场分量，早通过坐标变换成原坐标系各磁场分量，再将所有的多边形平面磁场值累加求和即可。其步骤为：一，建立个z轴向下的原始坐标系，原点o可任选，给出在该坐标系下，用来近似任意形体的多面体个面内所有角点的坐标值。
不同行业地下水潜在特征污染物类型、地球物理方法正演、不同污染调查区综合地球物理方法选择的主辅关系
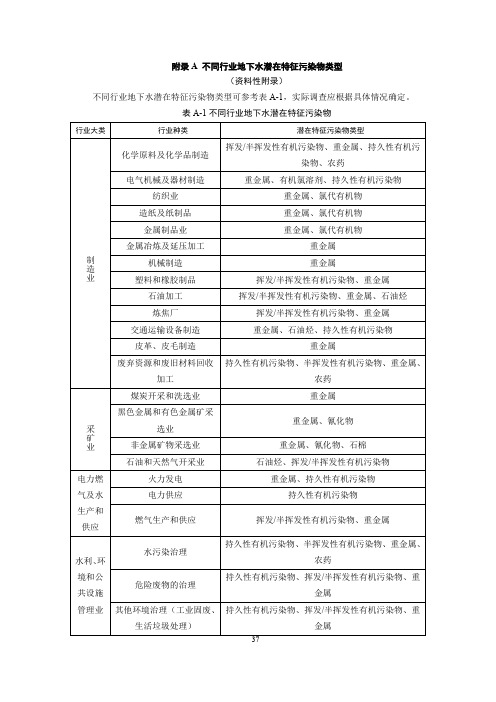
附录A不同行业地下水潜在特征污染物类型（资料性附录）不同行业地下水潜在特征污染物类型可参考表A-1，实际调查应根据具体情况确定。
表A-1不同行业地下水潜在特征污染物行业大类行业种类潜在特征污染物类型制造业化学原料及化学品制造挥发/半挥发性有机污染物、重金属、持久性有机污染物、农药电气机械及器材制造重金属、有机氯溶剂、持久性有机污染物纺织业重金属、氯代有机物造纸及纸制品重金属、氯代有机物金属制品业重金属、氯代有机物金属冶炼及延压加工重金属机械制造重金属塑料和橡胶制品挥发/半挥发性有机污染物、重金属石油加工挥发/半挥发性有机污染物、重金属、石油烃炼焦厂挥发/半挥发性有机污染物、重金属交通运输设备制造重金属、石油烃、持久性有机污染物皮革、皮毛制造重金属废弃资源和废旧材料回收加工持久性有机污染物、半挥发性有机污染物、重金属、农药采矿业煤炭开采和洗选业重金属黑色金属和有色金属矿采选业重金属、氰化物非金属矿物采选业重金属、氰化物、石棉石油和天然气开采业石油烃、挥发/半挥发性有机污染物电力燃气及水生产和供应火力发电重金属、持久性有机污染物电力供应持久性有机污染物燃气生产和供应挥发/半挥发性有机污染物、重金属水利、环境和公共设施管理业水污染治理持久性有机污染物、半挥发性有机污染物、重金属、农药危险废物的治理持久性有机污染物、挥发/半挥发性有机污染物、重金属其他环境治理（工业固废、生活垃圾处理）持久性有机污染物、挥发/半挥发性有机污染物、重金属行业大类行业种类潜在特征污染物类型其它军事工业挥发/半挥发性有机污染物、重金属研究，开发和测试设施挥发/半挥发性有机污染物、重金属干洗店挥发性有机污染物、有机氯溶剂交通运输工具维修重金属、石油烃附录B 地球物理方法正演（资料性附录）B-1电阻率法和激发极化法正演（1）微分方程根据点电源场论理论，在稳定的电流场中，地表、地井、井地和井间的电场与电势的关系、欧姆定律以及电荷守恒定律都满足：E=/j Ej q t ϕ-∇⎧⎪=σ⎨⎪∇⋅=-∂∂⎩式中，E 为电场强度；ϕ为电位；j 为电流密度；σ为地下介质的电导率；q 为电荷密度。
地球物理勘查名词术语
中华人民共和国国家标准GB XXXX--XX地球物理勘查名词术语Terms Of geophysical exploration1 主题内容及适用范围本标准规定了地球物理勘查(包括重力勘查、磁勘查、电勘查、地震勘查、测井及核物探)中常用的、主要的、本学科专有的名词术语。
本标准适用于地球物理勘查工作的语言和文字交流。
2 基本术语2.1 地球物理勘查geophysical exploration运用物理学的原理、方法和仪器以研究地质情况或寻查埋藏物的一类勘查。
同义词物探；地球物理勘探：(勘探地球物理；地球物理探矿)注：1.取决于使用场合，该术语可附加后缀“法”或“学”。
2.根据具体情况，可以使用“航空物探”，“海洋物探”，“地面物探”，“地下物探”，“深部物探”，“区域物探”，“工程物探”，“环境物探”，……等术语。
2.2 正常场normal field物理场的相对平稳部分。
2.3 异常anomaly物理场对正常场的偏离。
2.3.1 理论异常theoretical anomaly正演所获得的异常。
同义词计算异常2.4 物性physical properties岩(矿)石或其它探测对象的物理性质。
2.5 异向性系数coefficient of anisotropy描述介质垂直层理(片理、节理等)方向与平行层理方向的物性差异的一种参数。
同义词(各向异性系数;非各向同性系数)2.6 地球物理正演geophysical direct problem根据地质体或其它探测对象的几何参数和物理参数计算地球物理场值。
同义词物探正演2.7 地球物理反演geophysical inversion根据地球物理场值，计算地质体或其它探测对象的几何参数和物性参数。
同义词物探反演国家技术监督局XXXX—XX—XX批准 XXXX—XX—XX实施2.7.1 交互解释interactive modelling直接在计算机的显示器上反复修改地质体或其它探测对象模型的参数，使模型的理论异常逐步逼近于实测异常的一种反演方法。
一、正反演问题的概述解剖
（1）地球物理反演问题的陈述方式：
这是因为，地球物理反问题实质上可 化为微分方程的反问题：微分方程的中 心任务是寻求其定解问题的解，由微分 方程解的某种泛函，来确定方程的系数 、右端或解的定义域。
各种经典场形式上都满足下列偏微分方程（组）：
0, Lug(x),
,Willian Menke,College of Oceanography,Oregon State University,ACADEMIC PRESS, INC.,1984
本节课主要讲授: 一、正反演问题的概述（绪论）
主要内容:
․正反演问题一般原理及实例； ․地球物理反演的陈述方式和主要观点； ․对反问题的描述（数学形式、适定性、解及
课程重点
了解并认识地球物理反演理论和方法； 了解地球物理问题和数学物理问题的
内在本质联系；
把地球物理问题变为数学问题，反过
来又学会把解数学问题与地球物理实际 问题有机联系在一起。
课程主要内容：
（1）地球物理反演问题的一般理论，模型空 间，数据空间，零空间，解的存在性、惟一 性、稳定性，适定与不适定问题。 （2）线性反演理论及方法，长度的概念，模 型构制，解的非惟一性，稳定性和结果评价， 参数化模型的最小长度解。 （3）广义线性反演，广义逆矩阵，广义逆的 求解方法。
课程主要内容：
（ 4 ） Backus-Gilbert 反 演 理 论 ， 连 续 介质反演理论，BG线性评价。 （5）非线性反演方法，非线性问题的 线性化，最优化法，阻尼最小二乘法， 人工神经网络法，遗传算法，多尺度反 演。 （6）典型地球物理反演实例。
主要参考文献
[1]《地球物理反演基本理论与应用方法》，中国地质大学“211”工程 建设重点资助系列教材，姚姚主编，中国地质大学出版社，2002。 [2]《地球物理反演问题》，傅淑芳等编著，地震出版社，1998。 [3]《数字信号分析与处理》，朱光明，李庆春等编著，陕西人民教育 出版社，2003。 [4]《地球物理反演理论》，王家映编著，高等教育出版社，2002。 [5]《反演理论及其应用》，徐果明编著，地震出版社，2003。 [6]《地球物理反演的理论和方法》，杨文采编著，地质出版社，1997。 [7]《地球物理数据分析—离散反演理论》，王光明等译，地质出版社， 1988。 [8]Inverse Problem Theory—methods for data fitting and model parameter estimation, A.Tarantola(中译本,张先康译)。 [9] Geophysical Data Analysis : Discrete Inverse T的问题。
地球物理学中的电磁场积分方程正演初探
地球物理学中的电磁场积分方程正演初探摘要：在积分方程法使用过程中，需要对异常体进行剖分，具有计算速度快、占用内存少等特点，属于一种容易实现的三维电磁正演模拟算法。
本文根据以往工作经验，对积分方程正演的基本原理进行总结，并从并矢格林函数、散射场求解两方面，论述了地球物理学中的电磁场积分方程正演实际应用，希望对相关工作可以起到一定的帮助作用。
关键词：地球物理学；电磁场积分；方程正演引言：电磁场积分方程正演可利用积分方程对地下半空间中的电磁场进行模拟，将积分法推广到三维空间层面之中，从而实现三维体正演。
随着科学技术的不断发展，地球物理学知识也逐渐实现了丰富，越来越多的人投入到电磁场积分方程正演研究过程中。
我国在该领域的研究起步较晚，但取得的成绩和研究效果十分显著，为我国今后的物理学发展奠定了坚实基础。
1.积分方程正演的基本原理1.1散射方程在积分方程正演流程中，主要将异常体的散射作为等效电流的产生源，利用并矢格林函数对散射场进行描述，而场点处的总场利用背景和散射之和进行表示，具体表达式如下：在该式中，E(r）代表场点数的总场，代表背景场，而代表并矢格林函数，r代表场点坐标r’代表源点坐标。
在散射电场的作用下，再加上异常体和围岩电导率之间的差距，可利用电磁感应现象对相关特点进行解释。
而积分方程法的使用，可将异常体和背景体看作是点电流叠加而成的场源，从而将异常体和电磁场联系到一起，构成地球物流学中的电磁场三维正演。
1.2异常体部分在实际问题解决过程中，需要将异常体分成有很多个小的单元，而每个小的单元均可以被视为一个点电流源。
应用此种方式可以对矿体内的电场进行计算，并将计算过程推广到矿体之外的任意点总场上，由于单元内的总场数量人们并不清楚，需要对每个小单元总场进行求解。
当异常体需要剖分的单元较多时，线性方程的规模也会逐渐增加，此时需要利用散射场近似法或线性方程迭代进行求解，以保证整体计算结果的准确性。
2.地球物理学中的电磁场积分方程正演实际应用2.1并矢格林函数在积分方程正演过程中，需要对均匀半空间并矢格林函数进行应用，而该函数的推导正是应用到了积分方程正演。
《应用地球物理学》主要知识点
《应⽤地球物理学》主要知识点⼀、名词正演（问题）：已知地质体求其引起的异常。
（给定地球物理模型，通过数值计算或物理模拟，得出相应的地球物理场）反演（问题）：已知异常反推地质体的形状和产状。
（已知异常的分布特征和变化规律，求场源的赋存状态（如产状、形状和剩余密度等）重⼒勘探：重⼒勘探是观测地球表⾯重⼒场的变化，借以查明地质体构造和矿产分布的物探⽅法。
零长弹簧零点漂移：在相对重⼒测量中，由于重⼒仪灵敏系统的弹性疲劳、温度补偿不完全等因素，仪器读数的零点值随时间⽽不断变化。
重⼒场强度：单位质量的物体在场中某⼀点所受的重⼒作⽤。
⼤地⽔准⾯：以平静海平⾯的趋势延伸到各⼤陆之下所构成的封闭曲⾯，作为地球的基本形状。
重⼒异常：由地下岩矿⽯密度分布不均匀所引起的重⼒变化，或地质体与围岩密度的差异引起的重⼒变化。
⾃由空间重⼒异常：对实测重⼒值只做正常场与⾼度校正。
布格重⼒异常：观测重⼒差值经过正常场校正、地形校正和布格校正之后得到异常称为布格重⼒异常。
均衡重⼒异常：布格重⼒异常再进⾏均衡校正。
重⼒梯级带：重⼒异常等值线分布密集，异常值向某个⽅向单调上升或下降。
三度体：x,z,y,三个⽅向都有限的物体。
⼆度体：地质体沿⾛向⽅向⽆限延伸。
特征点法：根据异常曲线上的⼀些点或特征点（如极⼤值点、零值点、拐点）的异常值及相应的坐标求取场源体的⼏何或物性参数磁法勘探：利⽤地壳内各种岩矿⽯间的磁性差异所引起的磁异常来寻找有⽤矿产或查明地下地质构造的⼀种地球物理勘探⽅法磁异常：通常把研究对象引起的磁场部分叫做磁异常，⽽周围环境和围岩引起的磁场同归为正常场。
磁场强度：单位正磁荷在磁场中所受的⼒。
磁感应强度：磁感应强度为场源在观测点的磁场强度与磁化物体所形成的附加磁场强度的和。
磁化率：在⼀定磁场强度和⼀定温度范围内，M=κT，磁化率κ为由物质本⾝性质所决定外的参数，表⽰物质被磁化的难易程度。
值越⼤，越易磁化，⽆量纲。
磁化强度：单位体积内分⼦电流磁矩⽮量和，表现在外磁场中物质可被磁化的强度。
地球物理学中的电磁场正演与反演
第22卷 第4期地 球 物 理 学 进 展Vol.22 No.42007年8月(页码:1181～1194)PRO GRESS IN GEOP H YSICSAug. 2007地球物理学中的电磁场正演与反演汤井田, 任政勇, 化希瑞(中南大学信息物理工程学院,长沙410083)摘 要 本文在近年来众多的地球物理研究者的研究基础上,总结了当前地电磁模型正反演已有成果,定量分析了各种主要正反演的性能测试,指出不同正反演法的优点、缺点以及应用范围局限,提出了各种方法的发展趋势以及当前计算地球物理领域的核心内容,指出了计算地球物理领域的数值模拟发展方向.关键词 有限差分,有限元,积分方程,线性迭代,蒙特卡罗,电磁模型,正演,反演中图分类号 P318,P319 文献标识码 A 文章编号 100422903(2007)0421181214The forw ard modeling and inversion ingeophysical electrom agnetic f ieldTAN G Jing 2tian , REN Zheng 2yong , HUA Xi 2rui(S chool of I nf o -p hysics and Geomatics Engineering ,Changsha ,410083)Abstract Based on the excellent achievements by many geophysical researchers at present ,this paper has analyzed performances of the most used forward and inversion methods in electromagnetic quantitatively ,and then ,has pointed the merits and faults of this algorithms.So ,with the quantitative analysis and testing ,the development trend of a 2bove forward and inversion in geophysical electromagnetic filed is pointed and also the core of computational geophys 2ics is listed.At the end ,we have clearly listed the development trend of the numerical simulation in computational ge 2ophysics.K eyw ords finite difference method ,finite element method ,integral equation method ,linear iterate method ,monte 2carlo method ,electromagnetic simulation ,forward model ,inversion收稿日期 2007204210; 修回日期 2007206220.基金项目 国家863计划(2006AA06Z105,2007AA06Z134)项目资助.作者简介 汤井田,博士,博士生导师,中南大学教授,中国地球物理学会会员,美国勘探地球物理学家协会(SEG )会员.主要从事电磁场理论和应用、地球物理信号处理及反演成像等研究.(Email :jttang @ ).0 引 言在地球物理学,电磁场的复杂性决定了地球物理模型的复杂性,一般而言,地球物理模型无法以解析法得到解析解[1],因此,数值模拟方法在地球物理学中得到了广泛地应用,并以此,地球物理学家得到了许多经典的地电模型的电磁场分布数据.借助于这些电磁场分布数据,结合地电模型结构,我们可以初步建立电磁场数据与模型之间的对应关系.但对于复杂的模型来说,其电磁场分布也非常之复杂,在这种情况下,模型与电磁场数据之间的关系变得十分复杂,因此,需要一种高效的、准确的方法来建立模型与电磁模型之间的关系,这种方法即称为电磁模型的反演[2].目前而言,反演主要集中在完全2D 、3D 非线性模型上[3～5],在其中,3D 电磁场数值模拟是3D 电磁反演的核心引擎,因此反演与正演是相得益彰,互相促进的.限于篇幅,本文只讨论广泛应用于地球物理电磁场正演的有限差分[6～8],有限元[9,10],积分方程法[11,12]等,基于此的方法变种,如微分2积分法[13]等不具体讨论;对于反演来说,只讨论线性迭代法[14]、蒙特卡洛反演方法[3].而其它一些变种如微分2积分方法[13]等不具体论述.本文第一部分,讨论有限差分、有限元和积分方程法,分析其现有应用效果,其优点与缺点,基于此分析其发展趋势;第二部分详细论述反演算法的应用以及发展趋势,集中讨论线性化迭代法,蒙特卡洛地 球 物 理 学 进 展22卷非线性全局最优化方法等,分析其优点与缺点,并讨论解决当前阻碍其发展的解决方法,指出非线性反演的在电磁模型中发展趋势.表1 符号的意义T able1 The meaning of symbolsV Laplace算子ε介电常数μ磁导率σ介质电导率ω～角频率j ext外加电流σ～=σ-iωt复电导率e-iωt时间依赖常数E电场强度H磁感应强度E0初始电场强度H0初始磁感应强度r空间坐标V s体积A系统矩阵D空间维数X节点值向量B右边向量φ目标函数m目标模型δm模型增量λ罚函数因子J n×m灵敏矩阵H n×m海森矩阵i,n,k不清索引计数β调整因子M=N M模型集x模型参数w,v模型个体1 电磁场正演分析电磁正演模型的宏观控制方程为Maxwell方程,就其在频率领域的形式为[2]:Δ×H=σ～E+j ext,Δ×E=iωμH.(1)求解(1)式,便可获得H和E.对于绝大多数模型,(1)式只能够通常数值方法来求解,下面列举主要数值方法最新进展.1.1 有限差分法[4,7]有限差分(Finite-deference met hod,FDM)是最为古老的数值计算方法之一,其被用于应用地球物理邻域始于20世纪60代(Yee1966[7];Jones and Pascoe,1972[15];Dey and Morrison,1979[16]; Madden and Mackie,1989[17]),特别进入90年代,交错式样网格被广泛用于地电磁场的分析中来,使有限差分法步入全盛时期(Smit h and Booker, 1991[8];Mackie et al,1993,1994[18,19];Wang and Hohmann,1993[20];Weaver,1994[21];Newman and Alumbaugh,1995,1997[22,23];Smit h,1996a, b[24,25];Varent sov,1999[26];Champagne etal, 1999[27];Xiong et al.,2000[28];Fomenko and Mogi, 2002[29];Newman and Alumbaugh,2002[30]).有限差分的基本原理为:方程(Ⅰ)控制的模型被分为规则的网格,其规模为M=N x×N y×N z,N i为直角笛卡尔坐标系的坐标轴方向的节点距,电磁与磁场被离散到节点,并导致一些关于电磁场节点值的线性方程组,A FD X=B,A FD为3M×3M的复数、对称、大型、稀疏矩阵,X为3M长的各节点电场或磁场的三方向值的向量,B 为由j ext等激励和边界条件生成的长度为3M的向量.同上可知,有限差分的最大不足之处为,它要求模型能够被剖分成规则的单元如四边形,六面体等,严重制约了其在复杂地球物理模型中的应用;最大优点在于能够非常好的处理内部介质中电磁性差异引出的磁场与电磁不连续现象,这是由交错网格的基本性质决定.目前来说,作为电磁数值模拟方法的主导者,有限差分法(FD)正处于各向同性介质模型转向各向异性介质模型的升级(Weidelt,1999[31]; Weiss and Newman2002,2003[32,33]);正处于频率域电磁模型的模拟向时间域电磁模型模拟的空间转换,并借助于并行技术求解(Wang and Hohmann, 1993[20],Wang and Tripp,1996[34],Haber et al, 2002[35];Commer and Newman,2004[36]).1.2 有限单元法[4,8,9]有限单元法(Finite element met hod,FEM)并未广泛地被应用到地电磁场数值模拟计算当中来, FEM利用节点值与节点基函数来形成整个电磁场的分布.不同于FDM,FEM是基于电磁场的积分形28114期汤井田,等:地球物理学中的电磁场正演与反演式,它是由电磁场的微分形式通过Green等定理变换而得,通常也称有限法的解为微分形式的弱解.同于FDM,FEM最也形成大型,对称,复数,稀疏矩阵,A FE X=B.不同于FDM,FEM并不一定要求模型能够被剖分成规则单元,如三角形与六面体单元(其被理论与实践证明可以无限度精确地模拟地球物理模型),因此,FEM能够求解FDM不能够求解的复杂地球物理模型,并被应用于实际中(Reddy,1977[37] Coggen,1976[9];Pridmore,1981[38]Pasulsen, 1988[39]Boyce,1992[40]Livelybrooks,1993[41]Lager and Mur,1998[42]Sugeng,1999[43]unorbi,1999[44] Ratz,1999[45]Ellis,1999[46]Haber,1999[47]Zyserman and Santos,2000[48]Badea,2001[49]Mit subhata and Uchida,2004[50].由上可知,FEM不仅能够处理FDM能处理的简单模型,更能够处理复杂的模型,因此,FEM能够作为地电磁场数值模拟的通用者. FEM显然肯定一些不足之处:对于复杂的模型,其结果不能给人以绝对的信服,其解没有相应的误差分析,并且这种分析是非常之必要.FEM的发展趋势:(1)对复杂的模型给予相应的精确的误差分布,难以肯定结果的真实可靠性[24～30];(2)基于势理论的成长,电磁场借助于矢量势与(或)标量势的方程系统能够完美的代表电磁场分布,有限元求解这些系统是一种大势所趋[44,49,50].(3)虽然FD能够处理内部边界电磁场不连续现象,但是基于节点的有限元法不能处理此理解,从而给结果带来误差,基于边的矢量有限元能够很好的处理节点有限元的不足[43,50],因此,随着对误差的要求越来越小,矢量有限元将会越来越多的应用到地电磁场的分析中来.1.3 积分方程法[4,11,12]积分方程法实现了均匀导电半空间三维大地电磁响应的数值模拟.即求取张量格林函数积分时,采用二次剖分算法解决计算中奇异值问题,对于含有贝塞尔函数的积分项,利用结合连分式展开的高斯求积代替常规的快速汉克尔变换方法,确保了张量格林函数的正确计算并提高了计算精度.最后通过数值模拟结果的对比及模型试算验证了算法的正确性.积分方程法(Integral equation met hod,IE)把Maxwell方程变成Fredholm积分方程(Raiche, 1974[11,12])E(r)=E0(r)+∫V s G(r,r′)(σ～-σ～0)E(r′)dr′,(2)(2)式为电场表达式,此方程即为著名的散射方程(Scattering Equation,SE).(2)式中,E0(r)通常为已经项,G为3×3的Green函数在1D参考介质中矩阵,V s为(σ～-σ～0)不为0处的体积.通过离散化方程(2),产生线性方程组,AIEX=B为复数、密实矩阵.由此可见,IEM的主要优点为线性方程的维数相对FDM、FEM要小的多,可以快速求解模型;不足之处为,解的精度严重依赖于AIE的精确度,但一般来讲,AIE的精确无法得出有限保证,并且其本身也是一项十分耗时的工作.但是由于其速度快的优点,特别是在3D电磁模型计算中,被广泛地应用(Ting and Hohmann,1981[51];Wannamaker, 1984[52];Newman and HOhmann,1988[53];Hohm2 ann,1988[54];Wannamaker,1991[55];Dmit riev and Newmeyanova,1992[56];Xiong,1992[57];Xiong and Tripp,1995[58];Kauf man and Eaton,2001[59]).由于其速度快的原因,IE的发展趋势为求解三维大型、超大型基本电磁模型上面,由此可见,IE是所有电磁场数值模型中的效率快速者.积分方程法主要优点为,1.积分方程法只须对异常体进行剖分和求积,不涉及微分方法中的吸收边界等复杂问题,在三维电磁数值模拟研究中具有快速、方便等特点,与有限元和有限差分法相比,这种方法在模拟有限大小三维体电磁响应时更为有效,计算速度快,占用内存少因而积分方程法近年来受到人们的关注和重视,并取得较快的发展. 2.由于计算机的迅速发展,对异常体进行三维网格剖分和数值求积已变得越来越方便.同样的问题,用计算机计算的时间比以前大大降低.三维电磁响应数值模拟不再是“昂贵”和“费时”,从而可以成为一种廉价、快速、能推广的解释技术.1.4 频谱Lancsoz分解法[4]频谱Lancsoz分解法(Spectral Lancsoz Decompo2 sition Method,SLDM)是一种频率中非常有效的数值模拟方法(Druskin and Knizhernam,1994[60]; Druskin,1999[61]).特别是有模型多频率情况下的首先者,因为SLDM在求解多频模型所需时间与其它方法如FDM、FEM、IDM求解单频模型所需时间相当.SLDM由于其在多频模型模拟上的优点,算得上电磁场模型模拟中的高效者.目前而看,SDLM正转向各向异性模型的模拟(Wang and Fang,2001[62]),3811地 球 物 理 学 进 展22卷Davydycheva(2003)[63]提出了特别的电导率平均法与最优化网格法来减小网格大小与数目,从而加速了SDLM的速度,使其效率更上一层.综观上述各种数值模型方法,正演各种数值方法不外乎把地球物理模拟转化为复数,大型的线性方程组.因而如何快速、准确地求解此线性方程成为重中之重,在数据表明,此线性方程的求解时间约为总求解时间的80%[2].通常来说,由FEM、FDM、ID、SDL M等法生成的线性方程的条件数(Condi2tion Number,CN)非常之大(109-1012,Tamarch2enko,1999[64]),而求解速度与CN成正比,因此十分之有必要减小线性方程式的CN,从而加速成了方程组的预条件处理器(p reconditioners)的发展.在IEM方面,通常利用M ID E(modified iterative2dissipative met hod)来加快方程的收敛速度(Sing2er,1995[65];Pankratov,1995,1997[66][67];Singerand Fainberg,1995,1997[68][69];Avdeev and Zha2nov,2002[70]),通常与FDM法(Newman andAlumbaugh,2002[30])相对比,足见M IDE在ID中的作用,表2列出了IE与FD方法中各种预处理器的性能.表2 各种预处理器的性能,模型为三维感应测井(引用Avdeev(2002)[30])IE测试平台为PC P2350MH z,FD测试平台为IBM R S-6000590工作站T able2 The performance testing of differentpreconditioners,testing on3D induction loggingmodel(cited from Avdeev(2002)[30]).testing platform is PC P2350MH z for IE andIBM R S-6000590for FD正演方法网格大小N x×N y×N z=M频率(k Hz)预处理器迭代次数运行时间A(s)IE 31×31×32=30752101600MIDM72950500056332810L IN172121FD435334160J acobi60005686 4353345000J acobi12001101对于FDM、FEM、SLDM来说,最通常用预处理器则为J acobi,SSOR与不完全L U分解器(例如,M=25×22×21=11550,N bicgstab=396;T CPU= 18min在P31-Ghz PC上,Mit suhata and Uchida, 2004).另外,还有低感应数法(Low induction num2 ber,IN,Newman and Alumbaugh,2002[18])与多重网格预处理器等,表3、4列出L IN与J acobi处理器的测试性能.表3 IE法中的L IN与Jacobi处理器的测试性能,模型为3D感应测井模型的结果统计(采用Avdeev,2002[30]),本次Jacobi测试平台为P350MH z,LIN平台为IBM RS-6000590工作站T able3 The perform ance testing of L IN and Jacobi on IE method,testing models is3D induction logging models(cited from Avdeev,2002[30])Jacobi is tested on PC P2350MH z, L IN is tested on IBM RS26000590w orkstation预处理器迭代次数相对残差J acobi1 1.00E-035 2.00E-11L IN1 1.10E-011009.40E-051000 1.30E-10由上表各表定量分析可知,经预处理过的线性方程组不仅在收敛速度上加快,而且在精确度上也有所提高.因此,寻找最优的预处理器是今后地电模型电磁正演的发展趋势之一.2 电磁模型反演反演领域十分活跃,目前反演存在三个主要问题:(1)理论表明反演的收敛速度严重依赖于正演模型的精确,但目前正演的准确度仍然无法得以保证(Zhdanov,2000[70];Torres2Verdin and Ha2 bashy,2002[71];Zhang,2003[72]).(2)反演问题通常规模较大,通常需要在成千上万的节点上反演成千上万的参数.就目前而言,计算机速度较难以提供如此之动力.(3)地球物理模型的反演通常是非线性的、病态的,这有增加了数值模拟上的困难,结果很难以收敛到精确解,只可以把误差控制在一定的范围之内.非线性成倍增加了反演的计算负担,使反演很难在完全现实的状态中完成.(4)反演存在非唯一性、非稳定性,要解决此困难,通常要包括稳定罚顶(Stabilizing Penalty Func2 tion,SPF,Tikhonov and Arenin,1977[73]);通常SPF依赖于先念信息,可影响解的平稳性、精确性等等(Part niaguine and Zhdanov,1999[74];Sasaki, 2004[75];Heber,2005[76]).因此,选取合理的SPF 在反演过程是十分重要(Farquharson and Olden2 burg,1998[77]).因此,完全反演将会是十分活跃的领域,以下为48114期汤井田,等:地球物理学中的电磁场正演与反演当前反演的主要方法和最新进展.2.1 线性化迭代法线性化迭代法(linear iterator met hod,L IM)地电磁模型反演算法中最为古老的方法(Eato n,1989[78]),在其产生的10之中,发展较为缓慢.非约束非线性最优化(Unconst rained nonlinear optimi2zation,Nocedal and Wright,1999[79])思想的引入使得L IM得到快速发展,数学理论的完善更是推动了L IM的进步.L IM的标准迭代公式可表示为:φ(m,λ)=φd (m)+λR(m)→m,λmin,(3)一般来讲,要求解(3)式的最小值值问题,可应用非线性牛顿迭代性(nonlinear Newto n2type itera2 tions,NN I;如,Newton Iterations,N I、Gauss2 Newton Iterations,CN T、quasi2Newton Iterations, QN I)求解模型空间参数.一旦(3)式得到了满足,得是反演具休来说,在每的最优模型.L IM算法描述如下:Step1:初始化模型参数。
地球物理学报视电阻率正演计算程序
地球物理学报视电阻率正演计算程序摘要：一、引言二、地球物理学报视电阻率正演计算程序的概述三、程序的输入参数和输出结果四、程序的优缺点分析五、应用实例六、结论正文：一、引言随着地球物理勘探技术的发展，视电阻率正演计算在地球物理领域中的应用越来越广泛。
地球物理学报视电阻率正演计算程序作为一种重要的地球物理计算工具，为地球物理学家提供了便利。
本文将详细介绍地球物理学报视电阻率正演计算程序的相关内容。
二、地球物理学报视电阻率正演计算程序的概述地球物理学报视电阻率正演计算程序是一种基于地球物理原理的视电阻率正演计算方法。
该程序利用地球物理观测数据（如地震数据、电磁数据等）和地质模型，通过数值模拟方法，计算地下的视电阻率分布。
这种方法可以为地球物理学家提供关于地下地质结构和矿产资源的有效信息。
三、程序的输入参数和输出结果地球物理学报视电阻率正演计算程序需要输入以下参数：地球物理观测数据（如地震数据、电磁数据等）、地质模型、电导率剖面等。
程序运行后，将输出视电阻率分布图、地质结构图等。
四、程序的优缺点分析优点：地球物理学报视电阻率正演计算程序具有较高的计算精度和可靠性，能够为地球物理学家提供准确的地下地质结构信息。
此外，该程序具有较好的适应性，可以应用于多种地球物理勘探领域。
缺点：该程序的运行时间较长，对计算机硬件要求较高。
此外，程序的输入参数和输出结果的解释需要地球物理学家具备一定的专业知识。
五、应用实例地球物理学报视电阻率正演计算程序在我国多个矿产资源勘探项目中发挥了重要作用。
例如，在我国某地热资源勘探项目中，该程序成功地为地球物理学家提供了准确的地下地质结构信息，为地热资源的开发提供了有力支持。
六、结论地球物理学报视电阻率正演计算程序是一种具有广泛应用前景的地球物理计算工具。
该程序能够为地球物理学家提供准确的地下地质结构信息，为地球物理勘探领域的发展做出了重要贡献。
地球物理学报视电阻率正演计算程序
地球物理学报视电阻率正演计算程序地球物理学报视电阻率正演计算程序导言：地球物理学中的电阻率正演计算是一种重要的地球物理勘探方法，它可以通过模拟电流在地下介质中的传输和分布情况，推断出地下介质的电阻率分布。
这对于研究地下结构、寻找矿产资源、了解地下水分布等具有重要的意义。
本文将介绍一种基于有限差分法的地球物理学报视电阻率正演计算程序。
一、地球物理学报视电阻率正演原理电阻率正演是根据电磁场理论，通过模拟电流在地下介质中的传输和分布情况，计算出不同位置的电场、磁场以及观测点上的电压。
根据电磁感应原理，地下介质中的电阻率不同，电流的传输和分布情况也会不同。
通过观测电场、磁场和电压的分布情况，可以推断出地下介质的电阻率分布。
二、地球物理学报视电阻率正演的数学模型地球物理学报视电阻率正演可以通过求解Maxwell方程组来实现。
在空间电磁场中，Maxwell方程组可以写为：∇ × E = -∂B/∂t∇ × H = J + ∂D/∂t∇ · B = 0∇ · D = ρ其中，E是电场强度，B是磁感应强度，H是磁场强度，J是电流密度，D是电位移矢量，ρ是电荷密度。
为了简化计算，可以假设地下介质为均匀各向同性的电阻率体，此时Maxwell方程组可以简化为：∇ × E = -∂B/∂t∇ × H = σE + ∂D/∂t∇ · B = 0∇ · D = ρ其中，σ为电导率。
根据有限差分法的思想，可以将空间上的观测区域离散为网格点，将时间离散为时间步长。
通过迭代求解上述方程组，可以得到每个网格点的电场、磁场和电位移矢量的分布情况，从而推断地下介质的电阻率分布。
三、地球物理学报视电阻率正演计算程序由于描述数学模型的方程组较为复杂，本文将以伪代码的形式给出地球物理学报视电阻率正演计算的程序流程。
1. 初始化模型参数和计算网格参数：包括地下介质电阻率分布、观测区域大小、时间步长等。
地球物理正演与反演
反演的理论基础：褶积模型(时间域)
假设: 叠后地震数据道是零偏
移距的 没有多次波 没有AVO效应 噪声是随机的，与地震
数据不相关 子波是固定的，不随时
间变化 地震数据已做过偏移，
每一地震道只取决于地震 道位置处的反射系数序列
地震道可以用下面的模型表示 seismic = wavelet * reflectivity + noise
当研究客观世界存在的复杂事物和自然现象 时，最可靠的办法是对事物进行试验和观测，然 而由于种种原因，对事物进行直接观测，研究会 遇到很多困难，甚至不可能实现。在这些情况下， 较好的解决办法就是用模型来代替实物，也就是 所谓模型技术。
正演理论方法
• 地震模型技术
模型技术的基本思想就是研究某一类复杂事 物时，抓住它们的某些主要方面，而摈弃、忽略 一些非本质的次要方面，概括出一个能反映这类 事物的主要特点的模型。再用数学或物理的方法 研究发生在这个模型里的物理现象的基本规律，
测井资料和地震资料频带范围对比
为什要进行地震反演？
◙可以看出，地震资料中明显缺少测井曲线 中包含的低频及高频信息。低频成分提供了 地层的基本速度结构，高频成分提供了地层 的纵向分辨率。地震资料提供了稳定的中频 信息和可靠的横向分辨能力。因此，需要通 过测井约束的波阻抗反演来提高其分辨率。
反演理论方法
PY地震剖面与地质模型
速度分析
CDP叠加
PY地质模型与其地震响应
为什要进行地震反演？
• 在时间域中的褶积就 是频率域中的乘积.
• 从右图中可以看出,子 波的作用是将地震频 谱中高频和低频都消 除了.
• 理论上讲,反演就是试 图将这些失去的频率 区域进行恢复.
为什要进行地震反演？
地球物理正反演方法
地球物理正反演方法姓名:班级：学号：时间:2012.9.12参考文献：1.聂勋碧等. 有限元一虚谱法混合法正演模拟. 八十年代中国地球物理学进展，学术书刊出版社，1989,502~5102.Bir ch F. The velocit y o f compressio nal w aves in r ocks to 10kb. J Geop hy s, 1961, 66: 2199～22243.王山山等. 混合法双程无反射波动方程偏移.石油地球物理勘探，1 9 93 , 2 8 (5 ) : 53 6 ~ 5423.Cer jan C, Ko sloff D, Kosloff R a nd Reshef M . A no nreflecting bo undary co ndit ion for discr ete acousticw av e and elastic-w ave eqation. Geop hy sics, 1985, 50: 705～708正演模拟在地球物理勘探研究中，根据地质体的形状、产状和物性数据，通过构造数学模型计算得到其理论值（数学模拟），或通过构造实体模型来观测模型所产生的地球物理效应的数值（物理模拟）叫做正演模拟。
在地球物理资料解释过程中，常常利用正演模拟结果与实际地球物理勘探资料进行比较，不断修正模型，使模拟结果与实际资料尽可能地接近，进而使解释结果更接近客观实际。
这种比较的过程也叫做选择法。
地震波场正演模拟方法的研究在近十几年中取得了很大进展，出现了众多的正演方法。
正演模拟方法在地震资料和数字处理中有广泛的应用，如各种波场迭代计算型反演、A V O 特性研究、多波多分量资料分析等方面都需要进行正演模拟计算。
同时兼顾计算速度、精度等因素而又实用的正演方法是正演研究面临的重要问题之一。
特别是对于大量使用正演计算的处理方法，这个问题显得更加突出。
因此, 研究者非常重视提高正演算法综合性能的研究，混合型算法的不断推出证实了这一点。
《应用地球物理学》主要知识点
一、名词1.正演（问题）：由“源”求“场”。
即给定地球物理模型，通过数值计算或物理模拟，得出相应的地球物理场。
目的是认识和掌握地球物理场的特征与场源之间的对应关系。
2.反演（问题）：由“场”求“源”。
即根据已知的地球物理场，求解可能的地球物理解释，即地下地质结构的过程。
即已知异常的分布特征和变化规律，求场源的赋存状态。
3.重力勘探：通过观测与研究天然重力场的变化规律以查明地质构造和寻找矿产的一种物探方法。
其基础是地壳中不同岩、矿石间的密度差异。
物理学基础为牛顿万有引力。
4.零长弹簧：当弹簧受拉时,所受拉力与弹簧长度成正比的弹簧。
5.零点漂移：在相对重力测量中，由于重力仪灵敏系统的弹性疲劳、温度补偿不完全等因素，仪器读数的零点值随时间而不断变化称为零点漂移。
6.重力场强度：规定单位质量的物体在场中某一点所受的重力作用作为衡量场本身强弱的标准，这个单位质量所受的重力称为该点的重力场强度。
7.大地水准面：以平静海平面的趋势延伸到各大陆之下所构成的封闭曲面，作为地球的基本形状。
8.自由空间重力异常9.布格重力异常10.均衡重力异常11.重力梯级带：指重力异常图上等值线平行排列的密集带。
它主要反映构造断裂的升降或大规模的不同密度岩石的接触带。
12.三度体：各方向上都为有限量的物体，如球体。
13.二度体：某一方向无限延伸，而在该方向上埋藏深度、截面形状、大小和物性特点都稳定不变的物体。
14.特征点法：指根据异常曲线上的一些点或特征点（如极大值点、零值点、拐点）的异常值及相应的坐标求取场源体的几何或物性参数的一中反演方法。
但仅适用于剩余密度为常数的几何形体。
15.磁法勘探：岩、矿石间的磁性差异将引起正常地磁场的变化（即磁异常），通过观测和研究磁异常来寻找有用的矿产或查明地下地质构造的勘探方法称为磁法勘探。
它是以地壳中各种岩、矿石间的磁性差异为物质基础的。
16.磁异常：实际上测得的地球磁场强度和理论磁场强度之差称地磁异常，即磁异常。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
矩阵[M]的每个元素本身就是一个3X3阶矩阵:
Γmn是相对有限单元体积电流的并矢格林函数 解方程,求出异常体内每个单元中心处的电场值之后,再加上一次场值可求 内 得异常体外任一点处的电场 .对总电场方程应用法拉第定律,可计算任意点 外 的磁场H(r)
物理模拟方法
基本原理:相似原理 方法:按比例复制地质模型 (通常比例尺为1:100和1:100万之间) ;
2.时间域电磁场的模拟准则
3.模拟模型的种类-4种
导电性溶 液 或固体 作为均匀 介质
导电性 更好的 覆盖
4,物理模报实验装置
5.模型材料
超声波模拟 几何相似性
L为几何尺度,λ为波长
物理相似性
速度比和密 度比相似
纵,横波速度 比的相似性
谢谢大家!
地球模型建立的要求: 模型应能够反映主要地质构造和岩石,矿物特征, 具有代表性或普遍性(共性),针对性(目的性), 特殊性(特殊问题) 模型不宜太复杂,否则无法建立相应的数学模型; 或者计算结果太复杂,难以分析,辨认地质特征与地 球物理场特征之间的联系.
求边值问题,研究区域边界上位势(或其导数)是已知的(边界条件). 在对网格节点编号时先编区域内部的号,后对边界点编号,分区处理 可简化方程,以下角标f表示区域内节点,下角标p表示边界上节点
整理得 解线性矩阵方程式,求取研究区域内各节点的位势Vf,有唯一解. 其精度取决于三角元的尺度
三,积分方程法
不足:积分方程方法涉及较复杂的数学推导 优点:仅需在异常区求出未知场 模拟一个或少数几个小异常体的响应时,该方法比较经济 多用于3D数值模拟 假设大地电磁场的源是来自高空的 垂直入射到地面的平面电磁波,则 频域中无源麦克斯韦方程组
将比例关系代入野外方程得模型参数描述的野外方程
按照模拟准则,要使模拟结果与实际一致,野外和模型磁场满足的波动 方程应完全相同,对比可以写出
模拟准则——参数比例尺
上式两边为响应参数k2r2,亦称综合参数,右端=1,表明:具有相同综合 参数的每个系统必定产生相同的电磁响应 ,与ω,,σ及l的具体数值 无关.因此,模拟准则简化为
所谓单纯形,在平面上为三角形,三维空间为四面体 由于三角元以公共边界及顶点连接成网,势的分布在穿过单元 时保持连续.
2,将势场u展成某种简单函数和系数的线性组合 假定,单元内势可用线性(一阶)方程表示,有 V=a+bx+cy 沿三角元边缘势V可以由相应两角点势值线性内插而 来,如果两个三角元共用一条边,则位势在跨单元时 保持连续. 为求各系数,设三个顶点上势为V1,V2,V3
下角标dis表示组合前不连接的三角元.对应这两个元的未组合能量写为矩阵
未组合能量
两个三角元连接前,后满足以下关系
下角标con注记已联接,对应连接后的总能量变为
连续近似的势能分布被表示为与元顶点位势向量有关的二次型
5,方程求解计算
记k为网格节点(连接后多个三角形的顶点)的编号,则 Laplace方程的 有限元近似解要将连接网中的势能极小化.——变成了求极值问题 则势能极小化为
基本方程式的有限差分格式 (2D) )
有限差分波动方程模拟结果演示实例
地质模型
炮集1 快 照 炮集1
1
2
3 4 5 6 7
蝴蝶结
模型边界产生的 假象
山顶激发波动方程正演模拟记录
炮集2 快照 炮集2
1
蝴蝶结
2
4
3
5 6 7
山谷激发波动方程正演模拟记录
二,有限单元法 突出优点:界面刻画能力强.对与复杂介质结构有关的 偏微分方程边值问题的数值计算适应性强. 其一般只对基本方程中的空间微分算子作逼近,而与时 间微分有关的计算仍然多采用有限差分法. 基本原理:变分原理或最小势能原理 认为:对与势场能量有关的泛函极小化等效于直接解 相应的场的方程 对Laplace方程 势场能量表达式 ***满足Laplace方程的势场,同时也是满足势场能量 F(u)取极小的场.
有限差分法 计算方法选择很重 微分方程法 要:不同方法适应 边界刻化好 有限元法 性不同,计算效率, 易于处理有源问题 机时,周期,费用 积分方程法 等各不相同,要综 快速离散傅里叶变换法 F域计算 合考虑各种因素合 理选用计算方法. 拟谱法(伪,虚)谱法 有针对性地灵活运 用计算方法 射线追踪法 易刻化运动学特性
上式是一非齐次的第二类矢量弗雷德霍姆(Fredholm)积分方程式
并矢格林函数 Q(x',y',z') P(x,y,z) ● r r'
●
g是对应全空间 的标量格林函数
P/(x,y,-z)
数值积分,求解
将异常体剖分成N个线性尺寸为的立 方体单元.并假设在每个单元内电场是 常数,则积分可用求和式来逼近,再经 一系列推导得到分块矩阵方程式
计算速度快
常用数值 计算方法
�
总 场 σ表示地下任一点处的实际电导 率值,且有
σ2(r)
σ1
r表示矢径
V
σ=
σ1,异常体外 σ2,异常体内
定义:一次场 一次场为均匀地球场,并以上角标p表示,则一次场也满足无源 一次场 麦克斯韦方程组,有
一次场方程组——可求解
其是电导率为σ1的均匀介质内的场
定义:二次场为实测场(总场)与一次场之差,并用上角标s表示
正演方法
云美厚
河南理工大学资源与环境学院
基础
地球物 理学的 问题
正演 问题 反演 问题
目的
按事物一般原理(或模型)及相关的条 件(初始条件,边界条件)来预测事物 的结果(可由观测可得 据地球物理场的实际观测值(有时也用 理论计算值)定量或定性解释推断地球 内部结构(地质体形态和岩层物性).
应用地球物理学的基本方程式——阻尼标量波动方程
(1)区域离散化网格剖分:确立合适网格步长,边界节点定位 步长选择很重要——决定计算精度,速度 (2)微分方程离散化——构建差分方程 边界条件离散化——构建边界条件差分方程 初始条件离散化——构建初始条件差分方程 (4)线性方程组形成与求解
位场计算举例: 位场计算举例: 1,位场所满足的方程
有源 无源 模拟二维地电断面电场 边界节点 式中,u表示电位,f表 示源项.
整理得二次场方程
二次场方程组
可转换成积分方程,求解
是散射电流,仅在异常体中才存在 表明:二次场可以认为是由异常体中的散射电流Js引起的.
建立二次场方程的积分方程
二次电场可通过将散射电流源Js乘以适当的并矢格林函数G(r,r/), 并对异常体所占的体积做积分而得,
如假设异常体内的电导率为常数σ2,则可得到实测电场表达式为
计算精度:主要决定于步长h.一般说来,网格划分越细,即h
值越小,计算值与理论值越接近. 矛盾:减小步长h将成倍增加计算节点数目,增加计算机内存需 求和计算时间.降低了效率,增加了费用
解决计算速度与精度矛盾的较好方法:采用变步长,即在
近区将网格分得密些,远区影响较小,可分得稀些.
弹性波场计算举例 1,反射地震中波传播方程
内节点
2,区域网格剖分
3,微分方程离散化,构组差分方程
k i-1,k
i
i,k-1 i,k i+1,k
i,k+1
ux,uxx,…和uz,uzz,…分别表示u对x和z的一阶,二阶导数等
含源分区均匀岩石中位函数二维差分方程
无源分区均匀岩石中位函数二维差分方程
4,线性方程组的形成与求解
式中[A]是方程组的系数矩阵.其与 物性参数(如电阻率)分布有关; {u}是电位u的列向量,其分量为所 有节点上的电位; {F}是常向量. 当给定电阻率分布(空间分布,模型结构)及边界条件后,解 线性方程式便可求得电位的空间分布
用Cramer准则解线性方程组,求得系数a,b,c的表达式.代回原方程可 得三角元内任一点位势的一阶近似式
三角元内任一点位势的一阶近似式
系 数 为
A为三角元的 面积 ,且有
3,单个元内位势能
写成矩阵形式有
至此,对单个元的近似已经完成
4,三角元连接组合求取总势能
整个区域的势能为单个三角元势能之总和.根据最小势能准则,使整个 研究区域势能极小化,就是使所有三角元组合后的势能极小化 两个元组合方法:设一对元在连接前的顶点位势可写成以下列向量
密度不均匀介质弹性波标量波动方程
激发问题
在各向同性均匀介质,平面波入射假设条件下,标量波动方程
传播问题
在二维情况下,
初始条件 σzz|z=0=ux=0,σzx|z=0=uz=0 (自由表面)边界条件
2,区域离散化
采用正方形网格元进行网格划分, 步长h;m,n为当前网格节点的横 向及垂向编号;l时间取样号
地球模型建立的要求: 模型应能够反映主要地质构造和岩石,矿物特征, 具有代表性或普遍性(共性),针对性(目的性), 特殊性(特殊问题) 模型不宜太复杂,否则无法建立相应的数学模型; 或者计算结果太复杂,难以分析,辨认地质特征与地 球物理场特征之间的联系.
有限差分法 有限元法
计算速度快 边界刻化好
微分方程法,适于模拟复 杂的地质情况
式中,u表示地球物理场的一种,如声场.电磁场的某一分 量等;f(x,t)为源函数;x为空间的一个点;t为时间;系数h和 g对不同场有不同的物理意义.
位场: 位场:在场源外区域满足拉普拉斯方程的物理场称为,如 重力场,磁场和稳定电流场 波场: 波场:在场源外区域满足波动方程或扩散方程的物理场, 如电磁场,弹性波场
差分方程式
利用差分方程式,由上至下,由左至右并随时标l增加计算 空间任一点(m,n)的波场um,n,l+1便得到波传播图像, um,0,l是地面直达波和反射波场的合成记录.
有限差分计算必须满足的条件如下: (1)时间取样率t(t=lt)满足t≤h/c (2)震源信号的主周期T<10h/c,否则有严重的频散. (3)由于地下介质无限,而计算网格有限,计算网格 的边界必须是吸收边界. (4)震源必须作专门处理,即在源点加入f(t) 信号. 有限差分计算的优点与不足: 优点:简明快速 不足:边界刻划能力弱.因只能使用矩形网格,对复杂 的地质构造不能准确地模拟,如,反射地震中常见的倾 斜界面,电法勘探中的局部不规则电性不均匀体等.