河北省邯郸市成安县第一中学2017届高三高考保温金卷(考前模拟)数学(理)试题含答案
【河北省邯郸】2017学年高考一模数学年试题(理科)

,
1 k 3 k 2 或 1 ,
k
2
2
直线 l 的斜率为 k 2 或 k 1 . 2
- 4 -/18
21.解:(Ⅰ)
f( x)
2x
a
2
x
a 2
x
a
2
,
x
0
,
x
x
所以,当 0 x a 时, f x<0 ,当 x> a 时, f x>0 ,
Y
1 000 2 000
3 000
P
0.16
0.68
0.16
Y 的数学期望为 E Y 1000 0.16 2000 0.68 3000 0.16 1680 .
20.解:(Ⅰ)联立
y
x
p 2
,消去 x 得
y2
3py
p2
0,
x2 2 py
4
题设得
所以 a 2 .
(Ⅱ)由条件可得 f 2 xe2x 6mf xex 9m 0 ,
令 g x f xex x2 2ln x ex ,
则
g( x)
x2
2x
2 x
2lnx
e
x
,
令(r x) x2 2x 2 2lnx x 1 ,
22 2
由于 g'a 1 ln a ,故 a 2 时, g '2 0 ,
22
且 0 a 2 时, ga 0 , a 2 时, ga 0 ,
【方法】高三数学下学期第一次模拟考试试题理扫描版1

【关键字】方法河北省邯郸市2017届高三数学下学期第一次模拟考试试题理(扫描版)2017年高三一模理科数学答案一、选择题1--5 D A C B C 6- B D B A 10- A二、填空题13.14. 15. 16.三、解答题17.解:(Ⅰ)由已知及正弦定理易求得, …………………2分. …………………………………………………4分(II)…………………………………………………6分,……………………………………………………8分因为所以,……………………………………………10分即,所以的值域为. ………………………………12分18.解:(Ⅰ)取中点,连接,由题易得三点共线,过点作于,则底面平面,是等边三角形………………………………2分平面平面,平面平面. ……………………4分(II)连接,又,底面. ……………………………………………6分点与点重合.如图,以为原点,分别以的方向为轴,轴,轴正方向建立空间直角坐标系.易知底面的一个法向量……………………………………8分设平面的法向量,取则,…………………………10分因为二面角的法向量分别指向二面角的内外,即为二面角的平面角.所求二面角的余弦值为. ……………………………12分19.解:(Ⅰ)设“从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分”为事件A.………………..3分(Ⅱ)(Ⅲ)Y的分布列为Y -1000 2000 3000 P0.160.680.16…………………12分 20.解:(Ⅰ)联立 ,消去得 ………………………………1分 依题设得 ………………………………3分所以抛物线的方程为. …………………………………………4分 (II )设联立 ,消去得 ……………6分 由得 ,直线的方程分别为……………………………………8分 联立得点的坐标为 ……………………………………10分 所以或所以直线的斜率为或 . ……………………………………………12分 21.解:(Ⅰ)解: 且,所以,当时,,当时,,…………2分故min()()ln ln 222222a a a a a a f x f a ==-=-,由题意可得ln 1222a a a -=,即ln 10222a a a--=…………………………3分 记()ln 1(0)222a a ag a a =-->,则函数()g a 的零点即为方程ln 1222a a a-=的根;由于1()ln 22ag a '=-,故2a =时,(2)0g '=, 且02a <<时,()0g a '>,2a >时,()0g a '<,所以2a =是函数()g a 的唯一极大值点,所以()(2)g a g ≤,又(2)0g =,………………4分 所以2a =. ……………………5分(直接得2a =给3分). (II )由条件可得22()6()90xx f x e mf x e m -+=,令2()()(2ln )x x g x f x e x x e ==- (7)分则'2222()(2)(2ln )(22ln )x x x g x x e x x e x x x e x x=-+-=+-- 令22()22ln (1)r x x x x x x==+--≥则2'22222(1)()2220x r x x x x x x x-=++->-=≥ ………….9分()r x 在区间[1,)+∞内单调递增()(1)g x g e ∴≥=.所以原问题等价于方程2690t mt m -+=在区间[,)e +∞内有唯一解当0∆=时可得0m =或1m =,经检验1m =满足条件…………..11分当0∆>时可得0m <或1m >,所以2690e me m -+≤解之得269e m e ≥-综上,m 的取值范围是{|1,m m =或2}69e m e ≥-. ………12分 22.解:(Ⅰ)(方法一)由1C ,2C 极坐标方程分别为2sin ρθ=,cos 24πρθ⎛⎫-= ⎪⎝⎭. 化为平面直角坐标系方程分为()2211,20x y x y +-=+-=. …………………………2分 得交点坐标为()()0,2,1,1. ……………………………………………………3分 即1C 和2C 交点的极坐标分别为2,,2,24ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.………………………………………5分 (方法二)解方程组2sin (1)cos 2(2)4ρθπρθ=⎧⎪⎨⎛⎫-= ⎪⎪⎝⎭⎩所以2sin cos 24πθθ⎛⎫-= ⎪⎝⎭, ……………………………………………………2分化解得cos 2sin 04πθθ⎛⎫-= ⎪⎝⎭,即24ππθθ==或, ……………………………4分所以1C 和2C 交点的极坐表分别为2,2,24ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭. ……………………………5分(II )(方法一)由直线l 的参数方程:33212x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩ (t 为参数), 可得3(3)3y x =+, …………………………………………………………6分 由圆1C 的方程为()2211,x y +-=联立解得13(),B()2222A -……………………………8分因为(P ,所以4PA PB +==. ……………………10分 (方法二)把直线l的参数方程:12x y t ⎧=⎪⎪⎨⎪=⎪⎩ (t 为参数),代入()2211,x y +-=得221112t ⎛⎫⎛⎫+-= ⎪ ⎪ ⎪⎝⎭⎝⎭,……………………………………………………………7分 即2430t t -+=,124t t +=, ………………………………………………………………8分 所以4PA PB +=. …………………………………………………………………………10分当时,得 ………………………………………………2分 当1,221x x x <->+ 得13x <……………………………………………………3分 综上所述,解集为1,(3,)3⎛⎫-∞+∞ ⎪⎝⎭……………………………………………………5分 (II )22224ax ax ax ax -+--≥---= ……………………………………………7分此文档是由网络收集并进行重新排版整理.word 可编辑版本!。
河北省邯郸市成安县第一中学2017届高三高考保温金卷(

成安一中2017年高考保温金卷文科综合地理第Ⅰ卷(选择题共140分)本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
浙江古代盛产青瓷,其中越窑生产的青瓷(越瓷)远销东亚、东南亚、南亚、西亚和非洲东部地区等。
古代越瓷贸易船主要以风力和洋流为动力,晴夜观星定向,一般出航半年内到达非洲。
下图为越瓷外销西南航线示意图。
完成下列问题。
1. 与陆路运输相比,越瓷西南方向贸易选择海运方式可①缩短路程②增加运量③减少货物破损④增强贸易灵活性A. ①②B. ①④C. ②③D. ③④2. 在输出越瓷的贸易航程中,船上的人可能会在A. 甲处夜观北极星定向B. 乙处借船右后方来风作动力C. 丙处见到河水的暴涨D. 丁处眺望到大片茂盛的草地【答案】1. C 2. B【解析】试题分析:1. 读图,与陆陆运输相比,越瓷西南方向贸易选择海运方式可远销东亚、东南亚、南亚和非洲东部地区,贸易船主要以风力和洋流为动力,贸易船活动灵活性受季节和航线影响大,灵活性差,④错。
轮船运量比车马运量大,可增加运量,②对。
海运的路程长,①错。
海上风浪大,但与陆地上相比,海洋上硬性碰撞少,可减少货物破损,③对。
C对。
2. 在输出越瓷的贸易航程中,甲处临近赤道,北极星高度太低,不易被看到,不能利用北极星定向,A错。
乙处冬季受东北季风影响,可借助船后方风作动力,B对。
丙处为热带沙漠气候,很难见到河水的暴涨,C错。
丁处半岛受离岸风及季风影响,沿岸多沙漠分布,看不到大片的草地,D错。
【考点定位】交通运输方式的特点,大气环流分布规律,洋流分布规律,不同区域自然环境特征差异。
【名师点睛】北印度洋海区的季风洋流系统的形成原理和记忆方法在北印度洋海区,由于受季风影响,洋流流向具有明显季节变化。
在冬、夏两个季节,在海区的环流系统不仅流向不同,而且组成环流系统的洋流也不同。
冬季该海区盛行东北季风,洋流向西流,环流系统由季风洋流、索马里暖流和赤道逆流组成,呈逆时针方向流动(如图A);夏季该海区盛行西南季风,季风洋流向东流,此时索马里暖流和赤道逆流消失,索马里沿岸受上升流的影响,形成与冬季流向相反的索马里寒流。
2017年河北省邯郸市高考数学一模试卷(理科) Word版含解析

2017年河北省邯郸市高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合A={x|x2﹣2x﹣3<0},B={x|x≥2},则A∩B=()A.(2,3]B.[2,3]C.(2,3)D.[2,3)2.已知a,b∈R,i为虚数单位,当a+bi=i(1﹣i)时,则=()A.i B.﹣i C.1+i D.1﹣i3.已知向量,满足||=2,||=3,(﹣)•=7,则与的夹角为()A.B.C.D.4.已知椭圆C: +=1(a>b>0)的左焦点为F(﹣c,0),上顶点为B,若直线y=x与FB平行,则椭圆C的离心率为()A.B.C.D.5.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=,AB=2,则S△ABC=()A.3 B.2C.3D.66.从5种主料职工选2种,8种辅料中选3种烹制菜肴,烹制方式有5种,那么最多可以烹制出不同的菜肴种数为()A.18 B.200 C.2800 D.336007.执行如图所示的程序框图,则输出的结果是()A.8 B.13 C.21 D.348.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是()A.B.C.D.9.设{a n}是公差为2的等差数列,b n=a,若{b n}为等比数列,则b1+b2+b3+b4+b5=()A.142 B.124 C.128 D.14410.某几何体的三视图如图所示,则该几何体的体积为()A.πB.πC.πD.π11.已知棱长为的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则+的最小值为()A.B.4 C.D.512.设f(x)=e x,f(x)=g(x)﹣h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,则m 的最小值为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分).13.已知函数f(x)=,则f[f(﹣3)]=.14.已知函数f(x)=ax+b,0<f(1)<2,﹣1<f(﹣1)<1,则2a﹣b的取值范围是.15.已知三个命题p,q,m中只有一个是真命题,课堂上老师给出了三个判断:A:p是真命题;B:p∨q是假命题;C:m是真命题.老师告诉学生三个判断中只有一个是错误的,那么三个命题p,q,m中的真命题是.16.已知点A(a,0),点P是双曲线C:﹣y2=1右支上任意一点,若|PA|的最小值为3,则a=.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.已知a,b分别是△ABC内角A,B的对边,且bsin2A=acosAsinB,函数f(x)=sinAcos2x﹣sin2sin 2x,x∈[0,].(Ⅰ)求A;(Ⅱ)求函数f(x)的值域.18.如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG 上.(Ⅰ)求证:平面PBE⊥平面APG;=,△PBE点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.19.某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).20.已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+交抛物线E于A,B两点.(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;(Ⅱ)过点A,B作抛物线E的切线l1,l2,且l1,l2交点为P,若直线PF与直线l斜率之和为﹣,求直线l的斜率.21.已知函数f(x)=x2﹣alnx(a>0)的最小值是1.(Ⅰ)求a;(Ⅱ)若关于x的方程f2(x)e x﹣6mf(x)+9me﹣x=0在区间[1,+∞)有唯一的实根,求m的取值范围.从22、23题中任选一题作答.[选修4-4:坐标系与参数方程选讲]22.在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1,C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣)=.(Ⅰ)求C1和C2交点的极坐标;(Ⅱ)直线l的参数方程为:(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.[选修4-5:不等式选讲]23.已知函数f(x)=|ax﹣2|.(Ⅰ)当a=2时,解不等式f(x)>x+1;(Ⅱ)若关于x的不等式f(x)+f(﹣x)<有实数解,求m的取值范围.2017年河北省邯郸市高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合A={x|x2﹣2x﹣3<0},B={x|x≥2},则A∩B=()A.(2,3]B.[2,3]C.(2,3)D.[2,3)【考点】交集及其运算.【分析】先分别求出集合A和B,由此利用交集定义能求出A∩B.【解答】解:∵集合A={x|x2﹣2x﹣3<0}={x|﹣1<x<3},B={x|x≥2},∴A∩B={x|2≤x<3}=[2,3).故选:D.2.已知a,b∈R,i为虚数单位,当a+bi=i(1﹣i)时,则=()A.i B.﹣i C.1+i D.1﹣i【考点】复数代数形式的乘除运算.【分析】由a+bi=i(1﹣i)=1+i,求出a,b的值,然后代入,再由复数代数形式的乘除运算化简得答案.【解答】解:由a+bi=i(1﹣i)=1+i,得a=1,b=1.则=.故选:A.3.已知向量,满足||=2,||=3,(﹣)•=7,则与的夹角为()A.B.C.D.【考点】平面向量数量积的运算.【分析】运用向量的数量积的性质:向量的平方即为模的平方,可得•=﹣3,再由向量的夹角公式,计算即可得到所求角.【解答】解:向量,满足||=2,||=3,(﹣)•=7,可得2﹣•=4﹣•=7,可得•=﹣3,cos<,>===﹣,由0≤<,>≤π,可得<,>=.故选:C.4.已知椭圆C: +=1(a>b>0)的左焦点为F(﹣c,0),上顶点为B,若直线y=x与FB平行,则椭圆C的离心率为()A.B.C.D.【考点】双曲线的简单性质.【分析】求出直线FB的斜率,利用直线y=x与FB平行,建立方程,求出b=c,即可求出椭圆C的离心率.【解答】解:由题意,,∴b=c,∴a=c,∴e==,故选B.5.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=,AB=2,则S△ABC=()A.3 B.2C.3D.6【考点】正弦定理.【分析】由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,故B=60°,ABD中,由余弦定理可得BD的长,进而利用三角形面积公式即可计算得解.【解答】解:∵由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,∴B=60°,∵△ABD中,由余弦定理可得:AD2=AB2+BD2﹣2AB•BD•cosB,即:7=4+BD2﹣2BD,∴BD=3或﹣1(舍去),可得:BC=6,===3.∴S△ABC故选:C.6.从5种主料职工选2种,8种辅料中选3种烹制菜肴,烹制方式有5种,那么最多可以烹制出不同的菜肴种数为()A.18 B.200 C.2800 D.33600【考点】排列、组合的实际应用.【分析】根据题意,分3步进行分析:①、从5种主料之中选2种,②、从8种辅料中选3种烹制菜肴,③、从5种烹制方式选一种,分别计算每一步的情况数目,由分步计数原理计算可得答案.【解答】解:根据题意,分3步进行分析:①、从5种主料之中选2种,有C52=10种选法;②、从8种辅料中选3种烹制菜肴,有C83=56种选法;③、从5种烹制方式选一种,有C51=5种选法;则最多可以烹制出不同的菜肴种数为10×56×5=2880;故选:C.7.执行如图所示的程序框图,则输出的结果是()A.8 B.13 C.21 D.34【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量a,b,c的值,并输出满足退出循环条件时的b的值,模拟程序的运行,对程序运行过程中各变量的值进行分析,即可得解.【解答】解:模拟执行程序,可得a=1,b=1,i=1执行循环体,c=2,a=1,b=2,i=2不满足条件i>5,执行循环体,c=3,a=2,b=3,i=3不满足条件i>5,执行循环体,c=5,a=3,b=5,i=4不满足条件i>5,执行循环体,c=8,a=5,b=8,i=5不满足条件i>5,执行循环体,c=13,a=8,b=13,i=6满足条件i>5,退出循环,输出b的值为13.故选:B.8.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是()A.B.C.D.【考点】定积分在求面积中的应用.【分析】由题意,建立如图所示的坐标系,求出抛物线的方程,利用定积分求面积即可.【解答】解:由题意,建立如图所示的坐标系,则D(2,1),设抛物线方程为y2=2px,代入D,可得p=,∴y=,∴S===,故选D.9.设{a n}是公差为2的等差数列,b n=a,若{b n}为等比数列,则b1+b2+b3+b4+b5=()A.142 B.124 C.128 D.144【考点】等比数列的通项公式.【分析】由已知得a n=a1+(n﹣1)×2=a1+2n﹣2,且(a4)2=a2•a8,从而a1=2,=2+2×2n﹣2=2n+1,由此能求出b1+b2+b3+b4+b5的值.【解答】解:∵{a n}是公差为2的等差数列,b n=a,∴a n=a1+(n﹣1)×2=a1+2n﹣2,∵{b n}为等比数列,∴.∴(a4)2=a2•a8,∴=(a1+4﹣2)(a1+16﹣2),解得a1=2,∴=2+2×2n﹣2=2n+1b1+b2+b3+b4+b5=22+23+24+25+26=124.故选:B.10.某几何体的三视图如图所示,则该几何体的体积为()A.πB.πC.πD.π【考点】由三视图求面积、体积.【分析】由三视图可得,直观图为圆锥的与圆柱的组合体,由图中数据可得该几何体的体积.【解答】解:由三视图可得,直观图为圆锥的与圆柱的组合体,由图中数据可得几何体的体积为=,故选A.11.已知棱长为的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则+的最小值为()A.B.4 C.D.5【考点】基本不等式.=S△ACD,【分析】由题意可得: +=,其中S△BCDh为正四面体ABCD的高,可得h=2,a+b=2.再利用“乘1法”与基本不等式的性质即可得出.=S△【解答】解:由题意可得: +=,其中S△BCD,h为正四面体ABCD的高.ACDh==2,∴a+b=2.∴+==≥=,当且仅当a=2=时取等号.故选:C.12.设f(x)=e x,f(x)=g(x)﹣h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,则m 的最小值为()A.B.C.D.【考点】函数奇偶性的性质.【分析】由F(x)=g(x)+h(x)及g(x),h(x)的奇偶性可求得g(x),h (x),进而可把mg(x)+h(x)≥0表示出来,分离出参数后,求函数的最值问题即可解决.【解答】解:由f(x)=g(x)﹣h(x),即e x=g(x)﹣h(x)①,得e﹣x=g(﹣x)﹣h(﹣x),又g(x),h(x)分别为偶函数、奇函数,所以e﹣x=g(x)+h(x)②,联立①②解得,g(x)=(e x+e﹣x),h(x)=(e x﹣e﹣x).mg(x)+h(x)≥0,即m•(e x+e﹣x)+(e x﹣e﹣x)≥0,也即m≥,即m≥1﹣∵存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,1﹣≥,∴m≥.∴m的最小值为.故选A.二、填空题:本大题共4小题,每小题5分,共20分).13.已知函数f (x )=,则f [f (﹣3)]= ﹣ .【考点】函数的值.【分析】由已知得f (﹣3)==,从而f [f (﹣3)]=f (),由此能求出结果.【解答】解:∵函数f (x )=,∴f (﹣3)==,f [f (﹣3)]=f ()====﹣.故答案为:.14.已知函数f (x )=ax +b ,0<f (1)<2,﹣1<f (﹣1)<1,则2a ﹣b 的取值范围是.【考点】不等式的基本性质.【分析】由题意可得0<a +b <2,﹣1<﹣a +b <1,作出可行域如图,设z=2a ﹣b ,利用z 的几何意义,利用数形结合即可求出该线性规划问题中所有的最优解. 【解答】解:∵f (x )=ax +b ,0<f (1)<2,﹣1<f (﹣1)<1, ∴0<a +b <2,﹣1<﹣a +b <1, 作出可行域如图设z=2a ﹣b ,得b=2a ﹣z ,则平移直线b=2a ﹣z ,则由图象可知当直线经过点B 时,直线b=2a ﹣z 得截距最小,由可得a=,b=此时z 最大为z=2×﹣=,当直线经过点A 时,直线b=2a ﹣z 得截距最大,由可得a=﹣,b=,此时z 最小为z=2×(﹣)﹣=﹣,∴2a ﹣b 的取值范围是,故答案为:,15.已知三个命题p ,q ,m 中只有一个是真命题,课堂上老师给出了三个判断:A :p 是真命题;B :p ∨q 是假命题;C :m 是真命题.老师告诉学生三个判断中只有一个是错误的,那么三个命题p ,q ,m 中的真命题是 m .【考点】复合命题的真假.【分析】根据已知中老师告诉学生三个判断中只有一个是错误的,逐一分析论证,可得答案.【解答】解:由已知中三个命题p ,q ,m 中只有一个是真命题, ①若A 是错误的,则:p 是假命题;q 是假命题;m 是真命题.满足条件; ②若A 是错误的,则:p 是真命题;q 的真假不能确定;m 是真命题.不满足条件; ③若C 是错误的,则:p 是真命题;p ∨q 不可能是假命题;不满足条件;故真命题是m,故答案为:m16.已知点A(a,0),点P是双曲线C:﹣y2=1右支上任意一点,若|PA|的最小值为3,则a=﹣1或2.【考点】双曲线的简单性质.【分析】设P(x,y)(x≥2),则|PA|2=(x﹣a)2+y2=+﹣1,分类讨论,利用|PA|的最小值为3,求出a的值.【解答】解:设P(x,y)(x≥2),则|PA|2=(x﹣a)2+y2=+﹣1,a>0时,x=a,|PA|的最小值为﹣1=3,∴,a<0时,2﹣a=3,∴a=﹣1.故答案为﹣1或2.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.已知a,b分别是△ABC内角A,B的对边,且bsin2A=acosAsinB,函数f(x)=sinAcos2x﹣sin2sin 2x,x∈[0,].(Ⅰ)求A;(Ⅱ)求函数f(x)的值域.【考点】余弦定理.【分析】(Ⅰ)由已知结合正弦定理,求出tanA的值,从而求出A的值;(II)由A化简函数f(x)为正弦型函数,求出x∈[0,]时f(x)的值域.【解答】解:(Ⅰ)△ABC中,bsin2A=acosAsinB,由正弦定理得,sinBsin2A=sinAcosAsinB,∴tanA==,…又A∈(0,π),∴;…(II)由A=,∴函数f(x)=sinAcos2x﹣sin2sin 2x=cos2x﹣sinxcosx=•﹣•sin2x=﹣(sin2x﹣cos2x)+,=﹣sin(2x﹣)+,∵x∈[0,],∴﹣≤2x﹣≤,…∴﹣≤sin(2x﹣)≤1,∴≤﹣sin(2x﹣)+≤,所以f(x)的值域为.…18.如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG 上.(Ⅰ)求证:平面PBE⊥平面APG;=,△PBE点M在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.【考点】二面角的平面角及求法;平面与平面垂直的判定.【分析】(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,过点P作PO⊥AG于O,则PO⊥底面ABCDE,推导出BE⊥PO,BE⊥AG,由此能证明平面PBE⊥平面APG.(II)连接PF,推导出O点与F点重合,以O为原点,分别以的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.利用向量法能求出二面角M﹣AB﹣D的余弦值.【解答】证明:(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,过点P作PO⊥AG于O,则PO⊥底面ABCDE∵BE⊂平面ABCDE,∴BE⊥PO,∵△ABE是等边三角形,∴BE⊥AG…∵AG∩PO=O,∴BE⊥平面PAG,∵BE⊂平面PBE,∴平面PBE⊥平面APG.…解:(II)连接PF,∵又∵∠PAF=45°,∴PF⊥AF,∴PF⊥AF,∴PF⊥底面ABCDE.…∴O点与F点重合.如图,以O为原点,分别以的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.底面ABCDE的一个法向量…∵,∴,设平面ABM的法向量,∵,∴,∴,∴,取则,∴,…∵二面角的法向量分别指向二面角的内外,即为二面角的平面角,∴cos<>==.∴二面角M﹣AB﹣D的余弦值为.…19.某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(Ⅰ)计算“从样本中任意选取2名学生,恰好有一名学生的打分不低于4分”的概率值;(Ⅱ)由X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望;(Ⅲ)根据表格写出Y的分布列,计算对应的数学期望值.【解答】解:(Ⅰ)设“从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分”为事件A,则P(A)==≈0.51;…(Ⅱ)X的可能取值为4,5,6,7,8,9,10;则P(X=4)=0.2×0.2=0.04,P(X=5)=2×0.2×0.3=0.12,P(X=6)=2×0.2×0.3+0.3×0.3=0.21,P(X=7)=2×0.3×0.3+2×0.2×0.2=0.26,P(X=8)=2×0.2×0.3+0.3×0.3=0.21,P(X=9)=2×0.2×0.3=0.12,P(X=10)=0.2×0.2=0.04;X的分布列如下:X的数学期望为E(X)=4×0.04+5×0.12+6×0.21+7×0.26+8×0.21+9×0.12+10×0.04=7;…..(Ⅲ)Y的分布列为Y的数学期望为E(Y)=﹣1000×0.16+2000×0.68+3000×0.16=1680.…20.已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+交抛物线E于A,B两点.(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;(Ⅱ)过点A,B作抛物线E的切线l1,l2,且l1,l2交点为P,若直线PF与直线l斜率之和为﹣,求直线l的斜率.【考点】抛物线的简单性质.【分析】(Ⅰ)根据弦长公式即可求出p的值,问题得以解决,(Ⅱ)联立方程组,根据韦达定理,即可求出过点A,B作抛物线E的切线l1,l2方程,再求出交点坐标,根据斜率的关系即可求出k的值.【解答】解:(Ⅰ)联立,消去x得,题设得,∴p=2,∴抛物线E的方程为x2=4y.(II)设联立,消去y得x2﹣2pkx﹣p2=0,∴,由得,∴直线l1,l2的方程分别为,联立得点P的坐标为,∴,∴或,∴直线l的斜率为k=﹣2或.21.已知函数f(x)=x2﹣alnx(a>0)的最小值是1.(Ⅰ)求a;(Ⅱ)若关于x的方程f2(x)e x﹣6mf(x)+9me﹣x=0在区间[1,+∞)有唯一的实根,求m的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出f(x)的最小值,问题转化为﹣ln﹣1=0,记g(a)=﹣ln﹣1,(a >0),根据函数的单调性求出a的值即可;(Ⅱ)由条件可得f2(x)e2x﹣6mf(x)e x+9m=0,令g(x)=f(x)e x=(x2﹣2lnx)e x,原问题等价于方程t2﹣6mt+9m=0在区间[e,+∞)内有唯一解,通过讨论△的符号,求出m的范围即可.【解答】解:(Ⅰ)f′(x)=2x﹣=,(x>0),所以,当0<x<时,f′(x)<0,当x>时,f′(x)>0,故f(x)min=f()=﹣ln,由题意可得:﹣ln=1,即﹣ln﹣1=0,记g(a)=﹣ln﹣1,(a>0),则函数g(a)的零点即为方程﹣ln=1的根;由于g′(a)=﹣ln,故a=2时,g′(2)=0,且0<a<2时,g′(a)>0,a>2时,g′(a)<0,所以a=2是函数g(a)的唯一极大值点,所以g(a)≤g(2),又g(2)=0,所以a=2.(II)由条件可得f2(x)e2x﹣6mf(x)e x+9m=0,令g(x)=f(x)e x=(x2﹣2lnx)e x,则g′(x)=(x2+2x﹣﹣2lnx)e x,令r(x)=x2+2x﹣﹣2lnx(x≥1),则,r(x)在区间[1,+∞)内单调递增,∴g(x)≥g(1)=e;所以原问题等价于方程t2﹣6mt+9m=0在区间[e,+∞)内有唯一解,当△=0时可得m=0或m=1,经检验m=1满足条件,当△>0时可得m<0或m>1,所以e2﹣6me+9m≤0,解之得:m≥,综上,m的取值范围是{m|m=1或m≥}.从22、23题中任选一题作答.[选修4-4:坐标系与参数方程选讲]22.在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1,C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣)=.(Ⅰ)求C1和C2交点的极坐标;(Ⅱ)直线l的参数方程为:(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】(Ⅰ)求出C1和C2的直角坐标方程,得出交点坐标,再求C1和C2交点的极坐标;(Ⅱ)利用参数的几何意义,即可求|PA|+|PB|.【解答】解:(Ⅰ)由C1,C2极坐标方程分别为ρ=2sinθ,’化为平面直角坐标系方程分为x2+(y﹣1)2=1,x+y﹣2=0.…得交点坐标为(0,2),(1,1).…即C1和C2交点的极坐标分别为.…(II)把直线l的参数方程:(t为参数),代入x2+(y﹣1)2=1,得,…即t2﹣4t+3=0,t1+t2=4,…所以|PA|+|PB|=4.…[选修4-5:不等式选讲]23.已知函数f(x)=|ax﹣2|.(Ⅰ)当a=2时,解不等式f(x)>x+1;(Ⅱ)若关于x的不等式f(x)+f(﹣x)<有实数解,求m的取值范围.【考点】绝对值不等式的解法;绝对值三角不等式.【分析】(Ⅰ)把a=2代入不等式化简后,对x分类讨论,分别去掉绝对值求出每个不等式的解集,再取并集即得不等式的解集;(Ⅱ)利用绝对值三角不等式求出f(x)+f(﹣x)的最小值,结合题意列出不等式,求出实数m的范围.【解答】解:(Ⅰ)当a=2时,不等式为:|2x﹣2|>x+1,当x≥1时,不等式化为:2x﹣2>x+1,解得x>3…当x<1时,不等式化为:2﹣2x>x+1,解得…综上所述,解集为;…(II)因为f(x)+f(﹣x)=|ax﹣2|+|﹣ax﹣2|≥|ax﹣2﹣ax﹣2|=4…,所以f(x)+f(﹣x)的最小值为4,…,因为f(x)+f(﹣x)<有实数解,所以…2017年4月1日。
2017高考模拟试卷理数及答案
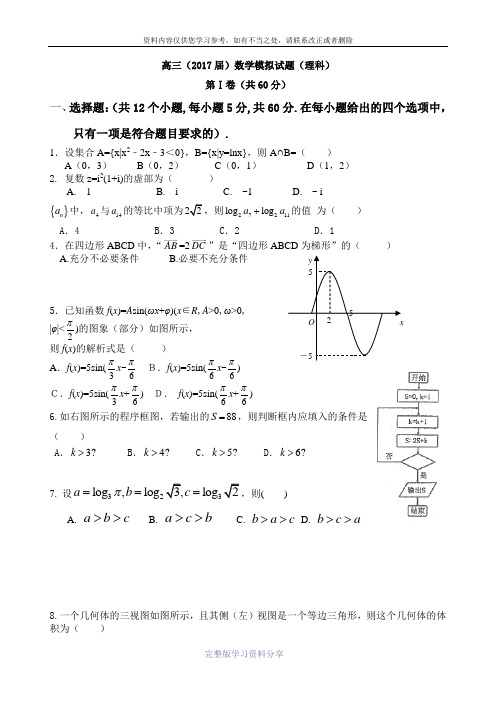
高三(2017届)数学模拟试题(理科)第Ⅰ卷(共60分)一、选择题:(共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.设集合A={x|x 2﹣2x ﹣3<0},B={x|y=lnx},则A ∩B=( )A (0,3)B (0,2)C (0,1)D (1,2) 2. 复数z=i 2(1+i)的虚部为( )A. 1B. iC. -1D. - i{}n a 中,4a 与14a 的等比中项为22,则27211log log a a +的值 为( )A .4B .3C .2D .1 4.在四边形ABCD 中,“AB =2DC ”是“四边形ABCD 为梯形”的( ) A.充分不必要条件 B.必要不充分条件 5.已知函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0, |φ|<2π)的图象(部分)如图所示,则f (x )的解析式是( )A .f (x )=5sin(3πx -6π B.f (x )=5sin(6πx -6π)C.f (x )=5sin(3πx +6π) D. f (x )=5sin(6πx +6π)6.如右图所示的程序框图,若输出的88S =,则判断框内应填入的条件是( )A .3?k >B .4?k >C .5?k >D .6?k >7. 设323log ,log 3,log 2a b c π===,则( )A.a b c >>B.a cb >>C.b ac >> D. b c a >>8.一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )x -5y O 5 2 5A .433 B .533 C .23 D .833x y 、满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩,如果目标函数z x y =-的最小值为-1,则实数m =( )A .6B .5C .4D .3 10.函数()2sin f x x x =+的部分图象可能是( )11. 已知双曲线()222210,0x y C a b a b-=>>:的右焦点为F ,过F 且斜率为3的直线交C 于A B 、两点,若4AF FB =,则C 的离心率为A .95 B. 75 C. 58 D. 6512、已知定义在R 上的可导函数f(x)的导函数为/()f x ,满足/()f x <()f x ,且()(2)f x f x -=+,(2)1f =,则不等式()x f x e <的解集为( )A. ()2,-+∞B. (0,+∞)C.(1, +∞)D.(2, +∞)第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共4个小题,每小题5分,共20分). 13. (4y x 的展开式中33x y 的系数为 。
河北省邯郸市2017届高三上学期质量检测理科数学试卷及答案解析

19.(本小题满分12分)
已知数列 的前n项和 ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)若 ,求数列 的前n项和 .
20.(本小题满分12分)
四棱锥 中,底面ABCD为矩形, , , ,E为线段AB上一点,且 ,点F、G、M分别为线段PA、PD、BC的中点.
(1)求证: ;
A. B. C. D.
10.已知抛物线 ( )的焦点为F,点P为C上一动点, , ,且 的最小值为 ,则等于()
A.4B. C.5D.
11.已知 , , , , 这3个函数在同一直角坐标系中的部分图像如下图所示,则函数 的图像的一条对称轴方程可以为()
A. B. C. D.
12.已知函数 若关于x的方程 存在2个实数根,则a的取值范围为()
(1)若 ,求 的面积;
(2)求 的最小值,并确定此时 的值.
18.(本小题满分12分)
已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
(1)试问这3年的前7个月中哪个月的平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
7.若正整数N除以正整数m后的余数为n,则记为 ,例如 .下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的 等于()
A.4B.8C.16D.32
8.如图是某几何体的三视图,则该几何体的体积为()
A.6B.9C.12D.18
9.设x,y满足约束条件 若 ,则 仅在点 处取得最大值的概率为()
16.已知四面体ABCD的每个顶点都在球O的表面上, , , ,G为 的重心,且直线DG与底面ABC所成角的正切值为 ,则球O的表面积为___________.
2017年河北省邯郸市高考数学一模试卷(理科)(解析版)

2017年河北省邯郸市高考数学一模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合A={x|x2﹣2x﹣3<0},B={x|x≥2},则A∩B=()A.(2,3]B.[2,3]C.(2,3) D.[2,3)2.已知a,b∈R,i为虚数单位,当a+bi=i(1﹣i)时,则=()A.i B.﹣i C.1+i D.1﹣i3.已知向量,满足||=2,||=3,(﹣)•=7,则与的夹角为()A.B.C. D.4.已知椭圆C: +=1(a>b>0)的左焦点为F(﹣c,0),上顶点为B,若直线y=x与FB平行,则椭圆C的离心率为()A.B.C.D.5.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=,AB=2,则S△ABC=()A.3 B.2 C.3 D.66.从5种主料职工选2种,8种辅料中选3种烹制菜肴,烹制方式有5种,那么最多可以烹制出不同的菜肴种数为()A.18 B.200 C.2800 D.336007.执行如图所示的程序框图,则输出的结果是()A.8 B.13 C.21 D.348.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是()A.B.C.D.9.设{a n}是公差为2的等差数列,b n=a,若{b n}为等比数列,则b1+b2+b3+b4+b5=()A.142 B.124 C.128 D.14410.某几何体的三视图如图所示,则该几何体的体积为()A.πB.πC.πD.π11.已知棱长为的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则+的最小值为()A.B.4 C.D.512.设f(x)=e x,f(x)=g(x)﹣h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,则m的最小值为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分).13.已知函数f(x)=,则f[f(﹣3)]=.14.已知函数f(x)=ax+b,0<f(1)<2,﹣1<f(﹣1)<1,则2a﹣b的取值范围是.15.已知三个命题p,q,m中只有一个是真命题,课堂上老师给出了三个判断:A:p是真命题;B:p∨q是假命题;C:m是真命题.老师告诉学生三个判断中只有一个是错误的,那么三个命题p,q,m中的真命题是.16.已知点A(a,0),点P是双曲线C:﹣y2=1右支上任意一点,若|PA|的最小值为3,则a=.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.已知a,b分别是△ABC内角A,B的对边,且bsin2A=acosAsinB,函数f(x)=sinAcos2x﹣sin2sin 2x,x∈[0,].(Ⅰ)求A;(Ⅱ)求函数f(x)的值域.18.如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.(Ⅰ)求证:平面PBE⊥平面APG;=,点(Ⅱ)已知AB=2,BC=,侧棱PA与底面ABCDE所成角为45°,S△PBEM在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.19.某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).20.已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+交抛物线E于A,B两点.(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;(Ⅱ)过点A,B作抛物线E的切线l1,l2,且l1,l2交点为P,若直线PF与直线l斜率之和为﹣,求直线l的斜率.21.已知函数f(x)=x2﹣alnx(a>0)的最小值是1.(Ⅰ)求a;(Ⅱ)若关于x的方程f2(x)e x﹣6mf(x)+9me﹣x=0在区间[1,+∞)有唯一的实根,求m的取值范围.从22、23题中任选一题作答.[选修4-4:坐标系与参数方程选讲]22.在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1,C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣)=.(Ⅰ)求C1和C2交点的极坐标;(Ⅱ)直线l的参数方程为:(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.[选修4-5:不等式选讲]23.已知函数f(x)=|ax﹣2|.(Ⅰ)当a=2时,解不等式f(x)>x+1;(Ⅱ)若关于x的不等式f(x)+f(﹣x)<有实数解,求m的取值范围.2017年河北省邯郸市高考数学一模试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合A={x|x2﹣2x﹣3<0},B={x|x≥2},则A∩B=()A.(2,3]B.[2,3]C.(2,3) D.[2,3)【考点】交集及其运算.【分析】先分别求出集合A和B,由此利用交集定义能求出A∩B.【解答】解:∵集合A={x|x2﹣2x﹣3<0}={x|﹣1<x<3},B={x|x≥2},∴A∩B={x|2≤x<3}=[2,3).故选:D.2.已知a,b∈R,i为虚数单位,当a+bi=i(1﹣i)时,则=()A.i B.﹣i C.1+i D.1﹣i【考点】复数代数形式的乘除运算.【分析】由a+bi=i(1﹣i)=1+i,求出a,b的值,然后代入,再由复数代数形式的乘除运算化简得答案.【解答】解:由a+bi=i(1﹣i)=1+i,得a=1,b=1.则=.故选:A.3.已知向量,满足||=2,||=3,(﹣)•=7,则与的夹角为()A.B.C. D.【考点】平面向量数量积的运算.【分析】运用向量的数量积的性质:向量的平方即为模的平方,可得•=﹣3,再由向量的夹角公式,计算即可得到所求角.【解答】解:向量,满足||=2,||=3,(﹣)•=7,可得2﹣•=4﹣•=7,可得•=﹣3,cos<,>===﹣,由0≤<,>≤π,可得<,>=.故选:C.4.已知椭圆C: +=1(a>b>0)的左焦点为F(﹣c,0),上顶点为B,若直线y=x与FB平行,则椭圆C的离心率为()A.B.C.D.【考点】双曲线的简单性质.【分析】求出直线FB的斜率,利用直线y=x与FB平行,建立方程,求出b=c,即可求出椭圆C的离心率.【解答】解:由题意,,∴b=c,∴a=c,∴e==,故选B.5.已知△ABC的三个内角A,B,C依次成等差数列,BC边上的中线AD=,AB=2,则S△ABC=()A.3 B.2 C.3 D.6【考点】正弦定理.【分析】由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,故B=60°,ABD中,由余弦定理可得BD的长,进而利用三角形面积公式即可计算得解.【解答】解:∵由于△ABC的三个内角A、B、C成等差数列,且内角和等于180°,∴B=60°,∵△ABD中,由余弦定理可得:AD2=AB2+BD2﹣2AB•BD•cosB,即:7=4+BD2﹣2BD,∴BD=3或﹣1(舍去),可得:BC=6,===3.∴S△ABC故选:C.6.从5种主料职工选2种,8种辅料中选3种烹制菜肴,烹制方式有5种,那么最多可以烹制出不同的菜肴种数为()A.18 B.200 C.2800 D.33600【考点】排列、组合的实际应用.【分析】根据题意,分3步进行分析:①、从5种主料之中选2种,②、从8种辅料中选3种烹制菜肴,③、从5种烹制方式选一种,分别计算每一步的情况数目,由分步计数原理计算可得答案.【解答】解:根据题意,分3步进行分析:①、从5种主料之中选2种,有C52=10种选法;②、从8种辅料中选3种烹制菜肴,有C83=56种选法;③、从5种烹制方式选一种,有C51=5种选法;则最多可以烹制出不同的菜肴种数为10×56×5=2880;故选:C.7.执行如图所示的程序框图,则输出的结果是()A.8 B.13 C.21 D.34【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变量a,b,c的值,并输出满足退出循环条件时的b的值,模拟程序的运行,对程序运行过程中各变量的值进行分析,即可得解.【解答】解:模拟执行程序,可得a=1,b=1,i=1执行循环体,c=2,a=1,b=2,i=2不满足条件i>5,执行循环体,c=3,a=2,b=3,i=3不满足条件i>5,执行循环体,c=5,a=3,b=5,i=4不满足条件i>5,执行循环体,c=8,a=5,b=8,i=5不满足条件i>5,执行循环体,c=13,a=8,b=13,i=6满足条件i>5,退出循环,输出b的值为13.故选:B.8.如图,在边长为2的正方形ABCD中,M是AB的中点,则过C,M,D三点的抛物线与CD围成阴影部分的面积是()A.B.C.D.【考点】定积分在求面积中的应用.【分析】由题意,建立如图所示的坐标系,求出抛物线的方程,利用定积分求面积即可.【解答】解:由题意,建立如图所示的坐标系,则D(2,1),设抛物线方程为y2=2px,代入D,可得p=,∴y=,∴S===,故选D.9.设{a n}是公差为2的等差数列,b n=a,若{b n}为等比数列,则b1+b2+b3+b4+b5=()A.142 B.124 C.128 D.144【考点】等比数列的通项公式.【分析】由已知得a n=a1+(n﹣1)×2=a1+2n﹣2,且(a4)2=a2•a8,从而a1=2,=2+2×2n﹣2=2n+1,由此能求出b1+b2+b3+b4+b5的值.【解答】解:∵{a n}是公差为2的等差数列,b n=a,∴a n=a1+(n﹣1)×2=a1+2n﹣2,∵{b n}为等比数列,∴.∴(a4)2=a2•a8,∴=(a1+4﹣2)(a1+16﹣2),解得a1=2,∴=2+2×2n﹣2=2n+1b1+b2+b3+b4+b5=22+23+24+25+26=124.故选:B.10.某几何体的三视图如图所示,则该几何体的体积为()A.πB.πC.πD.π【考点】由三视图求面积、体积.【分析】由三视图可得,直观图为圆锥的与圆柱的组合体,由图中数据可得该几何体的体积.【解答】解:由三视图可得,直观图为圆锥的与圆柱的组合体,由图中数据可得几何体的体积为=,故选A.11.已知棱长为的正四面体ABCD(四个面都是正三角形),在侧棱AB上任取一点P(与A,B都不重合),若点P到平面BCD及平面ACD的距离分别为a,b,则+的最小值为()A.B.4 C.D.5【考点】基本不等式.=S△ACD,h 【分析】由题意可得: +=,其中S△BCD为正四面体ABCD的高,可得h=2,a+b=2.再利用“乘1法”与基本不等式的性质即可得出.=S△ACD,【解答】解:由题意可得: +=,其中S△BCDh为正四面体ABCD的高.h==2,∴a+b=2.∴+==≥=,当且仅当a=2=时取等号.故选:C.12.设f(x)=e x,f(x)=g(x)﹣h(x),且g(x)为偶函数,h(x)为奇函数,若存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,则m的最小值为()A.B.C.D.【考点】函数奇偶性的性质.【分析】由F(x)=g(x)+h(x)及g(x),h(x)的奇偶性可求得g(x),h(x),进而可把mg(x)+h(x)≥0表示出来,分离出参数后,求函数的最值问题即可解决.【解答】解:由f(x)=g(x)﹣h(x),即e x=g(x)﹣h(x)①,得e﹣x=g(﹣x)﹣h(﹣x),又g(x),h(x)分别为偶函数、奇函数,所以e﹣x=g(x)+h(x)②,联立①②解得,g(x)=(e x+e﹣x),h(x)=(e x﹣e﹣x).mg(x)+h(x)≥0,即m•(e x+e﹣x)+(e x﹣e﹣x)≥0,也即m≥,即m≥1﹣∵存在实数m,当x∈[﹣1,1]时,不等式mg(x)+h(x)≥0成立,1﹣≥,∴m≥.∴m的最小值为.故选A.二、填空题:本大题共4小题,每小题5分,共20分).13.已知函数f(x)=,则f[f(﹣3)]=﹣.【考点】函数的值.【分析】由已知得f(﹣3)==,从而f[f(﹣3)]=f(),由此能求出结果.【解答】解:∵函数f(x)=,∴f(﹣3)==,f[f(﹣3)]=f()====﹣.故答案为:.14.已知函数f(x)=ax+b,0<f(1)<2,﹣1<f(﹣1)<1,则2a﹣b的取值范围是.【考点】不等式的基本性质.【分析】由题意可得0<a+b<2,﹣1<﹣a+b<1,作出可行域如图,设z=2a﹣b,利用z的几何意义,利用数形结合即可求出该线性规划问题中所有的最优解.【解答】解:∵f(x)=ax+b,0<f(1)<2,﹣1<f(﹣1)<1,∴0<a+b<2,﹣1<﹣a+b<1,作出可行域如图设z=2a﹣b,得b=2a﹣z,则平移直线b=2a﹣z,则由图象可知当直线经过点B时,直线b=2a﹣z得截距最小,由可得a=,b=此时z最大为z=2×﹣=,当直线经过点A时,直线b=2a﹣z得截距最大,由可得a=﹣,b=,此时z最小为z=2×(﹣)﹣=﹣,∴2a﹣b的取值范围是,故答案为:,15.已知三个命题p,q,m中只有一个是真命题,课堂上老师给出了三个判断:A:p是真命题;B:p∨q是假命题;C:m是真命题.老师告诉学生三个判断中只有一个是错误的,那么三个命题p,q,m中的真命题是m.【考点】复合命题的真假.【分析】根据已知中老师告诉学生三个判断中只有一个是错误的,逐一分析论证,可得答案.【解答】解:由已知中三个命题p,q,m中只有一个是真命题,①若A是错误的,则:p是假命题;q是假命题;m是真命题.满足条件;②若A是错误的,则:p是真命题;q的真假不能确定;m是真命题.不满足条件;③若C是错误的,则:p是真命题;p∨q不可能是假命题;不满足条件;故真命题是m,故答案为:m16.已知点A(a,0),点P是双曲线C:﹣y2=1右支上任意一点,若|PA|的最小值为3,则a=﹣1或2.【考点】双曲线的简单性质.【分析】设P(x,y)(x≥2),则|PA|2=(x﹣a)2+y2=+﹣1,分类讨论,利用|PA|的最小值为3,求出a的值.【解答】解:设P(x,y)(x≥2),则|PA|2=(x﹣a)2+y2=+﹣1,a>0时,x=a,|PA|的最小值为﹣1=3,∴,a<0时,2﹣a=3,∴a=﹣1.故答案为﹣1或2.三、解答题:本大题共5小题,共70分.解答写出文字说明、证明过程或演算过程.17.已知a,b分别是△ABC内角A,B的对边,且bsin2A=acosAsinB,函数f(x)=sinAcos2x﹣sin2sin 2x,x∈[0,].(Ⅰ)求A;(Ⅱ)求函数f(x)的值域.【考点】余弦定理.【分析】(Ⅰ)由已知结合正弦定理,求出tanA的值,从而求出A的值;(II)由A化简函数f(x)为正弦型函数,求出x∈[0,]时f(x)的值域.【解答】解:(Ⅰ)△ABC中,bsin2A=acosAsinB,由正弦定理得,sinBsin2A=sinAcosAsinB,∴tanA==,…又A∈(0,π),∴;…(II)由A=,∴函数f(x)=sinAcos2x﹣sin2sin 2x=cos2x﹣sinxcosx=•﹣•sin2x=﹣(sin2x﹣cos2x)+,=﹣sin(2x﹣)+,∵x∈[0,],∴﹣≤2x﹣≤,…∴﹣≤sin(2x﹣)≤1,∴≤﹣sin(2x﹣)+≤,所以f(x)的值域为.…18.如图,在五棱锥P﹣ABCDE中,△ABE是等边三角形,四边形BCDE是直角梯形且∠DEB=∠CBE=90°,G是CD的中点,点P在底面的射影落在线段AG上.(Ⅰ)求证:平面PBE⊥平面APG;=,点(Ⅱ)已知AB=2,BC=,侧棱PA与底面ABCDE所成角为45°,S△PBEM在侧棱PC上,CM=2MP,求二面角M﹣AB﹣D的余弦值.【考点】二面角的平面角及求法;平面与平面垂直的判定.【分析】(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,过点P 作PO⊥AG于O,则PO⊥底面ABCDE,推导出BE⊥PO,BE⊥AG,由此能证明平面PBE⊥平面APG.(II)连接PF,推导出O点与F点重合,以O为原点,分别以的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.利用向量法能求出二面角M﹣AB﹣D的余弦值.【解答】证明:(Ⅰ)取BE中点F,连接AF,GF,由题意得A,F,G三点共线,过点P作PO⊥AG于O,则PO⊥底面ABCDE∵BE⊂平面ABCDE,∴BE⊥PO,∵△ABE是等边三角形,∴BE⊥AG…∵AG∩PO=O,∴BE⊥平面PAG,∵BE⊂平面PBE,∴平面PBE⊥平面APG.…解:(II)连接PF,∵又∵∠PAF=45°,∴PF⊥AF,∴PF⊥AF,∴PF⊥底面ABCDE.…∴O点与F点重合.如图,以O为原点,分别以的方向为x轴,y轴,z轴正方向,建立空间直角坐标系.底面ABCDE的一个法向量…∵,∴,设平面ABM的法向量,∵,∴,∴,∴,取则,∴,…∵二面角的法向量分别指向二面角的内外,即为二面角的平面角,∴cos<>==.∴二面角M﹣AB﹣D的余弦值为.…19.某校后勤处为跟踪调查该校餐厅的当月的服务质量,兑现奖惩,从就餐的学生中随机抽出100位学生对餐厅服务质量打分(5分制),得到如图柱状图.(Ⅰ)从样本中任意选取2名学生,求恰好有1名学生的打分不低于4分的概率;(Ⅱ)若以这100人打分的频率作为概率,在该校随机选取2名学生进行打分(学生打分之间相互独立)记X表示两人打分之和,求X的分布列和E(X).(Ⅲ)根据(Ⅱ)的计算结果,后勤处对餐厅服务质量情况定为三个等级,并制定了对餐厅相应的奖惩方案,如表所示,设当月奖金为Y(单位:元),求E(Y).【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(Ⅰ)计算“从样本中任意选取2名学生,恰好有一名学生的打分不低于4分”的概率值;(Ⅱ)由X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望;(Ⅲ)根据表格写出Y的分布列,计算对应的数学期望值.【解答】解:(Ⅰ)设“从样本中任意选取2名学生,求恰好有一名学生的打分不低于4分”为事件A,则P(A)==≈0.51;…(Ⅱ)X的可能取值为4,5,6,7,8,9,10;则P(X=4)=0.2×0.2=0.04,P(X=5)=2×0.2×0.3=0.12,P(X=6)=2×0.2×0.3+0.3×0.3=0.21,P(X=7)=2×0.3×0.3+2×0.2×0.2=0.26,P(X=8)=2×0.2×0.3+0.3×0.3=0.21,P(X=9)=2×0.2×0.3=0.12,P(X=10)=0.2×0.2=0.04;X的分布列如下:X的数学期望为E(X)=4×0.04+5×0.12+6×0.21+7×0.26+8×0.21+9×0.12+10×0.04=7;…..(Ⅲ)Y的分布列为Y的数学期望为E(Y)=﹣1000×0.16+2000×0.68+3000×0.16=1680.…20.已知F为抛物线E:x2=2py(p>0)的焦点,直线l:y=kx+交抛物线E于A,B两点.(Ⅰ)当k=1,|AB|=8时,求抛物线E的方程;(Ⅱ)过点A,B作抛物线E的切线l1,l2,且l1,l2交点为P,若直线PF与直线l斜率之和为﹣,求直线l的斜率.【考点】抛物线的简单性质.【分析】(Ⅰ)根据弦长公式即可求出p的值,问题得以解决,(Ⅱ)联立方程组,根据韦达定理,即可求出过点A,B作抛物线E的切线l1,l2方程,再求出交点坐标,根据斜率的关系即可求出k的值.【解答】解:(Ⅰ)联立,消去x得,题设得,∴p=2,∴抛物线E的方程为x2=4y.(II)设联立,消去y得x2﹣2pkx﹣p2=0,∴,由得,∴直线l1,l2的方程分别为,联立得点P的坐标为,∴,∴或,∴直线l的斜率为k=﹣2或.21.已知函数f(x)=x2﹣alnx(a>0)的最小值是1.(Ⅰ)求a;(Ⅱ)若关于x的方程f2(x)e x﹣6mf(x)+9me﹣x=0在区间[1,+∞)有唯一的实根,求m的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出f(x)的最小值,问题转化为﹣ln﹣1=0,记g(a)=﹣ln﹣1,(a >0),根据函数的单调性求出a的值即可;(Ⅱ)由条件可得f2(x)e2x﹣6mf(x)e x+9m=0,令g(x)=f(x)e x=(x2﹣2lnx)e x,原问题等价于方程t2﹣6mt+9m=0在区间[e,+∞)内有唯一解,通过讨论△的符号,求出m的范围即可.【解答】解:(Ⅰ)f′(x)=2x﹣=,(x>0),所以,当0<x<时,f′(x)<0,当x>时,f′(x)>0,故f(x)min=f()=﹣ln,由题意可得:﹣ln=1,即﹣ln﹣1=0,记g(a)=﹣ln﹣1,(a>0),则函数g(a)的零点即为方程﹣ln=1的根;由于g′(a)=﹣ln,故a=2时,g′(2)=0,且0<a<2时,g′(a)>0,a>2时,g′(a)<0,所以a=2是函数g(a)的唯一极大值点,所以g(a)≤g(2),又g(2)=0,所以a=2.(II)由条件可得f2(x)e2x﹣6mf(x)e x+9m=0,令g(x)=f(x)e x=(x2﹣2lnx)e x,则g′(x)=(x2+2x﹣﹣2lnx)e x,令r(x)=x2+2x﹣﹣2lnx(x≥1),则,r(x)在区间[1,+∞)内单调递增,∴g(x)≥g(1)=e;所以原问题等价于方程t2﹣6mt+9m=0在区间[e,+∞)内有唯一解,当△=0时可得m=0或m=1,经检验m=1满足条件,当△>0时可得m<0或m>1,所以e2﹣6me+9m≤0,解之得:m≥,综上,m的取值范围是{m|m=1或m≥}.从22、23题中任选一题作答.[选修4-4:坐标系与参数方程选讲]22.在平面直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C1,C2的极坐标方程分别为ρ=2sinθ,ρcos(θ﹣)=.(Ⅰ)求C1和C2交点的极坐标;(Ⅱ)直线l的参数方程为:(t为参数),直线l与x轴的交点为P,且与C1交于A,B两点,求|PA|+|PB|.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】(Ⅰ)求出C1和C2的直角坐标方程,得出交点坐标,再求C1和C2交点的极坐标;(Ⅱ)利用参数的几何意义,即可求|PA|+|PB|.【解答】解:(Ⅰ)由C1,C2极坐标方程分别为ρ=2sinθ,’化为平面直角坐标系方程分为x2+(y﹣1)2=1,x+y﹣2=0.…得交点坐标为(0,2),(1,1).…即C1和C2交点的极坐标分别为.…(II)把直线l的参数方程:(t为参数),代入x2+(y﹣1)2=1,得,…即t2﹣4t+3=0,t1+t2=4,…所以|PA|+|PB|=4.…[选修4-5:不等式选讲]23.已知函数f(x)=|ax﹣2|.(Ⅰ)当a=2时,解不等式f(x)>x+1;(Ⅱ)若关于x的不等式f(x)+f(﹣x)<有实数解,求m的取值范围.【考点】绝对值不等式的解法;绝对值三角不等式.【分析】(Ⅰ)把a=2代入不等式化简后,对x分类讨论,分别去掉绝对值求出每个不等式的解集,再取并集即得不等式的解集;(Ⅱ)利用绝对值三角不等式求出f(x)+f(﹣x)的最小值,结合题意列出不等式,求出实数m的范围.【解答】解:(Ⅰ)当a=2时,不等式为:|2x﹣2|>x+1,当x≥1时,不等式化为:2x﹣2>x+1,解得x>3…当x<1时,不等式化为:2﹣2x>x+1,解得…综上所述,解集为;…(II)因为f(x)+f(﹣x)=|ax﹣2|+|﹣ax﹣2|≥|ax﹣2﹣ax﹣2|=4…,所以f(x)+f(﹣x)的最小值为4,…,因为f(x)+f(﹣x)<有实数解,所以…2017年4月1日。
河北省邯郸市成安县高考数学保温金卷 文

河北省邯郸市成安县2017届高考数学保温金卷文一、选择题1. 已知集合A={0,1,2},B={y|y=2x},则A∩B= ()A. {0,1,2}B. {1,2}C. {1,2,4}D. {1,4}2. [2017·吉大附中高三四模(文)]设i是虚数单位,则复数的虚部为 ()A. iB. -iC.1 D. -13. 已知向量a=(x,2),b=(2,1),c=(3,x),若a∥b,则a·c= ()A. 4B. 8C.12 D. 204. 程序框图如下:如果上述程序运行的结果S的值比2016小,若使输出的S最大,那么判断框中应填入( )A. B. C. D.5.若,,,则( )A. B. C. D.6. 从1,2,3,4,5中任取两个数,则这两个数的乘积为偶数的概率为 ()A. B. C. D.7. 若变量x,y满足约束条件则z=2x+y的最大值为 ()A. 1B. 2C. 3D. 48. 函数的图象大致是( )A. B. C.D.9.已知三棱锥S -ABC中,底面ABC为边长等于的等边三角形,SA垂直于底面ABC,SA=1,那么三棱锥S -ABC的外接球的表面积为 ( )A. 2πB. 4πC.6π D. 5π10. 为了得到函数的图象,只需将函数的图象( )A. 向左平移个单位B. 向右平移个单位C. 向左平移个单位D. 向右平移个单位11. 过(2,2)点与双曲线x2有共同渐近线的双曲线方程为( )A. B. C. D.12. 已知函数是R 上的增函数,则的取值范围是( )A. ﹣3≤a <0B. ﹣3≤a ≤﹣2C. a ≤﹣2D. a <0二、填空题13. 若△ABC 的三边a ,b ,c 及面积S 满足S =a 2-(b -c )2,则sin A = . 14. 不等式e x≥kx 对任意实数x 恒成立,则实数k 的最大值为 .15. 设数列满足: ,且,则数列的前项和等于 .16. 已知双曲线=1的一个焦点在圆x 2+y 2-4x -5=0上,则双曲线的渐近线方程为 .评卷人 得分 三、解答题17.已知数列{a n }满足a 1=,a n+1=10a n +1.(1)证明数列是等比数列,并求数列{a n }的通项公式;(2)数列{b n }满足b n =lg,T n 为数列的前n 项和,求证:T n <.18.如图所示,在四棱锥中,底面为菱形, 为与的交点, 平面为中点, 为中点.(1)求证:直线∥平面;(2)若点为中点, ,求三棱锥的体积.19. 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如下图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?20. 已知椭圆的一个焦点为,且离心率为.(1)求椭圆方程;(2)过点作直线与椭圆交于两点,求面积的最大值.21. 已知函数.(1)若函数的图象在处的切线方程为,求的值;(2)若函数在上是增函数, 求实数的最大值.22. 在直角坐标系中,直线的参数方程为,以坐标原点为极点, 轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)写出直线的普通方程和曲线的直角坐标方程;(2)直线与曲线交于两点,求.文数参考答案1. 【答案】B2. 【答案】D3. 【答案】D【解析】本题考查向量的坐标运算、向量平行和向量的数量积,属于基础题.∵a∥b,∴x×1-2×2=0,∴x=4,∴a·c=3x+2x=20,故选D.4. 【答案】C5. 【答案】A6. 【答案】D7. 【答案】C【解析】本题考查线性规划的相关知识.画出可行域(如图中阴影部分),由图可知,当直线y=-2x+z经过点A(1,1)时,z最大,最大值为2×1+1=3.8. 【答案】D9. 【答案】D10.【答案】D11. 11. 【答案】C12. 【答案】B13. 【答案】 14. 【答案】e15. 【答案】16. 【答案】y =±x17.(1) 【答案】由a n+1=10a n +1得a n+1+=10a n +=10,所以=10,所以数列是等比数列,首项为a 1+=100,公比为10,所以a n +=100×10n-1=10n+1,所以a n =10n+1-. (2) 【答案】由第1问得b n =lg =lg10n+1=n +1,所以,所以T n =+…+=.18.(1) 【答案】证明:取中点,连接,,四边形为平行四边形,,又平面平面,平面.(2) 【答案】由已知条件得所以.所以.19.(1) 【答案】根据统计数据作出2×2列联表如下:K2=≈7.287>6.635,因此可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关.(2) 【答案】分层抽样后,高茎玉米有2株,设为A,B,矮茎玉米有3株,设为a,b,c,从中取出2株的取法有AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,共10种,其中均为矮茎的选取方式有ab,ac,bc共3种,因此选取的植株均为矮茎的概率是.20.(1) 【答案】依题意有.可得. 故椭圆方程为.(2) 【答案】由题意可知过点M的直线斜率存在且不等于0,设直线方程为y=k(x-3).联立方程组,消去y得,所以,=,面积的最大值为.21、(1) 【答案】. 由题知,解得.,于是,解得.(2) 【答案】由题意即恒成立,恒成立, 设, 则,令,解得,列表得: 在上是减函数,在上是增函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成安一中2017年保温金卷理科数学一、选择题(本大题共12小题,共60。
0分)1。
全集U={1,2,3},M={x|x2-3x+2=0},则∁U M等于( )A.{1} B。
{1,2} C。
{2} D。
{3}2.已知复数为纯虚数,那么实数a的值为( )A。
—1 B。
0 C。
1 D。
23。
已知,则cos(60°—α)的值为( )A. B. C。
D.-4。
甲乙二人争夺一场围棋比赛的冠军,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为,且各局比赛结果相互独立,则在甲获得冠军的情况下,比赛进行了三局的概率为( )A. B. C。
D.5。
已知F为双曲线的一个焦点,则点F到C的一条渐近线的距离为()A. B.3 C. D。
66.一个几何体的三视图如图所示,则这个几何体的体积为( )A。
B.26 C。
80 D.7。
函数y=的图象大致是()A. B. C。
D。
8。
设a=0.64。
2,b=70。
6,c=log0。
67,则a,b,c的大小关系是()A.c<b<a B.c<a<b C。
a<c<b D.a<b<c9.执行如图所示的程序框图,输出的结果是( )A.13B.11 C。
9 D。
710。
已知抛物线C:y2=4x的焦点是F,过点F的直线与抛物线C相交于P、Q两点,且点Q在第一象限,若,则直线PQ的斜率是( )A. B。
1 C. D。
11.已知三棱柱ABC—A1B1C1的侧棱与底面垂直,体积为,底面的边长都为,若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为()A。
B. C。
D。
12.已知函数f(x)=sin(ωx+)(ω>0),f(x)在区间(0,2]上只有一个最大值1和一个最小值-1,则实数ω的取值范围为()A。
[,) B.[,π) C.[,) D。
[,]二、填空题(本大题共4小题,共20.0分)13.已知向量,,,若∥,则k= ______ .14。
的展开式的常数项为______ .15.已知点M(1,m)(m>1),若点N(x,y)在不等式组表示的平面区域内,且(O为坐标原点)的最大值为2,则m= ______ .16.在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2-a2=bc,,,则b+c的取值范围是______ .三、解答题(本大题共6小题,共72。
0分)17.已知函数f(x)=,数列{a n}是首项等于1且公比等于f(1)的等比数列;数列{b n}首项b1=,满足递推关系b n+1=f(b n).(Ⅰ)求数列{a n}和{b n}的通项公式;(Ⅱ)设c n=,求数列{c n}的前n项和T n.18.某超市从2017年1月甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:假设甲、乙两种酸奶独立销售且日销售量相互独立.(Ⅰ)写出频率分布直方图(甲)中的a值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为S12与S22,试比较S12与S22的大小(只需写出结论);(Ⅱ)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;(Ⅲ)设X表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求X的分布列和数学期望.19.如图所示,四棱锥P—ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=.(Ⅰ)证明:平面PBE⊥平面PAB;(Ⅱ)求二面角A—BE-P的大小.20。
曲线C1上任意一点M满足|MF1|+|MF2|=4,其中F1(-,0),F2(,0)抛物线C2的焦点是直线y=x-1与x轴的交点,顶点为原点O.(1)求C1,C2的标准方程;(2)请问是否存在直线l满足条件:①过C2的焦点F;②与C1交于不同两点M,N,且满足⊥?若存在,求出直线l的方程;若不存在,说明理由.21.设函数f(x)=e x(x2-x+1)(1)求f(x)的单调区间;(2)若当x∈[—1,1]时,不等式f(x)>m恒成立,求实数m的取值范围.22.在极坐标系中,O为极点,已知圆C的圆心为,半径r=1,点P在圆C上运动.(Ⅰ)求圆C的极坐标方程;(Ⅱ)在直角坐标系(与极坐标系取相同的长度单位,且以极点O为原点,以极轴为x轴正半轴)中,若Q为线段OP的中点,求点Q轨迹的直角坐标方程.成安一中2017年保温金卷理科数学答案和解析【答案】1.D 2。
B 3。
C 4.B 5。
A 6。
D 7。
C 8。
B 9.C 10.D 11.B 12。
A13。
5 14。
88 15.16.(,)17。
解:(Ⅰ)函数f(x)=,则:f(1)=由于:数列{a n}是首项等于1且公比等于f(1)的等比数列,所以:数列{b n}首项b1=,满足递推关系b n+1=f(b n).则:整理得:所以:{}是以为首项,3为公差的等差数列.解得:(Ⅱ)则:T n=c1+c2+…+c n=n—1① =n② 则:①—②得:所以:18.解:(Ⅰ)由各小矩形面积和为1,得(0。
010+a+0。
020+0.025+0.030)×10=1,解得a=0.015,由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,主要集中在20—30箱, 故s12>s22.(II)设事件A:在未来的某一天里,甲种酸奶的销售量不高于20箱;事件B:在未来的某一天里,乙种酸奶的销售量不高于20箱;事件C:在未来的某一天里,甲、乙两种酸奶的销售量恰好一个高于20箱且另一个不高于20箱.则P(A)=0.20+0。
10=0。
3,P(B)=0.10+0。
20=0.3.∴P(C)=P()P(B)+P(A)P()=0.42.(III)由题意可知X的所有可能取值为0,1,2,3,X~B(3,0.3)P (X=k)=,∴P(X=0)=0。
343,P(X=1)=0.441,P(X=2)=0。
189,P(X=3)=0。
027,∴X的分布列为:X 0 1 2 3P 0.343 0.441 0。
189 0。
027E(X)=3×0.3=0。
9.19。
证明:(I)如图所示,连接BD,由ABCD是菱形且∠BCD=60°知,△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,所以BE⊥AB,又因为PA⊥平面ABCD,BE⊂平面ABCD,所以PA⊥BE,而PA∩AB=A,因此BE⊥平面PAB.又BE⊂平面PBE,所以平面PBE⊥平面PAB.解:(II)由(I)知,BE⊥平面PAB,PB⊂平面PAB,所以PB⊥BE.又AB⊥BE,所以∠PBA是二面角A-BE—P的平面角.在R t△PAB中,..故二面角A—BE-P的大小为60°.20。
解:(1)∵曲线C1上任意一点M满足|MF1|+|MF2|=4,其中F1(-,0),F2(,0),∴曲线C1是以F1(—,0),F2(,0)为焦点,以4为实轴的椭圆,∴a=2,c=,∴b2=4-3=1,∴曲线C1的方程为.∵抛物线C2的焦点是直线y=x-1与x 轴的交点,顶点为原点O,∴抛物线C2的焦点是F(1,0)∴抛物线C2的标准方程为:y2=4x.…(6分)(2)假设存在存在直线直线l满足条件:①过C2的焦点F;②与C1交于不同两点M,N,且满足⊥,当直线l的斜率k不存在时,直线l的方程为x=0,不满足条件;当直线l的斜率k存在时,设直线l的方程为y=k(x—1),由,得(4k2+1)x2-8k2x+4k2-4=0,设M(x1,y1),N(x2,y2),则,, =k2[x1x2-(x1+x2)+1],∵⊥,∴=x1x2+y1y2=(1+k2)x1x2—k2(x1+x2)+k2=—+k2=0,解得k=2或k=—2,∴直线l满足条件,且l的方程为y=2x-2或y=—2x+2.…(13分) 21。
解:(1)函数f(x)的定义域为(—∞,+∞),…(1分)f′(x)=e x (x2—x+1)+e x(2x-1)=e x(x2+x).…(3分)由x2+x=0得x=—1,x=0,又e x>0,∴若x<-1,则f′(x)>0;若—1<x<0,则f′(x)<0;若x >0,则f′(x)>0.∴f(x)的增区间为(—∞,—1)和(0,﹢∞),减区间为(-1,0).…(8分)(2)由(1)知f(x)在[—1,1]上的最小值为f(0),∴[f(x)]min=f(0)=1,∴当m<1时,不等式f(x)>m恒成立.即实数m的取值范围是(—∞,1).…(12分)22。
解:(Ⅰ)设点P的极坐标为(ρ,θ),由余弦定理得,即,∴圆C的极坐标方程为.(Ⅱ)在直角坐标系中,圆心,圆C的方程为.设Q(x,y),则P(2x,2y),由点P在圆C上得,即,故点Q轨迹的直角坐标方程为.【解析】1. 解:由集合M中的方程解得:x=1或x=2,即M={1,2},∵全集U={1,2,3},∴∁U M={3}.故选D求出集合M中方程的解确定出M,根据全集U求出M的补集即可.此题考查了补集及其运算,熟练掌握补集的定义是解本题的关键.2。
解:∵=为纯虚数.∴a=0.故选:B.利用复数代数形式的乘除运算化简,再由实部为0且虚部不为0求得a值.本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.3. 解:cos(60°—α)=sin[90°-(60°—α)]=sin(30°+α)=,故选C.利用诱导公式把要求的式子化为sin(30°+α),利用条件求得结果.本题主要考查利用诱导公式求三角函数的值,属于基础题.4。
解:由题意,甲获得冠军的概率为×+×+×=,其中比赛进行了3局的概率为×+×=,∴所求概率为=,故选B.求出甲获得冠军的概率、比赛进行了3局的概率,即可得出结论.本题考查条件概率,考查相互独立事件概率公式,属于中档题.5. 解:双曲线的a=,b=,c=,则可设F(,0),设双曲线的一条渐近线方程为y=x,则F到渐近线的距离为d==,故选A.求出双曲线的a,b,c,可设F(,0),设双曲线的一条渐近线方程,运用点到直线的距离公式计算即可得到.本题考查双曲线的方程和性质,考查渐近线方程的运用,考查点到直线的距离公式,考查运算能力,属于基础题.6。
解:由三视图可得几何体的直观图如图所示,连接AC,且AP=2、BE=4,底面ABCD是边长为4的正方形,BE∥AP,AP⊥平面ABCD,所以V C—ABEP==16,V P-ACD==,所以几何体的体积V=16+=,故选D.由三视图画出几何体的直观图,并求出线段的长度、判断出线面的位置关系,由分割法和椎体的体积公式求出此几何体的体积.本题考查了由三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.7. 试题分析:函数为奇函数,首先作出函数y=在区间上的图象,由于函数图象关于原点对称,得出图象.由于,∴函数是奇函数,其图象关于原点对称.又当时,,当时,,∴原函数在上是增函数,在上是减函数,首先作出函数y=在区间上的图象,由于此函数为奇函数,所以在上的图象与函数在上的图象关于原点对称.故选C.8。
