(完整版)2017年对口高考数学模拟试题(一)
2017年对口高考数学模拟试题

对口高考数学模拟试题(一)班级______________姓名_______________一、选择题(共15题,每小题4分,共60分)1.“B A a ”是“B A a ”的( )A.充分条件B.充要条件C.必要条件D.既不充分也不必要条件 2.关于x 的不等式xxk k k k 122)252()252(的解集是( )A.21x B.2 x C.21x D.2 x3.若31)4sin(,则)4cos( 的值是 ( )A.31B.232 C.31 D.2324. 若1)1( x x f ,则)3(f 等于( )5. 在等差数列 n a 中,12010 S 那么83a a 等于( )6.下列命题中正确的是( )A.若数列}{n a 的前n 项和是122 n n S n ,则}{n a 是等差数列B.若数列}{n a 的前n 项和是c S n n 3,则1 c 是}{n a 为等比数列的充要条件C.常数列既是等差数列又是等比数列D.等比数列}{n a 是递增数列的充要条件是公比1 q 7.设是任意的非零平面向量,且相互不共线,则( ) ①0)()( •• ••;②•• ••)()(不与垂直; ③||||||b a b a ; ○422||4||9)23)(23(b a b a b a A.①② B.②③C.③○4D.②○4 8.已知方程12322 ky k x 表示椭圆,则k 的取值范围为( ) A.)23(, B.)3( , C.)2(, D.),(),221213( 9.两条异面直线指的是( )A.在空间两条不相交的直线B.一个平面内的一条直线和这个平面外的一条直线C.分别位于两个不同平面内的两条直线D.不同在任何一个平面内的两条直线10.如果7722107)21(x a x a x a a x ,那么721a a a 的值等于( )11.二面角 l 为60˚,平面 上一点A 到棱l 的距离为3,则A 到平面β的距离为( )A.23B.2312. 偶函数)(x f 在[0,6]上递减,那么)( f 与)5(f 的大小关系是( ) A.)5()(f f B. )5()(f f C. )5()(f f D.不确定 13.若直线062 y ax 与直线0)1()1(2a y a x 平行,则a 的值是( )或2 D.32 14.函数xx x x f ||)1()(0的定义域为( )A.)0( ,B.)0(,C.)01()1-(,,D.)0()01()1-( ,,,15.下列函数中,是奇函数且最小正周期为 的函数是( ) A.|sin |x y B.x y cos C.|tan |x y D.x y 2sin二、填空题(共5小题,每小题4分,共20分) 16.函数)24lg(2x x y 的定义域为_________.17. 与椭圆14922 y x 有公共焦点,且离心率为25的双曲线方程为__________________18.已知向量3,1 ,1,3,则与b 的夹角等于19.双曲线12222b y a x 和椭圆)00(12222b m a b ym x ,的离心率互为倒数,则以a 、b 、m 为边长的三角形是_________三角形.(填“锐角”、“钝角”或“直角”) 20.二次函数)(2R x c bx ax y 的部分对应值如下表:则不等式02bx ax 的解集是_________.三、解答题(共6小题,共70分,解答应写出文字说明或演算步骤)21. (本小题满分10分) 设二次函数)(x f 满足)2()2(x f x f ,且图像y 轴上的截距为3,被x 轴截得的线段长为22.求: (1)函数)(x f 的表达式;(2)写出)(x f 的单调递减区间和最小值.22. (本小题满分10分)设向量e 1,e 2满足| e 1|=2,| e 2|=1,e 1、e 2的夹角为60º,若向量2t e 1+7e 2与向量e 1+t e 2的夹角为钝角,求实数t 的取值范围.23.(本小题满分12分)已知16960cos sin,且24.求:(1) cos sin 的值;(2) tan 的值.24. (本小题满分12分)数列{n a }是首项为23,公差为整数的等差数列,且前6项为正,从第7项开始变为负的,回答下列各问:(1)求此等差数列的公差d;(2)设前n 项和为n S ,求n S 的最大值;(3)当n S 是正数时,求n 的最大值.25.(本小题满分13分)过点P(5,2)作圆9)2()2(22y x 的切线,试求:(1)切线所在的直线方程; (2)切线长。
湖南省2017年普通高等学校对口招生考试数学试题

机密★启用前湖南省2017年普通高等学校对口招生考试 数 学(对口)试 题 本试试题包括选择题.填空题和解答题三部分,共4页,时量120分钟.满分120分一、 选择题(本大题共10小题,每小题4分,共40分.在第小题给出的四个选项中,只有一项是符合题目要求的)1.设全集{}21,=A ,{}432,,=B ,则 =B A ∪( )A.{}2B. {},,,432C. {}431,,D. {}4321,,,2. 设3-2=a ,212=b ,221)(=c ,则c b a ,,的大小关系为( ) A.c b a << B.b c a << C.c a b << D.a b c <<3. 已知),(∈,=cos παα021,则αsin =( ) A. 23 B. 23- C.21 D. 21- 4.已知两条直线2-ax y =和12+)+(=x a y 互相垂直,则=a ( )A. 2B.1C. 0D. 1-5.下列函数中,在区间),0(∞+上是单调递增的是 ( ) A. x y sin = B. x1y = C.2y x = D. x y 31log =6.已知函数)(x f 的定义域为R ,则“)(x f 为偶函数”是“)(=(1)1-f f ”的A.充分必要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件7. 不等式065-2<+x x 的解集为 ( )A. }<|{2x xB. }>|{3x xC. }><|{3或2x x xD. }<<|{32x x8.已知l ,m 是两条不同的直线,α是平面,则下列命题正确的是A.若αm m l ⊂,⊥,则αl ⊥;B.若αl ⊥,m l //则a m ⊥;C.若a l //,αm ⊂则m l //,D. 若αl //,αm //则m l //;9.从1,2,3,4,5,6,7,8,9这9个数中取2个不同的数,使其和为偶数,则不同的取法共有( )A. 72种B. 36种C. 32种D.16种10.在三棱锥中P-ABC 中,PA ,PB ,PC 两两垂直,且PA=PB=PC=1,则该三棱锥的体积为( ) A. 61 B. 31 C. 21 D. 1 二.填空题(本大题词共5小题,每小题4分,共20分)11.在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如表所示:则这些运动员成绩的平均数是 (m )12. 若直线06-=+y kx 经过圆42-1-(22=)(+)y x 的圆心,则=k . 13.函数x x f cos =)(2-1的最小值为 .14.若关于x 的不等式32<+b x 的解集为{}03-<<x x ,则=b15.若双曲线1-2222=b y a x )>,>(00b a 上存在四点A,B,C,D,使四边形ABCD 为正方形,则此双曲线的离心率的取值范围为 。
河北省2017年对口升学高考数学试题

2017年高考试题一、选择题:1、设集合{}{}2,2,0,1A x x B =<=-,则A B =( )A 、{}02x x ≤<;B 、{}22x x -<<;C 、{}22x x -≤<;D 、{}21x x -≤<。
2、若,a b c d ><,则( )A 、22ac bc >;B 、a c b d +>+;C 、ln()ln()a c b d ->-;D 、a d b c +>+.3、“A B B =”是“A B ⊆”的( )A 、充分不必要条件;B 、必要不充分条件;C 、充要条件;D 、既不充分也不必要条件。
4、设奇函数()f x 在[1,4]上为增函数,且最大值为6,那么()f x 在[]4,1--为( )A 、增函数,且最小值为-6;B 、增函数,且最大值为6;C 、减函数,且最小值为—6;D 、减函数,且最大值为6。
5、在△ABC 中,若cos cos a B b A =,则△ABC 的形状为( )A 、等边三角形;B 、等腰三角形;C 、直角三角形;D 、等腰直角三角形。
6、已知向量(2,),(,1),(4,2),,//a x b y c a b b c =-=-=-⊥且,则( )A 、4,2x y ==-;B 、4,2x y ==;C 、4,2x y =-=-;D 、4,2x y =-=.7、设α是第三象限角,则点(cos ,tan )P αα在( )A 、第一象限;B 、第二象限;C 、第三象限;D 、第四象限。
8、设{}n a 为等差数列,34a a 和是方程2230x x --=的两个根,则其前16项的和16S 为( )A 、8;B 、12;C 、16;D 、20。
9、若函数2log a y x =在(0,)+∞内为增函数,且函数4xa y ⎛⎫= ⎪⎝⎭为减函数,则a 的取值范围是( )A 、()0,2;B 、()2,4;C 、()0,4;D 、()4,+∞。
2017四川对口高考数学试题

2017四川对口高考数学试题机密★启封并考试结束前四川省2017年普通高校职教师资班和高职班对口招生统一考试数学本试题卷分第一部分(选择题)和第二部分(非选择题)两部分,第一部分1至2页,第二部分3至4页,共4页.考生作答时,须将答案答在答题卡上,在考试题卷、草稿纸上答题无效.满分150分,考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.第一部分(选择题共60分)注意事项:1.选择题必须使用2B铅笔将答案标号填涂在答题卡上对应题目标号的位置上.2.本部分共1个大题,15个小题.每个小题4分,共60分.一、选择题:(每小题4分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合A={0,1},B={-1,0},则A∪B=()A.∅ B.{0} C.{ -1,0,1} D.{0,1}2.函数f(x)=√x+1的定义域是()A.(1,,+∞)B.[1,+∞)C.(-1,+∞)D. [-1,+∞)3.cos2π3=()A.√32B. −√32C.12D.− 124.函数y =12sin x cos x 的最小正周期是( )A.2πB.πC. π2D. π45.已知平面向量)1,1(0,1-==b a),(,则b a 2+=( ) A.(1,1) B.(3,-2) C.(3,-1) D.(-1,2) 6.过点(1,2)且与y 轴平行的直线的方程是( )A. y =1B. y =2C. x =1D. x =2 7.不等式| x -2|≤5的整数解有( )A.11个B.10个C.9个D.7个 8.抛物线y 2=4 x 的焦点坐标为( )A.(1,0)B.(2,0)C.(0,1)D.(0,2) 9.某班的6位同学与数学老师共7人站成一排照相,如果老师站在中间,且甲同学与老师相邻,那么不同的排法共有( ) A.120种 B.240种 C.360种 D.720种 10.设x =㏒2m ,y =㏒2n ,其中m ,n 是正实数,则mn ( ) A.2x+y B. 2xy C. 2x−y D. 2x +2y11.设某机械采用齿轮转动,由主动轮M 带着从动轮N 转动(如右图所示),设主动轮M 的直径为150mm ,从动轮N 的直径为300mm ,若主动轮M 顺时针旋转π2,则从动轮N 逆时针旋转( )A. π8B. π4C. π2 D.πD.如果α∥β,l α,那么l ∥β15.函数f (x )在定义域(-∞,+∞)上是增函数,且对任意的实数x 恒有f(f (x )−x 5−x +1)=2成立,则f (−1)=( ) A.-1 B.-2 C.-3 D.-4第二部分(非选择题共90分)注意事项:1.非选择题必须用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.答在试题卷上无效.2.本部分共2个大题,12个小题.共90分.二、填空题:(本大题共5个小题,每小题4分,共20分)16已知函数f (x )={−1,x <0 x −1,x ≥0则f (2)=__________(用数字作答)17二项式5)1(+x 展开式中含5x 有项的系数为__________18已知平面向量a =(1,m ),b =(-2,1)且ab ⊥,则m=19点p (0,23)到椭圆1422=+y x 上的点的最远距离是________ 20某公司为落实供给侧改革,决定增加高科技产品的生产,已知该公司2016年生产的高科技产品的产值占总产值的20%,计划2017年的总产值比上一年增长10%,且使2017年的高科技产品的产值占总产值的24%,则该公司2017生产的高科技产品的产值应比2016年生产的高科技产品的产值增长 (用百分数表示)。
2017年对口高考数学模拟试题(一)

b c8.已知方程x2A.(-3,2)B.(-3,-∞)C.(-∞,2)D.(-3,-) (-,)2 B.x>2 C.x<3.若sin(α-π3 B.2A.1C.-1A.32 B.2a|x|-x的定义域为(+0),0),0)+仅供个人参考For personal use only in study and research;not for commercialuse对口高考数学模拟试题(一)7.设a,,是任意的非零平面向量,且相互不共线,则()✍(a•b)•c-(c•a)•b=0;✍(b•c)•a-(c•a)•b不与c垂直;✍|a|-|b|<|a-b|;○4(3a+2b)(3a-2b)=9|a|2-4|b|2A.✍✍B.✍✍C. ✍4D. ✍4班级______________姓名_______________3+k+y22-k=1表示椭圆,则k的取值范围为()一、选择题(共15题,每小题4分,共60分)1.“a∈A B”是“a∈A B”的()A.充分条件B.充要条件C.必要条件D.既不充分也不必要条件552.关于x的不等式(k2-2k+)x>(k2-2k+)1-x的解集是()22112229.两条异面直线指的是()A.在空间两条不相交的直线B.一个平面内的一条直线和这个平面外的一条直线C.分别位于两个不同平面内的两条直线D.不同在任何一个平面内的两条直线A.x>112 D.x<2 1π4)=3,则cos(α+4)的值是2323D.-324.若f(x-1)=x+1,则f(3)等于()A.3B.4C.5D.6()10.如果(1-2x)7=a+a x+a x2+ +a x7,那么a+a+ +a的值等于()0127127A.-2B.-1C.0D.211.二面角α-l-β为60?,平面α上一点A到棱l的距离为3,则A到平面β的距离为(3C.2D.1)5.在等差数列{}中,Sn10=120那么a+a等于()3812.偶函数f(x)在[0,6]上递减,那么f(-π)与f(5)的大小关系是()A.f(-π)<f(5)B.f(-π)>f(5)C.f(-π)=f(5)D.不确定A.12B.24C.36D.486.下列命题中正确的是()A.若数列{a}的前n项和是S=n2+2n-1,则{a}是等差数列n n n 13.若直线ax+2y+6=0与直线x+(a-1)y+(a2-1)=0平行,则a的值是()A.-1B.2C.-1或2D.23B.若数列{a}的前n项和是S=3n-c,则c=1是{a}为等比数列的充要条件n n nC.常数列既是等差数列又是等比数列14.函数f(x)=(x+1)0)D.等比数列{a}是递增数列的充要条件是公比q>1n不得用于商业用途A.(0,∞) B.(-∞,C.(-∞-1) (-1,D.(-∞-1) (-1, (0,∞)9 + 4 = 1 有公共焦点,且离心率为- 仅供个人参考15.下列函数中,是奇函数且最小正周期为π 的函数是()A. y =| sin x |B. y = cos xC. y =| tan x |D. y = sin 2 x二、填空题(共 5 小题,每小题 4 分,共 20 分)16.函数 y = lg(4 + 2 x - x 2) 的定义域为_________.7 项开始变为负的,回答下列各问:(1)求此等差数列的公差 d;(2)设前 n 项和为 S ,求 S 的最大n n值;(3)当 S 是正数时,求 n 的最大值.n25.(本小题满分 13 分)过点 P(5,2)作圆 ( x - 2) 2 + ( y + 2) 2 = 9 的切线,试求:17. 与椭圆19.双曲线 x 2a 2- y 2 x 2 y 2 = 1 和椭圆 +b 2 m 2 b 2= 1(a > 0,m > b > 0) 的离心率互为倒数,则以 a 、b 、 (1)点 D 到 ∆ABC 所在平面的距离; (2) DB 与平面 ABC 所成角的余弦值;Dm 为边长的三角形是_________三角形.(填“锐角”、“钝角”或“直角”) (3)二面角 D - BC - A 的余弦值.20.二次函数 y = ax 2 + bx + c ( x ∈ R ) 的部分对应值如下表:ACx-3 -2 -1 0 1 2 3 4y6-4-6-6-46则不等式 ax 2 + bx + c > 0 的解集是_________.三、解答题(共 6 小题,共 70 分,解答应写出文字说明或演算步骤)21. (本小题满分 10 分) 设二次函数 f ( x ) 满足 f ( x - 2) = f (-2 - x ) ,且图像 y 轴上的截距为 3,被 x 轴截得的线段长为 2 2 .求:(1)函数 f ( x ) 的表达式;(2)写出 f ( x ) 的单调递减区间和最小值.22. (本小题满分 10 分)设向量 e 1,e 2 满足| e 1|=2,| e 2|=1,e 1、e 2 的夹角为 60o ,若向量 2t e 1+7e 2 与向量 e 1+t e 2 的夹角为钝角,求实数 t 的取值范围.B第 26 题图23.(本小题满分 12 分)已知 sin α cos α =60 π169 ,且 4 < α <π 2 .求:(1) sin α - cos α 的值; (2) tan α 的值.24. (本小题满分 12 分)数列{ a }是首项为 23,公差为整数的等差数列,且前 6 项为正,从第n不得用于商业用途仅供个人参考仅供个人用于学习、研究;不得用于商业用途。
(完整word版)2017年安徽对口升学数学模拟试卷
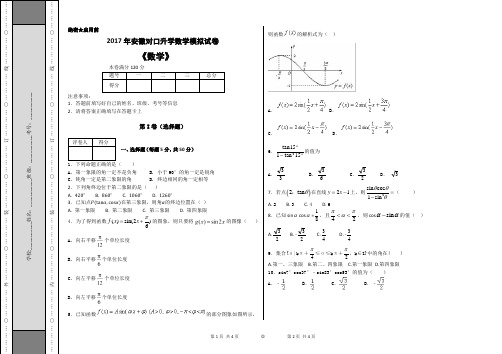
第1页 共4页 ◎ 第2页 共4页○…………外…………○…………装学校:___________姓名○…………内…………○…………装绝密★启用前2017年安徽对口升学数学模拟试卷《数学》注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(每题5分,共50分)1.下列命题正确的是( )A. 第一象限的角一定不是负角B. 小于90°的角一定是锐角C. 钝角一定是第二象限的角D. 终边相同的角一定相等 2.下列角终边位于第二象限的是( )A. 420∘B. 860∘C. 1060∘D. 1260∘3.已知点P(tanα,cosα)在第三象限,则角α的终边位置在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 4.为了得到函数()sin(2)6f x x π=+的图象,则只要将的图像( )A. 向右平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向左平移个单位长度5.已知函数的部分图象如图所示,则函数的解析式为( )A .B .C .D .6.οο15tan 115tan 2-的值为A .33B .63C .23 D . 37.若点()2tan θ,在直线21y x =-上,则2sin cos 1sin θθθ=-( )A. 2B. 3C. 4D. 6 8.已知sin αcos α=81,且24παπ<<,则cos ααsin -的值( ) A.23 B. -23 C.43 D. -439.集合{α|kπ+4π≤α≤kπ+2π,k ∈Z}中的角在( ) A.第一、三象限 B.第二、四象限 C.第一象限 D.第四象限10.sin7°cos37°﹣sin83°cos53°的值为( )A .﹣B .C .D .﹣第3页 共4页 ◎ 第4页 共4页第II 卷(非选择题)二、填空题(每题4分,共12分)11.已知半径为2的扇形面积为43π,则扇形的圆心角为 。
2017年安徽省对口高考数学模拟试题

2017年安徽省对口高考数学模拟试题(一)题型:选择题 共30小题,每小题4分,满分120分。
在每小题给出的四个选项中只有一项是符合题目要求,把正确选项写在表格中。
1.I ={0,1,2,3,4},M ={0,1,2,3} ,N ={0,3,4},)(N C M I =( )A.{2,4}B.{1,2}C.{0,1}D.{0,1,2,3} 2.下列命题中的真命题共有( );① x =2是022=--x x 的充分条件 ② x≠2是022≠--x x 的必要条件 ③y x =是x=y 的必要条件 ④ x =1且y =2是0)2(12=-+-y x 的充要条件A.1个B.2个C.3个D.4个3.设、、均为实数,且<,下列结论正确的是( )。
(A)< (B)< (C)-<- (D)<4.三个数30.7、3log 0.7、0.73的大小关系是 ( )A.30.730.73log 0.7<< B.30.730.7log 0.73<<C.30.73log 0.70.73<< D.0.733log 0.730.7<<5. y x a =-与log a y x=在同一坐标系下的图象可能是 ( )6.不等式0|)|1)(1(>-+x x 的解集是 ( )11 -1 A11 -1 B11 -1 C1 D-1 1A .}10|{<≤x xB .0|{<x x 且}1-≠xC .}11|{<<-x xD .1|{<x x 且}1-≠x7.函数xa y =在]1,0[上的最大值与最小值这和为3,则a = ( ) A .21B .2C .4D .41 8.在)2,0(π内,使x x cos sin >成立的x 的取值范围是 ( )A .)45,()2,4(ππππ B .),4(ππC .)45,4(ππD .)23,45(),4(ππππ9.椭圆5522=+ky x 的一个焦点是)2,0(,那么=k ( ) A .1-B .1C .5D .5-10.一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥轴截面顶角的余弦值是 ( ) A .43B .54C .53D .53-11.直线01)1(=+++y x a 与圆0222=-+x y x 相切,则a 的值为( ) A .1,1-B .2.2-C .1D .1-12.抛物线2y ax =的准线方程是2,y a =则的值为 ( )(A )18 (B )18- (C )8 (D )8- 13.等差数列{}n a 中,已知1251,4,33,3n a a a a n =+==则为( )(A )48 (B )49 (C )50 (D )5114.设函数⎪⎩⎪⎨⎧-=-2112)(xx f x 00>≤x x ,若1)(0>x f ,则0x 的取值范围是 ( ) (A )(1-,1) (B )(1-,∞+)(C )(∞-,2-)⋃(0,∞+) (D )(∞-,1-)⋃(1,∞+) 15.已知5()lg ,(2)f x x f ==则( )(A )lg 2 (B )lg32 (C )1lg32(D )1lg 2516.已知集合M ={x |x 2<4},N ={x |x 2-2x -3<0},则集合M ∩N =( )(A ){x |x <-2} (B ){x |x >3} (C ){x |-1<x <2} (D ){x |2<x <3} 17.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为 ( )(A )75°(B )60° (C )45°(D )30°18.已知向量a 、b 满足:|a |=1,|b |=2,|a -b |=2,则|a +b|=( )(A )1(B )2(C )5(D )619.双曲线19422=-y x 的渐近线方程是( ) A. x y 32±=B. x y 94±=C. x y 23±=D. x y 49±=20.已知向量a =(4,2),向量b =(x ,3),且a ∥b ,则x= ( )(A )9 (B )6 (C )5 (D )3 21.函数sin 2cos 2y x x =的最小正周期是( )(A )2π (B )4π (C )4π (D )2π22.如图,平面α⊥平面β,,,A B AB αβ∈∈与两平面α、β所成的角分别为4π和6π。
湖南省2017年普通高等学校对口招生考试数学模拟试题

湖南省2017年普通高等学校对口招生考试数学模拟试题————————————————————————————————作者:————————————————————————————————日期:湖南省2017年普通高等学校对口招生考试数学试题(附答案)本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分120分一、选择题(每小题4分,共40分.每小题只有一项是符合题目要求的)1.已知集合{},2,1=A ,{}4,32,=B ,则B A Y 等于 【答案】DA.{}2 B. {}4,32, C. {}4,3,1 D. {}4,3,2,12.已知32-=a,212=b ,2)21(=c ,则c b a ,,的大小关系为 【答案】BA .c b a <<B . b c a <<C .c a b <<D . a b c <<3.已知()παα,0,21cos ∈= ,则=αsin 【答案】A A .23 B . 23- C .21 D .21-4.已知两条直线1)2(2++=-=x a y ax y和互相垂直,则=a 【答案】DA .2B . 1C .0D .1-5.下列函数中,在区间()+∞,0上单调递增的是 【答案】C A.x ysin = B. x y 1=C. 2x y = D. x y 31log = 6.已知函数)(x f 的定义域为R ,则“)(x f 为偶函数” 是“)1()1(f f =-”的【答案】CA . 充分必要条件B . 必要不充分条件C . 充分不必要条件D . 既不充分也不必要条件 7.不等式0652<+-x x 的解集是 【答案】DA .{}2<x x B .{}3>x x C .{}32><x x x 或 D .{}32<<x x8.设m l 、 是两条不同的直线,α是平面,则下列命题正确的是 【答案】B A .若α⊂⊥m m l,,则α⊥l B .若l m l //,α⊥,则α⊥mC .若αα⊂m l ,//,则l m //D .若αα//,//m l ,则l m //9. 从1,2,3,4,5,6,7,8,9这9个数中取2个不同的数,使其和为偶数,则不同的取法共有A. 72种B. 36种C. 32种D. 16种 【答案】D10.在三棱锥ABC P - 中,PA ,PB ,PC 两两互相垂直,且PA=PB=PC=1 ,则该三棱锥的体积为 【答案】A A .61 B .31 C .21D .1 二、填空题(本大题共5小题,每小题4分,共20分)11、在一次中学生田径运动会上,参加男子跳高的10名运动员的成绩如下表所示:成绩/m 1.50 1.60 1.65 1.70 人数2242则这些运动员成绩的平均数是__________(m ). 【答案】1.62 12.若直线06=+-y kx 经过圆4)2()122=-+-y x (的圆心,则=k ______. 【答案】4-13.函数()x x f cos 21-=的最小值为 . 【答案】1-14.若关于x 的不等式32<+b x 的解集为{}03<<-x x ,则=b .【答案】3 15.若双曲线)0,0(12222>>=-b a by a x 上存在四点A ,B ,C ,D ,使四边形ABCD 为正方形,则此双曲线的离心率的取值范围为 .【答案】()∞+,2三、解答题(本大题共7小题,其中第21,22题为选做题.满分60分.解答题应写出文字说明、证明过程或演算步骤)16. (本小题满分10分) 已知函数()1)1(),1,0(1)5(log 2=-≠>-+=f a a x x f a 且.(I )求a 的值,并写出()x f 的定义域;(II )当[]11,4-∈x 时,求()x f 的取值范围.解:(I )依题意,有:()11)51(log 21=-+-=-a f ,解得:4=a ,由505->>+x x 得∴4=a ,()x f 的定义域为),(∞+-5 (II )由(1)得:()1)5(log 24-+=x x f ∵4>1,∴()1)5(log 24-+=x x f 为增函数,而314116log 2)11(,111log 2)4(44=-=-=-=-=-f f∴当[]11,4-∈x 时,()x f 的取值范围为[]3,1-.17. (本小题满分10分)某射击运动员射击3次,每次射击击中目标的概率为32,求: (I )3次射击都击中目标的概率; (II )击中次数ξ的分布列.解:(I )278323)3(==)(P(II )随机变量ξ的分布列为:18. (本小题满分10分)已知数列{}n a 为等差数列,若1231,1a a a a +==,求: (I )求数列{}n a 的通项公式;(II )设n an n a b )21(+=,求数列{}n b 的前n 项和n S .解:(I )设数列{}n a 的首项为1a ,公差为d ,依题意,有:⎩⎨⎧==⇒⎩⎨⎧++=+=,1,12111111d a a d a d a a ∴n d n a a n =-+=)1(1∴数列{}n a 的通项公式为n a n =;(II )n an n a b )21(+==nn )(21+∴n nn n n n n ⎪⎭⎫ ⎝⎛-++=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-++=21221211211212)1(S 2)(19. (本小题满分10分)已知向量),1(m a =ρ,向量)3,2(=b ρξ 0 1 2 3P271 92 94 278(I )若b a ρρ//,求m 的值; (II )若b a ρρ⊥,求)3()3a b a ρρρ-⋅(的值.解:(1)由b a ρρ//得:32=m ,23=∴m(2)由b a ρρ⊥得023=+m 32-=∴m∴ ),((3213)3-=a ρ=),(23- )(),()(5,1233,2)3(-=--=-a b ρρ ∴135213)3()3-=⨯-+-⨯=-⋅)()((a b a ρρρ20. (本小题满分10分)已知抛物线px y C 2:2=的焦点为().0,2F(I )求抛物线C 的方程;(II )过点M (1,2)的直线l 与C 相交于B A ,两点,且M 为AB 的中点,求直线l 的方程. 解:(I )∵抛物线px y C 2:2=的焦点为()0,2F ,∴22=p,解得4=p , 故抛物线C 的方程为:x y82=;(2)设)A 11y x ,(、)B 22y x ,( ,则依题意有422121=+=+y y x x ,易知若直线l 的斜率不存在,则直线方程为1=x ,此时4021≠=+y y ,不合题意,由⎪⎩⎪⎨⎧==22212188x y x y 得:)(8212221x x y y -=- 即2121218y y x x y y +=-- ∴2488212121==+=--==y y x x y y k k AB l∴ 直线l 的方程为02=-y x注意:第21题,22题为选做题,请考生选择其中一题作答. 21.(本小题满分10分) 已知c b a ,,,分别为△ABC 内角A ,B ,C 的对边,已知ab c22=,(I )若ο90=C ,且1=a ,求ABC ∆的面积; (II )若C A sin sin =,求C cos 的值解:(I )由ο90=C,且1=a ,则222c b a =+,又ab c 22=∴0122=+-b b ,解得1=b ∴2121S ==∆ab ABC (II )由正弦定理ca C A C c A a =⇒=sin sin sin sin , 又C A sin sin =, ∴c a =,又ab c22= ∴b c a 2==4122cos 2222==-+=ab b ab c b a C 由余弦定理得:22.某公司有40万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对乙项目投资的31倍,且对每个项目的投资都不能低于5万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对口高考数学模拟试题(一)
班级______________姓名_______________
一、选择题(共15题,每小题4分,共60分)
1.“B A a ∈”是“B A a ∈”的
( )
A.充分条件
B.充要条件
C.必要条件
D.既不充分也不必要条件 2.关于x 的不等式x
x k k k k -+->+-12
2
)2
52()2
52(的解集是
( )
A.2
1>
x B.2>x C.2
1<
x D.2<x
3.若31)4sin(=-
π
α,则)4
cos(πα+的值是 ( )
A.31
B.
232 C.31- D.23
2
- 4. 若1)1(+=-x x f ,则)3(f 等于( )
A.3
B.4
C.5
D.6
5. 在等差数列{}n a 中,12010=S 那么83a a +等于( ) A.12 B.24 C.36 D.48
6.下列命题中正确的是
( )
A.若数列}{n a 的前n 项和是122-+=n n S n ,则}{n a 是等差数列
B.若数列}{n a 的前n 项和是c S n n -=3,则1=c 是}{n a 为等比数列的充要条件
C.常数列既是等差数列又是等比数列
D.等比数列}{n a 是递增数列的充要条件是公比1>q 7.设c b a ,,是任意的非零平面向量,且相互不共线,则( ) ①0)()(=••-••b a c c b a ;②b a c a c b ••-••)()(不与c 垂直; ③||||||b a b a -<-; ○
422||4||9)23)(23(b a b a b a -=-+ A.①② B.②③
C.③○4
D.②○
4 8.已知方程
1232
2=-++k
y k x 表示椭圆,则k 的取值范围为( ) A.)23(,- B.)3(∞--, C.)2(,-∞ D.),(),22
121
3(--- 9.两条异面直线指的是
( )
A.在空间两条不相交的直线
B.一个平面内的一条直线和这个平面外的一条直线
C.分别位于两个不同平面内的两条直线
D.不同在任何一个平面内的两条直线
10.如果7
722107)21(x a x a x a a x ++++=- ,那么721a a a +++ 的值等于
( )
A.-2
B.-1
C.0
D.2
11.二面角βα--l 为60˚,平面α上一点A 到棱l 的距离为3,则A 到平面β的距离为( )
A.
2
3
B.
2
3 C.2 D.1
12. 偶函数)(x f 在[0,6]上递减,那么)(π-f 与)5(f 的大小关系是( ) A.)5()(f f <-π B. )5()(f f >-π C. )5()(f f =-π D.不确定 13.若直线062=++y ax 与直线0)1()1(2
=-+-+a y a x 平行,则a 的值是( ) A.-1
B.2
C.-1或2
D.
3
2 14.函数x
x x x f -+=||)1()(0
的定义域为( )
A.)0(∞+,
B.)0(,
-∞ C.)01()1-(,,--∞ D.)0()01()1-(∞+--∞,,,
15.下列函数中,是奇函数且最小正周期为π的函数是( ) A.|sin |x y = B.x y cos = C.|tan |x y = D.x y 2sin =
二、填空题(共5小题,每小题4分,共20分) 16.函数)24lg(2
x x y -+=的定义域为_________.
17. 与椭圆14
92
2=+y x 有公共焦点,且离心率为25的双曲线方程为__________________
18.已知向量()
3,1-=a , (
)
1,3-=
b
,则a 与b 的夹角等于
19.双曲线
122
22
=-b y
a x 和椭圆
)00(12
2
22
>>>=+b m a b y m x ,的离心率互为倒数,则以a 、b 、m 为边长的三角形是_________三角形.(填“锐角”、“钝角”或“直角”) 20.二次函数)(2
R x c bx ax y ∈++=的部分对应值如下表:
则不等式02
>++c bx ax 的解集是_________.
三、解答题(共6小题,共70分,解答应写出文字说明或演算步骤)
21. (本小题满分10分) 设二次函数)(x f 满足)2()2(x f x f --=-,且图像y 轴上的截距为3,被x 轴截得的线段长为22.求: (1)函数)(x f 的表达式;
(2)写出)(x f 的单调递减区间和最小值.
22. (本小题满分10分)设向量e 1,e 2满足| e 1|=2,| e 2|=1,e 1、e 2的夹角为60º,若向量2t e 1
+7e 2与向量e 1+t e 2的夹角为钝角,求实数t 的取值范围.
23.(本小题满分12分)已知16960cos sin =
αα,且24π
απ<
<.求:
(1) ααcos sin -的值;
(2) αtan 的值.
24. (本小题满分12分)数列{n a }是首项为23,公差为整数的等差数列,且前6项为正,从第7项开始变为负的,回答下列各问:(1)求此等差数列的公差d;(2)设前n 项和为n S ,求n S 的最大
值;(3)当n S 是正数时,求n 的最大值.
25.(本小题满分13分)过点P(5,2)作圆9)2()2(2
2
=++-y x 的切线,试求: (1)切线所在的直线方程; (2)切线长。
26.(本小题满分13分)已知一个正ABC ∆的边长为6cm ,点D 到ABC ∆各顶点的距离都是4cm.求:
(1)点D 到ABC ∆所在平面的距离;
(2)DB 与平面ABC 所成角的余弦值; (3)二面角A BC D --的余弦值.
A
B
C
D
第26题图。
