人教版七年级上有理数知识点总结及易错题
人教版七年级数学上册第一章有理数全章知识点总结归纳

人教版七年级数学上册第一章有理数全章知识点总结归纳人教版七年级数学上册第一章有理数全章知识点归纳一、知识要点1、正数和负数1) 大于的数为正数。
2) 在正数前面加上负号“-”的数为负数。
3) 数既不是正数也不是负数,是正数与负数的分界。
4) 在同一个问题中,分别用正数与负数表示的量具有相反的意义。
2、有理数1) 凡能写成分数形式的数,都是有理数,整数和分数统称有理数。
注意:即不是正数,也不是负数;-a不一定是负数,如:-(-2)=4,这个时候的a=-2.不是有理数;正有理数:正整数、正分数。
负有理数:负整数、负分数。
零。
3) 自然数:和正整数;a>:a是正数;a<:a是负数;a≥0:a是正数或是非负数;a≤0:a是负数或是非正数。
3、数轴1) 用一条直线上的点表示数,这条直线叫做数轴。
它满足以下要求:在直线上任取一个点表示数,这个点叫做原点;通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3…;从原点向左,用类似的方法依次表示-1,-2,-3…2) 数轴的三要素:原点、正方向、单位长度。
3) 画数轴的步骤:一画(画一条直线并选取原点);二取(取正反向);三选(选取单位长度);四标(标数字)。
数轴的规范画法:是条直线,数字在下,字母在上。
注意:所有的有理数都可以用数字上的点表示,但是数轴上的所有点并不都表示有理数。
4) 一般地,设a是一个正数,则数轴上表示数a的点在原点的右边,与原点的距离是a个单位长度;表示数-a的点在原点的左边,与原点的距离是a个单位长度。
4、相反数1) 只有符号不同的两个数叫做互为相反数。
注意:a的相反数是-a;a-b的相反数是b-a;a+b的相反数是-(a+b)=-a-b;非零数的相反数的商为-1;相反数的绝对值相等。
2、设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的两侧,表示a和-a。
2023年人教版七年级上有理数知识点总结及易错题

新课标人教版数学七年级(上)知识要点概括第一章有理数1.(1)正数:不小于零旳数;(2)负数:不不小于零旳数(在正数前面加上负号“—”旳数);注意:①0既不是正数也不是负数,它是正负数旳分界点;②对于正数和负数,不能简朴理解为带“+”号旳数是正数,带“—”号旳数是负数;③字母a可以表达任意数,当a表达正数时,-a是负数;当a表达负数时,-a是正数;当a表达0时,-a仍是0。
④正数有时也可以在前面加“+”,有时“+”省略不写。
因此省略“+”旳正数旳符号是正号。
2.有理数旳概念⑴正整数、0、负整数统称为整数;⑵正分数和负分数统称为分数;⑶正整数,0,负整数,正分数,负分数都可以写成分数旳形式,这样旳数称为有理数。
理解:只有能化成分数旳数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数;②有限小数和无限循环小数都可化成分数,都是有理数;③-a不一定是负数,+a也不一定是正数;3.有理数旳分类⑴按有理数旳定义分类⑵按性质符号来分正整数正整数整数 0 正有理数负整数正分数有理数有理数 0 (0不能忽视)正分数负整数分数负有理数负分数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数⑤0是整数不是分数。
4. 规定了原点,正方向,单位长度旳直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸旳直线;⑵原点、正方向、单位长度是数轴旳三要素,三者缺一不可;⑶同一数轴上旳单位长度要统一。
(4)数轴一般取右(或向上)为正方向,数轴旳原点旳选定,正方向旳取向,单位长度大小确实定都是根据实际需要规定旳。
5.数轴上旳点与有理数旳关系⑴所有旳有理数都可以用数轴上旳点来表达,正有理数可用原点右侧旳点表达,负有理数可用原点左侧旳点表达,0用原点表达。
⑵所有旳有理数都可以用数轴上旳点表达出来,但数轴上旳点不都表达有理数,也就是说,有理数与数轴上旳点不是一一对应关系。
人教版初一数学上册知识点归纳总结(精华版)

第一章有理数1.有理数: (1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数,整数和分数统称有理数. 注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 (3)注意:有理数中,1、0、-1是三个特殊的数,它们有自己的特性;这三个数把数轴上的数分成四个区域,这四个区域的数也有自己的特性;(4)自然数⇔ 0和正整数; a >0 ⇔ a 是正数; a <0 ⇔ a 是负数;a ≥0 ⇔ a 是正数或0 ⇔ a 是非负数; a ≤ 0 ⇔ a 是负数或0 ⇔ a 是非正数. 2.数轴:数轴是规定了原点、正方向、单位长度(数轴的三要素)的一条直线. 3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)注意: a-b+c 的相反数是-(a-b+c)= -a+b-c ;a-b 的相反数是b-a ;a+b 的相反数是-a-b ; (3)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. (4)相反数的商为-1. (5)相反数的绝对值相等 4.绝对值:(1)正数的绝对值等于它本身,0的绝对值是0,负数的绝对值等于它的相反数; 注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或 ⎩⎨⎧≤-≥=)0()0(a a a a a ; (3)0a 1aa >⇔= ;0a 1aa <⇔-=;(4) |a|是重要的非负数,即|a|≥0,非负性; 5.有理数比大小:(1)正数永远比0大,负数永远比0小; (2)正数大于一切负数;(3)两个负数比较,绝对值大的反而小;(4)数轴上的两个数,右边的数总比左边的数大;(5)-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
人教版七年级数学易错题讲解及答案_人教版七年级数学上册

人教版七年级数学易错题讲解及答案_人教版七年级数学上册第一章有理数易错题练习一.推断⑴ a与-a 必有一个是负数 .⑵在数轴上,与原点0相距5个单位长度的点所表示的数是5.⑶在数轴上,A 点表示+1,与A 点距离3个单位长度的点所表示的数是4.⑷在数轴的原点左侧且到原点的距离等于6个单位长度的点所表示的数的肯定值是-6. ⑸肯定值小于4. 5而大于3的整数是3、4. ⑺假如-x =- (-11),那么x = -11.⑻假如四个有理数相乘,积为负数,那么负因数个数是1个. ⑼若a =0, 则a=0. b⑽肯定值等于本身的数是1. 二.填空题⑴若-a =a -1,则a 的取值范围是: .⑵式子3-5│x │的最值是 .⑶在数轴上的A 、B 两点分别表示的数为-1和-15,则线段AB 的中点表示的数是 . ⑷水平数轴上的一个数表示的点向右平移6个单位长度得到它的相反数,这个数是________. ⑸在数轴上的A 、B 两点分别表示的数为5和7,将A 、B 两点同时向左平移相同的单位长度,得到的两个新的点表示的数互为相反数,则需向左平移个单位长度.⑹已知│a │=5,│b │=3,│a +b │= a +b ,则a -b 的值为;假如│a +b │= -a -b ,则a -b 的值为 .⑺化简-│π-3│= . ⑻假如a <b <0,那么11. a b⑼在数轴上表示数-1的点和表示-5的点之间的距离为:13121=-1,则a 、b 的关系是________. b a b ⑾若<0,<0,则ac 0.b c⑽a ⋅⑿一个数的倒数的肯定值等于这个数的相反数,这个数是 . 三. 解答题⑴已知a 、b 互为倒数,- c 与⑵数a 、b 在数轴上的对应点如图,化简:│a -b │+│b -a │+│b │-│a -│a ││.x d互为相反数,且│x │=4,求2ab -2c +d +的值.32⑶已知│a +5│=1,│b -2│=3,求a -b 的值. ⑷若|a |=4,|b |=2,且|a +b |=a +b ,求a - b 的值.⑸把下列各式先改写成省略括号的和的形式,再求出各式的值.①(-7)- (-4)- (+9) +(+2)- (-5);②(-5) - (+7)- (-6)+4.⑹改错(用红笔,只改动横线上的部分) :⑺比较4a 和-4a 的大小①已知5. 0362=25. 36,那么50. 3620. 050362 ②已知7. 4273=409. 7,那么74. 2730. 074273 ③已知3. 412=11. 63,那么2=116300;④近似数2. 40×104精确到百分位,它的有效数字是2,4;⑤已知5. 4953=165. 9,x 3=0. 0001659,则x ⑻在交换季节之际,商家将两种商品同时售出,甲商品售价1500元,盈利25%,乙商品售价1500元,但亏损25%,问:商家是盈利还是亏本? 盈利, 盈了多少? 亏本,亏了多少元? ⑼若x 、y 是有理数,且|x |-x =0,|y |+y =0,|y ||x |,化简|x |-|y |-|x +y |. ⑽已知abcd ≠0,试说明ac 、-ad 、bc 、bd 中至少有一个取正值,并且至少有一个取负值. ⑾已知a 0,推断(a +b )(c -b ) 和(a +b )(b -c ) 的大小. ⑿已知:1+2+3……+33=17×33,计算1-3+2-6+3-9+4-12+……+31-93+32-96+33-99的值.四.计算下列各题:1⎛2⎛137⑴(-42.75)×(-27.36)-(-72.64)×(+42.75) ⑵--- +⎛---- ⑶-7÷(35+)3⎛3⎛4495⎛2⎛3⎛1⎛226⑷-2000+ -1999⎛+4000+ -1⎛⑸⨯1.43-0.57⨯(-) ⑹(-5) ÷(-6) ÷(-)6⎛3⎛4⎛2⎛335221144 42⎛-2-(-3) ⑺9×18 ⑻-15×12÷6×5 ⑼-1-(1-0.5) ⨯÷⎛⑽-2-(-2)⎛3⎛18⑾(-3⨯2) 3+3⨯23有理数·易错题练习一.多种状况的问题(考虑问题要全面)(1)已知一个数的肯定值是3,这个数为_______;此题用符号表示:已知x =3, 则x=_______;-x =5, 则x=_______;(2)肯定值不大于4的负整数是________; (3)肯定值小于4.5而大于3的整数是________.(4)在数轴上,与原点相距5个单位长度的点所表示的数是________;(5)在数轴上,A 点表示+1,与A 点距离3个单位长度的点所表示的数是________;21(6) 平方得2的数是____;此题用符号表示:已知x = 412, 则x=_______; 4(7)若|a|=|b|,则a,b 的关系是________;(8)若|a|=4,|b|=2,且|a+b|=a+b ,求a -b 的值.二.特值法帮你解决含字母的问题(此方法只适用于选择、填空)正数有理数中的字母表示,从三类数中各取1——2个特值代入检验,做出正确的选择负数(1)若a 是负数,则a________-a ;-(2)已知-a 是一个________数;x =-x , 则x 满意________;若x =x , 则x 满意________;若x=-x,x 满意________;若a=____ ;(3)有理数a 、b 在数轴上的对应的位置如图所示:则()A.a + b<0 B.a + b>0; C.a -b = 0 D.a -b >0 (4)假如a 、b 互为倒数,c 、d 互为相反数,且,则代数式2ab-(c+d)m =3,+m2=_______。
《易错题》七年级数学上册第一单元《有理数》-选择题专项知识点总结(含答案)

一、选择题1.在数轴上距原点4个单位长度的点所表示的数是().A.4 B.-4 C.4或-4 D.2或-2C解析:C【解析】解:距离原点4个单位长度的点在原点的左边和右边各有一个,分别是4和-4,故选C.2.在数3,﹣13,0,﹣3中,与﹣3的差为0的数是()A.3 B.﹣13C.0 D.﹣3D解析:D【分析】与-3的差为0的数就是0+(-3),据此即可求解.【详解】解:根据题意得:0+(﹣3)=﹣3,则与﹣3的差为0的数是﹣3,故选:D.【点睛】本题考查了有理数的运算.熟练掌握有理数减法法则是解本题的关键.3.已知有理数a,b在数轴上表示的点如图所示,则下列式子中正确的是()A.a+b<0 B.a+b>0 C.a﹣b<0 D.ab>0A解析:A【分析】根据数轴判断出a、b的符号和取值范围,逐项判断即可.【详解】解:从图上可以看出,b<﹣1<0,0<a<1,∴a+b<0,故选项A符合题意,选项B不合题意;a﹣b>0,故选项C不合题意;ab<0,故选项D不合题意.故选:A.【知识点】本题考查了数轴、有理数的加法、减法、乘法,根据数轴判断出a、b的符号,熟知有理数的运算法则是解题关键.4.把实数36.1210-⨯用小数表示为()A.0.0612 B.6120 C.0.00612 D.612000C解析:C绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】6.12×10−3=0.00612,故选C.【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.5.已知实数m、n在数轴上的对应点的位置如图所示,则下列判断正确的是()A.m>0 B.n<0 C.mn<0 D.m-n>0C解析:C【解析】从数轴可知m小于0,n大于0,从而很容易判断四个选项的正误.解:由已知可得n大于m,并从数轴知m小于0,n大于0,所以mn小于0,则A,B,D 均错误.故选C.6.当A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,记作()A.海拔23米B.海拔﹣23米C.海拔175米D.海拔129米B解析:B【解析】由已知,当A地高于海平面152米时,记作“海拔+152米”,那么B地低于海平面23米时,则应该记作“海拔-23米”,故选B.7.2020年5月7日,世卫组织公布中国以外新冠确诊病例约为3504000例,把“3504000”用科学记数法表示正确的是()A.3504×103B.3.504×106C.3.5×106D.3.504×107B解析:B【分析】科学记数法表示较大的数形式为a×10n的形式,其中1≤|a|<10,n为整数,10的指数n比原来的整数位数少1.【详解】3504000=3.504×106,故选:B.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.8.如果向右走5步记为+5,那么向左走3步记为( )A.+3 B.-3 C.+13D.-13B解析:B【解析】试题用正负数来表示具有意义相反的两种量:向右记为正,则向左就记为负,由此得:如果向右走5步记为+5,那么向左走3步记为﹣3.故选B.9.一名粗心的同学在进行加法运算时,将“-5”错写成“+5”进行运算,这样他得到的结果比正确答案()A.少5 B.少10 C.多5 D.多10D解析:D【解析】根据题意得:将“-5”错写成“+5”他得到的结果比原结果多5+5=10.故选D.10.若|a|=1,|b|=4,且ab<0,则a+b的值为()A.3±B.3-C.3 D.5± A解析:A【分析】通过ab<0可得a、b异号,再由|a|=1,|b|=4,可得a=1,b=﹣4或者a=﹣1,b=4;就可以得到a+b的值【详解】解:∵|a|=1,|b|=4,∴a=±1,b=±4,∵ab<0,∴a+b=1-4=-3或a+b=-1+4=3,故选A.【点睛】本题主要考查了绝对值的运算,先根据题意确定绝对值符号中数的正负再计算结果,比较简单.11.如果a,b,c为非零有理数且a + b + c = 0,那么a b c abca b c abc+++的所有可能的值为(A.0 B.1或- 1 C.2或- 2 D.0或- 2A【分析】根据题意确定出a ,b ,c 中负数的个数,原式利用绝对值的代数意义化简,计算即可得到结果.【详解】解:∵a 、b 、c 为非零有理数,且a+b+c=0∴a 、b 、c 只能为两正一负或一正两负.①当a 、b 、c 为两正一负时,设a 、b 为正,c 为负,原式=1+1+(-1)+(-1)=0,②当a 、b 、c 为一正两负时,设a 为正,b 、c 为负原式1+(-1)+(-1)+1=0, 综上,a b c abc a b c abc+++的值为0, 故答案为:0.【点睛】此题考查了绝对值,有理数的混合运算,熟练掌握运算法则是解本题的关键.12.绝对值大于1且小于4的所有整数的和是( )A .6B .–6C .0D .4C 解析:C【解析】绝对值大于1且小于4的整数有:±2;±3,–2+2+3+(–3)=0.故选C .13.下列结论错误的是( )A .若a ,b 异号,则a ·b <0,a b <0 B .若a ,b 同号,则a ·b >0,a b >0 C .a b -=a b -=-a b D .a b--=-a b D 解析:D【解析】根据有理数的乘法和除法法则可得选项A 、B 正确;根据有理数的除法法则可得选项C 正确;根据有理数的除法法则可得选项D 原式=a b,选项D 错误,故选D. 14.若2020M M +-=+,则M 一定是( ) A .任意一个有理数B .任意一个非负数C .任意一个非正数D .任意一个负数B 解析:B【分析】直接利用绝对值的性质即可解答.【详解】解:∵M+|-20|=|M|+|20|,∴M≥0,为非负数.故答案为B.【点睛】本题考查了绝对值的应用,灵活应用绝对值的性质是正确解答本题的关键.15.-1+2-3+4-5+6+…-2011+2012的值等于A.1 B.-1 C.2012 D.1006D解析:D【解析】解:原式=(﹣1+2)+(﹣3+4)+(﹣5+6)+…+(﹣2011+2012)=+1+1+1+…+1=1006.故选D.点睛:本题考查了有理数的混合运算,正确根据式子的特点进行正确分组是关键.16.按如图所示的运算程序,能使输出的结果为12的是()A.x=-4,y=-2 B.x=3, y=3 C.x=2,y=4 D.x=4,y=0C解析:C【分析】根据y的正负然后代入两个式子内分别求解,看清条件逐一排除即可.【详解】当x=-4,y=-2时,-2<0,故代入x2-2y,结果得20,故不选A;当x=3,y=3时,3>0,故代入x2+2y,结果得15,故不选B;当x=2,y=4时,4>0,故代入x2+2y,结果得12,C正确;当x=4,y=0时,00≥,故代入x2+2y,结果得16,故不选D;故选C.【点睛】此题考查了整式的运算,重点是看清楚程序图中的条件,分别代入两个条件式中进行求解.17.计算11212312341254 2334445555555555⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+++---+++++⋯++⋯+⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭的值()A.54 B.27 C.272D.0C解析:C【分析】根据有理数的加减混合运算先算括号内的,进而即可求解.【详解】解:原式=﹣12+1﹣32+2﹣52+3﹣72+…+27=27×1 2=272.故选:C.【点睛】本题考查了有理数的加减混合运算,解决本题的关键是寻找规律.18.实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是()A.|a|>|b| B.|ac|=ac C.b<d D.c+d>0B解析:B【分析】先弄清a,b,c在数轴上的位置及大小,根据实数大小比较方法可以解得.【详解】从a、b、c、d在数轴上的位置可知:a<b<0,d>c>1;A、|a|>|b|,故选项正确;B、a、c异号,则|ac|=-ac,故选项错误;C、b<d,故选项正确;D、d>c>1,则c+d>0,故选项正确.故选B.【点睛】本题考核知识点:实数大小比较. 解题关键点:记住数轴上右边的数大于左边的数;两个负数,绝对值大的反而小.19.计算4(8)(4)(1)+-÷---的结果是()A.2 B.3 C.7 D.4 3 C解析:C【分析】先计算除法、将减法转化为加法,再计算加法可得答案.【详解】解:原式421=++7=,故选:C.【点睛】本题主要考查有理数的混合运算,解题的关键是掌握有理数的混合运算顺序和运算法则.20.已知a、b在数轴上的位置如图所示,将a、b、-a、-b从小到排列正确的一组是()A.-a<-b<a<b B.-b<-a<a<bC.-b<a<b<-a D.a<-b<b<-a D解析:D【解析】【分析】根据数轴表示数的方法得到a<0<b,且|a|>b,则-a>b,-b>a,然后把a,b,-a,-b从大到小排列.【详解】∵a<0<b,且|a|>b,∴a<-b<b<-a,故选D.【点睛】本题考查了数轴、有理数大小比较,解题的关键是熟知正数大于0,负数小于0;负数的绝对值越大,这个数越小.21.下列说法正确的是()A.近似数5千和5000的精确度是相同的B.317500精确到千位可以表示为31.8万,也可以表示为5⨯3.1810C.2.46万精确到百分位D.近似数8.4和0.7的精确度不一样B解析:B【解析】【分析】根据近似数的精确度对各选项进行判断.【详解】A.近似数5千精确度到千位,近似数5000精确到个位,所以A选项错误;B.317500精确到千位可以表示为31.8万,也可以表示为5⨯,所以B选项正确;3.1810C.2.46万精确到百位,所以C选项错误;D.近似数8.4和0.7的精确度是一样的,所以D选项错误.故选B.【点睛】本题考查了近似数和有效数字:精确到第几位”和“有几个有效数字”是精确度的两种常用的表示形式,它们实际意义是不一样的,前者可以体现出误差值绝对数的大小,而后者往往可以比较几个近似数中哪个相对更精确一些.22.下列四种说法:①减去一个数,等于加上这个数的相反数;②两个互为相反数的数和为0;③两数相减,差一定小于被减数;④如果两个数的绝对值相等,那么这两个数的和或差等于零.其中正确的说法有()A.4个B.3个C.2个D.1个B解析:B【分析】根据有理数的减法运算法则对各小题分析判断即可得解.【详解】①减去一个数等于加上这个数的相反数,故本小题正确;②互为两个相反数的两数相加得零,故本小题正确;③减数是负数时,差大于被减数,故本小题错误;④如果两个数的绝对值相等,这两个数可能相等,也可能互为相反数,故本小题正确;综上所述,正确的有①②④共3个.故选B.【点睛】本题考查了相反数的定义,有理数的减法,是基础题,熟记运算法则是解题的关键.23.在-1,2,-3,4,这四个数中,任意三数之积的最大值是()A.6 B.12 C.8 D.24B解析:B【分析】三个数乘积最大时一定为正数,二2和4的积为8,因此一定要根据-1和-3相乘,积为3,然后和4相乘,此时三数积最大.【详解】∵乘积最大时一定为正数∴-1,-3,4的乘积最大为12故选B.【点睛】本题考查了有理数的乘法,两个负数相乘积为正数,先将两个负数化为正数是本题的关键.24.一个因数扩大到原来的10倍,另一个因数缩小到原来的120,积()A.缩小到原来的12B.扩大到原来的10倍C.缩小到原来的110D.扩大到原来的2倍A解析:A根据题意列出乘法算式,计算即可.【详解】设一个因数为a ,另一个因数为b∴两数乘积为ab 根据题意,得1110202ab ab = 故选A .【点睛】本题考查了有理数乘法运算,根据有理数乘法运算法则计算即可.25.下列计算中,错误的是( )A .(2)(3)236-⨯-=⨯=B .()144282⎛⎫÷-=⨯-=- ⎪⎝⎭C .363(6)3--=-++=D .()()2399--=--= C解析:C【分析】根据有理数的运算法则逐一判断即可.【详解】 (2)(3)236-⨯-=⨯=,故A 选项正确;()144282⎛⎫÷-=⨯-=- ⎪⎝⎭,故B 选项正确; 363(6)9--=-+-=-,故C 选项错误;()()2399--=--=,故D 选项正确;故选C .【点睛】本题考查了有理数的运算,重点是去括号时要注意符号的变化.26.数轴上点A 和点B 表示的数分别为-4和2,若要使点A 到点B 的距离是2,则应将点A向右移动( )A .4个单位长度B .6个单位长度C .4个单位长度或8个单位长度D .6个单位长度或8个单位长度C解析:C【分析】A 点移动后可以在B 点左侧,或右侧,分两种情况讨论即可.【详解】∵到2距离为2的数为2+2=4或2-2=0∴-4移动到0需向右移动4个单位长度,移动到4需向右移动8个单位长度【点睛】本题考查了数轴表示距离,分两种情况一左一右讨论是本题的关键.27.下列说法中,①a - 一定是负数;② a -一定是正数;③倒数等于它本身的数是±1;④一个数的平方等于它本身的数是1;⑤两个数的差一定小于被减数;⑥如果两个数的和为正数,那么这两个数中至少有一个正数正确的有( )A .2个B .3个C .4个D .5个A 解析:A【分析】根据正数和负数、绝对值、倒数等相关的性质,逐一判断即可.【详解】①-a 不一定是负数,若a 为负数,则-a 就是正数,故说法不正确;②|-a|一定是非负数,故说法不正确;③倒数等于它本身的数为±1,说法正确;④0的平方为0,故说法不正确;⑤一个数减去一个负数,差大于被减数,故说法不正确;⑥如果两个数的和为正数,那么这两个数中至少有一个正数,故说法正确.说法正确的有③、⑥,故选A .【点睛】本题主要考查有理数的加法、正数和负数、绝对值、倒数,能熟记相关的定义及其性质是解决此类题目的关键.28.下列各组运算中,其值最小的是( )A .2(32)---B .(3)(2)-⨯-C .22(3)(2)-+-D .2(3)(2)-⨯- A解析:A【分析】根据有理数乘除和乘方的运算法则计算出结果,再比较大小即可.【详解】A ,()23225---=-;B ,()()326-⨯-=;C ,223(3)(2)941=++=--D ,2(3)(2)9(2)18-⨯-=⨯-=-最小的数是-25故选:A .【点睛】本题考查了有理数的混合运算和有理数大小的比较,熟练掌握相关的法则是解题的关键. 29.若12a =,3b =,且0a b <,则+a b 的值为( ) A .52 B .52- C .25± D .52± D 解析:D【分析】 根据a b判断出a 和b 异号,然后化简绝对值,分两种情况求解即可. 【详解】 ∵0a b< ∴a 和b 异号又∵12a =,3b = ∴12a =,3b =-或12a =-,3b = 当12a =,3b =-时,15322+-=-a b = 当12a =-,3b =时,15322+-+=a b = 故选D .【点睛】 本题考查了绝对值,有理数的除法,和有理数的加法,关键是根据a b 判断出a 和b 异号. 30.下列各组数中,互为相反数的是( )A .(﹣3)2和﹣32B .(﹣3)2和32C .(﹣2)3和﹣23D .|﹣2|3和|﹣23|A 解析:A【分析】各项中两式计算得到结果,即可作出判断.【详解】A 、(﹣3)2=9,﹣32=﹣9,互为相反数;B 、(﹣3)2=32=9,不互为相反数;C 、(﹣2)3=﹣23=﹣8,不互为相反数;D 、|﹣2|3=|﹣23|=8,不互为相反数,故选:A .【点睛】此题考查了有理数的乘方,相反数,以及绝对值,熟练掌握运算法则是解本题的关键.。
人教版初中七年级数学上册《有理数》易错题汇总

人教版初中七年级数学上册《有理数》易错题易错点1 (对“0”的认识错误)1.给出下列说法:①0可以表示没有,也可以表示具体的意义;②0是最小的正整数;③0是最小的有理数;④0既是负数又是正数;⑤0是最小的自然数.其中正确说法的序号是________.易错点2 (误认为带负号的数一定是负数)2.有理数﹣a是()A.负数B.正数C.0D.正数或负数或0 易错点3 (对π的认识错误)3.在数﹣2,0.3,+6,π,﹣0.3,15中,有理数的个数是()A.6B.5C.4D.34.化简|π﹣3.14|的结果是()A.0B.π﹣3.14C.3.14-πD.以上都不对易错点4 (对相反数的几何意义理解不透)5.如图,数轴上有A,B,C,D四个点,其中表示互为相反数的点是()A.点A与点DB.点A与点CC.点B与点DD.点B与点C易错点五(在条件|a|=﹣a下,误认为a的值一定是负数)6.已知|a|=﹣a,则a的值是()A.正数B.负数C.非正数D.非负数易错点6 (混淆绝对值符号或括号)7.下列式子中成立的是()A.﹣|﹣6|>5B.﹣8<﹣(﹣8)C.﹣|﹣7|=7D.|﹣8.5|<8疑难点1(数轴上的点与有理数的关系)1.下列说法正确的是( )A.数轴上的每一个点都表示一个整数B.数_上的每一个点都表示一个分数C.数轴上的每一个点都表示一个有理数D.每一个有理数都可以用数轴上的点表示疑难点2(有理数的大小比较)2.若﹣1<x <0,则x ,1丨x 丨,﹣x 的大小关系是( ) A.x >1丨x 丨>﹣x B 1丨x 丨>x >﹣x C.1丨x 丨>﹣x >xD.﹣x >1丨x 丨>x 疑难点3(绝对值问题中数形结合思想的应用)3.我们知道,点A ,B 在数轴上分别表示有理数a ,b ,A ,B 两点之间的距离AB=|a -b|,所以|x ﹣3|的几何意义是数轴上表示有理数3的点与表示有理数x 的点之间的距离.(1)若|x ﹣3|=5,则x=______;(2)若|x ﹣3|=|x+1|,则x=______.参考答案1.①⑤2.D【解析】解决本题的关键是知道a可以是正数、负数或0,则﹣a是负数、正数或0.故选D.易错分析当有理数是用一个字母表示时,要对这个字母分三种情况讨论求解,否则容易造成漏解.3.B【解析】解决本题的关键是知道π不是3.14,有理数.在﹣2,0.3,﹢6,π,﹣0.3,15中,除了π不是有理数外,其余各数都是有理数,所以共有5个有理数.故选B.易错分析小学数学解题经常用到π,因此受到习惯思维的影响而认为π就是有理数:实际上π是圆周率,不是整数,也不能化为分数,因此π不是有理数.4.B【解析】解决本题的关键是知道π不是3.14,π是一个比3.14大的数,因此π﹣3.14是一个正数,所以|π﹣3.14|=π﹣3.14.故选B.易错分析小学数学解题用到π时,一般把π看成3.14去计算,这样就习惯了遇到π就以为是3.14,实际上π是3.1415926535…,是一个大于3.14的数,这一点在解题中要注意.5.A【解析】由点A,B,C,D到原点的距离分别为2,1,0.5,2,知点A,D 到原点的距离相等,且在原点的两侧,所以点A与点D互为相反数.故选A.技巧点拨判断数轴上两个点所表示的数是否互为相反数,就是要看它是否满足两个条件:一是点在原点的两侧,二是点到原点的距离相等.6.C【解析】当a<0时,|a|=﹣a;当a=0时,|a|=a=﹣a.因此a的值是非正数.故选C.易错分析本题容易出现漏掉a=0的情况,从而错选B.7.B【解析】选项A,﹣|﹣6|=﹣6<5,所以A错误;选项B,﹣(﹣8)=8,﹣8<8,所以B正确;选项C,﹣|7|=﹣7 7,所以C错误;选项D,|﹣8.5|=8.5>8,所以D错误.故选B.易错分析本题的易错之处是对绝对值的意义理解不透,化简时由于受到负号的干扰导致出错.求一个数的绝对值通常有两种方法,分别为代数方法和几何方法,其中代数方法就是直接依据:绝对值的代数定义,即“一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0”;几何方法就是通过数轴,直接根据绝对值的几何定义(数轴上表示数a的点与原点的距离),结合图形,求出长度,即可得到答案.过疑难1.D【解析】选项A,虽然每一个整数都可以用数轴上的点表示,但反过来,数轴上的每一个点不都表示整数,如﹣32所以A错误;选项B,虽然每一个分数都可以用数轴上的点表示,但反过来,数轴上的每一个点不都表示分数,如1,所以B错误;选项C,虽然每一个有理数都可以用数轴上的点表示,但反过来,数轴上的每一个点不都表示有理数,如数轴上还有表示π的点,而π不是有理数,所以C错误.故选D.2.C【解析】因为﹣1<x<0,所以取x=﹣12,则1丨x丨=2,﹣x=12.因为2>12>﹣12,所以1丨x丨>﹣x>x.故选C.名师点睛本题的疑难点是比较大小的不是具体的数,不知道从哪入手解题.作为选择题可用特殊值代入法,可而化题目,降低难度.3.(1)﹣2或8;(2)1【解析】(1)|x﹣3|=5的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离为5,所以x=﹣2或8;(2)|x﹣3|=|x+1|的几何意义是数轴表示有理数3的点与表示有理数x的点之间的距离等于表示有理数﹣1的点与表示有理数x的点之间的距离,所以x=1.。
人教版七年级数学试题:第一章 有理数章节知识易错点 汇总

第一章有理数章节知识易错点易错点忽视0既不是正数也不是负数1.下列各数:0,+5,-312,+3.1,-24,2 018,-2π,其中负数有(B)A.2个B.3个C.4个D.5个易错点对有理数的相关定义理解不透彻2.下列说法正确的是(B)A.整数可分为正整数和负整数B.分数可分为正分数和负分数C.0不属于整数也不属于分数D.一个数不是正数就是负数易错点忽视到原点距离相等的点有两个3.到原点的距离是2 018个单位长度的点表示的数是(C) A.2 018 B.-2 018C.±2 018 D.2 019易错点对相反数的概念理解不清4.-a的相反数是a;-a的相反数是-5,则a=-5.易错点忽视绝对值等于一个正数的数有两个5.如果|x|=|-5|,那么x等于(C)A.5 B.-5C.5或-5 D.以上都不对易错点考虑不周全而致错5.绝对值大于2且不大于5的整数有±3、±4,±5.易错点对异号两数相加的法则理解不透彻6.计算:(-3.16)+2.08.解:原式=-(3.16-2.08)=-1.08.易错点将有理数范围内的减法与小学学过的减法混淆7.计算:(1)-4-2=-4+(-2)=-6 ; (2)-1-1=(-1)+(-1)=-2; (3)(-2)-(-3)=(-2)+(+3)=1. 易错点 运用运算律时出现符号错误 8.计算:(-112)+(-571320)-(-112)+42720.解:原式=-112-571320+112+42720=-112+112-571320+42720=0-15310=-15310.易错点 几个有理数相乘时忽视符号法则而致错 9.计算:(-3)×56×(-95)×(-14).解:原式=-(3×56×95×14)=-98.易错点 利用乘法对加法的分配律计算时,易漏乘或弄错符号 10.计算:-48×(12-3-58+56-112).解:原式=-48×12-3×(-48)-58×(-48)+56×(-48)-112×(-48)=-24+144+30-40+4 =114.易错点 不按运算顺序运算而出错 11.计算:-1÷13×(-3).解:原式=-1×3×(-3)=9.易错点 对底数的概念理解不透彻 12.(杭州中考)计算:-22=(B)A .-2B .-4C .2D .4易错点 当底数是分数或负数时,往往会忽略括号而导致错误13.计算:(1+12)×(-23)2÷13+(-1)3.解:原式=32×49×3+(-1)=2+(-1)=1.易错点 忽视科学记数法不改变数性14.-270 000用科学记数法表示为-2.7×105. 易错点 取近似数时忽视小数点的位置 15.205 001精确到万位的近似数是(D)A .20B .21C .2.0×105D .2.1×105附综合训练题:1.将下列各数按要求分别填入相应的集合中.-9.3,6,+314,-713,0,-100,-2.25,0.01,+65,-27,3100,0.2·1·.(1)正整数集合:{6,+65,…};(2)负整数集合:{-100,…};(3)正分数集合:{+314,0.01,3100,0.2·1·,…};(4)负分数集合:{-9.3,-713,-2.25,-27,…};(5)整数集合:{6,0,-100,+65,…}.2.某公司去年1~3月平均每月盈利2万元,4~6月平均每月亏损1.6万元,7~10月平均每月亏损1.5万元,11~12月平均每月盈利3.6万元.(设盈利为正,亏损为负) (1)该公司去年一年是盈利还是亏损?(2)该公司去年平均每月盈利(或亏损)多少万元?解:(1)3×2+3×(-1.6)+4×(-1.5)+2×3.6=2.4(万元). 答:该公司去年一年盈利2.4万元. (2)2.4÷12=0.2(万元).答:该公司去年平均每月盈利0.2万元.3.2018年国庆,全国从1日到7日放假七天,各地景区游人如织.其中广州白云山风景区,在9月30日的游客人数为0.9万人,接下来的七天中,每天的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).5.2万人;(2)七天假期里,游客人数最多的是10月2日,达到5.78万人;游客人数最少的是10月7日,达到0.65万人;(3)请问白云山风景区在这八天内一共接待了多少游客?(结果精确到万位)解:0.9+4+5.78+5.2+4.4+3.4+1.8+0.65=26.13≈26(万).答:白云山风景区在这八天内一共接待了约26万游客.。
七年级数学上册有理数知识点、重点、难点、易错点归纳总结
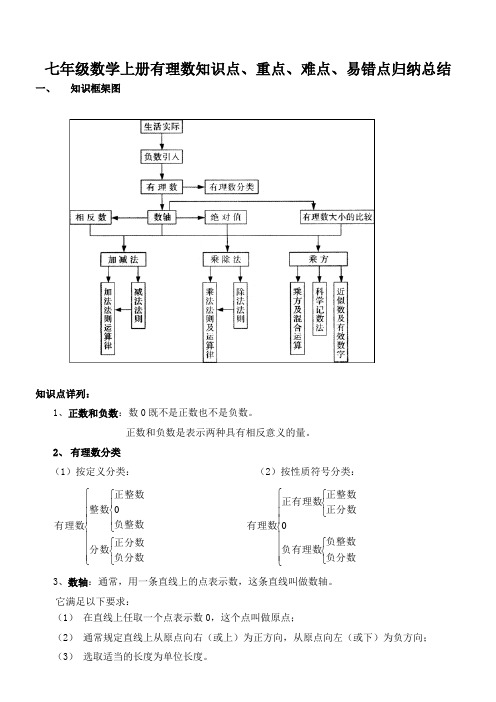
七年级数学上册有理数知识点、重点、难点、易错点归纳总结一、 知识框架图知识点详列:1、正数和负数:数0既不是正数也不是负数。
正数和负数是表示两种具有相反意义的量。
2、 有理数分类(1)按定义分类: (2)按性质符号分类: ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数正整数整数有理数0 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数正分数正整数正有理数有理数0 3、数轴:通常,用一条直线上的点表示数,这条直线叫做数轴。
它满足以下要求:(1) 在直线上任取一个点表示数0,这个点叫做原点;(2) 通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;(3) 选取适当的长度为单位长度。
4、相反数:绝对值相等,只有符号不同的两个数叫做互为相反数。
0的相反数仍是0.5、绝对值:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记做|a|。
由绝对值的定义可得:|a-b|表示数轴上a点到b点的距离。
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.6、有理数比较大小正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小。
7、有理数的四则运算(1)有理数的加法加法法则:①同号两数相加,取相同的符号,并把绝对值相加。
②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0.③一个数同0相加,仍得这个数。
运算律:加法交换律:a+b=b+a加法结合律:(a+b)+c=a+(b+c)(2)有理数的减法可转化为加法进行,减去一个数等于加上这个数的相反数,即a-b=a+(-b)。
正-正=正+负;正-负=正+正;负-正=负+负;负-负=负+正。
(4)有理数的乘法乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘。
②任何数同0相乘,都得0.③乘积是1的两个数互为倒数。
④几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积为负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新课标人教版数学七年级(上)知识要点概括第一章有理数1.(1)正数:大于零的数;(2)负数:小于零的数(在正数前面加上负号“—”的数);注意:①0既不是正数也不是负数,它是正负数的分界点;②对于正数和负数,不能简单理解为带“+”号的数是正数,带“—”号的数是负数;③字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
④正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.有理数的概念⑴正整数、0、负整数统称为整数;⑵正分数和负分数统称为分数;⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数;②有限小数和无限循环小数都可化成分数,都是有理数;③-a不一定是负数,+a也不一定是正数;3.有理数的分类⑴按有理数的定义分类⑵按性质符号来分正整数正整数整数 0 正有理数负整数正分数有理数有理数 0 (0不能忽视)正分数负整数分数负有理数负分数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数⑤0是整数不是分数。
4. 规定了原点,正方向,单位长度的直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸的直线;⑵原点、正方向、单位长度是数轴的三要素,三者缺一不可;⑶同一数轴上的单位长度要统一。
(4)数轴一般取右(或向上)为正方向,数轴的原点的选定,正方向的取向,单位长度大小的确定都是根据实际需要规定的。
5.数轴上的点与有理数的关系⑴所有的有理数都可以用数轴上的点来表示,正有理数可用原点右侧的点表示,负有理数可用原点左侧的点表示,0用原点表示。
⑵所有的有理数都可以用数轴上的点表示出来,但数轴上的点不都表示有理数,也就是说,有理数与数轴上的点不是一一对应关系。
(如,数轴上的点π不是有理数)6.数轴的画法(1)画一条直线,在这条直线上任取一个点作为原点;(2)通常规定直线上从原点向右(或左)为正方向,从原点向左(或右)为负方向;(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似的方法依次表示-1,-2,-3,….7.利用数轴表示两数大小⑴在数轴上数的大小比较,右边的数总比左边的数大;⑵正数都大于0,负数都小于0,正数大于负数;⑶两个负数比较,距离原点远的数比距离原点近的数小。
8.数轴上特殊的最大(小)数⑴最小的自然数是0,无最大的自然数;⑵最小的正整数是1,无最大的正整数;⑶最大的负整数是-1,无最小的负整数9.a可以表示什么数⑴a>0表示a是正数;反之,a是正数,则a>0;⑵a<0表示a是负数;反之,a是负数,则a<0;⑶a=0表示a是0;反之,a是0,,则a=0;10.数轴上点的移动规律根据点的移动,向左移动几个单位长度则减去几,向右移动几个单位长度则加上几,从而得到所需的点的位置。
11.归纳数轴上的点的意义:一般地,设a是一个正数,则数轴上表示a的点在原点的右边,与原点的距离是a个单位长度;表示-a的点在原点的左边,与原点的距离是a个单位长度.12.只有符号不同的两个数叫做互为相反数,其中一个是另一个的相反数。
注意:⑴相反数是成对出现的;⑵相反数只有符号不同,若一个为正,则另一个为负;⑶0的相反数是它本身;相反数为本身的数是0。
13.相反数的性质与判定⑴任何数都有相反数,且只有一个;⑵0的相反数是0;⑶互为相反数的两数和为0,和为0的两数互为相反数,即a,b互为相反数,则a+b=014.相反数的几何意义在数轴上与原点距离相等的两点表示的两个数,是互为相反数;互为相反数的两个数,在数轴上的对应点(0除外)在原点两旁,并且与原点的距离相等。
0的相反数对应原点。
说明:在数轴上,表示互为相反数的两个点关于原点对称。
15.相反数的求法⑴求一个数的相反数,只要在它的前面添上负号“-”即可求得(如:5的相反数是-5); ⑵求多个数的和或差的相反数是,要用括号括起来再添“-”,然后化简(如;5a+b 的相反数是-(5a+b )。
化简得-5a-b );⑶求前面带“-”的单个数,也应先用括号括起来再添“-”,然后化简(如:-5的相反数是-(-5),化简得5) 16.相反数的表示方法⑴一般地,数a 的相反数是-a ,其中a 是任意有理数,可以是正数、负数或0。
当a>0时,-a <0(正数的相反数是负数) 当a<0时,-a >0(负数的相反数是正数) 当a=0时,-a =0,(0的相反数是0) 17.多重符号的化简多重符号的化简规律:“+”号的个数不影响化简的结果,可以直接省略;“-”号的个数决定最后化简结果;即:“-”的个数是奇数时,结果为负,“-”的个数是偶数时,结果为正。
18.一般地,数轴上表示数a 的点与原点的距离叫做a 的绝对值,记作|a|,读作:a 的绝对值.19.因为数的绝对值是表示两点之间的距离,如:|a-b|表示数轴上a 点到b 点的距离。
所以一个数的绝对值不可能是负数。
即:任何数的绝对值都是非负数(0的绝对值是0) 20. 绝对值的计算规律:(1) 互为相反数的两个数的绝对值相等 (2) 若b a =,则a=b 或a=-b ; (3) 若0,0,0===+b a b a 则 21.绝对值的代数定义1)一个正数的绝对值是它本身 2)一个负数的绝对值是它的相反数3)0的绝对值是0 22.可用字母表示为:①如果a>0,那么|a|=a ; ②如果a<0,那么|a|=-a ; ③如果a=0,那么|a|=0。
可归纳为①:a ≥0<═> |a|=a (非负数的绝对值等于本身;绝对值等于本身的数是非负数。
) ②a ≤0<═> |a|=-a (非正数的绝对值等于其相反数;绝对值等于其相反数的数是非正数。
) 23.绝对值的性质任何一个有理数的绝对值都是非负数,也就是说绝对值具有非负性。
所以,a 取任何有理数,都有|a|≥0。
⑴0的绝对值是0;绝对值是0的数是0.即:a=0 <═> |a|=0; ⑵一个数的绝对值是非负数,绝对值最小的数是0.即:|a|≥0; ⑶任何数的绝对值都不小于原数。
即:即:|a|≥a ;0a 1a a>⇔= ; 0a 1aa<⇔-=; ⑷绝对值是相同正数的数有两个,它们互为相反数。
即:若|x|=a (a>0),则x=±a ; ⑸互为相反数的两数的绝对值相等。
即:|-a|=|a|或若a+b=0,则|a|=|b|;注意:|a|·|b|=|a ·b|,baba; ⑹绝对值相等的两数相等或互为相反数。
即:|a|=|b|,则a=b 或a=-b ;⑺若几个数的绝对值的和等于0,则这几个数就同时为0。
即|a|+|b|=0,则a=0且b=0。
(非负数的常用性质:若几个非负数的和为0,则有且只有这几个非负数同时为0) 24.有理数大小的比较⑴利用数轴比较两个数的大小:数轴上的两个数相比较,左边的总比右边的小;⑵利用绝对值比较两个负数的大小:两个负数比较大小,绝对值大的反而小;异号两数比较大小,正数大于负数。
(3)正数的绝对值越大,这个数越大; (4)正数永远比0大,负数永远比0小; (5)正数大于一切负数;(6)大数-小数 > 0,小数-大数 < 0. 25.已知一个数的绝对值,求这个数一个数a 的绝对值就是数轴上表示数a 的点到原点的距离。
一般地,绝对值为同一个正数的有理数有两个,它们互为相反数,绝对值为0的数是0,没有绝对值为负数的数。
26.有理数的加法法则⑴同号两数相加,取相同的符号,并把绝对值相加; ⑵绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;⑶互为相反数的两数相加,和为零; ⑷一个数与0相加,仍得这个数。
27.有理数加法的运算律 ⑴加法交换律:a+b=b+a⑵加法结合律:(a+b)+c=a+(b+c)28.在运用运算律时,一定要根据需要灵活运用,以达到化简的目的,通常有下列规律: ①互为相反数的两个数先相加——“相反数结合法”; ②符号相同的两个数先相加——“同号结合法”; ③分母相同的数先相加——“同分母结合法”; ④几个数相加得到整数,先相加——“凑整法”; ⑤整数与整数、小数与小数相加——“同形结合法”。
29.有理数减法法则减去一个数,等于加上这个数的相反数。
用字母表示为:a-b=a+(-b)。
30.有理数加减法统一成加法的意义在有理数加减法混合运算中,根据有理数减法法则,可以将减法转化成加法后,再按照加法法则进行计算。
在和式里,通常把各个加数的括号和它前面的加号省略不写,写成省略加号的和的形式。
如:(-8)+(-7)+(-6)+(+5)=-8-7-6+5.31.有理数加减混合运算中运用结合律时的一些技巧: Ⅰ.把符号相同的加数相结合(同号结合法) (-33)-(-18)+(-15)-(+1)+(+23)原式=-33+(+18)+(-15)+(-1)+(+23) (将减法转换成加法)=-33+18-15-1+23 (省略加号和括号) =(-33-15-1)+(18+23) (把符号相同的加数相结合) =-49+41 (运用加法法则一进行运算) =-8 (运用加法法则二进行运算) Ⅱ.把和为整数的加数相结合 (凑整法) (+6.6)+(-5.2)-(-3.8)+(-2.6)-(+4.8)原式=(+6.6)+(-5.2)+(+3.8)+(-2.6)+(-4.8) (将减法转换成加法)=6.6-5.2+3.8-2.6-4.8 (省略加号和括号)=(6.6-2.6)+(-5.2-4.8)+3.8 (把和为整数的加数相结合) =4-10+3.8 (运用加法法则进行运算) =7.8-10 (把符号相同的加数相结合,并进行运算) =-2.2 (得出结论) Ⅲ.把分母相同或便于通分的加数相结合(同分母结合法)-53-21+43-52+21-87 原式=(-53-52)+(-21+21)+(+43-87)=-1+0-81=-181Ⅳ.既有小数又有分数的运算要统一后再结合(先统一后结合)(+0.125)-(-343)+(-381)-(-1032)-(+1.25) 原式=(+81)+(+343)+(-381)+(+1032)+(-141)=81+343-381+1032-141=(343-141)+(81-381)+1032=221-3+1032=-3+1361=1061Ⅴ.把带分数拆分后再结合(先拆分后结合)-351+10116-12221+4157 原式=(-3+10-12+4)+(-51+157)+(116-221)=-1+154+2211=-1+308+3015 =-307Ⅵ.分组结合2-3-4+5+6-7-8+9…+66-67-68+69原式=(2-3-4+5)+(6-7-8+9)+…+(66-67-68+69)=0 Ⅶ.先拆项后结合(1+3+5+7…+99)-(2+4+6+8…+100) 32.有理数的乘法法则①两数相乘,同号得正,异号得负,并把绝对值相乘;(“同号得正,异号得负”专指“两数相乘”的情况,如果因数超过两个,就必须运用法则三) ②任何数同0相乘,都得0;③几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数;④几个数相乘,如果其中有因数为0,则积等于0.33.乘积是1的两个数互为倒数,其中一个数叫做另一个数的倒数,用式子表示为a ·a1=1(a ≠0),就是说a 和a 1互为倒数,即a 是a 1的倒数,a1是a 的倒数。
