光波导几何分析
合集下载
03光波导几何分析[41页]
![03光波导几何分析[41页]](https://img.taocdn.com/s3/m/3ec8c5ae964bcf84b8d57b3e.png)
图3.3 抛物型折射率波导中的多径光线
折返点 cos =1
n cos n( xm ) n1 cos0
n1 cos0 n1[1 ( xm / a)2 ]
xm a
1 cos0
15
第3章 光波导几何分析 3.2 折射率渐变波导中的光线
讨论 3. 导波条件
图3.3 抛物型折射率波导中的多径光线
折返点
dr / dS 0
利用不变量
dr dS
2
sin2 sin2
sin2 (1 cos2 ) sin2
a2 2
n2r 2
n2
dr
2
n2 (r ) 2 a2 2 / r 2
dS
光线判据函数 g(r) n2(r) 2 a2 2 / r2
光线存在的必要条件： g ≥0
图3.5 偏斜光线投影图
图3.6 偏斜光线立体图
光线始终不与光纤轴相交，存在一个内焦散面与光线相切。
光线传播过程中不变的几何参数
反射角；光线线段长度L；光线与轴线的夹角 ； 光线的旋进距离z；光线的旋转角 ；与轴线的距离l.
导波条件
可以证明 cos n2 / n1
n2
21
第3章 光波导几何分析
3.4 梯度光纤中的光线
3.4.1 柱坐标的光线方程
dr0 dS
d
dS
dr0
d
0
d
dS
d0
dS
d
dS
0
r0
d
dS
r0 分量式:
d
n dr
nr
d
2
dn
dS dS
dS dr
0 分量式:
d dS
nr
光波导理论PPT
模式所携带的能量基本上限制在导波层内，因此被成为束
缚模或导模。
③对于 k0n2 k0n0，图（2）中的d范围，方程 （1.4）解对应于覆盖层中的指数函数、导波层和衬底中的 振荡函数，这些模式称为衬底辐射模。
④对于 0 k0n2 ，图（2）中的（e）范围，方程 （1.4）的解在波导的三层介质中都是振荡函数，这类模式 称为辐射模或包层模。
(k1h)
1 p2
0
（2.11）
解之，可得
tan(k1h)
p0 p2
k1 (1
p0 p2 k12
)
（2.12）
式（2.12）为TE波的相位型色散方程，式（2.11）称为矩
阵形式的TE波的模式本征方程。
对于一般非对称n+2层平板波导，推广上述的结果，便 可得到TE波的矩阵形式的模式本征方程
在分界面上连续，所以最后的场分布如图2（a）所示。
场随着离开波导两界面的距离而无限制增加，这个解在物
理上是不能实现的，因此它并不对应于真实的波。
②对于 k0n0 两点的情况，因为
k0
1 Ey
n21xE2，y 对0，应由于方图程（（2）1.中4）（可b）知，和导（波c）层
中的解是正余弦形式，其余区域为指数形式的。由于这些
1b
1b
前面分析得到导模截止时，b=0,所以可得模式归一化截止 频率
Vcut m arctan a, m 0,1,2, 由上式可知波导进行单模传输的条件为
arctan a V arctan a
（1.26） （1.27）
对于完全对称波导（衬底与覆盖层的折射率相等）， a=0,此时的模式归一化截止频率
k0n0
N n0
②波导的归一化频率
第一章光波导基本理论
思考：光在1、2和1、3表面全反射时分别产生了一 个附加相位，为什么？
tan
12
p
tan
13
q
思考：全反射时相位是否会发生改变？
入射角对反射系数相位的影响
光疏光密
光密光疏
思考：全反射时发生的 相位变化大小怎么求？
只要想到反射折射的大小变化，首先 想到菲涅尔公式
rTE(或 rs)=n n1 1c co oss1 1 n n2 2c co oss2 2 代 入 折 射 定 律 n 1 s in 1 n 2 s in 2
13
q
思考：该方程中各字母的物理意义
是相位 的单位
1、2界面 反射时产 生的相位
K为x方向的 波矢
2 h 2 m 2 1 2 2 1 3
1、3界面 反射时产 生的相位
从射线光学角度重新分析 TE偏振的本征方程
2 h 2 m 2 1 2 2 1 3 ,m 0 , 1 ,2 . . .
估 算 h的 值
h 1 .8 7 6 1 c o s
思考：波导芯层厚 度对解的数量有什 么影响？
思考：波导芯层折
射率n1对解的数量 有什么影响？
思考：解的数量还和什
hk0n1hcos 么因素有关？
还需满足解出的θ大于临界角
sin c
n2 n1
影响平板波导本征解数量的因素
对一个多模波导或光纤，你是否 能辨别出每个模式？
线性独立本征解的线性叠加
从量子力学的角度来看平板波导对光的束缚
Helmholtz equation:
[ 2 x k 0 2 n 22]U (x) 0
几何光波导技术
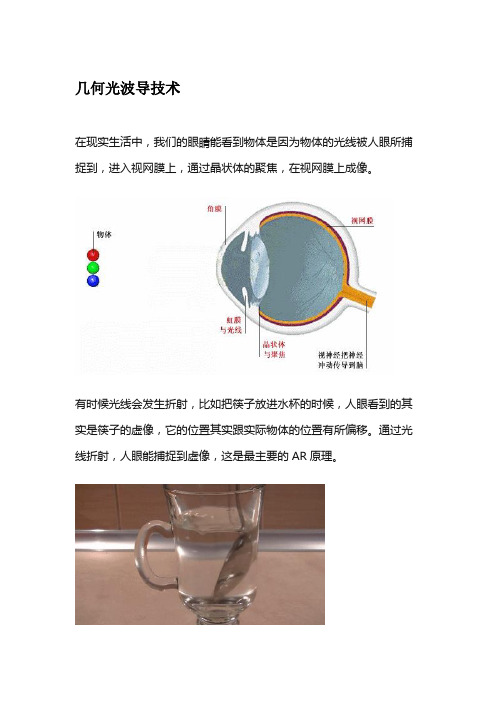
几何光波导技术在现实生活中，我们的眼睛能看到物体是因为物体的光线被人眼所捕捉到，进入视网膜上，通过晶状体的聚焦，在视网膜上成像。
有时候光线会发生折射，比如把筷子放进水杯的时候，人眼看到的其实是筷子的虚像，它的位置其实跟实际物体的位置有所偏移。
通过光线折射，人眼能捕捉到虚像，这是最主要的AR原理。
为何选择光波导当我们在了解Google Glass时，会知道它的光学显示系统主要由投影仪和棱镜组成。
投影仪把图像投射出来，然后棱镜将图像直接反射到人眼视网膜中，与现实图像相叠加。
但是，这一套系统，存在一个视场角vs体积的天然矛盾。
Google Glass有15度的视场角，光学镜片10mm厚度；爱普生的AR眼镜有23度的视场角，13mm厚度：视场角越大，光学镜片就越厚，体积越大。
这些AR眼镜无论采用的是棱镜或者自由曲面的方案，都是通过对基本AR光学系统结构和位置改变，来平衡视场角和体积之间的矛盾。
要解决这一矛盾，同时获得大的视场角和小的体积，光波导方案是不二之选。
那么它将会如何解决呢？光波导的定义是：能够实现视场折叠和复原，并且通过全反射无损传输的光系统。
光波导系统包括耦入、波导、耦出三部分。
具体的流程是，首先，一个大视角的完整图片会被切割成若干块，然后折叠起来形成一个视场细条，这样就可以通过很小的光学镜片耦入，耦出部分再将切割后的图片复原完整。
耦入部分其实做的事情就是视场折叠，耦出部分实现的是视场复原，波导实现光线无损传输。
这样一来，光波导就可以在轻薄的光学镜片实现大的视场角。
几何光波导的工作原理及优缺点“几何光波导”的概念最先由以色列公司Lumus提出并一直致力于优化迭代，至今差不多快二十年了。
•工作原理按上图所示，耦合光进入波导的一般是一个反射面或者棱镜。
在多轮全反射后光到达眼镜前方时，会遇到一个“半透半反”镜面阵列，这就是耦合光出波导的结构了，也就是几何光波导里的“光组合器”。
“半透半反”的意思是一部分光可穿透、另一部分被反射。
平板光波导
k0n f max( k0ns , k0nc )
根据边界条件，在x=a,-a处，有 E y , H z 连续（E y 和它的偏导数）
tan(ha ) q
h
tan(ha ) p
h
h(2a) m arctan(q ) arctan(p )
h
h
这就是TE模的特征方程
13
类似地，再研究TM模
To explain metal’s dispersion regulation, another more precise mode was demonstrate called Drude mode.
Where,
()
p2 2 i
p
Is totally caused by the transition of
令
2 1
k021
2
2 2
2
k02 2
在X=a处利用
1
dH y (x) dx
可以得到
tan( 1a)
1 2 2 1
T
1a m arctan(T )
16
对于奇对称的情况：
Hy(x)
Asin(1a)e 2 (xa) , x a Asin(1x),| x | a Asin(1a)e 2 (xa) , x a
2h 212 210
5
如果相干相长，即满足谐振条件，则此入射角对应的光 线（模式）可以被导波所接受
2h 212 210 2m
物理意义：在波导厚度h确定的情况下，平板波导所能 维持的导模模式数量是有限的，此时m只能取有限个整 数值，这个方程也称作平板波导的本征方程
每一模式对应的锯齿光路和横向光场分布
6
对于特征方程中的 12 10 是上下界面处全反射所引起的相移，那 么具体可根据菲涅尔公式求出。
根据边界条件，在x=a,-a处，有 E y , H z 连续（E y 和它的偏导数）
tan(ha ) q
h
tan(ha ) p
h
h(2a) m arctan(q ) arctan(p )
h
h
这就是TE模的特征方程
13
类似地，再研究TM模
To explain metal’s dispersion regulation, another more precise mode was demonstrate called Drude mode.
Where,
()
p2 2 i
p
Is totally caused by the transition of
令
2 1
k021
2
2 2
2
k02 2
在X=a处利用
1
dH y (x) dx
可以得到
tan( 1a)
1 2 2 1
T
1a m arctan(T )
16
对于奇对称的情况：
Hy(x)
Asin(1a)e 2 (xa) , x a Asin(1x),| x | a Asin(1a)e 2 (xa) , x a
2h 212 210
5
如果相干相长，即满足谐振条件，则此入射角对应的光 线（模式）可以被导波所接受
2h 212 210 2m
物理意义：在波导厚度h确定的情况下，平板波导所能 维持的导模模式数量是有限的，此时m只能取有限个整 数值，这个方程也称作平板波导的本征方程
每一模式对应的锯齿光路和横向光场分布
6
对于特征方程中的 12 10 是上下界面处全反射所引起的相移，那 么具体可根据菲涅尔公式求出。
光波导技术
ei ji z ( x , y ) e i h
一个特征解为一个模式，光纤中总的光场分布则是这些 模式的线性组合：
一系列模式可以看 a e E i i j iz ( x , y ) e 成是一个光波导的 b H 场分布的空间谱。 ih i i
（均匀光波导） 横向非均匀的光波导 （非均匀光波导） 缓变光波导 迅变光波导
突变光波导
模式的概念
不同类型的光波导相应于求解不同类型的微分方程。对 于光纤，还应注意结构的特征：纵向（光纤的轴向，即光传 输的方向）和横向的差别，这是光纤的基本特征。这个基本 特征决定了光纤中纵向和横向场解的不同。对于正规光波导 ，它表现出明显的导光性质，而由正规光波导引出的模式的 概念，则是光波导理论中最基本的概念。
正交性：一个正规光波导的不同模式之间满足正交关系。
光波导技术的广阔应用领域
光波导技术
信息获取
信息传输
信息处理
其它应用
位移、振动 温度、压力 应变、应力 电流、电压 电场、磁场 流量、浓度 可 以 测 量 70 多 个物理化学量
有源无源器件 光纤通信干线 光交换接入网 AON DWDM OADM OTDM FTTC,B,O,H
k 0
2 2
其中 代表 E 和H 在直角坐标系中的各个分量。
在推导的过程中，可以看到：影响光波导传输特 性的，主要是折射率的空间分布。
光波导的进一步分类
可根据折射率的空间分布，将光波导分类为：
正规光波导 （纵向均匀） 光波导 非正规光波导 （纵向非均匀）
横向分层均匀的光波导
n ( x ) cos ( x ) n ( 0 ) cos ( 0 ) 1 z 1 z
导波光学的分析方法有哪些
导波光学的分析方法有哪些
几何光学法和波动光学法是导波光学的两种重要分析方法，大多数光波导部都可以采用这两种方法进行分析.几何光学法较波动光学法简单直观,对结构简单的光波导,其分析结果和波动理论一致;但对复杂问题,几何光学法给出的结果相当粗糙,要得到较为精确的结果还要借助波动光学.教学中，可以先采用几何光学法分析,让学生建立一个初步的物理概念,再用较为严格的波动光学法得到光线入射角取不同值时，平板波导中光线将会出现不同的传输模式.若光线在薄膜层与衬底层的界面,薄膜层与包层的界面上部发生全反射,光会被限制在薄膜层中,形成导模.再通过横向谐振条件得到平板波导特征方程，结合导模截止条件求出传输模式数,截止波长，截止厚度.至此，学生已建立起光波导的概念了.但是,用几何光学法却无法进一步得到波导中各种模式的场分布及功率分布.这些还必须依靠波动光学来解决利用麦克斯韦方程导出波动方程，结合波导的边界条件求解不但可得导模的特征方程，还能求得波导场分布，并且通过对己知的场分布进行积分能得到导模的功率分布.将两种方法的分析结果进行比较，可知对结构简单的平板波导,两种方法所得导模特征方程和截止条件完全相同.通过这种由浅入深的讲解可以化解学生对复杂的波动方程的畏惧感轻松掌握导波光学中的众多概念.。
集成光学第三章 矩形(三维)光波导
x 2
2Ex y 2
nx2k02 n2yk02 n12k02 2
Ex 0
nx2
n32 n12
n52
xa a xa x a
n2y nn1222 n42
yb b y b y b
差别仅存在于4个阴影角区域，而在马卡梯里近似下， 角区是忽略不计的。
马卡梯里近似解法
13
➢ 采用分离变量法，假设 Ex x, y X xY y ，代入上
Hx
1
i0
Ez y
1
i0
y
1
i
Ex x
1
0
2Ex xy
Hy
2Ex
2Ex x 2
Hz
1
i0
E x y
Ez
1
i
E x x
马卡梯里近似解法
11
Hy
1
0
2Ex
2Ex x2
Hz
1
i0
E x y
代入下面的方程
H z y
i
Hy
i Ex
整理后得到
E
x mn
得到
r E 0
➢ 考虑 E y 0 ，得到
x
r
Ex
z
r
Ez
0
➢ 考虑波导折射率沿z方向不变，且 i ，得到
z
x
r Ex
ir Ez
0
即
Ez
1
ir
x
r
E
x
1
i
r
r
x
Ex
1
i
E x x
1
i
E x x
马卡梯里近似解法
10
➢ 电、磁场分量 H x、H y 、Hz 、Ez 与电场分量Ex的关系
2Ex y 2
nx2k02 n2yk02 n12k02 2
Ex 0
nx2
n32 n12
n52
xa a xa x a
n2y nn1222 n42
yb b y b y b
差别仅存在于4个阴影角区域，而在马卡梯里近似下， 角区是忽略不计的。
马卡梯里近似解法
13
➢ 采用分离变量法，假设 Ex x, y X xY y ，代入上
Hx
1
i0
Ez y
1
i0
y
1
i
Ex x
1
0
2Ex xy
Hy
2Ex
2Ex x 2
Hz
1
i0
E x y
Ez
1
i
E x x
马卡梯里近似解法
11
Hy
1
0
2Ex
2Ex x2
Hz
1
i0
E x y
代入下面的方程
H z y
i
Hy
i Ex
整理后得到
E
x mn
得到
r E 0
➢ 考虑 E y 0 ，得到
x
r
Ex
z
r
Ez
0
➢ 考虑波导折射率沿z方向不变，且 i ，得到
z
x
r Ex
ir Ez
0
即
Ez
1
ir
x
r
E
x
1
i
r
r
x
Ex
1
i
E x x
1
i
E x x
马卡梯里近似解法
10
➢ 电、磁场分量 H x、H y 、Hz 、Ez 与电场分量Ex的关系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图3.2 渐变折射率薄膜波导中的光线
n( x) n1[1 ( x / a)2]
n(0) n1 n(a) n2 芯层厚度：2a
相对折射率差
(relative refractive
n12 n22 2n12
n1 n2 n1
n1 n2 n2
介质波导和光纤 中的重要参数。
contrast)
11
• 内容
第1章 电磁场理论 第2章 几何光学 第3章 光波导几何分析 第4章 薄膜波导模式理论 第5章 三维光波导 第6章 光纤模式理论 第7章 电磁场分析的有限元法 第8章 模式耦合理论 第9章 无源光器件 第10章 有源光器件 第11章 光子晶体波导 第12章 光波导的制备
第3章 光波导几何分析
• 在无损耗的情况下，光波能量将无衰减地以封闭于芯层 中的形式传输。
• 导波光线在集成光路中的作用最为重要。
4
第3章 光波导几何分析 3.1 均匀介质薄膜波导
波导光线 辐射光线（折射光线）
衬底辐射：13 12
n3 n1 n2
n3
12 arcsin(n2 / n1 ) 13 arcsin(n3 / n1 )
n3 n1
n2
n1>n2n3
K1
n1 K 0
x
Kx
z
Kz
n2 K0 n1K0
n2 neff n1
满足导模条件的光波都能在波导中稳定传输吗？
NO！
若要形成稳定的传输，还必须满足相干加强条件。。
8
第3章 光波导几何分析 3.2 折射率渐变波导中的光线
阶跃式波导：折射率分层均匀，各自为常数。
讨论
1. 导波光线
➢ 光线不需界面反射而自行往返，蛇行前进。只要振幅适 当，不超出芯区，光线即为导波光线。
➢ 不但可以利用折射率突变介质构成波导，使光线在界面 折返，形成导波光线，也可以利用渐变折射率介质构成 传导光线的波导。
13
第3章 光波导几何分析 3.2 折射率渐变波导中的光线
讨论 2. 振幅
覆盖层
n3 x
z
T 芯层 n1 y 衬底层 n2
x
n2 n1
O
n3
n (x)
T
应用外延、沉积、旋涂等技术制作的波导大都属于这种情况。 波导介质层间有明显的分界面，制作中不可能形成理想的光 学界面，因此界面都有一定的不平整度。光在波导中传输时 在界面上会引起一定的散射损耗。
9
第3章 光波导几何分析
3.2 折射率渐变波导中的光线
K1
n1 K 0
x
Kx
z
Kz
n1K0 cos 也可看作光在n1cos 介质中自由传输时的波数。
neff ( ) / K0
n2 neff n1
与角 相比，分析波导中光传输问题时，使用传播常数来规范
模式更为方便，因为它会涉及到光波的相位、场分布等问题。
7
第3章 光波导几何分析 3.1 均匀介质薄膜波导
限大，光只在x方向受约束，沿z方向传播。
3Leabharlann 第3章 光波导几何分析3.1 均匀介质薄膜波导
波导光线
导波光线（束缚光线） n3
n1
n1>n2n3
12 arcsin(n2 / n1 ) 13 arcsin(n3 / n1 )
arcsin(n2 / n1 )
n2
均匀介质薄膜波导中的导波光线
• 光在芯层的上下界面之间不断地发生全反射，光波被束 缚在芯层内，以锯齿形光路传输。
n1>n2n3
n1
衬底、覆盖层辐射： 13 12 n2
• 光至少在芯层与覆盖层或芯层与衬底间的一个界面上不发
生全反射，有部分光波能量泄漏进覆盖层或衬底中。
5
第3章 光波导几何分析
3.1 均匀介质薄膜波导
导波条件和传播常数
n3
n1>n2n3
sin n2 / n1
n1
n2
K1
n1 K 0
x
d2 x 2 x[1 ( x2 / a2 )]
d z2
a2 cos2 0
忽略二阶小量2项得
d2 x d z2
p2 x
0
2
(p
)
a cos0
12
第3章 光波导几何分析
3.2 折射率渐变波导中的光线
光线轨迹
2
0
x xm sin( pz)
(p
)
a cos0
对于折射率呈抛物型分布的对称波导， 传输光线曲线近似为正弦曲线。
折射率渐变型波导：波导折射率不均匀，通常连续变化。
覆盖层
n3 x
z
0
T 芯层 n(x) y
. 0
. 5
. 0
. 5
. 0
1
0
0
0
1
B
衬底层 n2
5 0
1 0
A 0
1 5 0
B 2
0 0
n( x) n1
n2
n( x)
n1 n2
n3
O
x
O
x
扩散和离子交换波导折射率分布
在如扩散、离子交换、离子注入等制备工艺而形成的波导中，
3.1 均匀介质薄膜波导 3.2 折射率渐变薄膜波导中的光线 3.3 阶跃光纤中的光线 3.4 梯度光纤中的光线
3.5 传播时延与色散特性
2
第3章 光波导几何分析 3.1 均匀介质薄膜波导
波导结构 薄膜波导也称平板介质波导或二维波导
图3.1 薄膜波导结构及其中的传输光线
一般设定n1>n2n3
在y、z方向，波导的折射率均匀，y向宽度可视作无
第3章 光波导几何分析
3.2 折射率渐变波导中的光线
利用光线方程
d n dr n
dS dS
0
z分量式:
d dS
n
dz dS
0
n dz 为常数 dS
n cos n1 cos0
光波传输过程 中，传播常数 是一个不变量。
x分量式:
d
dS
n
dx dS
dn dx
2n1 x
/
a2
d dz d dS dS dz
图3.3 抛物型折射率波导中的多径光线
折返点 cos =1
n cos n( xm ) n1 cos0
n1 cos0 n1[1 ( xm / a)2 ]
xm a
1 cos0
Kx
z
Kz
波矢的x分量 K x n1K0 sin 随光的传输而变化，双值
波矢的z分量 Kz n1K0 cos
传播常数 即Kz 光传播过程中保持不变，重要的不变量。
导波条件 n2 K0 n1K0
6
第3章 光波导几何分析
3.1 均匀介质薄膜波导
有效折射率 n3
n1
n2
n1>n2n3
折射率连续变化。波导内部无明显的分界面，从而有效地降低
了散射损耗，并且和阶跃波导比较，渐变波导的模式色散小。
这种波导具有自聚焦作用，光束的大部分能量集中在介电常
数最大的位置附近，在一定程度上减小了界面的不平整对光束
传输的影响。
10
第3章 光波导几何分析 3.2 折射率渐变波导中的光线
分析对称抛物型折射率分布的波导