由三视图还原原图形教程
完整版三视图还原技巧

核心内容:三视图的长度特征一一“长对齐,宽相等,高平齐”,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。
还原三步骤:(1)先画正方体或长方体,在正方体或长方体地面上截取出俯视图形状;(2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短;(3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。
方法展示(1)将如图所示的三视图还原成几何体还原步骤:①依据俯视图,在长方体地面初绘ABCDE如图;②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D处不可能有垂直拉升的线条,而在E处必有垂直拉升的线条ES由正视图和侧视图中高度,确定点S的位置;如图I③将点S 与点ABCD 分别连接,隐去所有的辅助线条,便可得到还原的几何体SABCD 如图所示:o5/ VDR的(左)觇阁 匸)现图 厂1例题2: —个多面体的三视图如图所示,则该多面体的表面积为()经典题型:例题1:若某几何体的三视图,如图所示,则此几何体的体积等于()cm3 解答:(24)答案:21+ .. 3计算过程:S=2x2X6-y X 1X1 >x6 + y xV2 x72 X^yX2= 21+^3步骤如下:第一步:在正方体底面初绘制ABCDEFMN如图;第二步:依据正视图和左视图中显示的垂直关系,判断出节点 E F、M、N处不可能有垂直拉升的线条,而在点A、B、C、D处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点G,G',B',D',E',F'地位置如图;第三步:由三视图中线条的虚实,将点G与点E、F分别连接,将G'与点E'、F 分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。
特别讲座三视图复原绝技(艺体生专用)

1★高中数学特别讲座 三视图复原绝技基础知识精析1、三视图复原步骤: ⑴作长方体(或正方体);⑵在长方体的底面上画出“俯视图”;⑶再看主视图有没有直角顶点,侧视图有没有直角顶点,它们在“俯视图”的什么位置,如果有直角顶点,那么这个顶点可以向上引垂线,如果没有直角顶点,则不能向上引垂线;说明:确定俯视图直角顶点的位置是三视图复原步骤中最难掌控的一步,幸好我们有方法可以征服这一步,如图,第一个图正视图左边下方是直角,所以俯视图左边一条线上所有的顶点都可能是直角顶点,这个时候再看侧视图,如果侧视图对应的点也是直角顶点,则这个点一定向上引垂线,如果不是,则不能向上引垂线;第二个图正视图的中间有直角顶点,所以俯视图中间一条线上所有的顶点都可能是直角顶点,这个时候再看侧视图,如果侧视图对应的点也是直角顶点,则这个点一定向上引垂线,如果不是,则不能向上引垂线.⑷最后连线.说明:有些空间几体的三视图中俯视图可能是投影图,不过根本不影响这种方法的使用.⑸在把三视图的数据标在图上时,一定要标在长方体上,不要标在内部的图上,切记.正视图正视图2例1(2013·浙江·12)若某几何体的三视图所示,则此几何体的体积= cm 2.例2 [2014·重庆卷] 某几何体的三视图如图12所示,则该几何体的表面积为A .54B .60C .66D .72 ( )图12例3(2014·课标Ⅰ·12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )主视图 左视图43 32俯视图A.66B.6C.24D.431.某几何体的三视图如图所示,则该几何体的体积为( ) (A )2 (B )43(C )4 (D )5 2. 一个空间几何体的三视图如图所示,则这个几何体的体积为 ; 表面积为 .3. 某三棱锥的三视图如图所示,该三棱锥的体积是(A )183 (B )363 (C )123 (D )243 4.正三棱柱的左视图如右图所示,则该正三棱柱的侧面积为( )A .4B .12C .43D .24想 想 一6333333主视图侧视图俯视图正(主)视图 侧(左)视图5 2 1 3 2 111俯视图 11 1 第1题第2题第3题 2左视图 3 第4题45. 某几何体的三视图如图所示,则这个几何体的体积是 .6. 如右图是一几何体的三视图,则该几何体的体积为 .7.某几何体的三视图如图所示,则该几何体的体积是 (A )12 (B )36 (C )24 (D )728.一个空间几何体的三视图如图所示,该几何体的表面积为 .9.由两个四棱锥组合而成的空间几何体的三视图如图所示,其体积是 ;表面积是 .俯视图主视图侧视图侧视图 正视图俯视图 第5题第6题左视图俯视图左视图 俯视图 第7题第8题10.一个体积为16的三棱锥的三视图如图所示,其俯视图是一个等腰直角三角形,则这个三棱锥左视图的面积为.11.某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则()(A)2A,且4A(BA,且4A(C)2A,且A(DAA12.(2007·山东)下列几何体各自的三视图中,有且仅有两个视图相同的是( )A.①② B.①③ C.①④D.②④22俯视图侧视图正视图侧(左)视图①正方②圆锥③三棱④正四56E F D I A H G B C E F D A B C侧视 图1 图2 EA . EB . EC . ED . 13.(2008 广东卷理5文7)将正三棱柱截去三个角(如图1所示A B C ,,分别是GHI △三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )14.(2008山东卷理6文6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )(A)9π (B )10π (C)11π (D) 12π15.(2008海南宁夏卷理12)某几何体的一条棱长 为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为 A. 22 B. 32 C. 4 D. 52n mk。
三视图还原立体图圆柱体法

三视图还原立体图圆柱体法
简介
本文档将介绍三视图还原立体图的绘制方法,主要围绕圆柱体的表达展开。
步骤
以下是三视图还原立体图圆柱体法的步骤:
1.首先,绘制一个长方体作为基本结构,该长方体代表圆柱体的外形。
2.在长方体的顶面和底面上分别绘制两个同心圆,这两个圆代表圆柱体的顶面和底面。
3.在长方体的侧面上绘制两条垂直线段,将侧面分为三部分,中间的部分代表圆柱体的侧面。
4.确定视角,根据需要在正确位置上添加透视效果。
5.根据上述标记,绘制三视图:俯视图、前视图和左视图。
6.使用适当的线条和阴影表达立体效果。
注意事项
在进行三视图还原立体图圆柱体法时,需要注意以下事项:
确保准确测量和绘制圆柱体的尺寸和比例。
使用合适的比例尺来绘制三视图,以确保视图之间的一致性。
注意透视效果的表达,在正确的位置上添加透视线条与细节。
示例
以下是一个使用三视图还原立体图圆柱体法绘制的圆柱体示例:圆柱体示例](image.jpg)
结论
三视图还原立体图圆柱体法是一种简单且常用的绘制方法,通
过准确的测量和透视表达,可以有效展示圆柱体的形状和尺寸。
在
实际应用中,可以根据需要进行调整和添加细节,以满足具体要求。
三视图还原几何体的方法
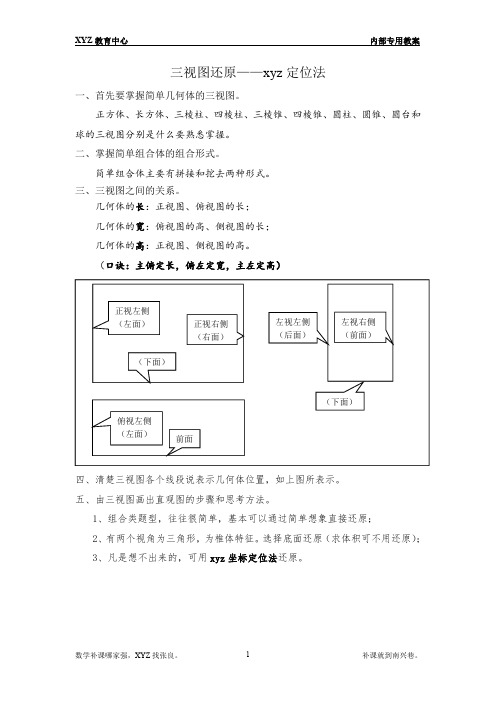
三视图还原——xyz 定位法一、首先要掌握简单几何体的三视图。
正方体、长方体、三棱柱、四棱柱、三棱锥、四棱锥、圆柱、圆锥、圆台和球的三视图分别是什么要熟悉掌握。
二、掌握简单组合体的组合形式。
简单组合体主要有拼接和挖去两种形式。
三、三视图之间的关系。
几何体的长:正视图、俯视图的长;几何体的宽:俯视图的高、侧视图的长;几何体的高:正视图、侧视图的高。
(口诀:主俯定长,俯左定宽,主左定高)(下面)左视左侧(后面)正视左侧(左面)正视右侧(右面)左视右侧(前面)(下面)四、清楚三视图各个线段说表示几何体位置,如上图所表示。
五、由三视图画出直观图的步骤和思考方法。
1、组合类题型,往往很简单,基本可以通过简单想象直接还原;2、有两个视角为三角形,为椎体特征。
选择底面还原(求体积可不用还原);3、凡是想不出来的,可用xyz 坐标定位法还原。
前面俯视左侧(左面)【类型一】:(三线交汇)例2:【类型二】:例3:连接这五个点的四棱锥,不满足俯视图。
而顶点又必须在这五点交点中,所以当点数超过4个,可能不需要全部连接,则这些点有所取舍。
第一法:俯视图看到的面不可以为上面四个点构成的整个四边形,而是中间有一条折痕,故只能说左半边三角形乡下折。
即舍弃前面左上方的点。
故得,第二:唯一法:正视图看,已标记下面的点必不可少;从俯视图看,上面有3个点必不可少;故只能舍弃前面左上方的点。
第三:口诀:实线两端的点保留,虚线两端的点待定。
从俯视图一看,便知道答案了。
取舍关键:墙角点是取舍的备选。
练习【类型三】:(八点齐飞,直观图不唯一)例4此题八点齐飞,通过类型二中的第三取舍法,我们很容易就能还原出来。
答案:然而,我们发现这个三视图也可以看成,是上图中的三棱锥与另外一个三棱锥组合而成。
如下图所示:M为顶点的三棱锥(四种)与上图的组合。
同理,还有其他两种形式,此处就不一一画图了。
由此得出,上题中的三视图至少有5种不同的直观图。
【三视图题目几点技巧】1,部分椎体求体积,直接用公式(可以不还原)2,斜二测画法与原图面积比例为定值(可以不还原)3,三视图中,和视线垂直的线段,长度不变。
三视图复原技巧

当物体某部分被其他部分遮挡时,需要在视图中进行相应的处理,如使用虚线表示被遮挡部分的轮廓。
处理遮挡关系
在复原三视图时,应注意细节部分的处理,如倒角、圆角、螺纹等。这些细节部分对于准确表达物体形状至关重要。
注意细节处理
在三视图中,各视图之间的比例关系应保持以确定长方体的宽度。
根据三个视图的信息,可以绘制出长方体的三维图。
主视图通常显示圆柱体的一个端面,呈现为一个圆。通过主视图可以确定圆的直径。
确定主视图
确定俯视图
确定左视图
绘制三维图
俯视图也显示圆柱体的上面,呈现为一个圆。这个圆应该与主视图的圆大小和位置一致。
左视图显示圆柱体的侧面,呈现为一个矩形。矩形的长度应该等于圆的直径,高度等于圆柱体的高度。
主视图
从物体的正面看去的视图,反映物体的主要形状和特征。
俯视图
从物体的上面看去的视图,反映物体的水平投影和上下位置关系。
左视图
从物体的左侧看去的视图,反映物体的左侧形状和左右位置关系。
02
CHAPTER
三视图复原步骤
仔细分析三视图中的每一个视图,理解其表达的空间形状和位置关系。
注意视图中的图线、符号等细节信息,特别是虚线和实线的含义。
根据三个视图的信息,可以绘制出圆柱体的三维图。
确定主视图
主视图通常显示圆锥体的一个侧面,呈现为一个等腰三角形。通过主视图可以确定圆锥体的高度和底面的直径。
确定俯视图
俯视图显示圆锥体的底面,呈现为一个圆。这个圆应该与主视图中三角形的底边大小和位置一致。
确定左视图
左视图也显示圆锥体的一个侧面,呈现为一个直角三角形。直角三角形的直角边应该等于圆的直径,斜边等于圆锥体的母线长。
x3.2由三视图还原成实物图PPT课件

Thank You
在别人的演说中思考,在自己的故事里成长
Thinking In Other People‘S Speeches,Growing Up In Your Own Story
讲师:XXXXXX XX年XX月XX日
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么?
正视图
侧视图
正视
俯视图
思考3:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考4:如图,桌子上放着一个长方体和 一个圆柱,若把它们看作一个整体,你 能画出它们的三视图吗?
俯视图
正视图 侧视图 俯视图
思考2:下图是简单组合体的三视图,想 象它们表示的组合体的结构特征,并作 适当描述.
正视图
侧视图
俯视图
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
正视
正视图侧视图Fra bibliotek俯视图
3.2由三视图还原成实物图
我们由实物图可以画出它的三视图, 实际生产中,工人要根据三视图加工零 件,需要由三视图还原成实物。这就要 求我们能由三视图想象它的空间实物形 状
思考1:下列两图分别是两个简单组合体 的三视图,想象它们表示的组合体的结 构特征,并画出其示意图.
正视图 侧视图
复习引入
1.柱、锥、台、球是最基本、最简单的 几何体,由这些几何体可以组成各种各 样的组合体,怎样画简单组合体的三视 图就成为研究的课题.
x32由三视图还原成实物图-31页PPT资料

思考1:下列两图分别是两个简单组合体 的三视图,想象它们表示的组合体的结 构特征,并画出其示意图.
正视图 侧视图
俯视图
正视图 侧视图 俯视图
思考2:下图是简单组合体的三视图,想 象它们表示的组合体的结构特征,并作 适当描述.
正视图
侧视图
俯视图
更多精品资请访问
画简单几何体的三视图 思考1:在简单组合体中,从正视、侧视、 俯视等角度观察,有些轮廓线和棱能看 见,有些轮廓线和棱不能看见,在画三 视图时怎么处理?
思考2:如图所示,将一 个长方体截去一部分, 这个几何体的三视图是 什么?
正视图
侧视图
正视
俯视图
思考3:观察下列两个实物体,它们的结 构特征如何?你能画出它们的三视图吗?
更多品资源请访问
正视图 侧视图 俯视图
正视图 侧视图 俯视图
思考4:如图,桌子上放着一个长方体和 一个圆柱,若把它们看作一个整体,你 能画出它们的三视图吗?
Hale Waihona Puke 正视正视图侧视图
俯视图
3.2由三视图还原成实物图
我们由实物图可以画出它的三视图, 实际生产中,工人要根据三视图加工零 件,需要由三视图还原成实物。这就要 求我们能由三视图想象它的空间实物形 状
(经典)高考数学三视图还原方法归纳

高考数学三视图还原方法归纳方法一:还原三步曲核心内容:三视图的长度特征——“长对齐,宽相等,高平齐”,即正视图和左视图一样高,正视图和俯视图一样长,左视图和俯视图一样宽。
还原三步骤:(1)先画正方体或长方体,在正方体或长方体地面上截取出俯视图形状;(2)依据正视图和左视图有无垂直关系和节点,确定并画出刚刚截取出的俯视图中各节点处垂直拉升的线条(剔除其中无需垂直拉升的节点,不能确定的先垂直拉升),由高平齐确定其长短;(3)将垂直拉升线段的端点和正视图、左视图的节点及俯视图各个节点连线,隐去所有的辅助线条便可得到还原的几何体。
方法展示(1)将如图所示的三视图还原成几何体。
还原步骤:①依据俯视图,在长方体地面初绘ABCDE如图;②依据正视图和左视图中显示的垂直关系,判断出在节点A、B、C、D处不可能有垂直拉升的线条,而在E处必有垂直拉升的线条ES,由正视图和侧视图中高度,确定点S的位置;如图③将点S与点ABCD分别连接,隐去所有的辅助线条,便可得到还原的几何体S-ABCD如图所示:经典题型:例题1:若某几何体的三视图,如图所示,则此几何体的体积等于()cm³。
解答:(24)例题2:一个多面体的三视图如图所示,则该多面体的表面积为()答案:21+3计算过程:步骤如下:第一步:在正方体底面初绘制ABCDEFMN 如图;第二步:依据正视图和左视图中显示的垂直关系,判断出节点E 、F 、M 、N 处不可能有垂直拉升的线条,而在点A 、B 、C 、D 处皆有垂直拉升的线条,由正视图和左视图中高度及节点确定点''''',,,,,F E D B G G 地位置如图;第三步:由三视图中线条的虚实,将点G 与点E 、F 分别连接,将'G 与点'E 、'F 分别连接,隐去所有的辅助线便可得到还原的几何体,如图所示。
例题3:如图所示,网格纸上小正方形的边长为4,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度是( )答案:(6)还原图形方法一:若由主视图引发,具体步骤如下:(1)依据主视图,在长方体后侧面初绘ABCM如图:(2)依据俯视图和左视图中显示的垂直关系,判断出在节点A、B、C出不可能有垂直向前拉升的线条,而在M出必有垂直向前拉升的线条MD,由俯视图和侧视图中长度,确定点D的位置如图:(3)将点D与A、B、C分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图所示:解:置于棱长为4个单位的正方体中研究,该几何体为四面体D—ABC,且AB=BC=4,2,可得DA=6.故最长的棱长为6.AC=24,DB=DC=5方法2若由左视图引发,具体步骤如下:(1)依据左视图,在长方体右侧面初绘BCD如图:(2)依据正视图和俯视图中显示的垂直关系,判断出在节点C、D处不可能有垂直向前拉升的线条,而在B处,必有垂直向左拉升的线条BA,由俯视图和左视图的长度,确定点A的位置,如图:(3)将点A与点B、C、D分别连接,隐去所有的辅助线条便可得到还原的几何体D—ABC如图:方法3:由三视图可知,原几何体的长、宽、高均为4,所以我们可以用一个正方体做载体还原:(1)根据正视图,在正方体中画出正视图上的四个顶点的原象所在的线段,用红线表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正视图
侧视图
俯视图
该几何体为四棱锥D1—ABCD
D1
D1
C1
A1
B1
D
C
D
C
A
B
A
B
正视图:等腰直角三角形;
侧视图:等腰直角三角形;
俯视图:正方形(要加对角线BD哟)
要三个这样的几何体才能拼成正方体,分别
四棱锥 D1 ABCD、四棱锥 D1AB1A B1 、 四棱锥 D1BC1B C1
变式训练二:
由三视图还原原图形教程
欣赏三视图
你认识它吗?
图1
图2
问题一:如果要做一个水管的三叉接头,工人事先看到的不是
图1,而是图2,你能替这位工人师傅根据这三个图形制造出水管 接头吗? 若已知一个几何体的三视图,我们如何去想象这个几何体的原形 结构,并画出其示意图呢?
复习回顾:
一、三视图:
1、从正面看到的图形叫做正视图;从左面看到的图形 叫侧视图;从上面看到的图形叫俯视图。这三张图, 称为三视图. 2、形体可见轮廓线画粗实线,不可见轮廓线画虚线
圆柱 正六棱柱
螺丝杆
❖ 如何把组合体的三视图还原成几何体的实形
❖ 1、把每个视图分解为基本图形(三角形,圆 等)
❖ 2、结合对应部分的三视图想象对应的基本几 何体
❖ 3、结合虚实线概括组合体
.
课外思考题
用小方块搭一个几何体,使得它的正视图和俯视图 如图所示,这样的几何体只有一种吗?它至少需要多 少个小立方块?最多需要多少个小立方块?分别画出 它们的几何体的侧视图.
1.一个零件的正视图和俯视图如图,请描述 这个零件的形状,并补画出它的侧视图.
正视图
球的一部分与圆柱的组 合体,侧视图同正视图.
俯视图
2、说出下面的三视图表示的几何体的结构特征
问题二:已知物体三视图的外轮廓,如何
构思该物体?
与同学交流你的看法和具体做法.
❖ 构思过程:
课堂活动
想一想下列三视图对 应的是生活中的哪些 实物
正视图
俯视图
正视图
俯视图
侧视图
正视图
俯视图
侧视图
正视图
俯视图
谢谢观赏
二、三视图的对应规律:
正视图和俯视图 ----长对正 正视图和侧视图 ----高平齐
俯视图和侧视图 ----宽相等
三、 基本几何体的三视图
(1)正方体的三视图都是—正—方—形 (2)圆柱的三视图中有两个是—长—方—形 另一个是—圆— (3)圆锥的三视图中有两个是三—角—形—,另 一(4个)球是的—圆三—和视—一图—个都—点是。—圆—
正视图 侧视图
俯视图
思考2:下列两图分别是两个简单组合体的三视 图,想象它们表示的组合体的结构特征,并 作适当描述.
正视图
侧视 图
俯视图
六棱锥与六棱柱 的组合体
正视图
1:、下图中的三视图表示哪个几何体?
正视图
侧视图
俯视图
A
B
2、如图是一个物体的三视图,试说出物体 的形状。
正 视 图
侧 视 图
俯 视 图
3、一空间几何体的三视图如图所示, 则该几何体是___
2
2
2
2
正视图
22 侧视图
俯视图
例2说出下面的三视图表示的几何体的结
构特征,并画出其示意图.
正视图 俯视图
侧视图
将一个长方体挖去两个 小长方体后剩余的部分
例 3 一个几何体的三视图如图所示,其中正视
图和侧视图是腰长为6的两个全等的等腰直角 三角形.用多少个这样的几何体可以拼成一个棱 长为6的正方体.
请找出下列三视图对应的几何体 第
一
a
b
c
组
A
B
C
第
二 e 俯
左
组
正三棱锥
E
f
俯
左
长方体
F
g 俯
左
正四棱 台
G
一个几何体的三视图如下,你能说出它是什么 立体图形吗?
正视图 俯视图
侧视图
与上一张三视图有何区别与联系?
思考1:下列两图分别是两个简单组合 体的三视图,想象它们表示的组合 体的结构特征,并画出其示意图.
