叶宏工程硕士第5次5.6
工程硕士学位论文工作中期情况报告表

工程硕士学位论文工作中期情况报告表
一、选题背景和研究内容
工程硕士学位论文选题为“基于机器学习的高压油管辅助控制系统研究”,主要研究高压油管辅助控制系统中利用机器学习算法提高控制精度的方法和应用。
二、研究进展
目前为止,本课题已完成文献综述、系统需求分析和系统设计等前期工作,并基于MATLAB/Simulink完成了初步的仿真实验,初步验证了机器学习算法在高压油管辅助控制系统中的应用优势。
三、存在的问题
在实验中发现,机器学习算法的应用对系统性能有着重要的影响,但随着强化学习或深度学习算法模型的复杂性提升,系统复杂度和计算量也将大幅增加。
因此,需要进一步研究在系统控制性能和复杂度之间的平衡问题,并探索更高效的算法设计和实现方案。
四、下一步工作计划
接下来,将针对存在的问题展开深入的研究和探索工作,主要包括以下几个方面:
1.进一步探究机器学习算法的应用优势,从多个角度分析其对高压油管系统性能的影响;
2.研究探索复杂算法模型的高效实现方案,优化系统的计算量和资源占用率;
3.进行进一步的仿真实验,验证模型的效果并对其性能进行评估;
4.总结和归纳研究成果,撰写完整的学位论文并提交答辩。
五、结论
本研究旨在探索机器学习算法在高压油管辅助控制系统中的应用,旨在提高控制精度和实时性。
虽然目前还存在一些挑战,但我们相信通过不断的研究和努力,一定能够取得理想的研究成果。
计算机学院工程硕士论文答辩.

计算机学院工程硕士论文答辩时间安排(2007年5月)论文答辩受理时间:请按上述时间提交授位材料,过时不予受理,责任自负。
附1:工程硕士学位登记表(一)(二)打印要求学位登记表(一)打印出来后请按A3规格正反两面复印。
正面:第1页,学位论文答辩委员会决议,第2页为“学位登记表(一)”;反面:第1页,“导师姓名等”,第2页,“学位论文答辩情况。
学位登记表(二)打印后按A4规格正反两面复印。
附2、计算机学院工程硕士论文答辩须知计算机学院工程硕士论文答辩须知一、硕士学位论文的基本要求1、工程硕士的学位论文应有一定技术难度、深度和先进性;表明作者具有综合运用科学技术理论和方法解决工程实际问题及进行技术攻关的能力。
论文应有解决工程实际问题的新见解、新方法和新进展,或者具有新工艺、新技术、新设计的先进性和实用性,并有良好的经济效益和社会效益。
无论论文是课题研究、技术改造或是工程设计,都应至少有局部深入的理论分析;论文应反映出本课题在企业中的作用,国内外解决这一问题的方法手段,基于企业实际条件为什么选定某种特定方案,或本课题的研究现状和国内外研究进展等,应表述明确。
2、论文字数一般应在3万字左右。
3、学位论文需经联合导师共同审阅批准后方可付印。
4、开题报告后,学位论文应保证有一年的工作量。
5、论文形式可以是工程项目技术报告、产品研制报告、关键技术的研究论文二、必修环节要求必修环节包括开题报告、论文工作中期报告和学术交流与学术报告等三项内容,各占1个学分。
工程硕士生须在学位论文答辩前完成此三项工作,通过考核后获得学分。
(1)开题报告:工程硕士生应在课程学习结束后的一学期内写出书面开题报告,并在我校公开举行开题报告会,由到会专家对所选题目的价值、难度和论文的可行性进行审查,通过审查者获得1学分。
(2)论文工作中期报告:工程硕士生应在开题一年内书面报告论文工作进展情况,按时完成计划通过指导小组检查者获得1学分。
(3)学术交流与学术报告:工程硕士生答辩前应在校内外参加5次以上的学术交流与学术报告会,并在“电子科技大学学术活动登记表”上做好登记,满5次方可获得1学分。
2012012学年第二学期新民校区研究生公共课表

生物
电镜
技术
生物
电镜
技术
生物
电镜
技术
生物
电镜
技术
生物
信息
学A
生物电镜技术
生物
信息
学A
周次
7
8
9
日期
2012.4.16~4.22
2012.4.23~4.29
2012.4.30~5.6
星期
一
二
三
四
五
六
日
一
二
三
四
五
六
日
一
二
三
四
五
六
日
1-4节
生物电镜技术
实验
医
学
遗
传
学
生物电镜技术
实验
医
学
遗
传
学
生物电镜技术
医学
工程
生物
医学
工程
生物
医学
工程
生物
医学
工程
生物
医学
工程
生物
医学
工程
5-8节
医
学
法
学
病
毒
学
医
学
法
学
医
学
法
学
医
学
法
学
医
学
法
学
医
学
法
学
请注意:此课表按《2011-2012年第二学期研究生教学周次表》执行;外语选修课课表另行公布。
基础解剖学系实验室
四肢局部解剖学(2周)
基础解剖学系实验室
胸腹局部解剖学(3周)
基础解剖学系实验室
周次
2011级工程硕士研究生集中授课第三学期课表

电子教材讲稿
Web技术
电子教材讲稿
14:00—17:30
18:30—22:00
5.5
5.6
5.12
5.13
六、日
8:00—11:40
计算机体系结构
14:00—17:30
18:30—22:00
5.26
5.27
6.9
6.10
六、日
8:00—11:40
Web技术
14:00—17:30
18:30—22:00
6.30
7.1
7.7
7.8
日
8:00—11:40
网络工程技术
14:00—17:30
18:30—20:10
课程名称
课时
学分
任课教师
数据库系统设计与开发
32
2
王传栋
计算机网络与通信
32
2
胡素君
计算机体系结构
32
2
洪龙
网络工程技术
32
2
叶晓国
Web技术
32
2
付雄
课程名称
教材
计算机网络与通信
电子教材讲稿
数据库系统设计与开发
电子教材讲稿
计算机体系结构
电子教材讲稿
2011级工程硕士研究生集中授课第三学期课表
计算机技术、软件工程、
日期
星期
时间
课程名称
地点
பைடு நூலகம்3.3
3.4
3.17
3.18
六、日
8:00—11:40
数据库系统设计与开发
本部教学主楼教东103教室
14:00—17:30
18:30—22:00
(工程建筑)级在职工程硕士研究生授课安排表精编

(工程建筑套表)级在职工程硕士研究生授课安排表2014-2015学年第壹学期在职工程硕士研究生教学课程表(此课表从9月20日开始执行)研究生学院2014年7月2014级在职工程硕士研究生教学课程表(工程领域:建筑和土木工程学科方向:建筑学)序号课程类别课程名称考核方式学时分配学分开课单位开课时间开课地点任课教师备注总学时理论学时实践学时第壹次第二次第三次第四次第五次第六次1学位课中国特色社会主义理论和实践研究* 36 36 2.0 思政部9月20日9月21日10月18日10月19日10月26日11月1日11月2日11月15日11月16日11月22日11月23日B2-201 刘春兰2 第壹外国语* 48 32 16 3.0 外语学院11月29日11月30日12月6日12月7日12月14日12月20日12月21日12月27日B2-201 韩松3 信息检索* 16 12 6 1.0 图书馆10月19日10月25日B2-201 曹丽娟4 知识产权法* 16 16 1.0 思政部12月14日12月20日12月21日12月27日B2-201 佟曾5 建筑学专业外语* 32 32 2.0 建筑学院3月7日3月8日3月14日3月15日C5-209 付瑶2015年6 低碳城市和生态建筑* 32 32 2.0 建筑学院3月21日3月22日3月28日3月29日C5-209 石铁矛2015年7 沈阳城和沈阳建筑* 32 32 2.0 建筑学院4月11日4月12日4月18日4月19日C5-209 吕海平2015年8 城市设计理论* 32 32 2.0 建筑学院4月25日4月26日5月9日5月10日C5-209 袁敬诚2015年9 现代建筑理论* 32 32 2.0 建筑学院5月16日5月17日5月23日5月24日C5-209 吕健梅2015年10 建筑设计1 * 32 16 16 2.0 建筑学院9月27日9月28日C5-209 李勇11 建筑设计2 * 32 32 2.0 建筑学院导师自上小计21.0“*”表示考试,“#”表示考查。
东南大学接收2013年在职人员攻读硕士学位调剂考生名单_东南大学考研
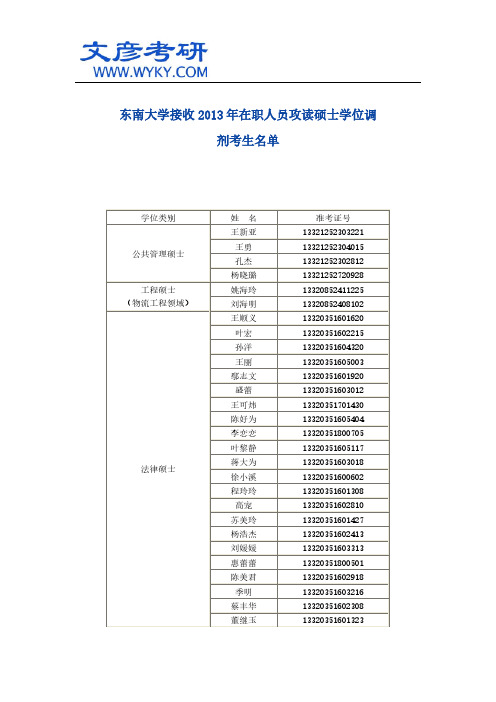
东南大学接收2013年在职人员攻读硕士学位调剂考生名单学位类别姓名准考证号公共管理硕士王新亚13321252303221王勇13321252304015孔杰13321252302812杨晓璐13321252720928工程硕士(物流工程领域)姚海玲13320852411225刘海明13320852408102法律硕士王顺义13320351601620叶宏13320351602215孙洋13320351604320王丽13320351605003鄢志文13320351601920盛蕾13320351603012王可炜13320351701430陈好为13320351605404李恋恋13320351800705叶黎静13320351605117蒋大为13320351603018徐小溪13320351600602程玲玲13320351601308高宠13320351602810苏美玲13320351601427杨浩杰13320351602413刘媛媛13320351603313惠蕾蕾13320351800501陈美君13320351602918季明13320351603216蔡丰华13320351602308董继玉13320351601323刘宏轩13320351601701田熏菁13320351604912龙华兰13320351701313韦晨虎13320351603218袁慧婷13320351601905唐文宣13320351602711赵彪13320351601016张宝兵13320351604026刘勇13320351800321张扬13320351701520丁云13320351602518李小雨13320351603519周备文13320351800109华纯13320351601323史明月13320351605009聂磊13320351602510徐娇13320351603417刘烨13320351604320陈超13320351604616丁晴晴13320351600217王丽13320351604823艺术硕士丁娟13321351109706文章来源:东南大学考研网(),更多东南大学考研相关信息和资料请关注文彦考研论坛。
18级非全日制双证工程硕士专业课课表--19年春季 (1)

32 赵晓群 408 康劲松 408
6月22日 6月29日
下午1:00--2:30 下午1:00--2:30
7 4089008 工程伦理讲座 0.5
59 赵晓群 408
7 4089008 工程伦理讲座 0.5
全体
59 万国春 408 7月6日
5月11日
晚上5:30--7:00
地点:档案馆楼
8
集中开题
晚上5:30--8:30
4 4080136 数字系统设计
2
34 万国春 408
5 4080122
现代电力系统 分析
2
36
电气工程、控制工 程
27 金立军 403
信息论基础及 6 4080132 应用
2
电子与通信工程、 36 集成电路工程、计 算机技术 全体
18/5、25/5、1/6、15/6:晚上5:30--8:30 22/6、29/6: 上午9:00--12:00 6/7: 上午9:00--12:00 、下午13:00-《信息 16:00
出版社:同济大学出版社, 2015.10 书 号 : ISBN 978-75608-5948-4 《电力系统分析》 上册 第三 版作者: 何仰赞 温增银出 版社: 华中科技大学出版社, 7-5609-2597-4 《 电 力 系 统 分 析》下册 第三版 作者:何仰赞 温增银出版社: 华中科技大学 出版社, 7-5609-2665-0 可以网购价在老师处买 论基础及应用教材》 作者:赵 晓群著 机械工业出版社, 2015 年8月 ISBN:9787111511267
电子与信息工程学院2018级工程硕士专业课课程表
(2018~2019学年第二学期 2019年春
序号 课号 名称 学分 学时 授课对象 人数 任课老师地点
高校课题申报:专业学位研究生培养模式改革研究

专业学位研究生培养模式改革研究学科分类:高等教育课题类别:重点课题关键词:专业学位,培养模式,改革预期研究成果:研究报告课题设计论证(一)问题的提出教育部、国家发展改革委、财政部于2013年3月联合颁布的《关于深化研究生教育改革的意见》明确要求,将培养模式改革作为综合改革的重中之重。
当前,专业学位研究生教育存在的突出问题为:一是现有研究生教育资源不足,亟需通过培养模式改革汇聚校内外教育资源;二是学术型研究生和专业学位研究生培养同质化,亟需通过专业学位培养模式改革,创新以培养实践能力为核心的专业学位研究生培养模式;三是专业学位研究生培养亟待建立行之有效的模式,需通过专业学位培养模式改革实践,探索可复制推广的专业学位研究生培养模式。
(二)课题界定专业学位研究生是具有从事某种专门职业技能,并掌握扎实的专业理论知识的人才。
关于人才培养模式概念的表述甚多:一是“教育运行方式”说,认为“人才培养模式是指在一定的教育思想和教育理论指导下为实现培养目标而采取的培养过程中的某种标准构造样式和运行方式”;二是“目标实现方式”说,认为“人才培养模式是学校为学生构建的知识、能力、素质结构,以及实现这种结构的方式,它从根本上规定了人才特征并集中地体现了教育思想和教育观念”;三是“人才培养系统”说,认为人才培养模式是一个系统,包括创新人才的培养模式和成长环境:创新人才培养模式是创新人才培养的核心,是在一定的教学组织管理下实施的,包括培养目标、专业结构、课程体系、教学制度、教学模式和日常教学管理;创新人才成长环境包括师资队伍、教学硬件和校园文化。
高素质的创新人才培养是从教师到学生、从观念到制度、从软件到硬件进行全方位、多角度的综合建设。
本课题针对专业学位研究生培养模式改革选取“人才培养系统”理论进行研究。
(三)国内外研究现状述评1.国外相关研究国外学者主要通过实证研究的方法对专业学位研究生培养模式进行研究。
一是多元模式研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
− (α + β ) z
(2) 并联的情况
X
L1
Y
L2
因为当且仅当都损坏时, 才停止工作, 因为当且仅当都损坏时,系统 L 才停止工作, 都损坏时 所以L的寿命 的寿命Z为 所以 的寿命 为 Z = max{X,Y}
Z的分布函数 的分布函数
FZ ( z ) = FX ( z ) FY ( z ) (1 − e −αz )(1 − e − βz ), z > 0, = 0, z ≤ 0.
解 (1) 串联的情况
X
L1
Y
L2
因为有一个损坏时,系统 L就停止工作, 就停止工作, 因为有一个损坏时, 有一个损坏时 就停止工作 所以 L的寿命为 Z = min{X ,Y }, 的寿命为
X , Y都服从指数分布,分布函数为
1 − e −αx , x > 0; 1 − e − βy , y > 0; FX ( x) = , FY ( y ) = 0, x ≤ 0, 0, y ≤ 0,
原公式
P131 例 设二维 r.v. (X ,Y ) 的 d.f. 为
8xy, 0 < x <1,0 < y < x, f (x, y) = 其它 0,
求E(X), E(Y), V(X), V(Y). 解 E( X ) = ∫ ∫ xf (x, y)dxdy −∞ −∞ 1 x 4 = ∫ dx∫ x ⋅ 8xydy = 0 0 5
应用概率统计
主讲教师 叶宏 山东大学数学院
5.6 二维随机变量函数的分布
3. 布 设连续型随机变量X , Y 相互独立, 问题 X , Y的分布函数分别为 F (x), F (y), X Y M = max{X ,Y }, N = min{X ,Y }, 求 M ,N 的分布函数.
设随机变量 X 的密度函数为
1 −|x| f (x) = e , − ∞ < x < +∞ 2
(1) E( X ), V( X )
(2) 求cov( X ,| X |), 问X 与| X |相关与否. (3) 问X 与| X | 是否独立?为什么? 解 (1)
1 −|x| E( X ) = ∫ x e dx = 0 −∞ 2
1 x
V (Y) = E(Y ) − E (Y)
2 2
P126.1 1 设 X , Y 是两个相互独立且服从正态分布 N (0 , ) 2 的随机变量,则 E X − Y = ____ , D X − Y = ____
法2 法1
Z =| X −Y |, E(Z) = ∫
+∞ +∞
−∞ −∞
∫
g(x, y) f (x, y)dxdy ?
+∞ +∞
E(Y) = ∫−∞ ∫−∞ yf (x, y)dxdy
+∞ +∞
V( X ) = E( X ) − E ( X )
2 2
E( X ) = ∫
2
+∞ −∞
∫
+∞ −∞
x f (x, y)dxdy
2
2
2 = ∫ dx∫ x ⋅ 8xydy= 8xydy 0 0 3 2 2 2 V( X ) = E( X ) − E ( X ) = 75
N=min(X1,…,Xn)的分布函数是 的分布函数是
FN (z) = 1− [1− FX1 (z)] … [1− FXn (z)]
特别,当X1,…,Xn相互独立且具有相 特别, 同分布函数F(x)时,有 同分布函数 时 FM(z)=[F(z)] n FN(z)=1-[1-F(z)] n
注意 是连续型随机变量, 若X1,…,Xn是连续型随机变量,在求得 M=max(X1,…,Xn)和N=min(X1,…,Xn)的分布 和 的分布 函数后,不难求得M和 的密度函数 的密度函数. 函数后,不难求得 和N的密度函数
Cov(X,Y)=E(XY) -E(X)E(Y)
cov( X,Y) ρXY = V ( X ) V(Y) D (5 X − 3Y ) = V (5 X ) + V (3Y ) − 2 cov(5 X ,3Y ) = 25V ( X ) + 9V (Y ) − 30 cov( X , Y )
P132
T = X −Y ∼ N(0,1), Z =| T |,
E(Z) = ∫ g(t) f (t)dt = ∫ | t | f (t)dt =
−∞ −∞ +∞ +∞
2
π
D(Z) = E(Z ) −[E(Z)] = E(T ) −
2 2 2
2
π
=1− .
2
π
5.8 协方差和相关系数
前面我们介绍了随机变量的数学期望 和方差,对于多维随机变量, 和方差,对于多维随机变量,反映分量之 间关系的数字特征中,最重要的, 间关系的数字特征中,最重要的,就是现 在要讨论的 协方差和相关系数
2 2 2 2
而 D(U) = a2D( X ) + b2D(Y) = (a2 + b2 )σ 2
D(V ) = a D( X ) + b D(Y) = (a + b )σ
2 2 2 2
2
故
ρUV
a −b = 2 2 a +b
2 2
思考:还有其他方法吗? 利用协方差的性质
cov(aX + bY, aX −bY) = a cov( X , X ) −b cov(Y,Y)
若 ( X ,Y ) ~ N ( µ1, σ12, µ2, σ22, ρ), 则X ,Y 相互独立 X ,Y 不相关
2. 协方差和相关系数的性质
(1)
cov( X ,Y) = cov(Y, X )
(2) cov(aX , bY ) = ab cov( X ,Y ) (3) cov( X +Y, Z) = cov( X , Z) + cov(Y, Z)
1 −|x | V ( X ) = E( X ) = ∫ x e dx = 2 −∞ 2
2 2 +∞
+∞
1 −|x| (2) E( X | X |) = ∫ x | x | e dx = 0 −∞ 2
cov( X ,| X |) = E( X | X |) − E( X )E(| X |) = 0
=1−[1− FX (z)][1− F (z)]. Y
推广
个相互独立的随机变量, 设X1 ,…, Xn是n个相互独立的随机变量 个相互独立的随机变量 它们的分布函数分别为
FXi (x)
(i =0,1,…, n) ,
M=max(X1,…,Xn)的分布函数为 的分布函数为: 的分布函数为
FM (z) = FX1 (z) … FXn (z)
FM (z) = P(m X,Y} ≤ z) ax{
= P( X ≤ z,Y ≤ z) = P( X ≤ z)P(Y ≤ z)
= FX (z)FY (z)
FN (z) = P(m X ,Y} ≤ z) in{
=1− P(m X ,Y} > z) in{
=1− P( X > z,Y > z)
=1− P( X > z)P(Y > z)
1. 协方差和相关系数的概念
定义
E([X − E(X )][Y − E(Y)])
称为 X ,Y 的协方差. 记为
cov( X,Y) = E([X − E(X )][Y − E(Y)])
若D (X ) > 0, D (Y ) > 0 ,称
cov( X,Y) D( X ) D(Y)
为X ,Y 的 相关系数,记为
教材P122.7
7. 设系统 L 是由 2个相互独立的子系统L1,L2 连接而成,并且 L1,L2 的寿命分别为 X , Y , 它们的密度分别为 α e −αx x > 0 β e − βy y > 0 f X (x ) = , fY ( y ) = x≤0 y≤0 0 0 求 L 在串联和并联方式下寿命 Z 的密度函数.
ρXY =
cov( X,Y) D( X ) D(Y)
若 ρXY = 0, 称 X ,Y 不相关.
计算协方差的一个简单公式 由协方差的定义及期望的性质, 由协方差的定义及期望的性质,可得 Cov(X,Y)=E{[ X-E(X)][Y-E(Y) ]} =E(XY)-E(X)E(Y)-E(Y)E(X)+E(X)E(Y) =E(XY)-E(X)E(Y) 即 Cov(X,Y)=E(XY) -E(X)E(Y)
X ,Y 相互独立
因为 ρXY
X , Y 不相关
X , Y 不相关
=0
cov( X ,Y) = 0
若 ( X , Y ) 服从二维正态分布, X , Y 相互独立 X , Y 不相关
P131
8xy, 0 < x <1,0 < y < x, f (x, y) = 其它 0,
+∞ +∞
求cov(X,Y), V(5X- 3Y). 解 E( XY) = ∫ ∫ xyf (x, y)dxdy −∞ −∞
故Z 的分布函数
FZ ( z ) = 1 − (1 − FX ( z ))(1 − FY ( z )) 1 − e = 0,
− (α + β ) z
, z > 0, z ≤ 0,
, z > 0; z ≤ 0.
于是,得Z的密度函数 于是, 的密度函数
(α + β )e f Z ( z) = 0,
绝对收敛, 则
E(Z) = ∫−∞ ∫−∞ g(x, y) f (x, y)dxdy
