理论力学习题集1
理论力学题库(含答案)---1

理论力学---11-1.两个力,它们的大小相等、方向相反和作用线沿同一直线。
这是(A)它们作用在物体系统上,使之处于平衡的必要和充分条件;(B)它们作用在刚体系统上,使之处于平衡的必要和充分条件;(C)它们作用在刚体上,使之处于平衡的必要条件,但不是充分条件;(D)它们作用在变形体上,使之处于平衡的必要条件,但不是充分条件;1-2. 作用在同一刚体上的两个力F1和F2,若F1 = - F2,则表明这两个力(A)必处于平衡;(B)大小相等,方向相同;(C)大小相等,方向相反,但不一定平衡;(D)必不平衡。
1-3. 若要在已知力系上加上或减去一组平衡力系,而不改变原力系的作用效果,则它们所作用的对象必需是(A)同一个刚体系统;(B)同一个变形体;(C)同一个刚体,原力系为任何力系;(D)同一个刚体,且原力系是一个平衡力系。
1-4. 力的平行四边形公理中的两个分力和它们的合力的作用范围(A)必须在同一个物体的同一点上;(B)可以在同一物体的不同点上;(C)可以在物体系统的不同物体上;(D)可以在两个刚体的不同点上。
1-5. 若要将作用力沿其作用线移动到其它点而不改变它的作用,则其移动范围(A)必须在同一刚体内;(B)可以在不同刚体上;(C)可以在同一刚体系统上;(D)可以在同一个变形体内。
1-6. 作用与反作用公理的适用范围是(A)只适用于刚体的内部;(B)只适用于平衡刚体的内部;(C)对任何宏观物体和物体系统都适用;(D)只适用于刚体和刚体系统。
1-7. 作用在刚体的同平面上的三个互不平行的力,它们的作用线汇交于一点,这是刚体平衡的(A)必要条件,但不是充分条件;(B)充分条件,但不是必要条件;(C)必要条件和充分条件;(D)非必要条件,也不是充分条件。
1-8. 刚化公理适用于(A)任何受力情况下的变形体;(B)只适用于处于平衡状态下的变形体;(C)任何受力情况下的物体系统;(D) 处于平衡状态下的物体和物体系统都适用。
理论力学习题册答案
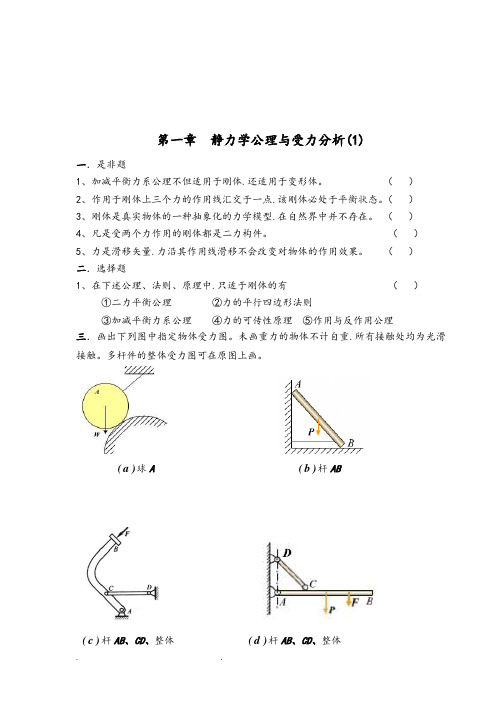
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中.只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N.放在水平梁AC的中央.如图所示。
理论力学习题集
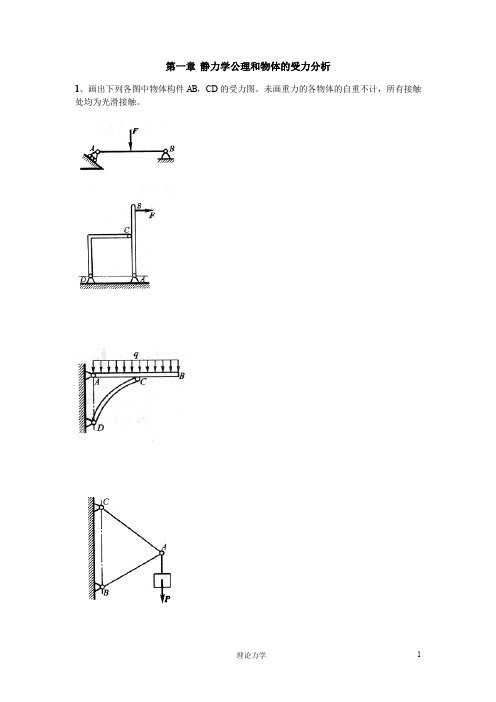
第一章静力学公理和物体的受力分析1、画出下列各图中物体构件AB,CD的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
2、画出下列每个标注字符的物体的受力图与系统整体受力图。
题图中未画重力的各物体的自重不计,所有接触处均为光滑接触。
第二章 平面汇交力系与平面力偶系1、物体重P =20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起。
设滑轮的大小、AB 与CB 杆自重及摩擦略去不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB 和支杆CB 所受的力。
2、铰链四杆机构CABD 的CD 边固定,在铰链A 、B 处有力1F 、2F 作用,如图所示。
该机构在图示位置平衡,杆重略去不计。
求力F 1与F 2的关系。
3、在图示结构中,各构件的自重略去不计。
在构件AB上作用一力偶矩为M的力偶,求支座A和C的约束反力。
4、在图示机构中,曲柄OA上作用一力偶,其矩为M;另在滑块D上作用水平力F。
机构尺寸如图所示,各杆重量不计。
求当机构平衡时,力F与力偶矩M的关系。
第三章 平面任意力系1、已知N 1501=F ,N 2002=F ,N 3003=F ,N 200'==F F 。
求力系向点O 的简化结果,并求力系合力的大小及其与原点O 的距离d 。
2、一水平简支梁结构,约束和载荷如图所示,求支座A 和B 的约束反力。
3、水平梁AB 由铰链A 和杆BC 支持,如图所示。
在梁的D 处用销子安装半径为r =0.1m 的滑轮。
有一跨过滑轮的绳子,其一端水平地系在墙上,另一端悬挂有重为P =1800N 的重物。
如AD =0.2m ,BD =0.4m ,ϕ=45°,且不计梁、滑轮和绳子的自重。
求固定铰支座A 和杆BC 的约束力。
4、由AC 和CD 构成的组合梁通过铰链C 连接。
它的支承和受力如图所示。
已知均布载荷强度kN/m 10=q ,力偶矩m kN 40⋅=M ,不计梁重。
(完整版)理论力学习题集册答案解析
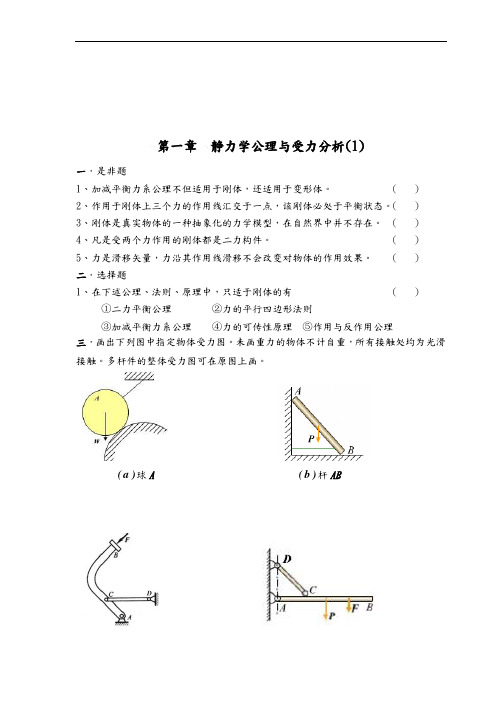
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆AB)a(球A )d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体 )b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
力学练习题——精选推荐

《理论力学》练习题一一.填空题1. 限制质点运动的物体(如曲线、曲面等 )称为( )。
2.惯性力( )对应的反作用力,( )牛顿第三定律。
3. 如果力只是位置的函数,并且它的旋度等于零,即满足0F F F z y x )(zyx=∂∂∂∂∂∂=⨯∇k j i r F 则这种力叫做( )。
4.真实力与参考系的选取( ),而惯性力却与参与系的选取( )。
5.质点系的动能等于质心的动能与各质点相对( )的动能之和。
6.同一质点系中各质点之间的相互作用力称为( )二.选择题1. e a r r θθθθ)2( +=称为质点的( )。
a. 法向加速度 b. 切向加速度c. 横向加速度d. 径向加速度 2.][)(r F m en '⨯⨯-=ωω称为a.平动惯性力b.离心惯性力c.科氏惯性力 3. ττdtdva =称为质点的( )。
a. 法向加速度 b. 横向加速度c. 切向加速度d. 径加速度4. 质点系中所有内力对任一力矩的矢量和a. 等于零b. 不等于零c. 不一定等于零5. e a rr r r )(2θ -=称为质点的( )。
a.径向加速度 b.横向加速度c.切向加速度d.法向加速度 6.质点系内力所作的功a. 等于零b. 不等于零c. 不一定等于零7. n a v n ρ2=称为质点的( )。
a. 横向加速度 b. 法向加速度c. 径向加速度d. 切向加速度8.如果作用在质点上的力都是保守力,或虽是非保守力作用但非保守力不作功或所作功之和等于零。
则质点系机械能a. 守恒b. 不守恒c. 不一定守恒三.简答题1.在曲线坐标系中,单位矢量和基矢有无区别?若有,区别何在? 2.瞬时速度中心;瞬时速度中心可以有加速度吗?3.写出质点系的动能定理,说明内力作功之和不为零的原因。
4.写出柯尼格定理的表达式并说明式中各项的意义。
5.科氏力。
四.计算题1.两根等长的细杆AC 和BC 在C 点用铰链连接,放在光滑的水平面上,如图所示。
理论力学试题及答案1精选全文完整版

可编辑修改精选全文完整版理论力学题库简答题1-1.简述伽利略相对性原理和牛顿运动定律成立的参考系。
答:(1)内容:不能借助任何力学实验来判断参考系是静止的还是在匀速直线运动;(2)相对与惯性系作匀速直线运动的参考系都是惯性参考系;(3)牛顿运动定理只能在惯性系成立。
1-2. 简述有心力的性质. 并证明质点在有心力作用下只能在一个平面内运动.证明:只要证明角动量是一个常矢量即可.性质:(1)力的作用线始终通过一定点;(角动量是一个常矢量或质点始终在垂直于角动量的平面内运动)(2) 角动量守恒,或掠面速度守恒;(3) 有心力是保守力, 或机械能守恒.1-3.什么情况下质心与几何中心、重心重合?质心系有何特性?(1) 密度均匀物体质心与几何中心重合;(2) 重力加速度为常量时物体质心与重心重合;质心系的特性:(1) 质心系中各质点相对于质心的总动量为零;(2) 质心系的惯性力矩为零;(3) 质心系的惯性力做功为零。
1-4.太阳和地球组成的两体系统中,分别以地球、太阳、质心为参照系,简述地球、太阳的运动情况。
答: (1)质心参照系中地球、太阳的运动:地球,太阳相对于质心作椭圆运动。
(2)地球参照系中太阳运动:太阳相对于地球作椭圆运动。
(3)太阳参照系中地球的运动:地球相对于太阳作椭圆运动。
2-1.分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立的条件。
2-2.说明 质点组 对某定点,如原点O ,的动量矩守恒定律成立的条件(要求写出分量式)。
质点组对原点O 的动量矩守恒定律成立的条件为:0)(1=⨯=∑=e i n i i F r M ,分量守恒。
即: 对x 轴:0)()(1=-∑=e iy i e iz n i i F z F y ;对y 轴:0)()(1=-∑=e iz i e ixn i i F x F z ; 对z 轴:0)()(1=-∑=e ixi e iy n i i F y F x 。
机械工业出版社理论力学习题解答1 (练习册P1-P6)

D
FO1 O1FO2
O2
O3 [ 整体 ] FO3
P3 习题:3(c)
FE
[ AB ] A
E
FAx FAy
E FE
[ OE ] O
B FBy FBx 铰链约束 D
FBx B F1 [ 铰 B ]
FBy
FB
FB
F2
B
C
O 二力杆 FO1
FO2 A
FAx FAy
[ 整体 ]
E
O FOx FOy
[ OD ] F1
FAx
FAy
B 三平力行汇力交系?
FBx 铰链约束
FBy
C
FC
FD
连杆约束
[ AB ]
[ BD ]
A FAx FAy
P1
B
P2
D
C
FC
FD
[ 整体 ]
P3 习题:3(b) [ AB ]
P
A
B 铰链约束
FA A
FA
C FCx
FCxFCy
FCy
C
[ AO1 ]
O1 FO1
FO2x
D FD O2 [ CO2 ] FO2y
静力学 1
习题解答 练习册
P1 习题:1 矢量与代数量 方法
二次投影法
sinj = 3/ 5 sinq = 4/ 5 Fx = Fcosj sinq = 64 N
cosj = 4/ 5 cosq = 3/ 5 Fy = Fcosj cosq = 48 N
Fz
jD
Fz = Fsinj = 60 N
l2
, , ,.
b
Fy F
2
2
,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章点的运动学
1-7 如图所示。
杆AB长为l,以等角速度ω绕点B转动,其转动方程为φ=ωt。
而与杆铰接的滑块B 按规律s=a+b sinωt沿水平线作谐振动。
其中a和b均为常数。
求点A轨迹。
1-8 如图所示,曲柄OB以匀角速度ω=2rad/s绕O轴顺时针转动,并带动杆AD上点A在水平槽内运动。
已知AB=OB=BC=CD=12 cm,求点D的运动方程和轨迹,以及当φ=45o时点D的速度和加速度。
1-9 如图所示。
摇杆机构的滑杆AB以等速u向上运动,试建立摇杆OC上C点的运动方程,并求
点在
π
4
ϕ=时的速度。
假定初瞬时0
ϕ=,摇杆长OC=a,距离OD=l。
1-12 如图所示,在曲柄摇杆机构中,曲柄
1
10cm
O A r
==,摇杆
2
24cm
O B l==,
12
10cm
O O=,若曲柄以
π
4
t
ϕ=rad绕O1轴转动,当t=0时0
ϕ=,求点B的运动方程、速度和加速度。
题1-7图
题1-9图
u
题题1-11图题1-12图
θ
2
10(m/s)10(m/s )
t v x t a v ====()()220rad s 20rad s t v R t a R ωα====222222
4210(m/s )
20(m/s )
1014(m/s )
t n t n a v a v R t a a a t =====+=+()()()
()()1112122112121112
22222222
21110
rad/s 30330104rad/s 7533
10
0.3m/s 3030
1640.75m/s 93
100100.3m/s 93AB BC CD DA AB CD BC DA n r i r r r n v v v v r a a a r a r πωπωωωωπππωππωππωππ======⋅======⋅=⋅====⋅=⋅==⋅=⋅=第二章 刚体的简单运动 2-2 试画出图中刚体上的M 点的轨迹以及在图示位置时的速度和加速度。
2-6 升降机装置由半径为R =50cm 的鼓轮带动,如图所示。
被升降物体的运动方程为x =5t 2(t 以s 计,x 以m 计)。
求鼓轮的角速度和角加速度,并求在任意瞬时,鼓轮轮缘上一点的全加速度的大小。
解: 轮缘上一点的速度与切向加速度为 从而,鼓轮的角速度与角加加速度为
鼓轮轮缘上一点的加速度 2-8 电动铰车由皮带轮Ⅰ和Ⅱ以及鼓轮Ⅲ组成,鼓轮Ⅲ和皮带轮Ⅱ刚性地固定在同一轴上。
各轮的
半径分别为r 1=30cm,r 2=75cm,r 3=40cm 。
轮Ⅰ的转速为n 1=100r/min 。
设皮带轮与皮带之间无滑动,求
重物Q 上升的速度和皮带各段上点的加速度。
解:
2-10 车床的走刀架机构如图所示。
已知各齿轮的齿数为z 1=40,z 2=84,z 3=28,z 4=80,主轴转速
n 1=120r/min ,丝杠螺距t =12mm 试求走刀速度v 2。
a 题2-6图题2-7图a
题2-8图W ⅡⅠ
Ⅲ题2-10图题
1M A v v O A ω==⋅2
1n n M A a a O A ω==⋅1t t
M A a a O A α==⋅
第三章 点的复合运动
3-6 图示两种机构中,已知1220cm O O a ==,1=3rad/s ω。
试求图示位置O 2A 的角速度。
3-9 杆OA 长为l ,由推杆BC 推动而在图平面内绕O 轴转动,如图所示。
试求杆端A 的速度大小(表示为由推杆至O 点距离的函数)。
假定推杆的速度为u ,其弯头长为a 。
3-10 如图所示。
摇杆机构的滑杆AB 以等速u 向上运动,初瞬时摇杆OC 处水平位置。
摇杆长OC=a ,距离OD=L 。
求当π
4
ϕ=
时C 点的速度大小。
3-11 图示曲柄滑道机构中,杆BC 水平,而杆DE 保持铅直。
曲柄长10cm OA r ==,并以角速度
=20rad/s ω绕O 轴匀速转动,通过滑块A 带动BC 杆作往复运动。
试求当曲柄与水平线交角30
ϕ=时,杆BC 的速度和加速度。
第 3 页共 21 页。
