2010~2018江苏高考解析几何汇编(文)
2018各地高考数学文科分类汇编_解析几何

(全国1卷4)答案:(全国1卷15)答案:(全国1卷20)答案:(全国2卷6)双曲线22221(0,0)x y a b a b-=>>A .y =B .y =C .y =D .y x = 答案:A(全国2卷11)已知1F ,2F 是椭圆C 的两个焦点,P 是C 上的一点,若12PF PF ⊥,且2160PF F ∠=︒,则C 的离心率为A .1B .2CD 1-答案:D(全国2卷20)设抛物线24C y x =:的焦点为F ,过F 且斜率为(0)k k >的直线l 与C 交于A ,B 两点,||8AB =.(1)求l 的方程;(2)求过点A ,B 且与C 的准线相切的圆的方程.答案:(1)由题意得F (1,0),l 的方程为y =k (x –1)(k >0).设A (x 1,y 1),B (x 2,y 2).由2(1)4y k x y x=-⎧⎨=⎩得2222(24)0k x k x k -++=. 216160k ∆=+=,故212224k x x k ++=. 所以212244(1)(1)k AB AF BF x x k +=+=+++=.由题设知22448k k+=,解得k =–1(舍去),k =1. 因此l 的方程为y =x –1.(2)由(1)得AB 的中点坐标为(3,2),所以AB 的垂直平分线方程为2(3)y x -=--,即5y x =-+.设所求圆的圆心坐标为(x 0,y 0),则00220005(1)(1)16.2y x y x x =-+⎧⎪⎨-++=+⎪⎩,解得0032x y =⎧⎨=⎩,或00116.x y =⎧⎨=-⎩, 因此所求圆的方程为22(3)(2)16x y -+-=或22(11)(6)144x y -++=.(全国3卷8)答案:A(全国3卷10)答案:D(全国3卷20)答案:(北京卷10)已知直线l过点(1,0)且垂直于ε,若l被抛物线截得的线段长为4,则抛物线的焦点坐标为________.答案:(1,0)(北京卷12)答案:4(北京卷20)已知椭圆的离心率为,焦距2.斜率为k的直线l与椭圆M有两个不同的交点A,B.(Ⅰ)求椭圆M的方程;(Ⅱ)若,求的最大值;(Ⅲ)设,直线PA与椭圆M的另一个交点C,直线PB与椭圆M的另一个交点D.若C,D和点共线,求k.(天津卷7)已知双曲线22221(0,0)-=>>x y a b a b的离心率为2,过右焦点且垂直于x轴的直线与双曲线交于,A B 两点,设,A B 到双曲线的同一条渐近线的距离分别为12和d d 且12+=6d d ,则双曲线方程为(A )22139-=x y (B )22193-=x y (C )221412-=x y (D )221124-=x y 答案:A解析:2==ce a,2=c a , 在梯形ABCD 中,+2=AC BD FE ,FE 为渐焦距=b ,1226∴+==d d b 3∴=b222+=a b c 2229,12=3,∴==a b c∴22139-=x y(天津卷12)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为答案:2220x x y -+= 解析:因为圆过(0,0)(2,0)所以圆心在x=1上,设其坐标为(1,b ) 又因为(1,1)在圆上所以10,1r b br =-=?=22(1)1,x y -+=即2220x x y -+=(天津卷19)(19)(本小题满分14分)设椭圆22221x y a b+=(0a b >>)的右顶点为A ,上顶点为B ,已知椭圆的离心率|AB =(I )求椭圆的方程;(II )设直线:l y kx = (k ∆0)与椭圆交于P,Q 两点,l 与直线AB 交于点M ,且点P,M 均在第四象限,若BPM 的面积是BPQ 面积的2倍,求k 的值。
2010-2018全国卷分类汇编(解析几何)1卷索引版
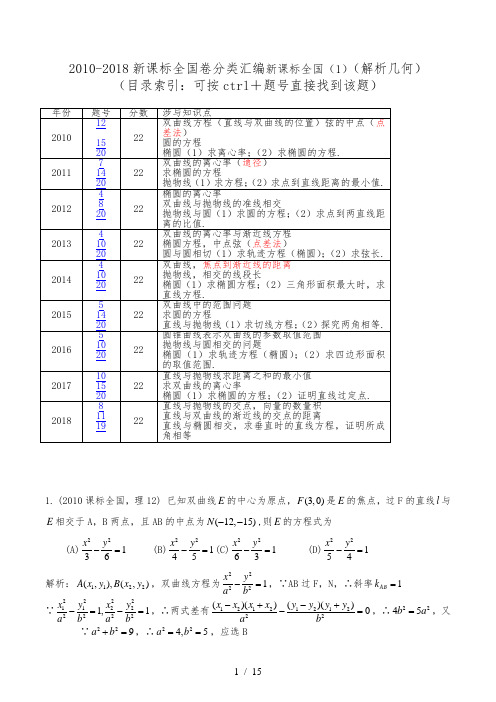
2010-2018新课标全国卷分类汇编新课标全国(1)(解析几何)(目录索引:可按ctrl +题号直接找到该题)1. (2010课标全国,理12) 已知双曲线E 的中心为原点,(3,0)F 是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为(12,15)N --,则E 的方程式为(A)22136x y -= (B)22145x y -=(C)22163x y -= (D)22154x y -= 解析:1122(,),(,)A x y B x y ,双曲线方程为22221x y a b-=,∵AB 过F ,N ,∴斜率1AB k =∵2222112222221,1x y x y a b a b -=-=,∴两式差有1212121222()()()()0x x x x y y y y a b-+-+-=,∴2245b a =,又∵229a b +=,∴224,5a b ==,应选B2. (2010课标全国,理15) 过点A(4,1)的圆C 与直线x-y-1=0相切于点B (2,1),则圆C 的方程为22(3)2x y -+=解析: 设圆心(,)O a b ,借助图形可知3a =,又11032b OB b -∴=-=-与切线垂直,即22C (3)2r OB x y ==-+=圆的方程为3.(2010课标全国,理20) 设12,F F 分别是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,过1F 斜率为1的直线i 与E 相交于,A B 两点,且22,,AF AB BF 成等差数列。
(1)求E 的离心率;(2) 设点(0,1)p -满足PA PB =,求E 的方程 解:(I )由椭圆定义知224AF BF AB a ++=,又222AB AF BF =+,得43AB a =l 的方程为y x c =+,其中c =设()11,A x y ,()22,B x y ,则A 、B 两点坐标满足方程组22221y x c x y a b=+⎧⎪⎨+=⎪⎩,化简得()()222222220a b x a cx a c b +++-= 则()2222121222222,a c b a cx x x x a b a b --+==++因为直线AB 斜率为1,所以AB=21x -=得22244,3ab a a b =+故222a b = 所以E的离心率2c e aa === (II )设AB 的中点为()00,N x y ,由(I )知212022223x x a c x c a b +-===-+,003cy x c =+=。
2018版高考数学文江苏专用大一轮复习讲义文档 第九章

1.双曲线定义平面内到两个定点F 1,F 2的距离的差的绝对值等于常数(小于F 1F 2的正数)的点的轨迹叫做双曲线,两个定点F 1,F 2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距. 集合P ={M ||MF 1-MF 2|=2a },F 1F 2=2c ,其中a ,c 为常数且a >0,c >0. (1)当2a <F 1F 2时,P 点的轨迹是双曲线; (2)当2a =F 1F 2时,P 点的轨迹是两条射线; (3)当2a >F 1F 2时,P 点不存在. 2.双曲线的标准方程和几何性质【知识拓展】 巧设双曲线方程(1)与双曲线x 2a 2-y 2b 2=1(a >0,b >0)有共同渐近线的方程可表示为x 2a 2-y 2b 2=t (t ≠0).(2)过已知两个点的双曲线方程可设为x 2m +y 2n =1(mn <0).【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内到点F 1(0,4),F 2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.( × ) (2)方程x 2m -y 2n=1(mn >0)表示焦点在x 轴上的双曲线.( × )(3)双曲线方程x 2m 2-y 2n 2=λ(m >0,n >0,λ≠0)的渐近线方程是x 2m 2-y 2n 2=0,即x m ±yn =0.( √ )(4)等轴双曲线的渐近线互相垂直,离心率等于 2.( √ )(5)若双曲线x 2a 2-y 2b 2=1(a >0,b >0)与x 2b 2-y 2a 2=1(a >0,b >0)的离心率分别是e 1,e 2,则1e 21+1e 22=1(此结论中两条双曲线称为共轭双曲线).( √ )1.(教材改编)若双曲线x 2a 2-y2b 2=1 (a >0,b >0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为________. 答案5解析 由题意得b =2a ,又a 2+b 2=c 2,∴5a 2=c 2. ∴e 2=c 2a2=5,∴e = 5.2.若方程x 22+m -y 2m +1=1表示双曲线,则m 的取值范围是____________.答案 (-∞,-2)∪(-1,+∞) 解析 由题意知(2+m )(m +1)>0, 解得m >-1或m <-2.3.(2016·无锡一模)已知焦点在x 轴上的双曲线的渐近线方程为y =±13x ,那么双曲线的离心率为________. 答案103解析 根据题意,设双曲线的方程为x 2a 2-y 2b 2=1,则b a =13,所以ca =1+(b a )2=103,即双曲线的离心率为103. 4.(2016·江苏)在平面直角坐标系xOy 中,双曲线x 27-y 23=1的焦距是________.答案 210解析 由已知,a 2=7,b 2=3,则c 2=7+3=10,故焦距为2c =210. 5.双曲线x 24-y 2=1的顶点到其渐近线的距离等于________.答案255解析 双曲线的一个顶点坐标为(2,0), 一条渐近线方程是y =12x ,即x -2y =0,则顶点到渐近线的距离d =|2-0|5=255.题型一 双曲线的定义及标准方程 命题点1 利用定义求轨迹方程例1 已知圆C 1:(x +3)2+y 2=1和圆C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1及圆C 2相外切,则动圆圆心M 的轨迹方程为____________________. 答案 x 2-y 28=1(x ≤-1)解析 如图所示,设动圆M 与圆C 1及圆C 2分别外切于A 和B .根据两圆外切的条件,得MC 1-AC 1=MA ,MC 2-BC 2=MB , 因为MA =MB ,所以MC 1-AC 1=MC 2-BC 2, 即MC 2-MC 1=BC 2-AC 1=2,所以点M 到两定点C 1、C 2的距离的差是常数且小于C 1C 2=6.又根据双曲线的定义,得动点M 的轨迹为双曲线的左支(点M 与C 2的距离大,与C 1的距离小), 其中a =1,c =3,则b 2=8.故点M 的轨迹方程为x 2-y 28=1(x ≤-1).命题点2 利用待定系数法求双曲线方程 例2 根据下列条件,求双曲线的标准方程: (1)虚轴长为12,离心率为54;(2)焦距为26,且经过点M (0,12); (3)经过两点P (-3,27)和Q (-62,-7). 解 (1)设双曲线的标准方程为 x 2a 2-y 2b 2=1或y 2a 2-x 2b 2=1(a >0,b >0). 由题意知,2b =12,e =c a =54.∴b =6,c =10,a =8.∴双曲线的标准方程为x 264-y 236=1或y 264-x 236=1.(2)∵双曲线经过点M (0,12),∴M (0,12)为双曲线的一个顶点,故焦点在y 轴上,且a =12. 又2c =26,∴c =13,∴b 2=c 2-a 2=25. ∴双曲线的标准方程为y 2144-x 225=1.(3)设双曲线方程为mx 2-ny 2=1(mn >0).∴⎩⎪⎨⎪⎧9m -28n =1,72m -49n =1,解得⎩⎨⎧m =-175,n =-125.∴双曲线的标准方程为y 225-x 275=1.命题点3 利用定义解决焦点三角形问题例3 已知F 1,F 2为双曲线C :x 2-y 2=2的左,右焦点,点P 在C 上,PF 1=2PF 2,则cos ∠F 1PF 2=________. 答案 34解析 ∵由双曲线的定义有PF 1-PF 2=PF 2=2a =22, ∴PF 1=2PF 2=42,则cos ∠F 1PF 2=PF 21+PF 22-F 1F 222PF 1·PF 2=(42)2+(22)2-422×42×22=34.引申探究1.本例中,若将条件“PF 1=2PF 2”改为“∠F 1PF 2=60°”,则△F 1PF 2的面积是多少? 解 不妨设点P 在双曲线的右支上, 则PF 1-PF 2=2a =22, 在△F 1PF 2中,由余弦定理,得cos ∠F 1PF 2=PF 21+PF 22-F 1F 222PF 1·PF 2=12,所以PF 1·PF 2=8,所以12F PF S △=12PF 1·PF 2·sin 60°=2 3.2.本例中,若将条件“PF 1=2PF 2”改为“PF 1→·PF 2→=0”,则△F 1PF 2的面积是多少? 解 不妨设点P 在双曲线的右支上, 则PF 1-PF 2=2a =22, 由于PF 1→·PF 2→=0,所以PF 1→⊥PF 2→,所以在△F 1PF 2中,有PF 21+PF 22=F 1F 22, 即PF 21+PF 22=16,所以PF 1·PF 2=4, 所以12F PF S △=12PF 1·PF 2=2.思维升华 (1)利用双曲线的定义判定平面内动点与两定点的轨迹是否为双曲线,进而根据要求可求出双曲线方程.(2)在“焦点三角形”中,常利用正弦定理、余弦定理,经常结合|PF 1-PF 2|=2a ,运用平方的方法,建立与PF 1·PF 2的联系.(3)待定系数法求双曲线方程具体过程中先定形,再定量,即先确定双曲线标准方程的形式,然后再根据a ,b ,c ,e 及渐近线之间的关系,求出a ,b 的值,如果已知双曲线的渐近线方程,求双曲线的标准方程,可设有公共渐近线的双曲线方程为x 2a 2-y 2b 2=λ(λ≠0),再由条件求出λ的值即可.(1)已知F 1,F 2为双曲线x 25-y 24=1的左,右焦点,P (3,1)为双曲线内一点,点A在双曲线上,则AP +AF 2的最小值为__________.(2)(2015·课标全国Ⅱ)已知双曲线过点(4,3),且渐近线方程为y =±12x ,则该双曲线的标准方程为________________.答案 (1)37-25 (2)x 24-y 2=1解析 (1)由题意知,AP +AF 2=AP +AF 1-2a ,要求AP +AF 2的最小值,只需求AP +AF 1的最小值,当A ,P ,F 1三点共线时,取得最小值,则AP +AF 1=PF 1=[3-(-3)]2+(1-0)2=37, ∴AP +AF 2的最小值为AP +AF 1-2a =37-2 5.(2)由双曲线的渐近线方程为y =±12x ,可设该双曲线的标准方程为x 24-y 2=λ(λ≠0),已知该双曲线过点(4,3),所以424-(3)2=λ,即λ=1,故所求双曲线的标准方程为x 24-y 2=1.题型二 双曲线的几何性质例4 (1)(2016·盐城三模)若圆x 2+y 2=r 2过双曲线x 2a 2-y 2b2=1的右焦点F ,且圆与双曲线的渐近线在第一、四象限的交点分别为A ,B ,当四边形OAFB 为菱形时,双曲线的离心率为______. (2)(2015·山东)在平面直角坐标系xOy 中,双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的渐近线与抛物线C 2:x 2=2py (p >0)交于点O ,A ,B .若△OAB 的垂心为C 2的焦点,则C 1的离心率为________. 答案 (1)2 (2)32解析 (1)若四边形OAFB 为菱形,且点A 在圆x 2+y 2=r 2上,则点A 坐标为(c 2,32c ),此时r=c .又点A 在渐近线上,所以32c =b a ·c 2,即ba=3, 所以e =1+(ba)2=2.(2)由题意,不妨设直线OA 的方程为y =ba x ,直线OB 的方程为y =-ba x .由⎩⎪⎨⎪⎧y =b a x ,x 2=2py ,得x 2=2p ·b ax ,∴x =2pb a ,y =2pb 2a2,∴A ⎝⎛⎭⎫2pb a ,2pb 2a 2.设抛物线C 2的焦点为F ,则F ⎝⎛⎭⎫0,p 2, ∴k AF =2pb 2a 2-p22pb a.∵△OAB 的垂心为F ,∴AF ⊥OB ,∴k AF ·k OB =-1, 即2pb 2a 2-p22pb a·⎝⎛⎭⎫-b a =-1,∴b 2a 2=54.设C 1的离心率为e ,则e 2=c 2a 2=a 2+b 2a 2=1+54=94.∴e =32.思维升华 双曲线的几何性质中重点是渐近线方程和离心率,在双曲线x 2a 2-y 2b 2=1(a >0,b >0)中,离心率e 与双曲线的渐近线的斜率k =±ba满足关系式e 2=1+k 2.(2016·全国甲卷改编)已知F 1,F 2是双曲线E :x 2a 2-y 2b2=1的左,右焦点,点M 在E 上,MF 1与x 轴垂直,sin ∠MF 2F 1=13,则E 的离心率为________.答案2解析 离心率e =F 1F 2MF 2-MF 1,由正弦定理得e =F 1F 2MF 2-MF 1=sin ∠F 1MF 2sin ∠MF 1F 2-sin ∠MF 2F 1=2231-13= 2.题型三 直线与双曲线的综合问题例5 (2016·苏州模拟)已知椭圆C 1的方程为x 24+y 2=1,双曲线C 2的左,右焦点分别是C 1的左,右顶点,而C 2的左,右顶点分别是C 1的左,右焦点. (1)求双曲线C 2的方程;(2)若直线l :y =kx +2与双曲线C 2恒有两个不同的交点A 和B ,且OA →·OB →>2(其中O 为原点),求k 的取值范围.解 (1)设双曲线C 2的方程为x 2a 2-y 2b 2=1(a >0,b >0),则a 2=4-1=3,c 2=4, 再由a 2+b 2=c 2,得b 2=1.故C 2的方程为x 23-y 2=1.(2)将y =kx +2代入x 23-y 2=1,得(1-3k 2)x 2-62kx -9=0.由直线l 与双曲线C 2有两个不同的交点,得⎩⎨⎧1-3k 2≠0,Δ=(-62k )2+36(1-3k 2)=36(1-k 2)>0,∴k 2≠13且k 2<1.①设A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=62k1-3k 2,x 1x 2=-91-3k 2. ∴x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2) =(k 2+1)x 1x 2+2k (x 1+x 2)+2=3k 2+73k 2-1.又∵OA →·OB →>2,得x 1x 2+y 1y 2>2, ∴3k 2+73k 2-1>2,即-3k 2+93k 2-1>0, 解得13<k 2<3,②由①②得13<k 2<1.故k 的取值范围为(-1,-33)∪(33,1). 思维升华 (1)研究直线与双曲线位置关系问题的通法:将直线方程代入双曲线方程,消元,得关于x 或y 的一元二次方程.当二次项系数等于0时,直线与双曲线相交于某支上一点,这时直线平行于一条渐近线;当二次项系数不等于0时,用判别式Δ来判定. (2)用“点差法”可以解决弦中点和弦斜率的关系问题,但需要检验.在平面直角坐标系xOy 中,已知双曲线C :x 24-y 23=1.设过点M (0,1)的直线l 与双曲线C 交于A ,B 两点.若AM →=2MB →,则直线l 的斜率为________. 答案 ±12解析 设A (x 1,y 1),B (x 2,y 2),则x 214-y 213=1,x 224-y 223=1. 又AM →=2MB →,AM →=(-x 1,1-y 1),MB →=(x 2,y 2-1).所以⎩⎪⎨⎪⎧ -x 1=2x 2,1-y 1=2y 2-2,即⎩⎪⎨⎪⎧x 1=-2x 2,y 1=3-2y 2,代入双曲线方程联立解得⎩⎪⎨⎪⎧ x 2=-2,y 2=0或⎩⎪⎨⎪⎧x 2=2,y 2=0,所以A (4,3),B (-2,0)或A (-4,3),B (2,0),故k =3-04+2=12或k =3-0-4-2=-12,即直线l 的斜率为±12.10.直线与圆锥曲线的交点典例 已知双曲线x 2-y 22=1,过点P (1,1)能否作一条直线l ,与双曲线交于A ,B 两点,且点P 是线段AB 的中点? 错解展示现场纠错解 设点A (x 1,y 1),B (x 2,y 2)在双曲线上,且线段AB 的中点为(x 0,y 0), 若直线l 的斜率不存在,显然不符合题意. 设经过点P 的直线l 的方程为y -1=k (x -1), 即y =kx +1-k . 由⎩⎪⎨⎪⎧y =kx +1-k ,x 2-y 22=1,得(2-k 2)x 2-2k (1-k )x -(1-k )2-2=0(2-k 2≠0).①∴x 0=x 1+x 22=k (1-k )2-k 2.由题意,得k (1-k )2-k 2=1,解得k =2.当k =2时,方程①可化为2x 2-4x +3=0. Δ=16-24=-8<0,方程①没有实数解.∴不能作一条直线l 与双曲线交于A ,B 两点,且点P (1,1)是线段AB 的中点. 纠错心得 (1)“点差法”解决直线与圆锥曲线的交点问题,要考虑变形的条件. (2)“判别式Δ≥0”是判断直线与圆锥曲线是否有公共点的通用方法.1.(2015·福建改编)若双曲线E :x 29-y 216=1的左,右焦点分别为F 1,F 2,点P 在双曲线E 上,且PF 1=3,则PF 2=________. 答案 9解析 由双曲线定义|PF 2-PF 1|=2a ,∵PF 1=3,∴P 在左支上,∵a =3,∴PF 2-PF 1=6, ∴PF 2=9.2.(2016·全国乙卷改编)已知方程x 2m 2+n -y 23m 2-n =1表示双曲线,且该双曲线两焦点间的距离为4,则n 的取值范围是________. 答案 (-1,3)解析 ∵方程x 2m 2+n -y 23m 2-n=1表示双曲线,∴(m 2+n )·(3m 2-n )>0,解得-m 2<n <3m 2,由双曲线性质,知c 2=(m 2+n )+(3m 2-n )=4m 2(其中c 是半焦距),∴焦距2c =2×2|m |=4,解得|m |=1,∴-1<n <3.3.(2016·盐城模拟)已知双曲线x 216-y 29=1的左,右焦点分别为F 1,F 2,过F 2的直线与该双曲线的右支交于A ,B 两点,若AB =5,则△ABF 1的周长为________. 答案 26解析 由双曲线x 216-y 29=1,知a =4.由双曲线定义AF 1-AF 2=BF 1-BF 2=2a =8, ∴AF 1+BF 1=AF 2+BF 2+16=21,∴△ABF 1的周长为AF 1+BF 1+AB =21+5=26.4.(2016·常州模拟)已知双曲线x 29-y 2m=1(m >0)的一个焦点在圆x 2+y 2-4x -5=0上,则双曲线的渐近线方程为____________.答案 y =±43x 解析 由⎩⎪⎨⎪⎧y =0,x 2+y 2-4x -5=0,得x 2-4x -5=0, 解得x =5或x =-1.又a =3,故c =5,所以b =4,双曲线的渐近线方程为y =±43x . 5.已知点F 是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点,点E 是该双曲线的右顶点,过F 且垂直于x 轴的直线与双曲线交于A 、B 两点,若△ABE 是锐角三角形,则该双曲线的离心率e 的取值范围是____________.答案 (1,2)解析 由题意易知点F 的坐标为(-c,0),A (-c ,b 2a ),B (-c ,-b 2a),E (a,0), ∵△ABE 是锐角三角形,∴EA →·EB →>0,即EA →·EB →=(-c -a ,b 2a )·(-c -a ,-b 2a)>0, 整理得3e 2+2e >e 4,∴e (e 3-3e -3+1)<0,∴e (e +1)2(e -2)<0,解得e ∈(0,2),又e >1,∴e ∈(1,2).6.(2016·浙江)设双曲线x 2-y 23=1的左,右焦点分别为F 1,F 2,若点P 在双曲线上,且△F 1PF 2为锐角三角形,则PF 1+PF 2的取值范围是________.答案 (27,8)解析 如图,由已知可得a =1,b =3,c =2,从而F 1F 2=4,由对称性不妨设P 在右支上,设PF 2=m ,则PF 1=m +2a =m +2,由于△PF 1F 2为锐角三角形,结合实际意义需满足⎩⎪⎨⎪⎧(m +2)2<m 2+42,42<(m +2)2+m 2,解得-1+7<m <3,又PF 1+PF 2=2m +2,∴27<2m +2<8.7.(2016·南京三模)设F 是双曲线的一个焦点,点P 在双曲线上,且线段PF 的中点恰为双曲线虚轴的一个端点,则双曲线的离心率为________.答案 5解析 不妨设双曲线方程为x 2a 2-y 2b 2=1 (a >0,b >0),设F (-c,0),线段PF 的中点为(0,b ),则P (c,2b ).由点P 在双曲线上,得c 2a 2-4=1,所以e = 5. 8.设双曲线x 24-y 25=1的左,右焦点分别为F 1,F 2,P 为双曲线上位于第一象限内的一点,且△PF 1F 2的面积为6,则点P 的坐标为____________.答案 (655,2) 解析 由双曲线x 24-y 25=1的左,右焦点分别为F 1,F 2,所以F 1F 2=6,设P (x ,y ) (x >0,y >0),因为△PF 1F 2的面积为6,所以12F 1F 2·y =12×6×y =6,解得y =2,将y =2代入x 24-y 25=1得x =655.所以P (655,2). 9.(2016·扬州一模)已知F 1,F 2分别是双曲线x 2a 2-y 2b2=1 (a >0,b >0)的左,右焦点,过点F 2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ,若点M 在以线段F 1F 2为直径的圆上,则双曲线的离心率为______.答案 2解析 由题意知渐近线y =b a x 与直线y =-b a (x -c )交于点M ,解得M (c 2,bc 2a).因为点M 在圆x 2+y 2=c 2上,所以c 24+b 2c 24a 2=c 2,解得b 2a 2=3,所以e = 1+b 2a2=4=2. 10.(2015·课标全国Ⅰ改编)已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是C 的两个焦点,若MF 1→·MF 2→<0,则y 0的取值范围是______________.答案 ⎝⎛⎭⎫-33,33 解析 由题意知a =2,b =1,c =3,∴F 1(-3,0),F 2(3,0),∴MF 1→=(-3-x 0,-y 0),MF 2→=(3-x 0,-y 0).∵MF 1→·MF 2→<0,∴(-3-x 0)(3-x 0)+y 20<0,即x 20-3+y 20<0.∵点M (x 0,y 0)在双曲线上,∴x 202-y 20=1,即x 20=2+2y 20, ∴2+2y 20-3+y 20<0,∴-33<y 0<33. 11.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的左,右焦点分别为F 1,F 2,点P 在双曲线的右支上,且PF 1=4PF 2,则此双曲线的离心率e 的最大值为________.答案 53解析 由定义,知PF 1-PF 2=2a .又PF 1=4PF 2,∴PF 1=83a ,PF 2=23a . 在△PF 1F 2中,由余弦定理,得cos ∠F 1PF 2=649a 2+49a 2-4c 22·83a ·23a =178-98e 2. 要求e 的最大值,即求cos ∠F 1PF 2的最小值,∴当cos ∠F 1PF 2=-1时,得e =53, 即e 的最大值为53. 12.设双曲线C 的中心为点O ,若有且只有一对相交于点O 且所成的角为60°的直线A 1B 1和A 2B 2,使A 1B 1=A 2B 2,其中A 1、B 1和A 2、B 2分别是这对直线与双曲线C 的交点,则该双曲线的离心率的取值范围是____________.答案 ⎝⎛⎦⎤233,2 解析 由双曲线的对称性知,满足题意的这一对直线也关于x 轴(或y 轴)对称.又由题意知有且只有一对这样的直线,故该双曲线在第一象限的渐近线的倾斜角范围大于30°且小于等于60°,即tan 30°<b a ≤tan 60°,∴13<b 2a 2≤3.又e 2=(c a )2=c 2a 2=1+b 2a 2,∴43<e 2≤4, ∴233<e ≤2. 13.(2016·泰州模拟)已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),求双曲线E 的方程.解 设双曲线的标准方程为x 2a 2-y 2b2=1(a >0,b >0), 由题意知c =3,a 2+b 2=9.设A (x 1,y 1),B (x 2,y 2).则有⎩⎨⎧ x 21a 2-y 21b 2=1,x 22a 2-y 22b 2=1,两式作差,得y 1-y 2x 1-x 2=b 2(x 1+x 2)a 2(y 1+y 2)=-12b 2-15a 2=4b 25a 2, 又AB 的斜率是-15-0-12-3=1,所以4b 25a 2=1. 将4b 2=5a 2代入a 2+b 2=9,得a 2=4,b 2=5.所以双曲线的标准方程是x 24-y 25=1. 14.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点是F 2(2,0),且b =3a . (1)求双曲线C 的方程;(2)设经过焦点F 2的直线l 的一个法向量为(m,1),当直线l 与双曲线C 的右支交于不同的两点A ,B 时,求实数m 的取值范围,并证明AB 中点M 在曲线3(x -1)2-y 2=3上;(3)设(2)中直线l 与双曲线C 的右支交于A ,B 两点,问是否存在实数m ,使得∠AOB 为锐角?若存在,请求出m 的取值范围;若不存在,请说明理由.解 (1)由已知,得c =2,c 2=a 2+b 2,b =3a ,∴4=a 2+3a 2,∴a 2=1,b 2=3,∴双曲线C 的方程为x 2-y 23=1. (2)由题意,得直线l :m (x -2)+y =0,由⎩⎪⎨⎪⎧y =-mx +2m ,x 2-y 23=1, 得(3-m 2)x 2+4m 2x -4m 2-3=0.由Δ>0,得4m 4+(3-m 2)(4m 2+3)>0,12m 2+9-3m 2>0,即m 2+1>0恒成立.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4m 2m 2-3,x 1x 2=4m 2+3m 2-3. 又⎩⎪⎨⎪⎧ x 1+x 2>0,x 1·x 2>0,∴⎩⎪⎨⎪⎧ 4m 2m 2-3>0,4m 2+3m 2-3>0,∴m 2>3,∴m ∈(-∞,-3)∪(3,+∞).∵x 1+x 22=2m 2m 2-3,y 1+y 22=-2m 3m 2-3+2m =-6m m 2-3, ∴AB 的中点M (2m 2m 2-3,-6m m 2-3), ∵3(2m 2m 2-3-1)2-36m 2(m 2-3)2=3×(m 2+3)2(m 2-3)2-36m 2(m 2-3)2=3×m 4+6m 2+9-12m 2(m 2-3)2=3, ∴M 在曲线3(x -1)2-y 2=3上.(3)设A (x 1,y 1),B (x 2,y 2),假设存在实数m ,使∠AOB 为锐角,则OA →·OB →>0,∴x 1x 2+y 1y 2>0.∵y 1y 2=(-mx 1+2m )(-mx 2+2m )=m 2x 1x 2-2m 2(x 1+x 2)+4m 2,∴(1+m 2)x 1x 2-2m 2(x 1+x 2)+4m 2>0,∴(1+m 2)(4m 2+3)-8m 4+4m 2(m 2-3)>0,即7m 2+3-12m 2>0,∴m 2<35, 与m 2>3矛盾,∴不存在实数m ,使得∠AOB 为锐角.。
2010-2018全国卷分类汇编(解析几何)1卷索引版

2010-2018全国卷分类汇编(解析几何)1卷索引版2010-2018新课标全国卷分类汇编新课标全国(1)(解析几何)(目录索引:可按ctrl +题号直接找到该题)1. (2010课标全国,理12) 已知双曲线E 的中心为原点,(3,0)F 是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为(12,15)N --,则E 的方程式为(A)22136x y -= (B) 22145x y -= (C) 22163x y -= (D) 22154x y -= 解析:1122(,),(,)A x y B x y ,双曲线方程为22221x y a b-=,∵AB 过F ,N ,∴斜率1AB k =∵2222112222221,1x y x y a b a b -=-=,∴两式差有1212121222()()()()0x x x x y y y y a b-+-+-=,∴2245b a =,又∵229a b +=,∴224,5a b ==,故选B2. (2010课标全国,理15) 过点A(4,1)的圆C 与直线x-y-1=0相切于点B (2,1),则圆C 的方程为22(3)2x y -+=解析: 设圆心(,)O a b ,借助图形可知3a =,又11032b OB b -∴=-=-与切线垂直,即22C (3)2r OB x y ==∴-+=圆的方程为3.(2010课标全国,理20) 设12,F F 分别是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,过1F 斜率为1的直线i 与E 相交于,A B 两点,且22,,AF AB BF 成等差数列。
(1)求E 的离心率;(2) 设点(0,1)p -满足PA PB =,求E 的方程 解:(I )由椭圆定义知224AF BF AB a ++=,又222AB AF BF =+,得43AB a =l 的方程为y x c =+,其中c =设()11,A x y ,()22,B x y ,则A 、B 两点坐标满足方程组22221y x c x y a b=+⎧⎪⎨+=⎪⎩,化简得()()222222220a b x a cx a c b +++-= 则()2222121222222,a c b a cx x x x a b a b--+==++ 因为直线AB 斜率为1,所以AB=21x -=得22244,3ab a a b =+故222a b = 所以E的离心率c e a===(II )设AB 的中点为()00,N x y ,由(I )知212022223x x a c x c a b +-===-+,003cy x c =+=。
2018年各地高考数学文科分类汇编——解析几何完整

3k 2
x2 y2 94 y kx
1 消去 y ,可得 x1
6 9k2
, 由 x2 4
5x1 可得
9k 2 当k
4 5(3k 2) ,两边平方,整理得 18k 2 25k 8
8 时, x2 9
9< 0 ,不合题意,舍去;当 k
0 ,解得 k 1 时, x2 2
8 ,或 k
1 .
9
2
12, x1 12 ,符合 5
A.1 3 2
答案: D
B. 2 3
C. 3 1 2
D. 3 1
(全国 2 卷 20)设抛物线 C:y 2 4 x 的焦点为 F ,过 F 且斜率为 k( k 0) 的直线 l 与 C 交于 A, B 两点, | AB | 8 .
( 1)求 l 的方程; ( 2)求过点 A , B 且与 C 的准线相切的圆的方程.
答案:
2
x
-
2x+
2
y=
0
解析:因为圆过( 0,0)(2,0) 所以圆心在 x=1 上,设其坐标为( 1,b) 又因为( 1,1)在圆上
所以 r = 1- b = 1+ b2 ? b 0, r = 1
( x - 1)2 + y2 = 1, 即 x2 - 2x + y 2 = 0
(天津卷 19)
(19) (本小题满分 14 分)
据医学文献记载 ,一个健康的青少年学生 30 分钟用脑 ,血糖浓度在 120 毫克 /100 毫升 ,大脑反应快 ,记忆力强; 90 分钟用脑, 血糖浓度降至 80 毫克 /100 毫升, 大脑功能尚正常; 连续 120 分钟用脑, 血糖浓度降至 60 毫克 /100 毫升,大脑反应迟钝,思维能力较 4
2010~2018江苏高考三角函数汇编(文)

2010~2018高考三角函数汇编1、考纲要求:三角函数的概念B同角的三角函数的基本关系式B正弦函数、余弦函数的诱导公式B三角函数图像与性质B函数y=Asin(ωx+φ)的图像与性质A 两角和与差的正弦、余弦及正切C二倍角的正弦、余弦及正切B正弦定理、余弦定理及应用B2、高考解读:高考中,对三角计算题的考查始终围绕着求角、求值问题,以和、差角公式的运用为主,可见三角式的恒等变换比三角函数的图象与性质更为重要.三角变换的基本解题规律是:寻找联系、消除差异.常有角变换、函数名称变换、次数变换等简称为:变角、变名、变次.备考中要注意积累各种变换的方法与技巧,不断提高分析与解决问题的能力.三角考题的花样翻新在于条件变化,大致有三类:第一类是给出三角式值见2014年三角解答题,第二类是给出在三角形中见2011年、2015年、2016年三角解答题,第三类是给出向量见2013年、2017年三角解答题.而2012年三角解答题则是二、三类的混合.通常一大一小也会出现两小一大情况,还有可能出现应用题,主要考察三角公式、三角函数的图像与性质、解三角形知识,一般都是容易题或中档题。
一、三角公式★7.(5分)(2011•江苏)已知,则的值为.★★11.(5分)(2012•江苏)设α为锐角,若cos(α+)=,则sin(2α+)的值为.(2015•江苏)已知tanα=﹣2,tan(α+β)=,则tanβ的值为.★8.(5分)★5.(5分)(2017•江苏)若tan(α﹣)=.则tanα=.★★★15.(14分)(2013•江苏)已知=(cosα,sinα),=(cosβ,sinβ),0<β<α<π.(1)若|﹣|=,求证:⊥;(2)设=(0,1),若+=,求α,β的值.★★★15.(14分)(2014•江苏)已知α∈(,π),sinα=.(1)求sin(+α)的值;(2)求cos(﹣2α)的值.★★★16.(14分)(2018•江苏)已知α,β为锐角,tanα=,cos(α+β)=﹣.(1)求cos2α的值;(2)求tan(α﹣β)的值.二、三角函数图像与性质★★★10.(5分)(2010•江苏)定义在区间上的函数y=6cosx的图象与y=5tanx的图象的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx 的图象交于点P2,则线段P1P2的长为.★★9.(5分)(2011•江苏)函数f(x)=Asin(ωx+φ),(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则f(0)=.★1.(5分)(2013•江苏)函数y=3sin(2x+)的最小正周期为.★5.(5分)(2014•江苏)已知函数y=cosx与y=sin(2x+φ)(0≤φ<π),它们的图象有一个横坐标为的交点,则φ的值是.★★★9.(5分)(2016•江苏)定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是.★★7.(5分)(2018•江苏)已知函数y=sin(2x+φ)(﹣φ<)的图象关于直线x=对称,则φ的值为.★★★16.(14分)(2017•江苏)已知向量=(cosx,sinx),=(3,﹣),x∈[0,π].(1)若,求x的值;(2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值.三、解三角形★★★13.(5分)(2010•江苏)在锐角△ABC中,角A、B、C的对边分别为a、b、c,若+=6cosC,则+的值是.★★★★14.(5分)(2014•江苏)若△ABC的内角满足sinA+sinB=2sinC,则cosC的最小值是.★★★★14.(5分)(2016•江苏)在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是.★★★13.(5分)(2018•江苏)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.★★★15.(14分)(2011•江苏)在△ABC中,角A,B,C的对边分别是a,b,c.(1)若sin(A+)=2cosA,求A的值.(2)若cosA=,b=3c,求sinC的值.★★★15.(14分)(2012•江苏)在△ABC中,已知.(1)求证:tanB=3tanA;(2)若cosC=,求A的值.★★★15.(14分)(2015•江苏)在△ABC中,已知AB=2,AC=3,A=60°.(1)求BC的长;(2)求sin2C的值.★★★15.(14分)(2016•江苏)在△ABC中,AC=6,cosB=,C=.(1)求AB的长;(2)求cos(A﹣)的值.★★★17.(14分)(2010•江苏)某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β.(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,请据此算出H 的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使α与β之差较大,可以提高测量精确度.若电视塔的实际高度为125m,试问d为多少时,α﹣β最大?★★★18.(16分)(2013•江苏)如图,游客从某旅游景区的景点A处下山至C 处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=,cosC=(1)求索道AB的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?★★★17.(14分)(2018•江苏)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围;(2)若大棚I内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.。
(2021年整理)2010~2018江苏高考立体几何试题汇编(文)

2010~2018江苏高考立体几何试题汇编(文)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2010~2018江苏高考立体几何试题汇编(文))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2010~2018江苏高考立体几何试题汇编(文)的全部内容。
2010~2018年高考立体几何试题汇编1、考纲要求:柱、锥、台、球及简单组合体A柱、锥、台、球的表面积和体积A平面及其性质A直线与平面平行、垂直的判定及性质B两平面平行、垂直的判定及性质B2、高考解读:通常一大一小,填空题主要考查空间几何体的表面积与体积,解答题主要考查空间的平行与垂直关系,其中三年也考查以几何体为背景的应用题。
这些题目难度不大,主要考查学生的基础知识和空间转换能力。
属于中档题。
一、空间几何体的表面积与体积★★7.(5分)(2012•江苏)如图,在长方体ABCD﹣A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A﹣BB1D1D的体积为cm3.★★8.(5分)(2013•江苏)如图,在三棱柱A1B1C1﹣ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F﹣ADE的体积为V1,三棱柱A1B1C1﹣ABC的体积为V2,则V1:V2= .★★8.(5分)(2014•江苏)设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是.★★9.(5分)(2015•江苏)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2,高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为.★★6.(5分)(2017•江苏)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则的值是.★★10.(5分)(2018•江苏)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.二、空间点、线、面的位置关系★★★16.(14分)(2010•江苏)如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求证:PC⊥BC;(2)求点A到平面PBC的距离.★★★16.(14分)(2011•江苏)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点,求证:(1)直线EF∥平面PCD;(2)平面BEF⊥平面PAD.★★★16.(14分)(2012•江苏)如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E 分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.★★★16.(14分)(2013•江苏)如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.★★★16.(14分)(2014•江苏)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.(14分)(2015•江苏)如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1,★★★16.设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.★★★16.(14分)(2016•江苏)如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F.★★★15.(14分)(2017•江苏)如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.★★★15.(14分)(2018•江苏)在平行六面体ABCD﹣A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.三、以空间几何体为背景的应用题★★★17.(14分)(2011•江苏)请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).(1)若广告商要求包装盒侧面积S(cm2)最大,试问x应取何值?(2)若广告商要求包装盒容积V(cm3)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值.★★★17.(14分)(2016•江苏)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1,下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.(1)若AB=6m,PO1=2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6m,则当PO1为多少时,仓库的容积最大?★★★★18.(16分)(2017•江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.。
2018年度0~2018年度8江苏高考解析汇报几何总汇编(文)

2010~2018年高考解析几何汇编1、考纲要求:直线的斜率和倾斜角B直线方程C直线的平行与垂直关系B两直线的交点B两点间的距离、点到直线的距离B圆的标准方程与一般方程C直线与圆、圆与圆的位置关系B椭圆标准方程与性质B双曲线标准方程与性质A 抛物线的标准方程与性质A2、高考解读:通常是两小一大,填空题一方面考查直线与圆的位置关系,另一方面考查圆锥曲线的概念与几何性质,解答题主要是直线与圆、直线与圆锥曲线的综合题,个别考题是基础题,多数考题是中档题,特别是解答题主要考查学生的运算能力和学生的观察、推理以及创造性地综合分析、解决问题的能力,有可能出现难题。
一、直线与圆的位置关系★★9.(5分)(2010•江苏)在平面直角坐标系xOy中,已知圆x2+y2=4上有且仅有四个点到直线12x﹣5y+c=0的距离为1,则实数c的取值范围是.★★★14.(5分)(2011•江苏)设集合,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是.★★★12.(5分)(2012•江苏)在平面直角坐标系xOy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是.★★9.(5分)(2014•江苏)在平面直角坐标系xOy中,直线x+2y﹣3=0被圆(x﹣2)2+(y+1)2=4截得的弦长为.★★10.(5分)(2015•江苏)在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx﹣y﹣2m﹣1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为.★★13.(5分)(2017•江苏)在平面直角坐标系xOy中,A(﹣12,0),B(0,6),点P在圆O:x2+y2=50上.若≤20,则点P的横坐标的取值范围是.★★★12.(5分)(2018•江苏)在平面直角坐标系xOy中,A为直线l:y=2x 上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为.★★★17.(14分)(2013•江苏)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4,设圆C的半径为1,圆心在l上.(1)若圆心C也在直线y=x﹣3上,过点A作圆C的切线,求切线方程;(2)若圆C上存在点M,使|MA|=2|MO|,求圆心C的横坐标的取值范围.★★★18.(16分)(2016•江苏)如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.二、圆锥曲线的定义与几何性质★★6.(5分)(2010•江苏)在平面直角坐标系xOy中,双曲线上一点M,点M的横坐标是3,则M到双曲线右焦点的距离是.★★8.(5分)(2012•江苏)在平面直角坐标系xOy中,若双曲线的离心率为,则m的值为.★★3.(5分)(2013•江苏)双曲线的两条渐近线方程为.★★★12.(5分)(2013•江苏)在平面直角坐标系xOy中,椭圆C的标准方程为(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d1,F到l的距离为d2,若d2=,则椭圆C的离心率为.★★12.(5分)(2015•江苏)在平面直角坐标系xOy中,P为双曲线x2﹣y2=1右支上的一个动点,若点P到直线x﹣y+1=0的距离大于c恒成立,则实数c的最大值为.★★3.(5分)(2016•江苏)在平面直角坐标系xOy中,双曲线﹣=1的焦距是.★★★10.(5分)(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是.★★8.(5分)(2017•江苏)在平面直角坐标系xOy中,双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P,Q,其焦点是F1,F2,则四边形F1PF2Q的面积是.★★8.(5分)(2018•江苏)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的值为.三、直线与椭圆的综合题★★★18.(16分)(2010•江苏)在平面直角坐标系xOy中,如图,已知椭圆=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.(1)设动点P满足PF2﹣PB2=4,求点P的轨迹;(2)设x1=2,x2=,求点T的坐标;(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).★★★★18.(16分)(2011•江苏)如图,在平面直角坐标系xOy中,M、N分别是椭圆的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k(1)若直线PA平分线段MN,求k的值;(2)当k=2时,求点P到直线AB的距离d;(3)对任意k>0,求证:PA⊥PB.★★★19.(16分)(2012•江苏)如图,在平面直角坐标系xOy中,椭圆(a >b >0)的左、右焦点分别为F 1(﹣c ,0),F 2(c ,0).已知(1,e )和(e ,)都在椭圆上,其中e 为椭圆的离心率. (1)求椭圆的方程;(2)设A ,B 是椭圆上位于x 轴上方的两点,且直线AF 1与直线BF 2平行,AF 2与BF 1交于点P . (i )若AF 1﹣BF 2=,求直线AF 1的斜率;(ii )求证:PF 1+PF 2是定值.★★★17.(14分)(2014•江苏)如图,在平面直角坐标系xOy 中,F 1,F 2分别为椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2C.并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1=,求椭圆的方程;(1)若点C的坐标为(,),且BF2(2)若FC⊥AB,求椭圆离心率e的值.1★★★18.(16分)(2015•江苏)如图,在平面直角坐标系xOy中,已知椭圆+=1(a>b>0)的离心率为,且右焦点F到左准线l的距离为3.(1)求椭圆的标准方程;(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.★★★17.(14分)(2017•江苏)如图,在平面直角坐标系xOy中,椭圆E:=1(a>b>0)的左、右焦点分别为F1,F2,离心率为,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.(1)求椭圆E的标准方程;(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.★★★18.(16分)(2018•江苏)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.实用标准文案(1)求椭圆C及圆O的方程;(2)设直线l与圆O相切于第一象限内的点P.①若直线l与椭圆C有且只有一个公共点,求点P的坐标;②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.精彩文档。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010~2018年高考解析几何汇编
1、考纲要求:直线的斜率和倾斜角B直线方程C直线的平行与垂直关系B两直线的交点B两点间的距离、点到直线的距离B圆的标准方程与一般方程C
直线与圆、圆与圆的位置关系B椭圆标准方程与性质B双曲线标准方程与性质A 抛物线的标准方程与性质A
2、高考解读:通常是两小一大,填空题一方面考查直线与圆的位置关系,另一方面考查圆锥曲线的概念与几何性质,解答题主要是直线与圆、直线与圆锥曲线的综合题,个别考题是基础题,多数考题是中档题,特别是解答题主要考查学生的运算能力和学生的观察、推理以及创造性地综合分析、解决问题的能力,有可能出现难题。
一、直线与圆的位置关系
★★9.(5分)(2010•江苏)在平面直角坐标系xOy中,已知圆x2+y2=4上有且仅有四个点到直线12x﹣5y+c=0的距离为1,则实数c的取值范围是.★★★14.(5分)(2011•江苏)设集合
,B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B≠∅,则实数m的取值范围是.
★★★12.(5分)(2012•江苏)在平面直角坐标系xOy中,圆C的方程为x2+y2﹣8x+15=0,若直线y=kx﹣2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是.
★★9.(5分)(2014•江苏)在平面直角坐标系xOy中,直线x+2y﹣3=0被圆(x﹣2)2+(y+1)2=4截得的弦长为.
★★10.(5分)(2015•江苏)在平面直角坐标系xOy中,以点(1,0)为圆心且与直线mx﹣y﹣2m﹣1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为.
★★13.(5分)(2017•江苏)在平面直角坐标系xOy中,A(﹣12,0),B(0,6),点P在圆O:x2+y2=50上.若≤20,则点P的横坐标的取值范围是.
★★★12.(5分)(2018•江苏)在平面直角坐标系xOy中,A为直线l:y=2x
上在第一象限内的点,B(5,0),以AB为直径的圆C与直线l交于另一点D.若=0,则点A的横坐标为.
★★★17.(14分)(2013•江苏)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4,设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x﹣3上,过点A作圆C的切线,求切线方程;(2)若圆C上存在点M,使|MA|=2|MO|,求圆心C的横坐标的取值范围.
★★★18.(16分)(2016•江苏)如图,在平面直角坐标系xOy中,已知以M 为圆心的圆M:x2+y2﹣12x﹣14y+60=0及其上一点A(2,4).
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,0)满足:存在圆M上的两点P和Q,使得+=,求实数t的取值范围.
二、圆锥曲线的定义与几何性质
★★6.(5分)(2010•江苏)在平面直角坐标系xOy中,双曲线上一
点M,点M的横坐标是3,则M到双曲线右焦点的距离是.
★★8.(5分)(2012•江苏)在平面直角坐标系xOy中,若双曲线
的离心率为,则m的值为.
★★3.(5分)(2013•江苏)双曲线的两条渐近线方程为.
★★★12.(5分)(2013•江苏)在平面直角坐标系xOy中,椭圆C的标准方程为(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d1,F到l的距离为d2,若d2=,则椭圆C的离心率为.
★★12.(5分)(2015•江苏)在平面直角坐标系xOy中,P为双曲线x2﹣y2=1右支上的一个动点,若点P到直线x﹣y+1=0的距离大于c恒成立,则实数c 的最大值为.
★★3.(5分)(2016•江苏)在平面直角坐标系xOy中,双曲线﹣=1的
焦距是.
★★★10.(5分)(2016•江苏)如图,在平面直角坐标系xOy中,F是椭圆
+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,
则该椭圆的离心率是.
★★8.(5分)(2017•江苏)在平面直角坐标系xOy中,双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P,Q,其焦点是F1,F2,则四边形F1PF2Q 的面积是.
★★8.(5分)(2018•江苏)在平面直角坐标系xOy中,若双曲线﹣=1(a>0,b>0)的右焦点F(c,0)到一条渐近线的距离为c,则其离心率的
值为.
三、直线与椭圆的综合题
★★★18.(16分)(2010•江苏)在平面直角坐标系xOy中,如图,已知椭圆=1的左、右顶点为A、B,右焦点为F.设过点T(t,m)的直线TA、
TB与椭圆分别交于点M(x1,y1)、N(x2,y2),其中m>0,y1>0,y2<0.(1)设动点P满足PF2﹣PB2=4,求点P的轨迹;
(2)设x1=2,x2=,求点T的坐标;
(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
★★★★18.(16分)(2011•江苏)如图,在平面直角坐标系xOy中,M、N分
别是椭圆的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P
在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB.
★★★19.(16分)(2012•江苏)如图,在平面直角坐标系xOy中,椭圆
(a>b>0)的左、右焦点分别为F1(﹣c,0),F2(c,0).已知(1,e)和(e,)都在椭圆上,其中e为椭圆的离心率.
(1)求椭圆的方程;
(2)设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.
(i)若AF1﹣BF2=,求直线AF1的斜率;
(ii)求证:PF1+PF2是定值.
★★★17.(14分)(2014•江苏)如图,在平面直角坐标系xOy中,F1,F2分别为椭圆+=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.(1)若点C的坐标为(,),且BF2=,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
★★★18.(16分)(2015•江苏)如图,在平面直角坐标系xOy中,已知椭圆
+=1(a>b>0)的离心率为,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
(2017•江苏)如图,在平面直角坐标系xOy中,椭圆E:(14分)
★★★17.
=1(a>b>0)的左、右焦点分别为F1,F2,离心率为,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
★★★18.(16分)(2018•江苏)如图,在平面直角坐标系xOy中,椭圆C过点(),焦点F1(﹣,0),F2(,0),圆O的直径为F1F2.
(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于A,B两点.若△OAB的面积为,求直线l的方程.。
