第七章应力状态1
合集下载
第七章应力状态及应变状态分析
第七章 应力状态及应变状态分析第一节 概 述在第一章中将应力定义为内力的集度或单位面积的内力值。
应力又分正应力σ和剪应力τ两种。
前面各章的知识表明，受力杆件中任一点的应力是随截面位置及点的位置的不同而不同，如7-1（a ）中a 、b 两点分别在两个截面上，其应力是不同的。
同一截面上的各点，如图7-1（b ）中b 、c 两点的应力一般情况下也是不同的。
同一点不同方向的应力也是不同的。
过一点各个方向上的应力情况称为该点的应力状态．．．．，应力状态分析就是要研究杆件中某一点（特别是危险点）各个方向上的应力之间的关系，确定该点处的最大正应力和最大剪应力，为强度计算提供重要依据。
研究应力状态的方法是过杆件中的任一点取出一个微小的六面体——单元．．体．。
如图7-1（a ）中过a 点取出的单元体放大如图7-2所示。
单元体三个方向的边长很小且趋于零，则该单元体代表一点，即a 点，互相平行的平面上的正应力相等，剪应力也相等。
杆件在任意荷载作用下，从中所取出的单元体表面上一般既有正应为又有剪应力，如图7-2所示。
当图7-2所示的单元体各面上的,0,0,0,0,0,0======zy zx yx yz xz xy ττττττ 即六个面上均没有剪应力作用时，这种面叫做特殊平面，并定义为主平面．．．。
该主(a)(b)图7-1各点的应力情况平面上作用的正应力称为主应力．．．，用,,,321σσσ表示（,321σσσ≥≥），如图7-3所示。
各面均为主平面的单元体，称为主单元体．．．．。
三个主应力中若有两个等于零一个不等于零，该单元体称为单向应力状态．．．．．．，如图7-4（a ）；三个主应力中有一个等于零，两个不等于零，该单元体称为二向应．．．力状态．．．，如图7-4（b ）；三个主应力均不等于零，该单元体称为三向应力状态．．．．．．，如7-3。
单向应力状态和二向应力状态属平面应力状态，三向应力状态属空间应力状．．．．．态．。
07章1-4应力状态
21m a x a (x ,xy)
o d’ (y ,yx) b
d c 21min
max
max min
min
ma4x5o
1m a x
min max
1m in
max 与 max 的作用面相差450
max min
ca
(
x
2
y )2
2 xy
max
min
2
( x y ) / 2
(1) 将原单元体上的剪应力等效汇合成两对流出和 流入的剪应力流。
(2) 最大主应力σmax的作用面偏向于流出的剪应力
流方向。
例：纯剪切应力状态及其主应力
等价流出的剪 应力流方向
等价流入的剪 应力流方向
xy , x y 0
等价流入的剪 应力流方向
主应力： max x min
主方向： tg20
1，
2，
；标注在单元体上。
3
3. max.
dx
１．应力在每个侧面上均布；
２．相互平行的面上应力等值、 反向。
■ 原始单元体（各侧面应力已知的单元体）
M y
Iz
QS
z
梁
Izb
T
轴
Ip
杆
■ 施用截面法（用截面法找到特殊截面）
N A
M y
Iz
QS
z
梁
Izb
0的平面
主
平
面 上 的 正
主 应 力
应
力
主平面
１第一主应力
２ 第二主应力 ３ 第三主应力
max
22
my in
mxax2
y
2
2 xy
• (3)式中两式相加:
材料力学第七章 应力状态
主平面的方位：
tan
2a0
2 xy x
y
主应力与主平面的对应关系： max 与切应力的交点同象限
例题：一点处的平面应力状态如图所示。
已知 x 60MPa， xy 30MPa, y 40MPa, a 30。
试求（1）a 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。
x y cos 2a
2
x sin 2a
x
a
x y sin 2a
2
x cos 2a
300
10 30 2
10 30 cos 60020sin 600
2
2.32 MPa
300
10 30 sin 600 2
20cos 600
1.33 MPa
a
20 MPa
c
30 MPa
b
n1
y xy
a x
解：（1）a 斜面上的应力
y xy
a
x
2
y
x
2
y
cos 2a
xy
sin 2a
60 40 60 40 cos(60 ) 30sin(60 )
2
2
a x 9.02MPa
a
x
y
2
sin
2a
xy
cos
2a
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
2
1.33 MPa
300 600 x y 40 MPa
在二向应力状态下，任意两个垂直面上，其σ的和为一常数。
在二向应力状态下，任意两个垂直面上，其σ 的和为
一常数。
证明： a
x y
应力状态的概念
t xy 10MPa
600
600
n
s
40 (20) 2
40 (20) cos(1200 ) (10) sin(1200 ) 2
13.67MPa
t
40 (20) sin(1200 ) (10) cos(1200 ) 21MPa 2
20MPa
10MPa
300
40MPa
300
xn
解： s x 20MPa
P
A
P sx
sx
A
y
B
C z
P
sx B sx
Mx
tzx
txz
课堂练习
t yx
t C
xy
用单元体表达圆轴受扭时，轴表面任一点旳应力状态。
用单元体表达矩形截面梁横力弯曲时，梁顶、梁底及其他各
点旳应力状态。
七、主平面、主应力：
sy
y
主平面(Principal Plane)： 剪应力为零旳截面。
sx
sz
z
1 2 3
体积应变与应力分量间旳关系:
1 2
E
(s 1
s2
s3)
例5 已知一受力构件自由表面上某一点处于表面内旳主应变分别
为：1=24010-6， 3=–16010-6，弹性模量E=210GPa，泊松比 为 =0.3， 试求该点处旳主应力及另一主应变。
1 E
s
z
s
x s
y
xy
t
xy
G
yz
t
yz
G
zx
t zx
G
上式称为广义胡克定律
主应力 --- 主应变关系
s1 s3
1
1 E
材料力学-7-应力状态分析
7.1 应力状态的基本概念
y
y
1 1 4
z
4
Mz
x
x
l
S FP
2
3
Mx
z
3
a
第7章 应力状态分析
7.2 平面应力状态任意方向面上的应力 ——解析法
7.2 平面应力状态任意方向面上的应力 ——解析法
一、方向角与应力分量的正负号约定
x
正应力
x
x
拉为正
压为负
x
7.2 平面应力状态任意方向面上的应力 ——解析法
？
第7章 应力状态分析 7.1 应力状态的基本概念
7.2 平面应力状态任意方向面上的应力 ——解析法 7.3 主应力、主平面与面内最大切应力 ——解析法 7.4 应力圆及其应用——图解法
7.5 三向应力状态的特例分析
7.6 广义胡克定律
7.7 应变能密度
第7章 应力状态分析
tan 2q p＝－ 2 τ
xy
x y
主平面（principal plane）：切应力q＝0的方向面，用 qp表示。 主应力（principal stress）：主平面上的正应力。 主方向（principal directions）：主平面法线方向，用方 向角qp表示。
7.3 主应力、主平面与面内最大切应力 ——解析法
第7章 应力状态分析
第7章 应力状态分析
1
3
2
max
max
拉压、弯曲正应力 扭转、弯曲切应力
这些强度问题的共同特点是：
1、危险截面上的危险点只承受正应力 或切应力； 2、都是通过实验直接确定失效时的极限应力，并以此为依据建立强度 设计准则。 复杂受力：危险截面上危险点同时承受正 应力和切应力，或者危险点的其他面上同 时承受正应力或切应力。 → 强度条件
《应力状态分析》课件
意义
揭示了物体在受力状态下 内部应力的分布规律，为 分析强度、刚度和稳定性 问题提供依据。
空间应力状态的分类
单向应力状态
物体只承受单向正应力作 用，即一维应力状态。
二向应力状态
物体承受两个正交方向的 正应力作用，即平面应力 状态。
三向应力状态
物体承受三个正交方向的 的正应力作用，即空间应 力状态。
02 平面应力状态分析
平面应力状态的概念
平面应力状态
在二维平面上，各应力分量均平行于平面，且均沿z轴方向变化的 应力状态。
平面应力状态的特点
各应力分量均平行于平面，且均沿z轴方向变化。
平面应力状态的应用
在工程中，许多问题可以简化为平面应力状态进行分析，如薄板、 薄壳等结构的应力分析。
平面应力状态的分类
数值法
通过有限元、有限差分等方法求解平面应力状态 的应力和应变。
3
实验法
通过实验测试和测量平面应力状态的应力和应变 。
03 空间应力状态分析
空间应力状态的概念
01
02
03
空间应状态
描述物体内部各点应力矢 量在空间位置和方向上的 分布情况。
定义
空间中任意一点处的应力 状态由三个正交的主应力 及相应的主方向组成。
将物体离散化为有限个小的单元，对 每个单元进行受力分析，再通过单元 的集合得到整体的平衡方程，求解得 到各点的应力分量。适用于复杂几何 形状和边界条件的物体。
通过实验测试得到物体的应力应变关 系，从而反推出物体的应力状态。适 用于无法通过理论分析求解的复杂问 题。
05 应变与应力的关系
应变的概念
复杂应力状态的分类
按主应力大小分类
分为三向主应力状态和二向主应力状态。
材料力学-应力状态分析
+
σ x σ y
2
cos 2α τ x sin 2α
sin 2α + τ x cos 2α
注意： 的正负号， 注意：1）σx 、σy 、τx 和 α的正负号， 2） 公式中的切应力是τx ，而非τy， 而非 的正负号。 3） 计算出的σα和τα 的正负号。
τα τ α>0
τα τ α<0
图示圆轴中， 已知圆轴直径d=100mm， 轴向拉 例 ： 图示圆轴中 ， 已知圆轴直径 ， 力 F=500kN，外力矩Me=7kNm。求 C点α = 30°截 ， 外力矩 。 点 ° 面上的应力。 面上的应力。 y
σy
τ
D
x
τx τy
σx
o A2
C
A1
σ
D
y
σ1 =
σ x +σ y
2
σ x +σ y + 2
2 +τ x
2
2
σ2 =
σ x +σ y
2
σ x +σ y 2 +τ x 2
σy
τ
D
x
τx τy
σx
o A2
2α0
C
A1
σ
D
y
2τ x 2α 0 = arctan σ x σ y
σ x σ y R= 2
+τ x2
2
σ x +σ y σ α 2
σy
σ x σ y 2 2 + τα = +τ x 2 τ
2 2
D
x
τx τy
σx
o
C D
y
σ
50MPa
材料力学 第七章 应力状态和强度理论
y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
30
yx
y
e
x y sin 2 xy cos 2 2
xy
x
300 n
18.3MPa
f
50
(2) 求主应力和主单元体的方位
x = -40MPa， y =60MPa，
tg 2
0
x
2
xy
y
2(50) 1 40 60
xy = -50MPa。
(d)
pD 4t
n
（2）包含直径的纵向截面上的应力 用两个横截面 mm , nn 从圆筒部分 取出 单位长的圆筒研究。
m
n
p
m
1
n
17
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。
包含直径的纵向平面
直径平面
研究对象
R 是外力在 y 轴上的投影， 包含直径的纵截面上的内力为轴力 FN 。 该截面上的应力为正应力 ”，且 假设为均匀分布。
y
t p z
D
（a）
（b）
解：
包围内壁任一点，沿直径方向
取一单元体，单元体的侧面为 横截面，上，下面为含直径的 纵向截面，前面为内表面。 包含直径的纵向截面
横截面
内表面
（1）横截面上的应力 假想地，用一垂直于轴线的平面将汽包分成两部分，取右边为研 究对象。n— n面为横截面 。
n
p
n
图（d）研究对象的剖面图，其上的外力为压强 p。
1 2 3
2
1
3
7
（1）单轴应力状态：只有一个主应力不为零
（2）平面应力状态 ：有个二主应力不等于零。（参见教材定义）
8
（3）空间应力状态 ：主单元体上的三个应力均不等于零
平面和空间应力状态称为复杂应力状态
9
梁上取单元体
10
图（a）为汽包的剖面图。内壁受压强 p 的作用 。 图（b）给出尺寸。
因而从 构件表层取出的微分单元体 就接近二向应力状态。
这是最有实际意义的。
例：分析滚珠轴承中滚珠与外圈接触点的应力状态。 F
A
包围点 A ,以垂直和平行于压力 F 的平面截取单元体。
F
3
1
A A
2
单元体三个互相垂直的面皆为主平面，且三个主应力皆不为零， 于是得到三向应力状态。
§7-2 平面应力状态的分析 主应力
x y x y cos 2 xy sin 2 2 2
得到 max 和 min (主应力）
max min
}
x
y
2
(
x y
2
2
)
xy
2
42
（2）主平面的位置
2 xy
tan 2 0
α1
α 2 α 1 90
34
设斜截面的面积为 dA , eb 的面积为 dAcos ， bf 的面积为 dAsin
e
x
xy
dA cos
dA cos
e
dA
dA
b
yx
f
y
yxdA sin
ydA sin
35
b
f
（ 2 ）平面应力状态下, 任一斜截面 ( 截面 ) 上的应力 ¸ 的计算公式
{
26 -96
MPa
1 26MPa
2 0
A
3 96MPa
x
3
1
48
例题：图示单元体，已知 x = -40MPa， y =60MPa，
xy = -50MPa。试求 ef 截面上的应力情况及主应力和主单 元体的方位。 y
e
yx
xy
x
300 n
f
49
(1) 求 ef 截面上的应力
3
F A A
a
d
σ
b
σ
A
c
4
2. 单元体特征
（1）单元体的尺寸无限小，每个面上应力均匀分布；
（2）任意一对平行平面上的应力相等。
三、主应力和应力状态的分类 从一点处以不同方位截取的诸单元体中，有一个特殊的单元体， 在这个单元体侧面上只有正应力而无切应力。这样的单元体称为 该点处的 主单元体。
FN FN
p R
O
y t
FN
R 2
FN
d O
FN
取圆心角为 d 的微元面积，其 弧上为 ds
ds R
D ds d 2
微元面积为 dS.1 微元面积上，压强的合力为 p.1.ds y
FN
d O
FN
ds R
( p dS 1) sin
y p.1.ds 在 y 方向的投影为 ( p dS 1) sin
yx
y
1 xy x
67.5
0
3
52
例题：求平面纯剪切应力状态的主应力及主平面方位。
53
解：（1）求主平面方位
tg 2
0
x y
2
xy
20
{
900 900
0
{
45
0 0
45
54
450
0
{
45
0 0
45
因为 x = y ，且 xy > 0，所以
0ห้องสมุดไป่ตู้
x y
max min
}
x
y
2
(
x y
2
2
)
xy
2
以 1 代表 max作用面的方位角， 2 代表 min 作用面的方位角。
43
（ 1 在 900 范围内取值 ）
（1） 若 x y ， (2) 若 x y ， 则 ，1 450 则 ， 1 450 x 0 ， x 0 ， 1 = -450 1 = 450
平面应力状态的普遍形式如图 所示 。 单元体上有 x ，xy 和 y ，y 。
y
y
yx
a d xy
xy
σx
yx
c
σx
x
z
b
σy
32
一、解析法
1.斜截面上的应力
（1） 截面法: 假想地沿斜截面 ef 将单元体截分为二 ,留下左边部 分的单体元 ebf 作为研究对象。
y n e x
= 2
= 3
pD 2t
''
σ p
'''
单元体为 空间应力状态 ，三个正应力为 主应力。
= 1
1
2
= 2
= 3
由于内壁的压强 = p 远小于 和 ，所以可忽略不计。 单元体看作 平面应力状态
注 意
从构件的扭转和弯曲问题看最大应力往往发生在的外表面。 因为构件的外表面一般为自由表面，即有一主应力为零。
dA cos
dA cos
e
dA
dA
b yxdA sin
ydA sin
f
t
对研究对象列 和 t 方向的平衡方程并解之得：
36
x y x y cos 2 xy sin 2 2 2
x y
=-300
0
20
{
45
0 0
0
135
{
0
22.5 67.5
0
因为 x< y ，所以 1 67.5
对应于 1
51
max min
}
x y ( x y ) 2 xy 2 2
2
{
80.7 -60.7
1 80.7
2 0
3 60.7
38
x y d 2[ sin 2 xy cos 2 ] 0 d 2
tan 2 0
2 xy
x y
α α 90
α1
2 1
0
1 和 2 确定两个互相垂直的平面，一个是最大正应力 所在的平面，另一个是最小正应力所在的平面。
39
x y x y cos 2 xy sin 2 2 2 x y sin 2 xy cos 2 2
第 七 章 应力状态和强度理论
§7-1 概述
§7-2 平面应力状态的应力分析 主应力 §7-3 空间应力状态的概念
§7-4 应力与应变间的关系
§7-5 空间应力状态下的应变能密度 §7-6 强度理论及其相当应力 §7-7 莫尔强度理论及其相当应力 §7-8 各种强度理论的应用
1
§7-1 概述
一、一点处的应力状态: 1. 受力构件内一点处不同方位的截面上应力的集合,称为 一点处的应力状态。
x y d 0 2[ sin 2 xy cos 2 ] 0 d 2
正应力达到极值的面上，切应力必等于零。
此平面为主平面,正应力的极值为主应力。
40
由公式
tan 2 0
2 xy
x y
求出 0 就可确定主平面的位置。
41
（1）主应力 将 0 代入公式
FN
d O R
FN
dS
D d 2
yx
y
e
x y sin 2 xy cos 2 2
xy
x
300 n
18.3MPa
f
50
(2) 求主应力和主单元体的方位
x = -40MPa， y =60MPa，
tg 2
0
x
2
xy
y
2(50) 1 40 60
xy = -50MPa。
(d)
pD 4t
n
（2）包含直径的纵向截面上的应力 用两个横截面 mm , nn 从圆筒部分 取出 单位长的圆筒研究。
m
n
p
m
1
n
17
由截面法，假想地用 直径平面将取出的单 位长度的圆筒分成两 部分。取下半部分为 研究对象。
包含直径的纵向平面
直径平面
研究对象
R 是外力在 y 轴上的投影， 包含直径的纵截面上的内力为轴力 FN 。 该截面上的应力为正应力 ”，且 假设为均匀分布。
y
t p z
D
（a）
（b）
解：
包围内壁任一点，沿直径方向
取一单元体，单元体的侧面为 横截面，上，下面为含直径的 纵向截面，前面为内表面。 包含直径的纵向截面
横截面
内表面
（1）横截面上的应力 假想地，用一垂直于轴线的平面将汽包分成两部分，取右边为研 究对象。n— n面为横截面 。
n
p
n
图（d）研究对象的剖面图，其上的外力为压强 p。
1 2 3
2
1
3
7
（1）单轴应力状态：只有一个主应力不为零
（2）平面应力状态 ：有个二主应力不等于零。（参见教材定义）
8
（3）空间应力状态 ：主单元体上的三个应力均不等于零
平面和空间应力状态称为复杂应力状态
9
梁上取单元体
10
图（a）为汽包的剖面图。内壁受压强 p 的作用 。 图（b）给出尺寸。
因而从 构件表层取出的微分单元体 就接近二向应力状态。
这是最有实际意义的。
例：分析滚珠轴承中滚珠与外圈接触点的应力状态。 F
A
包围点 A ,以垂直和平行于压力 F 的平面截取单元体。
F
3
1
A A
2
单元体三个互相垂直的面皆为主平面，且三个主应力皆不为零， 于是得到三向应力状态。
§7-2 平面应力状态的分析 主应力
x y x y cos 2 xy sin 2 2 2
得到 max 和 min (主应力）
max min
}
x
y
2
(
x y
2
2
)
xy
2
42
（2）主平面的位置
2 xy
tan 2 0
α1
α 2 α 1 90
34
设斜截面的面积为 dA , eb 的面积为 dAcos ， bf 的面积为 dAsin
e
x
xy
dA cos
dA cos
e
dA
dA
b
yx
f
y
yxdA sin
ydA sin
35
b
f
（ 2 ）平面应力状态下, 任一斜截面 ( 截面 ) 上的应力 ¸ 的计算公式
{
26 -96
MPa
1 26MPa
2 0
A
3 96MPa
x
3
1
48
例题：图示单元体，已知 x = -40MPa， y =60MPa，
xy = -50MPa。试求 ef 截面上的应力情况及主应力和主单 元体的方位。 y
e
yx
xy
x
300 n
f
49
(1) 求 ef 截面上的应力
3
F A A
a
d
σ
b
σ
A
c
4
2. 单元体特征
（1）单元体的尺寸无限小，每个面上应力均匀分布；
（2）任意一对平行平面上的应力相等。
三、主应力和应力状态的分类 从一点处以不同方位截取的诸单元体中，有一个特殊的单元体， 在这个单元体侧面上只有正应力而无切应力。这样的单元体称为 该点处的 主单元体。
FN FN
p R
O
y t
FN
R 2
FN
d O
FN
取圆心角为 d 的微元面积，其 弧上为 ds
ds R
D ds d 2
微元面积为 dS.1 微元面积上，压强的合力为 p.1.ds y
FN
d O
FN
ds R
( p dS 1) sin
y p.1.ds 在 y 方向的投影为 ( p dS 1) sin
yx
y
1 xy x
67.5
0
3
52
例题：求平面纯剪切应力状态的主应力及主平面方位。
53
解：（1）求主平面方位
tg 2
0
x y
2
xy
20
{
900 900
0
{
45
0 0
45
54
450
0
{
45
0 0
45
因为 x = y ，且 xy > 0，所以
0ห้องสมุดไป่ตู้
x y
max min
}
x
y
2
(
x y
2
2
)
xy
2
以 1 代表 max作用面的方位角， 2 代表 min 作用面的方位角。
43
（ 1 在 900 范围内取值 ）
（1） 若 x y ， (2) 若 x y ， 则 ，1 450 则 ， 1 450 x 0 ， x 0 ， 1 = -450 1 = 450
平面应力状态的普遍形式如图 所示 。 单元体上有 x ，xy 和 y ，y 。
y
y
yx
a d xy
xy
σx
yx
c
σx
x
z
b
σy
32
一、解析法
1.斜截面上的应力
（1） 截面法: 假想地沿斜截面 ef 将单元体截分为二 ,留下左边部 分的单体元 ebf 作为研究对象。
y n e x
= 2
= 3
pD 2t
''
σ p
'''
单元体为 空间应力状态 ，三个正应力为 主应力。
= 1
1
2
= 2
= 3
由于内壁的压强 = p 远小于 和 ，所以可忽略不计。 单元体看作 平面应力状态
注 意
从构件的扭转和弯曲问题看最大应力往往发生在的外表面。 因为构件的外表面一般为自由表面，即有一主应力为零。
dA cos
dA cos
e
dA
dA
b yxdA sin
ydA sin
f
t
对研究对象列 和 t 方向的平衡方程并解之得：
36
x y x y cos 2 xy sin 2 2 2
x y
=-300
0
20
{
45
0 0
0
135
{
0
22.5 67.5
0
因为 x< y ，所以 1 67.5
对应于 1
51
max min
}
x y ( x y ) 2 xy 2 2
2
{
80.7 -60.7
1 80.7
2 0
3 60.7
38
x y d 2[ sin 2 xy cos 2 ] 0 d 2
tan 2 0
2 xy
x y
α α 90
α1
2 1
0
1 和 2 确定两个互相垂直的平面，一个是最大正应力 所在的平面，另一个是最小正应力所在的平面。
39
x y x y cos 2 xy sin 2 2 2 x y sin 2 xy cos 2 2
第 七 章 应力状态和强度理论
§7-1 概述
§7-2 平面应力状态的应力分析 主应力 §7-3 空间应力状态的概念
§7-4 应力与应变间的关系
§7-5 空间应力状态下的应变能密度 §7-6 强度理论及其相当应力 §7-7 莫尔强度理论及其相当应力 §7-8 各种强度理论的应用
1
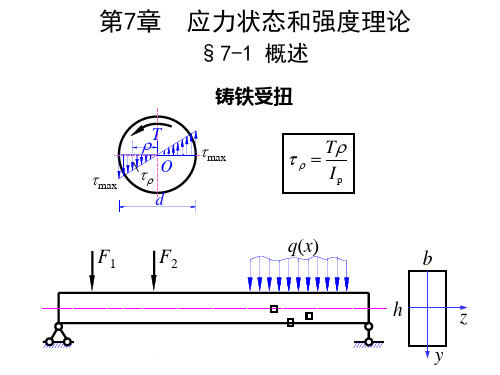
§7-1 概述
一、一点处的应力状态: 1. 受力构件内一点处不同方位的截面上应力的集合,称为 一点处的应力状态。
x y d 0 2[ sin 2 xy cos 2 ] 0 d 2
正应力达到极值的面上，切应力必等于零。
此平面为主平面,正应力的极值为主应力。
40
由公式
tan 2 0
2 xy
x y
求出 0 就可确定主平面的位置。
41
（1）主应力 将 0 代入公式
FN
d O R
FN
dS
D d 2