2(答案课件版)九年级上数学第五章反比例函数测试题
北师大版九年级数学上册第五章反比例函数(同步+复习)串讲精品课件

【例3】下列各题中,哪些是反比例函数关系
1. 三角形面积S一定时,它的底a与高h之间的 关系。 2. 多边形的内角和与边数的关系。 3. 正三角形的面积与边长之间的关系。 4. 长方形面积一定,长与宽的关系
正三角形面积=(√3/4)a2
【练习】下列各小题中,两个变量成 反比例的是( D )。
(A)时间不变时,匀速运动的路程与 速度. (B)商品的价格与需求量. (C)矩形的周长不变时,它的长与宽. (D)三角形面积不变时,它的底边与 这条底边上的高.
1. 2. 3. 形状及名称:双曲线(与两轴无交点)。 位置:k>0双曲线两个分支分别在一、三象 限;k<0双曲线两个分支分别在二、四象限 性质:
① 增减性: k>0时:图象在每个分支内是减函数; k<0时间:图象在每个分支内是增函数 ② 对称性:是轴对称图形,对称轴是直线y=x和y=x(两坐标轴的两条角平分线)。又是中心对称 图形,对称中心是原点。 ③ 过原点的任一直线与函数图象的两个分支的交点 是中心对称点(坐标互反,知一求一)。 ④ 特别注意每个分支这一条件,不在一个分支据实。
填表分析正比例函数和反比例函数的区别
函数 表达式
图象形状
位 置
正比例函数
y=kx ( k≠0 ) 直线 一三 象限
y随x的增大而增大
反比例函数
k y = x ( k是常数,k≠0 )
双曲线 一三 象限 每个象限内, y随
x的增大而减小
K>0
增 减 性
位 置
二四 象限
y随x的增大而减小
二四 象限
K<0
4.
反比例的意义:小学的名称,没有负数时的 算术概念。(可与正比例比较)。
【例1】
北师大版九年级上册数学第五章反比例函数复习题及答案

xyOA图2九年级数学上第五章反比例函数一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案1、(2010内蒙呼和浩特)已知:点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)是函数y=-x3图像上的三点,且x 1<0<x 2<x 3则y 1、y 2、y 3的大小关系是( ) A .y 1< y 2< y 3 B. y 2<y 3<y 1 C. y 3<y 2<y 1 D.无法确定2、已知函数1y x=的图象如图所示,当x≥-1时,y 的取值范围是( ) A.y <-1B.y≤-1C. y≤-1或y >0D. y <-1或y≥03、(2010吉林)反比例函数xky =的图象如图所示,则k 的值可能是( ) A .-1B .21C .1D .24、(2010云南曲靖)函数y=kx-k 与y )0(≠=k xk在同一坐标系中的大致图像是( )5、(2010湖北黄石)如图,反比例函数xk=y (k >0)与一次函数b x 21y +=的图象相交于两点A (1x ,1y ),B (2x ,2y ),线段AB 交y 轴与C ,当|1x -2x |=2 且AC = 2BC 时,k 、b 的值分别为( ) A.k =21,b =2 B.k =94,b =1 C.k =13,b =13 D.k =94,b =136、(2010辽宁大连)如图2,反比例函数11k y x=和正比例函数22y k x = 的图像都经过点(1,2)A -,若12y y >,则x 的取值范围是( ) A. 10x -<< B. 11x -<< C. 1x <-或01x << D. 10x -<<或1x >7、(2010 广西玉林、防城港)直线l 与双曲线C 在第一象限相交于A 、B 两点,AOy xB COAB Cxyy =x y1 xOA BC图3D P B y其图象信息如图4所示,则阴影部分(包括边界)横、纵坐标都是整数的点 (俗称格点)有( )A .4个B .5 个C .6个D .8个 8、(2010四川攀枝花)如图,等腰直角三角形ABC 位于第一象限,AB=AC=2, 直角顶点A 在直线y = x 上,其中A 点的横坐标为1,且两条直角边AB 、AC 分 别平行于x 轴、y 轴。
九年级上《反比例函数》单元测试卷含答案

《反比例函数》单元检测一.选择题(共10小题)1.已知函数y=(m+2)210mx-是反比例函数,且图象在第二、四象限内,则m 的值是( ) A .3 B .﹣3 C .±3D .﹣132.已知y 与x 成反比例函数,且x=2时,y=3,则该函数表达式是( ) A .y=6x B .y=16xC .y=6xD .y=16x - 3.函数y=ax ﹣a 与y=ax(a ≠0)在同一直角坐标系中的图象可能是( ) $A .B .C .D .4.若函数y=3m x+的图象在其所在的每一象限内,函数值y 随自变量x 的增大而减小,则m 的取值范围是( )A .m <﹣3B .m <0C .m >﹣3D .m >05.如图,点A 是反比例函数y=3x(x >0)的图象上任意一点,AB ∥x 轴交反比例函数 y=﹣2x的图象于点B ,以AB 为边作平行四边形ABCD ,其中C 、D 在x 轴上, 则S 平行四边形ABCD 为( )A .2B .3C .4D .5'6.(2016•天津)若点A (﹣5,y 1),B (﹣3,y 2),C (2,y 3)在反比例函数y=3x的图象上,则y 1,y 2,y 3的大小关系是( ) A .y 1<y 3<y 2 B .y 1<y 2<y 3C .y 3<y 2<y 1D .y 2<y 1<y 37.(2016•株洲)已知,如图一次函数y1=ax+b与反比例函数y2=kx的图象如图示,当y1<y2时,x 的取值范围是()A.x<2 B.x>5 C.2<x<5 D.0<x<2或x>58.在同一直角坐标平面内,如果直线y=k1x与双曲线y=2kx没有交点,那么k1和k2的关系一定是()A.k1+k2=0 B.k1•k2<0 C.k1•k2>0 D.k1=k2'9.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是()体积x(mL)10080604020、压强y(kPa)6075100150300A.y=3 000x B.y=6 000x C.y=3000xD.y=6000x10.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:25)能喝到不小于70℃的水,则接通电源的时间可以是当天上午的()|A.7:00 B.7:10 C.7:25 D.7:35二.填空题(共8小题)11.在①y=2x﹣1;②y=﹣ax;③y=5x﹣3;④y=15x中,y是x的反比例函数的有(填序号).12.(2016•邵阳)已知反比例函数y=kx(k≠0)的图象如图所示,则k的值可能是(写一个即可).】第10题图13.如图是三个反比例函数的图象的分支,其中k 1,k 2,k 3的大小关系是 . ,14.如图,正比例函数y=ax 的图象与反比例函数y=kx的图象相交于点A ,B ,若点A 的坐标为 、(﹣2,3),则点B 的坐标为 .15.已知反比例函数y=﹣8x,则有 ①它的图象在一、三象限:②点(﹣2,4)在它的图象上;③当l <x <2时,y 的取值范围是﹣8<y <﹣4;④若该函数的图象上有两个点A (x 1,y 1),B (x 2,y 2),那么当x 1<x 2时,y 1<y 2 以上叙述正确的是 .】16.(2016•荆州)若12x m ﹣1y 2与3xy n+1是同类项,点P (m ,n )在双曲线1a y x-=上,则a 的值为 .17.一定质量的二氧化碳,其体积V (m 3)是密度ρ(kg/m 3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=时,ρ= .&第13题图 第14题图第17题图第18题图18.在平面直角坐标系中,直线y=﹣x+2与反比例函数y=1x的图象有唯一公共点,若直线y=﹣x+b 与反比例函数y=1x的图象有2个公共点,则b 的取值范围是 .三.解答题(共6小题)19.己知函数y=25(2)k k x--为反比例函数.(1)求k 的值;(2)它的图象在第 象限内,在各象限内,y 随x 增大而 ;(填变化情况) `(3)求出﹣2≤x ≤﹣12时,y 的取值范围.20.在平面直角坐标系xOy 中,反比例函数y=kx(k >0)的图象经过点A (2,m ),连接OA ,在x 轴上有一点B ,且AO=AB ,△AOB 的面积为2. -(1)求m 和k 的值;(2)若过点A 的直线与y 轴交于点C ,且∠ACO=30°,请直接写出点C 的坐标.21.(2016•广安)如图,一次函数y 1=kx+b (k ≠0)和反比例函数y 2=mx(m ≠0)的图象交于点A (﹣1,6),B (a ,﹣2).(1)求一次函数与反比例函数的解析式; ](2)根据图象直接写出y 1>y 2时,x 的取值范围.22.如图,在平面直角坐标系xOy 中,菱形OABC 的顶点A 在x 轴的正半轴上,反比例函数y=12x的图象经过点C (3,m ). (1)求菱形OABC 的周长; (2)求点B 的坐标.)23.某物流公司要把3000吨货物从M 市运到W 市.(每日的运输量为固定值)(1)从运输开始,每天运输的货物吨数y (单位:吨)与运输时间x (单位:天)之间有怎样的函数关系式 &(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数. …24.已知反比例函数2ky x和一次函数y=2x ﹣1,其中一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点.(1)求反比例函数的解析式;(2)求反比例函数与一次函数两个交点A 、B 的坐标: (3)根据函数图象,求不等式2kx>2x ﹣1的解集;(4)在(2)的条件下,x轴上是否存在点P,使△AOP为等腰三角形若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.《反比例函数》单元检测—参考答案一.选择题(共10小题)1.B.2.C.3.D.4.C.5.D.6.D.7.D.8.B.9.D.10.B.二.填空题(共8小题)11.①④(填序号).12.﹣1(写一个即可).13.k1<k3<k2..14.(2,﹣3).15.②③.16.3.17.5kg/m3.18.b>2或b<﹣2.三.解答题(共6小题)?19.己知函数y=为反比例函数.(1)求k的值;(2)它的图象在第二、四象限内,在各象限内,y随x增大而增大;(填变化情况)(3)求出﹣2≤x≤﹣时,y的取值范围.【解答】解:(1)由题意得:k2﹣5=﹣1,解得:k=±2,∵k﹣2≠0,∴k=﹣2;!(2)∵k=﹣2<0,∴反比例函数的图象在二、四象限,在各象限内,y随着x增大而增大;故答案为:二、四,增大;(3)∵反比例函数表达式为4yx =-,∴当x=﹣2时,y=2,当12x=-时,y=8,∴当122x-≤≤-时,2≤y≤8.20.在平面直角坐标系xOy中,反比例函数y=kx(k>0)的图象经过点A(2,m),连接OA,在x轴上有一点B,且AO=AB,△AOB的面积为2.、(1)求m和k的值;(2)若过点A的直线与y轴交于点C,且∠ACO=30°,请直接写出点C的坐标.【解答】解:(1)由题意可知B(4,0),过A作AH⊥x轴于H.∵,AH=m,OB=4,∴,∴m=1,|∴A(2,1),∴k=2.(2)C(0,1+23)或C(0,1﹣23).21.(2016•广安)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=mx(m≠0)的图象交于点A(﹣1,6),B(a,﹣2).(1)求一次函数与反比例函数的解析式;(2)根据图象直接写出y1>y2时,x的取值范围.(【解答】解:(1)把点A (﹣1,6)代入反比例函数y 2=mx(m ≠0)得: m=﹣1×6=﹣6, ∴.将B (a ,﹣2)代入得:﹣2=6a-, a=3,∴B (3,﹣2), <将A (﹣1,6),B (3,﹣2)代入一次函数y 1=kx+b 得:632k b k b -+=⎧⎨+=-⎩∴24k b =-⎧⎨=⎩∴y 1=﹣2x+4.(2)由函数图象可得:x <﹣1或0<x <3.22.如图,在平面直角坐标系xOy 中,菱形OABC 的顶点A 在x 轴的正半轴上,反比例函数y=12x的图象经过点C (3,m ). (1)求菱形OABC 的周长; )(2)求点B 的坐标.【解答】解:(1)∵反比例函数y=12x的图象经过点C (3,m ),∴m=4.作CD ⊥x 轴于点D ,如图1, 由勾股定理,得OC==5.∴菱形OABC 的周长是20; ^(2)作BE ⊥x 轴于点E ,如图2, ∵BC=OA=5,OD=3, ∴OE=8.又∵BC ∥OA , ∴BE=CD=4, ∴B (8,4).23.某物流公司要把3000吨货物从M 市运到W 市.(每日的运输量为固定值) .(1)从运输开始,每天运输的货物吨数y (单位:吨)与运输时间x (单位:天)之间有怎样的函数关系式(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数. 【解答】解:(1)∵每天运量×天数=总运量 ∴xy=3000 ∴y=(x >0);(2)设原计划x 天完成,根据题意得:(1﹣20%)=,)解得:x=4经检验:x=4是原方程的根, 答:原计划4天完成.24.已知反比例函数2ky x和一次函数y=2x ﹣1,其中一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点.(1)求反比例函数的解析式;(2)求反比例函数与一次函数两个交点A 、B 的坐标: (3)根据函数图象,求不等式2kx>2x ﹣1的解集; (4)在(2)的条件下,x 轴上是否存在点P ,使△AOP 为等腰三角形若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由.【解答】解:(1)∵一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点, ∴b=2a ﹣1①,2a+2k ﹣1=b+k+2②,∴整理②得:b=2a ﹣1+k ﹣2, ∴由①②得:2a ﹣1=2a ﹣1+k ﹣2,∴k ﹣2=0,∴k=2,∴反比例函数的解析式为:y==1x; (2)解方程组, 解得:,,∴A (1,1),B (12,﹣2); (3)根据函数图象,可得出不等式2k x >2x ﹣1的解集; 即0<x <1或x ;(4)当AP 1⊥x 轴,AP 1=OP 1,∴P 1(1,0),当AO=OP 2,∴P 22,0),当AO=AP 3,∴P 3(2,0),当AO=P 4O ,∴P 42,0).∴存在P 点P 1(1,0),P 22,0),P 3(2,0),P 42,0).。
九年级(上)北师版数学第五章《反比例函数》测试题
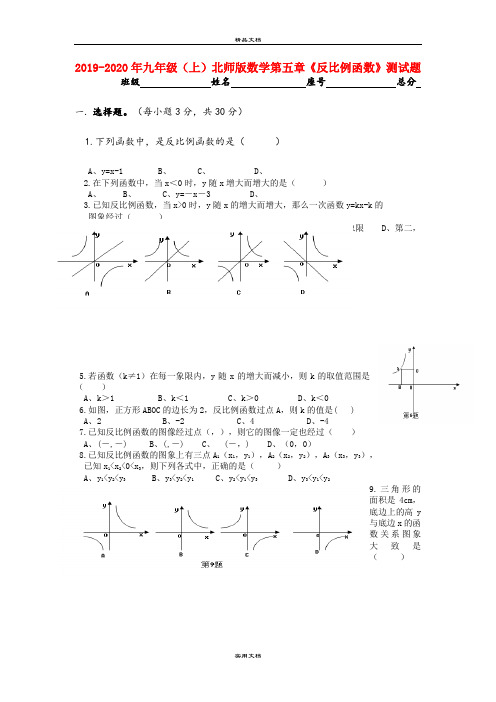
2019-2020年九年级(上)北师版数学第五章《反比例函数》测试题班级姓名座号总分一.选择题。
(每小题3分,共30分)1.下列函数中,是反比例函数的是()A、y=x-1B、C、D、2.在下列函数中,当x<0时,y随x增大而增大的是()A、 B、 C、y=-x-3 D、3.已知反比例函数,当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图象经过()A、第一,二,三象限B、第一,二,四象限C、第一,三,四象限D、第二,三,四象限4.函数y=kx(k≠0)和(k≠0)在同一坐标系中的图象是()5.若函数(k≠1)在每一象限内,y随x的增大而减小,则k的取值范围是()A、k>1B、k<1C、k>0D、k<06.如图,正方形ABOC的边长为2,反比例函数过点A,则k的值是( )A、2B、-2C、4D、-47.已知反比例函数的图像经过点(,),则它的图像一定也经过()A、(-,-)B、(,-)C、 (-,)D、(0,0)8.已知反比例函数的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1<x2<0<x3,则下列各式中,正确的是()A、y1<y2<y3B、y3<y2<y1C、y2<y1<y3D、y3<y1<y29.三角形的面积是4cm,底边上的高y与底边x的函数关系图象大致是()10.在同一直角坐标平面内,如果直线与双曲线没有交点,那么和的关系一定是( ) A 、 <0,>0 B 、 >0,<0 C 、、同号 D 、、异号 二.填空题。
(每小题3分,共30分)11、函数,当时没有意义,则 12、已知函数的图象如图所示,当x ≥-1时,y 的取值范围是_______________13、若反比列函数的图像经过二、四象限,则= _______14、如图,是反比例函数在第一象限内的图象,且过点A (2,1),与关于x 轴对称,那么图象的函数解析式为 。
部编版初中九年级数学反比例函数(含中考真题解析答案)

部编版初中九年级数学反比例函数(含中考真题解析答案)反比例函数(含答案)?解读考点知识点 1.反比例函数概念反比例函数概2.反比例函数图象念、图象和性3.反比例函数的性质质 4.一次函数的解析式确定名师点晴会判断一个函数是否为反比例函数。
知道反比例函数的图象是双曲线,。
会分象限利用增减性。
能用待定系数法确定函数解析式。
会用数形结合思想解决此类问题.反比例函5.反比例函数中比例系数的几何能根据图象信息,解决相应的实际问题.数的应用意义能解决与三角形、四边形等几何图形相关的计算和证明。
?2年中考【2021年题组】y?1.(2021崇左)若反比例函数kx的图象经过点(2,-6),则k的值为()A.-12 B.12 C.-3 D.3【答案】A.【解析】y?试题分析:∵反比例函数kx的图象经过点(2,��6),∴k?2?(?6)??12,解得k=��12.故选A.考点:反比例函数图象上点的坐标特征. 2.(2021苏州)若点A(a,b)在反比例函数A.0 B.��2 C.2 D.��6 【答案】B.【解析】y?y?2x的图象上,则代数式ab��4的值为()试题分析:∵点(a,b)反比例函数22b?x上,∴a,即ab=2,∴原式=2��4=��2.故选B.考点:反比例函数图象上点的坐标特征. 3.(2021来宾)已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是()- 1 -A. B. C.D.【答案】C.考点:1.反比例函数的应用;2.反比例函数的图象.4.(2021河池)反比例函数y1?mx(x?0)的图象与一次函数y2??x?b的图象交于A,B两点,其中A(1,2),当y2?y1时,x的取值范围是()A.x<1 B.1<x<2 C.x>2 D.x<1或x>2 【答案】B.【解析】试题分析:根据双曲线关于直线y=x对称易求B(2,1).依题意得:如图所示,当1<x<2时,y2?y1.故选B.考点:反比例函数与一次函数的交点问题.- 2 -5.(2021贺州)已知k1?0?k2,则函数y?k1x和y?k2x?1的图象大致是()A.【答案】C.B.C. D.考点:1.反比例函数的图象;2.一次函数的图象. 6.(2021宿迁)在平面直角坐标系中,点A,B的坐标分别为(��3,0),(3,0),点P在y?反比例函数2x的图象上,若△PAB为直角三角形,则满足条件的点P的个数为()A.2个 B.4个 C.5个 D.6个【答案】D.【解析】y?试题分析:①当∠PAB=90°时,P点的横坐标为��3,把x=��3代入此时P点有1个;22y??x得3,所以2222222(x?3)?()(x?3)?()22x,PB=x,AB2 ②当∠APB=90°,设P(x,x),PA=222222(x?3)?()?(x?3)?()222(3?3)xxPA?PB?AB==36,因为,所以=36,整理得2x4?9x2?4?0,所以x2?9?659?65x2?22,或,所以此时P点有4个;y?22y?x得3,所以此时P点有1个;③当∠PBA=90°时,P点的横坐标为3,把x=3代入综上所述,满足条件的P点有6个.故选D.考点:1.反比例函数图象上点的坐标特征;2.圆周角定理;3.分类讨论;4.综合题.7.(2021自贡)若点(的点,并且x1,y1),(x2,y2),(x3,y3y??),都是反比例函数1x图象上y1?0?y2?y3,则下列各式中正确的是()- 3 -A.D.x1?x2?x3 B.x1?x3?x2 C.x2?x1?x3x2?x3?x1【答案】D.【解析】试题分析:由题意得,点(的点,且(x1,y1)xy,xy,(2,2)(3,3)都是反比例函数y??1x上y1?0?y2?y3,xy,xy位于第三象限,x?x3,则(2,2)(3,3)y随x的增大而增大,2 x1,y1)位于第一象限,x1最大,故x1、x2、x3的大小关系是x2?x3?x1.故选D.考点:反比例函数图象上点的坐标特征.8.(2021凉山州)以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面y?直角坐标系,双曲线3x经过点D,则正方形ABCD的面积是()A.10 B.11 C.12 D.13 【答案】C.考点:反比例函数系数k的几何意义.y?9.(2021眉山)如图,A、B是双曲线kx上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()48A.3 B.3 C.3 D.4- 4 -【答案】B.考点:1.反比例函数系数k的几何意义;2.相似三角形的判定与性质. 10.(2021内江)如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点Ay?的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线有公共点,则k的取值范围为()kx与正方形ABCDA.1<k<9 B.2≤k≤34 C.1≤k≤16 D.4≤k<16 【答案】C.【解析】试题分析:点A在直线y=x上,其中A点的横坐标为1,则把x=1代入y=x解得y=1,则Ay?的坐标是(1,1),∵AB=BC=3,∴C点的坐标是(4,4),∴当双曲线kx经过点(1,1)时,k=1;当双曲线kx经过点(4,4)时,k=16,因而1≤k≤16.故选C.考点:1.反比例函数与一次函数的交点问题;2.综合题.- 5 -11.(2021孝感)如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函y?数1ky?x的图象上.若点B在反比例函数x的图象上,则k的值为()A.��4 B.4 C.��2 D.2【答案】A.考点:1.反比例函数图象上点的坐标特征;2.相似三角形的判定与性质;3.综合题.41012.(2021宜昌)如图,市煤气公司计划在地下修建一个容积为m3的圆柱形煤气储存室,则储存室的底面积S(单位:m2)与其深度d(单位:m)的函数图象大致是()- 6 -【答案】A.B. C. D.考点:1.反比例函数的应用;2.反比例函数的图象.y?13.(2021三明)如图,已知点A是双曲线2x在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为()A.n??2m B.【答案】B.【解析】n??24n??m C.n??4m D.m2试题分析:∵点C的坐标为(m,n),∴点A的纵坐标是n,横坐标是:n,∴点A 的坐22标为(n,n),∵点C的坐标为(m,n),∴点B的横坐标是m,纵坐标是:m,∴点B2nm?2222mmn??mn,∴m2n2?4,又∵m<0,n>0,∴的坐标为(m,m),又∵n,∴- 7 -mn??2,∴n??2m,故选B.考点:反比例函数图象上点的坐标特征.y?14.(2021株洲)从2,3,4,5中任意选两个数,记作a和b,那么点(a,b)在函数图象上的概率是()12x1111A.2 B.3 C.4 D.6【答案】D.考点:1.列表法与树状图法;2.反比例函数图象上点的坐标特征.OA3?OB4.15.(2021乌鲁木齐)如图,在直角坐标系xOy中,点A,B分别在x轴和y轴,∠y?AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数kx的图象2过点C.当以CD为边的正方形的面积为7时,k的值是()- 8 -A.2 B.3 C.5 D.7 【答案】D.考点:1.反比例函数综合题;2.综合题;3.压轴题. 16.(2021重庆市)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴y?平行,A,B两点的纵坐标分别为3,1.反比例函数ABCD的面积为()3x的图象经过A,B两点,则菱形A.2 B.4 C.22 D.42 【答案】D.【解析】y?试题分析:过点A作x轴的垂线,与CB的延长线交于点E,∵A,B两点在反比例函数3x的图象上且纵坐标分别为3,1,∴A,B横坐标分别为1,3,∴AE=2,BE=2,∴AB=22,S菱形ABCD=底×高=22×2=42,故选D.- 9 -考点:1.菱形的性质;2.反比例函数图象上点的坐标特征;3.综合题.17.(2021临沂)在平面直角坐标系中,直线y??x?2与反比例函数1y?x的图象有2个公共点,则b的取值范围是公共点,若直线y??x?b与反比例函数()y?1x的图象有唯一A.b>2 B.��2<b<2 C.b>2或b<��2 D.b<��2 【答案】C.考点:反比例函数与一次函数的交点问题. 18.(2021滨州)如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA12y??y?x、x的图象交于B、A两点,则∠OAB的大小的变化趋势为的两边分别与函数()- 10 -A.逐渐变小 B.逐渐变大 C.时大时小 D.保持不变【答案】D.考点:1.相似三角形的判定与性质;2.反比例函数图象上点的坐标特征;3.综合题. 19.(2021扬州)已知一个正比例函数的图象与一个反比例函数的一个交点坐标为(1,3),则另一个交点坐标是.【答案】(��1,��3).【解析】试题分析:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,∴另一个交点的坐标与点(1,3)关于原点对称,∴该点的坐标为(��1,��3).故答案为:(��1,��3).考点:反比例函数图象的对称性.20.(2021泰州)点(a��1,1)、(a+1,2)在反比例函数yyy?k?k?0?x的图象上,若y1?y2,- 11 -则a的范围是.【答案】��1<a<1.考点:1.反比例函数图象上点的坐标特征;2.分类讨论.y?21.(2021南宁)如图,点A在双曲线23ky?x(x?0)上,x(x?0)点B在双曲线上(点B在点A的右侧),且AB∥x轴.若四边形OABC是菱形,且∠AOC=60°,则k= .【答案】63.【解析】y?试题分析:因为点A在双曲线2323x(x?0)上,设A点坐标为(a,a),因为四23边形OABC是菱形,且∠AOC=60°,所以OA=2a,可得B点坐标为(3a,a),可得:3a?k=23a=63,故答案为:63.考点:1.菱形的性质;2.反比例函数图象上点的坐标特征;3.综合题. 22.(2021桂林)如图,以?ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直y?角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数交BC于D,连接AD,则四边形AOCD的面积是.kx的图象- 12 -【答案】9.考点:1.平行四边形的性质;2.反比例函数系数k的几何意义;3.综合题;4.压轴题. 23.(2021贵港)如图,已知点A1,A2,…,An均在直线y?x?1上,点B1,B2,…,y??Bn均在双曲线1x上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若则a2021= .a1??1,【答案】2.- 13 -考点:1.反比例函数图象上点的坐标特征;2.一次函数图象上点的坐标特征;3.规律型;4.综合题.24.(2021南京)如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1?1x,则y2与x的函数表达式是.【答案】【解析】y2?4x.试题分析:过A作AC⊥x轴于C,过B作BD⊥x轴于D,∵点A在反比例函数y1?1x上,11∴设A(a,a),∴OC=a,AC=a,∵AC⊥x轴,BD⊥x轴,∴AC∥BD,∴△OAC∽△ACOCOAACOCOA12?????OBD,∴BDODOB,∵A为OB的中点,∴BDODOB2,∴BD=2AC=a,- 14 -2k2y2?2a??4yx,∴k=aOD=2OC=2a,∴B(2a,a),设,∴2与x的函数表达式是:y2?44y2?x.故答案为:x.考点:1.反比例函数与一次函数的交点问题;2.综合题;3.压轴题.y?25.(2021攀枝花)如图,若双曲线kx(k?0)与边长为3的等边△AOB(O为坐标原点)的边OA、AB分别交于C、D两点,且OC=2BD,则k的值为.363【答案】25.- 15 -考点:1.反比例函数图象上点的坐标特征;2.等边三角形的性质;3.综合题.93(x>0)y?x26.(2021荆门)如图,点A1,A2依次在的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为.【答案】(62,0).- 16 -考点:1.反比例函数图象上点的坐标特征;2.等边三角形的性质;3.综合题;4.压轴题. 27.(2021南平)如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OCy?是△OAB的中线,点B,C在反比例函数于.3x(x?0)的图象上,则△OAB的面积等9【答案】2.考点:1.反比例函数系数k的几何意义;2.综合题. 28.(2021烟台)如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比y?例函数kx(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为.- 17 -15【答案】4.考点:1.反比例函数系数k的几何意义;2.反比例函数综合题;3.综合题. 29.(2021玉林防城港)已知:一次函数y??2x?10的图象与反比例函数y?kx(k?0)的图象相交于A,B两点(A在B的右侧).(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.(3)当A(a,��2a+10),B(b,��2b+10)时,直线OA与此反比例函数图象的另一支交BC5?BD2,求△ABC的面积.于另一点C,连接BC交y轴于点D.若y?【答案】(1)81?x,B(1,8);(2)(��4,��2)、(��16,2);(3)10.- 18 -【解析】y?试题分析:(1)把点A的坐标代入kx,就可求出反比例函数的解析式;解一次函数与反比例函数的解析式组成的方程组,就可得到点B的坐标;(2)①若∠BAP=90°,过点A作AH⊥OE于H,设AP与x轴的交点为M,如图1,对于y=��2x+10,当y=0时,��2x+10=0,解得x=5,∴点E(5,0),OE=5.∵A(4,2),∴OH=4,AH=2,∴HE=5��4=1.∵AH⊥OE,∴∠AHM=∠AHE=90°.又∵∠BAP=90°,∴∠AME+∠AEM=90°,∠AME+∠MAH=90°,∴∠MAH=∠AEM,∴△AHM∽△EHA,∴AHMH2MH??EHAH,∴12,∴MH=4,∴M(0,0),可设直线AP的解析式为y?mx,1?y?x??2??x?4811?y??y?xy?2?x,2,则有4m?2,解得m=2,∴直线AP的解析式为解方程组?得:??x??4?y??2,∴点P的坐标为(��4,��2)或?.1②若∠ABP=90°,同理可得:点P的坐标为(��16,2).?- 19 -1综上所述:符合条件的点P的坐标为(��4,��2)、(��16,2);?(3)过点B作BS⊥y轴于S,过点C作CT⊥y轴于T,连接OB,如图2,则有BS∥CT,CDCTBC5CTCD3????BD2.∵A(a,��2a+10)∴△CTD∽△BSD,∴BDBS.∵BD2,∴BS,B(b,��2b+10),∴C(��a,2a��考点:1.反比例函数综合题;2.待定系数法求一次函数解析式;3.反比例函数与一次函数的交点问题;4.相似三角形的判定与性质;5.压轴题.【2021年题组】1. (2021年湖南湘潭)如图,A、B两点在双曲线线段,已知S阴影=1,则S1+S2=()y?4x上,分别经过A、B两点向轴作垂- 20 -④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是(把所有正确的结论的序号都填上).【答案】①④.考点:1.反比例函数综合题;2. 反比例函数的图象和k的几何意义;3.平行四边形、矩形的性质和菱形的性质.- 26 -9. (2021年湖北荆州)如图,已知点A是双曲线y?2x在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线是.y?kx(k<0)上运动,则k的值【答案】��6.考点:1.单动点问题;2.曲线上点的坐标与方程的关系;3. 等边三角形的性质;4.相似三角形的判定和性质;5.锐角三角函数定义;6.特殊角的三角函数值.- 27 -10. (2021年江苏淮安)如图,点A(1,6)和点M(m,n)都在反比例函数y?kx(x>0)的图象上,(1)k的值为;(2)当m=3,求直线AM的解析式;(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.【答案】(1)6;(2)y=��2x+8;(3)直线BP与直线AM的位置关系为平行,.- 28 -考点:1.反比例函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.相似三角形的判定和性质;5.平行的判定.?考点归纳归纳 1:反比例函数的概念基础知识归纳:一般地,函数(k是常数,k0)叫做反比例函数。
北师大版九年级数学上册《6.1反比例函数》同步测试题及答案

北师大版九年级数学上册《6.1反比例函数》同步测试题及答案一、单选题1.下列函数:①y=x−2,②y=3x ,③y=x−1,④y=2x+1,⑤xy=11,⑥y=kx,⑦y=5x2,⑧yx=1.其中y是x的反比例函数的有()A.1个B.2个C.3个D.4个2.下列问题中,两个变量成反比例的是()A.商一定时(不为零),被除数与除数;B.等腰三角形周长一定时,它的腰长与它底边的长;C.一个因数(不为零)不变时,另一个因数与它们的积;D.货物的总价A一定时,货物的单价a与货物的数量x.3.当x=−3时,反比例函数y=−12x的函数值为()A.−14B.4C.−4D.144.下列各点在反比例函数y=−8x的图象上的是()A.(−2,−4)B.(2,4)C.(13,24)D.(−12,16)5.若一个反比例函数的图象经过A(2,−4)、B(m,−2)两点,则m的值为()A.−4B.4C.8D.−86.如果点A(a,−b)在反比例函数y=2x的图象上,则代数式ab−4的值为()A.0B.−2C.2D.−67.已知点A(3,m)和点B(n,2)关于x轴对称,则下列各点不在反比例函数y=mnx的图象上的点是()A.(3,−2)B.(−3,2)C.(−1,−6)D.(−1,6)8.现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).用小莉掷A立方体朝上的数字为x、小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在双曲线y=6x上的概率为()A.19B.23C.118D.16二、填空题9.已知反比例函数y=−8x的图像经过(−2,m),则m=10.已知反比例函数y=8x的图象经过点A(m,−2),则A关于原点对称点A′坐标为.11.已知y与x-2成反比例,且比例系数为k≠0,若x=3时,y=4,则k=.12.已知y−3与x+2成反比例,且x=2时y=7,则当y=1时,x的值为13.已知点A(x1,y1),B(x2,y2)都在反比例函数y=4x的图象上.若x1⋅x2=−2,则y1⋅y2的值为.14.点A(x1,y1),B(x2,y2)在反比例函数y=kx(k≠0)的图象上,若x1+x2=0,则y1+y2=.15.已知点P(a,b)是反比例函数y=1x 图像上异于点(-1,-1)的一个动点,则21+a+21+b=.16.如图,平面直角坐标系中,若反比例函数y=kx(k≠0)的图象过点A和点B,则a的值为.三、解答题17.已知y=(a−2)x a2−a−1,当a为何值时,y为x的正比例函数?当a为何值时,y为x的反比例函数?18.写出下列问题中的函数关系式,并指出其比例系数.(1)当圆锥的体积是150cm³时,它的高ℎ(cm)与底面积S(cm²)的函数关系式;(2)功是常数W时,力F与物体在力的方向上通过的距离s的函数关系式;(3)某实验中学八(2)班同学为校运动会制作小红花1000朵,完成的天数y与该班同学每天制作的数量x 之间的函数关系式;(4)某商场推出分期付款购买电脑的活动,一台电脑售价1.2万元,首期付款4千元后,分x次付清,每次付款相同. 每次的付款数y(元)与付款次数x的函数关系式.19.已知反比例函数y=−12x.(1)说出这个函数的比例系数和自变量的取值范围.(2)求当x=−3时函数的值.(3)求当y=−√3时自变量x的值.20.已知函数y=y1+y2,其中y1与x成正比例,y2与x−3成反比例,当x=2时y=16;当x=4时,y=20.求:(1)y关于x的函数解析式及定义域;(2)当x=5时的函数值.21.已知y−3与x+1成反比例关系,且当x=2时y=1.(1)求y与x的函数表达式.)是否在该函数图象上,并说明理由.(2)试判断点B(3,−1222.在面积为定值的一组矩形中,当矩形的一边长为7.5cm时,它的另一边长为8cm.(1)设矩形相邻的两边长分别为x(cm),y(cm),求y关于x的函数表达式.这个函数是反比例函数吗?如果是,指出比例系数.(2)若其中一个矩形的一条边长为5cm,求这个矩形与之相邻的另一边长.23.服装厂承揽一项生产1600件夏凉小衫的任务,计划用t天完成.(1)写出每天生产夏凉小衫w(件)与生产时间t(天)(t>4)之间的函数关系式;(2)服装厂按计划每天生产100件夏凉小衫,那么需要多少天能够完成任务?(3)由于气温提前升高,商家与服装厂商议调整计划,决定提前6天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务?参考答案:题号 1 2 3 4 5 6 7 8答案 C D B D B D C A(k≠0),xy=k(k≠0),y=kx−1(k≠0).1.解:反比例的三种形式分别为:y=kx①中x的次数是1,是一次函数,不是反比例函数;②,③是反比例函数;④中分母是x+1,故不是反比例函数;⑤是反比例函数;⑥中没有k≠0,故不是反比例函数;⑦分母是x2,故不是反比例函数;⑧中x的次数是1,是一次函数,不是反比例函数.故有三个是反比例函数.故选C.2.解:A、商一定时(不为零),被除数和除数成正比例关系,故A错误;B、等腰三角形周长一定时,它的腰长与它底边的长成一次函数关系;故B错误;C 、一个因数(不为零)不变时,另一个因数与它们的积成正比例关系;故C 错误;D 、货物的总价A 一定时,货物的单价a 与货物的数量x 成反比例关系;故D 正确. 故选D3.解:当x =−3时 故选:B .4.解:A.当x =−2时y =−8−2=4,故该点不在反比例函数y =−8x图象上;B. 当x =2时y =−82=−4,故该点不在反比例函数y =−8x 图象上; C. 当x =13时y =−813=−24,故该点不在反比例函数y =−8x 图象上;D. 当x =−12时y =−8−12=16,故该点在反比例函数y =−8x 图象上;故选:D .5.解:设反比例函数的表达式为y =kx(k ≠0)∵反比例函数的图象经过A(2,−4)、B(m ,−2)两点 ∵k =2×(−4)=−2m 解得:m =4 故选:B .6.解:∵点A(a ,−b)在反比例函数y =2x 的图象上 ∵−b =2a ∵ab =−2∵ab −4=−2−4=−6 故选D .7.解:∵点A (3,m )和点B (n,2)关于x 轴对称 ∵{m =−2n =3∵反比例函数解析式为y =mn x=−6x∵在反比例函数图象上的点一定满足横纵坐标的乘积为−6 ∵四个选项中只有C 选项符合题意 故选C .8.解:表格列示所有投掷情况如下小明小莉12345611,11,21,31,41,51,622,12,22,32,42,52,633,13,23,33,43,53,644,14,24,34,44,54,655,15,25,35,45,55,666,16,26,36,46,56,6点P若落在y=6x上,则xy=6.如上表,两人掷的组合情况共有6×6=36种,其中满足要求的有4种:2,3;3,2;1,6;6,1,故概率为436=19;故选:A9.解:把(−2,m)代入y=−8x即m=−8−2=4故答案为:4.10.解:∵反比例函数y=8x的图象经过点A(m,−2)∵−2m=8解得m=−4∴A(−4,−2)则A关于原点对称点A′(4,2)故答案为:(4,2).11.解:由题意知k=y(x-2)∵x=3时,y=4∵k=4×(3-2)=4.故答案为:412.解:∵y −3与x +2成反比例 ∵可设:y −3=k x+2(k ≠0)又∵x =2,y =7 ∵7−3=k 2+2解之得:k =16 ∵得:y −3=16x+2,即:y =16x+2+3∵当y =1时得:1=16x+2+3 解之得:x =−10 故答案为:−10.13.解:∵点A (x 1,y 1),B (x 2,y 2)都在反比例函数y =4x 的图象上∴x 1y 1=4,x 2y 2=4 ∴x 1y 1x 2y 2=16且x 1⋅x 2=−2 ∴y 1⋅y 2=−8. 故答案为:−8.14.解:∵点A(x 1,y 1),B(x 2,y 2)在反比例函数y =k x (k ≠0)的图象上 ∵y 1=k x 1,y 2=k x 2∵y 1+y 2=kx 1+kx 2=k(x 1+x 2)x 1x 2.∵x 1+x 2=0 ∵k(x 1+x 2)x 1x 2=0,即y 1+y 2=0.故答案为:0.15.解:∵点P(a,b)是反比例函数y =1x 图象上异于点(−1,−1)的一个动点∴ab =1∴ 21+a +21+b =2(1+b)(1+a)(1+b)+2(1+a)(1+a)(1+b)=2(1+b+1+a)1+b+a+ab=2(2+a+b)2+a+b=2.故答案为2.16.解:依题意,将点A (1,−3)代入y =kx ,得出k =−3∵反比例数解析式为y =−3x当x =−2时y =32即a =32 故答案为:32.17.解:当y 为x 的正比例函数时{a −2≠0a 2−a −1=1解得:a =−1.所以:当a =−1时,y 为x 的正比例函数. 当y 为x 的反比例函数时{a −2≠0a 2−a −1=−1解得:a =0或a =1.所以:当a =0或a =1时,y 为x 的反比例函数. 18.解:(1)∵hS=450,∵ℎ=450S,∵比例系数为450.(2)∵Fs=W ,∵F =W s,∵比例系数为W . (3)∵xy=1000,∵y =1000x,∵比例系数为1000.(4)∵xy=12000-4000,∵y =8000x,∵比例系数为8000.19.(1)解:∵y =−12x∵k =−12,x ≠0;(2)解:把x =−3,代入y =−12x 得:y =−12−3=4; ∵当x =−3时函数的值为:4;(3)解:把y =−√3,代入y =−12x 得:−√3=−12x ,解得:x =4√3;∵当y =−√3时x 的值为:4√3.20.(1)解:∵ y 1与x 成正比例,y 2与x −3成反比例 ∴设y 1=ax(a ≠0)∴y =y 1+y 2=ax +bx −3∵当x =2时y =16;当x =4时∴{2a +b2−3=164a +b4−3=20解得:a =6∴y =6x −4x −3∵x −3≠0 ∴x ≠3∴y =6x −4x −3(x ≠3) (2)解:由(1)可知y =6x −4x−3,则当x =5时y =6×5−45−3=28. 21.(1)解:设y −3=k x+1∵当x =2时y =1 ∵1−3=k2+1 ∵k =−6 ∵y =−6x+1+3; (2)不在;理由如下: 当x =3时y =−63+1+3=32∵B (3,−12)不在该函数图象上.22.(1)解:设矩形的面积为Scm 2,则S =7.5×8=60 即xy =60,y =60x即y 关于x 的函数解析式是y =60x,这个函数是反比例函数,系数为60;(2)解:当x =5时y =60x=12故这个矩形与之相邻的另一边长为12cm . 23.解:(1)根据题意,得wt =1600 所以w =1600t(t >4);(2)当w=100时1600t=100,解得t=16.即服装厂需要16天能够完成任务.(3)当t=16−6=10时w=1600t =160010=160(件).160−100=60(件)即服装厂每天要多做60件夏凉小衫才能完成任务.。
北师大版九年级上数学第五章反比例函数单元测试题
九年级上数学第五章《反比例函数》测试题(一)一、精心选一选,相信自己的判断!(每题2分共20分)1、下列函数中,反比例函数是( )A 、1)1(=-y xB 、11+=x y C 、21xy = D 、x y 31= 2、函数x k y =的图象经过点(-4,6),则下列各点中在xky =图象上的是( )A 、(3,8)B 、(3,-8)C 、(-8,-3)D 、(-4,-6) 3、若y 与-3x 成反比例,x 与z4成正比例,则y 是z 的( ) A 、正比例函数 B 、反比例函数 C 、一次函数 D 、不能确定 4、如果反比例函数xky =的图像经过点(-3,-4),那么函数的图像应在( ) A 、第一、三象限 B 、第一、二象限 C 、第二、四象限 D 、第三、四象限5、在同一坐标系中,函数ky =和3+=kxy 的图像大致是 ()6、正方形ABOC 的边长为2,反比例函数ky x=过点A ,则k 的值是( ) A .2B .2-C .4D .4-7、已知反比例函数的图像经过点(a ,b ),则它的图像一定也经过( ) A 、 (-a ,-b ) B 、 (a ,-b ) C 、 (-a ,b ) D 、 (0,0) 8、如上图,A 为反比例函数xky =图象上一点,AB 垂直x 轴于B 点,若S △AOB =3,则k 的值为( ) A 、6B 、3C 、23D 、不能确定9、若反比例函数22)12(--=m xm y 的图像在第二、四象限,则m 的值是( A 、-1或1 B 、小于21的任意实数 C 、-1 D、不能确定10、在同一直角坐标平面内,如果直线x k y 1=与双曲线xky 2=没有交点,那么1k 和2k 的关系一定是( )A 、1k <0,2k >0B 、1k >0,2k <0C 、1k 、2k 同号D 、1k 、2k 异号二、耐心填一填:(30分) 1、函数1y x a=-,当2x =时没有意义,则a 的值为 2、某物体对地面的压力为定值,物体对地面的压强p (Pa )与受力面积S (㎡)之间的函数关系如图所示.这一函数表达式为p=________3、反比例函数xky =的图像经过(-23,5)点、(a ,-3)及(10,b )点,则k = ,a = ,b = ;4、已知正比例函数kx y =与反比例函数3y x=的图象都过A (m ,1),则m = ,正比例函数与反比例函数的解析式分别是 、 ;5、反比例函数()0>=k xky 在第一象限内的图象如图,点M 是图像上一点,MP 垂直x 轴于点P ,如果 △MOP 的面积为1,那么k 的值是 ;6.在下列函数表达式中,表示y 是x 的反比例函数的有 。
第一学期北师大九年级数学上册:第五章反比例函数单元测试卷及答案
第一学期北师大九年级数学上册:第五章反比例函数单元测试卷及答案考试总分: 120 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 10 小题,每小题 3 分,共 30 分)1.当长方形面积一定时,长y与宽y之间的函数关系是()A.正比例函数B.反比例函数C.一次函数D.以上都不是2.圆柱的侧面积是10yyy2,则该圆柱的底面半径y(yy)关于高y(yy)的函数解析式的图象大致是()A. B.C. D.(y≠0)的图象的交点个数是()3.函数y=−yy与y=yyA.2B.1C.0D.不确定4.反比例函数y=6与一次函数y=y+1的图象交于点y(2, 3),利y用图象的对称性可知它们的另一个交点是()A.(3, 2)B.(−3, −2)C.(−2.−3)D.(−2, 3)5.三角形的面积为8yy2,这时底边上的高y(yy)与底边y(yy)之间的函数关系的图象大致是()第1页/共10页A.B.C.D.6.如图,矩形yyyy 的边分别与两坐标轴平行,对角线yy 经过坐标原点,点y 在反比例函数y =y 2−5y +10y(y >0)的图象上.若点y 的坐标为(−4, −4),则y 的值为( ) A.2B.6C.2或3D.−1或67.一个矩形面积为9,则这个矩形的一组邻边长y 与y 的函数关系的大致图象是( ) A.B.C.D.8.如图,在直角坐标系中,正方形的中心在原点y ,且正方形的一组对边与y 轴平行,点y (4y , y )是反比例函数y =yy (y >0)的图象上与正方形的一个交点,若图中阴影部分的面积等于16,则y 的值为( ) A.16 B.1 C.4D.−169.若函数y =y +1y是反比例函数,则y 的取值范围是( )A.y >−1B.y ≠−1C.y <−1D.y ≠010.如图.直线y =−y +y (y >0)与双曲线y =yy (y >0)交于y 、y 两点,连接yy 、yy ,yy ⊥y 轴于点y . yy ⊥y 轴于点y,以下结论错误的是()A.yy=yyB.△yyy≅△yyyC.当yy=√2时,yy=yy=yD.若yyyy=45∘,则y△yyy=y二、填空题(共 10 小题,每小题 3 分,共 30 分)11.函数y=12y的图象,在每一个象限内,y随y的值增大而________.12.反比例函数的图象是________.13.对于反比例函数y=15y,下列说法:①点(−3, −5)在它的图象上;②它的图象在第二、四象限;③当y>0时,y随y的增大而减小;④当y<0时,y随y的增大而增大.⑤它的图象不可能与坐标轴相交.上述说法中,正确的结论是________.(填上所有你认为正确的序号,答案格式如:“①②③④⑤”).14.如图,两个反比例函数y1=5y 和y2=3y,在第一象限内的图象依次是y1和y2,设点y在y1上,yy⊥y轴于点y,交y2于点y,yy⊥y轴于点y,交y2于点y,则四边形yyyy的面积为________.15.如图,设直线y=yy(y<0)与双曲线y=−5y相交于y(y1, y1),y(y2, y2)两点,则5y1y2−3y2y1的值为________.16.如图,y是反比例函数y=yy图象上一点,点y与坐标轴围成的矩形面积为3,则解析式为________.第3页/共10页17.阅读理解:对于任意正实数y、y,∵(√y−√y)2≥0,∴y−2√yy+y≥0,∴y+y≥2√yy,只有当y=y时,等号成立.结论:在y+y≥2√yy(y、y均为正实数)中,若yy为定值y,则y+y≥2√y,只有当y=y时,y+y有最小值2√y.根据上述内容,回答下列问题:(1)若y>0,只有当y=________时,y+1有最小值________.y(2)若y>0,只有当y=________时,2y+8有最小值________.y18.点(−1, y1),(2, y2),(3, y3)均在函数y=6的图象上,则y1,yy2,y3的大小关系是________.19.反比例函数y=−1的图象位于________.2y20.若y(3, 1),y(y, 4)均为某双曲线上的点,那么y=________.三、解答题(共 6 小题,每小题 10 分,共 60 分)21.已知y与y成反比例,且当y=3时,y=4.(1)求函数的关系式;(2)当y=3时,y的值是多少?222.如图,点y(y, 6),y(y, 1)在反比例函数图象上,yy⊥y轴于点y,yy⊥y轴于点y,yy=5.(1)求y,y的值并写出反比例函数的表达式;(2)连接yy,在线段yy上是否存在一点y,使△yyy的面积等于5?若存在,求出点y的坐标;若不存在,请说明理由.23.如图,一次函数y=yy+4的图象与y轴相交于点y,与反比例(y>0)的图象相交于点y(1, 6).函数y=yy(1)求一次函数和反比例函数的解析式;(2)设点y是y轴上一点,若y△yyy=18,直接写出点y的坐标.24.已知变量y−2与y成反比例,且y=2时,y=−2,求y和y之间的函数关系式,判断点y(4, 0)是否在这个函数的图象上.25.如图,在等腰梯形yyyy中,yy // yy,对角线yy⊥yy于y 点,点y在y轴上,点y、y在y轴上.(1)若yy=10,y(0, 8),求点y的坐标;(2)若yy=13√2,yy+yy=34,求过y点的反比例函数的解析式;(3)如图,在yy上有一点y,连接yy,过y作yy⊥yy交yy于y,交yy于y,在yy上取yy=yy,过y作yy⊥yy交yy于y,交yy于y,当y在yy上运动时,(不与y、y重合),yy的值是否发生yy变化?若变化,求出变化范围;若不变,求出其值.(y>0)的图象26.如图,直线yy:y=−y+7与反比例函数y=yy交点为y和y.(1)求反比例函数的解析式;(2)根据图象回答下列问题:①当y为何值时,一次函数的值等于反比例函数的值;②当y为何值时,一次函数的值大于反比例函数的值.答案1.B第5页/共10页2.C3.C4.B5.C6.D7.D8.C9.B 10.C 11.减小 12.双曲线 13.①③⑤ 14.2 15.10 16.y =−3y17.122818.y 1<y 3<y 2 19.第二、第四象限 20.3421.解:(1)设解析式y =yy,把y =3,y =4代入得y =3×4=12, 所以函数解析式为y =12y ;(2)当y =32时,y =1232=8.第7页/共10页22.解:(1)由题意得:{6y =yy +5=y,解得:{y =1y =6,∴y (1, 6),y (6, 1),设反比例函数解析式为y =yy , 将y (1, 6)代入得:y =6, 则反比例解析式为y =6y ; (2)存在,设y (y , 0),则yy =y −1,yy =6−y , ∵yy ⊥y 轴,yy ⊥y 轴, ∴yyyy =yyyy =90∘, 连接yy ,yy ,则y △yyy =y 四边形yyyy −y △yyy −y △yyy =12(yy +yy )⋅yy −12yy ⋅yy −12yy ⋅yy =12×(1+6)×5−12(y −1)×6−12(6−y )×1 =352−52y =5,解得:y =5, 则y (5, 0).23.解:(1)把y (1, 6)代入y =yy +4得:6=y +4, y =2,即一次函数的解析式是y =2y +4, 把y (1, 6)代入y =yy 得:6=y1,即反比例函数的解析式是y=6;y(2)把y=0代入y=2y+4得:2y+4=0,y=−2,即y的坐标是(−2, 0),分为两种情况:①当y在y的右边时,∵y△yyy=18,×yy×6=18,∴12yy=6,∵y(−2, 0),∴y(4, 0);②当y在y的左边时,y的坐标是(−8, 0).即y的坐标是(4, 0)或(−8, 0).24.解:∵变量y−2与y成反比例,∴可设y−2=y,y∵y=2时,y=−2,∴y=−2×2=−8,+2,∴y与y之间的函数关系式是y=−8y+2=0,把y=4代入得,y=−84∴点y(4, 0)在此函数的图象上.25.解:(1)在等腰梯形yyyy中,yy=yy=10又∵y(0, 8)∴yy=√102−82=6∴y(−6, 0)(2)作yy⊥yy于y,过y点作yy // yy交y轴于点y,∵yy // yy,yy // yy,∴yyyy是平行四边形,∴yy=yy,yy=yy,又∵yyyy为等腰梯形,∴yy=yy,∴yy=yy,而yy⊥yy,yy // yy,∴yyyy=yyyy=90∘,∵yy⊥yy,∴y为yy的中点,即yy为直角三角形yyy斜边yy上的中线,∴yy=12yy=12(yy+yy)=12(yy+yy)=12×34=17∵yy=13√2∴yy=√yy2−yy2=7∴yy=yy=yy=yy−yy=17−7=10∴y(10, 17)∴过y点的反比例函数的解析式为:y=170y(3)过点y作yy // yy交yy的延长线于点y,交yy的延长线于点y,过点y作yy // yy交yy于点y第9页/共10页易证四边形yyyy和四边形yyyy是平行四边形∴yy=yy=yy,yy=yy又∵yyyy=yyyy,yyyy=yyyy=yyyy∴△yyy≅△yyy∴yy=yy∵yy⊥yy,yy // yy,∴yyyy=yyyy=90∘,yyyy=yyyy=90∘−yyyy 由(2)知:yyyy=45∘,而yyyy=90∘,∴yy=yy∴△yyy≅△yyy∴yy=yy=yy=1∴yyyy(y>0)的图象过点y(1, 6),26.解:(1)∵反比例函数y=yy∴y=6.∴反比例函数的解析式为:y=6.y(2)由图象可知:①y=1或y=6;②1<y<6.。
北师大版九上数学第五章 反比例函数单元过关自测卷(含答案)
第五章 反比例函数单元过关自测卷(120分,90分钟)一、选择题(每题3分,共30分) 1.下列函数:①y =3x ;②y =3x ;③y =x -1;④y =1x+1,其中是反比例函数的有( ) A.1个 B.2个 C.3个 D.4个2.反比例函数y =21k x--的图象大致是图1中的( )图1 图23.反比例函数y =-2x的图象上有三个点A (-1,a ),B (-2,b ),C (2,c ),则下列结论正确的是( )A.c >b >aB.b >a >cC.c >a >bD.a >b >c4.如图2,正比例函数y 1=k 1x 和反比例函数y 2=2kx的图象交于A (-1,2)、B (1,-2)两点,若y 1<y 2,则x 的取值范围是( )A.x <-1或x >1B.x <-1或0<x <1C. -1<x <0或0<x <1D. -1<x <0或x >1 5.函数y =-ax +a 与y =a x-(a ≠0)在同一坐标系中的图象可能是图3中的( )图36.如图4,函数y =-x 与函数y =-4x的图象相交于A ,B 两点,过A ,B 两点分别作y 轴的垂线,垂足分别为点C ,D .则四边形ACBD 的面积为( ) A.2 B.4 C.6 D.8图4 图5 图67.如图5所示,过y 轴正半轴上的任意一点P 作x 轴的平行线,分别与反比例函数y =-4x和y =2x的图象交于点A 和点B .若点C 是x 轴上任意一点,连接AC ,BC ,则△ABC 的面积为( )A.3B.4C.5D.6 8.如图6所示,直线y =2x 与双曲线y =2x在第一象限的交点为A ,过点A 作AB ⊥x 轴于B ,将△ABO 绕点O 旋转90°,得到△A ′B ′O ,则点A ′的坐标为( ) A.(1,0) B.(1,0)或(-1,0) C.(2,0)或(0,-2) D.(-2,1)或(2,-1) 9.图7为反比例函数y =1x在第一象限的图象,点A 为此图象上的一动点,过点A 分别作AB ⊥x 轴和AC ⊥y 轴,垂足分别为B ,C .则四边形OBAC 的周长的最小值为( )A.4B.3C.2D.1 图710.如图8,若点M 是x 轴正半轴上任意一点,过点M 作PQ ∥y 轴,分别交函数y =1k x(x>0)和y =2k x(x >0)的图象于点P 和点Q ,连接OP 和OQ ,则下列结论正确的是( )A.∠POQ 不可能等于90°B.12k PM QM k C.这两个函数的图象一定关于x 轴对称 D.△POQ 的面积是12(|k 1|+|k 2|) 二、填空题(每题4分,共32分) 11.点P 在反比例函数y =kx(k ≠0)的图象上,点Q (2,4)与点P 关于y 轴对称,则反比例函数的关系式为.12.双曲线y=kx和一次函数y=ax+b的图象的两个交点分别为A(-1,-4)和B(2,m),则a+2b= .13.若函数y=(2m-1)x的图象与y=3mx-的图象的交点位于第一、三象限,则m的取值范围是.14.若反比例函数y=3kx-的图象位于第一、三象限,正比例函数y=(2k-9)x的图象经过第二、四象限,则k的整数值为.15.如图9,点A(x1,y1)、B(x2,y2)都在双曲线y=kx(x>0)上,且x2-x1=4,y1-y2=2.分别过点A、B向x轴、y轴作垂线,垂足分别为C、D、E、F,AC与BF相交于点G,四边形FOCG的面积为2,五边形AEODB的面积为14,那么k的值为.图9 图1016.在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图10所示,当V=10 m3时,气体的密度是.17.〈甘肃兰州〉如图11,点A在双曲线y=1x上,点B在双曲线y=3x上,且AB∥x轴,C、D在x轴上.若四边形ABCD为矩形,则它的面积为.图11 图1218.如图12,M为双曲线y过点M作x轴、y轴的垂线,分别交直线y=-x+m于D、C两点.若直线y=-x+m与y轴交于点A,与x轴交于点B,则AD·BC的值为.三、解答题(19,21题每题8分,20,22题每题9分,其余每题12分,共58分)19.已知反比例函数y=kx(k<0)的图象上有两点A(x1,y1)、B(x2,y2),且x1<x2,试确定y1-y2的符号.20.如图13所示,一次函数y=kx+b的图象与反比例函数y=mx的图象相交于A、B两点.(1)根据图象,分别写出A、B两点的坐标;(2)分别求出两函数的关系式;(3)根据图象回答:当x为何值时,一次函数的函数值大于反比例函数的函数值?图1321.已知一次函数y1=x+b(b为常数)的图象与反比例函数y2=kx(k为常数,且k≠0)的图象相交于点P(3,1).(1)求这两个函数的关系式;(2)当x>3时,试判断y1与y2的大小.22.某商场出售一批进价为2元的贺卡,在市场营销中发现,此贺卡的日销售单价x(单位:元)与日销售量y(单位:张)之间有如下关系:(1)根据表中数据在平面直角坐标系中描出实数对(x,y)的对应点;(2)确定y与x之间的函数关系式,并画出图象;(3)设销售此贺卡的日纯利润为w元,试求出w与x之间的函数关系式.若物价局规定该贺卡售价最高不超过10元/张,请你求出日销售单价x定为多少元时,才能获得最大日销售利润?23.如图14,已知正比例函数y =2x 的图象和反比例函数的图象交于点A (m ,-2). (1)求反比例函数的关系式;(2)观察图象,直接写出正比例函数的函数值大于反比例函数的函数值时自变量x 的取值范围;(3)若双曲线上点C (2,n )沿OA B ,判断四边形OABC的形状并证明你的结论.图1424.如图15所示,已知反比例函数y =13k x的图象与一次函数y =k 2x +m 的图象交于A (-1,a )、B 1,33⎛⎫⎪⎝⎭-两点,连接AO . (1)求反比例函数和一次函数的关系式;(2)设点C 在y 轴上,且与点A 、O 构成等腰三角形,请直接写出点C 的坐标.图15参考答案及点拨一、1. B 点拨:②③是反比例函数. 2. B 3. D4. D 点拨:y 1<y 2,反映在图象上就是直线在双曲线的下方,观察图象知,直线在双曲线的下方对应的x 的取值范围是-1<x <0或x >1,故选D .5. A 点拨:分两种情况来考虑:①当a >0时,函数y =-ax +a 的图象经过第一、二、四象限,函数y =a x-的图象经过第二、四象限.②当a <0时,函数y =-ax +a 的图象在第一、三、四象限,函数y =a x-的图象在第一、三象限.故只有A 选项正确. 6. D 点拨:∵过函数y =-4x的图象上A ,B 两点分别作y 轴的垂线,垂足分别为点C ,D ,∴S △AOC =S △ODB =12|k |=2,又∵OC =OD ,AC =BD ,∴S △AOC =S △ODA =S △OBC =2,∴四边形ACBD 的面积为:S △AOC +S △ODA + S △ODB +S △OBC =4×2=8.故选D .7. A 点拨:设OP =a (a >0),则点A的横坐标是-4a,点B的横坐标是2a .∴AB =2a-⎪⎭⎫ ⎝⎛-a 4=6a.∴S △ABC =12AB ·OP =12×6a×a=3.答图18. D 点拨:本题运用了方程思想,由题意得方程组2y 2x y x =⎧⎪⎨=⎪⎩,消去y 得:x 2=1.解得x =1或-1.∴y =2或-2,∴A (1,2),即AB =2,OB =1.根据题意画出相应的图形,如答图1所示,可得A ′B ′=A ″B ″=AB =2.OB ′=OB ″=OB =1,根据图形得所求点的坐标为(-2,1)或(2,-1).故选D.9. A点拨:根据已知条件可判断四边形OBAC为长方形.设宽OB=x,则AB=1 x.则x+1x≥2xx1⋅=2.当且仅当x=1x,即x=1时,取等号.故x+1x(x>0)的最小值为2,所以四边形OBAC的周长的最小值为2×2=4.10. D点拨:点P坐标未知,当PM=MO=MQ时,∠POQ=90°,故A错;根据图象可得k1>0,k2<0,而PM,QM为线段,故一定为正值,则PMQM=kk21,B错;C项中由于k1、k2不确定,所以这两个函数的图象不一定关于x轴对称,故C错;D项中,∵|k1|=PM·MO,|k2|=MQ·MO,∴S△POQ=12MO·PQ=12MO·(PM+MQ)=12MO·PM+12MO·MQ,∴S△POQ=12(|k1|+|k2|),故D正确.二、11. y=8x-点拨:∵Q(2,4)与点P关于y轴对称,∴P(-2,4).∵点P在反比例函数y=kx(k≠0)的图象上,∴4=2k-,即k=-8,∴y=-x8.12. -2 点拨:把(-1,-4)代入y=kx可得k=4.进而可求得m=2.将A,B两点的坐标分别代入y=ax+b,得a b42a b2-+=-⎧⎨+=⎩,,解得a2b2=⎧⎨=-⎩,,∴a+2b=2+2×(-2)=-2.13. 12<m<3 点拨:由题意得21030mm-⎧⎨-⎩>,>,解得12<m<3.14. 4 点拨:由题意可得k32k9-⎧⎨-⎩>,<,∴3<k<4.5,∴k的整数值为4.15. 616. 1 kg/m317. 2 点拨:过点A 作AE ⊥y 轴,垂足为E .∵点A 在双曲线y =1x 上,AE ⊥y 轴,AD ⊥x轴,∴四边形AEOD 的面积为1.∵点B 在双曲线y =3x上,且AB ∥x 轴,则E 、A 、B 三点共线,∴四边形BEOC 的面积为3.∴S 四边形ABCD =S 四边形BEOC -S 四边形AEOD =3-1=2.点拨:作CE ⊥x 轴于点E ,DF ⊥y 轴于点F ,由直线y =-x +m 易得A (0,m ),B (m ,0),则△OAB 为等腰直角三角形.又CE ∥y 轴,DF ∥x 轴,则△ADF 与△CEB 都是等腰直角三角形.设M (a ,b ),则ab且CE =b ,DF =a.则AD,BC,于是AD ·BC=2ab三、19. 解:①当A 、B 两点在同一象限,即x 1<x 2<0(或0<x 1<x 2)时,∵k <0,∴y 1<y 2,y 1-y 2<0,即y 1-y 2的符号为负;②当A 、B 两点在不同象限,即x 1<0<x 2时.∵k <0,∴y 1>0>y 2,y 1-y 2>0,即y 1-y 2的符号为正.综上可知,当A 、B 两点在同一象限时,y 1-y 2的符号为负,当A 、B 两点在不同象限时,y 1-y 2的符号为正.20. 解:(1)观察图象可知A (-6,-2)、B (4,3).(2)∵点B 在反比例函数y =m x 的图象上,∴把B 点的坐标代入y =mx ,得3=4m ,解得m =12.∴反比例函数的关系式为y =12x.又∵点A 、B 在一次函数y =kx +b 的图象上,∴把A 、B 两点的坐标分别代入y =kx +b ,得⎩⎨⎧=+-=+-.34,26b k b k 解得⎪⎩⎪⎨⎧==.1,21b k ∴一次函数的关系式为y =12x +1. (3)由图象可知,当-6<x <0或x >4时,一次函数的函数值大于反比例函数的函数值. 点拨:在比较两个函数的函数值的大小时,应注意分段比较.21. 解:(1)∵点P (3,1)在一次函数y 1=x +b 的图象上,∴1=3+b,解得b =-2.∴一次函数的关系式为y 1=x -2.∵点P (3,1)在反比例函数y 2=k x 的图象上,∴1=3k,解得k =3.∴反比例函数的关系式为y2=3 x.(2)y1>y2.22. 解:(1)略.(2)设函数关系式为y=kx,把点(3,20)代入y=kx中,得k=60.又将点(4,15),(5,12),(6,10)分别代入,均成立.∴y与x之间的函数关系式为y=60x.图象略.(3)w=(x-2)y=60-120x,∵函数值在x>0的范围内随x的增大而增大,又x≤10,∴当x=10时,w最大,即日销售单价x定为10元时,才能获得最大日销售利润.23. 解:(1)设反比例函数的关系式为y=kx(k>0),∵A(m,-2)在函数y=2x的图象上,∴-2=2m,∴m=-1,∴A(-1,-2).又∵点A在反比例函数y=kx的图象上,∴k=2.∴反比例函数的关系式为y=2 x.(2)观察图象可知正比例函数的函数值大于反比例函数的函数值时自变量x的取值范围为-1<x<0或x>1.(3)四边形OABC是菱形.证明:∵A(-1,-2),∴OA.由题意知:CB∥OA且CB CB=OA,∴四边形OABC是平行四边形.∵C(2,n)在反比例函数y=2x的图象上,∴n=1,∴C(2,1).则OC∴OC=OA,∴四边形OABC是菱形.24. 解:(1)∵反比例函数y=13kx的图象经过点B(13,-3),∴k1=3×13×(-3)=-3,∴反比例函数的关系式为y=-1x,又∵反比例函数y=-1x的图象经过点A (-1,a ),∴a =1.∴A (-1,1). 由一次函数y =k 2x +m 的图象经过点A (-1,1),B (13,-3)可得⎪⎩⎪⎨⎧-=+=+-,331,122m m k k ,解得23,2.m k ⎧⎪⎨⎪⎩=-=- ∴一次函数的关系式为y =-3x -2.(2)点C 的坐标为:(00,2)或(0,1).。
(数学试卷九年级)第五章反比例函数练习题及答案全套
一、判断题1.当x 与y 乘积一定时,y 就是x 的反比例函数,x 也是y 的反比例函数( ) 2.如果一个函数不是正比例函数,就是反比例函数 ( )3.y 与2x 成反比例时y 与x 并不成反比例( ) 二.填空题4.已知三角形的面积是定值S ,则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________; 5.如果y 与x 成反比例,z 与y 成正比例,则z 与x 成____ ___;6.如果函数222-+=k kkx y 是反比例函数,那么k=________,此函数的解析式是____ ____;7. 有一面积为60的梯形,其上底长是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是______________三、选择题:8.如果函数12-=m x y 为反比例函数,则m 的值是 ( )A 1-B 0C 21 D 19.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
在课堂上,李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图,同学们画出的示意图如下,你认为正确的是( )10、下列函数中,y 是x 反比例函数的是( )(A ) 12+=x y (B )22xy = (C )x y 51=(D )x y =2 四.辨析题(1)兄弟二人分吃一碗饺子,每人吃饺子的个数如下表:①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式(不要求写xy 的取值范围).②虽然当弟吃的饺子个数增多时,兄吃例吗? (2)水池中有水若干吨,若单开一个出水口,水流速v 与全池水放光所用时t 如下表:①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系. ②这是一个反比例函数吗? 兄(y )29 28 27 26 …… 3 2 1——……→逐渐减少弟(x )1 2 3 4 …… 27 28 29 ——……→逐渐增多§5.1反比例函数③与(1)的结论相比,可见并非反比例函数有可能“函数值随自变量增大而减小”,反之,所有的反比例函数都是“函数值随自变量的增大而减小吗?这个问题,你可以提前探索、尝试,也可以预习下一课时”反比例函数的图象和性质,也可以等到下一节课我们共同解决.五.已知□ABCD 中,AB = 4,AD = 2,E 是AB 边上的一动点,设AE=x ,DE 延长线交CB 的延长线于F ,设CF =y ,求y 与x 之间的函数关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
法2:(代入求值法)由 题意得 7 y1 5 y 2 2 2 2 y1 ,y 2 7 5 y1 y 2
3 y 2 x k 分析:由题意得可设 y 2 x k 把x 3, y 1代入上式 1 2 , 解得k 3 3 3 3 y2 整理得 y 2 x x
2 1 反比例函数的表达式为 y 2x x
解: (1)把 A (a, b),C (a 1, b k )代入y 2 x 1 中,
b 2a 1 得 b k 2a 1 ② ①, 得k 2 ① ②
2 1 反比例函数的表达式为 y 2x x
AD 3 1 2 1 1 10 10 S ABC BC AD 2 2 2 3 3
解: (1)把 A (a, b),C (a 1, b k )代入y 2 x 1 中,
b 2a 1 得 b k 2 a 1 1 ② ①, 得k 2 ① ②
m (3)根据图像可知当x 6或0 x 4时,kx b 0. x
注意:分段函数需 要把自变量的取值 范围写出来!!
解: (1) 设药物燃烧时m与t的关系式 (0 t 10) 为m k1 t 4 把(10,8)代入m k1 t中,得k1 5 4 药物燃烧时 m与t的关系式为m t(0 t 10) 5
一次函数的表达式为 y x 4 y x 4 x1 3 x 2 1 ( 2)解方程组 , 得 B为(3, 1) 3 y y 1 1 y 2 3 x
解: (1) A( 6,2)、B(4,3) m (2)把(4,3)代入y 中,得m 4 3 12 x 12 反比例函数解析式为 y x 把A(4,3),B(6,2)代入y kx b中,
A
ab
因为k a b ab 所以只要符合 xy ab即可
ab函数的定义. 反比例函数可以写成 y kx 1 ( k 0, k为常数)
2 m 1 m 2 1 解得 1 解:由题意得 m 2m 1 0 2
∵A在第一象限
∴A的坐标为 1, 1
m 得m 1 (3) 3 解:( 1)把( 1,3)代入y 中, x 3 反比例函数的表达式为 y x 3 k b 把 A (1,3),C (0,4)代入y kx b中,得 4 b k 1 解得 b 4
解: (1) 设药物燃烧时m与t的关系式为 m k1 t (0 t 10). 4 把(10,8)代入m k1 t中,得k1 5 4 药物燃烧时 m与t的关系式为m t(0 t 10) 5 k2 ( 2) 设药物燃烧后 m与t的关系式为m ( t 10). t k2 把(10,8)代入m 中,得k 2 80 t 80 药物燃烧后m与t的关系式为m (t 10) t 80 (3)由题意得 1.6,解得t 50 t 答:从消毒开始,经过50分钟后才可以回教室 .
D
k 考点:可以写成 y ( k 0, k为常数) x
A
B
C
D
1 可以写成 y 1 , 那么 y 1是x的反比例函数 x y是x 1的反比例函数
y是x 2的反比例函数
1 可以写成 y 3 , 所以y是x的反比例函数 x
B
因为k 4 6 24, 所以只要符合 xy 24即可
3m 2 0
1 3 点(m, 1)在反比例图像上,得m 1 3, 得m 3
3
1 把(3, 1)代入y kx中得1 3k , 解得k 3
①② ③④
三
20 S h
圆柱的体积 底面积 高
y1 y 2
法1:(图像性质法) k 0, 在每个象限内,y值随x值增大而增大 7 5 y1 y 2
24
A
考点:
k 3 4 12 0
当k 0时,在一、三象限 k 反比例函数 y 的图像 x 当k 0时,在二、四象限
A
画草图法:这种题型一 般要分情况讨论
①k 0
②k 0
D
分析: k S正方形ABOC 2 4
2
图像在第二象限 k 4
m 1
A
k 1 (1) 1
一次函数为y x 2 ①它的图像过( 0, 2) ②k 0,图像从左往右是下降的
C
1 三角形面积 底 高 2
1 xy 2 2 xy 4 4 y ( x 0) x
2
分母为 0时无意义 2 3
m 解: (1)把(1,2)代入y kx 1和y 中, x 2 k 1
k 1 得 , 解得 m 2 b2 1 2 反比例函数为y ,一次函数为y x 1. x
(2)在y x 1 中, 令x 3, 得y 4, 则B为(3,4) 2 2 2 在y 中,令x 3, 得y , 则C为(3, ) 3 x 3 2 10 BC 4 3 3 过点A作AD BC , 垂足为D
1 3 4k b k 得 解得 2 2 6k b b 1
m (3)根据图像可知当x 6或0 x 4时,kx b 0. x
v
v
v
v
(3)的题意为:当 x为何值时,一次函数的 值小于反比例函数的值?
m 分析:变形得kx b x
解: (1) 蓄水池的容积为 8 6 48m 3 48 ( 2) t与Q的关系式为 t (Q 0 ) Q 48 (3)由题意得 5,解得Q 9.6 Q 答:每小时的排水量 至少为 9.6m 3 48 48 (4)Q ,由题意得 12,解得t 4 t t 答:最少4小时可将满池水全部排空.
2 2 ②若OA OP, OA 1 1 2
OP 2
P为( 2, 0)或( 2, 0)
③若PO PA, A(1,1) AOP OAP 45 APO 90 OP 1 P为(1, 0)
综上所述:符合条件的 点为 ( 2,0)、 ( 2 ,0)、 ( 2 ,0)、 (1,0).
y 2x 1 ( 2)解方程组 1 y x 1 x 1 x , 得 2 或 y1 y 2
∵A在第一象限 ∴A的坐标为 1, 1,B的坐标为 1,-1 .
(2)存在。有 4个满足条件的点.
①若AO AP , 过点A作AD OP , 垂足为D, OP 2OD 2 P为(2, 0)
4
S1 S 2 3 1 2
0 y1
y 1或y 0
x2
x 2且x 0
分析:求两个函数的图 像交点,都是通过解方程组求得.
y x 解:解方程组 1 y x
x 1 1 x 2 1 , 得 , y 1 1 y 2 1
