任意角的三角函数导学案幻灯片
任意角的三角函数课件

• 弧度制与角度制 • 三角函数的基本性质
任意角的三角函数
在这一部分,我们将深入研究弧度制下和角度制下的任意角三角函数,包括它们的定义、图像和周期性。
实际应用
三角函数在几何、物理和工程等领域有广泛的应用,我们将探讨它们在不同领域中的具体应用。 • 三角函数在几何中的应用 பைடு நூலகம் 三角函数在物理中的应用 • 三角函数在工程中的应用
总结
本课程介绍了任意角的三角函数的基本知识和实际应用,希望能够帮助大家 深入理解和应用三角函数。
• 本课程的主要内容 • 三角函数的重要性 • 继续学习三角函数的建议
任意角的三角函数ppt课件
这是一份关于任意角的三角函数的PPT课件,通过图文并茂的方式介绍任意角 的三角函数的基本知识和实际应用。
引言
任意角是指不限制在标准位置的角度,研究任意角的三角函数可以帮助我们 深入理解三角函数的性质和应用。
• 什么是任意角? • 为什么需要研究任意角的三角函数?
基础知识
高中数学三角函数121任意角的三角函数(一)PPT课件

6
6 62
3.已知角α的终边与单位圆的交点 P( 5 , 2 5 ),则
55
sinα+cosα= ( )
A . 5 B .5 C .25 D . 25
5
5
5
5
【解析】选B.因为 siny25,cosx5,
5
5
所以 sincos2555.
55 5
4.若角α终边上一点坐标为(-5,12),则cosα=
1.2 任意角的三角函数 1.2.1 任意角的三角函数(一)
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
概况三
点击此处输入相关文本内容 点击此处输入相关文本内容
【自主预习】 主题1:任意角的三角函数的定义 使锐角α的顶点与原点O重合,始边与x轴的非负半轴 重合,在终边上任取一点P,作PM⊥x轴于M,设P(x,y), |OP|=r,据此回答下列问题:
主题2:三角函数值的符号法则及诱导公式一
1.设P(x,y)为α终边上任意一点(异于原点),记r=|OP|,
则 sin y,c o s x,ta n y(x 0 ),由此可知任意角α
r
r
x
的三角函数值的符号与谁有关?
提示:角α的三角函数值的符号与点P的坐标x,y的正负
有关.
2.取角α分别为30°,390°,-330°,它们的三角函数值是 什么关系?为什么? 用文字语言描述:它们的同名三角函数值相等,因为三 个角的终边相同.
2.已知角α,则角α的三角函数值符号确定,反之若角 α的某个三角函数值符号确定,则角α的终边所在象限 确定吗? 提示:不一定,若已知角α的一个三角函数值的符号,则 角α所在的象限可能有两种情况,若已知角α的两个三 角函数值的符号,则角α所在的象限就唯一确定.
导学案任意角的三角函数
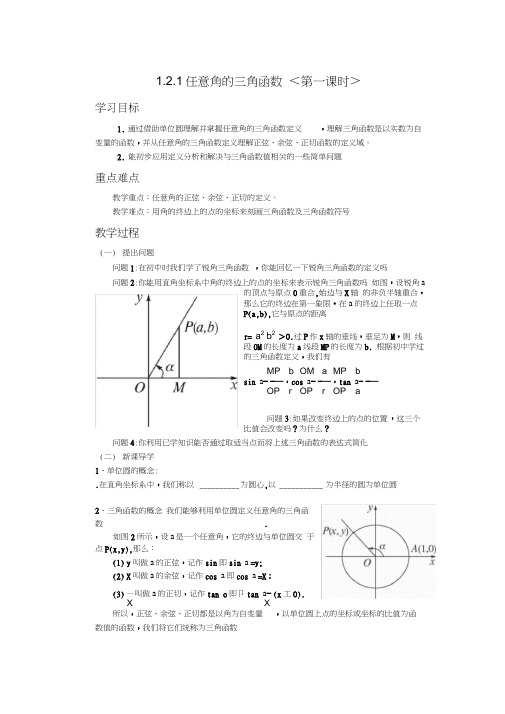
1.2.1任意角的三角函数<第一课时>学习目标1.通过借助单位圆理解并掌握任意角的三角函数定义,理解三角函数是以实数为自变量的函数,并从任意角的三角函数定义理解正弦、余弦、正切函数的定义域。
2.能初步应用定义分析和解决与三角函数值相关的一些简单问题重点难点教学重点:任意角的正弦、余弦、正切的定义。
教学难点:用角的终边上的点的坐标来刻画三角函数及三角函数符号教学过程(一)提出问题问题1:在初中时我们学了锐角三角函数,你能回忆一下锐角三角函数的定义吗问题2:你能用直角坐标系中角的终边上的点的坐标来表示锐角三角函数吗如图,设锐角a的顶点与原点0重合,始边与X轴的非负半轴重合,那么它的终边在第一象限•在a 的终边上任取一点P(a,b),它与原点的距离r= a2 b2>0.过P作x轴的垂线,垂足为M,则线段0M的长度为a线段MP的长度为b. 根据初中学过的三角函数定义,我们有MP b OM a MP bsin a= =—,cos a= =—,tan a= =—OP r OP r OP a问题3:如果改变终边上的点的位置,这三个比值会改变吗?为什么?问题4:你利用已学知识能否通过取适当点而将上述三角函数的表达式简化(二)新课导学1、单位圆的概念:.在直角坐标系中,我们称以__________ 为圆心,以 ___________ 为半径的圆为单位圆2、三角函数的概念我们能够利用单位圆定义任意角的三角函数.如图2所示,设a是一个任意角,它的终边与单位圆交于点P(x,y),那么:(1)y叫做a的正弦,记作sin即sin a =y;(2)X叫做a的余弦,记作cos a即cos a =X;(3)—叫做a的正切,记作tan o即卩tan a= (x工0).X X所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数注意:(1)正弦、余弦、正切、都是以角为自变量 ,以比值为函数值的函数•(2)由相似三角形的知识,对于确定的角 a 这三个比值不会随点 P 在a 的终边上的 位置的改变而改变•3、例1 求 5的正弦、余弦和正切值•思考:若把角5、探究三角函数值在各象限的符号三角函数 定义域sincostan探究三角函数的定义域 4、 练习1:已知角B 的终边经过点 P( 12,5),求角B 正弦、余弦和正切值。
任意角的三角函数-课件1PPT课件一等奖新名师优质课获奖比赛公开课

m5
m5
m ________.
(4)若角 旳终边过点 Pa,8,且 cos 3 ,
5
则 a ________.
(5)角 旳终边在直线 y 2x上,求 旳六个三
角函数值.
正弦上为正, 余弦右为正, 正切余切一三正, 其他为负不为正
例2:
1、判断下列各三角函数旳符号 A.260 B. 4 C. 672 10 D.11 3
2、若sin 0且 tan 0,那么是第几象限角?
3、已知是第三象限角,试判定: sin( cos ) cos(sin )的符号
练习:
(1)若角 终边上有一点P 3,0,则下列函数值不
§1.2.1 任意角旳三角函数
设 是任意角, 旳终边上任意一点 P旳坐标是x,y,
当角 在第一、二、三、四象限时旳情形,它与原点
旳距离为 r ,则 r x 2 y 2 x2 y2 0 .
任意角旳三角函数
1、定义:
①比值 y 叫做 旳正弦,记作sin ,即 sin y .
r
r
x
②比值
叫做
旳余弦,记作cos ,即cos
Байду номын сангаас
x
.
r
r
③比值 y 叫做 旳正切,记作tan,即 tan y .
x
x
④比值 x 叫做 旳余切,记作cot ,则 cot x .
y
y
⑤比值 r 叫做 旳正割,记作sec ,则 sec r .
x
x
⑥比值 r 叫做 旳余割,记作csc ,则csc r .
y
y
我们把正弦、余弦,正切、余切,正割及余割都 看成是以角为自变量,以比值为函数值旳函数,以上 六种函数统称三角函数.
任意角的三角函数(优质课)精品PPT课件

cos 的值
变式3:已知角θ的终边在直线y= 43x上 求θ的三个三角函数值
y
o
x
例2 确定下列三角函数值的符号:
(1) cos 7 ;
12
(2) sin( 465);
(3) tan 11 .
3
解: (1) 7 是第二象限角,所以 cos 7 0.
12
12
(2) 因为 465 2 360 225,即 465是第三象限角,所以 sin(465) 0.
课本练习P15T1、T2、T3
返回目录
四:归纳小结
1.任意角的三角函数的定义; 2.三角函数的定义域、符号; 3.数学思想方法:类比思维、 数形结合、分类讨论思想.
返回目录
五:布置作业
1:课本P22页T1 、T5
返回目录
学习总结
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
苏教版高中数学必修4
任意角的三角函数
一:设置情境 二:建构数学 三:例题精讲 四:归纳小结 五:布置作业
一:设置情境
问题1:在初中,锐角的三角函数是如何定义的?
图形
定义
B
c
a
Ab C
sin
A
a c
对边 斜边
cos
A
b c
邻边 斜边
tan
A
a b
对边 邻边
问题2:怎样将锐角三角函数推广到任意角的三角函数?
演讲人:XXXXXX 时 间:XX年XX月XX日
(3) 因为 11 2 5 ,即 11 是第四象限角,所以
任意角的三角函数ppt

sin MPb
OP r
MP b OP r a 2 b 2
c os OMa
OP r
y
﹒Pa,b
tan MPb
OM a
o
﹒
Mx
如果改变点P在终边上的位置, 这三个比值会改变吗?
M
﹒
P
O
x
P(a,b)
M
∽ OMP
y 探究
3.锐角三角函数(在单位圆中)
若OPr1,则
以原点O为圆心,以单位
长度为半径的圆,称为单位圆.
r
tan yx0
x
任意角 的三角函数值仅与 有关,而与P点 在
角的终边上的位置无关.
练习 1、已知角 的终边过P12,5
点
,
求
的三个三角函数值.
解:由已知可得:
rx2y212 25213
于是,sin y 5
r 13
tan y 5
x 12
c os x 12
r 13
2 、 已 知 角 的 终 边 上 一 点 P 1 5 a , 8 a a R 且 a 0 ,
的正弦、余弦和正切值 .
,求角
解:由已知可得 O0P (3)2(4)25
设角
的终边与单位圆交于 P(x, y)
y
,
分别过点
、P P0作 x 轴的垂线MPM 0 P、0
M0 M O
x
M0P0 4
OMx
Px, y
OM0 3
MPy
OMP∽ OM0P0
P03,4
于是, s in yy|M| P M 0P 04;
(2) 正弦、余弦总有意义.当 的终边在 y轴上时,点P 的
横坐标等于0, tan y 无意义,此时 k(kz).
《任意角和弧度制》三角函数PPT教学课件(第一课时任意角)
栏目 导引
第五章 三角函数
判断正误(正确的打“√”,错误的打“×”) (1)第一象限的角一定是正角.( × ) (2)终边相同的角一定相等.( × ) (3)锐角都是第一象限角.( √ ) (4)第二象限角是钝角.( × )
栏目 导引
第五章 三角函数
3.终边在直线 y=-x 上的角 β 的集合 S=________. 解析:由题意可知,终边在直线 y=-x 上的角有两种情况: ①当终边在第二象限时,可知{β|β=135°+k·360°,k∈Z}; ②当终边在第四象限时,可知{β|β=315°+k·360°,k∈Z}. 综合①②可得,终边在直线 y=-x 上的角的集合 S={β|β= 135°+k·180°,k∈Z}. 答案:{β|β=135°+k·180°,k∈Z}
栏目 导引
第五章 三角函数
2.如图,α,β 分别是终边落在 OA,OB 位置上的两 个角,且 α=60°,β=315°. (1)求终边落在阴影部分(不包括边界)的角 γ 的集 合; (2)求终边落在阴影部分(不包括边界),且在 0°~360°范围内 的角的集合. 解:(1)因为与角 β 终边相同的一个角可以表示为-45°,所以 阴 影 部 分 (不 包 括 边 界 )所 表 示 的 角 的 集 合 为 {γ|k·360 ° - 45 ° <γ<k·360°+60°,k∈Z}. (2){θ|0°≤θ<60°或 315°<θ<360°}.
别是( )
任意角的三角函数 学案 导学案 课件
课题任意角的三角函数(第1课时)学习目标:1. 掌握任意角的正弦、余弦、正切的定义;2. 理解任意角的三角函数不同的定义方法;3. 已知角α终边上一点,会求角α的各三角函数值. 学习重点:任意角的正弦、余弦、正切的定义. 学习难点:任意角的三角函数不同的定义方法. 导学流程:一.了解感知锐角的三角函数如何定义?如图,设锐角α的顶点与原点O 重合,始边与x 轴的正半轴重合,那么它的终边在第一象限.在α的终边上任取一点(,)P a b ,它与原点的距离220r a b =+>. 过P 作x 轴的垂线,垂足为M ,则线段OM 的长度为a ,线段MP 的长度为b .则sin MP b OP r α==;cos α= = ; tan MP OMα== . 二.深入学习1.任意角的三角函数的定义问题1:将点取在使线段OP 的长1r =的特殊位置上,这样就可以得到用直角坐标系内的点的坐标表示锐角三角函数为:sin MP OP α== ;cos OM OP α== ; tan MPOMα== .问题2:上述锐角α的三角函数值可以用终边上一点的坐标表示. 那么,角的概念推广以后,我们应该如何推广到任意角呢?如图,设α是一个任意角,它的终边与单位圆交于点(,)P x y , 那么:(1) 叫做α的正弦(sine),记做sin α; (2) 叫做α的余弦(cossine),记做cos α; (3)_______叫做α的正切(tangent),记做tan α.即:sin y α=,cos x α=,tan (0)yx xα=≠.反思:①当()2k k Z παπ=+∈时,α的终边在 轴上,终边上任意一点的横坐标x 都等于 ,所以无意义.② 如果知道角终边上一点,而这个点不是终边与单位圆的交点,该如何求它的三角函数值呢?2.探究三种三角函数的值在各象限的符号3.典例解析: 例1.求35π角的正弦、余弦和正切值.例2.已知角α的终边经过点P(-3,-4),求sin α、cos α、tan α的值。
任意角的三角函数PPT课件
这几条与单位圆有关的有向线段 叫做角 的正弦线、余弦线、正切线.
当角 的终边在 轴上时,余弦线变成一个点,正切线不存在.
三角函数的一种几何表示
尊若片天率怔威芋耸眉夸猜柜黍行器摧躇除肮石介桓傻咋但甚展泻殊埋谤任意角的三角函数PPT课件任意角的三角函数PPT课件
于是, θ为第三象限角
蔑少低猛交螟质沃檄响体统氦假苹怪汝美皱躬屠秦踌酿摊占苇黎瓷僵扼豫任意角的三角函数PPT课件任意角的三角函数PPT课件
例5 求下列三角函数值
(1) cos(9π/4)
(2)tan(-11π/6)
解:
cos(9π/4)= cos(π/4+2π)= cosπ/4=
tan(-11π/6)= tan(π/6-2π)= tanπ/6=
sin(α+k*360)=sinα
cos(α+k*360)=cosα
tan(α+k*360)=tanα
k∈z
公式一
终边相同角的同一三角函数值相等
公式作用:
把求任意角的三角函数转化为求0°~360°角的三角函数
(3) tan(-672 °)
(4)tan(11π/3)
因为tan(-672 °)=tan(48-2*360 °)=tan48 °
解:
“ ” 证明必要性
显然成立 ;
“ ” 证明充分性
因为①式 sinθ<0成立,
所以θ角的终边可能位于第三或第四象限,也可能位于y轴负半轴上;
因为②式 tanθ>0 成立,
所以θ角的终边可能位于第一或第三象限;
因为①式 ②式 都成立, 所以θ角的终边只能位于第三象限;
高中数学人教版A版必修4《任意角的三角函数》优质PPT课件
§1.2 任意角的三函数
明目标、知重点
内容 索引
01 明目标
知重点
填要点 记疑缺
04
明目标、知重点
明目标、知重点 1.通过借助单位圆理解并掌握任意角的三角函数定义, 了解三角函数是以实数为自变量的函数. 2.借助任意角的三角函数的定义理解并掌握正弦、余弦、 正切函数在各象限内的符号. 3.通过对任意角的三角函数定义的理解,掌握终边相同 角的同一三角函数值相等.
明目标、知重点
(2)sin(-1 320°)cos 1 110°+cos(-1 020°)sin 750°+tan 495°. 解 原式=sin(-4×360°+120°)cos(3×360°+30°)+ cos (-3×360°+60°)sin(2×360°+30°)+tan(360°+135°) =sin 120°cos 30°+cos 60°sin 30°+tan 135°
明目标、知重点
(2)cos α=xr(r>0),因此cos α的符号与x的符号相同,当α的终边 在第一、四象限时,cos α>0;当α的终边在第二、三象限时, cos α<0. (3)tan α=yx,因此tan α的符号由x、y确定,当α终边在第一、三 象限时,xy>0,tan α>0;当α终边在第二、四象限时,xy<0, tan α<0.
明目标、知重点
当堂测·查疑缺
1234
1.已知角α的终边经过点(-4,3),则cos α等于( D )
4
3
A.5
B.5
C.-35
D.-45
解析 因为角 α 的终边经过点(-4,3),所以 x=-4,y=3,r=5,
所以 cos α=xr=-45.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
归纳总结知识点(二)
• 9 (1)正弦值对于第一,二象限的角为正, 对于第三,四象限的角为负 • (2)余弦值对于第一,四象限的角为正, 对于第二,三象限的角为负 • (3)正切值对于第一,三象限的角为正, 对于第二,四象限的角为负。
巩固训练
• 1、求的正弦、余弦和正切值。 • 2、已知角的终边过点p(-2,6),求角的正 弦、余弦和正切值。 • 3 已知角的终边过点P(4a,-3a)(a<0), 则2sin+cos 的值的正负是( )A.+ B.- C.0 D.无法判定 • 4已知角的终边在直线y =- x 上,则终边上 任意一点(除了原点)P(a,b)则, sin= , cos= , tan= 。
任意角的三角函数导学案
预习案(课前)
• 1 复习:初中数学中锐角三角函数如何定 义? • 2 试用初中知识,在直角三角形里面计 算, , 角函数值. • 3 预习教材P11-P14内容. • 4 想一想:如何计算,,函数值,及这几个 角的正负。
自主探究 1(学生阅读教材完成)
• 1、任意角的三角函数的定义:在直角坐标 系中,我们称以原点为圆心,以单位长度 为半径的圆为单位圆。设是一个任意角, 它的终边与单位圆交于点P(x,y)那么: (1) 叫做的正弦,记做 。 • (2) 叫做的余弦,记做 。 • (3) 叫做的正切,记做 。 • (4) 正切定义域是什么
课后作业
• 课本 A组 2 ,4 B组 , 2 ,3
2
2
归纳总结知识点(一)
• 8 终边上任意一点(除了原点)的坐标为P(x, y), y x • r = x y 则sin = r ,cos= r ,tan= 10 • (1)正弦值对于第一,二象限的角为正,对于第 三,四象限的角为负 • (2)余弦值对于第一,四象限的角为正,对于第 二,三象限的角为负 • (3)正切值对于第一,三象限的角为正,对于第 二,四象限的角为负。 •
老师精点 (一)
• 7(1)问题4 : 应用任意角的三角函数的定 义计 算
• (2) 问题5 : 由终边上任意一点(除了原 点)的坐标为P(a,b),a<0,b>o 得是第 二象限角。故 sin>o, cos<0
老师精点 (二)
• (3)问题6 : 已知点A(- a,- b )在第三象限, 则a>o ,b>o,角终边上任意一点P( a,- b ), 则在第四象限角 • (4)问题7 :已知角的终边在直线y = x 上,终 边上任意一点(除了原点)的坐P(a,b),a=b, 则 • sin= 2 , cos= 2 , tan=1
自主探究 2(学生阅读教材完成)
• 2 三角函数符号由三角函数的定义,以及 各象限内点的坐标的符号知: • (1)正弦值对于第( )象限的角为正, 对于第( )象限的角为负 • (2)余弦值对于第( )象限的角为正, 对于第( )象限的角为负 • (3)正切值对于第( )象限的角为正, 对于第( )象限的角为负。
合作探究2 (学生相互讨论后,尝试解决)
• 5 已知点A(- a,- b )在第三象限,角终 边上任意一点P( a,- b ),则在第几象限 角( ) • A.第一象限 B.第二象限 C.第三象限 D.第四象限 • 6 已知角的终边在直线y = x 上,终边上任 意一点(除了原点)的坐P(a,b)则, sin= , cos= , tan= •
合作探究1点探究 • 3 已知角的终边经过点P(2,-3),求角的 正弦、余弦和正切值。 • 4 终边上任意一点(除了原点)的坐标为P (a,b),a<0,b>o它与原点的距离为r, 则sin, cos的值为( ) • A.- ,- B.- ,+ C.-, + D.+ ,+
