Excel在数学建模中的应用实例
EXCL在数学建模和土木工程中的应用

《环境质量评价》实验指导(适用专业:农业资源与环境、水土保持与荒漠化专业)黑龙江八一农垦大学植物科技学院资环系……………………………………………………………精品资料推荐…………………………………………………目录实验一 Excel 在建立数学模型的应用 (1)实验二用Excel进行等标污染指数、等标污染负荷、污染负荷比的运算方法 (9)实验三 Excel在大气环境质量评价中的应用 (13)实验四用Excel模板进行有关河流湖泊水质评价的应用 (21)实验五环境系统最优化 (26)实验一 Excel 在建立数学模型的应用一、实验目的:练习掌握线性回归分析、曲线拟合及参数估计等数学建模问题二、实验原理:数学模型的建立过程中,从数据分析、参数估计直至模型的检验,数据计算的工作量十分巨大,没有计算机的帮助要完成这些工作是很难想象的。
Microsoft Excel 就是完成该项工作的一种简便有效的工具。
三、实验内容:1、污水处理的线性回归分析:例2-2 某污水处理厂提供的3、4月份的日常监测台帐如表2-4所示,试根据3月份的数据建立其出水COD对应入水COD的线性回归模型,然后用4月份的数据进行验证。
解:首先建立Excel的工作表,输入污水处理厂监测的原始数据。
在2.2 中已介绍了Microsoft Excel的“分析工具库”。
线性回归也是属于该工具库的内容。
在“工具”菜单中,单击“数据分析”命令。
如果“数据分析”命令没有出现在“工具”菜单中,则需要通过加载宏安装“分析工具库”,与此同时也将“规划求解”安装备用。
如图2-5所示。
完成了加载宏的安装过程,在“工具”菜单中,单击“数据分析”命令,选择线性回归操作。
按照对话框要求在Y 值输入区域输入对因变量数据区域的引用,该区域必须由单列数据组成。
这里选择输入3月份的出水COD的数据区域;在X 值输入区域输入对应入水COD数据。
回归统计的一些主要结果如表2-5。
图2-5 加载宏安装“分析工具库”和“规划求解”表2-5 出水COD对应入水COD回归统计结果Multiple R 0.630237Intercept 43.25682X Variable 1 0.136996标准误差26.22009观测值24因此,出水COD 对应入水COD 的线性回归的模型形式是:Y = 0.137X + 43.257相关系数 R =0.63,观测值24个。
Excel在数学建模中的应用

环境系统分析
Excel规划求解 (四)Excel规划求解
的规划求解, 用Excel的规划求解,解农药管理问题。 的规划求解 解农药管理问题。
LP: S.t. Max Z=140X1+ 100X2 0.9X1+ 0.5X2 ≤632.5 X1+ X2 ≤1000 X1,X2≥0
环境系统分析
Excel的规划求解操作过程 的规划求解操作过程
ISCST3模型是由美国环保局开发并推广使用的一个城 ISCST3模型是由美国环保局开发并推广使用的一个城 市尺度的大气扩散模型, 市尺度的大气扩散模型,该模型是基于统计理论的正态 烟流模式,使用的公式为目前广范应用的稳态密封型高 烟流模式, 斯扩散方程。 斯扩散方程。
环境系统分析
气象参数预处理程序界面
环境系统分析
(一)多元回归模型的建立
环境系统分析
(一)多元回归模型的建立
环境系统分析
(二)模型参数估值
已 知 河 流 平 均 流 速 为 4.0km/h , 饱 和 溶 解 氧 (DO) 为 10.0mg/L,河流起点的 ,河流起点的BOD(L0)浓度为 浓度为20mg/L,沿程 浓度为 , 的溶解氧(DO)的测定数据在文件 的测定数据在文件BOD-DO.xls 给出。 给出。 的溶解氧 的测定数据在文件 试根据河流溶解氧的变化规律,确定耗氧速度常数K 试根据河流溶解氧的变化规律,确定耗氧速度常数 d 和复氧速度常数Ka。已知数学模型为: 已知数学模型为: 和复氧速度常数
工具”菜单中,单击“规划求解” 1 在“工具”菜单中,单击“规划求解”命令 目标单元格”编辑框中, 2 在“ 目标单元格 ”编辑框中 ,键入单元格引用或目标单元格 的名称。目标单元格必须包含公式。 的名称。目标单元格必须包含公式。 最大值” 、、“ 最小值” 3 目标单元格中数值可选 “ 最大值 ” 、、 “ 最小值 ” 或指定 “目标值” 。 目标值” 可变单元格”编辑框中, 4 在“ 可变单元格 ”编辑框中 ,键入每个可变单元格的名称或 引用,用逗号分隔不相邻的引用。 引用 ,用逗号分隔不相邻的引用。可变单元格必须直接或间 接与目标单元格相联系。 接与目标单元格相联系。
Excel在数模解题中的应用(董)

此题可列出微分方程并解出纯理论解, 但这里我们采用数值解法。
模型假设及构建
以坦克初始点为坐标原点,正东方向为x轴正方 向建立直角坐标系。假定在每个0.1秒时间间隔内, 坦克先向北行驶1.5米,然后导弹朝着对准坦克的方 向行驶6米。 Tk ~坦克第k个0.1秒末的纵坐标值 xk~导弹第k个0.1秒末的横坐标值 yk~导弹第k个0.1秒末的纵坐标值 Tk=1.5k; k=1,2, 0≤ xk ≤3000 ; 0≤ yk; k=1,2,
为解决此题,首先必须建立从k时刻到k+1时刻的 导弹轨迹坐标关系式:
(xk+1,yk+1)
由此可得出从k时刻到k+1时刻的导弹轨迹坐标关系式:
yk 1 yk Tk 1 yk xk 1 xk xk
xk 1 xk yk 1 yk
2
2
6
模型求解:
循环计算,直到可以覆盖整个轨道即可。
对于椭圆轨道:最少需要多少个测控站?
进一步讨论: 有必要求解β2吗? 假如将(θ+β1) 视为任意初始角θ, 从P1开始作为第一 个测控站,往下递 推,如何? 飞船最少测控站数
建模案例3:
如何预报人口的增长
•已知近200多年来美国人口数据(见上图) •问:如何预测2000年和2010年美国的人口数?
根据以上导弹坐标关系式,可推导出以下递推关系式
xk 1 xk
6 xk
Tk 1 yk
2
xk
2
yk 1 yk 36 xk 1 xk
2
有了这个导弹坐标递推公式,就可借助Excel表格软 件上机逐步计算出导弹运行轨迹。当: xk+1≤ 0且xk >0 时,即可近似确认导弹击中了坦克。追迹题解 所得结果为:当k≈533.3(即导弹运行53.3秒)时, 在Tk+1 ≈ 800(即坦克约向北行驶了800米)处,导弹 击中坦克。
【建筑工程管理】ECL在数学建模和土木工程中的应用

使用Excel 工作表进行曲线拟合的操作,是在图表菜单下,选定数据系列,使用趋势线命令,获得对话框,如图2-7所示。Excel趋势线所提供的模型结构形式,如表2-6所示。
表2-6 Excel趋势线所提供的模型结构
名称
趋势线计算方程
备注
线性
(2-11)
代表斜率b代表截距m
对数
(2-12)
c和b代表常数,函数ln代表自然对数
1.9459
5
7.5
20.2
2.6265
2.0149
5.4
8.17
20.4
2.7507
2.1005
5.8
8.5
19.7
2.8712
2.1401
6.6
9.5
21.7
3.1026
2.2513
表2-9 回归分析的一些主要结果
参数名称
参数估值
回归统计
Intercept
13.50766
Multiple R
0.94304
X Variable 1
6.72025
R Square
0.889324
X Variable 2
-4.30189
观测值
13
4空气污染指数
Excel在数学建模中的应用(例题+练习)
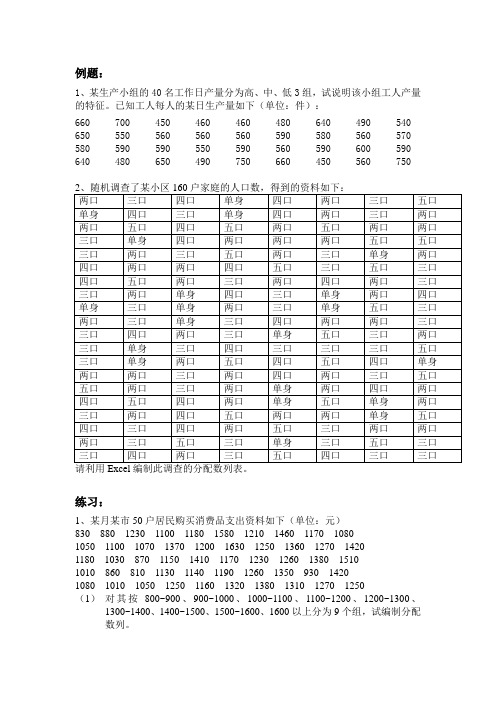
例题:
1、某生产小组的40名工作日产量分为高、中、低3组,试说明该小组工人产量的特征。
已知工人每人的某日生产量如下(单位:件):
660 700 450 460 460 480 640 490 540 650 550 560 560 560 590 580 560 570 580 590 590 550 590 560 590 600 590 640 480 650 490 750 660 450 560 750
练习:
1、某月某市50户居民购买消费品支出资料如下(单位:元)83088012301100118015801210146011701080 1050110010701370120016301250136012701420 118010308701150141011701230126013801510 1010860810113011401190126013509301420 1080101010501250116013201380131012701250
(1)对其按800~900、900~1000、1000~1100、1100~1200、1200~1300、1300~1400、1400~1500、1500~1600、1600以上分为9个组,试编制分配数列。
(2)根据编制的分配数列绘制折线图,直方图。
2、某银行为了提高客户满意度,在客户办完业务后,柜员会让客户在他的“客户满意度调查终端”上按一下,客户可以在“很满意”、“满意”、“比较满意”、“不满意”、“很不满意”几个按钮中选择一个,对这个柜员的服务进行即时评价。
excel软件的数据建模功能有哪些应用案例

excel软件的数据建模功能有哪些应用案例Excel 软件的数据建模功能有哪些应用案例在当今数字化的时代,数据的处理和分析变得越来越重要。
Excel 作为一款广泛使用的电子表格软件,其数据建模功能为我们提供了强大的工具,帮助我们从海量的数据中提取有价值的信息,并做出明智的决策。
下面将为您介绍一些 Excel 数据建模功能的应用案例。
一、销售数据分析假设一家公司拥有多个销售渠道和产品类别,每月都会产生大量的销售数据。
通过 Excel 的数据建模功能,可以对这些数据进行整合和分析。
首先,将不同渠道和产品类别的销售数据导入到 Excel 中。
然后,使用数据建模中的“关系”功能,建立各个数据表之间的关联,例如将销售订单表与产品表、客户表相关联。
接下来,运用“数据透视表”和“切片器”功能,可以快速地按产品类别、销售区域、时间段等维度对销售数据进行汇总和分析。
比如,轻松查看某个产品在特定地区的季度销售趋势,或者比较不同销售渠道的销售业绩。
通过这样的分析,销售团队可以发现销售的高峰和低谷,了解哪些产品和地区表现出色,哪些需要改进,从而制定更有针对性的销售策略,优化资源配置。
二、财务预算与预测对于企业的财务部门来说,准确的预算和预测至关重要。
Excel 的数据建模功能可以在这方面发挥重要作用。
以年度预算为例,将历史财务数据、市场趋势、业务计划等相关数据输入到 Excel 中。
利用数据建模中的“计算列”和“度量值”,可以根据设定的公式和规则自动计算各项费用和收入。
同时,结合“趋势线”和“预测函数”,可以基于历史数据对未来的财务状况进行预测。
比如预测未来几个月的销售额、成本支出等,帮助企业提前做好资金规划和风险防范。
通过不断调整输入的参数和假设条件,财务人员可以生成不同的预算和预测方案,为管理层提供决策支持,确保企业的财务健康和稳定发展。
三、人力资源管理在人力资源领域,Excel 的数据建模也有广泛的应用。
例如,对于员工的绩效评估数据,可以使用数据建模进行综合分析。
Excel在数学建模中的应用实例

Excel在数学建模中的应用实例一、Excel 基础1、自动填充公式函数等例1.1:自动填充编号:病例数据的统一编号例1.2:自动填充实现复制例1.3:自动填充生成序列:等差、等比例1.4:利用函数计算2e-ln3.例1.5:利用函数求逆矩阵及矩阵转置、数乘矩阵、矩阵和、积、行列式等运算如已知1101122222213153A⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥-⎣⎦,求A’,A-1解:A’:选择性粘贴,或用transpose()函数(可在名称框中输入范围以选中结果区域,然后填入公式=transpose(原矩阵区域),再按Ctrl+Shift+Enter即可)A-1:Excel中输入矩阵,在结果矩阵第一行一列处输入=MINVERSE(原矩阵区域),结果只显示一个数字,用鼠标选中结果区域,先F2,后Ctrl+Shift+ Enter.A+B:用自动填充,或选中结果区域,在第一格输入公式后Ctrl+Entern*A:用自动填充+绝对引用,也可同上A/n:用自动填充+绝对引用,也可同上A*B:选中结果区域,用MMult函数后Ctrl+Shift+ Enter求矩阵行列式的值:用MDETERM函数用矩阵运算解方程组:未知数X等于系数矩阵的逆矩阵和Y向量的乘积.例1.6:用公式计算11212312341...23353573579π=+++++计算π的近似值,使误差小于10-14解:令n=1; m=3; t=1; p=1,然后n=n+1; m=m+2; t=t*n/m; p=p+t; pi=p*2 10-14即计算出的前后两项相差小于10-14例1.7:利用公式及函数计算:当x=3,2,1,0,-1,-2,-3时分段函数sin,0cos,0xx x xye x x>⎧=⎨≤⎩的值。
解:先输入列x,后用if和三角函数解决。
例1.8:求连续复利问题假设银行活期存款年利率为r(如r=3.25%),若某储户存20000元活期存款,那么一年后,他可以得到利息20000r,本息合计20000(1+r)元,因活期可以随便什么时候支取,如果满半年就结算一次,此时的本息合计为20000(1+r/2),把本息取出后立即再存入的话可得复利,即半年后再次结算,则全年的本息合计为20000(1+r/2)2,因为(1+r/2)2=1+r+r 2/4>1+r ,如此可发现每半年结算一次获利比一年结算一次多,某储户就想是不是每季度、每月、每半月。
Excel在数学建模中的应用

第四步:将条形图转换成标准直方图
(如图所示)
35
二、用Excel绘制图表 (以文件“图表”为例)
图表是数据表现的另一种形式。数据的图表化就是将单 元格中的数据以各种统计图的形式显示。
1.图表种类 (1)独立的图表:单独占据一个工作表,打印时也将与数据 表分开打印。 (2)附属于工作表的嵌入式图表:它和数据源放置在同一张 工作表中,同时打印。
39
绘图实例: 用Excel绘制任意一元函数的图像
以 y 2sin x ln(1 x2 ) 为例介绍:
40
三、用Excel进行相关与回归分析 1、用Excel计算描述统计量 2、用Excel进行相关分析 3、用Excel进行回归分析
41
三-1、用Excel计算描述统计量 (1)用函数计算描述统计量 (2)描述统计菜单项的使用
6
函数的引用
手工输入:在编辑栏或单元格内输入 引用单元格地址:
7
相对引用
利用单元格间的相对位置关系引用单元格内容。公式中 的相对引用随单元格的移动而修改,但原来的位置不变。
例:打开文件“数据编辑”,在工作表“电视机的销售 统计表” 的G3中输入“=E3*F3,则可在G4、G5、G6、 G7、G8中填入相应公式来计算商品的销售金额。 绝对引用
3
自动输入数据
自动填充鼠标拖动填充柄向下、右拖数字 增量为1,向上、左拖增量为-1 .
自定义序列 ① 工具——选项——新序列——输入序列 内容,每个序列间按回车键——添加 ② 选中序列区域——工具——选项——导 入——确定
4
5
公式的使用
用公式计算 所有的公式运算均以“=”开头。错误的公式以#开头。 (1)数学运算符: +、-、*、/、^、%(计算准则:先乘方,再乘、除,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel在数学建模中的应用实例
一、Excel 基础
1、自动填充公式函数等
例1.1:自动填充编号:病例数据的统一编号
例1.2:自动填充实现复制
例1.3:自动填充生成序列:等差、等比
例1.4:利用函数计算2
e-
ln3.
例1.5:利用函数求逆矩阵及矩阵转置、数乘矩阵、矩阵和、积、行列式等运算
如已知
1101
1222
2221
3153
A
⎡⎤
⎢⎥
⎢⎥
=
⎢⎥
-
⎢⎥
-
⎣⎦
,求A’,A-1
解:
A’:选择性粘贴,或用transpose()函数(可在名称框中输入范围以选中结果区域,然后填入公式=transpose(原矩阵区域),再按Ctrl+Shift+Enter即可)A-1:Excel中输入矩阵,在结果矩阵第一行一列处输入=MINVERSE(原矩阵区域),结果只显示一个数字,用鼠标选中结果区域,先F2,后Ctrl+Shift+ Enter.
A+B:用自动填充,或选中结果区域,在第一格输入公式后Ctrl+Enter
n*A:用自动填充+绝对引用,也可同上
A/n:用自动填充+绝对引用,也可同上
A*B:选中结果区域,用MMult函数后Ctrl+Shift+ Enter
求矩阵行列式的值:用MDETERM函数
用矩阵运算解方程组:未知数X等于系数矩阵的逆矩阵和Y向量的乘积.
例1.6:用公式计算
1121231234
1...
23353573579
π
=+++++计算π的近似值,使误差
小于10-14
解:令n=1; m=3; t=1; p=1,然后n=n+1; m=m+2; t=t*n/m; p=p+t; pi=p*2 10-14即计算出的前后两项相差小于10-14
例1.7:利用公式及函数计算:当x=3,2,1,0,-1,-2,-3时分段函数
sin,0
cos,0
x
x x x
y
e x x
>
⎧
=⎨
≤
⎩
的值。
解:先输入列x,后用if和三角函数解决。
例1.8:求连续复利问题
假设银行活期存款年利率为r(如r=3.25%),若某储户存20000元活期存款,那么一年后,他可以得到利息20000r,本息合计20000(1+r)元,因活期可以随便什么时候支取,如果满半年就结算一次,此时的本息合计为20000(1+r/2),把本息取出后立即再存入的话可得复利,即半年后再次结算,则全年的本息合计
为20000(1+r/2)2,因为(1+r/2)2=1+r+r 2/4>1+r ,如此可发现每半年结算一次获利比一年结算一次多,某储户就想是不是每季度、每月、每半月。
,他发现:活期存款存期越短获利越多,假如可以按小时甚至按分钟结算,该储户是否可以发大财?
解:n 为一年中的结算次数,a k 为第k 次结算时的本息,a 0=20000是首次存入的全金,则结算次数分别为1,2,4,12,24,365,8760…时的利息为。
例1.9:奖金问题
某公式给员工发奖金,奖金与销售额挂钩(按销售额的一定比例提成),另一方面还与其他指标挂钩(提成比例分成三等:一等1.5%,二等1%,三等0.5%) 请计算销售额为2000、3000、…、6000时的三种等级的应发奖金数。
2、 相关数学函数的使用
例1.10:求排列数、求组合数、求阶乘.
Permut(个数n,选取数k)
Combin(个数n,选取数k)
Fact(n)
二、 线性规划
例2.1:
三、 求解方程
1、 线性方程的求解
解方程组:
例3.1: 解二元一次方程组211313x y x y +=⎧⎨+=⎩
例3.2:解方程组:
求解高次方程:
例3.3: 求解高次方程654322433420x x x x x x +-+-++=
2、 非线性方程的求解
例3.4: 用迭代法求非线性方程x-cosx=0的数值解,迭代公式是x k =cos(x k-1),取x 0=1,试用Excel 求解,要求精度达到10-12.
四、 统计
1、 计数与求和
例4.1:统计票数
例4.2:统计每类个数
例4.3:求和、汇总
2、 均值与最值
例4.4: 求平均/期望
例4.5: 求最大值、最小值
3、 筛选与排序
例4.6: 从一系列数据中筛选出符合某个条件的数据.
低级筛选和高级筛选
例4.7:对某系列数据排列以找出最优值.
4、 描述统计
例4.8: 统计某炼钢厂的120炉钢中的Si 含量,已知有如下数据:。
解:
①、安装“数据分析”工具包:点击“工具”->“加载宏”,在弹出的对话中选择“分析工具库”、“规划求解”、“与Access 链接”等项目,“确定”,如果需要,将Office 光盘放入光驱,然后按提示进行安装。
②、输入这120个数据
③、工具——>数据分析——>描述统计
5、 分类汇总与数据透视表
例4.9:按科室分类汇总工资.
例4.10:按地点和油类等汇总销售额.
6、 其他统计应用
例4.11:国有资产的核账
五、 作图
例5.1:分布图
例5.2:直方图
例5.3:函数曲线图
画出22sin ln(1)y x x =-+在区间48x -≤≤内的图像,设步长为0.1
使用无数据点平滑线散点图
六、 其他建模应用如VBA
用其他算法进行统计。
