数学实验复习题
深圳实验学校国际部小学数学二年级下册第五单元经典复习题(含答案解析)

一、选择题1.下面算式中的括号,去掉后不改变计算结果的是()。
A. (64-24)÷8B. (9×3)-18C. 150-(46-28)B解析: B【解析】【解答】解:去掉括号后不改变计算结果的是(9×3)-18。
故答案为:B。
【分析】A项中去掉括号之前,先算减法,再算除法,去掉括号后,先算除法,再算减法,所以结果会改变;B项中去掉括号之后,先算乘法,再算减法,去掉括号后,依然是先算乘法,再算减法,所以结果不会改变;C项中去掉括号之前,先算后两个数的减法,再算用第一个数减,去掉括号后,要按照顺序从左往右依次计算,所以结果会改变。
2.下面算式中的括号,去掉后不改变计算结果的是()。
A. (63-27)÷9B. (87-23)-17C. 62-(38-17)B解析: B【解析】【解答】解:A:去掉括号后就先算除法,再算减法,结果改变;B:去掉括号后仍然是先算87-23,结果不改变;C:去掉括号后先算62-38,结果改变。
故答案为:B。
【分析】在含有小括号的混合运算中,要先算小括号里面的,再算小括号外面的。
3.实验小学三年级同学去秋游,男生有3组,每组9人;女生有36人。
去秋游的男生和女生一共有()人。
A. 27B. 39C. 45D. 63D解析: D【解析】【解答】3×9+36=27+36=63(人)故答案为:D。
【分析】根据题意可知,用每组男生的人数×男生的组数+女生的人数=总人数,据此列式解答。
4.与6×2+6结果相等的是()。
A. 6×3B. 6×4C. 6×2A解析: A【解析】【解答】与6×2+6结果相等的是6×3。
故答案为:A。
【分析】6×2+6表示2个6与1个6相加,等于3个6相加,用乘法计算为6×3,据此解答。
5.把算式6÷3=2,5×2=10,合并成一个综合算式是()。
数学实验1-3章习题答案
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
2018-2019年介休市实验第二小学一年级下册数学复习题含答案(1)
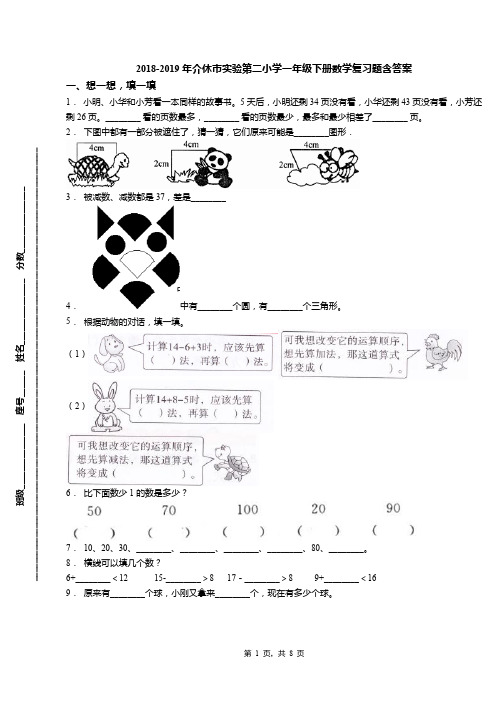
2018-2019年介休市实验第二小学一年级下册数学复习题含答案一、想一想,填一填1. 小明、小华和小芳看一本同样的故事书。
5天后,小明还剩34页没有看,小华还剩43页没有看,小芳还剩26页。
________ 看的页数最多,________ 看的页数最少,最多和最少相差了________ 页。
2. 下图中都有一部分被遮住了,猜一猜,它们原来可能是________图形.3. 被减数、减数都是37,差是________4.中有________个圆,有________个三角形。
5. 根据动物的对话,填一填。
(1)(2)6. 比下面数少1的数是多少?7. 10、20、30、________、________、________、________、80、________。
8. 横线可以填几个数?6+________<12 15-________>8 17-________>8 9+________<16 9. 原来有________个球,小刚又拿来________个,现在有多少个球。
班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10.一个数从右边起,第一位上是6,第二位上是3,这个数是________。
二、对号入座、选择填空(含多选)11.右图中是一个()边形。
A.6 B.5 C.412.直线、射线和线段三者比较()A. 直线比射线长B. 射线比线段长C. 线段比直线长D. 三者无法比13.下面最接近20的数是()。
A.23 B.18 C.1214.4×<38,方框中最大能填几()A. 9B. 10C. 815.一页信纸有18行,每行有22个字,一页信纸大约能写()个字。
数学实验练习整理(课本)

1. 统计推断(实验12)—区间估计、假设检验[mu,sigma,muci,sigmaci]=normfit(x,alpha); %%正态分布检验 [ht,sigt,cit]=ttest(x,mu); %%t 检验[hz,sigz,ciz,zval]=ztest(x,mu,sigma,alpha,tail); %%z 检验 tail 默认为0① P297第2题:(1)分别用两个月的数据验证这种说法的可靠性; 编程:x1=[]; x2=[]; alpha=0.05;[mu1,sigma1,muci1,sigmaci1]=normfit(x1,alpha) %%一月份的均值和标准差以及其置信区间 [mu2,sigma2,muci2,sigmaci2]=normfit(x2,alpha) %%二月份的均值和标准差以及其置信区间 运行结果:(1月)mu1 =115.1500; sigma1 =3.8699;muci1 =113.3388 116.9612; sigmaci1 = 2.9430 5.6523 (2月)mu2 =120.7500; sigma2 =3.7116muci2 =119.0129 122.4871; sigmaci2 =2.8227 5.4211(2)分别给出1月和2月汽油价格的置信区间(05.0=α); 编程:x1=[]; x2=[]; mu=115; alpha=0.05;[h1,sigma1,ci1]=ttest(x1,mu,alpha,0) %%一月份汽油价格的置信区间 [h2,sigma2,ci2]=ttest(x2,mu,alpha,0) %%二月份汽油价格的置信区间 运行结果:(1月)h1 =0; sigma1 =0.8642; ci1 =113.3388 116.9612(2月)h2 =1; sigma2 =1.3241e-006; ci2 =119.0129 122.4871(3)如何给出1月和2月汽油价格差的置信区间(05.0=α) 编程:x1=[]; x2=[]; alpha=0.05;[h1,sigma1,ci1]=normfit(x2-x1,alpha) %数据看成同一个加油的数据,其价格差和置信区间 [h2,sigma2,ci2]=ttest(x2,x1,alpha,0) %数据完全随机时,用总体的t 分布检验 运行结果:h1 = 5.6000; sigma1 =5.4715; ci1 =3.0393 8.1607 h2 =1; sigma2 =2.0582e-004; ci2 =3.0393 8.1607结果分析:根据运行结果,我们可以知道数据完全随机时,用t 分布检验获得的结果更为合理准确。
西南交通大学限修课数学实验题目及答案三

西南交通大学限修课数学实验题目及答案三实验课题三向量与曲线绘图第一大题:向量的创建与运算用元素输入法创建向量x11=(2 �C5 8 �C1 7 1 -8 3 2 5 9)x11=[2 -5 8 -1 7 1 -8 3 2 5 9]用冒号输入法创建向量x12=(2 4 6 8 10 12 14 16 18 20 22)x12=2:2:22用等分取值法创建向量x13,其初值为0,终值为2π,共20个元素.x13=linspace(0,2*pi,20) 用随机输入法创建8维行向量x14 x14=rand(1,8)用随机输入法创建6维整数列向量x15 x15=fix(rand(6,1)*100)取向量x11的绝对值大于3的元素构成向量x16. x16=x11(abs(x11)>3)求空间两点间距离M 1(5,?4,?9)、M2(8,?6,?3) d=norm([8 6 3]-[5 4 9])做向量的线性运算:x18=4十x11+7x12. x18=4+x11+7*x12做向量的数量积 x19=x11・x12.x19=dot(x11,x12)分别取x11与x12的前三个元素做向量的叉积赋给x10.x10=cross(x11([1:3]),x12([1:3])) 第二大题:曲线绘图:构造坐标向量绘出‘田’字的图形(先给出构成字的数据点坐标) figureaxis([0,6,0,6])x=[1 1 5 5 1 1 5 5 3 3]; y=[1 5 5 1 1 3 3 5 5 1]; line(x,y)绘制向量y=[4 5 5 3 2 3 5 6 7 8]的图形。
y=[4 5 5 3 2 3 5 6 7 8]; plot(y)数据数组x23=(0.1 0.11 0.12…10),函数y23=30/x23,绘出函数曲线图形。
x23=0.1:0.01:10; y23=30./x23; plot(x23,y23)数据数组x24为区间[-5,5]上等分的30个点列,绘出函数y24= 5・x24・cos(x24) 的曲线图。
《数学软件与数学实验》复习题解答及评注

《数学软件与数学实验》复习题解答及评注一.填空题(请自己回答,并能举一反三,复习这些知识点)1.若123456,ones(3)789A B⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦,在MATLAB中运行指令“A*B”,结果为________;若运行指令“A.*B”,结果为_________。
2.若在MATLAB的命令行窗口中输入如下指令:A=1:12;B=reshape(A,4,3);B=B’;则B(2,:)=_________。
3.请写出快速的调出在MATLAB中已经运行过的指令的两种方法:(1)________(2)_________。
4.绘图指令“legend”的含义是____________。
5.假设有一个你不知道其长度的一维数组A,现在要将该数组倒序后赋给变量B,指令为_________。
6.请写出在MATLAB环境下运行一个程序的两种方法:(1)________________;(2)_______________。
7.MATLAB中符号运算的好处是___________。
8.小明写了一个MATLAB程序,代码若直接在command window中运行是正确的,但当他将代码存成文件2__xiaoming.m后,运行却出错。
原因是___________。
9.给定一个二维数组A,请用一句MA TLAB代码得到A的最小值所位于的行和列___________。
10.函数tic和toc的功能是_____________。
11.函数pretty的功能是________________。
12.若在MATLAB中,运行如下指令:A=1:4; B=8-A;Eq=A==B;则Eq的值为___________。
13.若在MATLAB中,运行如下指令:A=1:4; B=8-A;Eq=find(A==B);则Eq的值为___________。
14.用MATLAB随机产生一个正整数x∈[0,99],正确的指令为____________。
教科版小学六年级下册数学实验题

教科版小学六年级下册数学实验题
本文档主要介绍教科版小学六年级下册数学实验题,内容涵盖以下几个方面:
实验目的
通过开展数学实验,激发学生的数学兴趣,提高学生的数学思维能力和创新意识。
实验内容
本册的数学实验包含以下几个方面:
1. 图形的旋转和对称性实验
2. 三角形的分类实验
3. 平行四边形与梯形的性质实验
4. 角的度量实验
5. 直角三角形的性质实验
每个实验都有详细的实验步骤和实验方法,帮助学生更好地理解和掌握数学知识。
实验意义
数学实验是数学教学的一种创新型教学方法,它能使学生在探究中研究,在实践中提高,加深学生对数学知识的理解和记忆,能够更好地培养学生的观察能力、动手能力和创新能力。
实验操作要求
为了保证实验的顺利进行和实验结果的准确可靠,学生在进行数学实验时,需要注意以下几点:
1. 仔细阅读实验操作方法,按照操作步骤进行实验。
2. 注意实验器材的使用和存放,保持实验桌面整洁。
3. 将实验结果记录在实验桌面上的实验记录表上,并认真分析实验结果。
4. 实验过程中要注意安全,遵守实验室安全规定,防止意外事故的发生。
实验总结
通过进行数学实验,学生能够更直观地感受和理解数学知识,培养学生的数学思维和创新意识,有利于提高学生的数学成绩和科学素养,同时也有利于激发学生对数学的兴趣和热爱。
希望本文档能够对教师和学生在进行数学实验时有所帮助。
吉林省实验中学小学数学六年级上册第二单元复习题(含解析)

一、选择题1.如图,小东从学校出发,步行去图书馆,正确的行走路线是()A. 向东偏北55°方向行走800米B. 向西偏南40°方向行走400米C. 向南偏西35°方向行走800米D. 向南偏东40°方向行走400米D解析: D【解析】【解答】解:根据图上的方向、夹角的度数和距离可知,小东向南偏东40°分析行走400米到图书馆。
故答案为:D。
【分析】图上的方向是上北下南、左西右东,根据图上的方向、夹角的度数和距离描述行走路线即可。
2.如图中,小明家在学校的()处.A. 南偏西30°1.8千米B. 南偏东30°1.8千米C. 南偏西60°1.8千米D. 南偏东60°1.8千米C解析: C【解析】【解答】如图中,小明家在学校的南偏西60°1.8千米处。
故答案为:C。
【分析】此题主要考查了根据方向和距离确定物体的位置,观察图可知,此题是按“上北下南,左西右东”来规定方向的,图中1厘米代表实际600米,以学校为观测点,根据角度和距离描述出小明家的位置。
3.观察下图的位置关系,其中说法错误的是()。
A. 学校在公园北偏西 40°方向400m处B. 公园在少年宫东偏北 70°方向300m处C. 公园在学校东偏南 40°方向400m处[D. 少年宫在公园北偏东 20°方向300m处B 解析: B【解析】【解答】观察下图的位置关系,其中说法错误的是:公园在少年宫东偏北70°方向300m处。
故答案为:B。
【分析】观察图可知,此题是按“上北下南,左西右东”来规定方向的,图中1格代表100m,根据方向和距离描述相对位置即可。
4.小丽从家里出发,先向东偏南45°方向走500m,再向正西方走100m,现在她的位置在家的()方向.A. 东北B. 西北C. 东南D. 西南C解析: C【解析】【解答】根据上北下南,左西右东可知,她的位置在家的东南方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学实验复习题
1、求2
30x
e
x -=的所有根。
(先画图后求解)(要求贴图) 2、求下列方程的根。
1) 5
510x x ++=
2)1sin 0
2x x -
=至少三个根
3、求解下列各题: 1)3
sin lim
x x x x
->-
2) (10)
cos ,
x
y e x y
=求
3)2
1/20
(17x
e dx
⎰
精确到位有效数字)
4)4
2
254x
dx
x
+⎰
5)求由参数方程ln arctan x y t
⎧⎪=⎨
=⎪⎩d y d x
与二阶导数
2
2
d y dx。
6)设函数y =f (x )由方程xy +e y = e 所确定,求y ′(x )。
7)0
sin 2x
e
xdx +∞-⎰
8)
08x =展开(最高次幂为)
9) 1sin
(3)
(2)x
y e
y
=求
10)求变上限函数2
x
x
⎰对变量x 的导数。
5、已知2
2
()2(),
x f x μσ
--
=分别在下列条件下画出()
f x 的图形:(要求贴
图)
(1)1,011σμ=时=,-,,在同一坐标系里作图 (2)0,124
μσ=时=,,,在同一坐标系里作图。
6、画下列函数的图形:(要求贴图)
(1)sin 020cos 02
4x u t t y u t
u t z ⎧
⎪=≤≤⎪
=⎨≤≤⎪⎪=
⎩
(2) sin()03,03z xy x y =≤≤≤≤
(3)sin (3cos )
02cos (3cos )
02sin x t u t y t u u z u ππ
=+⎧≤≤⎪=+⎨≤≤⎪=⎩
7、 已知
4221343
05,20315
321
1A B -⎛⎫⎛⎫
⎪ ⎪
=-=-- ⎪ ⎪ ⎪ ⎪-⎝
⎭⎝
⎭
,在MATLAB 命令窗口中建立A 、
B 矩阵并对其进行以下操作: (1) 计算矩阵A 的行列式的值det()A (2) 分别计算下列各式:1
122,*,.*,,,,T
A B A B A B AB
A B A A
---
8、 在MATLAB 中分别利用矩阵的初等变换及函数rank 、函数inv 求下列矩阵的秩:
(1) 1
6323
540,11124A -⎛⎫ ⎪
=- ⎪ ⎪--⎝⎭
求 rank(A)=? (2) 35011
200,10201
2
2B ⎛⎫ ⎪
⎪= ⎪ ⎪⎝⎭
求1
B -。
9、解线性方程组1231341243
45132
53241
x x x x x x x x x x x +-=⎧⎪
+-=⎪⎨---+=⎪⎪+=-⎩并求系数矩阵的行列式。
10、在MATLAB 中判断下列方程组解的情况,若有多个解,写出通解。
(1)1234123412341234420
20
372031260
x x x x x x x x x x x x x x x x -+-=⎧⎪
--+=⎪⎨
++-=⎪⎪--+=⎩
(2) 1231231231
23234
245
38213496
x x x x x x x x x x x x ++=⎧⎪
-+=-⎪⎨
+-=⎪⎪-+=-⎩
11、设()()3
f x ,y 4 sin x y =,求
2
2
3
x y f x y
==∂∂∂。
12、求方程433x 4x 20x 5 0+-+=的所有解。
13、使用两种方法
求积分2
1
2
1x
dx -
⎰的近似值。
14、 设11
7()/23n n n
x x x x +⎧
=+⎪⎨⎪=⎩,数列{}n x 是否收敛?若收敛,其值为多少?
精确到6位有效数字。
15、设 1111...,2
3
n
p
p
p
x
n
=+
+
++
{}n x 是否收敛?若收敛,其值为多少?精
确到17位有效数字。
16
、求二重极限1
lim y
x y →→
17、已知0,x
z e
xyz x
∂-=∂求。
18、求253
x
x x e -+=的在-1附近的根。
19、计算积分1(2)2
D
I x y dxdy =--⎰⎰,其中D 由直线2
y x y x ==与围成。
20、作函数22(,)310332f x y x y xy x y =++-+在|x|<2, |y|<1内的图。
21、对于迭代模型2
111 1.40.3k k k k k
x y x y x ++⎧=+-⎨
=⎩
,取初值x 0 = 0, y 0 = 0, 进行
3000次迭代,对于k>1000, 在(x k , y k ) 处亮一点(注意不要连线)。
要求:写出M 脚本文件,不必作图。
22、某公司投资2000万元建成一条生产线。
投产后,在时刻t 的追加成本和追加收益分别为G(t)= 3
/225t
t ++(百万元/年), H(t)=
3
/218t
-(百万元/年)。
试确定该生产线在合适何时停产可获最大利
润?最大利润是多少?
要求:写出数学模型、M 函数(如果需要的话)、运算命令和计算结果。
24、将函数1
()f x x =展开为(3)x -的幂级数。
