重庆市南开中学数学圆几何综合中考真题汇编[解析版]

合集下载

重庆市南开中学2024-2025学年九年级上学期数学开学考试模拟试题[含答案]

重庆市南开中学2024－2025学年九年级上学期数学开学考试模拟试卷一．选择题（共10小题，满分40分，每小题4分）1．下列图形中，既是中心对称图形又是轴对称图形的为（）A ．B ．C ．D ．2．下列方程中，有两个相等实数根的是（）A ．2x x=B ．2104x x ++=C ．240x -=D ．2240x x ++=3．在反比例函数3k y x -=图象的每一支曲线上y 都随x 的增大而减小，则k 的取值范围是（）A ．3k >B ．0k >C ．3k <D ．0k <4．如图，在平面直角坐标系中，ABC V 与ADE V 是以点A 为位似中心的位似图形，相似比为1:3，点A 在x 轴上，点A 的坐标是()1,0-，点B 的坐标是()2,2-，则点D 的坐标是（）A ．()3,4-B ．()4,6-C ．()4,5-D ．()3,5-5．某厂今年一月份新产品的研发资金为10万元，以后每月新产品的研发资金与上月相比增长率都是x ，则该厂今年一季度新产品的研发资金y （元）关于x 的函数关系式为（）A ．()3101y x =+B ．()()210101101y x x =++++C ．21010y x x =++D ．()2101y x =+6的值应在（）A ．8和9之间B ．9和10之间C ．10和11之间D ．11和12之间7．若13a c eb d f ===，则3232ac e bd f -+-+的值为（）A ．13B ．1C ．1.5D ．38．下列按照一定规律排列一组图形，其中图形①中共有2个小三角形，图形②中共有6个小三角形，图形③中共有11个小三角形，图形④中共有17个小三角形，……．按此规律，图形⑩中共有n 个小三角形，这里的n =（）A ．87B ．74C ．62D ．539．如图正方形ABCD 的对角线AC 与BD 相交于点O ，点E 为边AB 上一动点，连接DE ，作CF DE ^于点F ，连接OF ．若BDE α∠=，则DOF ∠的度数为（）A ．2αB ．30α°+C ．45α°-D ．602α°-10．给定一列数，我们把这列数中第一个数记为1a ，第二个数记为2a ，第三个数记为3a ，以此类推，第n 个数记为n a （n 为正整数），已知1a x =．并规定：111n na a +=-，123n n T a a a a =××K ，123n n S a a a a =+++¼+．则①25a a =；②1231000211x T T T T x -+++¼+=-；③对于任意正整数k ，()3333233132k k k k k k T S S T T T ++---=--成立，以上结论中正确的有（）A ．0个B ．1个C ．2个D ．3个二．填空题（共8小题，满分32分，每小题4分）11．计算：101()(2)2p -+-＝．12．已知关于x 的一元二次方程220x x m -+=的一个根是2，则2m = ．13．一个不透明的箱子里装有a 个球，其中红球有5个，这些球除颜色外都相同．每次将箱子里的球搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验后发现，摸到红球的频率稳定在0.25，那么可以估算出a 的值为．14．若一个多边形的内角和等于720°，则从这个多边形的一个顶点引出对角线条．15．如图，矩形ABCD 的顶点A 、B 分别在反比例函数()40y x x =>与()20y x x=-<的图象上，点C 、D 在x 轴上，AB 、BD 分别交y 轴于点E 、F ，则阴影部分的面积为．16．若关于x 的不等式组()02422x m x x -ì>ïíï-<-î的解集为0x >，且关于y 的分式方程1322y m y y -=---有非负整数解，则所有满足条件的整数m 的值的和是．17．如图，菱形ABCD 的边长为4，60BAD ∠=°，过点B 作BE AB ^交CD 于点E ，连接AE ，F 为AE 的中点，H 为BE 的中点，连接FH 和CF ，CF 交BE 于点G ，则GF 的长为．18．若一个四位自然数A ，满足百位数字与千位数字的平方差恰好是A 去掉千位与百位数字后得的两位数，则称这个四位数A 为“活泼数”，例如2521A =，因为225221-=，故2521是一个“活泼数”；若一个四位自然数B ，各个数位上的数字互不相等且满足十位数字比千位数字大1，个位数字比百位数字大1，则称这个四位数B 为“可爱数”，例如1425，因为211-=，541-=，故1425是一个“可爱数”．对于一个“活泼数”A abcd =，规定：22()a b b cd F Aab×+-=+，对于一个“可爱数”B mnpq =，规定：()G B p n =-，则(5611)(3142)F G ´= ；当B 的百位数字为4时，若()3()9G B F A +是整数，则所有满足条件的奇数四位数A 的和是．三．解答题（共8小题，满分78分）19．（1）解方程：11322x x x-=---（2）解不等式组：()328143x x x x ì--£ïí+-<ïî．20．先化简，再求值：22122121x x x x xx x x ---æö-¸ç÷+++èø，其中x 满足x 2﹣x ﹣1=0．21．学习了平行四边形的知识后，同学们进行了拓展性研究．他们发现作平行四边形一组对角的角平分线与另一组对角的顶点所连对角线相交，则这两个交点与这条对角线两侧的对角顶点的连线所围成的封闭图形是一个特殊四边形．他的解决思路是通过证明对应线段平行且相等得出结论．请根据她的思路完成以下作图和填空：用直尺和圆规，过点B 作ABC ∠的角平分线，交AC 于点F ，连接BE 、DF ．（只保留作图痕迹）已知：如图，四边形ABCD 是平行四边形，AC 是对角线，DE 平分ADC ∠，交AC 于点E ．求证：四边形BEDF 是平行四边形．证明：∵四边形ABCD 是平行四边形，∴AD CB =，① ，∴DAC BCA ∠=∠．∵DE 平分ADC ∠，BF 平分CBA ∠，∴12ADE ADC ∠=∠，12CBF ABC ∠=∠．∵ADC CBA∠=∠∴② ，∴()ASA ADE CBF V V ≌．∴DE BF =，DEA BFC ∠=∠．∴③ ，∴四边形BEDF 是平行四边形．同学们再进一步研究发现，过平行四边形任意一组对角的顶点作平行线与另一组对角顶点所连对角线相交，均具有此特征．请你依照题意完成下面命题：过平行四边形一组对角的顶点作平行线与另一组对角顶点所连对角线相交，则④ ．22．2022年，教育部制定了独立的《义务教育劳动课程标准》，其中规定：以劳动项目为载体，以孩子经历体验劳动过程为基本要求，培养学生的核心劳动素养，某校分别从该校七、八年级学生中各随机调查了100名学生，统计他们上周的劳动时间，劳动时间记为x 分钟，将所得数据分为5个组别（A 组：90100x ££；B 组：8090x £<；C 组：7080x £<；D 组：6070x £<；E 组：060x £<），将数据进行分析，得到如下统计：①八年级B 组学生上周劳动时间从高到低排列，排在最后的10个数据分别是：82，82，81，81，81，81，80，80，80，80.②八年级100名学生上周劳动时间频数分布统计表：分组A B C D E 频数14b 28136③七、八年级各100名学生上周带动时间的平均数、中位数、众数如表：年级平均数中位数众数七年级81.379.582八年级81.3c 83④七年级100名学生上周劳动时间分布扇形统计图如图．请你根据以上信息，回答下列问题：(1)a =______，b =______，c =______；(2)根据以上数据分析，你认为七、八年级哪个年级学生上周劳动情况更好，请说明理由；（写出一条理由即可）(3)已知七年级有800名学生，八年级有600名学生，请估计两个年级上周劳动时间在80分钟以上（含80分钟）的学生一共有多少人？23．四边形ABCD 中，AB CD ∥，BC AB ^，12AB =，6DC =，8BC =．动点P 从A 点出发，沿A B ®方向以每秒1个单位的速度运动，同时，动点Q 从点A 出发，沿折线A D C ®®方向以每秒2个单位的速度运动，当Q 点到达C 点时，P 、Q 两点都停止运动．设动点P 运动的时间为x 秒，1y AP DQ =+，(1)请直接写出1y 关于x 的函数关系式并注明自变量x 的取值范围；(2)在给定的平面直角坐标系中画出函数1y 的图象，并写出函数1y 的一条性质；(3)若函数2y x b =+的图象跟函数1y 的图象有两个交点，请直接写出b 的取值范围．24．新学期学校门口开了一家文具店，为了更好的迎接同学们，商家购进了一批笔记本和签字笔，商家用1600元购进笔记本，800元购进签字笔，每本笔记本比每支签字笔的进价贵6元，且购进签字笔的数量是笔记本的2倍．(1)求每本笔记本和每支签字笔的进价？(2)商家在销售过程中发现，当笔记本的售价为每本14元，签字笔的售价为每支5元时，平均每天可售出20本笔记本，40支签字笔．据调查，笔记本的售价每降低0.5元平均每天可多售出5本，且开学活动力度大，降价幅度不低于10%，商家在保证签字笔的售价和销量不变且不考虑其他因素的情况下，想使笔记本和签字笔平均每天的总获利为270元，则每本笔记本的售价应定为多少元？25．如图，直线122y x =+分别与x 轴，y 轴交于点A ，点C ，点P 是反比例函数(0)k y k x =¹图象与直线AC 在第一象限内的交点，过点P 作PB x ^轴于点B ，且6AB =．(1)求反比例函数的表达式；(2)点D 是直线PB 右侧反比例函数图象上一点，且92APD S =V ，直线PD 交y 轴于点E ，点M ，N 是直线AC 上两点，点M 在点N 的左侧且MN AP =，求EM DN +的最小值及此时点N 的坐标；(3)在（2）的条件下，点F 为反比例函数图象上一点，若45PEF PAB ∠-∠=°，请直接写出所有符合条件的点F 的横坐标．26．在ABC V 中，90BAC ∠=°，AB AC =，D 为线段BC 上一点（点D 不与B ，C 重合），连接AD ．(1)如图1，105ADB ∠=°，CD =BD 的长度；(2)如图2，D 为BC 中点，E 为平面内一点，连接DE ，CE ，AE ，BE ，将线段DE 绕D 顺时针旋转90°得到线段DF ，连接AF ，90FAC ECB ∠+∠=°，G 为线段EC 上一点，AG CE ^，求证：2CE AG =+；(3)如图3，P ，H 为射线AD 上两个点，90BHA ∠=°，2AP BH =，将BNP △沿直线BP 翻折至BHP V 所在平面内得到BKP △，直线PK 与直线AB 交于点T ．若AB =BP 取得最小值时，请直接写出APT △的面积．1．D【分析】本题考查了中心对称图形和轴对称图形的识别．根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【详解】解：A、不是轴对称图形，是中心对称图形，故本选项不符合题意；B、是轴对称图形，不是中心对称图形，故本选项不符合题意；C、是轴对称图形，不是中心对称图形，故本选项不符合题意；D、既是轴对称图形，又是中心对称图形，故本选项符合题意；故选：D．2．B【分析】本题主要考查了根的判别式．利用根的判别式对选项中方程根的情况依次进行判断即可．【详解】解：2x x=，则20x x-=，所以2(1)41010D=--´´=>，则此方程有两个不相等的实数根．故A选项不符合题意．210 4x x++=，则2114104D=-´´=，所以此方程有两个相等的实数根．故B选项符合题意．240x-=，2041(4)160D=-´´-=>，所以此方程有两个不相等的实数根．故C选项不符合题意．2240x x++=，22414120D=-´´=-<，所以此方程没有实数根．故D选项不符合题意．故选：B．3．A【分析】此题考查反比例函数图象的性质，根据题意得到反比例函数的系数大于0时得到30k ->，解可得k 的取值范围．【详解】解：根据题意得：30k ->，3k \>，故选：A ．4．B【分析】本题考查的是位似变换，以点A 为坐标原点，原来的x 轴为x 轴建立新的平面直角坐标系，根据位似变换的性质求出点D 在新坐标系中的坐标，进而求出点D 的坐标，解题的关键是正确理解在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或k -．【详解】以点A 为坐标原点，原来的x 轴为x 轴建立新的平面直角坐标系，则在新坐标系中，点A 的坐标为()0,0，点B 的坐标为 ()12-,，∵ABC V 与ADE V 是以点A 为位似中心的位似图形，相似比为1:3，∴点D 在新坐标系中的坐标为 ()13,23-´´，即 ()3,6-，则点D 在原坐标系中的坐标为()4,6-，故选：B ．5．B【分析】此题主要考查了根据实际问题抽象出二次函数解析式，直接利用二月的研发资金为：()101x +，故三月份新产品的研发资金为：()2101x +，再求和即可，正确表示出三月份的研发资金是解题关键．【详解】解：根据题意可得二月的研发资金为：()101x +，故三月份新产品的研发资金为：()2101x +，今年一季度新产品的研发资金()()210101101y x x =++++，故选：B ．6．B【分析】本题主要考查的是二次根式乘法运算，估算无理数的大小，夹逼法的应用是解题的关键．先利用二次根式的乘法法则计算，进而估算无理数的大小得出答案．6=∵91516<<∴34<<∴9610<<的值应在9和10之间．故选：B ．7．A【分析】先用b 、d 、f 分别表示出a 、c 、e ，再代入要求的式子即可．【详解】解：由13a c eb d f ===， 333b a ，dc ，f e \===，()323232132332333323a c e a c e a c eb d f ac e a c e -+-+-+\===-+´-´-´-+，故选：A ．【点睛】此题考查比例的性质，解题关键在于掌握其性质定义．8．B【分析】本题考查了规律型中的图形的变化类，根据图形中数的变化找出变化规律是解题的关键．设图形n 中三角形的个数是(n a n 为正整数），列出部分图形中三角形的个数，根据数据的变化找出变化规律第n 个图形三角形个数为(1)(21)2n n n ++-，依此规律即可得出结论．【详解】解：设图形n 中三角形的个数是(n a n 为正整数），1211a ==+Q ，26(12)3a ==++，311(123)5a ==+++，417(1234)7a ==++++，(1)12(21)(21)2n n n a n n n +\=++¼++-=+-．()1011010121015519742a \=´´++´-=+=．故选：B ．9．C【分析】根据正方形的性质及垂直定义得出OD OC =，90DOC DFH EFC ∠=∠=∠=°，利用三角形内角和定理得出BDE OCH α∠=∠=，利用AAS 即可证明ODN OCN V V ≌，得出OF 平分EFC ∠，利用三角形外角性质即可得答案．【详解】解：如图，过点O 作OM CF ^于M ，ON DE ^于N ，设CF 、BD 交于点H ，∵正方形ABCD 的对角线AC 与BD 相交于点O ，∴AC BD ^，OD OC =，∵CF DE ^，∴90DOC DFH EFC ∠=∠=∠=°，∵DHF OHC ∠=∠，∴BDE OCH α∠=∠=，在ODN △和OCM V 中，90OND OMC ODN OCM OD OC α∠=∠=°ìï∠=∠=íï=î，∴ODN OCN V V ≌，∴OM ON =，∴OF 平分EFC ∠，∴1452EFO OFC EFC ∠=∠=∠=°，∴45DOF EFO BDE α∠=∠-∠=°-．故选：C ．【点睛】本题考查正方形的性质、全等三角形的性质、角平分线的判定、三角形内角和定理及三角形外角性质，熟练掌握相关性质及判定定理是解题关键．10．D【分析】本题考查与有理数有关的规律探究，熟练掌握有理数的运算是解题的关键，根据题意逐一判断即可得到答案．【详解】解：∵1a x =，111n n a a +=-，∴211a x =-，31x a x-=，4a x =，511a x =-，∴25a a =，故①正确；∵123n nT a a a a =××K ∴1T x =，212111x T a a x x x===--g ，3123111x x T a a a x x-===--g g g ，41234T a a a a x ==-g g g ，5123451x T a a a a a x-==-g g g g ，61234561T a a a a a a ==g g g g g ，∴1234560T T T T T T +++++=，∵100061664¸=L ，12310001234211x T T T T T T T T x-+++¼+=+++=-，故②正确；由①②可得n n a T 、分别是以3和6为周期的数列，当k 为奇数时：()()3333233323k k k k k k T S S T S S ++++-=--()333132k k k T a a +++=-+11·1x x æö=-+ç÷-èø211x x x--=-，2331321111k k k x x x x x xT T T ------=---=--，∴()3333233132k k k k k k T S S T T T ++---=--，当k 为偶数时：()()3333233323k k k k k k T S S T S S ++++-=--()333132k k k T a a +++=-+11·1x x æö=+ç÷-èø211x x x-++=-，()2331321111k k k x x x T T T x x x----++--=---=--，∴()3333233132k k k k k k T S S T T T ++---=--，故③正确；故选：D ．11．3【分析】根据负整数指数幂，零指数幂的性质解答．【详解】解：原式=2+1=3，故答案为3 ．【点睛】本题考查整数指数幂的应用，熟练掌握负整数指数幂和零指数幂的性质是解题关键．12．1【分析】先将x =2代入220x x m -+=，然后求解关于m 的方程，再代入求值即可．【详解】把2x =代入220x x m -+=，得：22220m -+=，∴1m =-∴21m =．故答案为：1．【点睛】本题考查了一元二次方程的解以及解一元一次方程的解，理解方程的解是解答本题的关键．13．20【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，根据红球的个数除以总数等于频率，求解即可．【详解】解：∵大量重复试验后发现，摸到红球的频率在0.25，∴任意摸出一个球，摸到红球的概率为0.25，50.25a\=，解得20a =，经检验：20a =是原方程的解，故答案为：20．【点睛】此题主要考查了利用频率估计概率，解答此题的关键是利用红球的个数除以总数等于频率．14．3【分析】根据多边形的内角和公式求出边数，从而求出这个多边形从一个顶点出发引出的对角线的条数．【详解】设多边形的边数是n ，则（n ﹣2）•180°=720°，解得n=6，∴从这个多边形的一个顶点引出对角线是：6﹣3=3（条），故答案为3．【点睛】本题考查多边形的对角线，多边形内角与外角，关键是要先根据多边形的内角和公式求出边数.15．53##213【分析】设A （a ，4a），a ＞0，根据题意，利用函数关系式表示出线段OD ，OE ，OC ，OF ，EF ，利用三角形的面积公式，即可得答案．【详解】解：设点A 的坐标为（a ，4a ），a ＞0，则OD =a ，OE =4a ，∴点B 的纵坐标为4a，∴点B 的横坐标为-2a ，∴OC =2a ，∴BE =2a ，∵AB ∥CD ，∴12EF BE OF OD ==，∴EF =13OE =43a ，OF =23OE =83a，∴S △BEF =12EF •BE =12×43a ×2a =13，S △ODF =12OD •OF =12×a ×83a =43，∴S 阴影=S △BEF +S △ODF =13+43=53．故答案为：53．【点睛】本题主要考查了反比例函数的比例系数的几何意义，反比例函数的图象上点的坐标的特征，矩形的性质，利用点的坐标表示相应线段的长度是解题的关键．16．8-【分析】先按照不等式组的性质求出不等式的解集，进而确定m 取值范围；再解出分式方程，找到分式方程的非负整数解，进而求出m 的值，最后求和即可．【详解】解：()02422x m x x -ì>ïíï-<-î①②，解不等式①得x m >，解不等式②得0x >，Q 不等式的解集为：0x >，0m \£．解分式方程1322y m y y -=---，方程两边同时乘以()2y -得，()132y y m -=-+，解得：52m y +=．25m y \=-，0m £Q ，250y \-£，52y \£．Q 分式方程1322m y y y--=--有非负整数解，20y \-¹，0y ³，2y \¹且0y ³，y \的值为：0，1．m \对应的值为：5-，3-．\符合条件的所有m 的取值之和为：()538-+-=-．故答案为：8-．【点睛】本题考查了分式方程的解以及不等式的解集，解题的关键在于求出m 取值范围以及求出分式方程的解．17【分析】本题考查了菱形的性质、三角形中位线定理、全等三角形的判定与性质、含30°角的直角三角形的性质以及勾股定理等知识．由菱形的性质得4AB BC CD ===，AB CD ∥，60BAD BCE ∠=∠=°，再由三角形中位线定理得122FH AB ==，AB FH ∥，然后证()AAS FHG CEG ≌△△，得12EG GH EH ===，进而由勾股定理即可得出结论．【详解】解：Q 菱形ABCD 的边长为4，60BAD ∠=°，4AB BC CD \===，AB CD ∥，60BAD BCE ∠=∠=°，F Q 为AE 的中点，H 为BE 的中点，\12EH BE =，FH 是ABE V 的中位线，\122FH AB ==，AB FH ∥，\AB FH CD ∥∥，BE AB ^Q ，FH BE \^，CD BE ^，90FHE BEC °\∠=∠=，906030CBE \∠=°-°=°，\122CE BC ==，\BE ===，\12EH BE ==FH CE \=，在FHG △和CEG V 中，FHG CEG FGH CGE FH CE ∠=∠ìï∠=∠íï=î，()AAS FHG CEG \≌△△，\12EG GH EH ===在Rt FHG V中，由勾股定理得：GF ，18． 126905【分析】本题考查因式分解及新定义的运算，理解定义是解决问题的关键．根据题意即可求得(5611)(3142)F G ´的值，结合“活泼数”A abcd =，“可爱数”B mnpq =，百位数字为4，可得()33()93(23)G B m F A a b -=+-+是整数，可知30m -=，3，6，根据“可爱数”可知只有33m -=符合题意，进而可得()13()923G B F A a b =+-+是整数，得231a b -+=±，即24a b -=-或22a b -=-，求得a ，b 得值，结合“活泼数”定义及条件为奇数即可求得所有得满足条件的奇数四位数A 的和．【详解】解：由题意可得：2566211(5611)(3142)1256F G ´+-´´==+ ∵“活泼数”A abcd =，则22b a cd -=，∴22()a b b cd F A a b×+-=+()2222a b b b a a b ×+--=+222a b b a a b×-+=+()()2a b a b a b-+=+2a b =-，则()()3()933323F A F A a b éù+=+=-+ëû，∵“可爱数”B mnpq =，百位数字为4，则1p m =+，4n =，∴()143G B p n m m =-=+-=-，∵()33()93(23)G B m F A a b -=+-+是整数，30m \-=，3，6，当30m -=时，3m =，则4p =，4n =，不符题意，舍去；当33m -=时，6m =，则7p =，4n =，15q n =+=，符合题意；当36m -=时，9m =，则10p =，不符题意，舍去；()13()923G B F A a b \=+-+是整数，231a b \-+=±，24a b \-=-或22a b -=-，当24a b -=-时，1,6a b ==；2,8a b ==；1635A \=或2860A =（偶数，不符题意，舍去）；当22a b -=-时，1,4;2,6;3,8a b a b a b ======；1415A \=或2632A =（偶数，不符题意，舍去）或3855A =，1635141538556905\++=故答案为：12，6905．19．（1）无解；（2）1312x -£<【分析】本题考查了解分式方程和求一元一次不等式组解集．（1）分式方程两边都乘以()2x -，把分式方程化为整式方程，求解，再进行检验即可；（2）先求出两个不等式的解集，再求其公共解．【详解】解：（1）方程两边都乘以()2x -得：()1132x x =---，解得：2x =．检验：当2x =时，2220x -=-=，所以原分式方程无解；（2）()328143x x x x ì--£ïí+-<ïî①②，解不等式①得：1x ³-，解不等式②得：132x <，所以，不等式组的解集是1312x -£<．20．21x x +；1．【分析】根据分式的运算法则进行计算化简，再将x 2=x +1代入即可．【详解】解：原式=(1)(1)(2)(1)x x x x x x -+--+×2(1)(21)x x x +-=21(1)x x x -+×2(1)(21)x x x +-=21x x +，∵x 2﹣x ﹣1=0，∴x 2=x +1，∴21x x +=11x x ++=1．21．①AD CB ∥ ②ADE CBF ∠=∠ ③DE BF P ④形成的四边形是平行四边形【分析】本题考查了作图﹣复杂作图，平行四边形的性质和全等三角形的判定的知识，三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．（1）作ABC ∠的平分线，其中交AC 于F 即可；（2）由于()ASA ADE CBF V V ≌，根据全等三角形的性质得到()ASA ADE CBF V V ≌根据等角的补角相等可得DE BF =，DEA BFC ∠=∠，则DE BF P ，根据平行四边形的判定即可得到结论．【详解】如图，点F 即为所作；证明：∵四边形ABCD 是平行四边形，∴AD CB =，AD CB ∥，∴DAC BCA ∠=∠．∵DE 平分ADC ∠，BF 平分CBA ∠，∴12ADE ADC ∠=∠，12CBF ABC ∠=∠．∵ADC CBA∠=∠∴ADE CBF ∠=∠，∴()ASA ADE CBF V V ≌．∴DE BF =，DEA BFC ∠=∠．∴DE BF P ，∴四边形BEDF 是平行四边形．命题：过平行四边形一组对角的顶点作平行线与另一组对角顶点所连对角线相交，则形成的四边形是平行四边形．故答案为：①AD CB ∥ ②ADE CBF ∠=∠ ③DE BF P ④形成的四边形是平行四边形．22．(1)10，39，80；(2)八年级的较好，理由：八年级学生参加劳动的时间的中位数、众数均比七年级的大；(3)718．【分析】（1）在扇形统计图中，先求出“B 组”所占的百分比，再求出“A 组”所占的百分比，确定a 的值，根据八年级的频数之和等于100可求出b 的值，再根据中位数的定义求出c 的值；（2）从中位数、众数的大小比较得出答案；（3）求出七年级、八年级上周劳动时间在80分钟以上（含80分钟）的学生数即可．【详解】（1）解：根据扇形统计图可知，“B 组”所占的百分比为144100%40%360´=，所以“A 组”所占的百分比为140%25%18%7%10%----=，即10a =；100142813639b =----=；八年级的中位数在B 组，将100名学生的劳动时间从大到小排列，处在中间位置的两个数的平均数为8080802+=，即80c =；故答案为：10，39，80；（2）八年级的较好，理由：八年级学生参加劳动的时间的中位数、众数均比七年级的大；（3）()143980010%40%600718100+´++´=（人），答：七、八年级上周劳动时间在80分钟以上（含80分钟）的学生大约有718人．【点睛】本题考查扇形统计图，频数分布表、中位数、众数、平均数以及样本估计总体，理解平均数、中位数、众数的定义，掌握平均数、中位数、众数的计算方法是正确解答的前提．23．(1)()()1100531058x x y x x ì-££ï=í-<£ïî(2)图见解析，当05x ££时，1y 随x 的增大而减小（答案不唯一）(3)06b <£【分析】本题考查动点的函数图象问题、勾股定理、矩形的判定和性质等：（1）作DH AB ^于点H ，得到矩形DCBH ，当05x ££时，点Q 在线段AD 上，当58x <£时，点Q 在线段CD 上，列分段函数即可；（2）根据（1）中解析式描点作图，根据所得图象的增减性可得函数1y 的性质；（3）通过一次函数图象的平移解决问题．【详解】（1）解：如图，作DH AB ^于点H ，Q AB CD ∥，BC AB ^，DH AB ^，\90C B DHB Ð=Ð=Ð=°，\四边形DCBH 是矩形，\8DH BC ==，6BH CD ==，\1266AH AB BH =-=-=，\10AD ===，Q 动点Q 从点A 出发，沿折线A D C ®®方向以每秒2个单位的速度运动，\点Q 从点A 到点D 用时：()1025s ¸=，从点A 到点C 用时：()()10628s +¸=，当05x ££时，点Q 在线段AD 上，102DQ AD AQ x =-=-，AP x =，\110210y AP DQ x x x =+=+-=-；当58x <£时，点Q 在线段CD 上，2210DQ x AD x =-=-，AP x =，\1210310y AP DQ x x x =+=+-=-；综上可知，()()1100531058x x y x x ì-££ï=í-<£ïî；（2）解：1y 的图象如下图所示，由图可知，当05x ££时，1y 随x 的增大而减小，当58x <£时，1y 随x 的增大而增大；（3）解：如图，当06b <£时，函数2y x b =+的图象跟函数1y 的图象有两个交点．24．(1)每本笔记本的进价是8元，每支签字笔的进价是2元；(2)每本笔记本的售价应定为11元．【分析】本题主要考查了一元二次方程的应用、分式方程的应用，理解题意，找准等量关系，正确列出分式方程以及一元二次方程是解此题的关键．（1）设每本笔记本的进价是x 元，则每支签字笔的进价是()6x -元，根据“商家用1600元购进笔记本，800元购进签字笔，且购进签字笔的数量是笔记本的2倍”列出分式方程，解方程即可；（2）设每本笔记本的售价为y 元，则每本笔记本的销售利润为()8y -元，每天可售出()14205160100.5y y -+´=-本，根据“笔记本和签字笔平均每天的总获利为270元”列出一元二次方程，解方程即可得出答案．【详解】（1）解：设每本笔记本的进价是x 元，则每支签字笔的进价是()6x -元，根据题意得：800160026x x=´-，解得：8x =，经检验，8x =是所列方程的解，且符合题意，6862x \-=-=，答：每本笔记本的进价是8元，每支签字笔的进价是2元；（2）解：设每本笔记本的售价为y 元，则每本笔记本的销售利润为()8y -元，每天可售出()14205160100.5y y -+´=-本，根据题意得：()()()8160105240270y y --+-´=，整理得：2241430y y -+=，解得：121113y y ==，，当11y =时，141411100%100%21.4%10%1414y --´=´»>，符合题意；当13y =时，141413100%100%7.1%10%1414y --´=´»<，不符合题意，舍去，答：每本笔记本的售价应定为11元．25．(1)反比例函数解析式为6y x=；(2)EM DN +的最小值为，此时(4,4)N ；(3)符合条件的点F 5-．【分析】（1）先求出点A 坐标，利用6AB =求出点P 的坐标，继而求出反比例函数解析式即可；（2）过点D 作y 轴的平行线交直线AC 于点K ，根据面积求出点D 坐标，再求出直线PD解析式，得到点E 坐标，继而求出线段MN 长，将点D 沿着射线PA 方向平移个单位长度得到点(3,1)D ¢--，连接MD ¢，D E ¢，则四边形DD MN ¢是平行四边形，则D M DN ¢=，当点E 、M 、D ¢共线时取等号，此时EM DN +最小，最小值为D E ¢的长，据此求出最小值和点N 坐标即可；（3）分两种情况讨论①当EF 在ED 左侧时，②当EF 在ED 右侧时，根据条件分别求出点F 的横坐标即可．【详解】（1）解：在一次函数122y x =+中，令0y =时，4x =-，4\=OA ，6AB =Q ，2OB \=，当2x =时，12232y =´+=，(2,3)P \，Q 点P 在反比例函数图象上，6k \=，\反比例函数解析式为6y x=；（2）解：如图，过点D 作y 轴的平行线交直线AC 于点K ，设点6,D a a æöç÷èø，2a >，则1,22K a a æö+ç÷èø，92APD ADK PDK S S S =-=Q △△△，\11692(24)222a a æö´+-´+=ç÷èø，整理得：2120a a +-=，解得3a =或4a =-（舍去），(3,2)D \，设直线PD 的解析式为y kx b =+，3223k b k b +=ìí+=î，解得15k b =-ìí=î，\直线PD 的解析式为5y x =-+，)5(0,E \，(4,0)-Q A ，(2,3)P，MN AP \==将点D 沿着射线PA方向平移个单位长度得到点(3,1)D ¢--，连接MD ¢，D E ¢，则四边形DD MN ¢是平行四边形，则D M DN ¢=，EM DN EM D M D E \+=³¢¢+，当点E 、M 、D ¢共线时取等号，此时EM DN +最小，最小值为D E ¢的长，(3,1)D ¢--Q ，(0,5)E ，\直线D E ¢的解析式为25y x =+，D E ¢=，由12225y x y x ì=+ïíï=+î，解得21x y =-ìí=î，(2,1)M \-，则(4,4)N ，EM DN \+的最小值为，此时(4,4)N ；（3）解：①当EF 在ED 左侧时，如图所示，设PE 与x 轴交于点Q ，则(5,0)Q ，5OE OQ \==，则45OEQ OQE ∠=∠=°，Q 当0x =时，1222y x =+=，(0,2)C \，则2OC =，过点M 作MH y ^轴，垂足为H ，90MHE COA \∠=∠=°，2MH OC ==，4HE OA ==，()SAS MHE COA \V V ≌，HEM CAO \∠=∠，则45PEM HEM OEQ PAB ∠=∠+∠=∠+°，45PEF PAB ∠-∠=°Q ，45PEF PAB \∠=∠+°，PEF PEM \∠=∠，即点E 、M 、F 共线，则点F 为直线25y x =+与反比例函数6y x=图象的交点，由6y x y ì=ïíï=î得22560x x +-=，解得x =或x =，点F ②当EF 在ED 右侧时，如图，ES x ∥轴，则45SEP ∠=°，则4545PEF FES PAB ∠=∠+°=∠+°，FES PAB \∠=∠，则EF AP ∥，\直线EF 的解析式为152y x =+，由6152y x y x ì=ïïíï=+ïî得210120x x +-=，解得5x =-或5x =-，\在ED 右侧的点F 横坐标为5-综上分析，符合条件的点F 或5-．【点睛】本题考查了反比例函数的综合，涉及待定系数法求函数解析式、坐标与图形、平移性质、平行四边形的判定与性质、最短路径问题、全等三角形的判定与性质、解一元二次方程等知识，熟练掌握相关知识的联系与运用，灵活数形结合和分类讨论思想是解答本题的关键．26．(1)BD =；(2)(3)APT S V 【分析】（1）作DE AC ^于E ，由Rt CDE △求得DE ，由Rt ADE V 求得AE ，由Rt ABC △求得BC ，进一步得出结果；（2）可证得()SAS ADF BDE V V ≌，从而得出EBD FAB ∠=∠，BE AF =，可证得EBA AOE ∠=∠，从而点E B O A 、、、共圆, 从而得出45BEC BAD ∠=∠=°，从而12BEC BAC ∠=∠，12EH AF ==，EH BH =，进而得出点E 在以A 为圆心，AB 为半径的圆上，从而AE AC AB ==，可得出AH 是BE 的垂直平分线, 从而EAH BAH ∠=∠，AEH ABH ∠=∠，进而证得GAH AHG ∠=∠，从而AG GH =，进一步得出结论；（3）作CE AD ^于E ，可证得ACE BAH ≌V V ，从而得出AE BH =，进而得出 CP CA ==从而得出点P 在以C BC 交C e 于点 P ¢，可得出当点P 运动在P ¢处时，BP 最小，作AH BC ^于H ，可求得APC △的面积，根据BPT CPA ∽V V ，可求得BPT △的面积，进一步得出结果．【详解】（1）如图1，作DE AC ^于E ，∴AB AC =，90BAC ∠=°，∴45B C ∠==°∠，在Rt CDE △中，CD =45C ∠=°，∴由勾股定理得：DE CE ==，在Rt ADE V 中，1054560DAC ADB C ∠=∠-∠=°-°=° ，DE =∴1AE =∴1AC AE CE =+=，在Rt ABC △中，1AC =，45C ∠=°，∴BC =+，∴BD BC CD =-=（2）证明：如图2，设AD 和CE 交于点O∴AB AC =，D 是BC 的中点，∴AD BC ^，∵90BAC ∠=°∴12AD BD CD BC ===，∵线段DE 绕D 顺时针旋转90°得到线段DF ，∴90EFD ∠=°，DE DF =，∴90ADB EDF ∠==°，∴ADF BDE ∠=∠，∴()SAS ADF BDE V V ≌，∴EBD FAB ∠=∠，BE AF =，CAF CAD ∠=∠，∴4545EBA CAF ∠+°=∠+°，∴EAB CAF ∠=∠，∵90ADC ∠=°，∴90BCE COD ∠+∠=°，∵AOE COD ∠=∠，∴90BCE AOE ∠+∠=°，∵90BCE CAF ∠+∠=°，∴CAF AOE ∠=∠，∴EBA AOE ∠=∠，∴点E B O A 、、、共圆，∴45BEC BAD ∠=∠=°，∴12BEC BAC ∠=∠，12EH AF ==，EH BH =，AB AC =，∴点E 在以A 为圆心，AB 为半径的圆上，∴AE AC AB ==，∵AG CE ^，∴12EG CG CE ==，∵EH BH =，AE AB =，∴AH 是BE 的垂直平分线，∴EAH BAH ∠=∠，AEH ABH ∠=∠，∵BH AG ∥，∴BAG ABH ∠=∠，∴GAH BAH BAG EAH AEH ∠=∠+∠=∠+∠，∵AHG EAH AEH ∠=∠+∠，∴GAH AHG ∠=∠，∴AG GH =，∴EG EH GH AF AG =++，∴22EG AG +，∴2CE AG =+；（3）如图3，作CE AD ^于E ，∴90AEC ∠=°，∴90EAC ACE ∠+∠=°，∵90BAC ∠=°，∴90BAH CAE ∠+∠=°，∴BAH ACE ∠=∠，∵AB AC =，90AEC AHB ∠=∠=°，∴()ACE BAH AAS V V ≌，∴AE BH =，∵2AP BH =，∴2AP AE =，∴CP CA ==∴点P 在以C BC 交C e 于点P ¢，∴当点P 运动在P ¢处时,BP 最小，如图4，作AH BC ^于H ，。

2023年重庆南开中学中考数学模拟试卷(word版)附详细参考答案

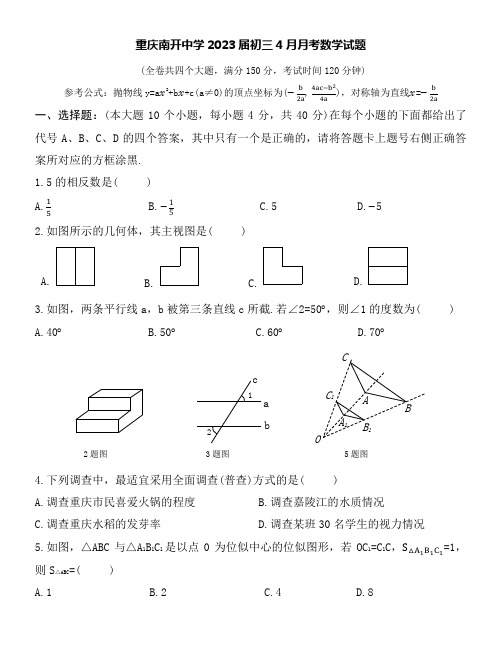
重庆南开中学2023届初三4月月考数学试题(全卷共四个大题，满分150分，考试时间120分钟)参考公式：抛物线y=a x 2+b x +c(a≠0)的顶点坐标为(−b2a ,4ac−b 24a)，对称轴为直线x =−b2a一、选择题：(本大题10个小题，每小题4分，共40分)在每个小题的下面都给出了代号A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑. 1.5的相反数是( )A.15 B.−15 C.5 D.−52.如图所示的几何体，其主视图是( )3.如图，两条平行线a ，b 被第三条直线c 所截.若∠2=50°，则∠1的度数为( ) A.40° B.50° C.60° D.70°4.下列调查中，最适宜采用全面调查(普查)方式的是( ) A.调查重庆市民喜爱火锅的程度 B.调查嘉陵江的水质情况 C.调查重庆水稻的发芽率 D.调查某班30名学生的视力情况5.如图，△ABC 与△A 1B 1C 1是以点0为位似中心的位似图形，若OC 1=C 1C ，S △A 1B 1C 1=1，则S △ABC =( )A.1B.2C.4D.82题图a 3题图bc125题图BACOA 1B 1C 1A.B. C.6.估计(2√3−√2)×√2的值应在( )A.0到1之间B.1到2之间C.2到3之间D.3到4之间 7.某口罩生产商今年一月的产量为150万只，由于疫情得到有效控制，到今年三月逐渐减少为90万只，设该厂二、三月的口罩产量的月平均减少率为x ，则可列方程为( )A.150(1−x )2=90B.150(1−2x )=90C.90(1+x )2=150D.150−150(1−x ) −150(1−x )2=908.用若干大小相同的开口笑图形按如图所示的规律拼成一列图案，其中第①个图案中有4个开口笑图形，第②个图案中有7个开口笑图形，第③个图案中有10个开口笑图形，…，按此规律排列下去，则第⑦个图案中开口笑图形的个数是( ) A.20 B.21 C.22 D.239.如图，AB 是⊙O 的直径，BC 为弦，D 是弧BC 的中点，连接AD 交BC 于E ，若∠BAD=30°，AB=2√3，则EC=( )A.1B.√2C.√3D.210.已知两个正整数a ，b ，可按规则c=(a+1)(b+1)−1扩充得到一个新数，再从a ，b ，c 三个数中任取两个数，按上述规则又可扩充得到一个新数，依次下去，将每扩充得到一个新数叫做一次操作.已知a=3，b=1，则以下结论正确的个数为( ) ①第一次操作后扩充得到的新数c=7； ②第三次操作后扩充得到的新数可能是63；③若n 次操作后扩充得到的新数大于2023，则n 至少是4.A.0B.1C.2D.39题图8题图①②③……二、填空题：(本大题8个小题，每小题4分，共32分)请将每小题的答案直接填在答题卡中对应的横线上11.计算(12)-1+(π−3)0=_________.12.已知点A(3，a)，B(−2，6)都在反比例函数y=kx(k≠0)图象上，则a=_________.13.如图，矩形ABCD 中，AB=2，BC=2√2，以点A 为圆心，AD 为半径作弧交BC 于E ，连接AE ，则图中阴影部分的面积为_________.14.有三张完全一样的卡片，正面分别标有数字−1，1，2，将其背面朝上洗匀，从中抽出一张记为P 点的横坐标x ，放回后洗匀，再从中抽出一张记为P 点的纵坐标y ，则点P(x ，y)在第一象限的概率是_________.15.已知正多边形的一个外角是60°，则这个正多边形的内角和为_________.16.如图，正方形ABCD 中，E 为DC 边上一点，连接AE 、BD ，点M 为AE 中点，点O 为BD 中点，连接BM ，点K 为BM 中点，连接KO ，若AB=3√5，DE=√5，则OK=________. 17.若关于x 的分式方程2x −3+2=1−a x 3−x有整数解，且关于y 的不等式组{y2−1≥y−23y +a ≥3(y −1)至少有1个整数解，则符合条件的所有整数a 的值之积为_________.18.如果一个三位自然数各个数位上的数字均不为0，且百位数字等于十位数字与个位数字的和，则称这个数为“百合数”.如：853，∵8=5+3，∴853是“百合数”.又如：432，∵4≠3+2，∴432不是“百合数”.已知M 是一个“百合数”，在M 的末位数字后添加数字1得到一个四位数A ，在M 的首位数字前添加M 的十位数字得到一个四位13题图16题图BAED CKOM数B，且A−B能被11整除.则“百合数”M的最小值是_________；“百合数”M所有的值的和为_________.三、解答题：(本大题8个小题，每小题10分，19题8分，共78分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形(包括辅助线)，请将解答过程书写在答题卡中对应的位置上.19.在学习等腰三角形性质中，小美遇到这样一个题目，如图，在△ABC中，AB=AC，点D在BC边上，连接AD.过点C作CE⊥AD于E，且∠ACE=1∠BAC，求证：AD=CD.小美2的解决方法是过点A作AF垂直BC于点F，利用等腰三角形和全等三角形的性质解决问题.请根据小美的思路完成下面的作图与填空.证明：用直尺和圆规，过点A作BC的垂线AF，垂足为F(只保留作图痕迹)∵AB=AC,①∴∠CAF=1∠CAB2∠CAB∵∠ACE=12∴②∵CE⊥AD，AF⊥CB∴③∵AC=AC∴△ACE≌△CAF∴④∴AD=CD20.计算：(1)6m 3n 2÷2m 2n+m(m −2n)−(m+n)(m −n)； (2)(4a−2−a+2)÷a 2−8a+162a−8.21.4月14日，某校初三年级学生参加了体育中考，为了解学生的考试情况，从该校初三年级男生、女生中各随机抽取20名同学的体考成绩(满分为50分)进行整理、描述和分析(体考成绩用x 表示，且均为整数，共分为四个等级：A.48≤x ≤50；B.46≤x ＜48；C.44≤x ＜46；D.0≤x ＜44)，下面给出了部分信息：抽取的20名男生体考成绩中A 等级包含的所有数据为：50，48，50，49，49，48，50，50，50，50，49，48，48，50.初三年级抽取的女生体考成绩条形统计图初三年级抽取的男生、女生体考成绩统计表BC 15% m%D 5% 初三年级抽取的男生体考成绩扇形统计图AACDBE根据以上信息，解答下列问题：(1)填空：a=_______； b=______；m=______；(2)根据以上数据，你认为该校初三年级男生和女生谁的体育中考成绩更优异？请说明理由；(写出一条理由即可)(3)若该校初二年级共有学生800人参加体育中考，估计该校初三年级体育中考成绩A 等级的学生人数.22.某班计划从商店购买“红龙”牌的饮料和“白乐”牌饼干，已知购买一盒饼干比购买一瓶饮料多用20元，若用400元购买饼干，用160元购买饮料，且购买饼干的盒数是购买饮料瓶数的一半.(1)购买一盒“白乐”牌饼干、一瓶“红龙”牌饮料各需要多少元？(2)经商谈，商店给予该班购买一盒“白乐”牌饼干赠送一瓶“红龙”牌饮料的优惠，如果该班需要“红龙”牌饮料瓶数是“白乐”牌饼干盒数的2倍还多8，且该班购买饮料和饼干的总费用不超过670元，那么该班最多可购买多少盒“白乐”牌饼干？23.如图，在平行四边形ABCD中，∠A=120°，AB=6，BC=8，点P从点B出发，沿线段BA向点A运动，到达点A时停止.过点P作AB的垂线PQ，交折线B-C-D于点Q，设BP=x(0≤x≤6)，CQ=y.(1)请直接写出y与x的函数表达式以及对应的x的取值范围；(2)在直角坐标系中画出y的图象，并写出函数y的一条性质；(3)当CQ＜AP时，请直接写出自变量x的取值范围.24.近日，小南和小开分别从点B 、C 处出发前往点A 处参加校园文化节活动.已知点A 位于点B 北偏东60°方向，点C 位于点A 南偏西15°方向，同时位于点B 南偏东45°方向，BC=4000米.(1)求BA 路段的长度；(结果保留根号)(2)由于当天要举行马拉松比赛，BA 路段实施交通管制，小南计划从B 处乘公交车沿B→D→A 前往A 处，点D 在点B 的正北方向，同时在点A 的正西方向.小开计划骑自行车沿C→A 前往A 处，若公交车速度为500米/分，小开骑自行车速度为200米/分，小开出发15分钟后小南从点B 出发，公交车到站停靠时间忽略不计，请计算小南和小开各自所需时间说明谁先到达A 处？(参考数据：√2≈1.41，√3≈1.73，√6≈2.45)A 15°60°DCB南东西北A DCQBP25.如图1，在平面直角坐标系中，抛物线y=√2x 2−2√2x −3√2与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴交于点C ，抛物线的对称轴交直线BC 于点D. (1)求点D 的坐标；(2)如图2，若P 是直线BC 下方抛物线上的一个动点，连接PC 、PD ，求△PCD 面积的最大值及此时P 点的坐标；(3)将抛物线y=√2x 2−2√2x −3√2沿射线CB 方向平移3√3个单位，得到的新抛物线与原抛物线交于点M.在新抛物线对称轴上是否存在一点N ，使得以点M 、N 、D 为顶点的三角形是以ND 为腰的等腰三角形？若存在，请直接与出N 点的坐标，并把求其中一个点N 的坐标的过程写出来；若不存在，请说明理由.26.在Rt△ABC 中，∠BAC=90°，D 是射线AB 上的一点.(1)如图1，连接CD ，过点A 作AE⊥DC 于E 交BC 于F ，若AB=AF ，∠D=40°，求∠ACB 的度数；(2)如图2，若AB=AC ，O 是BC 中点，连接DO 、AO ，点G 是OD 中点.连接AG 交B0于点H ，连接BG ，若∠BGA=90°，求证：AH=2BG+BH ；(3)如图3，若AB=2√3，AC=2，K 是平面内一点，∠BKC=45°，Q 是KC 中点，当AQ 的长取得最大值时，请直接写出△ABK 的面积.备用图图1 图2重庆南开中学2023届初三4月月考数学试题(全卷共四个大题，满分150分，考试时间120分钟)参考公式：抛物线y=a x 2+b x +c(a≠0)的顶点坐标为(−b2a ,4ac−b 24a)，对称轴为直线x =−b2a一、选择题：(本大题10个小题，每小题4分，共40分)在每个小题的下面都给出了代号A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑. 1.5的相反数是( )A.15 B.−15 C.5 D.−51.解：正数的相反数是负数，绝对值不变，故选D .2.如图所示的几何体，其主视图是( )2.解：C 是左视图，D 是主视图，故选D .A.B. C.图1ACEBDF图2ADOBGH C图33.如图，两条平行线a ，b 被第三条直线c 所截.若∠2=50°，则∠1的度数为( ) A.40° B.50° C.60° D.70°3.解：∠2的对顶角是∠1的同位角，∵a ∥b ，∴∠1=∠2=50°，故选B .4.下列调查中，最适宜采用全面调查(普查)方式的是( ) A.调查重庆市民喜爱火锅的程度 B.调查嘉陵江的水质情况 C.调查重庆水稻的发芽率 D.调查某班30名学生的视力情况 4.解：小样本可采用全面调查方式，故选D .5.如图，△ABC 与△A 1B 1C 1是以点0为位似中心的位似图形，若OC 1=C 1C ，S △A 1B 1C 1=1，则S △ABC =( )A.1B.2C.4D.8 5.解：∵OC 1=C 1C ，∴C 1为OC 的中点，∴A 1C 1AC=OC 1OC =12，S △A 1B 1C 1S △ABC=(12)2=14，故S △ABC =4，选C .6.估计(2√3−√2)×√2的值应在( )A.0到1之间B.1到2之间C.2到3之间D.3到4之间 6.解：(2√3−√2)×√2=2√6−2=√24−2，∵4=√16＜√24＜√25=5，∴2＜√24−2＜3，故选C .7.某口罩生产商今年一月的产量为150万只，由于疫情得到有效控制，到今年三月逐渐减少为90万只，设该厂二、三月的口罩产量的月平均减少率为x ，则可列方程为( )A.150(1−x )2=90B.150(1−2x )=90C.90(1+x )2=150D.150−150(1−x ) −150(1−x )2=902题图a 3题图bc125题图BACOA 1B 1C 17.解：二月产量为150×(1−x )，三月产量为150×(1−x )(1−x )=150(1−x )2，故选A . 8.用若干大小相同的开口笑图形按如图所示的规律拼成一列图案，其中第①个图案中有4个开口笑图形，第②个图案中有7个开口笑图形，第③个图案中有10个开口笑图形，…，按此规律排列下去，则第⑦个图案中开口笑图形的个数是( ) A.20 B.21 C.22 D.238.解：4=4+3×0，7=4+3×1，10=4+3×2，…，4+3×(n −1)，代入n=7得，4+3×6=22个，故选C .9.如图，AB 是⊙O 的直径，BC 为弦，D 是弧BC 的中点，连接AD 交BC 于E ，若∠BAD=30°，AB=2√3，则EC=( )A.1B.√2C.√3D.29.解：连接OD ，BD ，CD ，OD 交BC 于点F ，∵D 是弧BC 的中点，∴OD ⊥BC ，CD=BD ，∵∠BOD=2∠BAD=60°，∴∠COD=60°，又∵OD=OC ，∴△CD 为等边三角形，∴OF=DF=12OD=14AB=√32，CF=OC ×sin60°=12AB ×√32=32，EF=DF ×tan ∠ODA=DF ×tan ∠BAD=√32×√33=12，故CE=CF −EF=32−12=1，故选A .10.已知两个正整数a ，b ，可按规则c=(a+1)(b+1)−1扩充得到一个新数，再从a ，b ，c 三个数中任取两个数，按上述规则又可扩充得到一个新数，依次下去，将每扩充得到一个新数叫做一次操作.已知a=3，b=1，则以下结论正确的个数为( ) ①第一次操作后扩充得到的新数c=7； ②第三次操作后扩充得到的新数可能是63；③若n 次操作后扩充得到的新数大于2023，则n 至少是4.9题图8题图①②③……A.0B.1C.2D.310.解：第一次操作后扩充得到的新数c=(3+1)(1+1)−1=7，①正确；c=(a+1)(b+1)−1=ab+a+b ，从1、3、7种任选两数进行第二次操作可能得到新数3×7+3+7=31或1×7+1+7=15，第三次操作可能得到新数3×31+3+31=128或1×15+15+1=31或3×15+15+3=63或1×31+31+1=63或7×31+31+7=255或7×15+15+7=127，②正确；三次操作最大数为255，第四次操作可得最大数为31×255+255+31=8191＞2023，③正确，故选D .二、填空题：(本大题8个小题，每小题4分，共32分)请将每小题的答案直接填在答题卡中对应的横线上11.计算(12)-1+(π−3)0=_________.11.解：原式=2+1=3.12.已知点A(3，a)，B(−2，6)都在反比例函数y=kx(k≠0)图象上，则a=_________.12.解：k=(−2)×6=3a ，解得a=−4.13.如图，矩形ABCD 中，AB=2，BC=2√2，以点A 为圆心，AD 为半径作弧交BC 于E ，连接AE ，则图中阴影部分的面积为_________.13.解：由勾股定理知BE=√AE 2−AB 2=√AD 2−AB 2=√8−4=2，∵AB=BE ，∴△ABE 为等腰直角三角形，∴∠BAE=45°，∠DAE=45°，故阴影部分面积=AB ×BC −12AB 2−45360π×AD 2=2×2√2−12×22−45360π×(2√2)2=4√2−2−π.13题图16题图BAED CKOM14.有三张完全一样的卡片，正面分别标有数字−1，1，2，将其背面朝上洗匀，从中抽出一张记为P 点的横坐标x ，放回后洗匀，再从中抽出一张记为P 点的纵坐标y ，则点P(x ，y)在第一象限的概率是_________.14.解：x 为1或2的概率是23，y 为−1的概率是13，故点P(x ，y)在第一象限的概率是23×13=29. 15.已知正多边形的一个外角是60°，则这个正多边形的内角和为_________. 15.解：(36060−2)×180°=720°.16.如图，正方形ABCD 中，E 为DC 边上一点，连接AE 、BD ，点M 为AE 中点，点O 为BD 中点，连接BM ，点K 为BM 中点，连接KO ，若AB=3√5，DE=√5，则OK=________. 16.解：连接DM ，∵M 为Rt △ADE 斜边AE 中点，∴DM=12AE=12√AD 2+DE 2=5√2，∵O 为BD 中点，K 为BM 中点，∴OK=12DM=√22.17.若关于x 的分式方程2x −3+2=1−a x3−x有整数解，且关于y 的不等式组{y2−1≥y−23 y +a ≥3(y −1)至少有1个整数解，则符合条件的所有整数a 的值之积为_________. 17.解：原分式方程变形得2x −3+2x−6x −3=a x−1x −3，∴2x −4=a x −1，即x =32−a，∵x 为整数，∴a=1、3(舍去)、5、−1；解y 2−1≥y−23得y ≥1，解y+a ≥3(y −1)得y ≤a+32，依题意有a+32≥1，即a ≥−1，故符合条件的所有整数a 的值之积为1×5×(−1)= −5.18.如果一个三位自然数各个数位上的数字均不为0，且百位数字等于十位数字与个位数字的和，则称这个数为“百合数”.如：853，∵8=5+3，∴853是“百合数”.又如：432，∵4≠3+2，∴432不是“百合数”.已知M 是一个“百合数”，在M 的末位数字后添加数字1得到一个四位数A ，在M 的首位数字前添加M 的十位数字得到一个四位数B ，且A −B 能被11整除.则“百合数”M 的最小值是_________；“百合数”M 所有的值的和为_________.18.解：设百合数M为(a +b)ab ̅̅̅̅̅̅̅̅̅̅̅̅，A=(a +b )ab1̅̅̅̅̅̅̅̅̅̅̅̅̅̅，B=a(a +b)ab ̅̅̅̅̅̅̅̅̅̅̅̅̅̅，A −B=1000a+1000b+100a+10b+1−1000a −100a −100b −10a −b=909b −10a+1=82×11b+7b+a −11a+1，∵A −B 能被11整除，∴7b+a+1能被11整除，解得a=3，b=1，M=431；a=7，b=2，M=972；a=4，b=4，M=844；a=1，b=6，M=716，故“百合数”M 的最小值是431；“百合数”M 所有的值的和为=431+972+844+716=2963.三、解答题：(本大题8个小题，每小题10分，19题8分，共78分)解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形(包括辅助线)，请将解答过程书写在答题卡中对应的位置上.19.在学习等腰三角形性质中，小美遇到这样一个题目，如图，在△ABC 中，AB=AC ，点D 在BC 边上，连接AD.过点C 作CE ⊥AD 于E ，且∠ACE=12∠BAC ，求证：AD=CD.小美的解决方法是过点A 作AF 垂直BC 于点F ，利用等腰三角形和全等三角形的性质解决问题.请根据小美的思路完成下面的作图与填空.证明：用直尺和圆规，过点A 作BC 的垂线AF ，垂足为F(只保留作图痕迹) ∵AB=AC,① ∴∠CAF=12∠CAB∵∠ACE=12∠CAB ∴②∵CE⊥AD，AF⊥CB ∴③ ∵AC=AC ∴△ACE≌△CAF ∴④ ∴AD=CD19.解：∵AB=AC ，∴A 在BC 的中垂线上，故作BC 的中垂线交BC 于F 点即可. ①AF ⊥BC ，②∠CAF =∠ACE ，③∠AEC=∠CFA ，④∠CAE=∠ACF . 20.计算：(1)6m 3n 2÷2m 2n+m(m −2n)−(m+n)(m −n)； (2)(4a−2−a+2)÷a 2−8a+162a−8.20.解：(1)原式=3mn+m 2−2mn −m 2+n 2=n 2+mn . (2)原式=(4a−2−(a−2)(a−2)a−2)÷(a−4)(a−4)2(a−4)=a(4−a)a−2×2a−4=2a2−a.21.4月14日，某校初三年级学生参加了体育中考，为了解学生的考试情况，从该校初三年级男生、女生中各随机抽取20名同学的体考成绩(满分为50分)进行整理、描述和分析(体考成绩用x 表示，且均为整数，共分为四个等级：A.48≤x ≤50；B.46≤x ＜48；C.44≤x ＜46；D.0≤x ＜44)，下面给出了部分信息：抽取的20名男生体考成绩中A 等级包含的所有数据为：50，48，50，49，49，48，50，50，50，50，49，48，48，50.初三年级抽取的女生体考成绩条形统计图初三年级抽取的男生、女生体考成绩统计表ACDBE F根据以上信息，解答下列问题：(1)填空：a=_______； b=______；m=______；(2)根据以上数据，你认为该校初三年级男生和女生谁的体育中考成绩更优异？请说明理由；(写出一条理由即可)(3)若该校初二年级共有学生800人参加体育中考，估计该校初三年级体育中考成绩A 等级的学生人数. 21.解：(1)a=48+492=48.5，b=50，m=1÷20×100=5.(2)女生的体育中考成绩更优异，理由(任选其一)是女生的平均成绩高于男生，或女生成绩的中位数高于男生，或女生成绩的满分率高于男生. (3)800×13+1420+20=540，估计该校初三年级体育中考成绩A 等级的学生人数有540人.22.某班计划从商店购买“红龙”牌的饮料和“白乐”牌饼干，已知购买一盒饼干比购买一瓶饮料多用20元，若用400元购买饼干，用160元购买饮料，且购买饼干的盒数是购买饮料瓶数的一半.(1)购买一盒“白乐”牌饼干、一瓶“红龙”牌饮料各需要多少元？(2)经商谈，商店给予该班购买一盒“白乐”牌饼干赠送一瓶“红龙”牌饮料的优惠，如果该班需要“红龙”牌饮料瓶数是“白乐”牌饼干盒数的2倍还多8，且该班购买饮料和饼干的总费用不超过670元，那么该班最多可购买多少盒“白乐”牌饼干？ 22.解：(1)设购买一瓶饮料需要x 元，依题意有BC 15% m%D 5% 初三年级抽取的男生体考成绩扇形统计图A160x=400x +20×2解得x =5则一盒“白乐”牌饼干价格=x +20=5+20=25(元/盒)答：购买一盒“白乐”牌饼干、一瓶“红龙”牌饮料各需要25元、5元. (2)设该班最多可购买y 盒“白乐”牌饼干，依题意有 25y+5(2y+8)≤670 解得y ≤703=2313∵y 为正整数，∴y 有最大值23答：该班最多可购买23盒“白乐”牌饼干.23.如图，在平行四边形ABCD 中，∠A=120°，AB=6，BC=8，点P 从点B 出发，沿线段BA 向点A 运动，到达点A 时停止.过点P 作AB 的垂线PQ ，交折线B-C-D 于点Q ，设BP=x (0≤x ≤6)，CQ=y.(1)请直接写出y 与x 的函数表达式以及对应的x 的取值范围； (2)在直角坐标系中画出y 的图象，并写出函数y 的一条性质； (3)当CQ ＜AP 时，请直接写出自变量x 的取值范围.23.解：(1)过C 作CM ⊥AB 于M ，过A 作AN ⊥CD 于N ，∵AB ∥CD ，∴AN ∥CM ，∴四边形AMCN 为矩形，∴AM=CN ，∵∠B=180°−∠A=60°，CM ⊥AB ，∴BM=BC ×cos ∠B=4ADCQBP MN当0≤x≤4时，CQ=BC−BQ=BPcos∠B=8−2BP=8−2x 当4＜x≤6时，CQ=PM=BP−BM=x−4故y与x的函数表达式为{8−2x(0≤x≤4) x−4(4＜x≤6).(2)图象如图所示，函数的性质(增减性)当0≤x≤4时，y随x的增大而减小，当4＜x≤6时，y随x的增大而增大.(3)当0≤x≤4时，CQ=8−2x，AP=6− x，∵CQ＜AP，∴8−2x＜6− x，解得x＞2，即此时x的取值范围为2＜x≤4当4＜x≤6时，CQ=x−4，AP=6− x，∵CQ＜AP，∴x−4＜6− x，解得x＜5，即此时x的取值范围为4＜x＜5综上述，自变量x的取值范围为2＜x＜5.或AP=6−x，如图所示，画出AP所在直线y=6−x的函数图象，与CQ所在函数图象交于点(2,4)、(5,1),可直接写出自变量x的取值范围2＜x＜5.24.近日，小南和小开分别从点B、C处出发前往点A处参加校园文化节活动.已知点A 位于点B北偏东60°方向，点C位于点A南偏西15°方向，同时位于点B南偏东45°方向，BC=4000米.(1)求BA路段的长度；(结果保留根号)(2)由于当天要举行马拉松比赛，BA路段实施交通管制，小南计划从B处乘公交车沿B→D→A前往A处，点D在点B的正北方向，同时在点A的正西方向.小开计划骑自行车沿C→A前往A处，若公交车速度为500米/分，小开骑自行车速度为200米/分，小开出发15分钟后小南从点B出发，公交车到站停靠时间忽略不计，请计算小南和小开各自所需时间说明谁先到达A处？(参考数据：√2≈1.41，√3≈1.73，√6≈2.45)24.解：(1)依题意易知∠ABC=180°−60°−45°=75° ∵∠ABD=60°，∴∠BAD=30°，∠BAC=90°−30°−15°=45° 过B 作BE ⊥AC 于E ，则△ABE 为等腰直角三角形 ∴∠ABE=45°，BA=√2BE ，∠CBE=75°−45°=30°∴BE=BC ×cos ∠CBE=4000×√32=2000√3，故BA=√2BE=2000√6(米).(2)∵CE=BC ×sin ∠CBE=4000×12=2000，AE=BE=2000√3∴CA=CE+AE=2000+2000√3≈5460(米)，5460÷200=27.3(分钟)∵BD=BA ×cos ∠ABD=2000√6×12=1000√6，AD=BA ×sin ∠ABD=2000√6×√32=3000√2∴AD+BD=3000√2+1000√6≈6680(米),6680÷500=13.36(分钟) ∵27.3−15=12.3＜13.36，∴小开先到达A 处.25.如图1，在平面直角坐标系中，抛物线y=√2x 2−2√2x −3√2与x 轴交于A 、B 两点(点A 在点B 的左侧)，与y 轴交于点C ，抛物线的对称轴交直线BC 于点D. (1)求点D 的坐标；(2)如图2，若P 是直线BC 下方抛物线上的一个动点，连接PC 、PD ，求△PCD 面积的最大值及此时P 点的坐标；(3)将抛物线y=√2x 2−2√2x −3√2沿射线CB 方向平移3√3个单位，得到的新抛物线与原抛物线交于点M.在新抛物线对称轴上是否存在一点N ，使得以点M 、N 、D 为顶点的E A 15°60°DCB南东西北三角形是以ND 为腰的等腰三角形？若存在，请直接与出N 点的坐标，并把求其中一个点N 的坐标的过程写出来；若不存在，请说明理由.25.解：(1)将y=0代入y=√2x 2−2√2x −3√2得√2x 2−2√2x −3√2=0 解得x 1=−1，x 2=3，∴点A 坐标(−1,0)，点B 坐标为(3,0)将x =0代入y=√2x 2−2√2x −3√2得y=−3√2，即点C 坐标为(0, −3√2) 抛物线y=√2x 2−2√2x −3√2的对称轴为x =−b2a =1设直线BC 的解析式为y=k x +m ，分别代入点B(3,0)、点C(0, −3√2)得 {3k +m =0m =−3√2，解得k=√2，m=−3√2，即直线BC 的解析式为y=√2x −3√2 将x =1代入y=√2x −3√2得y=−2√2，即点D 坐标为(1, −2√2). (2)连接BP ，令对称轴交x 轴于点E ，∵DE ∥y 轴，∴BD DC =BE OE=3−11=2，即CD=13BC∴S △PCD =13S △BCP ，设点P 坐标为(t, √2t 2−2√2t −3√2)(0＜t ＜3) 过点P 作PF ∥y 轴交直线BC 于点F ，则点F 坐标(t, √2t −3√2) FP=√2t −3√2−(√2t 2−2√2t −3√2)=3√2t −√2t 2 S △PCD =13S △BCP =13×12×(x B − x C )×FP=16×3×(3√2t −√2t 2)=−√22(t −32)2+9√28∴当t=32时，S △PCD =有最大值9√28，此时点P 坐标为(32,−15√24). (3)由勾股定理知BC=√OB 2+OC 2=√9+18=3√3备用图图1 图2∴新抛物线由原抛物线向右平移3个单位长度，向上平移3√2单位长度所得，其解析式为y=√2(x −3)2−2√2(x −3)−3√2+3√2=√2x 2−8√2x +15√2其对称轴为x =4，与原抛物线交于点B ，即点M 与点B 重合，故点M 坐标为(3,0) 设点N 坐标为(4,n)①当ND=MD 时，由(2)知BD=MD=23BC=2√3∵ND 2=MD 2，∴(n+2√2)2+(4−1)2=12，解得n 1=√3−2√2，n 2=−√3−2√2 ②当ND=MN 时，有ND 2=MN 2，即(n+2√2)2+(4−1)2=n 2+(4−3)2，解得n=−2√2 综上述，满足条件的N 点坐标有(4, √3−2√2)、(4, −√3−2√2)、(4, −2√2). 26.在Rt△ABC 中，∠BAC=90°，D 是射线AB 上的一点.(1)如图1，连接CD ，过点A 作AE⊥DC 于E 交BC 于F ，若AB=AF ，∠D=40°，求∠ACB 的度数；(2)如图2，若AB=AC ，O 是BC 中点，连接DO 、AO ，点G 是OD 中点.连接AG 交B0于点H ，连接BG ，若∠BGA=90°，求证：AH=2BG+BH ；(3)如图3，若AB=2√3，AC=2，K 是平面内一点，∠BKC=45°，Q 是KC 中点，当AQ 的长取得最大值时，请直接写出△ABK 的面积.26.解：(1)∵AE ⊥CD ，∠D=40°，∴∠BAF=50° ∵AB=AF ，∴∠ABC=12(180°−∠BAF)=65°∵∠BAC=90°，∴∠ACB =90°−∠ABC=25°.E F M图1ACEBDF图2ADO BG H C图3(2)延长AO与BG交于点E，过D作DF∥BC交AE于点F，交BE于点M，连接OM∵DF∥BC，∴∠GBO=∠GMD，又∵∠BGO=∠MGD，OG=DG，∴△BGO≌△MGD(AAS)∴BO=DM，BG=GM，连接AM，∵AG⊥BM，∴AB=AM∵∠BAC=90°，AB=AC，O是BC中点，∴AO⊥BC，AO=BO，∠ABO=∠BAO=∠CAO=45°∵∠BGA=∠BOA=90°，∴A、B、G、O四点共圆，∴∠BAG=∠BOG∵DF∥BC，∴∠BOG=∠ODF，∴∠BAG=∠0DF∵AO⊥BC，DF∥BC，∴DF⊥AF，∵∠BAO=45°，∴AF=DF∵OA=OB，BO=DM，∴BO+MF=OA+OF，∴OF=MF，∴△DFO≌△AFM(SAS)∴DO=AM，∴DO=AB，又∵∠BGA=∠OFD=90°，∠BAG=∠0DF，∴△BAG≌△0DF(AAS) ∴OF=BG，∴MF=BG令∠GBO=α，则∠GAO=α，∴∠EBA=∠ABO+α=45°+α=∠CAO+∠GAO=∠HAC又∵∠BEA=90°−∠GBO=90°−α=90°−∠GAO=∠AHC，CA=AB∴△BEA≌△AHC(AAS)，∴AH=BE∵∠EMF=∠GMD=∠HBG，∠BGH=∠MFE=90°，MF=BG，∴△BGH≌△MFE(SAS)∴ME=BH∵BE=BG+GM+ME=2BG+BH，AH=BE，∴AH=2BG+BH.(3)由勾股定理知BC=√AB2+AC2=4，显然，当K与A在BC异侧时， AQ有最大值∵∠BKC=45°，∴点K在以BC为弦的优弧上运动，令该圆圆心为O，连接OB、OCBC=2√2则∠BOC=2∠BKC=90°，即△BOC为等腰直角三角形，∴⊙O的半径OB为√22连接OK，取OC中点E，连接EQ，∵Q为KC中点，∴EQ=1OK=√22故当K在⊙O圆弧上运动时，点Q在以E为圆心，半径为√2的⊙E上运动当A、E、Q三点共线时，AQ有最大值，此时点K位于CQ的延长线上，连接BK、AK以OC 所在直线为x 轴，OB 所在直线为y 轴建立平面直角坐标系，则B 、C 坐标分别为(0，2√2)、(2√2，0)，点E 坐标为(√2,0)过A 作AN ⊥x 轴于N ，过B 作BM ⊥AN 交NA 延长线于M ，令CN=t ∵∠BAC=90°，∴∠CAN+∠BAM=∠ABM+∠BAM=90°，∴∠CAN=∠ABM ∴△CAN ∽△ABM ，∴CN AM =AN BM =AC AB，即tAM =2√2+t =2√3解得AM=√3t ，AN=2√63+√33t ，∵AM+AN=MN=OB=2√2，∴√3t+2√63+√33t=2√2 解得t=√6−√22，故点A 坐标为(√6+3√22，√6+√22) 直线AE 的斜率k=√6+√22√6+3√22−√2=1连接OK ，∵AQ ∥OK ，∴直线OK 的斜率为1，即直线OK 表达式为y=x ∵OK=2√2，∴点K 坐标为(−2,−2) 设直线AK 的解析式为y=k ´x +b 分别代入(√6+3√22，√6+√22)、(−2,−2)可解得b=−√3√6+3√2+4故S △ABK =12×(√6+3√22+2)×(2√2+√3√6+3√2+4)=4√3+4√2+6.。

【新】2019-2020重庆南开中学初升高自主招生数学【4套】模拟试卷【含解析】

第一套：满分120分2020-2021年重庆南开中学初升高自主招生数学模拟卷一．选择题（共6小题，满分42分）1. （7分）货车和小汽车同时从甲地出发，以各自的速度匀速向乙地行驶，小汽车到达乙地后，立即以相同的速度沿原路返回甲地，已知甲、乙两地相距180千米，货车的速度为60千米/小时，小汽车的速度为90千米/小时，则下图中能分别反映出货车、小汽车离乙地的距离y （千米）与各自行驶时间t （小时）之间的函数图象是【】A. B. C. D.2. （7分）在平面直角坐标系中，任意两点规定运算：①；②；③当x 1= x 2且y 1=y 2时，A =B.有下列四个命题：（1）若A (1，2)，B (2，–1)，则，；（2）若，则A =C ；（3）若，则A =C ；()()1122,,，A x y B x y ()1212,⊕=++A B x x y y 1212=⊗+A B x x y y (),31⊕= A B 0=⊗A B ⊕=⊕A B B C =⊗⊗A B B C（4）对任意点A 、B 、C ，均有成立. 其中正确命题的个数为（）A. 1个B. 2个C. 3个D. 4个 3．（7分）如图，AB 是半圆直径，半径OC ⊥AB 于点O ，AD 平分∠CAB 交弧BC 于点D ，连结CD 、OD ，给出以下四个结论：①AC ∥OD ；②CE=OE ；③△ODE ∽△ADO ；④2CD 2=CE •AB ．正确结论序号是（）A ．①②B ．③④C ．①③D ．①④ 4. （7分）如图，在△ABC 中，∠ACB =90º，AC =BC =1，E 、F 为线段AB 上两动点，且∠ECF =45°，过点E 、F 分别作BC 、AC 的垂线相交于点M ，垂足分别为H 、G ．现有以下结论：①；②当点E 与点B 重合时，；③；④MG •MH =，其中正确结论为（）A. ①②③B. ①③④C. ①②④D. ①②③④ 5.（7分）在数学活动课上，同学们利用如图的程序进行计算，发现无论x 取任何正整数，结果都会进入循环，下面选项一定不是该循环的是（）A. 4，2，1B. 2，1，4C. 1，4，2D. 2，4，1 6. （7分）如图，在矩形ABCD 中，AB =4，AD =5，AD 、AB 、BC 分别与⊙O 相切于E 、F 、G 三点，过点D()()⊕⊕=⊕⊕A B C A B C 2AB =12MH =AF BE EF +=12作⊙O 的切线交BC 于点M ，则DM 的长为（）A.B. C. D.二．填空题（每小题6分，满分30分）7.（6分）将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为 . 8.（6分）如图，三个半圆依次相外切，它们的圆心都在x 轴上，并与直线33y x =相切．设三个半圆的半径依次为r 1、r 2、r 3，则当r 1＝1时，r 3＝．9.（6分）如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOB=60°，点A 在第一象限，过点A 的双曲线为k y x=．在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ´B ´．（1）当点O ´与点A 重合时，点P 的坐标是；（2）设P （t ，0），当O ´B ´与双曲线有交点时，t 的取值范围是．1339241332510.（6分）如图，正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数2(0)y x x=>的图象上，顶点A 1、B 1分别在x 轴、y 轴的正半轴上，再在其右侧作正方形P 2P 3A 2B 2，顶点P 3在反比例函数2(0)y x x=>的图象上，顶点A 2在x 轴的正半轴上，则点P 3的坐标为．11.（6分）如图，在⊙O 中，直径AB ⊥CD ，垂足为E ，点M 在OC 上，AM 的延长线交⊙O 于点G ，交过C 的直线于F ，∠1=∠2，连结CB 与DG 交于点N ．若点M 是CO 的中点，⊙O 的半径为4，cos ∠BOC=41，则BN= ．三．解答题（每小题12分，满分48分）12.（12分）先化简，再求值：，其中.13.（12分）如图，点A （m ，m ＋1），B （m ＋3，m －1）都在反比例函数的图象上．（1）求m ，k 的值；32221052422x x x x x x x x --÷++--+-2022(tan 45cos30)21x =-+︒-︒-xky =xO yAB （2）如果M 为x 轴上一点，N 为y 轴上一点，以点A ，B ，M ，N 为顶点的四边形是平行四边形，试求直线MN 的函数表达式．（3）将线段AB 沿直线进行对折得到线段，且点始终在直线OA 上，当线段与轴有交点时,则b 的取值范围为（直接写出答案）14.（12分）如图，在Rt △ABC 中，∠ABC=90°，以AB 为直径作⊙O 交AC 于点D ，DE 是⊙O 的切线，连接DE ．（1）连接OC 交DE 于点F ，若OF=CF ，证明：四边形OECD 是平行四边形；（2）若=n ，求tan ∠ACO 的值b kx y +=11B A 1A 11B A x OFCF15.（12分）如图1，抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为C （1，4），交x 轴于A 、B 两点，交y 轴于点D ，其中点B 的坐标为（3，0）。

重庆市沙坪坝区南开中学2023-2024学年九年级上学期开学数学试卷(原卷版+答案解析)

重庆市沙坪坝区南开中学2023-2024学年九年级上学期开学数学试卷（解析版）一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请在答题卡中将正确答案所对应的1．（4分）下列式子中是分式的是（）A．B．C．D．2．（4分）2023年第31届世界大学生运动会在成都举行，如图所示历届大运会会徽是轴对称图形的是（）A．B．C．D．3．（4分）已知关于x的一元二次方程x2+4x+3＝0的两根分别为a、b，则的值为（）A．B．C．﹣D．﹣4．（4分）下列说法错误的是（）A．三角形的中位线平行于第三边且等于第三边的一半B．顺次连接对角线相等的任意四边形各边中点所得的四边形是矩形C．有一个锐角相等的两个直角三角形相似D．对角线互相垂直的矩形是正方形5．（4分）若ab＞0，则一次函数y＝ax+2与反比例函数y＝在同一平面直角坐标系中的大致图象可能是（）A．B．C．D．6．（4分）如图，△ABC与△DEF位似，点O为位似中心，则BC：EF＝（）A．1：2B．2：1C．1：4D．4：17．（4分）如图，矩形ABCD对角线AC、BD相交于点O，DE平分∠ADC交AB于点E，若DF＝2，CD＝6（）A．B．1C．D．28．（4分）学校“自然之美”研究小组在野外考察时了发现一种植物的生长规律，即植物的1个主干上长出x个枝干，每个枝干又长出x个小分支，根据题意，下列方程正确的是（）A．1+（1+x）2＝73B．1+x2＝73C．1+x+x2＝73D．x+（1+x）2＝739．（4分）如图，点E是正方形ABCD对角线BD上一点，O为对角线BD的中点，连接CE、AE、FE、AF、OF，取AF中点G，当∠ECF＝∠EFC时，若EG＝，则△EOF的面积为（）A．1B．C．D．10．（4分）在数学学习中，复杂的知识往往都是简单的内容通过一定的规则演变而来的．例如对单项式x进行如下操作：规定a1＝b1＝x，且满足以下规律：a2＝2a1，a3＝2a2，a4＝2a3，…，a n＝2a n﹣1，…b2＝b1+1，b3＝b2+1，b4＝b3+1，…，b n＝b n﹣1+1，…c1＝，c2＝a2b2，c3＝，c4＝a4b4，…其中n为正整数，以此类推：①a8＝128x；②b1+b2+b3+b4+…+b15＝15x+105：③当x＝1时，c n＝；④当x＝1时，c1+c2+c3+c4+…+c20＝．以上说法正确的有（）A．1个B．2个C．3个D．4个二、填空题（本大题共8个小题，每小题4分，共32分）请将正确答案直接填写在答题卡11．（4分）计算：﹣（﹣3）2+（π﹣5）0＝．12．（4分）已知，则的值为．13．（4分）现有四张完全相同的刮刮卡，涂层下面的文字分别是“我”、“爱”、“学”、“习”．小光从中随机抽取两张并刮开，则这两张刮刮卡上的文字恰好是“我”和“学”的概率是．14．（4分）若关于x的一元二次方程x2+2x﹣k＝0有实数根，则k的取值范围是．15．（4分）如图，在平面直角坐标系中，点A、B为反比例函数y＝（k≠0），且点B横坐标为点A横坐标的两倍，分别过点A作x轴平行线，两直线交于点C，若S△OAB＝6，则S△ABC＝．16．（4分）已知关于x的分式方程有整数解，且关于x的不等式组，则符合条件的所有整数a的和为．17．（4分）如图，矩形ABCD的宽为8，长为12，CQ＝5，点P在线段BC上，若点C恰落在边AD上的点R处，点O在线段AB上，点A恰落在线段PR上的点H处，则点H 到线段DC的距离为．18．（4分）若对于一个四位正整数，其千位数字的2倍和百位数字之和为14，十位数字的2倍和个位数字的3倍之和为15，得到新四位数A′，规定F（A）＝（6233）的值为．若s＝2640+1000a+100b+10c+d（0≤a≤6，3＜b≤9，0≤c≤5，0≤d ≤9，其中a、b、c、d均为整数），则当s为“凸月数”，且s最大时F（s）．三、计算题：（本大题共2个小题，19题8分，20题10分，共18分）解答时给出必要的演19．（8分）化简：（1）；（2）．20．（10分）解方程：（1）（2x﹣1）2＝x（2x+6）﹣7；（2）＝1．四、解答题：（本大题共660分）解答时给出必要的演算过程.21．（10分）如图，在▱ABCD中，连接BD．（1）用直尺和圆规过点B作BC的垂线，交线段CD的延长线于点E，连接AE（用基本作图，要保留作图痕迹，不写作法，不下结论）．（2）若BD＝CD，求证：四边形ABDE为菱形．证明：∵BD＝CD，∴，∵在Rt△CBE中，∠CBE＝90°，∴∠CEB+∠C＝∠EBD+∠CBD＝90°，∴，∴BD＝ED，∵BD＝CD，∴，∵▱ABCD，∴AB≌CD，∴AB⊥ED，∴四边形ABDE为，∵▱ABDE，BD＝ED，∴四边形ABDE为菱形（）．22．（10分）第19届亚洲运动会将于2023年9月23日至10月08日在浙江省多地举行，此次杭州亚运会共设40个大项，现场观赛门票分项目开售，则可以只购买田径赛事门票．近期官方平台有意愿为学校免费提供四个比赛项目的门票若干张，包括田径、游泳、篮球、拳击，学校调查了a个同学（要求每个同学只能选择一个项目观看），并将调查结果绘制成如图所示两幅不完整的统计图．请根据图中提供的信息，回答下列问题：（1）a＝，b＝；（2）请补全条形统计图；（3）若全校共有3500名学生，请你估计选择“篮球”项目的学生人数．23．（10分）如图，△ABC是边长为4的等边三角形，动点E，E沿折线A→B→C方向运动，F沿折线A→C→B方向运动，点E，F的距离为y．（1）请直接写出y关于t的函数关系式并注明自变量t的取值范围；（2）在给定的平面直角坐标系中，画出这个函数图象，并写出该函数的一条性质；（3）结合函数图象，直接写出点E，F相距3个单位长度时t的值．24．（10分）今年七八月份世界大学生运动会在成都顺利召开，中国向世界展现了热情好客的一面，也获得了许多外国友人的喜爱与赞赏，熊猫周边供不应求：现成都一玩偶店销售“抱竹熊猫”、“打坐熊猫”两款熊猫玩偶，其中“抱竹熊猫”成本每件100元，“打坐熊猫”售价是“抱竹熊猫”售价的倍，大运会开幕第一天“抱竹熊猫”比“打坐熊猫”多卖3件（1）求两款熊猫玩偶的售价分别是多少元？（2）为了更好的宣传国宝熊猫，第二天店家决定降价出售，但是市场规定降价之后的售价不能低于成本价的，当天“抱竹熊猫”的销量在第一天的基础上增加了m%，结果“打坐熊猫”的销量在第一天的基础上增加了m%，求m的值．25．（10分）如图1，在平面直角坐标系中，Rt△ACD沿直线CD翻折得△BCD（0，﹣2），D（0，3），点B在x轴负半轴上，A、C、B三点在同一条直线上（1）求直线CD的解析式；（2）如图1，在线段CE上有一动点F，连接OF，K为y轴上一动点，连接PF、PK△DOF＝时，求PF+PK的最小值；（3）如图2，将△DOE沿直线DC平移得到△D'O'E'，若在平移过程中△BD'E'是以BE'为一腰的等腰三角形26．（10分）如图，在平行四边形ABCD中，AE⊥BC于点E．（1）如图1，若AB＝AD，EC＝1，求AD的长；（2）如图2，若AD＝AE，连接DE，在AB上截取AG＝AF，连接DG，∠DAE的角平分线AH与GD相交于点H，求证：GH＝DH；（3）在（2）的条件下，若AN：AD＝2：5，请直接写出点C到直线DE的距离．参考答案与试题解析一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请在答题卡中将正确答案所对应的1．（4分）下列式子中是分式的是（）A．B．C．D．【分析】根据分式的定义：一般地，如果A，B表示两个整式，并且B中含有字母，那么式子叫做分式，分别判断即可．【解答】解：是分式，故A符合题意，，，都不是分式，故B、C、D选项不符合题意，故选：A．【点评】本题考查了分式的定义，熟练掌握分式的定义是解题的关键．2．（4分）2023年第31届世界大学生运动会在成都举行，如图所示历届大运会会徽是轴对称图形的是（）A．B．C．D．【分析】根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．【解答】解：A，B，D选项中的图形都不能找到一条直线，直线两旁的部分能够互相重合；C选项中的图形能找到一条直线，使图形沿一条直线折叠，所以是轴对称图形；故选：C．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3．（4分）已知关于x的一元二次方程x2+4x+3＝0的两根分别为a、b，则的值为（）A．B．C．﹣D．﹣【分析】先根与系数的关系得a+b＝﹣4，ab＝3，再利用通分得到+＝，然后利用整体代入的方法计算．【解答】解：根据根与系数的关系得a+b＝﹣4，ab＝3，所以+＝＝﹣．故选：D．【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．4．（4分）下列说法错误的是（）A．三角形的中位线平行于第三边且等于第三边的一半B．顺次连接对角线相等的任意四边形各边中点所得的四边形是矩形C．有一个锐角相等的两个直角三角形相似D．对角线互相垂直的矩形是正方形【分析】由三角形中位线定理，相似三角形的判定，矩形、菱形、正方形的判定，即可判断．【解答】解：A、三角形的中位线平行于第三边且等于第三边的一半，故A不符合题意；B、顺次连接对角线相等的任意四边形各边中点所得的四边形是菱形；C、由两角对应相等的两三角形相似，故C不符合题意；D、对角线互相垂直的矩形是正方形，故D不符合题意．故选：B．【点评】本题考查三角形中位线定理，相似三角形的判定，矩形、菱形、正方形的判定，掌握以上知识点是解题的关键．5．（4分）若ab＞0，则一次函数y＝ax+2与反比例函数y＝在同一平面直角坐标系中的大致图象可能是（）A．B．C．D．【分析】根据ab＞0及一次函数与反比例函数图象的特点，可以从a＞0，b＞0和a＜0，b＜0两方面分类讨论得出答案．【解答】解：∵ab＞0，∴分两种情况：（1）当a＞0，b＞8时、二、三象限图象在第一，无选项符合；（2）当a＜0，b＜4时、二、四象限图象在第二，故D选项正确；故选：D．【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．6．（4分）如图，△ABC与△DEF位似，点O为位似中心，则BC：EF＝（）A．1：2B．2：1C．1：4D．4：1【分析】根据位似变换的概念得到△ABC∽△DEF，再根据相似三角形的面积比等于相似比的平方解答即可．【解答】解：∵△ABC与△DEF位似，∴△ABC∽△DEF，∵△DEF的面积是△ABC面积的4倍，∴△ABC与△DEF的相似比为1：5，∴BC：EF＝1：2，故选：A．【点评】本题考查的是位似变换、相似三角形的性质，熟记相似三角形的面积比等于相似比的平方是解题的关键．7．（4分）如图，矩形ABCD对角线AC、BD相交于点O，DE平分∠ADC交AB于点E，若DF＝2，CD＝6（）A．B．1C．D．2【分析】由角平分线的定义可得∠ADE＝45°，则△ADE为等腰直角三角形，AD＝AE，根据等腰直角三角形三线合一的性质得DF＝EF，∠AFD＝90°，进而易求得AD＝DF ＝4＝AE，于是BE＝2，由三角形中位线定理易知OF为△BDE的中位线，则OF＝BE ＝1．【解答】解：∵四边形ABCD为矩形，CD＝6，∴AB＝CD＝6，∠ADC＝∠BAD＝90°，∵DE平分∠ADC，∴∠ADE＝∠CDE＝∠ADC＝45°，∴△ADE为等腰直角三角形，AD＝AE，∵AF⊥DE，∴DF＝EF，∠AFD＝90°，∴△ADF为等腰直角三角形，∴AD＝DF＝6，∴AE＝AD＝4，∴BE＝AB﹣AE＝6﹣5＝2，∵DF＝EF，OD＝OB、O分别为DE，∴OF为△BDE的中位线，∴OF＝BE＝．故选：B．【点评】本题主要考查矩形的性质、角平分线的定义、等腰直角三角形的性质、三角形OD＝OB，根据等腰直角三角形的三线合一性质得到DF＝EF，进而得出OF为△BDE的中位线是解题关键．8．（4分）学校“自然之美”研究小组在野外考察时了发现一种植物的生长规律，即植物的1个主干上长出x个枝干，每个枝干又长出x个小分支，根据题意，下列方程正确的是（）A．1+（1+x）2＝73B．1+x2＝73C．1+x+x2＝73D．x+（1+x）2＝73【分析】根据在1个主干上的主干、枝干和小分支的数量之和是73个，即可得出关于x 的一元二次方程．【解答】解：依题意得：1+x+x2＝73，故选：C．【点评】本题考查由实际问题抽象出一元二次方程，解答本题的关键是明确题意，写出相应的方程．9．（4分）如图，点E是正方形ABCD对角线BD上一点，O为对角线BD的中点，连接CE、AE、FE、AF、OF，取AF中点G，当∠ECF＝∠EFC时，若EG＝，则△EOF的面积为（）A．1B．C．D．【分析】过点E作EM⊥BC于M，EN⊥CD于N，过F作FH⊥BD于H，先证四边形EMCN为矩形，再证△EFC为等腰三角形，设MC＝x，AG＝y，则MF＝MC＝x，CF＝2x，BM＝x+2，AB＝BC＝2x+2，然后证△ADE和△CDE全等得AE＝EC＝EF，进而根据等腰三角形的性质得AG＝GF＝y，则AF＝2y，在RtABF中由勾股定理得y2＝x2+2x+2①，证△BEM为等腰直角三角形得EM＝BM＝2+x，在Rt△EMF和Rt△EGF中，由勾股定理得EF2＝EM2+MF2＝EG2+GF2，据此得y2＝2x2+4x﹣6②，由①②解得x＝2，进而得AB＝6，EM＝CN＝4，EN＝2，最后再由勾股定理计算得出BD＝，DE＝，HF＝，则OE＝，据此可求出△EOF的面积．【解答】解：过点E作EM⊥BC于M，EN⊥CD于N，如图：则∠EMC＝∠ENC＝90°，∵四边形ABCD为正方形，BD为对角线，∴∠BCD＝90°，∠ADB＝∠CDB＝∠ABD＝∠CBD＝45°，∴∠EMC＝∠ENC＝∠BCD＝90°，∴四边形EMCN为矩形，∴EM＝CN，EN＝MC，∵∠ECF＝∠EFC，∴△EFC为等腰三角形，即：EC＝EF，又EM⊥BC，∴MC＝MF，设MC＝x，AG＝y，∴MF＝MC＝x，∴CF＝MC+MF＝2x，BM＝BF+MF＝x+2，在△ADE和△CDE中，，∴△ADE≌△CDE（SAS），∴AE＝EC＝EF，即△EAF为等腰三角形，又EG⊥AF，∴AG＝GF＝y，则AF＝AG+GF＝8y，在RtABF中，AF＝2y，BF＝2，由勾股定理得：AF4＝AB2+BF2，即：（4y）2＝（2x+6）2+28，整理得：y2＝x2+3x+2①，∵∠CBD＝45°，EM⊥BC，∴△BEM为等腰直角三角形，∴EM＝BM＝2+x，在Rt△EMF中，EM＝7+x，由勾股定理得：EF2＝EM2+MF3＝（2+x）2+x4＝2x2+8x+4，在Rt△EGF中，EG＝，由勾股定理得：EF2＝EG3+GF2＝10+y2，∴10+y5＝2x2+6x+4，整理得：y2＝8x2+4x﹣7②，由①②得：2x2+2x﹣6＝x2+5x+2，整理得：x2+7x﹣8＝0，解得：x＝3，或x＝﹣4（不合题意，∴AB＝2x+2＝6，EM＝CN＝2+x＝5，在Rt△ABD中，AB＝AD＝6，由勾股定理得：，∵点O为BD的中点，∴OD＝BD＝，∵∠CDB＝45°，EN⊥CD，∴△DEN为等腰直角三角形，∴DN＝EN＝2，由勾股定理得：，∴OE＝OD﹣DE＝＝，∵∠CBD＝45°，FH⊥BD，∴△BHF为等腰直角三角形，即：HF＝BH，由勾股定理得：HF2+BH8＝BF2，∴2HF7＝22，∴HF＝，∴S△EOF＝OE•HF＝．故选：A．【点评】此题主要考查了正方形的性质，矩形的判定及性质，等腰三角形的判定和性质，全等三角形的判定和性质，勾股定理等，理解正方形的性质和矩形判定和性质，熟练掌握全等三角形的判定和性质，灵活运用勾股定理构造方程进行计算是解答此题的关键．10．（4分）在数学学习中，复杂的知识往往都是简单的内容通过一定的规则演变而来的．例如对单项式x进行如下操作：规定a1＝b1＝x，且满足以下规律：a2＝2a1，a3＝2a2，a4＝2a3，…，a n＝2a n﹣1，…b2＝b1+1，b3＝b2+1，b4＝b3+1，…，b n＝b n﹣1+1，…c1＝，c2＝a2b2，c3＝，c4＝a4b4，…其中n为正整数，以此类推：①a8＝128x；②b1+b2+b3+b4+…+b15＝15x+105：③当x＝1时，c n＝；④当x＝1时，c1+c2+c3+c4+…+c20＝．以上说法正确的有（）A．1个B．2个C．3个D．4个【分析】根据题中的操作步骤，可知a i（i为正整数）是x的2i﹣1倍，b i是x加上i﹣1，再根据c i（i为正整数）与a i和b i的关系找出规律，即可解决问题．【解答】解：由题知，，b i＝x+i﹣8（i为正整数），所以．故①正确．b1+b7+b3+b4+…+b15＝x+x+3+x+2+…+x+14＝15x+＝15x+105．故②正确．因为，，，，…所以当n为奇数，且x＝5时，，当n为偶数，且x＝1时，．故③错误．由上面的结论可知，c1+c2+c5+c4+…+c20＝＝S．则24S＝1×22+2×28+…+9×220+10×322，故3S＝10×222﹣2×22﹣34﹣28﹣ (220)S＝．所以c1+c8+c3+c4+…+c20＝＝．故④正确．故选：C．【点评】本题考查实数的计算规律，能根据所给的等式找到a i，b i和c i的变化规律是解题的关键．二、填空题（本大题共8个小题，每小题4分，共32分）请将正确答案直接填写在答题卡11．（4分）计算：﹣（﹣3）2+（π﹣5）0＝﹣4．【分析】【解答】解：原式＝4﹣9+8＝﹣4．故答案为：﹣4．【点评】本题主要考查了实数的运算，算术平方根的意义，有理数的乘方法则和零指数幂的意义，熟练掌握上述法则与性质是解题的关键．12．（4分）已知，则的值为．【分析】两边都乘以5（a+b）得出5a＝3a+3b，求出2a＝3b，再根据比例的性质得出即可．【解答】解：＝，两边都乘以5（a+b）得：5a＝3a+7b，2a＝3b，＝，故答案为：．【点评】本题考查了比例的性质，能熟记比例的性质的内容是解此题的关键，如果ab＝cd，那么＝，反之亦然．13．（4分）现有四张完全相同的刮刮卡，涂层下面的文字分别是“我”、“爱”、“学”、“习”．小光从中随机抽取两张并刮开，则这两张刮刮卡上的文字恰好是“我”和“学”的概率是．【分析】列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．【解答】解：列表如下：我爱学习我（爱，我）（学，我）（习，我）爱（我，爱）（学，爱）（习，爱）学（我，学）（爱，学）（习，学）习（我，习）（爱，习）（学，习）由表知，共有12种等可能结果，所以这两张刮刮卡上的文字恰好是“我”和“学”的概率为＝，故答案为：．【点评】此题考查的是用列表法或树状图法求概率以及概率公式，画出树状图是解题的关键；用到的知识点为：概率＝所求情况数与总情况数之比．14．（4分）若关于x的一元二次方程x2+2x﹣k＝0有实数根，则k的取值范围是k≥﹣1．【分析】根据方程有实数根得出△≥0，据此列出不等式求解即可求出k的取值范围．【解答】解：∵关于x的一元二次方程x2+2x﹣k＝5有实数根，∴Δ＝22﹣7×1×（﹣k）≥0，解得k≥﹣7，故答案为：k≥﹣1．【点评】此题考查了根的判别式，掌握一元二次方程根的情况与判别式△的关系：（1）Δ＞0⇔方程有两个不相等的实数根；（2）Δ＝0⇔方程有两个相等的实数根；（3）Δ＜0⇔方程没有实数根是解决问题的关键．15．（4分）如图，在平面直角坐标系中，点A、B为反比例函数y＝（k≠0），且点B横坐标为点A横坐标的两倍，分别过点A作x轴平行线，两直线交于点C，若S△OAB＝6，则S△ABC＝2．【分析】过点A，B作AE，BD⊥x轴于E，D，然后根据点B横坐标为点A横坐标的两倍，且点A、B都在曲线上，设出A，B坐标，由图形的面积公式求出k的值，然后由反比例函数的性质求解即可．【解答】解：过点A，B作AE，D，如图：∵点B横坐标为点A横坐标的两倍，且点A，∴设A（﹣m，﹣），则B（﹣2m，﹣，k＞5），∵S△ABO＝S梯形ABDE+S△AEO﹣S△BDO＝6，∴（+）×m+﹣×5m×，∴＝6，∴k＝8，∴S△ABC＝AC•CB＝＝＝2．故答案为：2．【点评】本题考查反比例函数系数k的几何意义，反比例函数的性质，面积公式等，关键是对反比例函数性质的掌握．16．（4分）已知关于x的分式方程有整数解，且关于x的不等式组，则符合条件的所有整数a的和为1．【分析】分式方程去分母转化为整式方程，由分式方程有整数解，确定出a的值，再根据不等式组的解集确定出满足题意a的值，求出之和即可．【解答】解：去分母得：ax﹣2+x﹣1＝6，解得：x＝，∵分式方程有整数解，∴a+5＝±1或±2或±4，解得：a＝0或﹣2或2或﹣3或﹣5，不等式组整理得：，∵不等式组的解集为x≤﹣1，∴＞﹣1，解得：a＞﹣，则满足题意的整数a为0或6，之和为1．故答案为：1．【点评】此题考查了分式方程的解，解一元一次不等式组，一元一次不等式组的整数解，熟练掌握各自的解法是解本题的关键．17．（4分）如图，矩形ABCD的宽为8，长为12，CQ＝5，点P在线段BC上，若点C恰落在边AD上的点R处，点O在线段AB上，点A恰落在线段PR上的点H处，则点H到线段DC的距离为．【分析】过点H作EF∥CD，交AD于点E，交BC于点F，则四边形CDEF为矩形，由折叠得性质可知CQ＝RQ＝5，∠C＝∠PRQ＝90°，AR＝HR，利用勾股定理求得DR＝4，进而求得AR＝8＝HR，易证△RDQ∽△HER，根据相似三角形的性质可求得ER＝，DE＝DR+ER＝，以此即可得到答案．【解答】解：如图，过点H作EF∥CD，交BC于点F，∵矩形ABCD的宽为8，长为12，∴AB＝CD＝8，AD＝BC＝12，AD∥BC，∵EF∥CD，∴∠DEF＝90°＝∠D＝∠C，∴四边形CDEF为矩形，∵将△PQC沿PQ翻折，点C恰落在边AD上的点R处，∴CQ＝RQ＝4，∠C＝∠PRQ＝90°，∴DQ＝CD﹣CQ＝8﹣5＝7，在Rt△RDQ中，DR＝＝，∴AR＝AD﹣DR＝12﹣4＝8，∵将△AOR沿OR翻折，点A恰落在线段PR上的点H处，∴AR＝HR＝5，∵∠DRQ+∠ERH＝90°，∠DRQ+∠DQR＝90°，∴∠DQR＝∠ERH，∵∠RDQ＝∠HER，∴△RDQ∽△HER，∴，即，∵ER＝，∴DE＝DR+ER＝4+＝，∴点H到线段DC的距离为．故答案为：．【点评】本题主要考查矩形的判定与性质、折叠的性质、勾股定理、相似三角形的判定与性质，解题关键是正确作出辅助线，熟练掌握折叠的性质，利用相似三角形的性质解决问题．18．（4分）若对于一个四位正整数，其千位数字的2倍和百位数字之和为14，十位数字的2倍和个位数字的3倍之和为15，得到新四位数A′，规定F（A）＝（6233）的值为29．若s＝2640+1000a+100b+10c+d（0≤a≤6，3＜b≤9，0≤c≤5，0≤d≤9，其中a、b、c、d均为整数），则当s为“凸月数”，且s最大时F（s）9．【分析】（1）根据新定义进行解答；（2）分两种情况：当0≤b＜4时，当4≤b≤7时，根据新定义分别列出方程进行解答求得s，并求得s最大时，F（s）的值．【解答】解：（1）∵6×2+5＝14，3×2+8×3＝15，∴6233是“凸月数”．∴F（6233）＝＝29．故答案为：29．（2）当0≤b＜3时，∵s＝2640+1000a+100b+10c+d为“十四五数”，∴2（a+2）+（b+5）＝14，2（c+4）+3d＝15．即2a+b＝4，7c+3d＝7．∵4≤a≤6，0≤b＜5，0≤d≤9、b、c、d均为整数，∴a＝5，b＝2（或a＝2；c＝8．∴s＝3861或4661．当4≤b≤7时，∵s＝2640+1000a+100b+10c+d为“十四五数”，∴2（a+3）+（b﹣4）＝14，4（c+4）+3d＝15．即4a+b＝12，2c+3d＝2，∵0≤a≤6，8≤b≤7，0≤d≤3、b、c、d均为整数，∴a＝3，b＝6（或a＝7；c＝2．∴s＝6261或7061．故满足条件s的值为3861或4661或6261或7061．当s＝7061时，F（s）＝．即当s最大时F（s）的值为9．故答案为：7．【点评】本题主要考查了新定义，二元一次方程的整数解的求解，理解新定义是解本题的关键．三、计算题：（本大题共2个小题，19题8分，20题10分，共18分）解答时给出必要的演19．（8分）化简：（1）；（2）．【分析】（1）先根据分式的减法法则进行计算，再根据分式的除法法则把除法变成乘法，最后根据分式的乘法法则进行计算即可；（2）先根据分式的减法法则进行计算，再根据分式的除法法则把除法变成乘法，最后根据分式的乘法法则进行计算即可．【解答】解：（1）＝•＝•＝；（2）＝÷＝÷＝•＝﹣．【点评】本题考查了分式的化简求值，能正确根据分式的运算法则进行计算是解此题的关键，注意运算顺序．20．（10分）解方程：（1）（2x﹣1）2＝x（2x+6）﹣7；（2）＝1．【分析】（1）先把方程化为一般式，再利用因式分解法把方程转化为x﹣4＝0或x﹣1＝0，然后解一次方程即可；（2）先把方程化为（x+1）2﹣4＝x2﹣1，解整式方程，然后进行检验确定原方程的解．【解答】解：（1）（2x﹣1）2＝x（2x+6）﹣5，方程化为一般式为x2﹣5x+6＝0，（x﹣4）（x﹣7）＝0，x﹣4＝4或x﹣1＝0，所以x8＝4，x2＝6；（2）去分母得，（x+1）2﹣8＝x2﹣1，解得x＝5，检验：当x＝1时，（x+1）（x﹣2）＝0，所以原方程无解．【点评】本题考查了解一元二次方程﹣因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了解分式方程．四、解答题：（本大题共6个大题，共60分）解答时给出必要的演算过程.21．（10分）如图，在▱ABCD中，连接BD．（1）用直尺和圆规过点B作BC的垂线，交线段CD的延长线于点E，连接AE（用基本作图，要保留作图痕迹，不写作法，不下结论）．（2）若BD＝CD，求证：四边形ABDE为菱形．证明：∵BD＝CD，∴∠CBD＝∠C，∵在Rt△CBE中，∠CBE＝90°，∴∠CEB+∠C＝∠EBD+∠CBD＝90°，∴∠EBD＝∠CEB，∴BD＝ED，∵BD＝CD，∴CD＝ED，∵▱ABCD，∴AB≌CD，∴AB⊥ED，∴四边形ABDE为平行四边形，∵▱ABDE，BD＝ED，∴四边形ABDE为菱形（邻边相等的平行四边形为菱形）．【分析】（1）利用基本作图，过B点作BC的垂线即可；（2）先证明∠EBD＝∠CEB得到BD＝ED，所以CD＝DE，再根据平行四边形的性质得到AB＝CD，AB∥CD，所以AB＝ED，则可判断四边形ABDE为平行四边形，然后利用BD＝ED可判断四边形ABDE为菱形．【解答】（1）解：如图，BE；（2）证明：∵BD＝CD，∴∠CBD＝∠C，∵在Rt△CBE中，∠CBE＝90°，∴∠CEB+∠C＝∠EBD+∠CBD＝90°，∴∠EBD＝∠CEB，∴BD＝ED，∵BD＝CD，∴CD＝DE，∵▱ABCD，∴AB＝CD，AB∥CD，∴AB＝ED，∴四边形ABDE为平行四边形，∵▱ABDE，BD＝ED，∴四边形ABDE为菱形（邻边相等的平行四边形为菱形）．故答案为：∠CBD＝∠C，∠EBD＝∠CEB，平行四边形．【点评】本题考查了作图﹣基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了全等三角形的判定与性质、平行四边形的性质和菱形的判定．22．（10分）第19届亚洲运动会将于2023年9月23日至10月08日在浙江省多地举行，此次杭州亚运会共设40个大项，现场观赛门票分项目开售，则可以只购买田径赛事门票．近期官方平台有意愿为学校免费提供四个比赛项目的门票若干张，包括田径、游泳、篮球、拳击，学校调查了a个同学（要求每个同学只能选择一个项目观看），并将调查结果绘制成如图所示两幅不完整的统计图．请根据图中提供的信息，回答下列问题：（1）a＝160，b＝20；（2）请补全条形统计图；（3）若全校共有3500名学生，请你估计选择“篮球”项目的学生人数．【分析】（1）用拳击人数及其所占百分比可得总人数a；用总人数﹣其它各类人数得出游泳人数，再÷总人数可得b；（2）根据（1）中游泳人数从而补全条形图；（3）总人数乘以样本中选择“篮球”项目对应的百分比即可．【解答】解：（1）本次共调查学生a＝64÷40%＝160（名），游泳人数为：160﹣24﹣40﹣64＝32（名），∴b%＝×100%＝20%，∴b＝20；故答案为：160；20；（2）补全图形如下：（3）喜欢篮球运动的学生约有3500×＝875（名），答：估计选择“篮球”项目的学生人数875名．【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．23．（10分）如图，△ABC是边长为4的等边三角形，动点E，E沿折线A→B→C方向运动，F沿折线A→C→B方向运动，点E，F的距离为y．（1）请直接写出y关于t的函数关系式并注明自变量t的取值范围；（2）在给定的平面直角坐标系中，画出这个函数图象，并写出该函数的一条性质；（3）结合函数图象，直接写出点E，F相距3个单位长度时t的值．【分析】（1）根据动点E、F运动的路线和速度分段进行分析，写出不同时间的函数表达式并注明自变量t的取值范围即可；（2）根据画函数图象的方法分别画出两段函数图象，然后写出这个函数的其中一条性质即可；（3）根据两个函数关系式分别求出当y＝3时的t值即可解决问题．【解答】解：（1）当点E、F分别在AB，△AEF为边长等于t的等边三角形，∴点E，F的距离等于AE，∴当0≤t≤4时，y关于t的函数表达式为y＝t，当点E、F都在BC上运动时，F的距离等于8﹣2（t﹣4），∴当7＜t≤6时，y关于t的函数表达式为y＝4﹣2（t﹣4）＝12﹣2t，∴y关于t的函数表达式为；（2）由（1）中得到的函数表达式可知：当t＝0时，y＝3，y＝4，y＝0，分别描出三个点（2，0），4）（7，然后顺次连线根据函数图象可知这个函数的其中一条性质：当0≤t≤4时，y随t的增大而增大，正确即可）（3）把y＝7分别代入y＝t和y＝12﹣2t中，得：3＝t，5＝12﹣2t，解得：t＝3或t＝3.5，∴点E，F相距3个单位长度时t的值为7或4.5．【点评】本题是一道三角形综合题，主要考查等边三角形的性质、一次函数的图象和性质，以及一次函数的应用，深入理解题意是解决问题的关键．24．（10分）今年七八月份世界大学生运动会在成都顺利召开，中国向世界展现了热情好客的一面，也获得了许多外国友人的喜爱与赞赏，熊猫周边供不应求：现成都一玩偶店销售“抱竹熊猫”、“打坐熊猫”两款熊猫玩偶，其中“抱竹熊猫”成本每件100元，“打坐熊猫”售价是“抱竹熊猫”售价的倍，大运会开幕第一天“抱竹熊猫”比“打坐熊猫”多卖3件（1）求两款熊猫玩偶的售价分别是多少元？（2）为了更好的宣传国宝熊猫，第二天店家决定降价出售，但是市场规定降价之后的售价不能低于成本价的，当天“抱竹熊猫”的销量在第一天的基础上增加了m%，结果“打坐熊猫”的销量在第一天的基础上增加了m%，求m的值．【分析】（1）设“抱竹熊猫”的售价是x元，则“打坐熊猫”的售价是x元，利用数量＝总价÷单价，结合大运会开幕第一天“抱竹熊猫”比“打坐熊猫”多卖3件，可列出关于x的分式方程，解之经检验后可得出“抱竹熊猫”的售价，再将其代入x中，即可求出“打坐熊猫”的售价；（2）利用总利润＝每个的销售利润×销售数量，可列出关于m的一元二次方程，解之取其符合题意的值，即可得出结论．【解答】解：（1）设“抱竹熊猫”的售价是x元，则“打坐熊猫”的售价是，根据题意得：﹣＝3，解得：x＝150，经检验，x＝150是所列方程的解，∴x＝．答：“抱竹熊猫”的售价是150元，“打坐熊猫”的售价是200元；（2）根据题意得：[150（1﹣m%）﹣100]×m%）+（200×85%﹣120）×。

重庆市南岸区重庆南开融侨中学2024届中考联考数学试卷含解析

重庆市南岸区重庆南开融侨中学2024年中考联考数学试卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）1．在Rt△ABC中，∠C=90°，AC=5，AB=13，则sinA的值为（）A．B．C．D．2．16的算术平方根是（）A．4 B．±4 C．2 D．±23．如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为（）A．83B．8 C．43D．64．一元二次方程x2﹣3x+1=0的根的情况（）A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．以上答案都不对5．不等式组1040xx+>⎧⎨-≥⎩的解集是（）A．﹣1≤x≤4B．x＜﹣1或x≥4C．﹣1＜x＜4 D．﹣1＜x≤46．如图，小明为了测量河宽AB，先在BA延长线上取一点D，再在同岸取一点C，测得∠CAD=60°，∠BCA=30°，AC=15 m，那么河AB宽为（）A．15 m B．53m C．3m D．123m7．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是（）A ．B ．C ．D ．8．如图，在,//ABC DE BC ∆中，,D E 分别在边,AB AC 边上，已知13AD DB =，则DE BC 的值为（）A ．13B ．14C ．15D ．259．下面四个几何体中，左视图是四边形的几何体共有（）A ．1个B ．2个C ．3个D ．4个10．在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（）A ．①B ．②C ．③D ．④二、填空题（共7小题，每小题3分，满分21分）11．计算（2a ）3的结果等于__．12．已知A （0,3），B （2,3）是抛物线上两点，该抛物线的顶点坐标是_________.13．反比例函数k y x=的图象经过点（﹣3，2），则k 的值是_____．当x 大于0时，y 随x 的增大而_____．（填增大或减小） 14．一个n 边形的内角和为1080°，则n=________.15．Rt △ABC 中，∠ABC=90°，AB=3，BC=4，过点B 的直线把△ABC 分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是_____．16．已知双曲线k 1y x+=经过点（－1，2），那么k 的值等于_______. 17．如图所示：在平面直角坐标系中，△OCB 的外接圆与y 轴交于A （0，），∠OCB=60°，∠COB=45°，则OC= ．三、解答题（共7小题，满分69分）18．（10分）某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同．求每件甲种、乙种玩具的进价分别是多少元？商场计划购进甲、乙两种玩具共48件，其中甲种玩具的件数少于乙种玩具的件数，商场决定此次进货的总资金不超过1000元，求商场共有几种进货方案？19．（5分）已知：如图，梯形ABCD 中，AD ∥BC ，DE ∥AB ，DE 与对角线AC 交于点F ，FG ∥AD ，且FG=EF. （1）求证：四边形ABED 是菱形；（2）联结AE ，又知AC ⊥ED ，求证：21·2AE EF ED .20．（8分）在平面直角坐标系中，二次函数y=x 2+ax+2a+1的图象经过点M （2，-3）。

重庆市南开中学校2024-2025学年九年级上学期期中数学试题(解析版)

重庆南开中学2024-2025学年度上学期期中考试初2025届数学试题（全卷共三个大题，满分150分，考试时间120分钟）一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡．．．上题号右侧正确答案所对应的方框涂黑．1.17−的相反数是( )．A.17− B.17C. −7D. 7【答案】B【解析】【分析】本题考查了相反数的定义，解答本题的关键是熟练掌握相反数的定义，只有符号不同的两个数是互为相反数， 0的相反数是0．【详解】解：17−的相反数是17，故选：B．2. 下列化学仪器示意图中，是轴对称图形的是（）A. 蒸馏烧瓶B. 烧杯C. 圆底烧瓶D. 分液漏斗【答案】C【解析】【分析】本题考查了轴对称图形的定义，熟练掌握轴对称图形的定义是解答本题的关键．根据轴对称图形的定义逐项分析即可．【详解】解：选项A、B、D均不能找到这样的一条直线，使图形沿该直线对折后直线两旁的部分能够完全重合，所以不是轴对称图形，选项C能找到这样的一条直线，使图形沿该直线对折后直线两旁的部分能够完全重合，所以是轴对称图形．故选C ．3. 二次函数()20y ax bx c a ++≠的图象如图所示，则下列选项正确的是（）A. 0a >B. 0b >C. 240b ac −<D. 0c >【答案】A【解析】【分析】本题考查根据二次函数图象判断各项系数和式子的符号，熟练掌握二次函数图象与系数的关系是解题的关键．根据抛物线的开口方向和对称轴的位置确定a 、b 的符号，由抛物线与x 轴的交点个数确定∆的符号，由抛物线与y 轴的交点位置确定c 的符号，即可得出答案．【详解】解：A 、∵抛物线的开口向上，∴0a >，故此选项符合题意；B 、∵抛物线的对称轴在y 轴右侧，∴02b a−>， ∵0a >，∴0b <，故此选项不符合题意；C 、∵抛物线与x 轴的两个交点，∴240b ac ∆=−>，故此选项不符合题意；D 、∵抛物线与y 轴的交点在负半轴上，∴0c <，故此选项不符合题意；故选：A ．4. 将ABC 沿BC 方向平移至DEF ，点A ，B ，C 的对应点分别是D ，E ，F ，使得:5:3BC EC =，则ABC 与GEC 的周长之比为（）A. 2:3B. 2:5C. 5:3D. 3:5【答案】C【解析】【分析】本题考查平移的性质，相似三角形的判定与性质，熟练掌握平移的性质、相似三角形的判定与性质是解题的关键．根据平移的性质得到AB GE ∥，从而可得到ABC GEC △∽△，利用相似三角形周长于相似比可得答案．【详解】解：∵ABC 沿BC 方向平移至DEF ，∴AB DE ∥，即AB GE ∥，∴A EGC ∠=∠,B GEC ∠=∠,∴ABC GEC △∽△，∴ABC 与GEC 的周长之比:5:3BCEC =，故选：C ．5. 中国选手郑钦文顺利入围2024年WTA 年终总决赛女子单打项目，该项目第一阶段采用组内循环赛制，即每两名选手之间比赛一场．现计划安排28场组内循环赛，共有几名选手参加组内循环赛？设一共有x 名选手参加组内循环赛，根据题意可列方程为（）A. ()128x x −=B. ()128x x +=C. ()11282x x +=D. ()11282x x −= 【答案】D【解析】【分析】此题主要考查了有实际问题抽象出一元二次方程，解决本题的关键是得到比赛总场数的等量关系，注意2队之间的比赛只有1场，最后的总场数应除以2．设一共有x 名选手参加组内循环赛，则每个队参加()1x −场比赛，则共有()112x x −场比赛，可以列出一个一元二次方程．【详解】解：由题意可列方程为：()11282x x −=，故选：D ．6. 估计+）A. 6和7之间B. 7和8之间C. 8和9之间D. 9和10之间【答案】D【解析】【分析】本题考查二次根式的混合运算，无理数的估算，解题的关键是熟练掌握二次根式的运算法则．先利用二次根式的运算法则将原式化简，再对无理数进行估算．【详解】解：++，3<<∵67∴9310+<故选：D．7. 南南用相同的小圆圈按照一定的规律摆成了“中”字，第①个图形中有10个小圆圈，第②个图形中有16个小圆圈，第③个图形中有22个小圆圈，…，按照此规律排列下去，则第⑧个图形中小圆圈的个数是（）A. 42B. 52C. 46D. 58【答案】B【解析】【分析】考查了图形的变化类问题，解题的关键是仔细观察图形并找到进一步解题的规律，难度不大．仔细观察图形变化，找到图形变化规律，利用规律求解．×+=个小圆圈，【详解】第①个图形中一共有16410×+=个小圆圈，第②个图形中一共有26416×+=个小圆圈，第③个图形中一共有36422…，∴第n 个图形中一共有()64n +个小圆圈，∴第⑧个图形中小圆圈的个数是86452×+=，故选：B ．8. 如图，AB 是O 的直径，AE 、CE 、CB 为O 的弦，132AO =，12AE =，则sin BCE ∠=（）A. 512B. 1312C. 513D. 125【答案】C【解析】【分析】本题考查了圆周角定理，求一个角的正弦值，勾股定理；根据AB 是O 的直径，得出90AEB ∠=°，再运用勾股定理算出5BE ，再结合 EBEB =，则BCE BAE ∠=∠，所以5sin sin 13BE BCE BAE AB ∠=∠==，即可作答．【详解】解：连接BE ，如图：∵AB 是O 的直径，∴90AEB ∠=°， ∵132AO =， ∴13AB =，在Rt ABE △中，5BE ，∵ EBEB =，∴BCE BAE ∠=∠， ∴5sin sin 13BE BCE BAE AB ∠=∠==，故选：C ． 9. 如图，在正方形ABCD 中，O 是对角线BD 的中点，E 为正方形内的一点，连接BE ，CE ，使得CB CE =，延长BE 与ECD ∠的角平分线交于点F ．若BEC α∠=，连接OF ，则FOD ∠的度数为（）A. 290α−°B. 1452α°+C. 1902α°−D. 245α−°【答案】A【解析】【分析】连接DF ，先证明∴()SAS CEF CDF ≌，得到CEF CDF ∠=∠，从而得180CDF CEF α∠=∠=°−，继而90BFD ∠=°，然后利用直角三角形的性质，得出OF OB =，从而有45OFB OBF α∠=∠=−°，然后由三角形外角的性质可求解．【详解】解：连接DF ，如图，∵正方形ABCD∴BC CD =，45CBD CDB ∠=∠=°，∵CB CE =∴CE CD =，CBE BEC α∠=∠=， ∴45DBE α∠=−°，∵CF 是ECD ∠角平分线∴ECF DCF ∠=∠ ∵CF CF =，ECF DCF ∠=∠，CE CD =， ∴()SAS CEF CDF ≌∴CEF CDF ∠=∠，∴180CDF CEF α∠=∠=°−∴18045135BDFCDF CDB αα∠=∠−∠=°−−°=°− ∴1354590BDF DBE αα∠+∠=°−+−°=° ∴90BFD ∠=°∵O 是对角线BD 的中点，∴OF OB =∴45OFB OBF α∠=∠=−° ∴4545290FOD OFB OBF ααα∠=∠+∠=−°+−°=−° 故选：A ．【点睛】本题考查正方形的性质，直角三角形的性质，等腰三角形的性质，三角形外角的性质，全等三角形的判定与性质，证明90BFD ∠=°是解题的关键．10. 给定三个互不相等的代数式，先将任意两个代数式作差（相同的两个代数式只作一次差），再将这些差“绝佳操作”．例如：对于m ，n ，p 作“绝佳操作”，得到m n m p n p −+−+−．下列说法：①对2，4−，5作“绝佳操作”结果是18；②对m ，n ，p 作“绝佳操作”的结果一共有8种；③对22a ，66a −，42a 作“绝佳操作”的结果为28，则a的值为1−或1−；其中正确的个数为（）A. 0B. 1C. 2D. 3【答案】B【解析】【分析】本题考查新定义和绝对值化简，解一元二次方程，理解万岁新定义是解题的关键，注意分类讨论．利用绝对值的性质进行逐个计算判断即可．【详解】解：①()242545−−+−+−−的的18=，故①正确；②当m n p >>时，则22m n m p n p m n m p n p m p −+−+−=−+−+−=−，当m p n >>时，则22m n m p n p m n m p n p m n −+−+−=−+−−+=−，当n m p >>时，则22m n m p n p m n m p n p n p −+−+−=−++−+−=−，当n p m >>时，则22m n m p n p m n m p n p n m −+−+−=−+−++−=− 当p m n >>时，则22m n m p n p m n m p n p p n −+−+−=−−+−+=−当p n m >>时，则22m n m p n p m n m p n p p m −+−+−=−+−+−+=− ∴对m ，n ，p 作“绝佳操作”的结果一共有6种，故②错误；③当226642a a a >−>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：2260a a −−=，解得：1a =+1a =−；当224266a a a >−>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：2340a a −−=，解得：4a =（舍去）或1a =−；当266242a a a −>>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：6828a −=，解得：6a =（舍去）；当266422a a a −>−>时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：23100a a −+=，∵()234110310∆=−−××=−<∴无解；当242266a a a −>>−时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：8a −=，解得：8a =−（舍去），当242662a a a −>−>时，则()()()22266242664228a a a a a a −−+−−+−−−=，化简得：4828a −+=，解得：5a =−（舍去），综上，a 的值为11−，故③错误；∴只有①正确，共1个，二、填空题：（本题共8个小题，每小题4分，共32分）请将每个小题的答案直接填在答题．．卡．中对应的横线上． 11. 计算：()01tan3012−°−−=________．【答案】12##0.5 【解析】【分析】本题主要考查实数混合运算，零指数幂，负整理指数幂，特殊角的三角函数，解题的关键是掌握分负整数指数幂、零指数幂的规定，熟记特殊锐角的三角函数值．【详解】解：()01tan3012−°−−112 =−−112=− 12=．故答案为：12． 12. 正八边形每个外角的度数为_____．【答案】45°##45度【解析】【分析】本题主要考查了正多边形外角和定理，根据任何一个多边形的外角和都是360°求解即可．【详解】解：因为任何一个多边形的外角和都是360°，所以正八边形的每个外角的度数是：360845°÷=°．故答案为：45°．13. 为了全面推进素质教育，助力学生健康成长，公能学校开设了多门选修课程．其中南南和开开想从刺绣、糖画、国家疆土、巧匠工坊中选修一门课程，两名同学恰好选修同一门课程的概率为________．【答案】14【解析】【分析】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n ，再从中选出符合事件A 或B 的结果数目m ，然后利用概率公式计算事件A 或事件B 的概率．画树状图展示所有16种等可能的结果数，再找出他们两人恰好选修同一门课程的结果数，然后根据概率公式求解．【详解】解：用A 、 B 、C 、D 分别表示刺绣、糖画、国家疆土、巧匠工坊，画树状图如图，共有16种等可能的结果，其中他们两人恰好选修同一门课程的结果数为4，所以他们两人恰好选修同一门课程的概率为：41164=． 14. 如图，点A 在反比例函数()0k yk x=≠图象上，过点A 作AB x ⊥轴于点B ，连接OA ，若ABO 的面积为2，则k =________．【答案】4【解析】【分析】本题考查反比例函数系数k 的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于k ．本知识点是中考的重要考点，同学们应高度关注．根据在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是122k =，再根据反比例函数的图象位于第二象限即可求出k 的值．【详解】解：根据题意可知：221AOB S k == ，又反比例函数的图象位于第一象限，0k >，则4k =．故答案为：4．15. 若二次函数232y x x =−+过点(),3m ，则代数式2262023m m −+=________．【答案】2025【解析】【分析】本题考查的是抛物线的性质．掌握“点在抛物线上，则点的坐标满足函数解析式”是解本题的关键．由于抛物线经过点(),3m ，则231m m −=，把2262023m m −+整理后整体代入即可．【详解】∵二次函数232y x x =−+过点(),3m ， ∴2323m m −+=， ∴231m m −=，∴()222620232320232120232025m m m m −+=−+=×+=．故答案为：2025．16. 关于x 的一元一次不等式组()341221x x x x m − ≤−+≥−+至少有2个整数解，且关于y 的分式方程13222m y y−=−−−的解为非负整数，则符合条件的整数m 的值之和为________．【答案】2 【解析】【分析】本题考查了分式方程的解，以及解一元一次不等式组，掌握相应的计算方法是关键．先解不等式组，确定m 的取值范围25<≤m ，再把分式方程去分母转化为整式方程，解得22m y −=，由分式方程有非负整数解，确定出的值，即可解答．【详解】解：()341221x x x x m − ≤−+≥−+①② 解①得：2x ≤，解②得：23m x −≥， ∴223m x −≤≤， ∵不等式组至少有2个整数解， ∴213m −≤，解得：5m ≤；13222m y y−=−−−，去分母得：1243m y −=−+，解得：2my =， ∵分式方程的解为非负整数，且2y ≠ ∴0m ≥且4m ≠的偶数，又∵5m ≤ ∴2m =，0∴符合条件的整数m 的值之和为202+=．故答案：2．17. 如图，在矩形ABCD 中，4=AD ，点E 为AB 中点，将矩形沿着EF 所在的直线翻折至矩形ABCD 所在的平面，点B ，C 的对应点分别是B ′，C ′，B E ′与CD 交于点G ，使得CF GF =，连接AB ′，B F ′，AF ，若25B G GF ′=，则GF =________；AB F S ′= ________．【答案】 ①. 5 ②. 985【解析】【分析】过点G 作GH C F ′⊥，则四边形B C HG ′′是矩形，根据矩形的性质，结合折叠的性质可得4GH B C ′′==，GF GE =，令5GF CF a ==，则2B G C H a ′′==，5CF C F a ′==，可知3HF C F C H a ′′=−=，根据勾股定理即可求解，则2B G ′=，7BE B E ′==，令AB ′与CD 交于点O ，过点B ′作B M CD ′⊥，则90D B MO ′∠=∠=°，再证明B OG B AE ′′△∽△，DOA MOB ′△∽△，结合相似三角形的性质求得2855B M AD ′==，由1122AB F AOF B OF S S S OF AD OF B M ′′′=+=⋅+⋅△△△，即可求解．【详解】解：在矩形ABCD 中，4AD BC ==，AB CD =，90B C D ∠==∠=°，AB CD ∥，则BEF DFE ∠=∠，由折叠可知，BE B E ′=，CF C F ′=，4BC B C ′′==，90C C ′∠=∠=°，90EB C B ′∠=∠=°，BEF B EF ′∠=∠，则B EF DFE ′∠=∠， ∴GF GE =，为过点G 作GH C F ′⊥，则四边形B C HG ′′是矩形， ∴4GHB C ′′==，B G C H ′′=， ∵25B G GF ′=，CF GF =，令5GFCF a ==，则2B G C H a ′′==，5CF C F a ′==， ∴3HF C F C H a ′′=−=，由勾股定理可得：222GH GF HF =−，即：()()222453a a =−，解得：1a =，∴5GF =，则2B G ′=，7BEB E ′==，令AB ′与CD 交于点O ，过点B ′作B M CD ′⊥，则90D B MO ′∠=∠=°，∵点E 是AB 的中点，∴7AE BE ==，即14ABCD ==， ∵AB CD ∥，∴B OG B AE ′′△∽△，B G B O GF OA ′′==∴OG B GAE B E ′=′，即277OG =， ∴2OG =，∴7OF OG GF =+=，则2OD CD OF CF =−−=， ∵DOA MOB ′∠=∠ ∴DOA MOB ′△∽△，∴25B M B O AD OA ′′==，则2855B M AD ′==， ∴1118987422255AB F AOF B OF S S S OF AD OF B M ′′′=+=⋅+⋅=××+=，故答案为：5，985．【点睛】本题考查矩形与折叠问题，勾股定理，相似三角形的判定及性质，平行线分线段成比例等知识点，熟练掌握相关图形的性质是解决问题的关键．18. 一个四位数M 各数位上的数字均不为0，若将M 的千位数字和个位数字对调，百位数字和十位数字对调，得到新的四位数N ，则称N 为M 的“翻折数”，规定()11M NF M +=．例如：1235的“翻折数”为5321，()12355321123559611F +==，则()2678F =________；若()5001200101M x y =+++（M ，y 为整数，59x ≤≤，18y ≤≤），M 的“翻折数”N 能被17整除，则()F M 的最大值为________．【答案】 ①. 1040 ②. 757 【解析】【分析】根本题主要考查了有理数的混合运算，二元一次方程的解，列代数式，本题是阅读型题目，准确理解题干中的定义和公式并熟练应用是解题的关键．据()11M NF M +=代入求解()2678F 即可；首先表示出s 和t 的“翻折数”，然后求出3153x y ++的取值范围，进而分类讨论求得x ，y 的值，然后代入()11M NF M +=求解即可．【详解】根据题意可得，()267887622678104011F +==；∵()5001200101M x y =+++（M ，y 为整数59x ≤≤，18y ≤≤）， ∴M 的千位数字为6，百位数字为210x −，十位数字为1y +，个位数字为1， ∴M 的“翻折数”N 为()()10001001102106y x +++−+201001006x y =++()175593153x y x y =+++++，∵59x ≤≤，18y ≤≤， ∴333153150x y ≤++≤， ∵M 的“翻折数”N 能被17整除， ∴3153x y ++能被17整除， ∵x ，y 都是整数， ∴3153x y ++是整数，∴431533x y +=+，51，68，85，102，119，136，∴当431533x y +=+时，x ，y 无整数解，当131535x y +=+时，13x y = = （舍去）或62x y = =，当831536x y +=+时，x ，y 无整数解，当531538x y +=+时，x ，y 无整数解，当2315310x y +=+时，36x y == （舍去）或85x y = = ，当9315311x y +=+时，x ，y 无整数解，当6315313x y +=+时，x ，y 无整数解，∴当62x y = =时，()5001200610216231M =+×+×+=，1326N =，()6231132668711F M +==，当85x y = =时，()5001200810516661M =+×+×+=，1666N =，()6661166675711F M +==， ∴()F M 的最大值为757，故答案为：1040，757．三、解答题：（本大题共8个小题，第19题8分，其余每题10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡．．．中对应的位置上． 19. 计算：（1）()22()m m n m n +−+（2）2214123a a a a −+÷ +【答案】（1）2n −；（2）321a a +−．【解析】【分析】本题考查了整式的运算和分式的混合运算．解题的关键是掌握整式和分式混合运算顺序和运算法则．（1）利用完全平方公式和单项式乘多项式展开，再合并即可；（2）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果即可．【小问1详解】解：()22()m m n m n +−+2222(2)m mn m mn n =+−++22222m mn m mn n =+−−− 2n =−；【小问2详解】解：2214123a a a a −+÷ + 2221413a a a a a+−÷+ ()()()321·2121a a a a a a ++=+− 321a a +=−． 20. 为了全面了解学生对校史的掌握情况，公能学校开展了校史知识竞赛．现从七、八年级的学生中各随机抽取20名学生的比赛成绩（百分制）进行收集、整理、描述、分析．所有学生的成绩均高于60分（成绩得分用x 表示，共分为四组：A ．90100x <≤；B ．8090x <≤；C ．7080x <≤；D ．6070x <≤；），下面给出了部分信息：七年级20名学生的竞赛成绩为：68，76，78，79，84，85，86，86，86，86， 88，89，89，91，91，94，94，95，95，100．八年级20名学生的竞赛成绩在B 组的数据为：80，83，86，87，87，89，89．七、八年级所抽学生的校史知识竞赛成绩统计表年级七年级八年级平均数8787中位数 87 b众数 a92根据以上信息，解答下列问题：（1）填空：a =________；b =________；m =________；（2）根据以上数据分析，你认为在此次知识竞赛中，该校七、八年级中哪个年级学生对校史的掌握情况更好？请说明理由（写出一条理由即可）；（3）公能学校七年级有500名学生、八年级有600名学生参加此次校史知识竞赛，请估计七、八年级参加此次知识竞赛的成绩优秀(90)x >的学生共有多少人？【答案】（1）86；87；40（2）八年级学生安全知识竞赛成绩较好，理由见解析（3）415 【解析】【分析】（1）根据众数和中位数定义求a 、b 值，先求出B 组人数占的百分比为35%，即可由%110%15%35%m =−−−求出m 值；（2）根据两个年级成绩的平均数相同，但八年级的中位数高于七年级，可得出结论；（3）用各年级的总人数乘以年级的优秀率，再相加，列式计算即可求解. 【小问1详解】解：在七年级20名学生的竞赛成绩中86出现的次数最多，故众数86a =； ∵八年级20名学生的竞赛成绩在B 组的数据为：80，83，86，87，87，89，89． ∴B 组人数占的百分比为：7100%35%20×=， ∵C 组人数占的百分比为15%，D 组人数占的百分比为10%， ∴A 组人数占的百分比为%110%15%35%40%m =−−−=，即40m =． ∴八年级20名学生竞赛成绩的中位数在B 组，的∴把八年级20名学生的竞赛成绩从小到大排列，排在中间的两个数分别是87，89，故中位数8789872b +=，故答案：86；87；40．【小问2详解】解：八年级学生安全知识竞赛成绩较好，理由如下：因为两个年级成绩的平均数相同，但八年级的中位数高于七年级，所以得到八年级学生安全知识竞赛成绩较好（答案不唯一）；【小问3详解】解：750060040%20×+× 175240+415=（人），答：估计该校七、八年级参加此次安全知识竞赛成绩优秀()90x >的学生人数大约是415人．【点睛】本题考查众数，中位数，统计表，扇形统计图，用样本估计总体，掌握相关统计量的意义以及计算方法是解答本题的关键．21. 在学习了平行四边形与正方形的相关知识后，智慧小组进行了更深入的探究．他们发现，如图所示的正方形ABCD ，分别取BC ，CD 的中点M ，N ，连接AM ，DN 交于点E ，过B 作AM 的垂线，交AM 于点Q ，交AD 于点P ．则四边形BPDN 是平行四边形．（1）用尺规完成以下基本作图：过B 作AM 的垂线，交AM 于点Q ，交AD 于点P （只保留作图痕迹）．（2）根据（1）中所作图形，智慧小组发现四边形BPDN 是平行四边形成立，并给出了证明，请补全证明过程．证明：∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．又∵M ，N 分别为BC ，CD 的中点，∴12DM CD =，12CN BC =，∴ ① ，在ADM 与DCN 中，为AD CD ADM C DM CN =∠=∠ =∴()ADM DCN SAS ≌．∴ ② ．又∵90CDN ADN ∠+∠=°，∴90DAM ADN ∠+∠=°，∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°，∴ ③ ．又∵DP BN ∥ ∴四边形BPDN 是平行四边形．进一步思考，智慧小组发现任取BC ，CD 的上点N ，M （M 不与C ，D 重合），DM CN =，连接AM ，DN ，过B 作AM 的垂线，交AD 于点P ，则四边形BPDN 是 ④ ．【答案】（1）见解析（2）DM CN =；DAM CDN ∠=∠；∥BP DN ；进一步思考：四边形BPDN 是平行四边形【解析】【分析】（1）利用尺规基本作图——经过直线外一点作已知直线的第一线作法作出图形即可；（2）先证明()SAS ADM DCN ≌，得到DAM CDN ∠=∠．从而证得90AQP AED ∠=∠=°，即可得到∥BP DN ．又由正方形的性质得DP BN ∥，即可得出结论；进一步思考：证明()SAS ADM DCN ≌，得到DAM CDN ∠=∠，再证明∥BP DN ，又由正方形的性质得DP BN ∥，即可得出结论．【小问1详解】解：如图所示，BP 就是所求作的经过点B 垂直于AM 于Q ，交AD 于P 的直线，【小问2详解】证明：∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．又∵M ，N 分别为BC ，CD 的中点， ∴12DM CD =，12CN BC =， ∴DM CN =，在ADM 与DCN 中，AD CD ADM C DM CN =∠=∠ =∴()SAS ADM DCN ≌． ∴DAM CDN ∠=∠．又∵90CDN ADN ∠+∠=°， ∴90DAM ADN ∠+∠=°， ∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°， ∴∥BP DN ．又∵DP BN ∥∴四边形BPDN 是平行四边形．进一步思考：如图，∵四边形ABCD 是正方形，∴AD CD BC ==，90ADC C ∠=∠=°，AD BC ∥．在ADM 与DCN 中，AD CD ADM C DM CN =∠=∠ =∴()SAS ADM DCN ≌． ∴DAM CDN ∠=∠．又∵90CDN ADN ∠+∠=°， ∴90DAM ADN ∠+∠=°， ∴90AED ∠=°，又∵BP AE ⊥，∴90AQP AED ∠=∠=°， ∴∥BP DN ．又∵DP BN ∥∴四边形BPDN 是平行四边形．故答案为：平行四边形．【点睛】本题考查正方形的性质，全等三角形的判定与性质，尺规基本作图—作垂线，平行四边形的判定．熟练掌握正方形的性质，和平行四边形的判定是解题的关键．22. 重庆金沙天街某家蛋糕店推出了“流沙羊角”和“开心果羊角”两款特色蛋糕．（1）购买1个“流沙羊角”和1个“开心果羊角”需要37元，购买1个“流沙羊角”和2个“开心果羊角”需要54元，求“流沙羊角”和“开心果羊角”的单价分別为多少元？（2）国庆节当天，蛋糕店进行促销活动，将“流沙羊角”的单价降低了2m 元，“开心果半角”单价降低了m 元，节日当天“流沙羊角”的销量是“开心果羊角”销量的1.2倍，且“流沙羊角”的销售额为960元，“开心果羊角”的销售额为750元，求m 的值．【答案】（1）“流沙羊角”的单价为20元，“开心果羊角”的单价为17元（2）2 【解析】【分析】本题考查二元一次方程组的应用，分式方程的应用，正确列出方程组或方程是解题的关键．（1）设“流沙羊角”的单价为x “开心果羊角”的单价为y 元，根据购买1个“流沙羊角”和1个“开心果羊角”需要37元，购买1个“流沙羊角”和2个“开心果羊角”需要54元，列出方程组，求解即可．（2）根据销量等于销售额除以销售单价，以“流沙羊角”的销量是“开心果羊角”销量的1.2倍，列出分式方程求解即可．【小问1详解】解：设“流沙羊角”的单价为x 元，“开心果羊角”的单价为y 元，根据题意，得37254x y x y +=+= ，解得：2017x y = =，答：“流沙羊角”的单价为20元，“开心果羊角”的单价为17元．【小问2详解】解：根据题意，得960750 1.220217m m=×−−，解得：2m =，经检验，2m =是方程的解且符合题意， ∴m 的值为2．23. 如图1，在菱形ABCD 中，5AB =，8BD =，动点P 从点A 出发，沿着A B C −−的路线运动，到达C 点停止，过点P 作PQ BD ∥交菱形的另一边于点Q ．设动点P 行驶的路程为x ，点P 、Q 的距离为y ．（1）请直接写出y 关于x 的函数表达式，并注明自变量x 的取值范围；（2）在给定的平面直角坐标系中画出函数y 的图象，并写出函数y 的一条性质；（3）函数11y x b 2=+与函数y 只有一个交点，求b 的取值范围．【答案】（1）()()80558165105x x y x x ≤≤ =−+<≤ ；（2）作图见解析，当05x ≤≤时，y 随x 的增大而增大；当510x <≤时，y 随x 的增大而减小；（3）50b −≤<或112b =．【解析】【分析】（1）分点P 在AAAA 上和点P 在BC 上两种情况讨论，利用相似三角形的判定及性质构造等量关系，即可得到答案；（2）根据（1）所得函数关系式，利用描点法画图，再写出该函数的性质即可；（3）结合函数图象，将()5,8、()0,0和()10,0代入11y x b 2=+，分别求出b 的值，即可得出b 的取值范围．【小问1详解】解：如图，点P 在AAAA 上时，05x ≤≤，∵PQ BD ∥， ∴APQ ABD ∽，∴AP PQ AB BD =即58x y=， ∴85y x =， ∵5AB =，如图，点P 在BC 上时，∵四边形ABCD 是菱形， ∴5BC AB ==， ∴10PC x =−，当点P 在BC 上时，510x <≤， ∵PQ BD ∥， ∴CPQ CBD ∽，∴CP PQ CB BD =即1058x y −=， ∴8165y x =−+，综上可知，y 关于x 的函数表达式为()()80558165105x x y x x ≤≤ =−+<≤ 【小问2详解】解：由（1）所得关系式可知，x0 5 8 10 y83.2函数图象如下：性质：当05x ≤≤时，y 随x 的增大而增大；当510x <≤时，y 随x 的增大而减小；（答案不唯一）【小问3详解】解：如图，由图象可知，函数11y x b 2=+的图象在3l 和2l 之间时，与函数y 只有一个交点，将()5,8代入11y x b 2=+，得：1852b =×+，解得：112b =，将()0,0代入11y x b 2=+，得：0b =，将()10,0代入11y x b 2=+，得：5b =−， ∴b 的取值范围为50b −≤<或112b =．【点睛】本题考查了菱形的性质，相似三角形的判定及性质，求一次函数解析式，描点法画函数图象，一次函数图象和性质，两直线交点问题等知识，利用数形结合和分类讨论的思想解决问题是关键．24. 如图，M 为沙坪坝区物流中心，N ，P ，Q 为三个菜鸟驿站，N 在M 的正南方向4.3km 处，Q 在M 的正东方向，P 在Q 的南偏西37°方向2.5km 处，N 在P 南偏西64°方向．（sin370.60°≈，cos370.80°≈，tan370.75°≈，sin640.90°≈，cos640.44°≈，tan64 2.05°≈）（1）求驿站P ，驿站N 之间的距离（结果精确到0.1km ）；（2）“双11”期间，派送员从沙坪坝区物流中心M 出发，以30km/h 的速度沿着M N P Q ———的路线派送快递到各个驿站，派送员途径N ，P 两个驿站各停留6min 存放快递，请计算说明派送员能否在40min 内到达驿站Q ？【答案】（1）5.2km （2）能，理由见解析【解析】【分析】本题考查解直角三角形的应用，将实际问题转化成解直角三角形的问题，利用解直角三角形的知识求解是解题的关键．（1）过点P 作PA MN ⊥于A ，PB MQ ⊥于B ，先解Rt PBQ △，求得2km PB =，再证明2km AM PB ==，从而得出 2.3km AN =，然后解Rt PAN △，即可求解．（2）求出派送员所需总时间，再与40min 比较即可得出答案．【小问1详解】解：过点P 作PA MN ⊥于A ，PBMQ ⊥于B ，如图，根据题意，得37BPQ PQD ∠=∠=°，64PNA NPC ∠=∠=°， 4.3km MN =， 2.5km PQ =，在Rt PBQ △中，∵cos PB BPQ PQ∠=， ∴()cos 2.5cos37 2.50.802km PBPQ BPQ =⋅∠=×°≈×=， ∵PA MN ⊥，PBMQ ⊥，90NMQ ∠=°，∴四边形AMBP 是矩形， ∴2km AM PB ==，∴()4.32 2.3km AN MN AM =−=−=，在Rt PAN △中，∵cos PNA ∠∴()2.3 2.3 5.2km cos cos 640.44ANPNPNA ==≈≈∠°，答：驿站P ，驿站N 之间的距离约为5.2km ．【小问2详解】解：∵30km/h 0.5km/min =，∴()()4.3 5.2 2.50.56236min ++÷+×=， ∵36min<40min ，∴派送员能在40min 内到达驿站Q ．25. 如图1，在平面直角坐标系中，直线112y x =−+与抛物线()230y ax x a =−+≠交于A ，B 两点，且点A 在x 轴上，直线与y 轴交于点C ．（1）求抛物线的表达式；（2）P 是直线AB 上方抛物线上一点，过P 作PQ y ∥轴交直线AB 于点Q ，求PQ AQ 的最大值，并求此时点P 的坐标；（3）在（2）PQ AQ 的最大值的条件下，连接BP ，将抛物线沿射线BA 方向平移，使得点A 在新抛物线的对称轴上，M 是新抛物线上一动点，当MAB BPQ ∠=∠时，直接写出所有符合条件的点M 的坐标．【答案】（1）2134y x x =−−+（2）PQ AQ +的最大值为4，()2,4P −（3）点M 的坐标为()2,2或【解析】【分析】（1）先由一次函数解析式求出点()2,0A ，再把()2,0A 代入23y ax x =−+，求出a 值即可；（2）延长PQ 交y 轴于D ，证明OAC DAQ ∽，得AC OC AQ DQ =1DQ =，求得DQ AQ =，再设21,34P x x x −−+ ，则1,12Q x x−+ ，则211242PQ x x =−−+，112QD x =−+，所以()21244PQ AQ PQ QD PD x +=+==−++，利用二次函数最值即可求解．（3）根据平移的性质求得抛物线平移后的解析式为2114y x x =−++，再分两种情况：当点M 在直线AB 上方时，当点M 在直线AB 下方时，分别求解即可．【小问1详解】解：对于直线112y x =−+，令0y =，则1102x −+=，解得：2x =， ∴()2,0A ，把()2,0A 代入23y ax x =−+，得0423a −+，解得：14a =−， ∴抛物线的表达式2134y x x =−−+．【小问2详解】解：延长PQ 交y 轴于D ，对于直线112y x =−+，令0x =，则1y =， ∴CC (0,1)， ∵()2,0A∴AC ==∵PQ y ∥轴，即QD OC ∥， ∴OAC DAQ ∽∴AC OC AQ DQ =1DQ=，∴DQ AQ =，设21,34P x x x −−+ ，则1,12Q x x −+，∴2211113124242PQ x x x x x=−−+−−+=−−+，112QD x =−+∴()221132444PQ AQ PQ QD PD x x x =+==−−+=−++ ∵104−< ∴当2x =−时，PQ AQ +的最大值为4； ∴()2,4P −．【小问3详解】解：联立，2134112y x x y x =−−+=−+，解得：1143x y =− = ，2220x y = = ，∴()4,3B −，由（2）知，在PQ AQ +的最大值的条件下，抛物线的顶点为点()2,4P −，对称为直线PQ ，当2x =−时，则()12122y =−×−+=， ∴()2,2Q −，则2PQ =，PB QB∴BPQ BQP ∠=∠， ∵将抛物线沿射线BA 方向平移，使得点A 在新抛物线的对称轴上， ∴点Q 平移后与点A 重合， ∵()2,2Q −，()2,0A ，∴抛物线沿射线BA 方向平移，是向下平移了2个单位，向右平移了4个单位，∴抛物线顶点()2,4P −平移后到点()2,2P ′，点()4,3B −平移后到点()0,1B ′，即B ′与C 重合，∴BPQ B P A ′′ ≌，抛物线平移后的解析式为()221122144y x x x =−−+=−++，∴BPQ B P A ′′∠=∠， ∵()0,1B ′，()2,2P ′，∴P B =′=′∵()0,1B ′，()2,0A ，∴AB ′=，∴P B AB ′′′=， ∴B AP B P A ′′′′∠=∠，当点M 在直线AB 上方时，∵MAB BPQ ∠=∠， ∴MAB B P A ′′∠=∠， ∴点M 与点P ′重合， ∴()2,2M ，当点M 在直线AB 下方时，设21,14M x x x−++，过点M 作ME PQ ∥，交AB 于E ，交x 轴于N ，则MEA BQP ∠=∠，1,12E x x−+，则AOC ANE △∽△，∴AC OCAE EN=，则E AE EN AC =⋅=， ∵MAB BPQ ∠=∠， ∴BPQ MAE △∽△，∴BQ PQ ME AE=，则BQ ME PQ AE =，=，整理得：32E M y y =−，即：231111224x x x −+=−−++，解得：x =（x =，此时，M y =∴M ，综上，符合条件的点M 的坐标为()2,2或．【点睛】本题属二次函数综合题目，主要去向不明了待定系数法求抛物线解析式，抛物线的性质，抛物线的平移，相似三角形的判定与性质，综合性较强，熟练掌握相关性质是解题的关键．26. 在ABC 中，AC BC =，D 为线段AB 上一点，连接CD ．（1）如图1，若30B ∠=°，AC AD =，过A 作AE CD ⊥于O ，交BC 于E ，2CE =，求线段BE 的长；（2）如图2，过点B 作BF CD ⊥交CD 延长线于点F ，以BC 为斜边在ABC 的右侧作等腰直角三角形BCG ，过点G 作GH AB ∥，交DC 的延长线于点H ，HC FB =．猜想线段AD ，BD ，CD 的数量关系，并证明你的猜想；（3）如图3，60ACB ∠=°，过A 作AQ BC ⊥于Q ，作ACB ∠的角平分线交AQ 于M ，取CM 的中点N ，连接QN ．点K 为直线BC 上的动点，连接NK ，将QKN 沿着NK 所在直线翻折至ABC 所在平面得到Q KN ′ ，连接MQ ′，取MQ ′中点P ，连接CP ．将12CD 绕着点D 顺时针旋转至直线AB 上方DR 处，使得BDR ACD ∠=∠．当CP 取得最小值时，连接AP ，PR ，AR ，当ARP △以AP 为腰的等腰三角形时，请直接写出DR AP的值．【答案】（1）（2）AD BD =+（3 【解析】【分析】（1）利用等腰三角形的性质得120ACB ∠=°，75ACD ∠=°，得45DCE ∠=°，根据线段垂直平分线性质，得2CE DE ==，得90CED ∠=°，即得BE = （2）过点C 作CI AB ⊥于I ，得AI BI =，根据等腰直角BCG 中，90BG CG BGC =∠=°，，BF CD ⊥，得点G 、C 、F 、B 在以BC 为直径的圆上，得GCH GBF ∠=∠，结合HC FB =，得()SAS GCH GBF ≌，得GF GH BGF CGH =∠=∠，，得90FGH ∠=°，证明45IDC H ∠=∠=°，得DI =，根据BI BD DI =+，AD AI DI =+，即得AD BD =+；（3）证明当'Q 与C 重合时，点P 与点N 重合，PC 取得最小值，当AP AR =时，设CD 中点为T ，连接RT BR CR ，，，由对称性知，点R 在ABC ∠的平分线上，得CR AR =，由BDR ACD ∠=∠，得60CDR CAD ∠=∠=°，根据RT DT CT ==，得DTR 是等边三角形，得30RCT ∠=°，90CRD ∠=°，得tan DR DCR CR ∠=；②延长CM 交AB 于L ，过B 作BS AC ∥，交DR 延长线于S ，连接CS ，则AL BL =，60CBS ACB ∠=∠=°，得60CBS CDS ∠=∠=°，得B 在过C 、D 、S 三点的圆上，得60CSD CBD ∠=∠=°，得 CDS 是等边三角形，当D 与点B 重合时，T 与Q 重合，点R 在BS 上，根据150NQB NQR ∠=∠=°，BQ RQ NQ NQ ==，，得()SAS BQN RQN ≌,得BN RN =，得AN RN =，设ABC 的边长为2，则1AL =，CL =，根据23CM CL =，N 是CM 中点，得NL =，得AN =DR AP =【小问1详解】解：AC BC = ，30B ∠=°。

重庆市南开中学校2024-2025学年九年级上学期入学考试数学试题

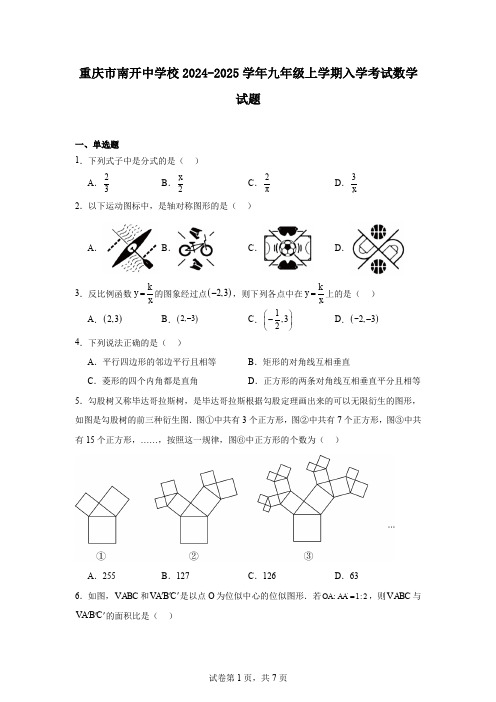
重庆市南开中学校2024-2025学年九年级上学期入学考试数学试题一、单选题1．下列式子中是分式的是（） A ．23B ．2xC ．2πD ．3x2．以下运动图标中，是轴对称图形的是（）A ．B ．C ．D ．3．反比例函数k y x =的图象经过点()2,3-，则下列各点中在ky x=上的是（） A ．()2,3B ．()2,3-C ．1,32⎛⎫- ⎪⎝⎭D ．()2,3--4．下列说法正确的是（） A ．平行四边形的邻边平行且相等 B ．矩形的对角线互相垂直C ．菱形的四个内角都是直角D ．正方形的两条对角线互相垂直平分且相等5．勾股树又称毕达哥拉斯树，是毕达哥拉斯根据勾股定理画出来的可以无限衍生的图形，如图是勾股树的前三种衍生图．图①中共有3个正方形，图②中共有7个正方形，图③中共有15个正方形，……，按照这一规律，图⑥中正方形的个数为（）A ．255B ．127C ．126D ．636．如图，ABC V 和A B C '''V 是以点O 为位似中心的位似图形．若:1:2OA AA '=，则ABC V 与A B C '''V 的面积比是（）A ．1:2B ．1:3C ．1:4D ．1:97．已知(m =，则实数m 的范围是（） A ．12m <<B ．23m <<C ．34m <<D ．45m <<8．在物理学中，压强p 等于物体所受压力F 的大小与受力面积S 之比，即FpS=．小明将底面积为2m S 、重100N 的均匀长方体铁块A 和底面积为()21m S +、重150N 的均匀长方体铁块B 放置在水平桌面上，A 、B 两个铁块对桌面的压强之比为2:1，求底面积S 为多少？则可列方程（） A ．10015021S S =⨯+ B ．10015021S S ⨯=+ C ．10015021S S=⨯+ D ．10015021S S⨯=+ 9．如图，正方形ABCD 的对角线AC BD 、交于点O ，将BA 绕点B 顺时针旋转60︒，得到BE ，连接AE DE 、，过A 作AF BE ⊥于点F ．若DE =AF =（）A1 B ．3C D ．10．已知多项式2232A x x =--，多项式21B x mx =-+． ①当0A =时，代数式220241xx x --的值为4048；②当3m =时，若22225B A B A --+-+≥，则x 的取值范围是12x ≤或136x ≥； ③当0m =时，若p 、q 为自然数，且整式p B q A ⋅-⋅所有项的系数和不超过10，则p q -的值有9种可能．以上说法正确的个数是（）A ．0B ．1C ．2D ．3二、填空题11．若34x y =，则x yx+=． 12．若一个多边形内角和等于1260°，则该多边形边数是．13．重庆因其魔幻建筑，被网友称为“8D 魔幻城市”，小南与小开打算来重庆旅游，他们将分别在A 、B 、C 、D 四家旅行社中随机选择一家，小南与小开选择同一家旅行社的概率为． 14．若m ，n 是一元二次方程210x x --=的两个实数根，则代数式2232n mn m -+=． 15．黄金分割在生活中有着非常广泛的应用，如图，在国旗上的五角星中，C 、D 两点都是线段AB 的黄金分割点．若2AC =，则AB 的长为．（结果保留根号）16．若关于x 的一元一次不等式组234223x m x +≤⎧⎪+⎨<-⎪⎩的解集是2x <-，且关于y 的分式方程322m yy y-=--有非负整数解，则符合条件的所有整数m 的和为． 17．如图，在矩形ABCD 中，E 为AD 边的四等分点（AE ED >），连接BE ，将矩形沿BE 折叠，点C 落在点C '处，点D 落在点D ¢处，BC '与AD 交于点F ，连接C E '．若4BC =，2AB =，则EF =，点F 到C E '的距离为．18．如果一个四位正整数的各数位上的数字互不相同且均不为0，且满足十位数字比千位数字大6，个位数字比百位数字大4，那么称这个四位数为“清活数”．记“清活数”M 的千位数字和个位数字之积与百位数字和十位数字之积的和为()F M ．例如：四位数1276，∵716=+，624=+，∴1276是“清活数”，()1276162720F =⨯+⨯=；四位数3295，∵936=+，但524≠+，∴3295不是“清活数”．若38a b 为“清活数”，则()38F a b =．若N 为“清活数”，且()F N 能被12整除，则满足条件的N 的最大值与最小值的平均数为．三、解答题 19．因式分解： (1)236x y xy +； (2)2249a b -． 20．解方程： (1)2250x x +-=； (2)22341x x x x-=--． 21．先化简，再求值：2222111x x x x x x -+⎛⎫-÷ ⎪++⎝⎭，其中3x =．22．如图，在菱形ABCD 中．(1)尺规作图：作BAC ∠的角平分线AE 交BC 于点E ，并在线段AB 上截取AF CE =，连接CF ．（不写作法，保留作图痕迹）(2)在（1）所作图形中，求证：CF 平分ACB ∠．证明：∵菱形ABCD ∴AB =__________ ∴ACB BAC ∠=∠ 在ACE △和CAF V 中∵AC AC =，ACB BAC ∠=∠，CE = ______∴()SAS ACE CAF V V≌ ∴CAE ∠=__________ ∵AE 平分BAC ∠ ∴12CAE BAC ∠=∠∵ACB BAC ∠=∠ ∴ACF ∠=__________ ∴CF 平分ACB ∠．23．北关中学在七、八年级各选取10名学生参加学校举办的“我爱我校”知识竞赛．竞赛成绩整理、描述和分析如下：（成绩得分用x 表示，共分成四组：A ．85x <；B ．8590x ≤<；C ．9095x ≤<；D ．95100x ≤≤）七年级10名学生的成绩：82，84，90，92，93，93，93，93，100，100 八年级10名学生的成绩在C 组中的数据是：91，91，93，94 七、八年级选取的学生竞赛成绩统计表八年级选取的学生竞赛成绩统计图根据以上信息回答下列问题：(1)a =______，b =_______，c =______． (2)哪个年级的学生成绩更好？请说明理由．(3)若该校七年级有700人，八年级有800人，均参加此次知识竞赛，估计成绩优秀（90x ≥）的学生共有多少人？24．巴黎奥运会的吉祥物“弗里热”玩偶共有两种尺寸．分别为大款和小款，小渝购置了一定数量的两款玩偶，各自花费2400元，已知大款比小款单价高90元，小款数量是大款数量的85． (1)请问大，小款单价各多少元？(2)为了送给其他的朋友，小渝决定再买一定数量的吉祥物，此时，在第一次购买的基础上，小款的单价减少了m 元，购买数量增加了23m 个，大款的单价不变，购买数量减少了14m 个，总费用为4800元，请求出m 的值．25．如图1，在四边形ABCD 中，AD BC ∥，AB BC ⊥，4AB =，3AD =，6BC =．点P 以每秒1个单位长度的速度从点A 出发，沿折线A D C →→方向匀速运动，到达点C 时停止运动，点Q 以每秒2个单位长度的速度从点C 出发，沿C B →方向匀速运动，到达点B 时停止运动．两点同时出发，设点P 运动时间为x 秒，CPQ V 的面积为y ．(1)请直接写出y 与x 之间的函数关系式及对应的x 的取值范围；(2)在如图2所示的平面点角坐标系中画出y 的图象，并写出函数y 的一条性质； (3)结合你所画的函数图象，当6y ≤时，请直接写出x 的取值范围_______．26．如图1，在平面直角坐标系中，直线l ：2y x =+与x 轴交于点A ，与y 轴交于点B ，点C 在x 轴的正半轴上，且3OC OB =．(1)求直线BC 的表达式；(2)点P 是线段BC 上一动点，点E 是直线AB 上一动点，点F 为x 轴上一动点，过P 作PQ AB ⊥于Q ，连接PE EF 、，当PQ =PE EF +的最小值；(3)如图2，在（2）问条件下，点M 为直线AB 上一动点，当QPM ACB BAC ∠=∠+∠时，直接写出所有符合条件的点M 的坐标．27．如图，在等腰Rt ABC △中，AB AC =，在AC 边上取一点D ，连接BD ，点E 为BD 上一点，以BE 为斜边向下作等腰Rt BEF △．(1)如图1，连接AE AF 、，AF 交BD 于G ，若AE 垂直平分DG ，设ABD α∠=，求AFE ∠的度数（用含α的代数式表示）；(2)如图2，连接AF CE 、，以A 为顶点，在AF 右侧作45FAM ∠=︒，AM 交CE 于点M ，求证：CM EM =；(3)如图3，连接AE CE 、，设EF 与BC 交于点O ，若AE BD ⊥，4AB =，点D 从点A 运动到点C 的过程中，当CE 的长度取得最小值时，请直接写出COE V的面积．。

2020年重庆市南开中学(融侨)中考数学综合卷四(含答案)

第 3 题图
第 4 题图
第 6 题图
5．已知正比例函数 y1 的图象与反比例函数 y2 的图象相交于点 A（2，4），下列说法正确的是（）
A．反比例函数 y2 的解析式是 y2＝﹣ 8 B．两个函数图象的另一交点坐标为（2，﹣4） x
C．当 x＜﹣2 或 0＜x＜2 时，y1＜y2
D．函数 y1 与函数 y2 都随 x 的增大而增大
度．如图，某路口的斑马线路段 A﹣B﹣C 横穿双向行驶车道，其中 AB＝BC＝6 米，在
绿灯亮时，小明共用 11 秒通过 AC，其中通过 BC 的速度是通过 AB 速度的 1.2 倍，求小
明通过 AB 时的速度．设小明通过 AB 时的速度是 x 米/秒，根据题意列方程得：
．
17. 在平面直角坐标系中，A，B，C 三点的坐标分别为（4，0），（4，4），（0，4），点 P 在 x
顶 B 点的仰角 BAO 35 ，山坡 AC 的坡度 i = 1: 2 ， OA 500 米，则山顶 C 的垂直
高度约为（）（参考数据：sin13 0.22 tan13 0.23 ，，sin 35 0.57 ，tan 35 0.70 ）
A．161.0 B．116.4
C．106.8
D． 76.2 y D
AO
CM x
E B
第 10 题
第 11 题图
11.如图，直线 y 1 x 2 与 x 轴交于 C，与 y 轴交于 D，以 CD 为边作矩形 CDAB，点 A 2
在
x
轴上，双曲线
y
k x
(k
0)
经过点
B
与直线
CD
交于
E，EM⊥x
轴于
M，则

2020年重庆市南开中学(融侨)中考数学综合卷五(PDF版含答案) (1)

I. 规定：巨2)表示向右移动2记作+2'则（七3)表示向左移动3记作<&
A. +3
n. -3
C. --I 3
2. 语句" X 的SI 与x的和不超过5"可以表示为 (tii
D. +-I 3
A. �+x�5
B. 斗,�5
C. �天5
D. �+x=5
<C 8
8
3. 如图，A, B, C为00上三点，乙AOB=l 10° , 贝； :�CB等千
（20 题图）
21. 某校初三有 2000 名学生，为了解初三学生的体能，从人数相等的甲、乙两个班进行了抽样调查，过程
如下，请补充完整.
收集数据：从甲、乙两个班各随机抽取 20 名学生．进行了体能测试，测试成绩（百分制）如下：
甲：78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
、�
3题图
l_',, ｀夕
二 A. 55°
13. 110°
C. 125°
D. 140°
4. 卜而足投影屏上出示的抢答题，衙拟回答横线上符号代表的内容，则回答止确的足<C)
B
已求证则和又芷
知汪明
气，
... .
廷』.. E
如 AB
图 “ 长
一
豆：
3 E C 立 3 乙 C
二宁
l,
七芒、、＂ i,i-．角
）
A.3
B.6
C. 3 5
二、填空
13.
计算：Biblioteka 1 20 1

七年级上册重庆市南开中学数学期末试卷中考真题汇编[解析版]

七年级上册重庆市南开中学数学期末试卷中考真题汇编[解析版]一、初一数学上学期期末试卷解答题压轴题精选（难）1．将一副三角板放在同一平面内，使直角顶点重合于点O（1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数.（2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论.（3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由.【答案】（1）解：∵而同理：∴∴（2）解：∠AOD与∠BOC的大小关系为：∠AOB与∠DOC存在的数量关系为：（3）解：仍然成立.理由如下：∵又∵∴【解析】【分析】（1）先计算出再根据（2）根据(1)中得出的度数直接写出结论即可.（3）根据即可得到利用周角定义得∠AOB+∠COD+∠AOC+∠BOD=360°，而∠AOC=∠BOD=90°，即可得到∠AOB+∠DOC=180°．2．点A、B在数轴上分别表示实数a、b，A、B两点之间的距离记作AB．当A、B两点中有一点为原点时，不妨设A点在原点．如图①所示，则AB＝OB＝|b|＝|a﹣b|．当A、B两点都不在原点时：⑴如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB﹣OA＝|b|﹣|a|＝b﹣a＝|b﹣a|＝|a﹣b|⑵如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB﹣OA＝|b|﹣|a|＝﹣b﹣(﹣a)＝a﹣b＝|a﹣b|⑶如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB+OA＝|b|+|a|＝a+(﹣b)＝|a﹣b|回答下列问题：（1）综上所述，数轴上A、B两点之间的距离AB＝________．（2）数轴上表示2和﹣4的两点A和B之间的距离AB＝________．（3）数轴上表示x和﹣2的两点A和B之间的距离AB＝________，如果AB＝2，则x的值为________．（4）若代数式|x+2|+|x﹣3|有最小值，则最小值为________．【答案】（1）（2）6（3）；0或－4（4）5【解析】【解答】(1)综上所述，数轴上A、B两点之间的距离 (2)数轴上表示2和－4的两点A和B之间的距离 (3)数轴上表示和－2的两点A和B之间的距离如果，则的值为或由题意可知：当x在−2与3之间时，此时，代数式|x+2|+|x−3|取最小值，最小值为故答案为：（1）；（2）6；（3），0或－4；（4）5.【分析】（1）发现规律：在数轴上两点之间的距离为这两点所表示的数的差的绝对值，故可求解；（2）根据（1），即可直接求出结果；（3）先根据（1）即可表示出AB；当AB=2时，得到方程，解出x的值即可；（4）|x+2|+|x-3|表示数轴上一点到-2与3两点的距离的和，当这点是-2或5或在它们之间时和最小，最小距离是-2与3之间的距离。

2025届重庆市沙坪坝区南开中学九年级数学第一学期期末联考试题含解析

2025届重庆市沙坪坝区南开中学九年级数学第一学期期末联考试题注意事项:1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题(每小题3分,共30分)1．若点 A 1(2,)y 、B 2(2,)y 、C 3(2,)y -都在二次函数()231y x k =-+的图象上，则123、、y y y 的大小关系为（）A ．123y y y >>B ．213y y y >>C ．312y y y >>D ．321y y y >> 2．如图，在正方形网格上，与△ABC 相似的三角形是（）A ．△AFDB ．△FEDC ．△AED D ．不能确定3．若△ABC ∽△ADE ，若AB ＝9，AC ＝6，AD ＝3，则EC 的长是（）A ．2B ．3C ．4D ．54．不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，两次都摸到颜色相同的球的概率为( )A ．23B ．13C ．12D ．145．如图，阳光透过窗户洒落在地面上，已知窗户AB 高1.5m ，光亮区的顶端距离墙角3m ，光亮区的底端距离墙角1.2m ，则窗户的底端距离地面的高度(BC )为( )A ．1mB ．1.2mC ．1.5mD ．2.4m6．如图，在△ABC 中，DE ∥BC ，13AD AB =，BC =12，则DE 的长是（）A ．3B ．4C ．5D ．67．下列图形是中心对称图形的是（）A ．B ．C ．D ．8．若正方形的外接圆半径为2，则其内切圆半径为（）A ．22B ．2C ．22D ．19．如图，在ABC 中，点P 在边AB 上，则在下列四个条件中：：ACP B ∠∠=①；APC ACB ∠∠=②；2AC AP AB =⋅③；AB CP AP CB ⋅=⋅④，能满足APC 与ACB 相似的条件是（）A ．①②④B ．①③④C ．②③④D ．①②③ 10．在平面直角坐标系中，二次函数269y x x =-+-与坐标轴交点个数（）A ．3个B ．2个C ．1个D ．0个二、填空题(每小题3分,共24分)11．如图，抛物线y ＝﹣2x 2+2与x 轴交于点A 、B ，其顶点为E ．把这条抛物线在x 轴及其上方的部分记为C 1，将C 1向右平移得到C 2，C 2与x 轴交于点B 、D ，C 2的顶点为F ，连结EF ．则图中阴影部分图形的面积为______．12．若一个反比例函数的图像经过点(),A a a 和()3,2B a -，则这个反比例函数的表达式为__________．13．如图，在平面直角坐标系中，一次函数y=kx+b 与反比例函数m y x =的图象相交于点(2,3)A 和点(,1)B n -，则关于x 的不等式m kx b x+>的解集是_____．14．如图，将矩形ABCD 绕点A 旋转至矩形AB ′C ′D ′位置，此时AC ′的中点恰好与D 点重合，AB ′交CD 于点E ．若AB ＝3，则△AEC 的面积为_____．15．不等式组的解是________．16．如图，在4×4的正方形网格中，若将△ABC 绕着点A 逆时针旋转得到△AB ′C ′，则BB '的长为_____．17．一个口袋中放有除颜色外，形状大小都相同的黑白两种球，黑球6个，白球10个．现在往袋中放入m 个白球和4个黑球，使得摸到白球的概率为35，则m ＝__． 18．如图，正方形ABCD 的边长为5，E 、F 分别是BC 、CD 上的两个动点，AE ⊥EF ．则AF 的最小值是_____．三、解答题(共66分)19．（10分）如图，点E为□ABCD中一点，EA=ED，∠AED=90º，点F，G分别为AB，BC上的点，连接DF,AG，AD=AG=DF，且AG⊥DF于点H，连接EG，DG，延长AB,DG相交于点P．（1）若AH=6，FH=2，求AE的长；（2）求证：∠P=45º；（3）若DG=2PG，求证：∠AGE=∠EDG．20．（6分）用适当的方法解下列一元二次方程（1）x2+2x＝3；（2）2x2﹣6x+3＝1．21．（6分）如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（3，1）在反比例函数kyx=的图象上．（1）求反比例函数kyx=的表达式；（2）在x轴的负半轴上存在一点P，使得S△AOP=12S△AOB，求点P的坐标；（3）若将△BOA绕点B按逆时针方向旋转60°得到△BDE，直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．22．（8分）如图，在ABC ∆中，CD 是AB 边上的高，且2CD AD BD =⋅．（1）求ACB ∠的度数；（2）在（1）的条件下，若4,10AC AB ==，求AD 的长．23．（8分）甲口袋中装有3个小球，分别标有号码1，2，3；乙口袋中装有2个小球，分别标有号码1，2；这些球除数字外完全相同．从甲、乙两口袋中分别随机地摸出一个小球，则取出的两个小球上的号码恰好相同的概率是多少？24．（8分）如图，某数学兴趣小组为测量一棵古树BH 和教学楼CG 的高，先在点A 处用高1.5米的测角仪测得古树顶端点H 的仰角HDE ∠为45︒，此时教学楼顶端点G 恰好在视线DH 上，再向前走7米到达点B 处，又测得教学楼顶端点G 的仰角GEF ∠为60︒，点A 、B 、C 点在同一水平线上．（1）计算古树BH 的高度；（2）计算教学楼CG 的高度．（结果精确到0.12 1.4≈3 1.7≈）．25．（10分）综合与探究：如图所示，在平面直角坐标系中，直线2y x =+与反比例函数()0k y k x=>的图象交于(),3A a ，()3,B b -两点，过点A 作AC x ⊥轴于点C ，过点B 作BD x ⊥轴于点D ．（1）求a ，b 的值及反比例函数的函数表达式；（2）若点P 在线段AB 上，且ACP BDP S S ∆∆=，请求出此时点P 的坐标；（3）小颖在探索中发现：在x 轴正半轴上存在点M ，使得MAB ∆是以A ∠为顶角的等腰三角形.请你直接写出点M 的坐标.26．（10分）小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现：每月的销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数y ＝－10x ＋500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%.(1)设小明每月获得利润为w(元)，求每月获得利润w(元)与销售单价x(元/件)之间的函数表达式，并确定自变量x 的取值范围；(2)当销售单价定为多少元/件时，每月可获得最大利润？每月的最大利润是多少？参考答案一、选择题(每小题3分,共30分)1、D【分析】根据反二次函数图象上点的坐标特征比较y 1、y 2、y 3的大小，比较后即可得出结论．【详解】解：∵A 12y ，)、B (2，2y )、C (32y -，)在二次函数y=()23x-1+k 的图象上，∵y=()23x-1+k 的对称轴x=1，∴当x=0与x=2关于x=1对称，∵A,B 在对称轴右侧,y 随x 的增大而增大，则y 2＞y 1，C 在对称轴左侧，且2<0 ，则y 3＞y 2，∴y 3＞y 2＞y 1，故选：D ．【点睛】本题考查了二次函数图象上点的坐标特征，利用二次函数图象上点的坐标关于对称轴对称的特征比较y 1、y 2、y 3的大小是解题的关键．2、A【分析】根据题意直接利用三角形三边长度，得出其比值，进而分析即可求出相似三角形．【详解】解：∵AF ＝4，DF ＝4，AD ＝4 AB ＝2，BC ＝2 AC ＝2 ∴2AF DF AD AB AB AC===， ∴△AFD ∽△ABC ．故选：A ．【点睛】本题主要考查相似三角形的判定以及勾股定理，由勾股定理得出三角形各边长是解题的关键．3、C【分析】利用相似三角形的性质得，对应边的比相等，求出AE 的长，EC=AC-AE ，即可计算DE 的长；【详解】∵△ABC ∽△ADE ， ∴AB AC AD AE=， ∵AB ＝9，AC ＝6，AD ＝3，∴AE=2，即EC=AC-AE=6-2=4；故选C.【点睛】本题主要考查了相似三角形的判定与性质，掌握相似三角形的判定与性质是解题的关键.4、C【分析】用列表法或树状图法可以列举出所有等可能出现的结果，然后看符合条件的占总数的几分之几即可【详解】解：两次摸球的所有的可能性树状图如下：共有4种等可能的结果，其中两次都摸到颜色相同的球结果共有2种， ∴两次都摸到颜色相同的球的概率为2142=. 故选C ．【点睛】本题考查用树状图或列表法求等可能事件发生的概率，关键是列举出所有等可能出现的结果数，然后用分数表示，同时注意“放回”与“不放回”的区别．5、A【分析】根据光沿直线传播的原理可知AE ∥BD ，则BCD ∽ACE △，根据相似三角形的对应边成比例即可解答．【详解】解：∵AE ∥BD∴BCD ∽ACE △ ∴BC CD CA CE= ∵ 1.5AB m =， 1.2CD m =，3CE m ∴1.21.53BC BC =+ 解得：1BC =经检验1BC =是分式方程的解．故选：A ．【点睛】本题考查了相似三角形的判定及性质，解题关键是熟知：平行于三角形一边的直线和其他两边或延长线相交，所截得的三角形与原三角形相似．6、B【解析】试题解析：在△ABC 中，DE ∥BC ，.ADE ABC ∴∽1.3DE AD BC AB ∴== 12.BC =4.DE ∴=故选B.7、B【解析】根据中心对称图形的定义，在平面内，把图形绕着某个点旋转180︒，如果旋转后的图像能与原图形重合，就为中心对称图形.【详解】选项A ，不是中心对称图形.选项B,是中心对称图形.选项C,不是中心对称图形.选项D,不是中心对称图形.故选B【点睛】本题考查了中心对称图形的定义.8、B【解析】试题解析：如图所示，连接OA 、OE ，∵AB 是小圆的切线，∴OE ⊥AB ，∵四边形ABCD 是正方形，∴AE =OE ，∴△AOE 是等腰直角三角形，2 2.OE ∴== 故选B.9、D【分析】根据相似三角形的判定定理，结合图中已知条件进行判断.【详解】当ACP B ∠∠=，A A ∠∠=，所以APC ∽ACB ,故条件①能判定相似，符合题意；当APC ACB ∠∠=，A A ∠∠=，所以APC ∽ACB ，故条件②能判定相似，符合题意；当2AC AP AB =⋅，即AC ：AB AP =：AC ，因为A A ∠=∠所以APC ∽ACB ，故条件③能判定相似，符合题意；当AB CP AP CB ⋅=⋅，即PC ：BC AP =：AB ，而PAC CAB ∠∠=，所以条件④不能判断APC 和ACB 相似，不符合题意；①②③能判定相似，故选D ．【点睛】本题考查相似三角形的判定，熟练掌握判定定理是解题的关键.10、B【分析】首先根据根的判别式判定与x 轴的交点，然后令0x =，判定与y 轴的交点，即可得解.【详解】由题意，得()()2641936360=-⨯-⨯-=-=△ ∴该函数与x 轴有一个交点当0x =时，9y =-∴该函数与y 轴有一个交点∴该函数与坐标轴有两个交点故答案为B.【点睛】此题主要考查利用根的判别式判定二次函数与坐标轴的交点，熟练掌握，即可解题.二、填空题(每小题3分,共24分)11、1【分析】由S 阴影部分图形＝S 四边形BDFE ＝BD×OE ，即可求解．【详解】令y ＝0，则：x ＝±1，令x ＝0，则y ＝2，则：OB ＝1，BD ＝2，OB ＝2，S 阴影部分图形＝S 四边形BDFE ＝BD×OE ＝2×2＝1．故：答案为1．【点睛】本题考查的是抛物线性质的综合运用，确定S 阴影部分图形＝S 四边形BDFE 是本题的关键．12、36y x= 【分析】这个反比例函数的表达式为k y x=，将A 、B 两点坐标代入，列出方程即可求出k 的值，从而求出反比例函数的表达式．【详解】解：设这个反比例函数的表达式为k y x =将点(),A a a 和()3,2B a -代入，得23k a a k a ⎧=⎪⎪⎨⎪-=⎪⎩化简，得260a a +=解得：126,0a a =-=（反比例函数与坐标轴无交点，故舍去）解得：36k = ∴这个反比例函数的表达式为36y x =故答案为：36y x =．【点睛】此题考查的是求反比例函数的表达式，掌握待定系数法是解决此题的关键．13、-6＜x ＜0或x ＞2；【解析】观察一次函数和反比例函数图象，一次函数比反比例函数高的部分就是所求.【详解】解：本题初中阶段只能用数形结合，由图知-6＜x ＜0或x ＞2；点睛：利用一次函数图象和反比例函数图象性质数形结合解不等式：形如式0m kx b x +->不等式，构造函数1y kx b =+，2y =m x，如果12y y >,找出1y 比2y ,高的部分对应的x 的值,12y y <,找出1y 比2y ,低的部分对应的x 的值.14、3【分析】先求出∠ACD=30°，进而可算出CE、AD，再算出△AEC的面积．【详解】如图，由旋转的性质可知：AC=AC'，∵D为AC'的中点，∴AD=1122AC AC='，∵ABCD是矩形，∴AD⊥CD，∴∠ACD=30°，∵AB∥CD，∴∠CAB=30°，∴∠C'AB'=∠CAB=30°，∴∠EAC=30°，∴AE=EC，∴DE=1122AE EC=，∴CE=222 33CD AB==，DE=11 3AB=，AD3∴132AECS EC AD==3【点睛】本题考查了旋转的性质、矩形的性质、直角三角形中30度角的性质，三角形面积计算等知识点，难度不大．清楚旋转的“不变”特性是解答的关键．15、x ＞4【分析】分别解出不等式组中的每一个不等式，然后根据同大取大得出不等式组的解集.【详解】由①得:x ＞2;由②得 :x ＞4;∴此不等式组的解集为x ＞4;故答案为x ＞4.【点睛】考查了解一元一次不等式组，一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到.16、π【分析】根据图示知45BAB ∠'=︒ ，所以根据弧长公式180n r l π=求得'BB 的长．【详解】根据图示知，45BAB ∠'=︒ ，∴'BB 的长为：454180ππ⨯=．故答案为：π ．【点睛】本题考查了弧长的计算公式，掌握弧长的计算方法是解题的关键．17、1【分析】根据概率公式列出方程，即可求出答案．【详解】解：由题意得，10m 3610m 45+=+++ 解得m ＝1，经检验m ＝1是原分式方程的根，故答案为1．【点睛】本题主要考查了概率公式，根据概率公式列出方程是解题的关键．18、254【分析】设BE ＝x ，CF ＝y ，则EC ＝5﹣x ，构建二次函数了，利用二次函数的性质求出CF 的最大值，求出DF 的最小值即可解决问题．【详解】解：设BE＝x，CF＝y，则EC＝5﹣x，∵AE⊥EF，∴∠AEF＝90°，∴∠AEB+∠FEC＝90°，而∠AEB+∠BAE＝90°，∴∠BAE＝∠FEC，∴Rt△ABE∽Rt△ECF，∴ABEC＝BECF，∴55x-＝xy，∴y＝﹣15x2+x＝﹣15（x﹣52）2+54，∵﹣15＜0，∴x＝52时，y有最大值54，∴CF的最大值为54，∴DF的最小值为5﹣54＝154，∴AF的最小值＝22AD DF+＝221554⎛⎫+ ⎪⎝⎭＝254，故答案为254．【点睛】本题考查了几何动点问题与二次函数、相似三角形的综合问题，综合性较强，解题的关键是找出相似三角形，列出比例关系，转化为二次函数，从而求出AF的最小值．三、解答题(共66分)19、（1）52；（2）见详解；（3）见详解【分析】（1）在Rt △ADH 中，设AD=DF=x ，则DH=x-2，由勾股定理，求出AD 的长度，由等腰直角三角形的性质，即可求出AE 的长度；（2）根据题意，设∠ADF=2a ，则求出∠FAH=a =，然后∠ADG=∠AGD=45a ︒+，再根据三角形的外角性质，即可得到答案；（3）过点A 作AM ⊥DP 于点M ，连接EM ，EF ，根据等腰直角三角形的判定和性质，全等三角形的判定和性质，得到角之间的关系，从而通过等量互换，即可得到结论成立．【详解】解：（1）∵AG ⊥DF 于点H ，∴∠AHD=90°，∵AH=6，FH=2，在Rt △ADH 中，设AD=DF=x ，则DH=DF -FH=x-2，由勾股定理，得：222AD DH AH =+，∴222(2)6x x =-+，∴10x =，即AD=DF=AG=10，∵EA=ED ，∠AED=90º，∴△ADE 是等腰直角三角形，∴AE=DE=210522⨯=；（2）如图：∵∠AED=90º，AG ⊥DF ，∴∠EAH=∠EDH ，设∠ADF=2a ，∵DA=DF ，则∠AFH=∠DAF=1(1802)902a a ⨯︒-=︒-， ∴∠FAH=90(90)a a ︒-︒-=，∴∠DAH=90902a a a ︒--=︒-，∵AD=AG ，∴∠ADG=∠AGD=1[180(902)]452a a ⨯︒-︒-=︒+， ∴4545P AGD FAH a a ∠=∠-∠=︒+-=︒；（3）过点A 作AM ⊥DP 于点M ，连接EM ，EF ，如图：∵AD=AG ，DG=2PG ，∴PG=GM=DM ，∵∠P=45°，∴△APM 是等腰直角三角形，∴AM=PM=DG ，∵∠ANO=∠DNM ，∠AED=∠AMD=90°，∴∠OAM=∠ODG ，∵AE=DE ，AM=DG ，∴△AEM ≌△DEG ，∴EM=EG ，∠AEM=∠DEG ，∴∠AED+∠DEM=∠DEM+∠MEG ，∴∠MEG=∠AED=90°，∴△MEG 是等腰直角三角形；∴∠EMG=45°，∵AM ⊥DP ，∴∠AME=∠EMG=45°，∴ME 是∠AMP 的角平分线，∵AM=PM ，∴ME ⊥AP ，∵∠AOH=∠DOE ，∴∠OAH=∠ODE ，∴△AEG ≌△DEF （SAS ），∴∠AEG=∠DEF ，∴∠AED+∠AEF=∠AEF+∠FEG ，∴∠FEG=∠AED=90°，∴∠FEG+∠MEG=180°，即点F 、E 、M ，三点共线，∴MF ⊥AP ，∵AM 平分∠DAG ，∴∠GAM=∠DAM ，∵∠EAN+∠DAM=45°，∴∠EAN+∠GAM=45°，∵∠PAG+∠GAM=45°，∴∠EAN=∠PAG ，∵∠PAG+∠AFH=∠DFE+∠AFH=90°，∴∠EAN=∠PAG=∠DFE ，∵△AEG ≌△DEF ，∴∠AGE=∠DFE=∠EAN ，∵∠EAN=∠EDM ，∴∠AGE=∠EDM ，∴∠AGE=∠EDG ．【点睛】本题考查了平行四边形的性质，等腰直角三角形的判定和性质，全等三角形的判定和性质，三角形的内角和定理，以及角平分线的性质，解题的关键是熟练掌握所学的性质进行证明，注意正确做出辅助线，找出角之间的关系，边之间的关系，从而进行证明．20、（1）x 1＝﹣3，x 2＝1；（2）12x x ==【分析】（1）移项，方程左边分解因式后，利用两数相乘积为1，两因式中至少有一个为1转化为两个一元一次方程来求解；（2）方程二次项系数化为1，常数项移到右边，两边加上一次项系数一半的平方，开方即可求出解．【详解】解：（1）移项得：x 2+2x ﹣3＝1，分解因式得：（x +3）（x ﹣1）＝1，可得x +3＝1或x ﹣1＝1，解得：x 1＝﹣3，x 2＝1；（2）方程变形得：x 2﹣3x ＝﹣32，配方得：x 2﹣3x +94＝﹣32+94，即（x ﹣32）2＝34，解得：12x x == 【点睛】此题考查了解一元二次方程-因式分解法及配方法，熟练掌握各种解法是解本题的关键．21、（1）y =；（2）P （-，0）；（3）E （1），在．【分析】（1）将点A ，1）代入k y x=，利用待定系数法即可求出反比例函数的表达式；（2）先由射影定理求出BC=3，那么B ，﹣3），计算求出S △AOB =124=S △AOP =12S △AOB 点P 的坐标为（m ，0），列出方程求解即可；（3）先解△OAB ，得出∠ABO=30°，再根据旋转的性质求出E 1），即可求解．【详解】（1）∵点A ，1）在反比例函数k y x=的图象上，∴k=∴反比例函数的表达式为y x=；（2）∵A 1），AB ⊥x 轴于点C ，∴AC=1，由射影定理得2OC =AC•BC ，可得BC=3，B 3），S △AOB =12×4=∴S △AOP =12S △AOB 设点P 的坐标为（m ，0），∴12×|m|×，∴|m|=∵P 是x 轴的负半轴上的点，∴m=﹣∴点P 的坐标为（-，0）；（3）点E 在该反比例函数的图象上，理由如下：∵OA ⊥OB ，OA=2，OB=AB=4，∴sin ∠ABO=OA AB =24=12， ∴∠ABO=30°，∵将△BOA 绕点B 按逆时针方向旋转60°得到△BDE ，∴△BOA ≌△BDE ，∠OBD=60°，∴BO=BD=OA=DE=2，∠BOA=∠BDE=90°，∠ABD=30°+60°=90°，而BD﹣BC ﹣DE=1，∴E （1），∵（﹣1）∴点E 在该反比例函数的图象上．考点：待定系数法求反比例函数解析式；反比例函数系数k 的几何意义；坐标与图形变化-旋转．22、（1）90ACB ∠=︒；（2） 1.6AD =【分析】(1) CD 是AB 边上的高，且2CD AD BD =⋅，就可以得出ADC CDB ∆~∆，可得∠A=∠BCD ，由直角三角形的性质可求解；(2证明~ACD ABC ∆∆，可得AD AC AC AB=，再把4,10AC AB ==代入可得答案．【详解】（1）证明：在ABC ∆中，∵CD 是AB 边上的高，∴090ADC CDB ∠=∠=，∵2CD AD BD =， ∴AD CD CD BD =， ∴ADC CDB ∆~∆， ∴A BCD ∠=∠，∴090ACB ACD BCD ACD A ∠=∠+∠=∠+∠=；（2）由（1）知ABC ∆是直角三角形，在Rt ABC ∆中，∵090ACD A B A ∠+∠=∠+∠=，∴ACD B ∠=∠，又∵A A ∠=∠，∴~ACD ABC ∆∆，∴AD AC AC AB=，又∵4,10AC AB ==，∴4410AD =， ∴ 1.6AD =【点睛】本题考查了相似三角形的判定和性质，证明三角形相似是关键．23、两个小球的号码相同的概率为13. 【解析】【试题分析】利用树状图求等可能事件的概率，树状图见解析.【试题解析】画树状图得：∵共有6种等可能的结果，这两个小球的号码相同的有2情况， ∴这两个小球的号码相同的概率为：2163=． 24、 (1)8.5米；(2)18.0米【分析】（1）先根据题意得出DE=AB=7米，AD=BE=1.5米，在Rt △DEH 中，可求出HE 的长度，进而可计算古树BH的高度；（2）作HJ ⊥CG 于G ，设HJ=GJ=BC=x ，在Rt △EFG 中，利用特殊角的三角函数值求出x 的值，进而求出GF ，最后利用 CG=CF+FG 即可得出答案．【详解】解：（1）由题意：四边形ABED 是矩形，可得DE=AB=7米，AD=BE=1.5米，在Rt △DEH 中，∵∠EDH=45°，∴HE=DE=7米．∴BH=EH+BE=8.5米．答：古树BH 的高度为8.5米．（2）作HJ ⊥CG 于G ．则△HJG 是等腰直角三角形，四边形BCJH 是矩形，设HJ=GJ=BC=x ．在Rt △EFG 中，tan60°=73GF x EF x +==， ∴7(31)2x =， ∴3x ≈16.45∴CG=CF+FG=1.5+16.45≈17.95≈18.0米．答：教学楼CG 的高度为18.0米．【点睛】本题主要考查解直角三角形，能够数形结合，构造出直角三角形是解题的关键．25、（1）1a =，1b =-，3y x =；（2）点P 的坐标为()0,2；（3）()123,0M + 【分析】（1）利用点在直线上，将点的坐标代入直线解析式中求解即可求出a ，b ，最后用待定系数法求出反比例函数解析式；（2）设点(),p p P x y ，用三角形的面积公式得到()()111322p p AC x DB x ⋅-=⋅+求解即可得出结论；（3）设出点M 坐标，表示出MA 2=（m-1）2+9，AB 2=32，根据等腰三角形的性质建立方程求解即可得出结论．【详解】解：（1）∵直线2y x =+与反比例函数()0k y k x =>的图象交与(),3A a ，()3,B b -两点 ∴23a +=，32b -+=.∴1a =，1b =-.∴()1,3A ，()3,1B --.∵点()1,3A 在反比例函数k y x =上， ∴133k =⨯=. ∴反比例函数的函数表达式为3y x =. （2）设点(),p p P x y ，∵()1,3A ，∴()1,0C .∴3AC =.∵()3,1B --，∴()3,0D -.∴1BD =，∵ACP BDP S S ∆∆= ∴()()111322p p AC x DB x ⋅-=⋅+. 解得：0p x =，∴2p y =.∴点P 的坐标为()0,2.（3）设出点M 坐标为（m,0），∴MA 2=（m-1）2+9，AB 2=（1+3）2+（3+1）2=32，∵MAB ∆是以A ∠为顶角的等腰三角形∴AM=AB,故（m-1）2+9=32解得m=1m=1-（舍去）∴()1M +【点睛】此题主要考查反比例函数与一次函数综合，解题的关键是熟知待定系数法求解析式、三角形的面积公式及等腰三角形的性质.26、 (1)w ＝－10x 2＋700x －10000(20≤x ≤32)；(2)当销售单价定为32元/件时，每月可获得最大利润，最大利润是2160元．【解析】分析：（1）由题意得，每月销售量与销售单价之间的关系可近似看作一次函数，利润=（定价-进价）×销售量，从而列出关系式；（2）首先确定二次函数的对称轴，然后根据其增减性确定最大利润即可；详解：（1）由题意，得：w=（x-20）•y=（x-20）•（-10x+500）=-10x2+700x-10000，即w=-10x2+700x-10000（20≤x≤32）.(2)w＝－10x2＋700x－10000＝－10(x－35)2＋2250.对称轴为：x=35，又∵a＝－10＜0，抛物线开口向下，∴当20≤x≤32时，w随着x的增大而增大，∴当x＝32时，w最大＝2160.答：当销售单价定为32元/件时，每月可获得最大利润，最大利润是2160元．点睛：二次函数的应用.重点在于根据题意列出函数关系式.。

重庆市南开中学数学几何模型压轴题中考真题汇编[解析版]

重庆市南开中学数学几何模型压轴题中考真题汇编[解析版]一、初三数学旋转易错题压轴题（难）1．已知如图1，在ABC 中，90ABC ∠=︒，BC AB =，点D 在AC 上，DF AC ⊥交BC 于F ，点E 是AF 的中点．（1）写出线段ED 与线段EB 的关系并证明；（2）如图2，将CDF 绕点C 逆时针旋转()090a α︒<<︒，其它条件不变，线段ED 与线段EB 的关系是否变化，写出你的结论并证明；（3）将CDF 绕点C 逆时针旋转一周，如果6BC =，32CF =，直接写出线段CE 的范围．【答案】（1）ED EB =，DE BE ⊥，证明见解析；（2）结论不变，理由见解析；（3）最大值22=最小值322=．【解析】【分析】（1）在Rt △ADF 中，可得DE=AE=EF ，在Rt △ABF 中，可得BE=EF=EA ，得证ED=EB ；然后利用等腰三角形的性质以及四边形ADFB 的内角和为180°，可推导得出∠DEB=90°；（2）如下图，先证四边形MFBA 是平行四边形，再证△DCB ≌△DFM ，从而推导出△DMB 是等腰直角三角形，最后得出结论；（3）如下图，当点F 在AC 上时，CE 有最大值；当点F 在AC 延长线上时，CE 有最小值．【详解】（1）∵DF ⊥AC ，点E 是AF 的中点∴DE=AE=EF ，∠EDF=∠DFE∵∠ABC=90°，点E 是AF 的中点∴BE=AE=EF ，∠EFB=∠EBF∴DE=EB∵AB=BC ，∴∠DAB=45°∴在四边形ABFD中，∠DFB=360°－90°－45°－90°=135°∠DEB=∠DEF+∠FEB=180°－2∠EFD+180°－2∠EFB=360°－2(∠EFD+∠EFB)=360°－2×135°=90°∴DE⊥EB（2）如下图，延长BE至点M处，使得ME=EB，连接MA、ME、MF、MD、FB、DB，延长MF交CB于点H∵ME=EB，点E是AF的中点∴四边形MFBA是平行四边形∴MF∥AB，MF=AB∴∠MHB=180°－∠ABC=90°∵∠DCA=∠FCB=a∴∠DCB=45°+a，∠CFH=90°－a∵∠DCF=45°，∠CDF=90°∴∠DFC=45°，△DCF是等腰直角三角形∴∠DFM=180°－∠DFC－∠CFH=45°+a∴∠DCB=∠DFM∵△ABC和△CDF都是等腰直角三角形∴DC=DF，BC=AB=MF∴△DCB≌△DFM(SAS)∴∠MDF=∠BDC，DB=DM∴∠MDF+∠FDB=∠BDC+∠FDB=90°∴△DMB是等腰直角三角形∵点E是MB的中点∴DE=EB，DE⊥EB（3）当点F在AC上时，CF有最大值，图形如下：∵BC=6，∴在等腰直角△ABC中，AC=62∵CF=32，∴AF=32∴CE=CF+FE=CF+12AF922=当点F在AC延长线上时，CE有最小值，图形如下：同理，CE=EF－CF322 =【点睛】本题考查三角形的旋转变换，用到了等腰直角三角形的性质和平行四边形的性质，解题关键是构造并证明△BDM是等腰直角三角形．2．在△AOB中，C，D分别是OA，OB边上的点，将△OCD绕点O顺时针旋转到△OC′D′．（1）如图1，若∠AOB=90°，OA=OB，C，D分别为OA，OB的中点，证明：①AC′=BD′；②AC′⊥BD′；（2）如图2，若△AOB为任意三角形且∠AOB=θ，CD∥AB，AC′与BD′交于点E，猜想∠AEB=θ是否成立？请说明理由．【答案】（1）证明见解析；（2）成立，理由见解析【解析】试题分析：（1）①由旋转的性质得出OC=OC′，OD=OD′，∠AOC′=∠BOD′，证出OC′=OD′，由SAS证明△AOC′≌△BOD′，得出对应边相等即可；②由全等三角形的性质得出∠OAC′=∠OBD′，又由对顶角相等和三角形内角和定理得出∠BEA=90°，即可得出结论；（2）由旋转的性质得出OC=OC′，OD=OD′，∠AOC′=∠BOD′，由平行线得出比例式，得出，证明△AOC′∽△BOD′，得出∠OAC′=∠OBD′再由对顶角相等和三角形内角和定理即可得出∠AEB=θ．试题解析：（1）证明：①∵△OCD旋转到△OC′D′，∴OC=OC′，OD=OD′，∠AOC′=∠BOD′，∵OA=OB，C、D为OA、OB的中点，∴OC=OD，∴OC′=OD′，在△AOC′和△BOD′中，，∴△AOC′≌△BOD′（SAS），∴AC′=BD′；②延长AC′交BD′于E，交BO于F，如图1所示：∵△AOC′≌△BOD′，∴∠OAC′=∠OBD′，又∠AFO=∠BFE，∠OAC′+∠AFO=90°，∴∠OBD′+∠BFE=90°，∴∠BEA=90°，∴AC′⊥BD′；（2）解：∠AEB=θ成立，理由如下：如图2所示：∵△OCD旋转到△OC′D′，∴OC=OC′，OD=OD′，∠AOC′=∠BOD′，∵CD∥AB，∴，∴，∴，又∠AOC′=∠BOD′，∴△AOC′∽△BOD′，∴∠OAC′=∠OBD′，又∠AFO=∠BFE，∴∠AEB=∠AOB=θ．考点：相似三角形的判定与性质；全等三角形的判定与性质；旋转的性质．3．在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°.(1)将△ADF绕着点A顺时针旋转90°，得到△ABG(如图①)，求证：△AEG≌△AEF；(2)若直线EF与AB，AD的延长线分别交于点M，N(如图②)，求证：EF2=ME2+NF2；(3)将正方形改为长与宽不相等的矩形，若其余条件不变(如图③)，请你直接写出线段EF，BE，DF之间的数量关系.【答案】（1）证明见解析；（2）证明见解析；（3）EF2=2BE2+2DF2.【解析】试题分析：（1）根据旋转的性质可知AF=AG，∠EAF=∠GAE=45°，故可证△AEG≌△AEF；（2）将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．由（1）知△AEG≌△AEF，则EG=EF．再由△BME、△DNF、△CEF均为等腰直角三角形，得出CE=CF，BE=BM，NF=DF，然后证明∠GME=90°，MG=NF，利用勾股定理得出EG2=ME2+MG2，等量代换即可证明EF2=ME2+NF2；（3）将△ADF绕着点A顺时针旋转90°，得到△ABG，根据旋转的性质可以得到△ADF≌△ABG，则DF=BG，再证明△AEG≌△AEF，得出EG=EF，由EG=BG+BE，等量代换得到EF=BE+DF．试题解析：（1）∵△ADF绕着点A顺时针旋转90°，得到△ABG，∴AF=AG，∠FAG=90°，∵∠EAF=45°，∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）设正方形ABCD的边长为a．将△ADF绕着点A顺时针旋转90°，得到△ABG，连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2考点：四边形综合题4．阅读材料：小胖同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的顶角的顶点，并把它们的底角顶点连接起来则形成一组旋转全等的三角形．小胖把具有这个规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，小胖发现若∠BAC＝∠DAE，AB＝AC，AD＝AE，则BD＝CE,(1)在图1中证明小胖的发现；借助小胖同学总结规律，构造“手拉手”图形来解答下面的问题：(2)如图2，AB＝BC，∠ABC＝∠BDC＝60°，求证：AD+CD＝BD；(3)如图3，在△ABC中，AB＝AC，∠BAC＝m°，点E为△ABC外一点，点D为BC中点，∠EBC＝∠ACF，ED⊥FD，求∠EAF的度数（用含有m的式子表示）．【答案】（1）证明见解析；（2）证明见解析；（3）∠EAF =12 m°.【解析】分析：（1）如图1中，欲证明BD=EC，只要证明△DAB≌△EAC即可；（2）如图2中，延长DC到E，使得DB=DE．首先证明△BDE是等边三角形，再证明△ABD≌△CBE即可解决问题；（3）如图3中，将AE绕点E逆时针旋转m°得到AG，连接CG、EG、EF、FG，延长ED到M，使得DM=DE，连接FM、CM．想办法证明△AFE≌△AFG，可得∠EAF=∠FAG=12m°.详（1）证明：如图1中，∵∠BAC=∠DAE，∴∠DAB=∠EAC，在△DAB和△EAC中，AD AEDAB EACAB AC⎧⎪∠∠⎨⎪⎩＝＝＝，∴△DAB≌△EAC，∴BD=EC．（2）证明：如图2中，延长DC到E，使得DB=DE．∵DB=DE，∠BDC=60°，∴△BDE是等边三角形，∴∠BD=BE，∠DBE=∠ABC=60°，∴∠ABD=∠CBE，∵AB=BC，∴△ABD≌△CBE，∴AD=EC，∴BD=DE=DC+CE=DC+AD．∴AD+CD=BD．（3）如图3中，将AE绕点E逆时针旋转m°得到AG，连接CG、EG、EF、FG，延长ED到M，使得DM=DE，连接FM、CM．由（1）可知△EAB≌△GAC，∴∠1=∠2，BE=CG，∵BD=DC，∠BDE=∠CDM，DE=DM，∴△EDB≌△MDC，∴EM=CM=CG，∠EBC=∠MCD，∵∠EBC=∠ACF，∴∠MCD=∠ACF，∴∠FCM=∠ACB=∠ABC，∴∠1=3=∠2，∴∠FCG=∠ACB=∠MCF，∵CF=CF，CG=CM，∴△CFG≌△CFM，∴FG=FM，∵ED=DM，DF⊥EM，∴FE=FM=FG，∵AE=AG，AF=AF，∴△AFE≌△AFG，∴∠EAF=∠FAG=12 m°．点睛：本题考查几何变换综合题、旋转变换、等腰三角形的性质、全等三角形的判定和性质等知识，解题的关键是学会利用“手拉手”图形中的全等三角形解决问题，学会构造“手拉手”模型，解决实际问题，属于中考压轴题．5．已知，如图：正方形ABCD，将Rt△EFG斜边EG的中点与点A重合，直角顶点F落在正方形的AB边上，Rt△EFG的两直角边分别交AB、AD边于P、Q两点，（点P与点F重合），如图1所示：（1）求证：EP2+GQ2=PQ2；（2）若将Rt△EFG绕着点A逆时针旋转α（0°＜α≤90°），两直角边分别交AB、AD边于P、Q两点，如图2所示：判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系？若存在，证明你的结论．若不存在，请说明理由；（3）若将Rt△EFG绕着点A逆时针旋转α（90°＜α＜180°），两直角边所在的直线分别交BA、AD两边延长线于P、Q两点，并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系？按题意完善图3，请直接写出你的结论（不用证明）．【答案】（1）见解析；（2）PF2+FQ2=EP2+GQ2；（3）四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2．【解析】【分析】（1）过点E作EH∥FG，由此可证△EAH≌△GAQ，然后根据全等三角形的性质得到EH=QG，又PQ=PH，在Rt△EPH中，EP2+EH2=PH2，由此可以得到EP2+GQ2=PQ2；（2）过点E作EH∥FG，交DA的延长线于点H，连接PQ、PH，由此可证△EAH≌△GAQ，然后根据全等三角形的性质得到EH=QG，又PH=PQ，在Rt△EPH中，EP2+EH2=PH2，即EP2+GQ2=PH2，在Rt△PFQ中，PF2+FQ2=PQ2，故PF2+FQ2=EP2+GQ2；（3）四条线段EP、PF、FQ、QG之间的关系为PE2+GQ2=PF2+FQ2，证明方法同上．【详解】（1）过点E作EH∥FG，连接AH、FH，如图所示：∵EA=AG，∠HEA=∠AGQ，∠HAE=∠GAD，∴△EAH≌△GAQ，∴EH=QG，HA=AQ，∵FA⊥AD，∴PQ=PH．在Rt△EPH中，∵EP2+EH2=PH2，∴EP2+GQ2=PQ2；（2）过点E作EH∥FG，交DA的延长线于点H，连接PQ、PH，∵EA=AG，∠HEA=∠AGQ，∠HAE=∠GAD，∴△EAH≌△GAQ，∴EH=QG，HA=AQ，∵PA⊥AD，∴PQ=PH．在Rt△EPH中，∵EP2+EH2=PH2，∴EP2+GQ2=PH2．在Rt△PFQ中，∵PF2+FQ2=PQ2，∴PF2+FQ2=EP2+GQ2．（3）四条线段EP、PF、FQ、QG之间的关系为PF2+GQ2=PE2+FQ2．【点睛】本题主要考查了旋转的性质，全等三角形的判定与性质，三线合一，勾股定理，正确作出辅助线是解答本题的关键.6．两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．（1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为______和位置关系为______；（2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；（3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？直接写出结论，不用证明．【答案】（1）相等，垂直．（2）成立，证明见解析；（3）成立，结论是FH=FG，FH⊥FG．【解析】试题分析：（1）证AD=BE，根据三角形的中位线推出FH=12AD，FH∥AD，FG=12BE，FG∥BE，即可推出答案；（2）证△ACD≌△BCE，推出AD=BE，根据三角形的中位线定理即可推出答案；（3）连接BE、AD，根据全等推出AD=BE，根据三角形的中位线定理即可推出答案．试题解析：（1）解：∵CE=CD，AC=BC，∠ECA=∠DCB=90°，∴BE=AD，∵F是DE的中点，H是AE的中点，G是BD的中点，∴FH=12AD，FH∥AD，FG=12BE，FG∥BE，∴FH=FG，∵AD⊥BE，∴FH⊥FG，故答案为相等，垂直．（2）答：成立，证明：∵CE=CD，∠ECD=∠ACD=90°，AC=BC，∴△ACD≌△BCE∴AD=BE，由（1）知：FH=12AD，FH∥AD，FG=12BE，FG∥BE，∴FH=FG，FH⊥FG，∴（1）中的猜想还成立．（3）答：成立，结论是FH=FG ，FH ⊥FG ．连接AD ，BE ，两线交于Z ，AD 交BC 于X ，同（1）可证∴FH=12AD ，FH ∥AD ，FG=12BE ，FG ∥BE ， ∵三角形ECD 、ACB 是等腰直角三角形， ∴CE=CD ，AC=BC ，∠ECD=∠ACB=90°， ∴∠ACD=∠BCE ，在△ACD 和△BCE 中AC BC ACD BCE CE CD ⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△ACD ≌△BCE ， ∴AD=BE ，∠EBC=∠DAC ，∵∠DAC+∠CXA=90°，∠CXA=∠DXB ， ∴∠DXB+∠EBC=90°， ∴∠EZA=180°﹣90°=90°，即AD ⊥BE ， ∵FH ∥AD ，FG ∥BE ， ∴FH ⊥FG ，即FH=FG ，FH ⊥FG ，结论是FH=FG ，FH ⊥FG.【点睛】运用了等腰直角三角形的性质、全等三角形的性质和判定、三角形的中位线定理，旋转的性质等知识点的理解和掌握，能熟练地运用这些性质进行推理是解此题的关键．7．在矩形ABCD 中，2AB =，1BC =，以点A 为旋转中心，逆时针旋转矩形ABCD ，旋转角为(0180)αα<<，得到矩形AEFG ，点B 、点C 、点D 的对应点分别为点E 、点F 、点G ．()1如图①，当点E 落在DC 边上时，直写出线段EC 的长度为______；()2如图②，当点E 落在线段CF 上时，AE 与DC 相交于点H ，连接AC ，①求证：ACD ≌CAE ； ②直接写出线段DH 的长度为______．()3如图③设点P 为边FG 的中点，连接PB ，PE ，在矩形ABCD 旋转过程中，BEP 的面积是否存在最大值？若存在请直接写出这个最大值；若不存在请说明理由．【答案】（1）23；（2）①见解析；34②；（3）存在，PBE 的面积的最大值为21，理由见解析【解析】【分析】()1如图①中，在Rt ADE 中，利用勾股定理即可解决问题； ()2①证明：如图②中，根据HL 即可证明ACD ≌CAE ；②如图②中，由ACD ≌CAE ，推出ACD CAE ∠∠=，推出AH HC =，设AH HC m ==，在Rt ADH 中，根据222AD DH AH +=，构建方程即可解决问题； ()3存在.如图③中，连接PA ，作BM PE ⊥交PE 的延长线于M.由题意：PF PC 1==，由AG EF 1==，G F 90∠∠==，推出PA PE 2==PBE12SPE BM 22=⋅⋅=，推出当BM 的值最大时，PBE 的面积最大，求出BM 的最大值即可解决问题；【详解】()1四边形ABCD 是矩形，AB CD 2∴==，BC AD 1==，D 90∠=，矩形AEFG 是由矩形ABCD 旋转得到，AE AB 2∴==，在Rt ADE 中，22DE 213=-=CE 23∴=，故答案为23．()2①当点E 落在线段CF 上，AEC ADC 90∠∠∴==，在Rt ADC 和Rt AEC 中，{AC CACD AE ==，Rt ACD ∴≌()Rt CAE HL ；ACD ②≌CAE ，ACD CAE ∠∠∴=，AH HC ∴=，设AH HC m ==，在Rt ADH 中，222AD DH AH +=，2221(2m)m ∴+-=，5m 4∴=， 53DH 244∴=-=，故答案为34； ()3存在．理由如下：如图③中，连接PA ，作BM PE ⊥交PE 的延长线于M ，由题意：PF PC 1==，AG EF 1==，G F 90∠∠==， PA PE 2∴==PBE12SPE BM 2∴=⋅⋅=， ∴当BM 的值最大时，PBE 的面积最大，BM PB ≤，PB AB PA ≤+，PB 22∴≤， BM 22∴≤∴的最大值为22BM+，PBE∴的面积的最大值为21+．【点睛】本题是四边形综合题，考查了矩形的性质，旋转变换，全等三角形的判定和性质，勾股定理，三角形的面积，三角形的三边关系等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．8．如图1，点O是正方形ABCD两对角线的交点. 分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．(1)求证：DE⊥AG；(2)正方形ABCD固定，将正方形OEFG绕点O逆时针旋转角(0°< <360°)得到正方形，如图2．①在旋转过程中，当∠是直角时，求的度数；(注明：当直角边为斜边一半时，这条直角边所对的锐角为30度)②若正方形ABCD的边长为1，在旋转过程中，求长的最大值和此时的度数，直接写出结果不必说明理由．【答案】（1）DE⊥AG （2）①当∠为直角时，α=30°或150°.②315°【解析】分析：（1）延长ED交AG于点H，证明≌，根据等量代换证明结论；（2）根据题意和锐角正弦的概念以及特殊角的三角函数值得到，分两种情况求出的度数；（3）根据正方形的性质分别求出OA和OF的长，根据旋转变换的性质求出AF′长的最大值和此时的度数．详解：如图1，延长ED交AG于点H，点O是正方形ABCD两对角线的交点，，，在和中，，≌，，，，，即；在旋转过程中，成为直角有两种情况：Ⅰ由增大到过程中，当时，，在中，sin∠AGO=，，，，，即；Ⅱ由增大到过程中，当时，同理可求，．综上所述，当时，或．如图3，当旋转到A、O、在一条直线上时，的长最大，正方形ABCD的边长为1，，，，，，，此时．点睛：考查了正方形的性质，全等三角形的判定与性质，锐角三角形函数，旋转变换的性质的综合应用，有一定的综合性，注意分类讨论的思想.二、初三数学圆易错题压轴题（难）9．如图①，已知Rt△ABC中，∠ACB＝90°，AC＝8，AB＝10，点D是AC边上一点（不与C 重合），以AD为直径作⊙O，过C作CE切⊙O于E，交AB于F．（1）若⊙O半径为2，求线段CE的长；（2）若AF＝BF，求⊙O的半径；（3）如图②，若CE＝CB，点B关于AC的对称点为点G，试求G、E两点之间的距离．【答案】（1）CE＝2；（2）⊙O的半径为3；（3）G、E两点之间的距离为9.6【解析】【分析】（1）根据切线的性质得出∠OEC=90°，然后根据勾股定理即可求得；（2）由勾股定理求得BC ，然后通过证得△OEC ∽△BCA ，得到OE OC BC BA =，即8610r r-= 解得即可；（3）证得D 和M 重合，E 和F 重合后，通过证得△GBE ∽△ABC ，GB GEAB AC=，即12108GE =，解得即可. 【详解】解：（1）如图①，连接OE ，∵CE 切⊙O 于E ， ∴∠OEC ＝90°，∵AC ＝8，⊙O 的半径为2， ∴OC ＝6，OE ＝2，∴CE ＝2242OC OE -= ；（2）设⊙O 的半径为r ，在Rt △ABC 中，∠ACB ＝90°，AB ＝10，AC ＝8， ∴BC 22AB A C -＝6， ∵AF ＝BF ， ∴AF ＝CF ＝BF ， ∴∠ACF ＝∠CAF ， ∵CE 切⊙O 于E ， ∴∠OEC ＝90°， ∴∠OEC ＝∠ACB ， ∴△OEC ∽△BCA ， ∴OE OC BC BA =，即8610r r-= 解得r ＝3， ∴⊙O 的半径为3；（3）如图②，连接BG ，OE ，设EG 交AC 于点M ，由对称性可知，CB＝CG，∵CE＝CG，∴∠EGC＝∠GEC，∵CE切⊙O于E，∴∠GEC+∠OEG＝90°，∵∠EGC+∠GMC＝90°，∴∠OEG＝∠GMC，∵∠GMC＝∠OME，∴∠OEG＝∠OME，∴OM＝OE，∴点M和点D重合，∴G、D、E三点在同一直线上，连接AE、BE，∵AD是直径，∴∠AED＝90°，即∠AEG＝90°，又CE＝CB＝CG，∴∠BEG＝90°，∴∠AEB＝∠AEG+∠BEG＝180°，∴A、E、B三点在同一条直线上，∴E、F两点重合，∵∠GEB＝∠ACB＝90°，∠B＝∠B，∴△GBE∽△ABC，∴GB GEAB AC=，即12108GE=∴GE＝9.6，故G、E两点之间的距离为9.6．【点睛】本题考查了切线的判定，轴的性质，勾股定理的应用以及三角形相似的判定和性质，证得G、D、E三点共线以及A、E、B三点在同一条直线上是解题的关10．在直角坐标系中，⊙C过原点O，交x轴于点A（2，0），交y轴于点B（0，）．（1）求圆心C的坐标．（2）抛物线y=ax2+bx+c过O，A两点，且顶点在正比例函数y=-的图象上，求抛物线的解析式．（3）过圆心C作平行于x轴的直线DE，交⊙C于D，E两点，试判断D，E两点是否在（2）中的抛物线上．（4）若（2）中的抛物线上存在点P（x0，y0），满足∠APB为钝角，求x0的取值范围．【答案】（1）圆心C的坐标为（1，）；（2）抛物线的解析式为y=x2﹣x；（3）点D、E均在抛物线上；（4）﹣1＜x0＜0，或2＜x0＜3．【解析】试题分析：（1）如图线段AB是圆C的直径，因为点A、B的坐标已知，根据平行线的性质即可求得点C的坐标；（2）因为抛物线过点A、O，所以可求得对称轴，即可求得与直线y=﹣x的交点，即是二次函数的顶点坐标，利用顶点式或者一般式，采用待定系数法即可求得抛物线的解析式；（3）因为DE∥x轴，且过点C，所以可得D、E的纵坐标为，求得直径AB的长，可得D、E的横坐标，代入解析式即可判断；（4）因为AB为直径，所以当抛物线上的点P在⊙C的内部时，满足∠APB为钝角，所以﹣1＜x0＜0，或2＜x0＜3．试题分析：（1）∵⊙C经过原点O∴AB为⊙C的直径∴C为AB的中点过点C作CH垂直x轴于点H，则有CH=OB=，OH=OA=1∴圆心C的坐标为（1，）．（2）∵抛物线过O、A两点，∴抛物线的对称轴为x=1，∵抛物线的顶点在直线y=﹣x上，∴顶点坐标为（1，﹣）．把这三点的坐标代入抛物线y=ax2+bx+c，得，解得，∴抛物线的解析式为y=x2﹣x．（3）∵OA=2，OB=2，∴AB==4，即⊙C的半径r=2，∴D（3，），E（﹣1，），代入y=x2﹣x检验，知点D、E均在抛物线上．（4）∵AB为直径，∴当抛物线上的点P在⊙C的内部时，满足∠APB为钝角，∴﹣1＜x0＜0，或2＜x0＜3．考点：二次函数综合题．11．如图，在平面直角坐标系中，O为坐标原点，△ABC的边BC在y轴的正半轴上，点A在x 轴的正半轴上，点C的坐标为（0，8），将△ABC沿直线AB折叠，点C落在x轴的负半轴D（−4，0）处．（1）求直线AB的解析式；（2）点P从点A出发以每秒45个单位长度的速度沿射线AB方向运动，过点P作PQ⊥AB，交x轴于点Q，PR∥AC交x轴于点R，设点P运动时间为t（秒），线段QR长为d，求d与t的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，点N是射线AB上一点，以点N为圆心，同时经过R、Q两点作⊙N，⊙N交y轴于点E，F．是否存在t，使得EF=RQ？若存在，求出t的值，并求出圆心N的坐标；若不存在，说明理由．【答案】（1）132y x=-+（2）d=5t （3）故当 t=85，或815，时，QR=EF，N（-6，6）或（2，2）．【解析】试题分析：（1）由C（0，8），D （-4，0），可求得OC ，OD 的长，然后设OB=a ，则BC=8-a ，在Rt △BOD 中，由勾股定理可得方程：（8-a ）2=a 2+42,解此方程即可求得B 的坐标，然后由三角函数的求得点A 的坐标，再利用待定系数法求得直线AB 的解析式；（2）在Rt △AOB 中，由勾股定理可求得AB 的长，继而求得∠BAO 的正切与余弦，由PR//AC 与折叠的性质，易证得RQ=AR ，则可求得d 与t 的函数关系式；（3）首先过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ，易证得四边形NTOS 是正方形，然后分别从点N 在第二象限与点N 在第一象限去分析求解即可求解;试题解析：（1）∵C （0，8），D （-4，0），∴OC=8，OD=4，设OB=a ，则BC=8-a ，由折叠的性质可得：BD=BC=8-a ，在Rt △BOD 中，∠BOD=90°，DB 2=OB 2+OD 2，则（8-a ）2=a 2+42，解得：a=3，则OB=3，则B （0，3），tan ∠ODB=34OB OD = ，在Rt △AOC 中，∠AOC=90°，tan ∠ACB=34OA OC = ，则OA=6，则A （6，0），设直线AB 的解析式为：y=kx+b ，则60{3k b b +== ，解得：1{23k b =-= ，故直线AB 的解析式为：y=-12x +3；（2）如图所示：在Rt △AOB 中，∠AOB=90°，OB=3，OA=6，则AB=22135,tan 2OB OB OA BAO OA +=∠== ，255OA cos BAO AB∠==，在Rt △PQA 中，9045APQ AP t ∠=︒=，，则AQ=10cos AP t BAO=∠ , ∵PR ∥AC ，∴∠APR=∠CAB ，由折叠的性质得：∠BAO=∠CAB ，∴∠BAO=∠APR ，∴PR=AR ，∵∠RAP+∠PQA=∠APR+∠QPR=90°，∴∠PQA=∠QPR ，∴RP=RQ ，∴RQ=AR ，∴QR=12AQ=5t, 即d=5t; （3）过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ，∵EF=QR ，∴NS=NT ，∴四边形NTOS 是正方形，则TQ=TR=1522QR t = ， ∴1115151022224NT AT AQ TQ t t t ==-=-=（）（），分两种情况，若点N 在第二象限，则设N （n ，-n ），点N 在直线132y x =-+ 上，则132n n -=-+ ，解得：n=-6，故N （-6，6），NT=6，即1564t = ，解得：85t = ; 若点N 在第一象限，设N （N ，N ），可得：132n n =-+ , 解得：n=2，故N （2，2），NT=2，即1524t =, 解得：t=815∴当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）。

重庆市南开中学2024届中考数学考试模拟冲刺卷含解析

重庆市南开中学2024届中考数学考试模拟冲刺卷注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．下列计算正确的是（）A．（a2）3＝a6B．a2•a3＝a6C．a3+a4＝a7D．（ab）3＝ab32．在一个不透明的袋子中装有除颜色外其余均相同的m个小球，其中5 个黑球，从袋中随机摸出一球，记下其颜色，这称为依次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球．以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：摸球试验次数100 1000 5000 10000 50000 100000摸出黑球次数46 487 2506 5008 24996 50007根据列表，可以估计出m 的值是（）A．5 B．10 C．15 D．203．已知反比例函数y＝﹣6x，当﹣3＜x＜﹣2时，y的取值范围是（）A．0＜y＜1 B．1＜y＜2 C．2＜y＜3 D．﹣3＜y＜﹣24．等腰三角形两边长分别是2 cm和5 cm，则这个三角形周长是（）A．9 cm B．12 cm C．9 cm或12 cm D．14 cm5．如图，AB∥CD，点E在线段BC上，若∠1＝40°，∠2＝30°，则∠3的度数是()A．70°B．60°C．55°D．50°6．如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )A．该班总人数为50 B．步行人数为30C．乘车人数是骑车人数的2.5倍D．骑车人数占20%7．如图是二次函数y =ax2+bx + c(a≠0)图象如图所示，则下列结论，①c<0，②2a + b=0；③a+b+c=0，④b2–4ac<0，其中正确的有( )A．1个B．2个C．3个D．48．下列计算正确的是()A．a2•a3＝a6B．(a2)3＝a6C．a2+a2＝a3D．a6÷a2＝a39．如图，一次函数y1＝x与二次函数y2＝ax2＋bx＋c图象相交于P、Q两点，则函数y＝ax2＋（b－1）x＋c的图象可能是（）A． B．C．D．10．已知点A为某封闭图形边界上一定点，动点P从点A出发，沿其边界顺时针匀速运动一周．设点P运动的时间为x，线段AP的长为y．表示y与x的函数关系的图象大致如右图所示，则该封闭图形可能是( )A ．B ．C ．D ．11．如图，在平面直角坐标系中，已知点A （―3，6）、B （―9，一3），以原点O 为位似中心，相似比为，把△ABO 缩小，则点A 的对应点A′的坐标是（）A ．（―1，2）B ．（―9，18）C ．（―9，18）或（9，―18）D ．（―1，2）或（1，―2）12．如图，在6×4的正方形网格中，△ABC 的顶点均为格点，则sin ∠ACB=（） A ．12B ．2C ．255D ．134二、填空题：（本大题共6个小题，每小题4分，共24分．） 13．如图，O 的半径为3，点A ，B ，C ，D 都在O 上，30AOB ∠=︒，将扇形AOB 绕点O 顺时针旋转120︒后恰好与扇形COD 重合，则AD 的长为_____．（结果保留π）14．如图，在等腰Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，BC ＝2，点D 是AC 边上一动点，连接BD ，以AD 为直径的圆交BD 于点E ，则线段CE 长度的最小值为___．15．如图，E 是▱ABCD 的边AD 上一点，AE=ED ，CE 与BD 相交于点F ，BD=10，那么DF=__．16．如图，在Rt ABC 中，CM 平分ACB ∠交AB 于点M ，过点M 作MN //BC 交AC 于点N ，且MN 平分AMC ∠，若AN 1=，则BC 的长为______．17．在一个不透明的口袋中装有4个红球和若干个白球，它们除颜色外其他完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有_____个.18．已知正方形ABCD ，AB ＝1，分别以点A 、C 为圆心画圆，如果点B 在圆A 外，且圆A 与圆C 外切，那么圆C 的半径长r 的取值范围是_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）如图，已知矩形 OABC 的顶点A 、C 分别在 x 轴的正半轴上与y 轴的负半轴上，二次函数228255y x x =--的图像经过点B 和点C ．（1）求点 A 的坐标；（2）结合函数的图象，求当 y<0 时，x 的取值范围．20．（6分）二次函数y=ax 2+bx+c （a ，b ，c 为常数，且a ≠1）中的x 与y 的部分对应值如表x ﹣1 1 1 3y ﹣1 3 5 3下列结论：①ac＜1；②当x＞1时，y的值随x值的增大而减小．③3是方程ax2+（b﹣1）x+c=1的一个根；④当﹣1＜x＜3时，ax2+（b﹣1）x+c＞1．其中正确的结论是．21．（6分）石狮泰禾某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“十一”国庆节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价1元，那么平均可多售出2件．设每件童装降价x元时，每天可销售______ 件，每件盈利______ 元；（用x的代数式表示）每件童装降价多少元时，平均每天赢利1200元．要想平均每天赢利2000元，可能吗？请说明理由．22．（8分）如图，⊙O的直径DF与弦AB交于点E，C为⊙O外一点，CB⊥AB，G是直线CD上一点，∠ADG＝∠ABD．求证：AD•CE＝DE•DF；说明：(1)如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来(要求至少写3步)；(2)在你经历说明(1)的过程之后，可以从下列①、②、③中选取一个补充或更换已知条件，完成你的证明．①∠CDB＝∠CEB；②AD∥EC；③∠DEC＝∠ADF，且∠CDE＝90°．23．（8分）如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．证明：DE为⊙O的切线；连接OE，若BC＝4，求△OEC的面积．24．（10分）某工厂生产部门为了解本部门工人的生产能力情况，进行了抽样调查．该部门随机抽取了30名工人某天每人加工零件的个数，数据如下：20 21 19 16 27 18 31 29 21 22 25 20 19 22 35 33 19 17 18 29 18 35 22 15 18 18 31 31 19 22 整理上面数据，得到条形统计图：样本数据的平均数、众数、中位数如下表所示：统计量平均数众数中位数数值23m21根据以上信息，解答下列问题：上表中众数m 的值为；为调动工人的积极性，该部门根据工人每天加工零件的个数制定了奖励标准，凡达到或超过这个标准的工人将获得奖励．如果想让一半左右的工人能获奖，应根据来确定奖励标准比较合适．（填“平均数”、“众数”或“中位数”）该部门规定：每天加工零件的个数达到或超过25个的工人为生产能手．若该部门有300名工人，试估计该部门生产能手的人数． 25．（10分）先化简，再求值：（1﹣11a +）÷221aa -，其中a=﹣1．26．（12分）在第23个世界读书日前夕，我市某中学为了解本校学生的每周课外阅读时间(用t 表示，单位：小时)，采用随机抽样的方法进行问卷调查，调查结果按0t 2≤<，2t 3≤<，3t 4≤<，t 4≥分为四个等级，并依次用A ，B，C，D表示，根据调查结果统计的数据，绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：（）求本次调查的学生人数；1（）求扇形统计图中等级B所在扇形的圆心角度数，并把条形统计图补充完整；2（）若该校共有学生1200人，试估计每周课外阅读时间满足3t4≤<的人数．327．（12分）如图，AB是⊙O的直径，∠BAC=90°，四边形EBOC是平行四边形，EB交⊙O于点D，连接CD并延长交AB的延长线于点F．（1）求证：CF是⊙O的切线；（2）若∠F=30°，EB=6，求图中阴影部分的面积．（结果保留根号和π）参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1、A【解题分析】分析：根据幂的乘方、同底数幂的乘法、积的乘方公式即可得出答案．详解：A、幂的乘方法则，底数不变，指数相乘，原式计算正确；B、同底数幂的乘法，底数不变，指数相加，原式=5a，故错误；C、不是同类项，无法进行加法计算；D、积的乘方等于乘方的积，原式=33a b，计算错误；故选A．点睛：本题主要考查的是幂的乘方、同底数幂的乘法、积的乘方计算法则，属于基础题型．理解各种计算法则是解题的关键．2、B【解题分析】由概率公式可知摸出黑球的概率为，分析表格数据可知的值总是在0.5左右，据此可求解m值.【题目详解】解：分析表格数据可知的值总是在0.5左右，则由题意可得，解得m=10,故选择B.【题目点拨】本题考查了概率公式的应用.3、C【解题分析】分析：由题意易得当﹣3＜x＜﹣2时，函数6yx=-的图象位于第二象限，且y随x的增大而增大，再计算出当x=-3和x=-2时对应的函数值，即可作出判断了. 详解：∵在6yx=-中，﹣6＜0，∴当﹣3＜x＜﹣2时函数6yx=-的图象位于第二象限内，且y随x的增大而增大，∵当x=﹣3时，y=2，当x=﹣2时，y=3，∴当﹣3＜x＜﹣2时，2＜y＜3，故选C．点睛：熟悉“反比例函数的图象和性质”是正确解答本题的关键.4、B【解题分析】当腰长是2 cm时，因为2+2<5，不符合三角形的三边关系，排除；当腰长是5 cm时，因为5+5>2，符合三角形三边关系，此时周长是12 cm．故选B．5、A【解题分析】试题分析：∵AB ∥CD ，∠1=40°，∠1=30°，∴∠C=40°．∵∠3是△CDE 的外角，∴∠3=∠C+∠2=40°+30°=70°．故选A ．考点：平行线的性质． 6、B 【解题分析】根据乘车人数是25人，而乘车人数所占的比例是50%，即可求得总人数，然后根据百分比的含义即可求得步行的人数，以及骑车人数所占的比例．【题目详解】A 、总人数是：25÷50%=50（人），故A 正确；B 、步行的人数是：50×30%=15（人），故B 错误；C 、乘车人数是骑车人数倍数是：50%÷20%=2.5，故C 正确；D 、骑车人数所占的比例是：1-50%-30%=20%，故D 正确．由于该题选择错误的，故选B ．【题目点拨】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题． 7、B 【解题分析】由抛物线的开口方向判断a 与1的关系，由抛物线与y 轴的交点判断c 与1的关系，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【题目详解】①抛物线与y 轴交于负半轴，则c ＜1，故①正确； ②对称轴x 2ba=-=1，则2a +b =1．故②正确； ③由图可知：当x =1时，y =a +b +c ＜1．故③错误；④由图可知：抛物线与x 轴有两个不同的交点，则b 2﹣4ac ＞1．故④错误．综上所述：正确的结论有2个．故选B ．【题目点拨】本题考查了图象与二次函数系数之间的关系，会利用对称轴的值求2a 与b 的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用． 8、B 【解题分析】试题解析：A.235,a a a ⋅=故错误. B.正确.C.不是同类项，不能合并，故错误.D.624.a a a ÷= 故选B.点睛：同底数幂相乘，底数不变,指数相加. 同底数幂相除，底数不变,指数相减. 9、A 【解题分析】由一次函数y 1=x 与二次函数y 2=ax 2+bx+c 图象相交于P 、Q 两点，得出方程ax 2+（b-1）x+c=0有两个不相等的根，进而得出函数y=ax 2+（b-1）x+c 与x 轴有两个交点，根据方程根与系数的关系得出函数y=ax 2+（b-1）x+c 的对称轴x=-12b a-＞0，即可进行判断．【题目详解】点P 在抛物线上，设点P （x ，ax 2+bx+c ），又因点P 在直线y=x 上， ∴x=ax 2+bx+c ， ∴ax 2+（b-1）x+c=0；由图象可知一次函数y=x 与二次函数y=ax 2+bx+c 交于第一象限的P 、Q 两点， ∴方程ax 2+（b-1）x+c=0有两个正实数根． ∴函数y=ax 2+（b-1）x+c 与x 轴有两个交点，又∵-2ba ＞0，a ＞0 ∴-12b a -=-2b a +12a＞0∴函数y=ax 2+（b-1）x+c 的对称轴x=-12b a-＞0， ∴A 符合条件，故选A ． 10、A 【解题分析】解：分析题中所给函数图像，O E-段，AP随x的增大而增大，长度与点P的运动时间成正比．E F-段，AP逐渐减小，到达最小值时又逐渐增大，排除C、D选项，F G-段，AP逐渐减小直至为0，排除B选项．故选A．【题目点拨】本题考查了动点问题的函数图象，函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．用图象解决问题时，要理清图象的含义即会识图．11、D【解题分析】试题分析：方法一：∵△ABO和△A′B′O关于原点位似，∴△ ABO∽△A′B′O且OA'OA＝13.∴A EAD'＝0E0D＝13.∴A′E＝13AD＝2，OE＝13OD＝1.∴A′（－1,2）.同理可得A′′（1,―2）.方法二：∵点A（―3，6）且相似比为13，∴点A的对应点A′的坐标是（―3×13，6×13），∴A′（－1,2）.∵点A′′和点A′（－1,2）关于原点O对称，∴A′′（1,―2）. 故答案选D.考点：位似变换.12、C【解题分析】如图，由图可知BD=2、CD=1、BC=5，根据sin ∠BCA=BD BC可得答案．【题目详解】解：如图所示，∵BD=2、CD=1，∴22BD CD +2221+5则sin ∠BCA=BD BC 525，故选C ．【题目点拨】本题主要考查解直角三角形，解题的关键是熟练掌握正弦函数的定义和勾股定理．二、填空题：（本大题共6个小题，每小题4分，共24分．）13、52π．【解题分析】根据题意先利用旋转的性质得到∠BOD=120°，则∠AOD=150°，然后根据弧长公式计算即可.【题目详解】解：∵扇形AOB 绕点O 顺时针旋转120°后恰好与扇形COD 重合，∴∠BOD=120°， ∴∠AOD=∠AOB+∠BOD=30°+120°=150°，∴AD 的长=150351802ππ⋅⋅=．故答案为:52π．【题目点拨】本题考查了弧长的计算及旋转的性质，掌握弧长公式l=180n R π⋅⋅（弧长为l ，圆心角度数为n ，圆的半径为R ）是解题的关键.14、5 2【解题分析】连结AE，如图1，先根据等腰直角三角形的性质得到AB=AC=4，再根据圆周角定理，由AD为直径得到∠AED=90°，接着由∠AEB=90°得到点E在以AB为直径的O上，于是当点O、E、C共线时，CE最小，如图2，在Rt△AOC中利用勾股定理计算出OC=25，从而得到CE的最小值为25﹣2.【题目详解】连结AE，如图1，∵∠BAC=90°,AB=AC,BC=42，∴AB=AC=4，∵AD为直径，∴∠AED=90°，∴∠AEB=90°，∴点E在以AB为直径的O上，∵O的半径为2，∴当点O、E. C共线时,CE最小,如图2在Rt△AOC中，∵OA=2，AC=4，∴2225+AC OA=∴52，即线段CE长度的最小值为5 2.故答案为5﹣2.【题目点拨】此题考查等腰直角三角形的性质，圆周角定理，勾股定理，解题关键在于结合实际运用圆的相关性质.15、4【解题分析】∵AE=ED，AE+ED=AD，∴ED=AD，∵四边形ABCD是平行四边形，∴AD=BC，AD//BC，∴△DEF∽△BCF，∴DF：BF=DE：BC=2：3，∵DF+BF=BD=10，∴DF=4，故答案为4.16、1【解题分析】根据题意，可以求得∠B的度数，然后根据解直角三角形的知识可以求得NC的长，从而可以求得BC的长．【题目详解】∵在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，∴∠AMN=∠NMC=∠B，∠NCM=∠BCM=∠NMC，∴∠ACB=2∠B，NM=NC，∴∠B=30°，∵AN=1，∴MN=2，∴AC=AN+NC=3，∴BC=1，故答案为1．【题目点拨】本题考查含30°角的直角三角形、平行线的性质、等腰三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．17、1.【解题分析】由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率，进而求出白球个数即可．【题目详解】设白球个数为：x个，∵摸到红色球的频率稳定在25%左右，∴口袋中得到红色球的概率为25%，∴=，解得：x=1，故白球的个数为1个．故答案为：1．【题目点拨】此题主要考查了利用频率估计概率，根据大量反复试验下频率稳定值即概率得出是解题关键．182﹣1＜r2．【解题分析】首先根据题意求得对角线AC的长，设圆A的半径为R，根据点B在圆A外，得出0＜R＜1，则-1＜-R＜0，再根据圆A与圆C外切可得2，利用不等式的性质即可求出r的取值范围．【题目详解】∵正方形ABCD中，AB=1，∴2，设圆A的半径为R，∵点B在圆A外，∴0＜R＜1，∴-1＜-R＜0，22-R2∵以A、C为圆心的两圆外切，2，∴22-R，2＜r22＜r2．【题目点拨】本题考查了圆与圆的位置关系，点与圆的位置关系，正方形的性质，勾股定理，不等式的性质．掌握位置关系与数量之间的关系是解题的关键．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19、（1）(40)，；（2）15x -<<【解题分析】（1）当0x =时，求出点C 的坐标，根据四边形OABC 为矩形，得出点B 的坐标，进而求出点A 即可；（2）先求出抛物线图象与x 轴的两个交点，结合图象即可得出．【题目详解】解：（1）当0x =时，函数228255y x x =--的值为-2， ∴点C 的坐标为(0,2)-∵四边形OABC 为矩形， ,2OA CB AB CO ∴=== 解方程2282255x x --=-，得120,4x x ==． ∴点B 的坐标为(4)2-，． ∴点A 的坐标为(40)，．（2）解方程2282055x x --=，得121,5x x =-=．由图象可知，当0y <时，x 的取值范围是15x -<<．【题目点拨】本题考查了二次函数与几何问题，以及二次函数与不等式问题，解题的关键是灵活运用几何知识，并熟悉二次函数的图象与性质．20、①③④．【解题分析】试题分析：∵x=﹣1时y=﹣1，x=1时，y=3，x=1时，y=5，∴a-b 1{35c c a b c +=-=++=，解得a 1{33c a =-==，∴y=﹣x 2+3x+3，∴ac=﹣1×3=﹣3＜1，故①正确；对称轴为直线332(1)2x =-=⨯-，所以，当x ＞32时，y 的值随x 值的增大而减小，故②错误；方程为﹣x 2+2x+3=1，整理得，x 2﹣2x ﹣3=1，解得x 1=﹣1，x 2=3，所以，3是方程ax 2+（b ﹣1）x+c=1的一个根，正确，故③正确；﹣1＜x ＜3时，ax 2+（b ﹣1）x+c ＞1正确，故④正确；综上所述，结论正确的是①③④．故答案为①③④．【考点】二次函数的性质．21、（1）（20+2x ），（40﹣x ）；（2）每件童装降价20元或10元，平均每天赢利1200元；（3）不可能做到平均每天盈利2000元．【解题分析】(1)、根据销售量=原销售量+因价格下降而增加的数量；每件利润=原售价－进价－降价，列式即可；(2)、根据总利润=单件利润×数量，列出方程即可；(3)、根据(2)中的相关关系方程，判断方程是否有实数根即可．【题目详解】(1)、设每件童装降价x 元时，每天可销售20+2x 件，每件盈利40-x 元，故答案为（20+2x ），（40-x ）；(2)、根据题意可得：(20+2x)(40－x)=1200，解得：121020x x ==，，即每件童装降价10元或20元时，平均每天盈利1200元；(3)、(20+2x)(40－x)=2000， 230x 6000x -+=，∵此方程无解，∴不可能盈利2000元．【题目点拨】本题主要考查的是一元二次方程的实际应用问题，属于中等难度题型．解决这个问题的关键就是要根据题意列出方程．22、 (1)见解析；(2)见解析.【解题分析】连接AF ，由直径所对的圆周角是直角、同弧所对的圆周角相等的性质，证得直线CD 是⊙O 的切线，若证AD •CE ＝DE •DF ，只要征得△ADF ∽△DEC 即可．在第一问中只能证得∠EDC ＝∠DAF ＝90°，所以在第二问中只要证得∠DEC ＝∠ADF 即可解答此题．【题目详解】(1)连接AF ，∵DF 是⊙O 的直径，∴∠DAF ＝90°，∴∠F+∠ADF＝90°，∵∠F＝∠ABD，∠ADG＝∠ABD，∴∠F＝∠ADG，∴∠ADF+∠ADG＝90°∴直线CD是⊙O的切线∴∠EDC＝90°，∴∠EDC＝∠DAF＝90°；(2)选取①完成证明∵直线CD是⊙O的切线，∴∠CDB＝∠A．∵∠CDB＝∠CEB，∴∠A＝∠CEB．∴AD∥EC．∴∠DEC＝∠ADF．∵∠EDC＝∠DAF＝90°，∴△ADF∽△DEC．∴AD：DE＝DF：EC．∴AD•CE＝DE•DF．【题目点拨】此题考查了切线的性质与判定、弦切角定理、相似三角形的判定与性质等知识．注意乘积的形式可以转化为比例的形式，通过证明三角形相似得出．还要注意构造直径所对的圆周角是圆中的常见辅助线．23、(1)证明见解析；（2）3 2【解题分析】试题分析：（1）首先连接OD，CD，由以BC为直径的⊙O，可得CD⊥AB，又由等腰三角形ABC的底角为30°，可得AD=BD，即可证得OD∥AC，继而可证得结论；（2）首先根据三角函数的性质，求得BD，DE，AE的长，然后求得△BOD，△ODE，△ADE以及△ABC的面积，继而求得答案．试题解析：（1）证明：连接OD，CD，∵BC为⊙O直径，∴∠BDC=90°，即CD⊥AB，∵△ABC是等腰三角形，∴AD=BD，∵OB=OC，∴OD是△ABC的中位线，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∵D点在⊙O上，∴DE为⊙O的切线；（2）解：∵∠A=∠B=30°，BC=4，∴CD=12BC=2，3∴33∴S△ABC=12AB•CD=12×33∵DE⊥AC，∴DE=12AD=12× AE=AD•cos30°=3，∴S △ODE =12OD•DE=12×，S △ADE =12AE•DE=12×3=2，∵S △BOD =12S △BCD =12×12S △ABC =14×∴S △OEC =S △ABC -S △BOD -S △ODE -S △ADE 24、 (1)18；（2）中位数；（3）100名.【解题分析】【分析】（1）根据条形统计图中的数据可以得到m 的值；（2）根据题意可知应选择中位数比较合适；（3）根据统计图中的数据可以计该部门生产能手的人数．【题目详解】（1）由图可得，众数m 的值为18，故答案为：18；（2）由题意可得，如果想让一半左右的工人能获奖，应根据中位数来确定奖励标准比较合适，故答案为：中位数；（3）300×11231230+++++=100（名），答：该部门生产能手有100名工人．【题目点拨】本题考查了条形统计图、用样本估计总体、加权平均数、中位数和众数，解答本题的关键是明确题意，利用数形结合的思想解答．25、原式=12a -=﹣2．【解题分析】分析：原式利用分式混合运算顺序和运算法则化简，再将a 的值代入计算可得．详解：原式=112()+11(1)(1)a a a a a a +-÷++-=(1)(1)·12a a aa a+-+=1 2a-，当a=﹣1时，原式=312--=﹣2．点睛：本题主要考查分式的化简求值，解题的关键是熟练掌握分式混合运算顺序和运算法则．26、()1本次调查的学生人数为200人；()2B所在扇形的圆心角为54，补全条形图见解析；()3全校每周课外阅读时间满足3t4≤<的约有360人．【解题分析】【分析】()1根据等级A的人数及所占百分比即可得出调查学生人数；()2先计算出C在扇形图中的百分比，用()1[A D C-++在扇形图中的百分比]可计算出B在扇形图中的百分比，再计算出B在扇形的圆心角；()3总人数⨯课外阅读时间满足3t4≤<的百分比即得所求．【题目详解】()1由条形图知，A级的人数为20人，由扇形图知：A级人数占总调查人数的10%，所以：1002010%20200(10÷=⨯=人)，即本次调查的学生人数为200人；()2由条形图知：C级的人数为60人，所以C级所占的百分比为：60100%30% 200⨯=，B级所占的百分比为：110%30%45%15%---=，B级的人数为20015%30(⨯=人)，D级的人数为：20045%90(⨯=人)，B所在扇形的圆心角为：36015%54⨯=，补全条形图如图所示：；()3因为C 级所占的百分比为30%，所以全校每周课外阅读时间满足3t 4≤<的人数为：120030%360(⨯=人)，答：全校每周课外阅读时间满足3t 4≤<的约有360人．【题目点拨】本题考查了扇形图和条形图的相关知识，从统计图中找到必要的信息进行解题是关键.扇形图中某项的百分比100%=⨯该项人数总人数，扇形图中某项圆心角的度数360=⨯该项在扇形图中的百分比． 27、（1）证明见解析；（2）9﹣3π 【解题分析】试题分析：(1)、连接OD ，根据平行四边形的性质得出∠AOC=∠OBE ，∠COD=∠ODB ，结合OB=OD 得出∠DOC=∠AOC ，从而证明出△COD 和△COA 全等，从而的得出答案；(2)、首先根据题意得出△OBD 为等边三角形，根据等边三角形的性质得出EC=ED=BO=DB ，根据Rt △AOC 的勾股定理得出AC 的长度，然后根据阴影部分的面积等于两个△AOC 的面积减去扇形OAD 的面积得出答案.试题解析：（1）如图连接OD ．∵四边形OBEC 是平行四边形，∴OC ∥BE ，∴∠AOC =∠OBE ，∠COD =∠ODB ，∵OB =OD ，∴∠OBD =∠ODB ，∴∠DOC =∠AOC ，在△COD 和△COA 中，，∴△COD ≌△COA ，∴∠CDO =∠CAO =90°，∴CF ⊥OD ， ∴CF 是⊙O 的切线．（2）∵∠F =30°，∠ODF =90°，∴∠DOF =∠AOC =∠COD =60°，∵OD =OB ，∴△OBD 是等边三角形，∴∠4=60°，∵∠4=∠F +∠1，∴∠1=∠2=30°，∵EC ∥OB ，∴∠E =180°﹣∠4=120°，∴∠3=180°﹣∠E ﹣∠2=30°，∴EC =ED =BO =DB ，∵EB =6，∴OB =OD ═OA =3，在Rt △AOC 中，∵∠OAC =90°，OA =3，∠AOC =60°， ∴AC =OA •tan60°=3， ∴S 阴=2•S △AOC ﹣S 扇形OAD =2××3×3﹣=9﹣3π．。

重庆南开中学2021年中考一轮复习几何综合 (一)

几何综合（一）（讲义）➢ 课前预习1. 如图，在梯形ABCD中，AB∥CD，∠B=∠C=90°，点E在BC边上，AB=3，CD=2，BC=7．若∠AED=90°，则C E=_____．提示：多个直角（一线三等角），考虑三等角模型．具体操作：∠ABE=∠ECD=∠AED=90°，考虑△ABE∽△ECD．2. 如图，将三角板放在矩形ABCD上，使三角板的一边恰好经过点B，三角板的直角顶点E落在矩形对角线AC上，另一边交C D于点F．若AB=3，BC=4，则=________．提示：斜直角要放正（关键是与其他直角配合），利用互余转移角后，寻找三角形相似或全等．具体操作：过点E分别作EM⊥CD于M，EN⊥BC于N，则△EMF∽△EN B．3. 如图，将长为4cm，宽为2 cm的矩形纸片ABCD折叠，使点B落在CD边的中点E处，压平后得到折痕MN，则线段AM的长为__________．提示：折叠，对称轴上的点到对应点的距离相等．具体操作：连接BM，ME，则BM=ME，在Rt△BAM和Rt△MDE中表达BM2，ME2，利用相等建等式求解．4. 如图，P是等边三角形ABC内的一点，连接PA，PB，PC，以BP为边作∠PBQ=60°，且BQ=BP，连接PQ，CQ．若PA:PB:PC=3:4:5，则∠PQC=________．提示：利用旋转可以重新组合条件．当看到等线段共端点时往往会考虑利用旋转思想构造全等．具体操作：由等线段共端点AB=BC，PB=BQ，先考虑△APB和△BQC的旋转关系，证明△APB≌△CQB后验证，重新组合条件后利用勾股定理逆定理进行求解．➢ 知识点睛1. 几何综合问题的处理思路①标注条件，合理转化②组合特征，分析结构③由因导果，执果索因2. 常见的思考角度3. 常见结构、常用模型➢ 精讲精练1. 如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°并缩小，恰好使DE=CD，连接AE，则△ADE的面积是________．2. 如图，在平面直角坐标系中，已知直线y=x上一点P(1，1)，C为y轴上一点，连接PC．线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x 轴，垂足为B，直线AB与直线y=x交于点A，且BD=2AD．若直线CD与直线y=x交于点Q，则点Q的坐标为__________．3. 如图，在Rt△ACB中，∠ACB=90°，AC=BC=3，CD=1，CH⊥BD于H，点O是AB的中点，连接OH，则OH=_______．4. 如图，把矩形ABCD沿直线AC折叠，点B落在点E处，连接DE．若DE:AC=3:5，则的值为_________．5. 如图1，将正方形纸片ABCD对折，使AB与CD重合，折痕为EF；如图2，展开再折叠一次，使点C落在线段EF上，折痕为BM，BM交EF于O，且△NM O的周长为．如图3，展开再折叠一次，使点C与点E重合，折痕为GH，点B的对应点为P，EP交AB于Q，则△A Q E的周长为_______．6. 如图1，在矩形纸片ABCD中，AB=，AD=10，点E是CD的中点．将这张纸片依次折叠两次：第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME，NE；第二次折叠纸片使点N与点E重合，如图3，点B落在B′处，折痕为HG，连接HE，则tan∠EHG=_______．图1 图2 图37. 如图，矩形ABCD中，BC=2，将矩形ABCD绕点D顺时针旋转90°，点A，C分别落在点A′，C′处，如果点A′，C′，B在同一条直线上，那么tan∠ABA′的值为__________．8. 如图，在四边形ABCD中，∠ABC=30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE．若AB=3，BC=4，则BD=__________．9. 如图，在Rt△ABC中，∠ACB=90°，tan∠CBA=，AB=5.将△ABC绕点A顺时针旋转得到△A B′C′，连接CC′并延长，交AB于点O，交BB′于点F．若CC′=CA，则BF=_____．10. 如图，在△ABC中，∠BAC=30°，AB=AC，AD是BC边上的中线，∠ACE=∠BAC，CE交AB于点E，交AD于点F．若BC=2，则EF的长为________．11. 如图，在△ABC中，AB=10，∠B=60°，点D，E分别在AB，BC上，且BD=BE=4，将△BDE沿DE所在直线折叠得到△B′DE（点B′在四边形ADEC内），连接A B′，则A B′的长为________．12. 如图，已知菱形ABCD的边长为2，∠A=60°，点E，F分别在边AB，AD上，若将△AEF沿直线EF折叠，使得点A恰好落在CD边的中点G处，则EF=__________．13. 如图，在正方形ABCD中，E，F分别为BC，CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA的延长线于点Q．下列结论：①AE=BF；②AE⊥BF；③tan∠BQP=；④．其中正确的个数是（）A．4 B．3 C．2 D．1【参考答案】➢∙课前预习1. 1或62.3. cm4. 90°➢∙精讲精练1. 22.3.4.5. 126.7.8. 59.10.11.12.13. C几何综合（一）（习题）➢ 例题示范例1：如图，在矩形ABCD中，点E是AD边的中点，∠EBC的平分线交CD 于点F．将△DEF沿EF折叠，点D恰好落在BE上的点M处，延长BC，EF交于点N．有下列四个结论：①DF=CF；②BF⊥EN；③△BEN是等边三角形；④S△BEF =3S△DEF．其中正确结论的序号是（）A．①②③B．①②④C．②③④D．①②③④【思路分析】1. 标注条件，合理转化对“E是中点，BF是角平分线，△DEF沿EF折叠”进行适当的转化标注．2. 组合条件，分析结构多结论问题，层层推进，问与问之间联系紧密，一般情况下，从前向后依次推证．①要证DF=CF，由折叠知DF=MF，所以只需证明CF=MF即可；已知∠BCF=90°，∠FMB=90°，BF是∠MBC的平分线，所以FM=FC=FD，△FBC≌△FBM．②要证BF⊥EN，就是证∠BFE=90°，由△FBC≌△FBM可以得知，∠BFM=∠CFB，由折叠又知，∠EFD=∠EFM，所以∠BFE=∠BFM+∠MFE=，即BF ⊥EN，所以△EBN为等腰三角形．③若△BEN是等边三角形，则∠ABE=30°，设ED=t，则BC=2t，所以BE=3t，si n∠ABE=，所以△BEN不是等边三角形．④∵B M=2EM，∴S△BFM=2S△EFM，∴S△BFE=3S△EFM，由折叠知，S△EFM=S△EFD∴S△BEF =3S△DEF．所以，正确结论为①②④，答案为选项B．➢ 巩固练习1. 如图，正方形ABCD边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB的延长线于点F，则EF的长为___________．第1题图第2题图2. 如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=cm，且tan∠EFC=，则矩形ABCD的周长为_______cm．3. 如图，在平面直角坐标系中，已知点A，B的坐标分别(8，0)，(0，)，C是AB的中点，过C作y轴的垂线，垂足为D．动点P从点D出发，沿DC 向C匀速运动，过点P作x轴的垂线，垂足为E，连接BP，EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为_________．4. 如图，在梯形ABCD中，AD∥BC，BE平分∠ABC交CD于E，且BE⊥CD，CE:ED=2:1．如果△BEC的面积为2，那么四边形ABED的面积是__________．5. 如图，△AOB为等腰三角形，顶点A的坐标为(2，)，底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为（）A．(，)B．(，)C．(，)D．(，)6. 如图，已知正方形ABCD的边长为5，E在BC边上运动，G是DE的中点，EG绕E顺时针旋转90°得EF，当CE为（）时，点A，C，F在一条直线上．A． B． C． D．7. 如图，正方形ABCD的边长为6，点E，F分别在AB，AD上，若CE=，且∠ECF=45°，则CF的长为（）A．B．C．D．8. 如图，矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P与点B，C都不重合），现将△PCD沿直线PD折叠，使点C落到点F处；过点P作∠BPF的平分线交AB于点E．设BP=x，BE=y，则y关于x的函数关系式为________．第8题图第9题图9. 如图，D是等边三角形ABC边A B上的一点，且AD:DB=1:2，现将△ABC折叠，使点C与点D重合，折痕为EF，点E，F分别在AC，BC上，则（）A．B．C．D．10. 如图，在矩形纸片ABCD中，AB=6，BC=10，点E在CD上，将△BCE沿BE折叠，点C恰落在边AD上的点F处；点G在AF上，将△ABG沿BG 折叠，点A恰落在线段BF上的点H处．有下列结论：①∠EBG=45°；②△DEF∽△ABG；③；④AG+DF=FG．其中正确的有__________（填写序号）．11. 如图，在△ABC中，∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，MN．有下列四个结论：①PM=PN；②；③△PMN为等边三角形；④当∠ABC=45°时，．其中正确结论的序号是_______．12. 如图，分别以Rt△ABC的斜边AB、直角边AC为边，向△ABC外作等边三角形ABD和等边三角形ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．有以下结论：①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④．其中正确结论的序号为________．第12题图第13题图13. 如图，在一张矩形纸片ABCD中，AB=4，BC=8，点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点H处，点D落在点G处，连接CE，CH．有以下四个结论：①四边形CFHE是菱形；②CE平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时，EF=．其中正确的有（）A．1个B．2个C．3个D．4个➢ 思考小结回顾下列角平分线的思考角度，并结合本讲讲义预习中的题目尝试自我总结中点、直角、旋转、折叠的思考角度．1. 相关定理①角平分线上的点到角两边的距离相等；②到角两边距离相等的点在这个角的角平分线上；③在下图中，成立．2. 组合搭配①等腰三角形“三线合一”②平行线+角平分线，出现等腰三角形③圆中有角平分线，遇角考虑弧（由弧找角，由角看弧）3. 模型结构①三个小结论两条内角平分线相交内角平分线与外角平分线相交两条外角平分线相交②二倍角（构造角平分线）【参考答案】数学➢ 巩固练习1.2. 363.4.5. C6. C7. A8.9. B10. ①③④11. ①②③④12. ①③④13. C。

2020年重庆市南开中学中考数学综合卷六(PDF版含答案) (1)

米，则建筑物 CD 的高度约为（）米．（精确到 0.1 米，参考数据：sin 37 0.60 ，
cos37 0.80 ， tan 37 0.75 ）
A． 38.5 米
B． 39.0 米
C． 40.0 米
D． 41.5 米
11．若数
a
使关于
x
的不等式组
3x 2
2
x
5 2
有且只有
4
个整数解，且使关于
b
c
a
第6页共8页
25．如图，平行四边形 ABCD 中， E 、 F 分别为对角线 AC 上两点，且 AE CF ，连接 BE 、 DF ．（1）如图 1，若 ABE ACB 30 ， AC BC ， CE 4 ，求 AE 的长；（2）如图 2，延长 DF 交 BC 于点 G ，连接 EG ． H 为 AD 边上一点，连接 EH ．若 GD 平分 CGE ， DH 2BG ，求证： EF EH ．
23．某商店经销甲、乙两种商品，已知一件甲种商品和一件乙种商品的进价之和为 30 元，每件甲种商品的利润是 4 元，每件乙种商品的售价比其进价的 2 倍少 11 元，小明在该商店购买 8 件甲种商品和 6 件乙种商品一共用了 262 元．（1）求甲、乙两种商品的进价分别是多少元？（2）在（1）的前提下，经销商统计发现：平均每天可售出甲种商品 400 件和乙种商品 300 件，如果将甲种商品的售价每提高 0.1 元，则每天将少售出 7 件甲种商品；如果将乙种商品的售价每提高 0.1 元，则每天将少售出 8 件乙种商品．经销商决定把两种商品的价格都提高
b
c
整理得 a ac 1 则 c 1 ac 1 1
aa
（1）已知 a 1 1， b 1 1，则 c 1

重庆市南开中学数学平面图形的认识(一)中考真题汇编[解析版]

一、初一数学几何模型部分解答题压轴题精选（难）1．如图，EF⊥AB于F，CD⊥AB于D，点在AC边上，且∠1=∠2= ．（1）求证：EF∥CD；（2）若∠AGD=65°，试求∠DCG的度数.【答案】（1）证明：∵EF⊥AB于F，CD⊥AB于D，∴∠BFE=∠BDC=90°，∴EF∥CD.（2）解：∵EF∥CD，∴∠2=∠DCE=50°，∵∠1=∠2，∴∠1=∠DCE,∴DG∥BC，∴∠AGD=∠ACB=65°，∴∠DCG=【解析】【分析】（1）由垂直的定义，可求得∠BFE=∠CDF=90°，可证明EF∥CD；（2）利用（1）的结论，结合条件可证明DG∥BC，利用平行线的性质可得∠AGD=∠ACB= ，则∠DCG=∠ACB-∠2即可求得．2．如图，点C在∠AOB的边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于C.（1）若∠O＝40°，求∠ECF的度数；（2）试说明CG平分∠OCD；（3）当∠O为多少度时，CD平分∠OCF？并说明理由．【答案】（1）解：∵DE//OB ，∴∠O=∠ACE，（两直线平行，同位角相等）∵∠O =40°，∴∠ACE =40°，∵∠ACD+∠ACE= (平角定义)∴∠ACD=又∵CF平分∠ACD ，∴ (角平分线定义)∴∠ECF=（2）证明：∵CG⊥CF，∴ .∴又∵）∴∵∴ (等角的余角相等）即CG平分∠OCD（3）解：结论：当∠O=60°时，CD平分∠OCF ．当∠O=60°时∵DE//OB，∴∠DCO=∠O=60°.∴∠ACD=120°.又∵CF平分∠ACD∴∠DCF=60°，∴即CD平分∠OCF【解析】【分析】（1）根据平行线“两直线平行，同位角相等”，求得∠ACE＝40°，根据平角的定义以及CF平分∠ACD ，可得到∠ACF＝70°，然后求出∠ECF的度数；（2）根据∠DCG＋∠DCF＝90°，∠GCO＋∠FCA＝90°，以及∠ACF＝∠DCF，可得到∠GCO ＝∠GCD，即可证明CG平分∠OCD；（3）根据两直线平行，内错角相等得出∠DCO＝∠O＝60°，根据角平分线可得到∠DCF＝60°，以此可得∠DCO＝∠DCF，即CD平分∠OCF．3．探究题学习完平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【答案】（1）圆心 C 的坐标为（1，）；
（2）抛物线的解析式为 y= x2﹣ x；（3）点 D、E 均在抛物线上；（4）﹣1＜x0＜0，或 2＜x0＜3．【解析】试题分析：（1）如图线段 AB 是圆 C 的直径，因为点 A、B 的坐标已知，根据平行线的性质即可求得点 C 的坐标；
（2）因为抛物线过点 A、O，所以可求得对称轴，即可求得与直线 y=﹣ x 的交点，即是二次函数的顶点坐标，利用顶点式或者一般式，采用待定系数法即可求得抛物线的解析式；
∵ P 是半圆 O 上的点，P 在 y 轴上，∴ OP=2，∠ AOP=90°，∴ AC=2，∴ 四边形 AOPC 是正方
形，
∴ 正方形的面积是 4，
又∵ BD⊥AB，BD=6，∴ 梯形 OPDB 的面积= (OP DB) OB (2 6) 2 8 ，
2
2
∴ 点 P 的关联图形的面积是 12．
（2）
，AB 是圆的直径，所以 OB=5；
于点，交于
点，F 是 BC 的中点；
，BF=4；在直角三角形 OBF 中由勾股定理得
OF=
；根据题意
，
，则
，所以
，从而
，解得 DF= ，
的面积
= 考点：直线与圆相切，相似三角形点评：本题考查直线与圆相切，相似三角形；解本题的关键是会判断直线与圆是否相切，能判定两个三角形相似
的两根，则其；；矩形两邻边的长、是方
程
的两根，则
；因为
，所以
由
得
；解得
（3）矩形变为正方形，则 a=b；、是方程
的两根，所以
方程有两个相等的实数根，即
，由
题乙：（1）BD 是切线；如图所示，
得是弧 AC 所对的圆周角，
；因为，所以
，所以，
；
于点，
，在三角形 OBD 中
，所以 OB⊥BD；BD 是切线
【答案】（1）12；（2）判断△ OCD 是直角三角形，证明见解析；（3）连接 OC，交半圆
O 于点 P，这时点 P 的关联图形的面积最大，理由风解析， 8 4 2 .
【解析】
试题分析：（1）判断出四边形 AOPC 是正方形，得到正方形的面积是 4，根据 BD⊥AB，
BD=6，求出梯形 OPDB 的面积= (OP DB) OB (2 6) 2 8 ，二者相加即为点 P 的
重庆市南开中学数学圆几何综合中考真题汇编[解析版]
一、初三数学圆易错题压轴题（难）
1．在平面直角坐标系 xOy 中，已知 A(-2，0)，B(2，0)，AC⊥AB 于点 A，AC=2，BD⊥AB 于点 B，BD=6，以 AB 为直径的半圆 O 上有一动点 P（不与 A、B 两点重合），连接 PD、 PC，我们把由五条线段 AB、BD、DP、PC、CA 所组成的封闭图形 ABDPC 叫做点 P 的关联图形，如图 1 所示. （1）如图 2，当 P 运动到半圆 O 与 y 轴的交点位置时，求点 P 的关联图形的面积. （2）如图 3，连接 CD、OC、OD,判断△ OCD 的形状，并加以证明. （3）当点 P 运动到什么位置时，点 P 的关联图形的面积最大，简要说明理由，并求面积的最大值.
题乙：如图，是直径，
点，且
．
于点，交于
（1）判断直线和
（2）当
，
的位置关系，并给出证明；
时，求
的面积．
【答案】题甲（1）
（2）
（3）
题乙：（1）BD 是【解析】
切线；证明
所以 OB⊥BD，BD 是切线（2）S=
试题分析：题甲：（1）、是方程
由
得
（2）矩形两邻边的长、，矩形的对角线的平方=
∴ PC 在半圆外，设在半圆 O 上的任意一点 P′到 CD 的距离为 P′H，则 P′H+P′O＞OH＞OC， ∵ OC=PC+OP，∴ P′H＞PC，∴ 当点 P 运动到半圆 O 与 OC 的交点位置时，点 P 的关联图形的面积最大．
∵ CD= 4 2 ，CP= 2 2 2 ，
∴ △ PCD 的面积= ( AC DB) AB (2 6) 4 16 ，
2
2
∴ 点 P 的关联图形的最大面积是梯形 ACDB 的面积﹣△ PCD 的面积
=16 (8 4 2) 8 4 2 ．
考点：圆的综合题．
2．选做题：从甲乙两题中选作一题，如果两题都做，只以甲题计分
题甲：已知矩形两邻边的长、是方程
的两根.
（1）求的取值范围；（2）当矩形的对角线长为时，求的值；（3）当为何值时，矩形变为正方形？
（2）判断△ OCD 是直角三角形．
证明：延长 CP 交 BD 于点 F，则四边形 ACFB 为矩形，∴ CF=DF=4，∠ DCF=45°，
∴ ∠ OCD=90°， ∴ OC⊥CD，∴ △ OCD 是直角三角形．
（3）连接 OC 交半圆 O 于点 P，则点 P 即为所确定的点的位置．
理由如下：连接 CD，梯形 ACDB 的面积= ( AC DB) AB (2 6) 4 16 为定值，
2
2
关联图形的面积是 12．
（2）根据 CBiblioteka =DF=4，∠ DCF=45°，求出∠ OCD=90°，判断出△ OCD 是直角三角形．
（3）要使点 P 的关联图形的面积最大，就要使△ PCD 的面积最小，确定关联图形的最大面
积是梯形 ACDB 的面积﹣△ PCD 的面积，根据此思路，进行解答．
试题解析：（1）∵ A（﹣2，0），∴ OA=2，
2
2
要使点 P 的关联图形的面积最大，就要使△ PCD 的面积最小，
∵ CD 为定长，∴ P 到 CD 的距离就要最小，
连接 OC，设交半圆 O 于点 P，
∵ AC⊥OA，AC=OA，∴ ∠ AOC=45°，过 C 作 CF⊥BD 于 F，则 ACFB 为矩形，
∴ CF=DF=4，∠ DCF=45°，∴ OC⊥CD，OC= 2 2 ，
3．在直角坐标系中，⊙C 过原点 O，交 x 轴于点 A（2，0），交 y 轴于点 B（0，）．（1）求圆心 C 的坐标．
（2）抛物线 y=ax2+bx+c 过 O，A 两点，且顶点在正比例函数 y=- 的图象上，求抛物线的解析式．（3）过圆心 C 作平行于 x 轴的直线 DE，交⊙C 于 D，E 两点，试判断 D，E 两点是否在（2）中的抛物线上．（4）若（2）中的抛物线上存在点 P（x0，y0），满足∠ APB 为钝角，求 x0 的取值范围．