第22讲唯一性定理第4章 介质中的电动力学2§2唯一性定理
《电动力学第三版》chapter2_2唯一性定理

E2t E1t
D
2n
D1n
如果我们假设 E仍保持球对称性,即
E1
A r3
r
E2
A r3
r
(左半部) (右半部)
(A为待定常数),分界面两侧电场与界面相切,并有相同数值,因 而边值关系得到满足.
球对称的E在球面上处处与球面垂直,保证导体球面为等
势面. 为了满足内导体总电荷等于Q,我们计算内导体球面上
对于第一类边界条件,只要把导体存在的空间扣除,将导 体看成是区域边界之一,即可证明电场被唯一确定.
对于第二类边界条件,在导体外,电荷分布给定,大区域表 面上电势或电势的法向导数给定;每个导体上的总电荷给定.
设区域V 内有一些导体,给定导体之外的电荷分布x 给定
各导体上的总电荷Qi以及V的边界S上的或/n值,则V内的电
有球对称性. 试解释之.
子区域 2
子区域 4
子区域 3
i ( S i i )d S i V i i d V(1)
i
V ii( )2dVV i(i 2)dV
i
i 2dV
Vi
i S i(i )d S i S i(i n i)d S 0 (2)(3)
i S i i d S i V i i 2 d V 0
场唯一地确定. 存在唯一的解,它在导体以外满足泊松方程
2/
在第i个导体上满足总电荷条件和等势面条件
Si ndSQ i, |Sii 常量
以及在V的边界S上具有给定的|s 或/n|s值.
证明: 设有 和 同时满足上述条件. 令 '''
2 0
|si 0,
dS 0 Si n
|s 0 或
第二章 静电场
电动力学22唯一性定理共18页

41、俯仰终宇宙,不乐复何如。 42、夏日长抱饥,寒夜无被眠。 43、不戚戚于贫贱,不汲汲于富贵。 44、欲言无予和,挥杯劝孤影。 45、盛年不重来,一日难再晨。及时 当勉励 ,岁月 不待人Байду номын сангаас。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
18
唯一性定理

唯一性定理蒋文佼(080320124)宋宝璋(080320125)夏世宇 (080320126) 李宝平 (080320127) 章文显 (080320129) 常 悦 (080320130) 1、试用唯一性定理证明:封闭导体壳内部的电场不受壳外电荷(包括壳外表面)的影响。
证:导体壳无论是用电势还是用总电量给定,壳的内外一般存在着四部分电荷。
如图所示,壳内外的电荷分布分别为 ρ 和 ρe ,壳内、外表面1S 、2S 上各自的面电荷分布为σ 和 σe 。
壳内外的场是这四部分电荷共同激发的。
根据定理,首先写出壳内空间电势应满足的条件:(一) 2ρϕε∇=- ,ρ 为壳内电荷分布。
(二)壳内表面1S 上的边界条件是:2S 上的总电量 1s dS q σ=-⎰ (1)其中 Vq dV ρ=⎰ 是壳内的总电量,V 是壳内区域的体积。
在壳层内作一高斯面 0S 后(如图中虚线所示),用高斯定理很容易证明(1)成立。
因此在给定 ρ 布后, 1S 上边界条件也已经给定为 q - ,和导体壳本身是有电势还是用总电量给定无关。
根据唯一性定理,满足(一)、(二)的ϕ 就是解。
由于(一)e和(二)与壳外的ρe 和 σρ 的电势并不唯一,可以差一个常数。
当然当壳用电势 0φ 给定时,1S 上的边界条件就是10|S ϕφ= 。
所以壳内不但电场唯一,而且电势也是唯一。
2.如图,有一电势为0φ的导体球壳,球心有一点电荷q ,球壳内外半径分别为2R 和1R 。
试用唯一性定理: (一)判断0R φ是否球壳外空间的电势分布。
(二)求球壳内空间的电势分布解:(一)首先必须找出球内外电势应满足的条件,他们是:(a )20∇ϕ=(b )球壳外表面1S 上的边界条件,10s ϕ=φ (c )无穷远边界条件,0R →∞ϕ→若R φ是解,根据唯一性定理,它必须满足以上三个条件。
下面来检验:220010R Rφ∇=φ∇= (0),R ≠ 方程已满足。
第2节唯一性定理

M 在圆心缩为一点,条件不变,解不变。
由此得出
Q 4 0 r
1
r R0
请说明原因,并画出电力线图示。
例:求偶极子在远区的场。 偶极子:1 其线度 l r 2 电荷线度线度 l 定义——偶极矩 P ql
(r ) 1
q q q r r' r' ( ) 4 0 r r' 4 0 rr ' q l cos 1 Pr 2 3 q l q 4 0 r 4 0 r
或
u
n s
0
使等式左端=0,则右端
2 2 ( u ) 0 u 0 ( u ) dV 0
v
u 0
V内 u =常数 1)若 u 0即1 2,同一个势,对应同一 个场。 2)1 , 2 可相差一个常数,不影响场分布。 电场分布唯一确定。
r
1 Pr 1 1 E 3 ( P ) 4 0 r 4 0 r 1 3( P r )r P ( 3) 5 4 0 r r 1 P cos ( E ) r E er 2 0 r3 1 P sin ( E ) E e 3 4 r 0 (E) E e 0
2 s'
2u 0
s'
uu dS uu dS uu dS
s si
v'
(u ) dV uu dS
2 s'
在 Si 表面上 u 常数
u u dS u u dS u dS 0 su si si n i
E1 E2 n
电动力学uniquenesstheorem唯一性定理完全解读

引入标量函数Φ ,令Φ = '- ″
2 , 2 , 2 0
i
i
在区域边界面S 上
S
S
0 S
(给定第一类边界条件)
或 ,
n S n S
0
n S
(给定第二类边界条件)
下面需要证明旳是,满足以上方程和边界条件旳'和
1) 绝缘介质静电问题旳唯一性定理及证明 在有限旳边界区域V 内有几种均匀旳绝缘介质Vi 、εi
(i = 1、2、3 …) ,V 中旳自由电荷分布(ρ或σ) 为已知,那
么,当V 旳边界面S 上旳电势 给 定(或电势旳法向导数边
界条件) ,则V 内旳电场有唯一拟定旳解。
数学表述如下:
2 i
i
(在每个小区Vi)
V′旳全部内、外表面上都有一定旳值或 值,应用有关绝缘介
质旳唯一性定理,则V′内旳电场必有唯一解. n
b)区域V 内有若干导体,假设除导体以外旳区域V′内旳自由电荷分
布ρ已知,V′旳外表面S 上有已知旳值或 值,另外,若每个导
n 体所带旳总电量Qi 为已知,则区域V′内旳电场有唯一解。
数学表达为:
场有唯一解。这么,有导体存在时静电问题旳唯一性定理 也得到证明。
最终需要强调一点,尽管唯一性定理并不给出求解泊松方程旳详细措 施与环节,但它对于处理实际旳边值问题有着主要旳意义. 首先,它明 确了在哪些条件下能够唯一地拟定一种静电场,即给出了求解静电场 旳根据;其次,它使我们能够灵活地选用最简朴、最合适旳解题措施, 甚至能够猜一种解(即提出尝试解) . 只要这个解确实满足了问题中 旳场方程和全部定解条件,那么,根据唯一性定理我们就能够肯 定地说,它就是该问题中旳唯一正确旳解.
唯一性定理
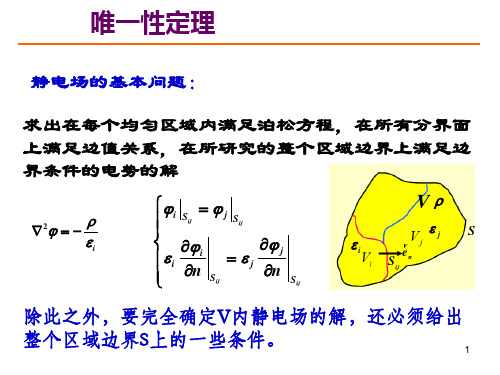
静电场的基本问题:
求出在每个均匀区域内满足泊松方程,在所有分界面 上满足边值关系,在所研究的整个区域边界上满足边 界条件的电势的解
2 i
i
Sij
j
Sij
i
i
n
Sij
j
j
n
Sij
V
j S
i
Sij evn
除此之外,要完全确定V内静电场的解,还必须给出 整个区域边界S上的一些条件。
1
到底需要给定哪些条件,才能求得静电场的解,并且 解是唯一的?
Ra
(2) 介质内无自由电荷分布; (3) R=a处导体球带总电量Qf 该定解问题有唯一解。
9
1. 给出边值关系和边界条件 设左、右介质的电势分别为 1 和 2
Ñ dS Qi
Si n
根据唯一性定理,只要能找到一个满足上面定解条件 的特解,那该解就一定是该问题的唯一解。
10
2. 提出尝试解
C与 0为待定系数,且 0与外球壳半径a’有关 3. 由边值关系和边界条件确定待定系数
2 0 Qf 2 1 2 a2
相同
v
2
0Q f
1 2 a2
(, 右半球)
P1
v P2
15
所以,由于有束缚电荷的存在,在内导体球壳两半球 面上束缚电荷与自由电荷之和是球对称的,所以电场 强度E是球对称的。
首先判断该问题是否满足唯一性定理。 1. 给出边值关系和边界条件 2. 提出尝试解 3. 由边值关系和边界条件确定待定系数 4. 求电场和球壳上的电荷分布
Ñ i
Vi
i
2dV
v
Si i dS i
2 0
Vi i 2 dV
积分区域包括沿区域V的边界S上的面积分和沿各分区的分界面Sij的面积4分
唯一性定理的内容及其意义

唯一性定理的内容及其意义
唯一性定理是数学中的一个重要概念,它表明一个函数的极限存在着唯一的可能性,也就是说,在一定的条件下,任何一个可以组成极限函数的一系列函数都只能有一个极限。
即使函数的系数都不同,其形式也不同,但是它们的极限仍然是一样的。
这就是唯一性定理提出的。
唯一性定理的定义也非常简单,就是指在特定的条件下,任何一个收敛的函数序列都只能存在一个极限值。
在实际应用中,唯一性定理要求极限函数必须存在,而且必须满足一定的数学模型和性质。
唯一性定理的具体内容包括:
一、极限函数的存在:极限函数是指在定义域内,当给定变量x 的值逐渐增加或减少时,函数f(x)可以达到一个确定的最终值,这个确定的最终值就是函数的极限值。
二、唯一性定理的证明:当极限函数的存在可以被证明时,唯一性定理的证明也就容易了。
就是说,在一定条件下,任意一个收敛的函数序列只有一个极限值,其他的所有的函数序列的极限值都是一样的。
三、唯一性定理的应用:唯一性定理在数学应用当中具有很重要的意义,它能帮助我们验证各种数学性质,如函数解析和微积分等。
另外,唯一性定理还可以用于描述从函数变换中产生的相应的形态变化情况。
综上所述,唯一性定理是数学中一个重要的概念,它表明,在一
定条件下,任何一个可以组成极限函数的一系列函数都只能有一个极限,即使函数的系数和形式都不同,它们的极限仍然是一样的。
唯一性定理的具体内容是极限函数的存在,以及证明唯一性定理的方法,它在数学应用当中发挥着重要作用,上述内容对于更好地理解唯一性定理是很有帮助的。
3.2 唯一性定理

唯 性定 唯一性定理汪 毅静电问题的唯一性定理均匀分区的区域V,即V可以分为若干个均匀区域Vi, 每个均匀区域的电容率为ε 设 内有给定的自由 每个均匀区域的电容率为 i,设V内有给定的自由 电荷分布ρ(x)。
电势ϕ在均匀区域Vi内满足泊松方 ρ ϕ 程:ρ ∇ ϕ =− εi2在两区域Vi和Vj的分界面上满足边值关系:ϕi = ϕ j∂ϕ j ∂ϕi εi =εj ∂n ∂n静电问题的唯一性定理要完全确定V内电场,还必须给出V的边界S上的一 些条件。
下面提出的唯 性定理具体指出所需给定 些条件。
下面提出的唯一性定理具体指出所需给定 的边值条件: 1)给定边界S的电势 2)给定边界S的电势法向偏导数 或者说V内存在唯一的解,它在每个均匀区域内满 足泊松方程,在两均匀区域分界面上满足边值关系, 并在 的边界上满足给定的ϕ或者∂ϕ/∂ 并在V的边界上满足给定的ϕ或者∂ϕ/∂n唯 性定理证明 唯一性定理证明 证明:假定泊松方程有两个解 ϕ1 , ϕ 2 ,满足:在边界上:ρ ∇ ϕ1 = ε2ρ ∇ ϕ2 = ε2ϕ1 S = ϕ 2令:S=ϕ S∂ϕ1 ∂nS∂ϕ ∂ϕ2 = = ∂n S ∂nSΦ = ϕ1 − ϕ2 ∇2Φ =∇2ϕ1 −∇2ϕ2 = 0 ∇ ∇唯一性定理证明Φ S = ϕ1 S − ϕ2 S∂ϕ2 ∂ϕ1 ∂Φ − =0 = ∂n S ∂n ∂n S =0S考虑第i个均匀区域Vi的界面Si上的积分∫Siε i Φ ∇Φ ⋅ dS∫根据格林第一公式: 根据格林第 公式Si ViεiΦ ∇Φ⋅ dS = ∫ ∇ (εiΦ ∇Φ )dV ∇Φ ∇⋅= ∫ εi (∇Φ ) dV + ∫ ϕεi∇ Φ dV2 2 Vi Vi唯一性定理证明 2 ε i Φ ∇Φ ⋅ dS = ∫ ε i (∇Φ ) dV ∫S Vi i对所有分 域 求 对所有分区域Vi求和∑∫iSiε i Φ ∇Φ ⋅ dS = ∑ ∫ ε i (∇Φ ) dV2 i ViΦ 在两均匀区域Vi和Vj界面上, 和ε ∇Φ 的法向分 量分别相等,但 dSi = − dS j ,因此上式左边的和 式中,内部分界面的积分互相抵消,因此只剩下整 式中 内部分界面的积分互相抵消 因此只剩下整 Φ 个V的边界面S上的积分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第22讲 唯一性定理 第4章 介质中的电动力学(2)§4.2 唯一性定理在上节中我们说明静电学的基本问题是求出所有边界上满足边值关系或给定边界条件的泊松方程的解。
本节我们把这问题确切地表述出来,即需要给出哪一些条件,静电场的解才能唯一地被确定。
静电场的唯一性定理对于解决实际问题有着重要的意义。
因为它首先告诉我们,哪些因素可以完全确定静电场,这样在解决实际问题时就有所依据。
其次,对于许多实际问题,往往需要根据给定的条件作一定的分析,提出尝试解。
如果所提出的尝试解满足唯一性定理所要求的条件,它就是该问题的唯一正确的解。
下面我们先提出并证明一般形式的唯一定理,然后再证明有导体存在时的唯一性定理。
1. 静电问题的唯一性定理 下面我们研究可以均匀分区的区域V ,即V 可以分为若干个均匀区域 V i ,每一个区域的电容率为 ε i 。
设V 内有给定的电荷分布 ρ(x )。
电势 φ 在均匀区域 V i 内满足泊松方程 2i ρϕε∇=- (4.2---1)在两区域 V i 和 V j 的分界上满足边值关系()()i j i i j j nn ϕϕϕϕεε=⎧⎪∂∂⎨=⎪∂∂⎩ (4.2---2)泊松方程(4.2---1)式和边值关系(4.2---2)式是电势所必须满足的方程,它们属于电场的基本规律。
除此之外,要完全确定V 内的电场,还必须给出V 的边界S 上的一些条件。
下面提出的唯一性定理具体指出所需给定的边界条件。
唯一性定理: 设区域V 内给定自由电荷分布,在V 的边界上S 上给定 (1)电势φ| s 或(2)电势的法向导数 ∂φ/∂n | s ,则V 内的电场唯一确定。
也就是说,在V 内存在唯一的解,它在每个均匀区域内满足泊松方程(4.2---1),在两均匀区域分界面上满足边值关系,并在V 的边界S 上满足该给定的φ或∂φ/∂n 值。
证明 设有两组不同的解 φ' 和 φ'' 满足唯一性条件定理的条件。
令,ϕϕϕ'''=- (4.2---3) 则由 ▽2φ' = −ρ/εi ,▽2φ'' = −ρ/εi ,得20ϕ∇= (在每个均匀区V i 内) (4.2---4) 在两均匀区界面上有i j ϕϕ= ()()i i j j n nϕϕεε∂∂=∂∂ (4.2---5)在整个区域V 的边界S 上有 0SS S ϕϕϕ'''=-= (4.2---6a )或SSSnnnϕϕϕ'''∂∂∂=-∂∂∂=0 (4.2---6b )考虑第i 个均匀区 V i 的界面 S i 上的积分iiS d εϕϕ∇⋅⎰ÑS由附录(Ⅰ.7)式,这积分可以变换为体积分()iiii S V d dV εϕϕεϕϕ∇⋅=∇⋅∇⎰⎰ÑS22()iii i V V dV dV εϕϕεϕ=∇+∇⎰⎰由(4.2---4)式,右边最后一项为零,因此2()iii i S V d dV Ñεϕϕεϕ∇⋅=∇⎰⎰S 对所有分区 V i 求和得2()iiii S V iid dV εϕϕεϕ∇⋅=∇∑∑⎰⎰ÑS (4.2---7)在两均匀区 V i 和 V j 的界面上,由(4.2---5)式,φ 和ε▽φ的法向分量分别相等,但 d S i = −d S j 。
因此,在(4.2---7)式左边的和式中,内部分界面的积分互相抵消,因而只剩下整个V 的边界S 上的积分。
但在S 上,由(4.2---6)式,或者 φ| s ,或者 ∂φ/∂n | s ,两情形下面积分都等于零。
因此由(4.2---7)式有2()0ii V idV εϕ∇=∑⎰由于被积分函数 ε(▽φ)2 ≥0,上式成立的条件是在V 内各点上都有 0ϕ∇= 即在V 内ϕ=常量由(4.2---3)式, φ' 和 φ'' 至多只能相差一个常量。
但电势的附加常量对电场没有影响,这就证明了唯一性定理。
2. 有导体存在时的唯一性定理 当有导体存在时,由实践经验我们知道,为了确定电场,所需条件有两种类型:一类是给定每个导体上的电势 φi ,另一个是给定每个导体上的总电荷 Q i 。
为简单起见,我们只讨论区域内含一种均匀介质的情形。
如图2-3,设在某区域V 内有一些导体,我们把除去导体内部以后的区域称为V ' ,因而V ' 的边界包括界面S 以及每个导体的表面 S i 。
设V ' 内有给定电荷分布 ρ ,S 上给定 φ| s 或 ∂φ/∂n | s 值。
对上述第一种类型的问题,每个导体上的电势 φi 亦给定,即给出了V ' 所有边界上的φ或 ∂φ/∂n 值,因而由上一小节证明了的唯一性定理可知,V ' 内的电场唯一地被确定。
对于第二种类型的问题,唯一性定理表述如下:设区域V 内由一些导体,给定导体之外的电荷分布ρ,给定各导体上的总电荷 Q i 以及V 的边界S 上的φ或 ∂φ/∂n 值,则V 内的电场唯一确定。
也就是说,存在唯一的解,它在导体以外满足泊松方程2/ϕρε∇=- (4.2---8) 在第i 个导体上满足总电荷条件(4.2---9) i i S Q dS n ϕε∂-=∂⎰Ñ (4.2---9)(n 为导体面的外法线)和等势面条件 iS i ϕϕ==常量, (4.2---10)以及在V 的边界 S 上具有给定的 φ| s 或 ∂φ/∂n | s 值。
证明 设有两个解φ'和φ" 满足上述条件,令 ,ϕϕϕ'''=- 则φ满足20,ϕ∇=(V '体内) (4.2---11) 0,i S dS nϕ∂-=∂⎰Ñ iS ϕ=常量 (4.2---12)S ϕ=0或Snϕ∂∂=0 (4.2---13)对区域 V ' 用公式()V d dV ϕϕϕϕ'∇⋅=∇⋅∇⎰⎰ÑS22''()V V dV dV ϕϕϕ=∇+∇⎰⎰ (4.2---14)上式左边的面积分包括V 的边界S 以及每个导体的表面 S i 上的积分。
作为 V ' 的边界, S i 的法线指向导体内部。
若我们用n 表示导体向外的法线分量,由(4.2---12)式,在 S i 上的积分为0ii i S S d dS nϕϕϕϕ∂∇⋅=-=∂⎰⎰蜒S 由(4.2---13)式,在S 上的面积分亦为零。
因而(4.2---14)式左边等于零。
该式右边最后一项由(4.2---11)式得零,因此, 2()0dV ϕ∇=⎰ 由此得0ϕ∇=即φ'和φ" 至多只能相差一个常量,因而电场唯一确定。
当导体外的电势确定后,由边值关系 iS nϕεσ∂-=∂ (4.2---15)因而导体上的电荷面密度亦同时确定。
由本定理的证明可以看出电场与电荷的相互制约关系。
若空间内有一些导体,给定各导体上的总电荷后,在空间中就激发了电场。
同时导体上的电荷受到电场作用。
在静止情况,导体上的电荷分布使得导体表面为一个等势面。
因此,由导体上的总电荷和导体面为等势面的条件同时确定空间中的电场以及导体上的电荷面密度。
例 如图2-4,两同心导体球壳之间充以两种介质,左半部电容率为 ε1,右半部电容率为 ε2。
设内球壳带总电荷Q ,外球壳接地,求电场和球壳上的电荷分布。
解 设两介质内的电势、电场强度和电位移分别为 φ1, E 1,D 1 和 φ2 ,E 2,D 2。
由于左右两半是不同介质,因此电场一般不同于只有一种均匀介质时的球对称解。
在找尝试解时,我们先考虑两介质分界面上的边值关系21,t t E E = (4.2---16) 21,n n D D = (4.2---17) 如果我们假设E 仍保持球对称性,即 13Ar =r E ,(左半部) 23Ar=r E ,(右半部) (4.2---18) (A 为待定常数),则在分界面两侧电场与界面相切,并有相同数值。
因而边值关系(4.2---16)得到满足。
而且由于 D 2n = D 1n = 0 ,因而(4.2---17)式亦被满足。
球对称的E 再到体面上处处与球面垂直,因而保证导体球面为等势面。
为了满足内导体总电荷等于Q 的条件,我们计算内导体球面上的积分121122,S S d d d εε⋅=⋅+⋅=⎰⎰⎰ÑD S E S E S Q (4.2---19)其中 S 1和 S 2 分别为左右半球面。
把(4.2---18)式代入得 122().A Q πεε+= 解得122()A πεε=+Q代入(4.2---18)式得 1312,2()rπεε=+QrE (左半部) 2312.2()r πεε=+QrE (右半部) (4.2---20)此解满足唯一性定理的所有条件,因此是唯一正确的解。
虽然 E 仍保持球对称性,但是D 和导体上的电荷面密度σ不具有球对称性。
设内导体球半径为a ,则球面上的电荷面密度为 11111212,2()r r D E a εσεπεε===+Q(左半部)22222212.2()r r r D E aεσεπεε===+Q(右半部) 注意导体两半球上的面电荷密度是不同的,但E 却保持球对称性。
读者试解释这一点。
第21讲 习题解答:第35-36页,第7,8,9,11,12,13题。
7.有一内外半径分别为1r 和2r 的空心介质球,介质的介电常数为ε使介质内均匀带静止自由点荷f ρ求:(1) 空间各点的电场(2) 极化体电荷和极化面电荷分布解:(1)在1r 内取同心球面,以r (1r r <)为半径 ∵D ρ∇⋅=u u v∴0SD d σ⋅=⎰⎰u u vu u vÒ ∴0D E ==u v u u v在12r r r <<内取同心球面r ,233144()3f D d E r r r σεππρ⋅=⋅=-⎰⎰u u vu u v Ò ∴3313()3f r r E r r ρε-=u u vuv 在2r r >取同心球:23302144()3f D d S E r r r εππρ⋅=⋅=-⎰⎰u u v u vÒ∴333210()/3f E r r r r ρε=-u u v u v方向:f ρ为正,均为圆心射线方向,f ρ为负,均为汇聚圆心方向(2)∴0000()(1)p f f p E D χεχεερχερρεεε=-∇⋅=-∇⋅=-∇⋅=-=-u vu u vu u v ∴1r r <或2r r >处是真空 ∴0p ρ= 在12r r r << 0(1)p f ερρε=- ∴1100p r r Eσε=== (1r r =)2332122200))()3((f r r p r r rEσρεεεεε==-=--3302122(1)3f r r r ερε-=- 2122211223333002121444440()(1)()(1)033r p p P r f f r r r drr r r r πσπσρπεεπρπρεε++=+--+--=⎰即,介质的总极化电荷为零。
