MIMO信道容量
MIMO信道容量极限

结果,描述了一些尚未解决的问题以及与 MIMO 系统相关的设计问题。 记号上的提示:我们用黑体表示矩阵和向量,用 表示期望, S 表示行 列式,S 1 表示方阵 S 的逆。对于一般性的矩阵 M ,M † 表示共轭变换,Tr M 表 示迹。 I 代表单位阵, diag i 表示对角元素 i, i 等于 i 的对角阵。对于对称矩 阵,记号 Q 0 表示 Q 是一个半正定阵。 全文中缩写的表格在表格 I 中给出。
表格 I 缩写表
CSI 信道状态信息 CDI 信道分布信息 CSIT 发送端信道状态信息 CSIR 接收端信道状态信息 CDIT 发送端信道分布信息 CDIR 接收端信道分布信息 ZMSW 零均值空间白色 CMI 信道均值信息 CCI 信道协方差信息 DPC 脏纸编码 MAC 多址接入信道 BC 广播信道 本文中剩下部分的安排如下。在第二节中,我们讨论了发送端和接收端在不 同信道状态和分布信息的假设下的单用户 MIMO 系统的容量。这一节中也描述 了波束形成和训练序列问题的最优性。第三节中也描述了 MIMO 多址接入信道 的容量区域和脏纸编码可获得的 MIMO 广播信道的容量区域,以及这些区域之 间的对偶连接。多小区系统在脏纸编码(DPC)和波束形成下的容量在第四节中讨 论,第四节中也讨论了容量,分集,扇区化之间的折中。第六节总结了这些容量
2
话并且发送数据丢失。 在这一场景下,每一个发送速率都有一个与之有关的掉话 概率,容量由相应的掉话概率来测量(容量 CDF)[20]。一篇关于单天线信道的 衰落信道容量的极好的学习材料可以在[4]中找到。对于有着发送端和接收端理 想 CSI 的单用户 MIMO 信道,遍历容量和中断容量的获得是容易的,因为对于每 一个信道状态 容量都已经知晓了。因此,对于单用户 MIMO 系统本文重点放在 容量结果上,假定发送端获得理想 CDI 接收端获得理想 CSI 或 CDI。尽管最近在 这一领域内获得很大进步,还有很多未解决的问题。 在多用户信道中, 容量变成一个由所有速率向量 R1 , , RK 集合定义的 K 维 区域, 这一速率向量由 K 个用户同时获得。 时变信道在不同发送端和接收端 CSI、 CDI 假设下的多个容量定义可以以显然的方式扩展到多址接入信道(MAC)和广播 信道(BC)的容量区域[28],[48],[49],[70]。 然而, 这些 MIMO 多用户容量区域即使对 于时不变信道也是很难找到的。 。多用户 MIMO 时变信道的容量结果基本上是没 有的,尤其是在发送端和(或)接收端只有 CDI 的实际情况下。因此对于多用户 MIMO 系统,本文的重点是在发送端和接收端获得理想 CSI 假设下的遍历容量, 对已知的结果以及其他容量定义和 CSI/CDI 假设下的尚未解决的问题进行了简要 讨论。 注意到此处描述的 MIMO 技术对于任何由矩阵描述的信道都是适用的。矩 阵信道不仅能描述多天线系统也能描述带有串扰的信道[85]和宽带信道[72]。尽 管本文的重点是无记忆信道(平坦衰落) ,我们会在一节中讨论使用广泛知道的 将信道时延扩展合并到信道矩阵中的方法,结果也可以扩展到有记忆信道(ISI)。 已经发展了很多实际的 MIMO 技术来利用香农理论预测的理论容量增益。 这一方面主要的工作是空时编码:这一方面最近的工作总结在[21]中。MIMO 系 统其他的技术包括空时调制[30], [33], 自适应调制和编码[10], 空时均衡[2], [51], 空时信号处理[3],空时 CDMA[14],[34],以及空时 OFDM[50],[52],[82]。对这些领 域近期的发展以及其他技术和这些技术的性能的总结可以在[25]中找到。
MIMO—OFDM系统无线衰落信道容量分析

便 构成 了 MI O O D 系统 。如果 用 和 分别 M .F M 表示发送 天线 和接 收天 线 的个 数 , 发送 数 据 需要 经
aeae rcie in os ai S R) whc es ic t aa tr d tr nn ecp ct;tei a t f e t ea pe do v rg eev ds a n i rt gl e o( N , ih a i f a r mees eemii t aa i h mp c i d l sra n r g in p n g h y o t me h y
Ab ta t Th ro i c p ct n pi lp we lo ain p lc fb o d a d MI sr c e e g dc a a iy a d o tma o ralc t iy o r a b o o n MO— DM y tms i rls a ig c a n l s OF s se n wiee sfdn h n esi d rv d b sd o h y tm d 1 Th n, eu p rb u d o a a i d i an o e i l ne naOF e ie a e n t e s se mo e . e t p e o n fc p ct a t g i v rsnge a tn DM r ac ltd frt eso fdng h yn s aec u ae o lw a i l h
c a n lwi qu — we l y. e rs lsidc t a e c a n lc p ct fMI h n e t e a p h l o rp i T e ut n iaet tt h n e a a i o MO— o c h h h y OFDM y tm rwswi e n mb ro tn a d s se go t t u e fa e n sa h h n n
《MIMO及信道模型》课件

MIMO技术的应用场景
MIMO技术广泛应用于无线通信系统,如4G、5G移 动通信系统、无线局域网(WLAN)、无线个人域网
(WPAN)等。
输标02入题
在4G和5G移动通信系统中,MIMO技术被用于提高 小区的覆盖范围和边缘用户的传输速率,同时也可以 提高系统的整体吞吐量。
01
03
以上内容仅供参考,具体内容可以根据您的需求进行 调整优化。
MIMO技术利用了无线信道的散射和 反射特性,通过空间复用和分集增益 ,提高了无线通信系统的传输速率和 可靠性。
MIMO技术的原理
MIMO技术的基本原理是利用多天线之间的独立性,将数据流分解成多个并行子流,在多个子流上同时传输,从而提高了传 输速率。
在接收端,多个天线接收到的信号经过处理后,可以恢复出原始的数据流。MIMO技术通过信号处理算法实现信号的分离和 合并,从而提高了信号的抗干扰能力和传输可靠性。
在此添加您的文本16字
天线选择
在此添加您的文本16字
最大信噪比 (Max-SNR): 选择能提供最大信噪比的发射天 线。
在此添加您的文本16字
轮询 (Round Robin): 轮流使用每个天线进行传输,确保 均衡使用。
05
CHAPTER
MIMO系统实现难点及挑战
信号处理复杂度
MIMO信号检测算法复杂度
考虑了信号在传播过程中因反射、折射和散射产生的多径 效应,适用于室内和室外非视距(NLoS)环境。
MIMO信道模型的特点
高数据速率
通过在发射端和接收端使用多个天线,提高 了数据传输速率。
抗干扰能力强
通过分集技术,降低了信号被干扰的风险。
频谱效率高
通过空间复用技术,提高了频谱利用率。
2、MIMO信道容量推导

二、信道容量的推导主要研究基于VBLAST 的MIMO 系统:系统:串并变换调制调制调制VBLAST 检测器y1y2ym 比特分配功率分配b1bnb2信道估计丰富的散射信道2p 1p pn 数据图2.1 采用VBLAST 结构MIMO 系统框图系统框图MIMO 信道容量的推导:信道容量的推导:(信道容量定义为MIMO 系统在单位带宽上的数据传输速率)系统在单位带宽上的数据传输速率)根据奇异值分解(SVD)理论,在k 时刻,任何一个M ×N 矩阵H 可以写成可以写成HH =UDV 式中,D 是M ×N 非负对角矩阵;U 和V 分别是M ×M 和N ×N 的酉矩阵,且有H HM =UU I 和H N =VV I ,其中M I 和N I 是M ×M 和N ×N 单位阵。
D 的对角元素是矩阵H HH 的特征值的非负平方根。
H HH 的特征值(用l 表示)定义为定义为 H l =HH y y ,0¹y式中,y 是与l 对应的M ×1维矢量,称为特征矢量。
特征值的非负平方根也称为H 的奇异值,而且U 的列矢量是H HH 的特征矢量,V 的列矢量是HH H 的特征矢量。
矩阵H HH 的非零特征值的数量等于矩阵H 的秩,用m 示,其最大值为),min(N M m =。
则可以得到接收向量。
则可以得到接收向量 H =r UDV x +n引入几个变换H r'=U r ,H x'=V x ,H'n =U n ,这样等价的信道可以描述为:'''r =Dx +n 对于M ×N 矩阵H ,秩的最大值),min(N M m =,也就是说有m 个非零奇异值。
值。
将i l 代入上式,可以得到接收信号为:代入上式,可以得到接收信号为:'''i i i i r x n l =+(m i ,,2,1 =)''i i n r =(1,2,,i m m M =++ )可以看出等效的MIMO 信道是由m 去耦平行子信道组成的。
MIMO信道容量计算公式

MIMO信道容量计算公式
MIMO(Multiple-Input Multiple-Output)是一种通过同时使用多个发射天线和接收天线来增加无线通信系统容量的技术。
MIMO技术可以利用信道的冗余和多路径效应,提高信号的传输速率和可靠性。
1.SISO信道容量计算公式:
SISO信道容量的计算公式使用香农公式,用于计算传输速率。
香农公式如下:
C = B * log2(1 + SNR)
其中,C是信道容量,B是带宽,SNR是信噪比(Signal-to-Noise Ratio)。
SISO信道容量计算公式适用于只有一个天线的系统。
2.MIMO信道容量计算公式:
C = log2(det(I + H*SNR*H^H))
其中,C是信道容量,H是MIMO信道的传输矩阵,SNR是信噪比。
除了以上基本的MIMO信道容量计算公式,还有一些进一步考虑调制方式、信道状态信息等因素的改进公式,如ZF(Zero Forcing)和MMSE (Minimum Mean Square Error)等方法,用于提高MIMO系统的容量。
这些方法考虑了天线之间的干扰和多径效应,可以优化信号的传输和接收性能。
总结起来,MIMO信道容量的计算公式可以通过SISO信道容量公式和MIMO信道容量公式来表示,具体的计算方法需要综合考虑信道状况和系
统参数,并结合数值计算方法进行分析。
通过合理设计和优化,MIMO技术可以显著提高无线通信系统的容量和性能。
MIMO信道的信道容量

Pi 1/ 0 1/ i 0 P
其中 0 为某个门限值。由此得到信道容量为
i 0 i 0 (1-6)
C B log 2 (
i: i 0
i ) 0
对于有一个发送天线和多个接收天线的单入多出系统,或者有多个发送天线 一个接收天线的多入单出系统,也可以定义出收发都有理想信道信息时的容量。 这些信道可以通过多天线获得分集增益和阵列增益,但没有复用增益。当发送端 和接收端都已知信道信息时, 其容量等于信号在发送端或接收端进行最大比合并 后得到的 SISO 信道的容量为
1 引言
信道容量的计算是研究噪声信道的主要关注点之一。信道容量的定义是以任 意小的差错率传输信息的最大速率,它建立了可靠通信的基本极限。因此,信道 容量广泛应用于衡量通信系统的性能。本文的主要目标是研究与 MIMO 无线信 道有关的信道容量。 MIMO 信道的香农容量是能够以任意小的差错率传输的最大数据率。中断容 量则定义为能使中断率不超过某个数值的最大数据率。 信道容量的大小和收发两 端是否已知信道增益矩阵或其分布有关。 下文先给出不同信道信息假设下静态信 道的容量,它是其后讨论的衰落信道容量的基础。
MIMO 信道的信道容量
摘要
由于 MIMO 可以在不需要增加带宽或总发送功率耗损(transmit power expenditure)的情况下大幅地增加系统的资料吞吐量(throughput)及传送距离, 使得此技术于近几年受到许多瞩目。MIMO 的核心概念为利用多根发射天线与 多根接收天线所提供之空间自由度来有效提升无线通信系统之频谱效率, 以提升 传输速率并改善通信品质。研究 MIMO 信道的容量是对 MIMO 进行深入分析的 基础,本文分析了 MIMO 信道的容量计算方法,分别介绍了在静态信道中的注 水法、平均功率分配法信道容量,以及衰落信道中遍历容量和中断容量。 关键词:MIMO,信道容量,注水法,平均功率分配,遍历容量,中断容量
MIMO通信系统的信道容量分析及MATLAB仿真实现

3 MI MO 系 统 信 道 模 型
研 究 MI MO系统 必 须考虑 信 道模 型 , 设研 究 的信道 为基 于瑞 利衰 落 的随机信 道 , MI 设 MO系统 信道模 型有 J V根发 射 天线 和 M 根接 收天 线 ,信道矩 阵 H( J 表 示第 i 发射 天线 到第 7 接 收天线 的信道 衰落 系 i) , 根 根 数 ,每根 发射 天线 的功 率为 P Ⅳ,每 根接 收天 线 的噪声 功率 为 ,故 信 噪 比 S R为 : =P/ I.通过分 / N 4 】
21 0 2年 4月
Apr 201 . 2
MI MO通信系统 的信道容 量分析及 MA L B仿真实现 TA
朱琳璐
( 丽水广播 电视 大 学 ,浙 江 丽水 3 3 0 2 0 0)
摘
要 :在 多入 多 出( MO) MI 系统原 理和模 型 的基础 上 ,分析 了基 于单入 单 出(I O 、单入 多 出( I SS ) SMO) 、多
解信道特征矩阵 Q的特征值 ,由香农公式导出 MI MO信道容量 C= o:el +P( ̄) } Wl dt 【/ r 】 ,其中威沙 g { N Q
特矩 阵 Q=HH“,M <N ;Q=日“ , M ≥N ; I 是 mi( n M,N) 阶单位 矩 阵 ;W 为 每个子 信道 的带宽 ,
还是 提高 频谱 的资源 利用率 .在无线 通信 中,使 用 多输入 、多输 出( MO:Mut l Ip t lpeOup t MI lpe n u— t l— tu) i — Mu i
技术 既能增 加 系统容量 ,也 能增强 系统 性能 ,在其 他条 件相 同 的前 提下 ,可 以成倍地 提 高频谱 效率 .
‘4 1 5‘
MIMO信道容量计算公式
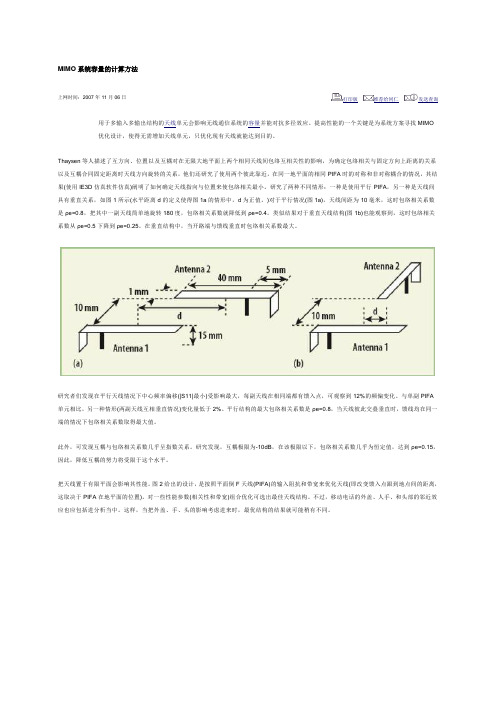
MIMO系统容量的计算方法上网时间:2007年11月06日打印版推荐给同仁发送查询用于多输入多输出结构的天线单元会影响无线通信系统的容量并能对抗多径效应。
提高性能的一个关键是为系统方案寻找MIMO优化设计,使得无需增加天线单元,只优化现有天线就能达到目的。
Thaysen等人描述了互方向、位置以及互耦对在无限大地平面上两个相同天线间包络互相关性的影响,为确定包络相关与固定方向上距离的关系以及互耦合同固定距离时天线方向旋转的关系,他们还研究了使用两个彼此靠近,在同一地平面的相同PIFA时的对称和非对称耦合的情况,其结果(使用IE3D仿真软件仿真)阐明了如何确定天线指向与位置来使包络相关最小。
研究了两种不同情形:一种是使用平行PIFA,另一种是天线间具有垂直关系,如图1所示(水平距离d的定义使得图1a的情形中,d为正值。
)对于平行情况(图1a),天线间距为10毫米,这时包络相关系数是ρe=0.8,把其中一副天线简单地旋转180度,包络相关系数就降低到ρe=0.4。
类似结果对于垂直天线结构(图1b)也能观察到,这时包络相关系数从ρe=0.5下降到ρe=0.25。
在垂直结构中,当开路端与馈线垂直时包络相关系数最大。
研究者们发现在平行天线情况下中心频率偏移(|S11|最小)受影响最大,每副天线在相同端都有馈入点,可观察到12%的频偏变化。
与单副PIFA单元相比,另一种情形(两副天线互相垂直情况)变化量低于2%。
平行结构的最大包络相关系数是ρe=0.8,当天线彼此交叠垂直时,馈线均在同一端的情况下包络相关系数取得最大值。
此外,可发现互耦与包络相关系数几乎呈指数关系。
研究发现,互耦极限为-10dB,在该极限以下,包络相关系数几乎为恒定值,达到ρe=0.15,因此,降低互耦的努力将受限于这个水平。
把天线置于有限平面会影响其性能。
图2给出的设计,是按照平面倒F天线(PIFA)的输入阻抗和带宽来优化天线(即改变馈入点跟到地点间的距离,这取决于PIFA在地平面的位置)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ρ=
σ
2
3.5.2 MIMO无线信道的容量
• 定义
若由x的实部和虚部构成2n维实随机向量
ˆ x = [Re( xT ) Im( xT )]T是高斯随机向量,则称x
为n维复高斯随机向量。 如存在非负定(特征值都小于零)的Hermitian 矩阵QєCn×n,使得n维复高斯随机向量x所对应 的2n维实随机向量 x 的协方差满足 ˆ
λi
yi ' = λi xi '+ ni ', i = 1,L, r
yi ' = ni ', i = r +1,L, MR
3.5.3 用SVD方法对MIMO的进一步分析
Q
Ry′y′ = U H RyyU Rx′x′ = V RxxV
H
tr ( Ry′y′ ) = tr ( Ryy ) tr ( Rx′x′ ) = tr ( Rxx ) tr ( Rn′n′ ) = tr ( Rnn )
| hij |2 = M T , (i = 1, 2,L M R ) ∑
j =1 MT
HH H = MI M
MP P T C = F log det( I M + I M ) = F log det(diag (1 + T2 )) 2 Mσ σ P M P T = F log(1 + 2 ) = MF log(1 + T2 )
nn MR
•
C = EH {log[det( I M R
PT H + 2 HH )]} σ MT
= EH {log[det( I M R +
ρ
MT
HH )]}
H
3.5.2 MIMO无线信道的容量
• 中断容量 中断容量:指信道瞬时容量值小于某个指 定容量值的概率等于某一给定中断概率 Poutage时,该给定的信道容量称为对应于该 中断概率的中断容量Coutage,即
i
MT
r λi PT λi PT ∴ C = F ∑ log(1 + ) = F log ∏ (1 + ) 2 2 M Tσ M Tσ i =1 i =1 r
3.5.3 用SVD方法对MIMO的进一步分析
HH H , M R ≤ M T m = min( M R , M T ) G = H H H , M R ≥ M T PT C = F log det( I m + G) 2 M Tσ
i
yi′ = ni′ (i=r+1,r+2,L M R )
3.5.3 用SVD方法对MIMO的进一步分析
• 等效的MIMO信道可看成由r个相分离的并 行子信道组成,每个子信道指配一个H矩阵 的奇异值(或HHH的特征值),该奇异值 λi 相当于该子信道的幅度增益,而子信道的 功率增益相当于HHH的特征值λi。
λi
3.5.3 用SVD方法对MIMO的进一步分析
Pyi = (λν − σ ) i
C = F ∑ log(1 +
i =1 r
2 +
Pyi
σ
2
)
C = F ∑ log(1 +
i =1
r
1
σ
2
(λi µ − σ ) )
2 +
3.5.3 用SVD方法对MIMO的进一步分析
• 例2 正交传送的MIMO信道 令发送天线数和接收天线数相等,发送 机与相应的接收机之间通过正交、并行的子 信道相连接,因而各个子信道之间无干扰。
y = Hx + n
n ~ N (0, σ 2 I )
Model applies to any channel described by a matrix (e.g. ISI channels)
3.5.1 MIMO系统模型
• 发送信号:第j根天线发送xj为零均值i.i.d高 斯变量,发送信号的协方差矩阵为:
3.5 MIMO信道及其容量(总结)
• 采用空间分集技术的MIMO系统是对抗无线衰落、 提高传输信道容量的一种行之有效的方法。 • 在相同发射功率和传输带宽下,MIMO系统较单天 线系统的信道容量大大提高,有时甚至高达几十倍。 • 这些增加的信道容量既可用来提高信息传输速率, 也可不提高信息速率而通过增加信息冗余度提高通 信系统的性能,或者在两者之间取得折中。
• 矩阵HHH的非零特征值数目m等于矩阵H的秩r。 对于MR×MT矩阵H,其秩最大为 m = min( M R , M T ) 即H的非零奇异值最多有m个。 • 用 λi (i = 1, 2,L r ) 表示H的奇异值,则
yi′ = λi xi′ + ni′ (i=1,2,L r)
• 从第1个到第r个接收分量,子信道增益为 λi , 而从第r+1接收分量起,子信道的增益为0,相应 的接收分量不再依赖发送分量 x′ 。
σ
σ
3.5.3 用SVD方法对MIMO的进一步分析
• 当MR= MT=M=8 ,SNR=24bit / sec/ Hz F
各子信道不相关联地给出了M倍增益。
3.5 MIMO信道及其容量(总结)
• MIMO系统的信道容量主要由H的奇异值决定,即 HHH的特征值。反映各支路的相关程度。 • 发送端未知CSI,采用功率均分
∑h
j =1
MT
2
ij
= M T , i = 1, 2,L M R
3.5.1 MIMO系统模型
• 接收端的噪声:各分量为独立的零均值高 斯变量,具有独立的和相等方差的实部和 虚部。 • 噪声协方差矩阵 Rnn = E{nn }
H
• 若n的分量间不相关, Rnn = σ I M R
2
• 每根接收天线具有相等的噪声功率σ2。 • 每根接收天线输出端的信号功率为PT,故 接收功率信噪比为 PT
Rxx = E{ xx H }
• 总的发送功率约束为 PT = tr ( Rxx ) • 若每根天线发送相等的信号功率PT/MT,
PT Rxx = I MT MT
3.5.1 MIMO系统模型
• 信道矩阵:H为复矩阵,hij表示第j根发送天 线至第i根接收天线的信道衰落系数。 • 归一化约束:每一根天线的接收功率均等 于总的发送功率
λi PT C = F ∑ log(1 + ) 2 M Tσ i =1
r
• 发送端已知CSI:采用water-filling,增加容量 r 1 C = F ∑ log(1 + 2 (λν − σ 2 ) + ) i
i =1
σ
• 发送端未知CSI时的信道容量小于或等于已知CSI 时的信道容量,是因为发送端可利用CSI对发送 模块进行优化处理。
ˆ ˆ ˆ ˆ E ( x − E{x})( x − E{x})
{
H
}
1 Re (Q ) − I m (Q ) = 2 I m (Q ) Re (Q )
则称x为循环对称复高斯随机向量。
3.5.2 MIMO无线信道的容量
• 定理1 设x єCn为零均值n维循环高斯复随机向量, H 且满足 E{xx } =,即 Q
E{xi x } = Qij , (1 ≤ i, j ≤ n)
* j
则x的熵满足
H ( x) ≤ log det(π eQ)
当且仅当x为循环对称复高斯分布时等式成立。
3.5.2 MIMO无线信道的容量
• 循环对称复高斯向量的性质 循环对称复高斯向量的性质: 若x єCn为零均值n维循环对称复向量,则 对任意的A єCn×n ,y=Ax也服从循环对称 高斯分布,且 E{ yy H } = AQAH 若x,y єCn为n维循环对称复高斯向量,且 相互独立, {xx H } = A , { yy H } = B , E E 则z=x+y也服从循环对称复高斯分布,且
3.5 MIMO信道及其容量
3.5.1 MIMO系统模型 3.5.2 MIMO无线信道的容量 3.5.3 用SVD方法对MIMO的进一步分析
3.5.1 MIMO Channel Model
MT TX antennas h11 h31 h21 h22 h32 h13 h23 h33 h12 MR RX antennas
H
• z为关于特征值λ的MR×1特征向量。U的列是HHH的 特征向量,V的列是HHH的特征向量。
HH z = λ z , z ≠ 0
H
3.5.3 用SVD方法对MIMO的进一步分析
y = UDV x + n
H
令 y′ = U y
H
x′ = V x
H
n′ = U n
H
则
y′ = Dx′ + n′
3.5.3 用SVD方法对MIMO的进一步分析
Rn′n′ = U H RnnU
• 即y’、x’ 和n’的协方差矩阵与变换前y,x, n的协方差阵具有相同的迹(对角线元素 之和)或功率。
3.5.3 用SVD方法对MIMO的进一步分析
• 各子信道是分开的,因而它们的容量相加。 假定在等效MIMO信道模型中每根天线发送 PT 的功率为 ,总的信道容量可利用 MT r Pi Shannon公式求出: C = F ∑ log(1 + 2 ) σ i =1 • 式中F为每个子信道的带宽,Pi为第i个子信 道的接收信号功率: P = λi PT
PT = F log det( I m + HH H ) M Tσ 2 PT 或 F log det( I m + HHH) M Tσ 2
若信道系数是随机变量,上式表示瞬时容 量。遍历容量可通过对信道系数求统计得出。
3.5.3 用SVD方法对MIMO的进一步分析
例1:自适应发送功率情况下的MIMO信道容量 在系统呈闭环 闭环情况下,发送端可知信道 闭环 的状态信息(CSI),可根据注水法则,将 发送功率分配给各发送天线,即将较大的发 送功率分配给状态较好的信道,则可以增大 容量。 2 σ + Pi = (ν − ) i = 1, 2,L r (a)+表示max(a,0)
