勾股定理的应用1
勾股定理的应用(1)

S3
S2
S1
心,在森林公园附近有 B、C 两个村庄,现要在 B、C两
村庄之间修一条长为 1000 m 的笔直公路将两村连通,
经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森
林公园?请通过计算说明.
解: ∵∠B=60°,∠C=30°,
400
A
∴∠BAC=90°
∴AB=½ BC=500m,
由AC勾股定10理00,2 得5002 500 3 60° ┐
l h
┐
b
解:10 1.52 32 33.5(m2 )
5. 如图,在甲村到乙村的公路旁有一块山地正在开发, 现有A处需要爆破.已知点A与公路上的停靠站B,C的距离 分别为400m和300m,且AC⊥AB.为了安全起见,如果爆 破点A周围半径250m的区域内不能有车辆和行人,问在 进行爆破时,公路BC段是否需要暂时封闭?为什么?
解:由勾股定理,得 A
BC AB2 AC 2 l 2 h2 122 82
4 5 8.9(m)
lh
B
C
答:点B离电线杆底部点C的距离
约为8.9米.
4. 如图要修一条塑料蔬菜大棚,棚宽 b=3m,高 h=1.5m, 长 l=10m.求覆盖在顶上的长方形塑料薄膜需要多少平方 米?(精确到 0.1m²)
解:过A作AD⊥BC,垂足为D.
甲
由勾股定理,得
B
BC²=AB²+AC²=400²+300²=250000
∴BC=500
D
勾股定理在生活中的应用

勾股定理在生活中的应用
勾股定理又称勾股论,即毕达哥拉斯设计的一个无理定理:“任意三角形的两边之积等于另外一边的平方之和”。
这个定理具有广泛的应用:
1、勾股定理在日常生活中可以用来确定三角形各边之间的关系:例如可以判断其中一边是不是一个倍数关系或者一个反比例关系。
通过建立对应方程,容易得到三角形三边的数值,作为三角形的参数。
2、也可以依据勾股定理来测量距离。
例如,构建一个直角三角形,让其一条边固定为一个值,我们使用两个斜边长度表示其他边的长度。
可以用i中国的三角测量法来求得某个距离的长度。
3、另外可以用勾股定理判断特殊的三角形。
例如可以判断一个三角形是不是等腰三角形、等边三角形或是直角三角形,只需要判断两边之积是否等于另外一边的平方之和。
4、勾股定理在空间中也有极大的作用,尤其是研究四面体或是更高维度的几何图形时。
例如可以用它来判断四面体的面面角是否都相等,以及求出该四面体的各个角。
另外还可以用它来求棱锥的体积、双曲线的起始点和极点等。
5 、另外勾股定理在物理学中也有广泛的应用,比如可以分析绳子长度或梯形长宽间的关系等。
总之,勾股定理由其卓越的简洁得到广泛应用,从日常生活到飞空实验都能发挥着无穷的作用,它被越来越多的人向科学家们赞美。
勾股定理的应用的例子

勾股定理的应用的例子:
一、圆柱侧面上两点间的最短距离圆柱侧面的展开图是一个矩形,圆柱上两点之间最短距离的求法,是把圆柱展开成平面图形,依据两点之间线段最短,以最短路线为构造直角三角形,利用勾股定理求解.
二、长方体(或正方体)表面上两点间的最短距离长方体每个面都是平面图形,所以计算同一个面上的两点之间的距离比较容易,若计算不同平面上的两点之间的距离,就变成了两个面之间的问题,必须将它们转化到同一平面内,即把四棱柱设法展开成一个平面图形,再构造直角三角形利用勾股定理解决,正方体的展开图从哪一面上展开都一样,而长方体的展开图一定要注意打开哪一个侧面,并且向上、下与向左、右展开会出现长度不的路线,应通过尝试从几条路线中选一条符合要求的.
三、折叠问题关于折叠问题的解题步骤:(1)利用重叠的图形传递数据(一般不用重叠的图形进行计算);(2)选择或构造直角三角形,这个直角三角形一般一边已知,另两边可通过重叠图形找到数量关系,从而利用勾股定理列方程求解.。
勾股定理的应用及方法

勾股定理的应用及方法勾股定理是数学中的一个重要定理,它描述了直角三角形中,直角边的平方和等于斜边的平方。
具体表述为:在一个直角三角形中,设直角边的长度分别为a 和b,斜边的长度为c,则有a²+ b²= c²。
勾股定理的应用非常广泛,在几何学、物理学和工程学等领域都有重要的应用。
下面我将介绍一些常见的勾股定理的应用及解题方法。
1. 求解三角形的边长和角度:勾股定理可以用于求解三角形的边长和角度。
当我们已知两条边长,可以利用勾股定理计算出第三条边长。
而已知两边长和夹角时,可以利用勾股定理计算出第三边长或者求解夹角的大小。
例如,已知直角三角形的斜边长为5,一条直角边长为3,我们可以利用勾股定理计算出另一条直角边的长度:3²+ b²= 5²9 + b²= 25b²= 16b = 4同样地,已知直角三角形的两条直角边长度为3和4,可以利用勾股定理计算斜边的长度:3²+ 4²= c²9 + 16 = c²c²= 25c = 52. 解决实际问题:勾股定理也可以应用于解决实际问题。
例如,在测量中,我们经常需要通过已知的边长计算其他未知边长的问题。
有一道经典的应用题是“房子问题”:如果一个房子的两堵墙的长度分别为6米和8米,房子的对角线长度是多少?根据勾股定理可知,对角线的长度即斜边的长度c,可以通过勾股定理求解:6²+ 8²= c²36 + 64 = c²c²= 100c = 10因此,房子的对角线长度为10米。
3. 判断三角形的形状:勾股定理还可以用来判断三角形的形状。
根据勾股定理,如果一个三角形的三条边满足a²+ b²= c²,那么这个三角形就是直角三角形。
例如,如果一个三角形的三条边长分别为3、4和5,我们可以通过勾股定理验证这个三角形是否为直角三角形:3²+ 4²= 5²9 + 16 = 2525 = 25由此可见,三角形的三条边满足勾股定理,所以这个三角形是一个直角三角形。
勾股定理的应用1
C
B
A
1,你能从点A到点B沿圆柱侧面 画出几条路线,你觉得哪条线路 最短呢?
C
B
A
2,将圆柱侧面开展成一个长方形, 从点A到点B的最短路线是什么?
C
B
C
B
A
A
3.蚂蚁从点A出发,想吃到点B处的食物,它沿 圆柱侧面爬行的最短路程是多少? (圆柱体的底面周长为18cm, 高AC为12cm)
C
B
C
B
3.有一圆形油罐底面圆的周长为24m,高为6m,一 只老鼠从距底面1m的A处爬行到对角B处 吃食物,它爬行的最短路线长为多少?
B
C A
B
A
分析:由于老鼠是沿着圆柱的 表面爬行的,故需把圆柱展开 成平面图形.根据两点之间线段 最短,可以发现A、B分别在 圆柱侧面展开图的宽1m处和长 24m的中点处,即AB长为最短 路线.(如图)
A
A
4,若蚂蚁先从点A 直接向上爬到点C, 然后再从点C沿底 C 面直径爬到点B, 这样爬的总路程与 沿圆柱侧面爬行的 A 最短路程比较,哪 条最短?
B
李叔叔想要检测雕塑底座正面的边AD 和边BC是否分别垂直于底边AB,但 他随身只带了卷尺, 1.你能替他想办法完成任务吗?
D C
A B
2,李叔叔量得边AD长是30cm,边AB 长是40cm,点B,D之间的距离是 50cm,边AD垂直于边AB吗? 3,小明随身只有一个长度 为20cm的刻度尺,他能有办法 检验边AD是否垂直于边AB吗? 边BC与边AB呢?
这是测量 B
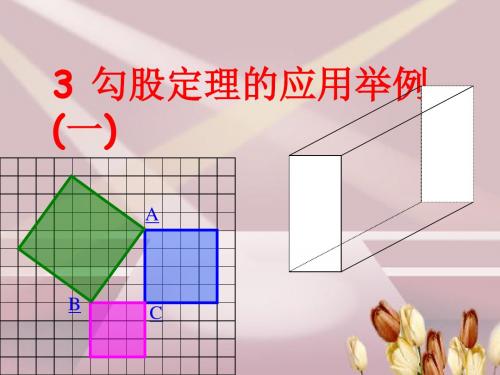
3 勾股定理的应用举例 (一 )
A
B
C
B 勾a C 弦c 股b
一、 勾股定理: 字母表示:
如果在Rt∆ABC中,
勾股定理的应用举例与解题方法

勾股定理的应用举例与解题方法勾股定理是一条著名的数学定理,它在几何学和代数学中具有广泛的应用。
本文将通过举例和解题方法来探讨勾股定理的应用。
一、求解直角三角形的边长勾股定理最常见的应用就是求解直角三角形的边长。
直角三角形是指一个角度为90度的三角形。
在这种三角形中,直角边即为斜边相对的两条边。
根据勾股定理,斜边的平方等于两条直角边的平方和。
举例1:已知一个直角三角形的一条直角边长度为5,另一条直角边长度为12,求斜边的长度。
解题方法:根据勾股定理可以得到:斜边的平方 = 直角边1的平方 + 直角边2的平方代入已知条件可得:斜边的平方 = 5² + 12² = 25 + 144 = 169开方得到斜边的长度为13。
因此,该直角三角形的斜边长度为13。
二、验证三条边是否构成直角三角形通过勾股定理,我们还可以验证三条边是否构成直角三角形。
举例2:已知三条边的长度分别为3、4、5,判断它们是否构成直角三角形。
解题方法:按照勾股定理,如果三条边的平方和等于斜边的平方,那么它们所构成的就是直角三角形。
代入已知条件可得:3² + 4² = 9 + 16 = 25而斜边的平方为5² = 25由此可见,两者相等,所以这三条边构成了直角三角形。
三、解决几何问题勾股定理不仅可以用于解决三角形问题,还可以应用于其他几何问题。
举例3:已知一个矩形的两条边长分别为5和12,求对角线的长度。
解题方法:由于矩形的对角线可以看作是直角三角形的斜边,我们可以利用勾股定理来求解。
根据勾股定理可以得到:对角线的平方 = 矩形的一条边长的平方 +矩形的另一条边长的平方代入已知条件可得:对角线的平方 = 5² + 12² = 25 + 144 = 169开方得到对角线的长度为13。
因此,该矩形的对角线长度为13。
四、应用于物理问题勾股定理还可以应用于物理问题的求解中。
举例4:一个投射角度为45度的物体以10 m/s的速度抛出,求物体在水平方向上的飞行距离。
勾股定理生活中的应用

勾股定理生活中的应用
勾股定理是数学中的一个重要定理,可以应用于许多实际问题中。
在生活中,勾股定理有以下应用:
1. 测量直角三角形的直角边和斜边的长度。
例如在建筑工程中,
使用勾股定理可以测量房间的对角线长度、屋顶的倾斜角度等。
2. 计算物体的投影距离。
例如,在射击运动中,使用勾股定理可
以计算弹道的投影距离,帮助射手瞄准目标。
3. 计算电路中电压、电流和电阻之间的关系。
例如,在电子工程中,使用勾股定理可以计算电路中不同元件之间的参数,帮助工程师
设计电路。
4. 计算航空航天器的飞行轨迹和速度。
例如,在航空航天领域中,使用勾股定理可以计算卫星的轨道位置和速度,帮助天文学家和工程
师进行航天探测任务。
总之,勾股定理是一种非常实用的数学工具,可以广泛应用于生
活中的各个领域,帮助人们解决实际问题。
勾股定理生活中的应用

勾股定理生活中的应用
勾股定理是数学中的一条重要定理,它在生活中有着广泛的应用。
勾股定理是
指直角三角形中,直角边的平方和等于斜边的平方。
这个简单的公式在我们的日常生活中有着很多实际的应用。
首先,勾股定理在建筑设计中起着重要作用。
在设计房屋或其他建筑物时,建
筑师需要使用勾股定理来计算房屋的结构和角度。
这有助于确保建筑物的结构稳固,同时也能够确保建筑物的外观符合设计要求。
其次,勾股定理在地理测量中也有着重要的应用。
地理学家和测量员们经常使
用勾股定理来计算地球上不同地点之间的距离和角度。
这有助于我们更好地理解地球的形状和大小,同时也能够帮助我们更准确地进行地图绘制和导航。
此外,勾股定理在工程领域也有着广泛的应用。
工程师们经常使用勾股定理来
计算机械设备的角度和距离,以确保设备能够正常运行并且安全稳定。
这对于工程项目的顺利进行至关重要。
最后,勾股定理还在日常生活中有着一些小小的应用。
比如在装修房屋时,我
们可能需要使用勾股定理来确保墙角的垂直度;在购买家具时,我们可能需要使用勾股定理来计算家具的尺寸和摆放位置。
总之,勾股定理在我们的生活中有着广泛的应用,它不仅帮助我们更好地理解
世界,同时也为我们的生活和工作提供了便利。
因此,我们应该更加重视数学知识的学习,以便更好地应用数学知识解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和为
.
2. 如图,在由单位正方形组成的网格图中标有AB,CD,EF,GH
四条线段,其中能构成一个直角三角形三边的是(
A CD,EF,GH B AB,EF,GH
) CE
C AB,CD,GH D AB,CD,EF
FA
G
B H D
3、如图,在由单位正方形组成的网格图 (1)求四边形ABCD的面积; (2) 你能判断 AD与CD的关系吗?说出你的理由
D
A
C
B
如图,小明的家位于一条南北走向的河流MN的东侧A处,某一天小明从家 出发沿南偏西30°方向走60 m到达河边B处取水,然后沿另一方向走80 m到达菜地C处浇水,最后沿第三方向走100 m回到家A处.问小明在河 边B处取水后是沿哪个方向行走的?并说明理由.
解:小明在河边B处取水后是沿南偏东60°方向行走的. 理由如下: ∵AB=60 m,BC=80 m,AC=100 m, ∴AB2+BC2=AC2. ∴∠ABC=90°. 又∵AD∥NM, ∴∠NBA=∠BAD=30°. ∴∠MBC=180°-90°-30°=60°.∴小明在河边B处取水后是沿南偏东60°方向行走的.
只最早何时进入我国领海?
例1、已知:如图,四边形ABCD,AB=1,BC=2,
CD=2,AD=3, 且AB⊥BC.
求四边形 ABCD的面积.
C
B
A
D
练习: 如图AB⊥BC,AB=BC=AD=2,CD=2 3
,
求∠DAB的度数。
例2、已知:在△ABC中,AB=15 cm,AC=13 cm,高AD=12 cm, 求S△ABC.
ห้องสมุดไป่ตู้
练习、如图,南北方向PQ以东为我国领海,以西为公海.晚上10:28,我边防反偷渡 巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我国领海靠近,便立 即通知正在PQ上B处巡逻的103号艇注意其动向.经检测,AC=10 n mile,AB =6 n mile,BC=8 n mile.若该可疑船只的速度为12.8 n mile/h,则该可疑船
棵大树从离地面6米处折断倒下,量得倒下部分的长是10米.出门在外的张
大爷担心自己的房子被倒下的大树砸到.大树倒下时能砸到张大爷的房子
吗?( )
A.一定不会 B.可能会
C.一定会
D.以上答案都不对
2、练习、如图,有两棵树,一棵高8m,另一棵高2m,两树相 距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ()
A.7m
B.8m
C.9m
D.10m
A
8m
C
B
2m
8m
3、见课本P56 4
4、一种盛饮料的圆柱形杯(如图),测得内部底面直径为5㎝,高为 12㎝,吸管放进杯里,杯口外面露出5㎝,问吸管要做多长?
C
A
B
• 例1、现有一楼房发生火灾,消防队员决定用消防车上的云梯去 救人。已知云梯最多只能伸长到10m,消防车高3m。救人时云梯 伸至最长,在完成从9m高处救人后,还要从12m高处救人,这 是消防车要从原处再向着火的楼房靠近多少米?(精确到0.1m)
1、在一块平地上,张大爷家屋前9米远处有一棵大树.在一次强风中,这
