第四章水轮机相似理论
水轮机的相似理论

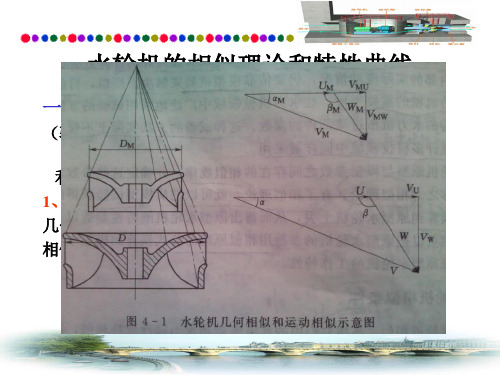
第三章水轮机的相似理论及综合特性曲线§3.1 相似理论概述一、几个基本概念1、水轮机特性水轮机在不同工况下运行时,各运行参数(H,Q,n,N,η,б)及这些参数之间的关系,称水轮机的特性。
水轮机设计、制造、选型、最佳运行方案、限制条件。
由于水轮机水流条件复杂,研究水轮机特性靠理论与实验相结合。
2、模型试验试验研究:原型:尺寸大,试验困难,不经济。
模型:(D: 250~460mm,H:2~6m)快、方便,易测量数据,较准确。
3、相似理论研究相似水轮机之间存在的相似规律,并确立这些参数之间的换算关系的理论。
二、水轮机相似条件保证模型水轮机与原型水轮机相似,只有符合一定的相似条件(水流运动相似)。
1、几何相似:过流通道几何形状相似(1)、过流通道的对应角相等:βe1=βe1M ;βe2=βe2M ;Φ=ΦM……(2)、对应尺寸成比例:D1/D1M=b0/b0M=a0/a0M=…….(3)、对应部位的相对糙率相等:△/ D1=△M/D1M几何相似: 大大小小的一套水轮机系列——轮系,同一轮系的水轮机才能建立运动相似和动力相似。
2、运动相似:同一轮系水轮机、工况相似(1)、过流通道的对应点的速度方向相同(2)、过流通道的对应点的速度大小对成比例即速度三角形相似。
3、 动力相似: (压力、惯性力、重力、摩擦力等)同一轮系水轮机,水流对应点所受的作用力是同名力、方向相同、大小成比例。
3.2 水轮机的相似定律、单位参数及比转速一、水轮机的相似定律相似定律:建立模型击原型水轮机各个参数(H 、n 、N 、η)之间的关系。
1. 流量相似律:几何相似、相似工况下流量之间的关系。
(a=a M )=SMM M rMM H DQ ηη21CH DQ Sr =ηη2111,,,D H D H M M 均为固定值,Q M 可以测得,若ηrM 、ηsM 、ηr 、ηs 已知,可求出Q 。
2. 转速相似律:即原型和模型水轮机转速之间的关系。
第4章 水轮机相似理论与特性曲线

二、单位参数
H=1m的标准水轮机参数 1、定义:指转轮直径D1=1m,水头H=1m的标准水轮机参数。 定义:指转轮直径D =1m,水头H=1m的标准水轮机参数。 称为单位转速,表示转轮直径D =1m,水头H=1m H=1m时水轮机具有的 1)n11—称为单位转速,表示转轮直径D1=1m,水头H=1m时水轮机具有的 7 转速;( ;(P86 12) 转速;(P86 公式 4-12)
6
第四章 水轮机相似理论与特性曲线 §4.2 相似律与单位参数
水轮机相似律(参数之间关系) 一、 水轮机相似律(参数之间关系)
1、转速相似律:(P85 公式4-8) 转速相似律:(P85 公式4 :( 物理含义:表示原型与模型水轮机在相似工况下转速之间的相互关系, 物理含义:表示原型与模型水轮机在相似工况下转速之间的相互关系, 它适用于同一系列的水轮机在相似工况下, 转速与直径成反比 与直径成反比, 它适用于同一系列的水轮机在相似工况下,其转速与直径成反比,与水头平方 根成正比。 根成正比。 流量相似律:(P86公式 10) :(P86公式4 2、流量相似律:(P86公式4-10) 物理含义:表示原型与模型水轮机在相似工况下流量之间的相互关系, 物理含义:表示原型与模型水轮机在相似工况下流量之间的相互关系, 它适用于同一系列的水轮机在相似工况下, 流量与直径平方成正比 与直径平方成正比, 它适用于同一系列的水轮机在相似工况下,其流量与直径平方成正比,与水头 平方根成正比。 平方根成正比。 出力相似律: P86公式 11) 公式4 3、出力相似律:(P86公式4-11) 物理含义:表示原型与模型水轮机在相似工况下出力之间的相互关系, 物理含义:表示原型与模型水轮机在相似工况下出力之间的相互关系, 它适用于同一系列的水轮机在相似工况下, 出力与直径平方成正比 与直径平方成正比, 它适用于同一系列的水轮机在相似工况下,其出力与直径平方成正比,与水头 平方根的三次方成正比。 平方根的三次方成正比。
第四章水轮机相似理论

见课本P89页(新)或课本P69页(老)
虽然高比转速水轮机存在转轮出口动能损 失大、气蚀不佳等不足之处,但它的能量特性 好是十分明显的,在同样水头下提高比转速是 水轮机的一种发展趋势,它可使水轮机尺寸和 电站开挖量不增加的情况下增加出力。 如:美国大古力三厂第二期工程与第一期一 样,H=86.9米,D1=8.9米,将ns从210提高到 270,出力则由60万kw增大到70万kw。 在世界范围内,从60年代到80年代,HL 式水轮机的ns提高了17%,ZZ式提高了15%, CJ式提高了9%。
二、单位流量
水轮机转轮直径为1m,在有效水头为1m 时,水轮机的实际有效流量,称为单位流量 ,用符号 Q11 表示,单位 m 3 s
QT D
2 1T
H T T
QM D
2 1M
H MM
C Q11
表达式为
Q11
Q D
2 1
H
Q Q11 2 D1 H
上式表明: 在相同转轮直径 D1 和水头
b0 21.47 0.44 D1 ns
轴流式:
②
ns
D1 与转轮进、出口直径比 D2
的关系
依照经验公式
D1 1 D2 0.96 0.00038 n s
可以看出,
D1 ns 在D1相同下D2 D2
③
n s 与转轮叶片数 Z
ns Z
ns
ns
的关系
④
与叶片形状的关系
H
条件下,
单位流量越大,则水轮机的实际过流能力越大 ,因此,在一定出力条件下,选择单位流量大 的机型,可缩小水轮机直经,或在一定直径 D1 下,选择单位流量大的机型,可获得较大的水 轮机出力。
水轮机的相似原理.pptx

e2 e2M
M ,
(2) D1 = b0 = a0 L(常数) D1M b0M a 0M
2、运动相似
前提:几何相似
相似工况 (1) 1 1M 1 1M ,
(2) v1 = u1 = w1 常数 v1M u1M w1M
3、动力相似
p = F = G L(常数) pM FM GM M
二、水轮机的相似定律
相似定律:水轮机在相似工况下运行时,各工 作参数(H、Q、n、N、η)之间的固定关系。 包括转速相似率、流量相似率和出力相似率。
1、 转速相似律:转速 有效水头 直径
Vx kvx 2gHH
转 速 相 似 律
1、 转速相似律:转速 有效水头 直径
Vx kvx 2gHH
n D1M HH C nM D1 H MHM
水轮机的相似原理
知识回顾:
水流在水轮机内运动复杂
H Q n N
试验
原型试验 校核与检测 模型试验 设计与研究 D 1m
问题:
水轮机的相似原理
1 模型如何模拟原相型似水条轮件机? 相似条件 相似原理
2 模型结果如何应相用似到定原律型中? 相似定律
一、水轮机相似条件
1、几何相似
轮系
(1) e1 e1M
2、 流量相似律:有效流量 有效水头 直径
流 量 相 似 律
2、 流量相似律:有效流量 有效水头 直径
QV D12 HH C QMVM D1M 2 HMHM
3、出力相似律:出力 有效水头 直径
出 力 相 似 律
3、出力相似律:出力 有效水头 直径
N NM
m D12 mM D12M
(HH )3/2 (H M HM )3/水轮机直径 D1M 0.25m ,模型水头HM 3.5m , 模型效率 M 90% ,相应的模型转速nM 500 r min , 模型流量 QM 0.15 m3 s
5水轮机的相似理论和特性曲线

水轮机的相似理论和特性曲线
• 混流式及轴流定桨式水轮机飞逸特性
水轮机的相似理论和特性曲线
轴流转桨式水轮机飞逸特 性
• 机组甩负荷,导水机构和转 叶机构同失灵,失去协联关 系:(实线) 某开度a0范围内,Ф 角越小, nrun11越大。 机组甩负荷,导水机构和转 叶机构同失灵不动,但有协 联关系: 最大nrun11不出现在最大开 度下,而是在较小开度(最 大开度70%)和较小Ф 角下。 保持协联时的飞逸转速低于 非协联时的飞逸转速。
1( - 1 -M )(0.3 0.7 5 D1M / D1 10 H M / H )
水轮机的相似理论和特性曲线
我国混流式:①H<150m时,
1( - 1 - M ) 5 D1M / D1 D1M / D1 20 H M / H
- 1 -M ) 5 ②H>150m时, 1(
11
H
Q11
Q D
2 1
(QM=Q11)
H
P11
P (PM=P11) 2 3/ 2 D1 H
水轮机的相似理论和特性曲线
同型号的水轮机在相似工况下的单位转速、单位流量、 单位功率相同,不同工况有不同的转速、流量、功率。 4、比转速 ①水轮机比转速: 水轮机特性的一个综合性参数,反映水轮机转速n、水 头H、功率P之间的关系,概括反映水轮机特性。 n P (m.kw) ns 5 / 4 H ns 3.13n11 Q11 (m.kw) 相似工况下,n11、Q11同,ns也同。 ns随工况而变,不同型水轮机性能比较,常用最优效率 工况或设计工况的比转速。
η ——原水轮机的最高效率η max η M——模型最优工况效率η Mmax ②非最优工况下的换算: 采用简化的等差修正法
水轮机的相似原理2

疆大学电气学 华
轮机
论
水轮机相似: 水轮机相似:两个水流中同名称运动要素特征值 相等或对应特征值比值存在共同的比例。 相等或对应特征值比值存在共同的比例。 一、水轮机相似条件 水轮机相似必须满足水轮机相似条件, 水轮机相似必须满足水轮机相似条件,包括应满 足它们的几何相似 运动相似和动力相似。 几何相似、 足它们的几何相似、运动相似和动力相似。 1. 几何相似 指原型与模型水轮机过流通道的几何形状相似, 指原型与模型水轮机过流通道的几何形状相似, 即所有对应空间角度相等, 即所有对应空间角度相等,并且一切线形尺寸成 一定的比例。 一定的比例。
疆大学电气学 华
节
条件
3. 动力相似 模型和原型流道内各对应点的流体质点所受的同 名称力的方向相同,大小成比例且比值相等。 名称力的方向相同,大小成比例且比值相等。 流体在泵与风机中流动时受到四种力的作用 ①惯性力 ②黏性力 ③重力 ④压力 主导作用 可忽略 表征惯性力和黏性力动力相似的准则数是 雷诺数 若 Rep = Rem 满足动力相似
疆大学电气学 华
节
条件
为了保证流体流动相似,必须具备几何相似、 为了保证流体流动相似,必须具备几何相似、运 几何相似 动相似和动力相似三个条件 三个条件。 动相似和动力相似三个条件。 即必须满足模型和原型中任一对应点上的同一 物理量之间保持比例关系。 物理量之间保持比例关系。 几何尺寸、运动参数和动力参数 几何尺寸、运动参数和 下标“ 表示模型的各参数 下标“ 表示原型 表示模型的各参数, 下标“m”表示模型的各参数,下标“p”表示原型 的各参数。 的各参数。 1. 几何相似 模型和原型各对应点的几何尺寸成比例, 模型和原型各对应点的几何尺寸成比例,且比值 相等,各对应角、叶片数相等。 相等,各对应角、叶片数相等。
4_水轮机相似理论

vm1 vm1M
2 vm1 Qv D1M 2 vm1M QMvM D1
D13 D1M Q v 3 QmvM D1 M D1
h hM vM v
vm1 u1 D1n v m1M u1M D1M nM nD13 Q v H h QMvM nM D13M H M hM
对于水斗式水轮机,它的单位参数亦可按同样 的方法求得,不过这些参数是用射流直径d0、喷嘴个 数z0和转轮直径D1来表示的。
水斗式水轮机的单位参数分别为:
第三节 原、模型单位参数的换算
一、水轮机的效率换算
模型与原型不可能保持完全的力学相似,雷诺 数并不相等。因此由粘性力引起的水力摩擦相对损 失在原、模型中就不相等。 1.最优工况下的效率修正
单位参数的修正
n11T n11M n11
Q11T Q11M Q11
T 1n11M 3%n11M 在设计中一般规定,若n11 M
单位转速可不予修正,即
n11T n11M
Q11T Q11M
单位流量的修正值一般较小,可不作修正,
★几点说明:
③ 单位参数可由模型试验资料整理得出,这样在 水轮机设计、选型和运行中,可以很方便地应用它们 确定原形水轮机在相应工况下的参数。 ④ 可借助特征工况(如最优工况或限制工况)下 的单位参数,来进行水轮机不同轮系之间的比较。 最优单位参数可表示为:
五、水斗式水轮机的单位参数
以上所得出的相似律公式仅适用于反击式水轮 机。
N D H
2 1 3 2
NM D H M2 M
2 1M 3
1.单位转速: 直径为D1=1m,H1=1m 时,水轮机所具有的转速称为水轮机 的单位转速,单位为r/min.习惯用 n11 表示。 Dn n11 1 H
5水轮机的相似理论和特性曲线解析
水轮机的相似理论和特性曲线
水轮机运转综合特性曲线: • 用水轮机工作参数(P、H、 η)直接表达水轮机运行特性 的曲线。 • 选型设计中方案分析、比较 的依据 • 水电站运行管理、拟定机组 的运行方式及考察机组动力 特性的主要依据 • 机组运行人员检查水轮机运 行情况的依据
水轮机的相似理论和特性曲线
η ——原水轮机的最高效率η max η M——模型最优工况效率η Mmax ②非最优工况下的换算: 采用简化的等差修正法
max M max
M
水轮机的相似理论和特性曲线
2、单位参数的修正 模型与原型水轮机效率不同,单位参数也不完全相同。 单位转速修正(P91修正式) 单位流量修正 3、例析(综合应用) P92 例4-2 思考练习 • P107 2~6题 • 反复看例4-2,理解不同工况参数的分析、计算方法. • 为什么高比转速水轮机只适用于低水头水电站?(P88)
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
水轮机的相似理论和特性曲线
混流式水轮机综合特性曲线包含: • 等效率曲线 • 导叶等开度曲线 • 等空化系数曲线 • 5%功率限制线:各单位转速下95%(使水轮机有一定 的功率储备)最大功率工况点的连线。左侧是可运 行区,右侧是不可运行区。 • 不同工况下稳定性的等压力脉动A线 • 飞逸特性曲线 • 模型转轮的流道参数和模型试验条件 水轮机综合特性曲线是正确选择水轮机、分析水轮机性 能的依据。
水轮机的相似理论和特性曲线
④ 提高比转速——设法提高n11、Q11(研究方向) ns 3.13n11 Q11 (m.kw) 提问:为什么高比转速水轮机只适用于低水头水电站? (P88)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4-1 水轮机相似条件及相似定律
由于水流在水轮机内的运动情况十分复 杂,到目前为止,尚没有完全掌握这种规律。 因此,在进行理论设计时,不得不引入一些 假设条件,这样,理论计算不能十分正确地 反映水流在水轮机的运动规律。况且,水轮 机的某些过流部件,至今还没有足够精确的 计算方法。因此,必须通过试验,对理论计 算加以校核。
1、最优工况下的效率换算
最优工况下,水轮机损失最小、效率最高。目 前,我国通常采用的换算公式为: ① 混流式水轮机
max 1 1 M max 5
② 轴流式水轮机
D1M D1
D1M HM m ax 1 1 M m ax 0.3 0.7 5 10 D H 1
v Eu C(常数) p
2
②惯性力相似(斯特洛哈数)
vt Sh C L
③粘性力相似(雷诺数)
Re
vL
2
C
④重力相似(弗汝德数)
v Fr C gL
注意:几何相似是运动相似的必要条件, 几何相似和运动相似是动力相似的必要
条件。
三、水轮相似定律
水轮机相似规律主要是研究几何相似的
的。
四、单位参数的近似公式
单位参数的表达式中均包含水轮机效率 (实际上是水轮机的水力效率),在计算时 比较麻烦,因为很难把水力效率从水轮机效 率中分离出来,因此,初步计算时,常忽略
水力效率的影响,采用近似公式。
1、一次近似公式(不考虑效率的影响)
n11
nD1 H
Q11
Q D
2 1
H
P 11
ns 3.13n11 Q11
比转速用m.hp表示,则
ns 3.65n11 Q11
注意:
比转速
ns 是水轮机相似工况的准则数,按
n11 、单
一定相 、单
照相似原理,则有,若水轮机工况相似,那么
比转速
ns 必然相等,但比转速 n s 相等,则
两水轮机工况未必相似。即单位转速 位流量 Q11 分别相等,则比转速 等;但比转速
u H
则上式可变为
( 1)
H T T v mT vT uT wT v M u M wM v mM H MM
1、转速相似律 nD1 由于
u1
代入(1)式得
60
nT D1T H T T
由于 v m1
n M D1M H MM
C
2、流量相似律
Q 4Q 2 F1 D1
T M
T M
3、动力相似
指几何相似的水轮机对应液流质点所受的 同名力方向相同,大小成比例,且具有相同的 边界条件。
根据流体力学的量纲分析,要获得两个流
动场之间的动力相似,需满足四个参数不变(
水轮机的流场), 即:压力相似、惯性力相似
、粘性力相似、重力相似。 ①压力相似(欧拉数)
代入(1)式得
QT D
2 1T
H T T
QM D
2 1M
H MM
C
3、出力相似律
P 由于 Q 9.81H
代入上式得
D
2 1T
H T T
PT
3
2
D
2 1M
H M M 2
3
PM
C
两台水轮机相似,就存在以上相似 定律
§4-2 水轮机的单位参数
单位参数——转轮直径为1米,有效水头为1 米的水轮机参数。 一、单位转速 水轮机转轮直径为1m,在有效水头为1m 时,水轮机所具有的实际转速,称为单位 转速,用符号 n11 表示,单位 r min
ns 叶片形状越平坦
⑤ 与应用水头
H
的关系
ns 应用水头H
⑥ 型由 ⑦
n s 与水轮机机型的关系
ns
由小→大的变化, 则水轮机机
CJ HL ZL 的变化
n s 与空化系数
的关系
依照经验公式有
ns
30 20000
1.8
可以看出, n s 轮机越容易发生空化。
,说明水
2、比转速与水轮机的能量关系 根据转轮进、出口速度三角形的变化可以看出: ①
ns
增大,则转轮进口绝对速度
v1
减小,
从而水轮机的反击度
R
增大,表明转轮转换
的水流能量中压能所占比重增大。
反击度——转轮内压能的变化与总能量变化
之比。
vu1 HP R 1 H 2u1
ns
与转轮出口动能的关系
§4-4 水轮机的效率换算及单位参数修正
一、效率换算 在推导水轮机相似公式时,曾假定相似 水轮机在相似工况下,其效率是相等的, 事实上是不相等的,这是因为原、模型水 轮机的几何尺寸不同,很难满足完全的力 学相似,如相对粗糙度,水力损失,容积 损失均不能相同。所以,要求得原型水轮 机的实际效率,必须对模型水轮机效率进 行修正。 效率换算分两种情况:
水轮机,在满足运动相似条件下,其工作参
数之间的关系,根据这些关系,可进行原、 模型水轮机参数之间的换算。
水轮机相似律以宏观的运动相似为基础导出 ,转轮流道中任意一点的水流速度三角形相似, 则有
v mT vT uT wT C vM uM wM v mM
由于两台水轮机速度三角形相似,则存在比 vu u 例关系 代入水轮机基本方程式,整理得
计算出最优工况时原型水轮机的最高效率 max
max 0
M max 0 M
②计算出原、模型水轮机的最高效率差值 0
0 0 0 M
b0 21.47 0.44 D1 ns
轴流式:
②
ns
D1 与转轮进、出口直径比 D2
的关系
依照经验公式
D1 1 D2 0.96 0.00038 n s
可以看出,
D1 ns 在D1相同下D2 D2
③
n s 与转轮叶片数 Z
ns Z
ns
nsBiblioteka 的关系④与叶片形状的关系
ns
ns
相等,单位转速 n11
Q11 位流量
不一定相等。
二、比转速与水轮机的关系
1、比转速与水轮机几何参数
b0 ① n s 与导叶相对高度 b0 的关系 D1
b0 ns Q11 Q Q D1b0 vm b0 D1
混流式:
bo 0.1 0.00065 n s D1
2、非最优工况下的效率换算
采用定值简化修正方法,即假设非最优工况的
原、模型效率差值 M 与最优工况的相 同,则可按照步骤换算: ①先由公式 混流式 D1M max 1 1 M max 5 D1
轴流式
D1M HM m ax 1 1 M m ax 0.3 0.7 5 10 D1 H
nT D1T H T T n M D1M H MM C n11
表达式为
n11
nD1 H
n11
nD1 H
上式表明:在相同转轮直径 D1 和水头 H 条件下,单位转速越大,则该系列水轮机的 实际转速就越高,因此,在选择水轮机时, 尽可能选择单位转速较高的水轮机,以缩小
发电机直径,降低机组造价。
ns Q11 Q 发电机出力
缺点:
ns 出口动能 水力损失
ns 水轮机容易发生气蚀
综上所述:比转速越高,水轮机的能量特性也
愈好。反之,则愈差。
综上所述:
因此,比转速的上限受到空化的限制,最
大不超过1000;比转速的下限受到能量特性
的限制,最小不低于50。
2 2 4
v ns 3 ns 出口动能 0.42 水力损失 2 gH 1000
因此,比转速越高的水轮机,有更多的转轮 出口水流剩余能量需要依靠尾水管回收。
三、高比转速水轮机的特性 优点:不同型号的水轮机,在转轮直径及水 头相同情况下。
ns n11 n 发电机尺寸 厂房投资
H
条件下,
单位流量越大,则水轮机的实际过流能力越大 ,因此,在一定出力条件下,选择单位流量大 的机型,可缩小水轮机直经,或在一定直径 D1 下,选择单位流量大的机型,可获得较大的水 轮机出力。
三、单位出力
水轮机转轮直径为1m,在有效水头为1m
时,水轮机所具有的出力,称为单位出力,
用符号
P11
表示,单位kw。
ns 表示,单
2、比转速的表达式
①
ns
n P H
5 4
其中:P ——单位kw或hp ns ——单位m.kw或m.hp ②若出力 P 的单位用kw 、比转速 用m.hp表示, 则
ns
7n P ns 5 6 H 4
其中: P ——单位kw ns ——单位m.hp
7 ns 用k w计算 即: ns 用hp计算 6 ③若用单位参数表示 比转速用m.kw表示,则
nD1 H
Q Q11 2 D1 H
P 11
P D H
2 1 3 2
注意:
n11
、 Q11 、 P11 是水轮机的三个相似准 则数,几何相似的同系列水轮机在相似工况 下,对应的三个单位参数分别相等。三个单 位参数中,单位转速 n11 和单位流量 Q11 是 两个独立的参数,通常用 n11 、 Q11 表示水 轮机运行工况,它们是水轮机工况相似的判 据。两个几何相似的水轮机,当其 n11 和 Q11 分别相等时,则这两个水轮机的工况是相似
见课本P89页(新)或课本P69页(老)
