质点运动的描述,自然坐标系
质点运动的坐标系

r
y
1
位置矢量可表示为
r xi yj zk
j 其中 i 、和 k 分别是x、y和z方向的单位矢量。
位矢大小 r r x 2 y 2 z 2
可用方向余弦来表示位置矢量方向。
y x cos , cos , r r
z cos r
小球的加速度可表示为 :
a ut 2 u
2
由上式可以看到, 径向加速度是时间的线性函
数, 横向加速度则为常量。
22
三、自然坐标系 (natural coordinates) 沿着质点的运动轨道所建立的坐标系。 取轨道上一固定点为原点, 规定两个随质点位置
变化而改变方向的单位矢量, 一个是指向质点运动
ˆ d
dt
dt dt
dt dt
dt
dt dt
a [
d2
d d ˆ ˆ ( ) ] [ 2 2 ] 2 dt dt dt dt dt
2
d
d 2
ˆ ˆ a a a
18
a
d2 dt 2
d d d 2 d 2 ( ) , a 2 2 dt dt dt dt
分别称为径向加速度和横向加速度。
质点直线运动, 取该直线为极径,极角为常量:
d2 a 2 , a 0 dt
质点圆周运动, 极径是圆周半径, 为常量, 有
d 2 d 2 a ( ) , a 2 dt dt
19
2 d 2 d 2 1 v 继续推算 a ( ) ( ) dt dt
方向的切向单位矢量, 用 表示, 另一个是垂直于
质点力学

ɺ ɺ a y = ɺɺ = (ɺɺ − rθɺ 2 ) sin θ + (rθɺ + 2rθɺ) cosθ y r
ɺ ∴ ar = a x cosθ + a y sin θ = ɺɺ − rθ 2 r
ɺ ɺɺ aθ = −a x sin θ + a y cosθ = rθɺ + 2rθ =
(径向加速度) 径向加速度)
运动学方程式是质点运动学的核心
r = r (t )
⇔
x = x(t ) y = y (t ) z = z (t )
x = x(t ) 若已知 r ,即 y = y (t ) 则可通过求导数求出 z = z (t )
v
ɺ ax = vx v x , v y , v z 则可通过求导数求出 a ,即 ay = vy ɺ 若已知 v ,即 a = v z ɺz
ɺ2 + y2 + z2 ɺ ɺ 大小: 大小:v = v + v + v = x
2 x 2 y 2 z
方向余弦: 方向余弦:
cos α =
vy vx v ,cosγ = z ,cosβ = v v v
α,β,γ 分别为 v 与x、y、z轴正方向之间的夹角
(3)加速度 )
t时刻: v = v(t )
t+△t时刻: v(t+△t)
速度增量: v = v(t+△t)-v(t) △ 平均加速度: a= △v △t 瞬时加速度: a =
△v dv i d 2 r ɺɺ lim △t = dt = v = dt 2 = r (t ) △ t →0
ˆ x ˆ yj z ˆ ˆ a = a xi + a y ˆ + a z k = ɺɺi + ɺɺˆ + ɺɺk j
3-2 自然坐标 极坐标
r a
o
θ
此时总加速度的大小为 r r a与v的夹角为 a = aτ + an = 1.22 + 9.82 = 9.87 (m ⋅ s−2 )
2 2
an 9.8 o α = arctg = arctg = 83.0 aτ 1.2
四. 刚体的运动 1. 基本形式 平动 —— 刚体运动时, 刚体运动时,若其上任意两点连线的方位 始终不变, 始终不变,这种运动称为刚体的平动。 这种运动称为刚体的平动。平动时刚体上 各质点的速度、 各质点的速度、加速度、 加速度、轨道均相同, 轨道均相同,可归结为质点 运动。 运动。 转动 —— 刚体上各质点都绕同一直线作圆周运动, 刚体上各质点都绕同一直线作圆周运动,叫 做刚体的转动。 做刚体的转动。该直线叫刚体的转轴 该直线叫刚体的转轴。 转轴。 定轴转动: 定轴转动:转轴为固定直线的转动叫做刚体的定轴转动。 转轴为固定直线的转动叫做刚体的定轴转动。 一般运动 —— 平动与转动叠加。 平动与转动叠加。
教材第44页例6
某发动机工作时, 某发动机工作时,主轴边缘一点作圆周运动方程为
θ = t + 4t + 3
3
( SI )
(1)t =2s 时,该点的角速度和角加速度为多大? 该点的角速度和角加速度为多大? (2)若主轴直径 D = 40 cm,求 t = 1 s 时, 该点的速度和加速度 思路: 思路:(1) θ ( t ) → ω ( t ) → β ( t ) → t = 2 (2)由角量与线量的关系
v vA
v vA
∆s
∆
v v
v vB
B
A
r D r ∆v r C v A ∆vn ∆ vτ r E ∆θ vB
1-2 质点运动的描述-1

1-2 质点运动的描述
第1章 质点运动学
3. 平均速率 ——质点在 △t 时间内所走过的路程△s与时间 △t 的比值.
Δs v = Δt
1-2 质点运动的描述
第1章 质点运动学
4. 瞬时速率: ——速度 v 的大小称为速率.
Δr Δs ds = lim = v v = lim = Δt → 0 Δt Δt → 0 Δt dt
ds v= et = v et dt
1-2 质点运动的描述
第1章 质点运动学
六、加速度 1) 平均加速度 ——单位时间内的速度增量。
y
A
O
vA
B
vB
Δv a = Δt
a 与 Δv 同方向 .
2)(瞬时)加速度
x
vA
Δv dv a = lim = Δt →0 Δt dt
Δv
vB
1-2 质点运动的描述
从中消去参数 t 得轨道方程
F(x, y, z) = 0
z
z (t )
o
x
1-2 质点运动的描述
第1章 质点运动学
例1. 已知质点的运动方程 r = 2ti + ( 2 − t 2 ) j ( SI ) 求:(1) 质点的轨迹。 (2) t = 0 及t = 2s 时,质点的位置矢量。
⎧ x = 2t 解:(1) 先写参数方程:⎨ y = 2 − t2 ⎩
dv a= = −10 j dt
(2) x : v x = 5
ax = 0 a y = −10 ≈ g
y : v y = 15 − 10t
1-2 质点运动的描述
第1章 质点运动学
(2) x : v x = 5
ax = 0 a y = −10 ≈ g
1-3 描述质点运动的坐标系
质点运动学两类基本问题
Ⅰ Ⅱ
(1006A)
x 5 t2
1、已知质点运动方程为: y 3 5t t 2 ,
z 1 2t2
第二秒末质点的速度和加速度,长度和时间的单位 分别是米和秒。
解:vx
dx d(5 t2 ) 2t
dt
dt
4 (m / s)
0
x1
=
0式是抛射点的位置, 另一个是射程
x2
v02 g
sin 20
dx2
d0
2v02 g
cos 20
0
0
π 4
最大射程
xmax
v02 g
物体的飞行时间
T
x2
v0 cos 0
2v0 g
sin 0
当物体到达最大高度时, 必有 v y 0
物体达最大高度的时间 y
t1
v0 g
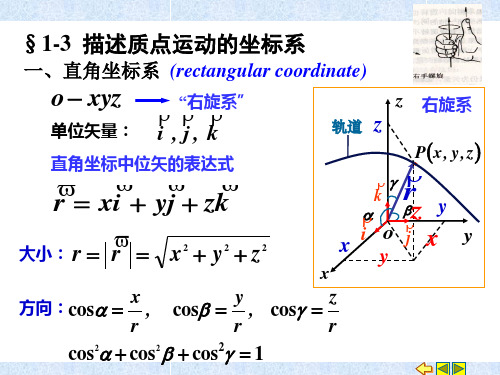
§1-3 描述质点运动的坐标系
一、直角坐标系 (rectangular coordinate)
o xyz “右旋系”
单位矢量: i , j , k
直角坐标中位矢的表达式
r
xi
yj
zk
大小: r r x2 y2 z2
z 右旋系
轨道 z
Px, y,z
dt
A
at
dv dt
2(m
/
s2 )
an
v2 R
402 1500
16 (m / 15
s2 )
av
at
tˆ
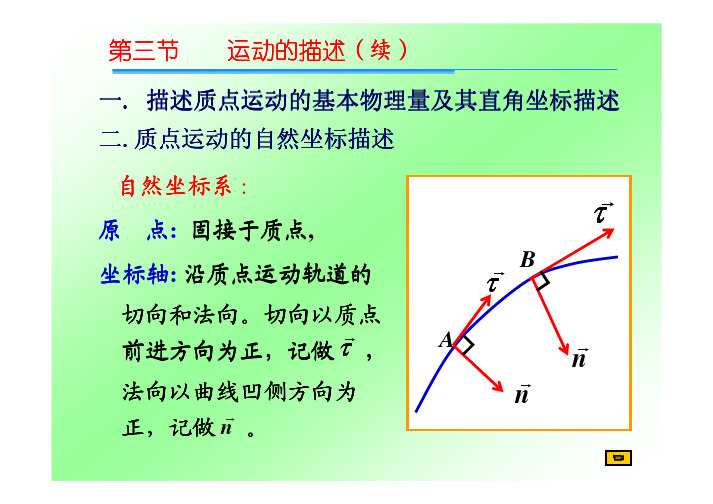
质点运动的自然坐标描述

a R x s i it y i n j R z k c o t j s h 2 k
R 2 ct i o R s 2 st j in
§1-5 质点运动的自然坐标描述
v x 2 y 2 z 2R 2 ( h 24 π 2 ) 常量
切向加速度
at vt 0
§1-5 质点运动的自然坐标描述
利用质点运动轨道本身的几何特性 (如切线、法线方 向等)来描述质点的运动. 这种方法称为自然坐标法.
1. 弧长方程
在轨道上取一点 作原O点, 规定沿轨道的某一方向为弧
长的正方向, 质点位置可由原点 到质点间的一段O弧长 来
确定, 称为弧坐s标.
s
s s(t)
弧长方程和轨道方程一起与 质点的运动学方程等价.
ebeten
§1-5 质点运动的自然坐标描述
3. 速度和加速度表达式
速度 加速度
v a v sddetvte tt dsds tde d (etsttet)
dsd
d d e tt s1d d t ve tn e n s e n
§1-5 质点运动的自然坐标描述
切向加速度
法向加速度
a
set
s2
en
在自然坐标描述中, 需要已知质点运动的轨道, 而对轨道 的数学描述又需要一个坐标系, 所以必须掌握自然坐标描述
中联有的系不物的同理基的a量本表与依达其据形他 是 式:,坐速 但标度 它系们中和的的加大物速小理度和量方在之向不间是同的惟的联一描系确述. 建定方立的法v这.中个
§1-5 质点运动的自然坐标描述
弧坐标为可正可负的标量,与恒正的路程是不同的.
§1-5 质点运动的自然坐标描述
2. 相关的微分几何知识
质点运动学

质点运动学1.描述质点的运动的物理量:位矢、位移、速度和加速度。
(1)位矢:从坐标原点引向质点所在位置的有向线段,记为r。
在直角坐标系中r=x i+y j+z k。
(2)运动方程:质点的位置随时间变化的关系:r=r(t)称为运动方程。
在直角坐标系中的矢量表示式:r(t)=x(t)i+y(t)j+z(t)k。
在自然坐标中:s=s(t)(3)位移:由质点初始位置指向末位置的矢量,△r=r(t+△t)-r(t).在直角坐标系中:△r=△x i+△y j+△z k。
(4)路程:物体运动时沿轨迹实际通过的路径长度称为路程,用s 表示。
一般情况下,|△r|≠△s。
(5)速度:质点位置对时间的一阶倒数称为速度v=d r/d t.在直角坐标系中:v=v x i+v y j+v z k=(dx/dt)i+(dy/dt)j+(dz/dt)k在自然坐标系中:v=(ds/dt)e t速度大小称为速率,速率是标量。
v=|v|=|d r/dt|=ds/dt(6)加速度:质点速度对时间的一阶求导a=d v/dt=d2r/dt2 在直角坐标系中:a=a x i+a y j+a z k=(dv x/dt)i+(dv y/dt)j+(dv z/dt)k=(d2x/dt2)i+(d2y/dt2)j+(d2z/dt2)k 在自然坐标系中:a=a t e t+a n e n=(dv/dt)e t+(v2/ρ)e n2.常见的几种运动形式(1)匀速直线运动:v=v0+atx=x0v0t+1/2*at2v2-v20=2a(x-x0)(2)抛体运动:a x=0,a y=-gv x=v0cosθ,v0=v0sinθ-1/2*gt2x=(v0cosθ)t,y=(v0sinθ)t-1/2*gt2 (3)圆周运动:角位置:θ=θ(t)角位移:△θ=θ(t+△t)-θ(t)角速度:ω=dθ/dt=v/R角加速度:β=dω/dt=d2θ/dt2法向加速度:a n=v2/R=Rω2切向加速度:aτ=dv/dt=Rβ3.伽利略变换伽利略速度变换式:v=v0+u。
1-4 自然坐标系中质点运动描述

v2 R
nv
三 变速圆周运动中的加速度
Δv vB vA Δvv Δvvn Δvv
Δvn 反映速度方向变化。
Δvv 反映速度大小变化。
av lim vv lim vvn lim vv t0 t t0 t t0 t
an
lim vn t0 t
av avn av
av
lim vv t0 t
vB
B vA
Δ r Δθ
oR A
Δv vB
Δ
vv
Δvn vA
Δθ
o
a反n 映出质点速度方向的变化,称为法向加速度。
avn
lim
t 0
vvn t
= lim t 0
|
Δvvn|nv= v 2 Δt R
2
(2)根据加速度的定义
an
v2 R
(v 0
bt)2 R
at
dv dt
b
a
at2 an2
b2
(v 0
bt)4 R2
a 1 R
R2b2 (v0 bt)4
由
a 1 R
R2b2 (v0 bt)4 b
解得 t v0 b
这时质点运行的圈数为
n
s 2R
v
0
(v 0 b
) 1 b(v0 2b
2πR
)
2
v02 4πRb
解题思路 自然坐标中质点运动学问题也分为两类问题。 1. 第一类问题:已知自然坐标中运动方程s(t),求质点运动 的速度、切向加速度、法向加速度,用求导法。 2. 第二类问题:已知质点运动的速度或切向加速度及初始条 件,求运动方程,用积分法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x R cost , y R sin t
x2 y 2 R2
o
P2 v1 R an P 1 t x
dr v (R sin t )i (R cost ) j dt
2 2
r ( R cost )i ( R sin t ) j
a ( R cost )i ( R sin t ) j r
讨论:切向加速度和法向加速度为零时的运动 情况:
(a ) an 0, a 0
匀速率直线运动
( b) an 0, a 0
(c) 0, a 0
(d ) an 0, a 0
变速率直线运动
匀速率曲线运动 变速(率)曲线运动
圆周运动:
直角坐标系描述(匀速圆周运动) y v2
问题:饲养员能否打中猴子? 动画
27
至此,我们学习了描述运动的物理量在直
角坐标系和自然坐标系中的描述方法。我们看
到,选用不同的参考系对物理量的描述是
不同的。这反映了描述运动的相对性。
在《相对运动》一节中我们将学习同一质 点在有相对运动的两个参考系中的位移、速 度和加速度之间的关系。
相对运动
运动具有相对性:选取的参考系不同,对物体运动的 描述就不同 运动是绝对的,静止是相对的 现在要研究同一质点在有相对运动的两个参考系 中的位移、速度和加速度之间存在着怎样的关系。 本节只考虑参考系S’相对于参考系S作平移运动 的情况,即S’系的原点O’相对于S系作任意的直线或 曲线运动,但它们的坐标轴的方向保持平行。
说明:以上各式都是在认为长 度的测量,时间的测量与参考 系无关的前提下得出的。这些 变换式再加上时间变换 t t ', 总称为伽利略变换式。
结论:
z K
r
R
z K P
r
o
y
o x
y
运动目标
(船)
绝
相
牵 动系 (水)
对
对
对
静系 (岸)
对
对
对
对
对
对
人骑车以速率
向正西行驶
遇到从北向南刮的风 , 速率也是
ds d
曲率半径愈大则曲线的弯曲程度愈小
加速度的表达式: 2 d s ds 2 1 a ( ) n 2 dt dt
d 2 n a an n dt
故切向加速度和法向加速度大小分别为:
d a , dt
an
2
n
a
描述速度大小改变的快慢,不影响速度的方向。 法向加速度:
v an n
2
描述速度方向改变的快慢,不影响速度的大小。
自然坐标系中总加速度为:
改变
a a an
a a
2
1
改变
速度大小
速度方向
加速度 的大小 和方向
a
2 n
a
tan
2
a
v2 2 2 ax a y 2 R R
自然坐标系描述: 圆周运动中 s R 则
y v2
R
v1
ds d d v ( R ) R R dt dt dt
d dt
o
x
是 随时间的变化率,称为角速度
dv d a R dt dt
在自然坐标系中,作曲线运动的质点的加速度可以 分解为两个分量:一个是反映速度大小变化的切向加速 度 a ,一个是反映速度方向变化的法向加速度 a n .
dv v a n a an dt
切向加速度:
2
a an
dv a dt
v ( R ) 2 an R R
2 2
求抛体轨道顶点的曲率半径.
v v0 cos 0 an g
2 2
解:
y
vo
o
o
x
x
v0 cos 0 v g g
2
2
讨论
质点沿固定的圆形轨道, 若速率 v 均匀增加, at 、an、a以及加速度与速度间的夹角中哪些 量随时间变化?
ˆ
•法向坐标 n 沿运动轨迹的法线方向并指向曲线凹侧。
ˆ ˆ, n 为单位矢量, 大小不变
(模为1不变),但方向随时 间改变。
n
n
强调:自然坐标系是建立在 运动质点上的,它随质点一 起运动在轨道曲线上。轨道 上各点的自然坐标系的二个 坐标轴的方位是不断变化的。
s 0O s 0
各 自 独 立
无 依 赖 关 系
一个复杂的运动,可看成几个独立的运动的叠加。 称为
应用:
运动叠加原理
先分别求解各坐标分量的一维运动参量, 然后进行二维运动合成。方便易行。
23
24
抛物运动
25
26
枪打落猴 :
动物园里的一个猴子从笼子里逃 了出来,爬到树上。饲养员为了逮住 猴子,决定用麻醉枪。饲养员用麻醉 枪瞄准猴子,在他开枪时惊慌的猴子 也同时从树上落下。
设 R 表示S
有:
r r R
系原点相对于 S
dR u 此处 为 S 系相对 S系的速度,称为牵连速度。 dt z P z
u
dr dr dR dt dt dt
系原点的位矢,
dv dv du dt dt dt
车对地
h
雨对地
雨对车
解: 所求雨滴速度和卡车速度都是相对于地面而言的。
雨对地 的方向与地面夹角 tan-1 63.4,于 由题意可知, d 是三个速度间的关系如上右图所示。雨滴速度大小为:
d 1m
雨对地 雨对车 车对地
h
车对地 雨对地 33.5km/h cos
人感到风 从 什么方向吹来
人对地 风对人 风对人 人对地
实质: 已知 北偏西45° 北 由 45° 得 西
人对地
风对人
和
风对地
求
风对地
风对地 风对地
人对地 人对地
人对地
45°
风对地 风对人
人感到风 从 北偏西45° 方向吹来
有一带蓬的卡车,蓬高h=2m,当它停在马路上时,雨点可 落入车内,达到蓬后沿前方d=1m处。当卡车以速度 15km/h沿平直马路行驶时,雨滴恰好不能落入车内。求 雨滴的速度。
此处的 d
dt
是什么呢?
由右图可知: d d 1d
d 方向与 n
1
A
d d n dt dt
B d d
1
一致,故有:
d 1d n
d n n
2
代入加速度公式,有:
d 2 s ds d d 2 s ds ds d a 2 n 2 n dt dt dt dt dt dt ds A 轨迹上任一点的弯曲程度不同, ds . 引入曲率半径的概念: d
r
r
a a A
o
x
R
o
y
y
总结:
绝 绝
相
相
牵
绝 绝 绝
相
相 相
牵
绝
相
相 相 牵
牵
牵
牵
绝 绝
牵
rP对K rP对K rK 对K P对 K P对 K K 对 K a P对 K a P对 K a K 对 K
自然坐标系
如果质点做平面曲线运动,且被约束在已知 的轨道上,则可采用“自然坐标系”。
所谓“自然”,意即“顺其自然”,把轨道 当作坐标的“轴”。
质点的坐标是代表路程, 演示动画 质点的运动方向规定为轨道切线的正方向。
自然坐标系的建立
O
ˆ n
s
ˆ n
ˆ
将此轨道曲线作为一维坐标的轴线,在其上任意选一 点O作为坐标原点。 质点在轨道上的位置可以用从原点O算起的弧长 度s 来表示,s 称为弧坐标。 运动方程:s s (t ) 自然坐标系是建立在物体运动的轨迹上的。 在质点上建立两个的坐标轴:切向坐标和法向坐标。 •切向坐标 沿运动轨迹的切线并指向质点运动的方向;
在此坐标系中速度和加速度怎么表示?
速度:因为瞬时速度的大小等于瞬时速率(注意平均
ds 速度的大小不等于平均速率),故速度大小为 ,方 dt
向就是切向单位矢量 的方向,故 对加速度: a dν dt 将速度的表达式代入,得:
ds . dt
2 d d ds d s ds d a ( ) 2 dt dt dt dt dt dt
的大小为最小
直接判断得 此时
t=1时
18
x =2t=2m
y =(2t2-4t)=-2m
注意:只有当积分表达式和被积分变量统一时,才 可以直接积分,否则就要做数学变换后才可以积分
19
20
21
斜抛运动 :
可以看成是水平方向的匀速直线运动和垂直 方向的上抛落体运动合成。 动画
22
轴上的运动 轴上的运动
相对运动
z
z
P r
看图:
o x
r
R
S
y
o
y
只考虑参考系S’ 相对于参考系S 作平移运动的情 况。也就是 S’系的原点相对S系作任意的直线或 曲线运动,但要保持它们的坐标轴方向平行。 质点P在 S 系和 S’ 系中的位矢、速度和加速度 分别为 r,, a 和 r ,. a
