3.1.1方程的根与函数的零点导学案
3.1方程的根与函数的零点(导学案)

3.1.1方程的根与函数零点一、教学目标1.结合二次函数,知道函数零点的概念;2.能说出函数零点与相应方程根的关系;3.会根据零点存在的判定条件求方程的根和函数的零点.二、重点与难点重点:零点的概念及存在性的判定.难点:零点的确定.三、教法与建议学生分组讨论,教师引导总结。
四、学生情况分析初中阶段,学生掌握了二次函数、二次方程的相关知识,又刚刚结束了指数函数、对数函数的学习,故学生已具备了接受本节内容的知识基础和心理储备。
尽管如此,还要采取有具体到抽象、有特殊到一般的讲课方式,灵活运用数形结合的思想以降低学习难度。
五、教学练评活动程序【活动1】设计问题,创设情境问题1:求下列方程的根。
(1)610x -= 2(2)3610x x +-=5(3)610x x +-=.(如何解,会解吗?)阿拉伯数学家花拉子米给出了一次方程和二次方程的一般解法。
挪威数学家阿贝尔证明了五次以上的方程的一般解法。
问题2:求下列方程的实数根。
ln 260x x +-=问题3:方程()0f x =的根与函数()y f x =有什么关系?【活动2】引导探究,获得新知问题1:先来观察几个具体的一元二次方程的根及其相应的二次函数的图象:○1方程0322=--x x 与函数223y x x =-- ○2方程0122=+-x x 与函数122+-=x x y ○3方程0322=+-x x 与函数322+-=x x y 请同学们解出方程,画出函数图象,分析方程的根与图象和x 轴交点坐标有什么关系? 你能将结论推广到))((D x x f y ∈=吗?函数零点的概念:对于函数))((D x x f y ∈=,把使0)(=x f 成立的实数x 叫做函数))((D x x f y ∈=的零点.反思:函数()y f x =的零点、方程0)(=x f 实数根、函数)(x f y =的图象与x 轴的交点的交点横坐标有什么关系?问题2:所有函数都存在零点吗?什么条件下才能确定零点的存在呢?(Ⅰ)让学生画出二次函数32)(2--=x x x f 的图象:○1 在区间]1,2[-上有零点______; =-)2(f _______,=)1(f _______,)2(-f ·)1(f _____0(<或>).○2 在区间]4,2[上有零点______; )2(f ·)4(f ____0(<或>).(Ⅱ)观察下面函数)(x f y =的图象○1 在区间],[b a 上______(有/无)零点; )(a f ·)(b f _____0(<或>).○2 在区间],[c b 上______(有/无)零点; )(b f ·)(c f _____0(<或>).○3 在区间],[d c 上______(有/无)零点; )(c f ·)(d f _____0(<或>).由以上两步探索,你可以得出什么样的结论?【活动3】信息交流,揭示规律函数零点的判定(零点存在性定理)如果函数y =f (x )在区间[a ,b ]上的图象是连续不断的一条曲线,并且f (a )·f (b )<0,那么函数y =f (x )在区间(a ,b )内有零点,即存在c ∈(a ,b ),使得f (c )=0,这个c 也就是f (x )=0的根.问题1:这个定理的前提有几个条件?问题2:“有零点”是指有几个零点?只有一个吗?问题3:再加上什么条件就“有且仅有一个零点”呢?问题4:若函数y =f (x )在区间(a ,b )内有零点,一定能得出f (a )·f (b )<0的结论吗? 问题5:这个定理有什么作用呢?【活动4】运用规律,解决问题例1.求函数62ln )(-+=x x x f 的零点个数.问题:1)你可以想到什么方法来判断函数零点个数?2)判断函数的单调性,由单调性你能得该函数的单调性具有什么特性?例2.求函数2223+--=x x x y ,并画出它的大致图象【活动5】形成性评价1.利用函数图象判断下列方程有没有根,有几个根:(1)0532=++-x x ;(2)3)2(2-=-x x ;(3)442-=x x ;(4)532522+=+x x x .2.利用函数的图象,指出下列函数零点所在的大致区间:(1)53)(3+--=x x x f ;(2)3)2ln(2)(--=x x x f ;(3)44)(1-+=-x e x f x ;(4)x x x x x f ++-+=)4)(3)(2(3)(.六、小结与反思1.本节课学习了哪些主要内容?2.零点存在定理有什么样的限制条件?七、展与延伸(选学)求下列函数的零点:(1)452--=x x y ;(2)202++-=x x y ;(3))13)(1(2+--=x x x y ;(4))23)(2()(22+--=x x x x f .求下列函数的零点,图象顶点的坐标,画出各自的简图,并指出函数值在哪些区间上大于零,哪些区间上小于零:(1)12312+-=x x y ; (2)1422+--=x x y .已知124)1(2)(2-+++=m mx x m x f :(1)m 为何值时,函数的图象与x 轴有两个零点;(2)如果函数至少有一个零点在原点右侧,求m 的值.附:总结性评价一、选择题1.已知函数f (x )=log 2x -(13),若实数x 0是方程f (x )=0的解,且0<x 1<x 0,则f (x 1)的值为A .恒为负B .等于零C .恒为正D .不小于零2.在下列哪个区间内,函数f (x )=x 3+3x-5一定有零点 ( )A .(—1,0)B .(0,1)C .(1,2)D .(2,3)3.函数f (x )=(x 2-2)(x 2-3x +2)的零点个数为 ( )A .4B .3C .2D .14.若函数f (x )在区间[a ,b ]上的图象是连续不断的一条曲线,并且f (a )·f (b )>0. 则函数f (x )在区间[a ,b ]上( )A 一定没有零点B 至少有一个零点C 只有一个零点D 零点情况不确定二、填空题5.定义在R 上的奇函数f (x )满足:当x >0时,f (x )有一个零点,则在R 上,函数f (x )零点的个数为________.三、解答题6.求下列函数的零点: (1)()53xf x =-; (2)2(1)(43)()3x x x f x x --+=-; (3)7()3f x x =-. 7.是否存在这样的实数a ,使函数f (x )=x 2+(3a -2)x +a -1在区间[-1,3]上与x 轴有且只有一个交点.若存在,求出a 的范围;若不存在,说明理由.8.(选做)m为何值时,f(x)=x2+2mx+3m+4.(1)有且仅有一个零点;(2)有两个零点且均比-1大。
3.1.1方程的根与函数的零点导学案

教法指导
通过引导、探究,发现方程的根与函数零点的关系;通过观察函数图象与 轴的交点的情况,来研究函数零点的情况;通过研究:①函数图象不连续;② ;③ ,函数在区间上不单调;④ ,函数在区间上单调,等各种情况,加深对零点存在性定理的理解.
2.零点存在性定理:如果函数 在区间 上的图象是连续不断的一条曲线,并且有 ,那么,函数 在区间 内有零点.
问题1. 不是连续函数,结论还成立吗?请举例说明。
问题2. ,那么,函数 在区间 内一定没有零点吗?
问题3.若 ,那么,函数 在区间 内一定只有一个零点吗?
问题4.若函数 在区间 内有零点,那么一定有 吗?
问题5.若 ,那么,增加什么条件可确定函数 在区间 内一定只有一个零点?
例2.求函数 的零点的个数。
达标检测
1.函数 的零点为( )
A.(0,0),(4,0) B.0,4 C.(– 4 ,0), (0,0),(4,0) D.– 4 ,0,4
2.对于定义在R上的函数 ,若 ,则函数 在 内()
A.只有一个零点B.至少有一个零点C.无零点D.无法确定有无零点
二次备课
1.三分钟德育教育:
2.预习评价情况反馈:
3.教学措施:
课堂学习研讨、合作交流
1.比较二次函数图象与 轴的交点和相应方程的根的关系,可知:
函数 的零点就是方程 的,也就是函数 的图象与的交点的横坐标。
方程 有实数根 函数 的图象 函数 。
例1.(1)求函数 的零点。(2)利用函数图象判断方程根的情况:
3.1.1方程的根与函数的零点
班级:姓名:小组:
教学目标知识与技能:1.ຫໍສະໝຸດ 解并掌握方程的根与相应函数零点的关系.
高中数学《方程的根与函数的零点》导学案

3.1.1方程的根与函数的零点1.函数零点的概念函数的零点:□1对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.注意:函数的零点不是一个点,而是f(x)=0的根.2.方程的根与函数零点的关系方程f(x)=0有实数根⇔□2函数y=f(x)的图象与x轴有交点⇔□3函数y=f(x)有零点.3.零点的存在性定理□4如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.注意:(1)函数y=f(x)在(a,b)内有零点,f(a)·f(b)<0不一定成立.(2)若连续不断的曲线y=f(x)在区间[a,b]上有f(a)·f(b)<0,y=f(x)在(a,b)内一定有零点,但不能确定有几个.1.判一判(正确的打“√”,错误的打“×”)(1)所有的函数都有零点.()(2)若方程f(x)=0有两个不等实根x1,x2,则函数y=f(x)的零点为(x1,0),(x2,0).()(3)若函数y=f(x)在区间(a,b)上有零点,则一定有f(a)·f(b)<0.()答案(1)×(2)×(3)×2.做一做(1)(教材改编P88T1)函数f(x)=x2+3x的零点是________.(2)(教材改编P88例1)若函数f(x)在区间(2,5)上是减函数,且图象是一条连续不断的曲线,f(2)·f(5)<0,则函数f(x)在区间(2,5)上零点的个数是________.(3)已知函数y=f(x)的定义域为R,图象连续不断,若计算得f(1)<0,f(1.25)<0,f(1.5)>0,则可以确定零点所在区间为________.答案(1)0和-3(2)1(3)(1.25,1.5)『释疑解难』(1)若函数f(x)在区间[a,b]上的图象是连续不断的,且在两端点处的函数值f(a),f(b)异号,则函数y=f(x)的图象至少穿过x轴一次,即方程f(x)=0在区间(a,b)内至少有一个实数根c.(2)零点的存在性定理只能判断出零点的存在性,而不能判断出零点的个数.如图(1)(2),虽然都有f(a)·f(b)<0,但图(1)中函数在区间(a,b)内有4个零点,图(2)中函数在区间(a,b)内仅有1个零点.(3)零点的存在性定理是不可逆的,因为f(a)·f(b)<0可以推出函数y=f(x)在区间(a,b)内存在零点.但是,已知函数y=f(x)在区间(a,b)内存在零点,不一定推出f(a)·f(b)<0.如图(3),虽然在区间(a,b)内函数有零点,但f (a )·f (b )>0.(4)如果单调函数y =f (x )在区间[a ,b ]上的图象是连续不断的一条曲线,并且有f (a )·f (b )<0,那么函数y =f (x )在区间(a ,b )内有唯一的零点,即存在唯一的c ∈(a ,b ),使得f (c )=0,这个c 也就是方程f (x )=0的根.探究1 求函数的零点例1 判断下列函数是否存在零点,如果存在,请求出.(1)f (x )=x 2+7x +6;(2)f (x )=1-log 2(x +3);(3)f (x )=2x -1-3;(4)f (x )=x 2+4x -12x -2. 解 (1)解方程f (x )=x 2+7x +6=0,得x =-1或x =-6,所以函数的零点是-1,-6.(2)解方程f (x )=1-log 2(x +3)=0,得x =-1,所以函数的零点是-1.(3)解方程f (x )=2x -1-3=0,得x =log 26,所以函数的零点是log 26.(4)解方程f (x )=x 2+4x -12x -2=0,得x =-6,所以函数的零点为-6.拓展提升求函数零点的方法函数的零点就是对应方程的根,求函数的零点常有两种方法:(1)令y =0,解方程f (x )=0的根就是函数的零点;(2)画出函数y =f (x )的图象,图象与x 轴交点的横坐标就是函数的零点.【跟踪训练1】若函数f(x)=x2+x-a的一个零点是-3,求实数a的值,并求函数f(x)其余的零点.解由题意知f(-3)=0,即(-3)2-3-a=0,a=6,∴f(x)=x2+x-6.解方程x2+x-6=0,得x=-3或2.∴函数f(x)其余的零点是2.探究2判断函数零点所在的区间例2若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间()A.(a,b)和(b,c)内B.(-∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(-∞,a)和(c,+∞)内解析∵f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a),∴f(a)=(a-b)(a-c),f(b)=(b-c)(b-a),f(c)=(c-a)(c-b),∵a<b<c,∴f(a)>0,f(b)<0,f(c)>0,∴f(x)的两个零点分别位于区间(a,b)和(b,c)内.答案A拓展提升确定函数零点所在区间的方法(1)判断一个函数是否有零点,首先看函数f(x)在区间[a,b]上的图象是否连续,并且是否存在f(a)·f(b)<0,若存在,则函数y=f(x)在区间(a,b)内必有零点.(2)对于连续函数f (x ),若存在f (a )·f (b )<0,则f (x )在区间(a ,b )内有零点,若只有一个零点,则称此零点为变号零点,反过来,若f (a )与f (b )不变号,而是同号,即不满足f (a )·f (b )<0,也不能说函数无零点,如f (x )=x 2,f (-1)·f (1)=1>0,但0是f (x )的零点.【跟踪训练2】 根据表格中的数据,可以判定方程e x -x -2=0的一个根所在的最小区间为________.答案 解析 解题的关键是e x 与x +2的差的符号,构造函数f (x )=e x -x -2,将求方程e x -x -2=0的根所在的区间转化为求函数的零点问题.令f (x )=e x -x -2,由表格中数据知f (-1)=0.37-1=-0.63<0,f (0)=1-2=-1<0,f (1)=2.72-3=-0.28<0,f (2)=7.39-4=3.39>0,f (3)=20.09-5=15.09>0,由于f (1)·f (2)<0,所以根据表格,可知根所在的最小区间为(1,2).探究3 判断函数零点的个数例3 f (x )=⎩⎪⎨⎪⎧x +2,x <0,x 2-1,x >0的零点个数是( ) A .0B .1C .2D .3解析 解法一:方程x +2=0(x <0)的根为x =-2,方程x 2-1=0(x >0)的根为x =1,所以函数f (x )有2个零点:-2与1.解法二:画出函数f (x )=⎩⎨⎧ x +2,x <0,x 2-1,x >0的图象,如图所示,观察图象可知,f (x )的图象与x 轴有2个交点,所以函数f (x )有2个零点.答案 C拓展提升 判断函数零点个数的方法(1)直接求出函数的零点进行判断.(2)结合函数图象进行判断.(3)借助函数的单调性进行判断.若函数f (x )在区间[a ,b ]上的图象是一条连续不断的曲线,且在区间(a ,b )上单调,满足f (a )·f (b )<0,则函数f (x )在区间(a ,b )上有且仅有一个零点,如图所示.【跟踪训练3】 判断下列函数零点的个数.(1)f (x )=x 2-34x +58;(2)f (x )=ln x +x 2-3.解 (1)由f (x )=0,即x 2-34x +58=0, 得Δ=⎝ ⎛⎭⎪⎫-342-4×58=-3116<0, 所以方程x 2-34x +58=0没有实数根,即f (x )零点的个数为0.(2)解法一:函数对应的方程为ln x +x 2-3=0,所以原函数零点的个数即为函数y =ln x 与y =3-x 2的图象交点个数.在同一直角坐标系下,作出两函数的图象(如图所示).由图象知,函数y =3-x 2与y =ln x 的图象只有一个交点.从而方程ln x +x 2-3=0有一个根,即函数y =ln x +x 2-3有一个零点.解法二:由于f (1)=ln 1+12-3=-2<0,f (2)=ln 2+22-3=ln 2+1>0,所以f (1)·f (2)<0,又f (x )=ln x +x 2-3的图象在(1,2)上是不间断的,所以f (x )在(1,2)上必有零点,又f (x )在(0,+∞)上是递增的,所以零点只有一个.探究4 函数零点的应用例4 已知关于x 的方程x 2-2ax +4=0,在下列条件下,求实数a 的取值范围.(1)一个根大于1,一个根小于1;(2)一个根在(0,1)内,另一个根在(6,8)内.解 (1)方程x 2-2ax +4=0的一个根大于1,一个根小于1,设f (x )=x 2-2ax +4,结合二次函数的图象与性质及零点的存在性定理得f (1)=5-2a <0,解得a >52.(2)方程x 2-2ax +4=0的一个根在(0,1)内,另一个根在(6,8)内,结合二次函数的图象与性质及零点的存在性定理得⎩⎪⎨⎪⎧ f (0)=4>0,f (1)=5-2a <0,f (6)=40-12a <0,f (8)=68-16a >0,解得103<a <174.拓展提升 解决根的分布的注意事项及方法(1)解决有关根的分布问题应注意以下几点:①首先画出符合题意的草图,转化为函数问题.②结合草图考虑四个方面:a.Δ与0的大小;b.对称轴与所给端点值的关系;c.端点的函数值与零的关系;d.开口方向.③写出由题意得到的不等式并检验条件的完备性.(2)解决此类问题可设出方程对应的函数,根据函数的零点所在的区间分析区间端点函数值的符号,建立不等式,使问题得解.当函数解析式中含有参数时,要注意分类讨论.【跟踪训练4】 函数y =x 2+2px +1的零点一个大于1,一个小于1,求p 的取值范围.解 解法一:记f (x )=x 2+2px +1,则函数f (x )的图象开口向上,当f (x )的零点一个大于1,一个小于1时,即f (x )与x 轴的交点一个在(1,0)的左方,另一个在(1,0)的右方,∴必有f (1)<0,即12+2p +1<0.∴p <-1.∴p 的取值范围为(-∞,-1).解法二:设y =x 2+2px +1的零点为x 1,x 2,则⎩⎨⎧ Δ=4p 2-4>0,(x 1-1)(x 2-1)<0⇔⎩⎨⎧ p 2>1,x 1x 2-(x 1+x 2)+1<0 ⇔⎩⎨⎧ p 2>1,1+2p +1<0,得p <-1.1.函数的零点 (1)函数的零点是一个实数,当自变量取该值时,其函数值等于零.(2)根据函数零点定义可知,函数f (x )的零点就是f (x )=0的根,因此判断一个函数是否有零点,有几个零点,就是判断方程f (x )=0是否有实根,有几个实根.(3)函数F (x )=f (x )-g (x )的零点就是方程f (x )=g (x )的实数根,也就是函数y =f (x )的图象与y =g (x )的图象交点的横坐标.2.判断函数y =f (x )零点的存在性的两个条件(1)函数的图象在区间[a ,b ]上是一条连续不断的曲线.(2)由f (a )·f (b )<0就可判断函数y =f (x )在区间(a ,b )内至少有一个零点.但应用时应注意以下问题:①并非函数所有的零点都能用这种方法找到.如y =x 2的零点在x=0附近就没有这样的区间.只有函数值在零点的左右两侧异号时才能用这种方法.②利用上述结论只能判别函数y=f(x)在区间(a,b)上零点的存在性,但不能确定其零点的个数.1.函数y =4x -2的零点是( ) A .2B .(-2,0) C.⎝ ⎛⎭⎪⎫12,0 D.12答案 D解析 令y =4x -2=0,得x =12.∴函数y =4x -2的零点为12. 2.函数f (x )=e x +x -2的零点所在的一个区间是( ) A .(-2,-1) B .(-1,0) C .(0,1) D .(1,2)答案 C解析 因为函数f (x )的图象是连续不断的一条曲线,又f (-2)=e-2-4<0,f (-1)=e -1-3<0,f (0)=-1<0,f (1)=e -1>0,f (2)=e 2>0,所以f (0)·f (1)<0,故函数的零点所在的一个区间是(0,1).3.方程x 3-x -1=0在[1,1.5]上实数解有( ) A .3个 B .2个 C .至少一个 D .0个答案 C解析 令f (x )=x 3-x -1,则f (1)=-1<0,f (1.5)=1.53-1.5-1=1.53-2.5>0,故选C.4.已知函数f (x )的图象是不间断的,且有如下的x ,f (x )对应值表:则函数f (x )在区间[-2,2]内的零点个数至少为________. 答案 3解析由f(-2)·f(-1.5)<0,f(-0.5)·f(0)<0,f(0)·f(0.5)<0可知,函数f(x)在区间[-2,2]内至少有3个零点.5.已知函数f(x)=x2-2x-3,x∈[-1,4].(1)画出函数y=f(x)的图象,并写出其值域;(2)当m为何值时,函数g(x)=f(x)+m在[-1,4]上有两个零点?解(1)依题意,f(x)=(x-1)2-4,x∈[-1,4],其图象如图所示.由图可知,函数f(x)的值域为[-4,5].(2)∵函数g(x)=f(x)+m在[-1,4]上有两个零点.∴方程f(x)=-m在x∈[-1,4]上有两相异的实数根,即函数y=f(x)与y=-m的图象有两个交点.由(1)所作图象可知,-4<-m≤0,∴0≤m<4.∴当0≤m<4时,函数y=f(x)与y=-m的图象有两个交点,即当0≤m<4时,函数g(x)=f(x)+m在[-1,4]上有两个零点.A级:基础巩固练一、选择题1.二次函数f(x)=ax2+bx+c的部分对应值如下表:x-3-2-101234f(x)6m-4-6-6-4n6不求a ,b ,c 的值,判断方程ax 2+bx +c =0的两根所在区间是( )A .(-3,-1)和(2,4)B .(-3,-1)和(-1,1)C .(-1,1)和(1,2)D .(-∞,-3)和(4,+∞)答案 A解析 因为f (-3)=6>0,f (-1)=-4<0,所以在(-3,-1)内必有根.又f (2)=-4<0,f (4)=6>0,所以在(2,4)内必有根.2.对于函数f (x ),若f (-1)·f (3)<0,则( ) A .方程f (x )=0一定有实数解 B .方程f (x )=0一定无实数解 C .方程f (x )=0一定有两实根 D .方程f (x )=0可能无实数解 答案 D解析 因为函数f (x )的图象在(-1,3)上未必连续,故尽管f (-1)·f (3)<0,但方程f (x )=0在(-1,3)上不一定有实数解.3.函数y =lg x -9x 的零点所在的大致区间是( ) A .(6,7) B .(7,8) C .(8,9) D .(9,10)答案 D解析 因为f (9)=lg 9-1<0,f (10)=lg 10-910=1-910>0,所以f (9)·f (10)<0,所以y =lg x -9x 在区间(9,10)上有零点,故选D.4.已知f (x )是定义域为R 的奇函数,且在(0,+∞)内的零点有2018个,则f (x )的零点的个数为( )A .2018B .2019C .4036D .4037答案 D解析 ∵f (x )为奇函数,且在(0,+∞)内有2018个零点,∴在(-∞,0)上也有2018个零点,又∵f (0)=0,∴共有4036+1=4037个.5.设a 是函数f (x )=2x -log 12x 的零点,若x 0>a ,则( )A .f (x 0)=0B .f (x 0)>0C .f (x 0)<0D .f (x 0)的符号不确定答案 B解析 如图所示,画出函数y =2x 与y =log 12x 的图象,可知当x 0>a 时,2 x 0>log 12x 0,故f (x 0)>0.二、填空题6.已知函数f (x )=x 2-ax -b 的两个零点是2和3,则函数g (x )=bx 2-ax -1的零点是________.答案 -12,-13解析 由题意知,方程x 2-ax -b =0的两根为2,3,∴⎩⎨⎧2+3=a ,2×3=-b ,即a =5,b =-6,∴方程bx 2-ax -1=-6x 2-5x -1=0的根为-12,-13,即为函数g (x )的零点.7.函数f (x )=3ax +1-2a 在区间(-1,1)上存在一个零点,则a 的取值范围是________.答案 (-∞,-1)∪⎝ ⎛⎭⎪⎫15,+∞ 解析 由零点存在性定理得f (-1)·f (1)<0, 即(3a +1-2a )·(-3a +1-2a )<0,整理(a +1)(-5a +1)<0,解得a <-1或a >15.8.若函数f (x )=|2x -2|-b 有两个零点,则实数b 的取值范围是________.答案 (0,2)解析 由f (x )=|2x -2|-b =0,得|2x -2|=b .在同一平面直角坐标系中画出y =|2x -2|与y =b 的图象,如图所示,则当0<b <2时,两函数图象有两个交点,从而函数f (x )=|2x -2|-b 有两个零点.三、解答题9.已知f (x )=2(m +1)x 2+4mx +2m -1.(1)当m 满足什么条件时,函数f (x )有两个零点?(2)若函数f (x )有两个零点x 1,x 2,且x 1<0<x 2,求实数m 的取值范围.解(1)由题意,知⎩⎨⎧2(m +1)≠0,(4m )2-4×2(m +1)(2m -1)>0,解得m <1且m ≠-1.(2)根据二次函数的图象,可知函数f (x )的两个零点满足x 1<0<x 2,有两种情况(如图):开口向上与开口向下.因为⎩⎨⎧2(m +1)>0,f (0)=2m -1<0或⎩⎨⎧2(m +1)<0,f (0)=2m -1>0,解得-1<m <12.所以实数m 的取值范围是⎝ ⎛⎭⎪⎫-1,12.B 级:能力提升练10.已知关于x 的方程4x 2-2(m +1)x +m =0,若该方程的一根在区间(0,1)上,另一根在区间(1,2)上,求实数m 的取值范围.解 设f (x )=4x 2-2(m +1)x +m ,则函数f (x )的图象与x 轴的交点分别在区间(0,1)和(1,2)内,画出示意图(如图):则有⎩⎪⎨⎪⎧f (0)=m >0,f (1)=4-2(m +1)+m <0,f (2)=4×22-2×2(m +1)+m >0,解得2<m <4,所以实数m 的取值范围(2,4).。
3.1.1 方程的根与函数的零点

3.1.1 方程的根与函数的零点【学习目标】1.理解函数零点的概念,掌握函数的零点与方程的根的关系;2.能够找出函数的零点的个数.【重点难点】重点:函数零点的概念、函数的零点与方程的根的关系。
难点:函数零点存在性定理【学法指导】通过研究一元二次方程的根与其对应的二次函数的图像与x 轴的交点的横坐标之间的关系,让学生明确“方程的根”与“函数的零点”的密切关系.【知识链接】一元二次方程、二次函数图像之间的关系.【问题探究】探究一:函数零点的概念1.观察下列一元二次方程的根与其相应的二次函数图像有什么关系?(1)方程2230x x --=与函数223y x x =--; (2)方程2210x x -+=与函数221y x x =-+; (3)方程2230x x -+=与函数223y x x =-+;2.对一般的一元次方程()200ax bx c a ++=≠的根与二次函数2y ax bx c =++(a ≠0)的图像有什么关系?设24b ac ∆=-,有如下结论: (1)当0∆>时,一元二次方程有两个不等的实数根12,x x , 相应的二次函数的图像与x 轴有两个交点为 ;(2)当0∆=时,一元二次方程有两个相等实数根12x x =, 相应的二次函数的图像 ;(3)当0∆<时,一元二次方程没有实数根,相应的二次函数的图像 .3.根据一元二次方程的根与其相应的二次函数图像的关系,推广到一般情况,可得到函数零点的概念: 探究二:函数零点的存在性定理引导:观察二次函数223y x x =--的图像,我们发现函数()223f x x x =--在区间[]2,1-上有零点.计算()2f -与()1f 的乘积,你能发现这个乘积有什么特点? 在区间[]2,4是否也具有这种特点?试一试:请同学们任意画几个函数的图像,观察图像,看是否能得出同样的结果? 函数零点的存在性定理:【典例分析】例1.求下列函数的零点:⑴()223f x x x =-+; ⑵()41f x x =-.引导:求函数的零点就是求该函数相应方程的根. 解:点拨:求函数的零点就是求该函数相对应方程的根,一般可借助求根公式或因式分解等办法,求出方程的根,从而求出函数的零点. 例2.判断下列函数在给定区间上是否存在零点:⑴()[]2318,1,8f x x x x =--∈; ⑵()[]31,1,2f x x x x =--∈-. 引导:利用函数的零点的存在性定理或图像进行判断. 解:点拨:判断函数在某一给定区间上是否存在零点,既是对函数零点的存在性定理的应用,只需看端点值是否异号即可.例3.求函数()ln 26f x x x =+-的零点的个数.引导:(1)用计算器或计算机作出(),x f x 对应值表;(2)作出函数()f x 的图像;(3)确定函数()f x 的单调性;(4)若在区间[],a b 上连续,且()()0f a b ⋅<,则在区间(),a b 内有一个零点;(5)结合单调性,确定零点的个数.解:【总结提升】1.判断函数在某个区间上是否存在零点,要根据具体题目灵活处理,当能直接求出零点时,就直接求出进行判断,当不能直接求出时,可根据零点存在性定理,当用定理也无法判断时,可利用计算机画出图形判断;2.判断二次函数()f x 零点的个数,就是判断一元二次方程()200ax bx c a ++=≠的实数根的个数.可利用判别式完成.而对于二次函数在某区间上的零点的个数,以及不能用判别式判断的二次函数零点,则要结合二次函数的图像进行.【总结反思】知识 . 重点 . 能力与思想方法 .【自我评价】你完成本节课的学案情况为( )A.很好B.较好C.一般D.较差3.1.1 方程的根与函数的零点一、选择题 1.若y =f(x)在区间[a ,b]上的图象为连续不断的一条曲线,则下列说法正确的是( ) A .若f(a)f(b)<0,不存在实数c ∈(a ,b),使得f(c)=0B .若f(a)f(b)<0,存在且只存在一个实数c ∈(a ,b),使得f(c)=0C .若f(a)f(b)>0,不存在实数c ∈(a ,b),使得f(c)=0D .若f(a)f(b)>0,有可能存在实数c ∈(a ,b),使得f(c)=02.设137x=,则 ( ) A.21x -<<- B.32x -<<- C.10x -<< D.01x <<3.函数()2ln f x x x=-的零点所在的大致区间为( )A.()1,2B.()2,3C.()11,,3,4e ⎛⎫⎪⎝⎭D.(),e +∞4.函数f(x)=x +1x的零点个数为 ( )A .0B .1C .2D .35.如果二次函数23y x mx m =+++的一个零点在原点,则另一个零点是 ( ) A.3 B.-3 C.32 D.-326.定义在R 上的奇函数f(x)满足:当x>0时,f(x)=2008x +log 2008x ,则函数f(x)的零点的个数为( )A .1B .2C .3D .20067.设函数3y x =与y =2-x 21⎪⎭⎫⎝⎛的图象的交点为(x 0,y 0),则x 0所在的区间是 ( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)8.已知f(x)是定义域为R 的奇函数,且在(0,+∞)内的零点有1003个,则f(x)的零点的个数为 ( ) A .1003 B .1004 C .2006 D .20079.若函数y =f(x)在区间[0,4]上的图象是连续不断的曲线,且方程f(x)=0在(0,4)内仅有一个实数根,则f(0)·f(4)的值 ( ) A .大于0 B .小于0 C .等于0 D .无法判断 二、填空题10.方程210ax x --=在()0,1内恰有一解,则a 的取值范围为 ;11.若函数()f x 在定义域R 上是奇函数,且在()0,+∞上是减函数,()20f =,则函数的零点是 .12.x ________.13.二次函数y =ax 2则使ax 2 三、解答题14.已知函数()()23263f x x m x m =-+++至多只有一个零点,求实数m 的取值范围. 解:15.已知函数()()221f x x a x =+-+的零点为正数,求实数a 的取值范围.16.如果函数)10()(f ≠>--=a a a x a x x 且有两个不同的零点,求a 的取值范围.。
方程的根与函数的零点导学案2课时

3.1.1方程的根与函数的零点导学案(2课时)课前预习案【使用说明和学法指导】1、仔细阅读课本,课前完成好预习学案,牢记基础知识,掌握基本题型,时间不超过20分钟。
在做题过程中,如遇不会的问题再回去阅读课本;AA 完成所有题目,BB 完成除★★外所有题目,CC 完成不带★题目。
2、认真限时完成,书写规范;课上小组合作探究,答疑解惑。
3、小组长在课上讨论环节时要在组内起引领作用,控制讨论节奏。
4、必须掌握的数学方法和数学思想:数形结合思想;利用零点的概念、方程的根与函数的零点的关系、零点存有性定理准确处理和解决具体问题。
课前准备:1、课本、《方程的根与函数的零点导学案》、典题本、练习本、双色笔。
2、分析错因,自纠学案。
3、标记疑难,以备讨论。
一.学习目标:1、理解函数的零点概念,理解并掌握函数零点与相对应方程根的联系 。
2、掌握判定函数零点存有的条件,并能确定具体函数存有零点的区间;3、学会将求方程的根的问题转化为求相对应函数零点的问题,转化为求相对应函数的图象与x 轴的交点问题,转化为求两函数图象的交点问题;4、激情投入,高效学习,培养学生形成扎实严谨的科学态度和勇于探索的数学精神。
重点:体会函数的零点与方程的根之间的联系,掌握零点存有的判定条件及应用.难点:探究发现函数零点的存有性.求函数零点的个数、方程根的个数、两函数图象交点的个数问题二.预习导学:自主学习教材P86~P87页内容,思考下列问题,找出疑惑之处。
复习:①函数零点定义:对于函数()y f x =,把使得 的实数x 叫做()y f x =的零点复习:②函数()y f x =有零点的等价条件函数 ()y f x =有零点⇔方程()0f x =有⇔函数()y f x =的图像函数()y f x =的零点⇔方程()0f x =的⇔函数()y f x =的图像复习:③函数零点的求法:代数法、图象法基础落实:④函数零点存有性定理如果函数()y f x =在区间[a,b]上的图象是 的一条曲线,并且有,那么,函数()y f x =在区间(a,b )内有零点,即存有c ∈(a,b ),使得()0f c =,这个c 也就是方程()0f x =的根三.小试牛刀:(1)函数82xy =-的零点为(2)函数()2x f x x =+ 的一个零点所在的大致区间为( )A.(-2,-1)B.(-1,0)C.(0,1)D. (1,2)一、合作探究重点讨论内容:1、零点存有的判定条件;(结合思考1-6及例1)2、函数零点的个数、方程根的个数与两函数图象交点的个数问题的等价转化。
3.1.1 方程的根与函数的零点导学案
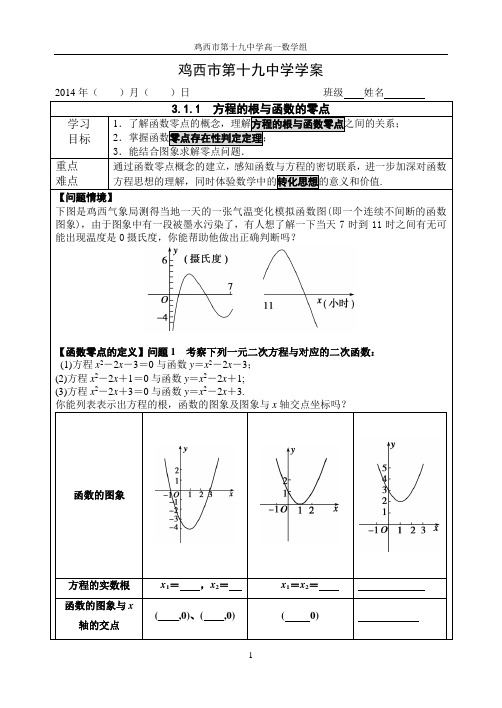
鸡西市第十九中学学案
【函数零点的定义】问题1考察下列一元二次方程与对应的二次函数:
=0与函数y=x2-2x-3;
0与函数y=x2-2x+1;
0与函数y=x2-2x+3.
你能列表表示出方程的根,函数的图象及图象与x轴交点坐标吗?
判断函数的零点的个数,可以转化为判断函数对应方程的实根的个数,也可以转化为判断函数图象与x轴交点的个数.
上的图象是一条的曲线,且,
)在区间[a,b]上的图象是连续不断的一条曲线,并且有这两个条件后,函数的零点是唯一的吗?
函数零点不一定唯一,由下图可知,还需添加函数y=。
方程的根与函数的零点导学案
3.1.1 方程的根与函数的零点导学案一、预习目标复习1:一元二次方程2ax +bx+c=0 (a ≠0)的解法.判别式∆= . 当∆ 0,方程有两根,为1,2x = ;当∆ 0,方程有一根,为0x = ;当∆ 0,方程无实数.复习2:方程2ax +bx+c=0 (a ≠0)的根与二次函数y=ax 2+bx+c (a ≠0)的图象之间有什么关系?判别式 一元二次方程 二次函数图象0∆>0∆=0∆<二、学习过程探究任务一:函数零点与方程的根的关系问题:① 方程2230x x --=的解为 ,函数223y x x =--的图象与x 轴有 个交点,坐标为 .② 方程2210x x -+=的解为 ,函数221y x x =-+的图象与x 轴有 个交点,坐标为 .③ 方程2230x x -+=的解为 ,函数223y x x =-+的图象与x 轴有 个交点,坐标为 .根据以上结论,可以得到:一元二次方程20(0)ax bx c a ++=≠的根就是相应二次函数20(0)y ax bx c a =++=≠的图象与x 轴交点的 .新知:对于函数()y f x =,我们把使()0f x =的实数x 叫做函数()y f x =的零点(zero point ).反思:函数()y f x =的零点、方程()0f x =的实数根、函数()y f x = 的图象与x 轴交点的横坐标,三者有什么关系?试试:(1)函数244y x x =-+的零点为 ; (2)函数243y x x =-+的零点为 .小结:方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.探究任务二:零点存在性定理问题:① 作出243y x x =-+的图象,求(2),(1),(0)f f f 的值,观察(2)f 和(0)f 的符号② 观察下面函数()y f x =的图象,在区间[,]a b 上 零点;()()f a f b 0;在区间[,]b c 上 零点;()()f b f c 0;在区间[,]c d 上 零点;()()f c f d 0.新知:如果函数()y f x =在区间[,]a b 上的图象是连续不断的一条曲线,并且有()()f a f b <0,那么,函数()y f x =在区间(,)a b 内有零点,即存在(,)c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根.讨论:零点个数一定是一个吗? 逆定理成立吗?试结合图形来分析.三、 典型例题例1求函数()ln 26f x x x =+-的零点的个数.变式一:求函数()ln 2f x x x =+-的零点所在区间.小结:函数零点的求法.① 代数法:求方程()0f x =的实数根;② 几何法:对于不能用求根公式的方程,可以将它与函数()y f x =的图象联系起来,并利用函数的性质找出零点.例2求函数23x y =-的零点大致所在区间.变式训练二求下列函数的零点:(1)254y x x =--;(2)2(1)(31)y x x x =--+.课后练习:1. 函数22()(2)(32)f x x x x =--+的零点个数为( ).A. 1B. 2C. 3D. 42.若函数()f x 在[],a b 上连续,且有()()0f a f b >.则函数()f x 在[],a b 上( ).A. 一定没有零点B. 至少有一个零点C. 只有一个零点D. 零点情况不确定3. 函数1()44x f x e x -=+-的零点所在区间为( ).A. (1,0)-B. (0,1)C. (1,2)D. (2,3)。
方程的根与函数的零点 导学案——高一上学期数学人教A版必修1
第三章函数的应用3.1.1 方程的根与函数的零点(导学案)【课时目标】1.理解函数零点的概念以及函数零点与方程根的联系.2.掌握函数零点的存在性定理.3.能够结合二次函数的图象判断一元二次方程根的存在性及根的个数,理解二次函数的图象与x轴的交点和相应的一元二次方程根的关系.【知识梳理】预习课本P86-P881.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应的ax2+bx+c=0(a≠0)的根的关系Δ>0 Δ=0 Δ<02.对于函数y=f(x),我们把________________叫做函数y=f(x)的零点.3.方程、函数、图象之间的关系方程f(x)=0__________⇔函数y=f(x)的图象______________⇔函数y =f(x)__________.【探究讨论】请观看视频——穿越国门若将中俄两国国界看成x 轴,火车途径的两个站点抽象到平面中来为点A ,B (两点对应的横坐标分别为a,b ),回到函数问题中来,请在下列四个图中分别画出过A ,B 两点的一条连续不断的曲线表示一个函数。
(1) (2)(3) (4)【思考1】满足什么条件,函数()y f x =在区间()b a ,上一定有零点?4.函数零点的存在性定理如果函数y =f(x)在区间[a ,b]上的图象是________的一条曲线,并且有____________,那么,函数y =f(x)在区间(a ,b)内________,即存在c ∈(a ,b),使得__________,这个c 也就是方程f(x)=0的根.【思考2】如果函数有零点,有几个零点?【牛刀小试】()21.log 1f x x =-求函数的零点.()2.23 A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)x f x x =-函数的零点所在的区间是( )3.()35x f x x =+-判断的零点个数.【课后思考】如何求出函数()ln 26f x x x =+-的零点?。
高中数学 第三章 3.1.1 方程的根与函数的零点导学案 新人教版必修1
§3.1.1 方程的根与函数的零点1. 结合二次函数的图象,判断一元二次方程根的存在性及根的个数,从而了解函数的零点与方程根的联系;2. 掌握零点存在的判定定理.8688复习1:一元二次方程2ax +bx +c =0 (a ≠0)的解法.判别式∆= .当∆ 0,方程有两根,为1,2x = ;当∆ 0,方程有一根,为0x = ;当∆ 0,方程无实根.复习2:方程2ax +bx +c =0 (a ≠0)的根与二次函数y =ax 2+bx +c (a ≠0)的图象之间有什么关系?二、新课导学※ 学习探究探究任务一:函数零点与方程的根的关系问题:① 方程2230x x --=的解为 ,函数223y x x =--的图象与x 轴有 个交点,坐标为 .② 方程2210x x -+=的解为 ,函数221y x x =-+的图象与x 轴有 个交点,坐标为 .③ 方程2230x x -+=的解为 ,函数223y x x =-+的图象与x 轴有 个交点,坐标为 .根据以上结论,可以得到:一元二次方程20(0)ax bx c a ++=≠的根就是相应二次函数20(0)y ax bx c a =++=≠的图象与x 轴交点的 .你能将结论进一步推广到()y f x =吗?新知:对于函数()y f x =,我们把使()0f x =的实数x 叫做函数()y f x =的零点(zero point ).反思:函数()y f x =的零点、方程()0f x =的实数根、函数()y f x = 的图象与x 轴交点的横坐标,三者有什么关系?试试:(1)函数244y x x =-+的零点为 ; (2)函数243y x x =-+的零点为 .小结:方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.探究任务二:零点存在性定理问题:① 作出243y x x =-+的图象,求(2),(1),(0)f f f 的值,观察(2)f 和(0)f 的符号② 观察下面函数()y f x =的图象,在区间[,]a b 上 零点; ()()f a f b 0;在区间[,]b c 上 零点;()()f b f c 0;在区间[,]c d 上 零点;()()f c f d 0.新知:如果函数()y f x =在区间[,]a b 上的图象是连续不断的一条曲线,并且有()()f a f b <0,那么,函数()y f x =在区间(,)a b 内有零点,即存在(,)c a b ∈,使得()0f c =,这个c 也就是方程()0f x =的根.讨论:零点个数一定是一个吗? 逆定理成立吗?试结合图形来分析.※ 典型例题例1求函数()ln 26f x x x =+-的零点的个数.变式:求函数()ln 2f x x x =+-的零点所在区间.小结:函数零点的求法.① 代数法:求方程()0f x =的实数根;② 几何法:对于不能用求根公式的方程,可以将它与函数()y f x =的图象联系起来,并利用函数的性质找出零点.※ 动手试试练1. 求下列函数的零点:(1)254y x x =--;(2)2(1)(31)y x x x =--+.练2. 求函数23x y =-的零点所在的大致区间.三、总结提升※ 学习小结①零点概念;②零点、与x 轴交点、方程的根的关系;③零点存在性定理※ 知识拓展图象连续的函数的零点的性质:(1)函数的图象是连续的,当它通过零点时(非偶次零点),函数值变号. 推论:函数在区间[,]a b 上的图象是连续的,且()()0f a f b <,那么函数()f x 在区间[,]a b 上至少有一个零点. .※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 函数22()(2)(32)f x x x x =--+的零点个数为( ).A. 1B. 2C. 3D. 42.若函数()f x 在[],a b 上连续,且有()()0f a f b >.则函数()f x 在[],a b 上( ).A. 一定没有零点B. 至少有一个零点C. 只有一个零点D. 零点情况不确定3. 函数1()44x f x e x -=+-的零点所在区间为( ).A. (1,0)-B. (0,1)C. (1,2)D. (2,3)4. 函数220y x x =-++的零点为 .5. 若函数()f x 为定义域是R 的奇函数,且()f x 在(0,)+∞上有一个零点.则()f x 的零点个数为 .1. 求函数3222y x x x =--+的零点所在的大致区间,并画出它的大致图象.2. 已知函数2()2(1)421f x m x mx m =+++-.(1)m 为何值时,函数的图象与x 轴有两个零点;(2)若函数至少有一个零点在原点右侧,求m 值.。
311方程的根与函数的零点导学案.doc
3.1.1方程的根与函数的零点教学目标:1.理解函数(结合二次函数)零点的概念,领会函数零点与相应方程要的关系,掌握零点存在的判定条一件・2. 理解零点存在性的判定3. 在函数与方程的联系中体验数学中的转化思想的意义和价值.重点:零点的概念及存在性的判定.难点:零点的确定一、创设情境:1>先来观察几个具体的一元二次方程的根及其相应的二次函数的图彖:①方程Jr? 一2兀一3 = 0与函数〉‘=兀2一2兀一3・Q方程x2一2兀+ 1二0与函数歹=/一2尤+1思考:表中一元二次方程的实数根与相应的二次函数图象与x轴的交点的关系。
总结:1)方程根的个数就是函数图象与X轴交点的个数。
2)方程的实数根就是函数图象与x轴交点的横坐标。
2、提出问题:若将上面特殊的一元二次方程推广到一般的一元二次方程ax2+bx+c=0(a#0) 及相应的二次函数y= ax2+bx+c(a7^0)的图彖与x轴交点的关系,上述结论是否仍然成立?溜式戶=b?—4ac 方程ax2 +bx+c=(a^O)的根。
函数y二ax2+bx+c(a^0)的图彖函数的图象与X轴的交占A>0两个不相等静实報根共q 、笑2x\■■J(X p 0),(x2, 0)A=0有两个相等的实数根X]二X2(x p 0)A<0没有实根 2 -iyB总结:可见上述关系对一般的一元二次ax2+bx+c=O(a^O)及相应的二次函数y= ax2+bx+c(a^O)也是成立的二、讲授新课:3、函数零点的概念:对于函数y = f(x)(xe D),把使/(x) = 0成立的实数兀叫做函数y 二/(X)(XG£>)的零点.函数零点的意义:函数y = /(%)的零点就是方程/(X)= 0实数根,亦即函数y = /(x)的图象与兀轴交点的横坐标.即:方程/(%) = 0有实数根o函数y = /(x)的图象与兀轴有交点o函数y = fM有零点.(1)求函数丁 = /(兀)零点的方法:①方程法:求方程fM = 0的实数根;®图像法:画出函数yh(x)的图象,其图象与x轴交点的横坐标是函数yh(x)的零点例1.求下列函数的零点:1 /(x) = x2-x-2 2 /(兀)二3兀一23 f(X)= e x 4. /W = lnx+2x-64、零点存在性的探索:(I )观察二次函数f(x) = x2-2x-3的图象:®在区间[-2,1]±有零点_______ ;/(-2) = ______ , /(D= _______/(-2)• /(D _____ 0 (<或>)・©在区间[2,4]上有零点______ ;/⑵• /⑷—0 (V或〉).(II)观察下面函数y = /(x)的图象®在区间[恥]上 _____ (有/无)零点;/⑺)•0 (<或>)・©在区间|Z?,c]±_______ (有/无)零点;/的• /(c)_____ 0(<或〉)・©在区间[c,〃]上____ (有/无)零点;/(C)• /(d)___ 0(V或〉)・由以上两步探索,你可以得出什么样的结论?(结合函数图象,思考、讨论、总结归纳得出函数零点存在的条件,并进行交流、评析)总结:函数零点存在性定理5、怎样利用函数零点存在性定理,断定函数在某给定区间上是否存在零点.三、例题讲解:例:1.求函数/(兀)=lnx + 2x-6的零点个数.问题:1) 你可以想到什么方法来判断函数零点个数?2) 判断函数的单调性,由单调性你能得该函数的单调性具有什么特性?(引导学生探索判断函数零点的方法,指出可以借助计算机或计算器来画函数的图象,结合图象对函数有一个零点形成直观的认识・)四、当堂训练:1. 利用函数图象判断下列方程有没有根,有几个根:(1) —兀~ + 3x + 5 = 0;(2) 2x(x — 2) = —3 ;(3) x2 = 4x —4;(4) 5X2+2X =3X2+5・2. 利用函数的图象,指出下列函数零点所在的大致区间:(1) / (x)=—无‘ 一3x + 5 ;(2) /(x) = 2xln(x-2)-3 ;(3) f(x) = e x~{(4) /(x) = 3(x+ 2)(x-3)(x + 4) + 兀五•、布置作业:教材P92 (A组)第1、2题;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y ax2 bx c (a 0) 的图象有什么关系?
2.函数的零点的概念: 对于函数 y=f(x),把 叫做函数 y=f(x)的零点。 注: 函数的零点是一个实数,而不是一个点。 3.方程、函数、图象之间的关系: 方程 f(x)=0 ⇔函数 y=f(x)的图象 ⇔函数 y=f(x) 。 练习: Al.函数 y=x-1 的零点是 ( ) A.(1,0) B.(0,1) C.0 D.1 A2.函数 f(x)=x2-3x-4 的零点是________ B3.若函数 f(x)=x2+2x+a 没有零点,则实数 a 的取值范围是 ( ) A.a<1 B.a>1 C.a≤1 D.a≥1 C4.已知函数 f(x)为奇函数,且该函数有三个零点,则三个零点之和等于 ( ) A.0 B.1 C.-1 D.不能确定 (二) 、认真阅读教材 P87---P88 页内容,探究:函数 y=f(x)在某个区间上是否一定有零 点?怎样的条件下,函数 y=f(x)一定有零点? 2 2 1 观察二次函数 y x 2x 3 的图象 我们发现函数 y x 2x 3 在区间 [2,1] 上 有零点。计算 f (2) 和 f (1) 的乘积,你能发现这个乘积有什么特点?在区间 [2,4] 上是否 也具有这种特点呢?
第 2 页 共 2 页
A 例 1、求证:函数 f(x)=2x -3x-2 有两个零点。
2
A 例 2 、求函数 f ( x) ln x 2 x 6 的零点个数。
五、达标检测: 练习:教材 88 页第 1 题(1) (2)第 2 题(1) ( 2) (3) 2 A1.函数 f(x)=lnx- 的零点所在的大致区间是( )
第 1 页 共 2 页
2 猜想:若函数在区间[a,b]上图象是连续的,如果有 成立,那么函数在 区间(a,b)上有零点。 3.函数零点存在定理:如果函数 y=f(x)在区间[a, b]上的图象是 的 一条曲线,并且有 , 那么, 函数 y=f(x) 在区间 内有零点, 即 存在 c∈(a, b),使 , 这个 也就是方程 f(x) = 0 的根。 思考:若函数 y=f(x) 在区间(a, b)内有零点,一定能得出 f(a)·f(b)<0 的结论吗?
x
A.(1,2)
B.(2,3)
1 C.(1, )和(3,4)
e
D.(e,+∞)
B2.函数 f(x)=x2-ax-b 的两个零点是 2 和 3,求函数 g(x)=bx2-ax-1 的零点。
六、学习小结: 1.函数零点的定义。 2.等价关系。 3.函数的零点或相应方程的根的存在性以及个数的判断。 七、布置作业: 八、课后反思:
3.1.1 方程的根与函数的零点导学案
一、学习目标: 结合二次函数的图象,理解函数的零点概念,领会函数零点与相应方程根的关系 二、学习重、难点: 函数的零点的概念以及零点存在的判定方法。 三、学法指导:认真阅读教材,在熟练掌握二次函数的有关知识的基础上,结合二次函数 图象,由特殊到一般逐渐理解零点的概念,并会判断零点的存在。 四、学习过程: (一) 、认真阅读教材 P86---P87 页内容,思考: 1.通过书中三个具体一元二次方程的根与相应的二次函数的图像与 x 轴的交点的关 系 归 纳 一 元 二 次 方 ax bx c 0 (a 0) 的 根 与 相 应 的 二 次 函 数
