第四章 生产论
第四章 生产理论

第四章出产论第一节出产函数一、概述出产者也称厂商,指能够作出统一的出产决策的单个经济单元。
包罗个人、合伙和公司性质的经营组织形式。
厂商被假定为是符合理性的经济人,提供产物的目的在于追求最大的利润。
厂商进行出产的过程就是从出产要素的投入到产物的产出的过程。
出产要素的类型一般被划分为以下四种:•劳动〔L〕:指人类在出产过程中提供的体力和智力的总和。
•地盘〔N〕:包罗地盘和地上、地下的一切自然资源。
•成本〔K〕:包罗成本品〔实物形态〕和货币成本〔货币形态〕。
•企业家才能〔E〕:指企业家组织成立和经营办理企业的才能。
出产函数暗示在一按时期内,在技术程度不变的情况下,出产中所使用的各种出产要素的数量与所能出产的最大产量之间的关系。
假定X1、X2……Xn依次暗示某产物出产过程中所使用的n种出产要素的投入数量,Q暗示所能出产的最大产量,那么出产函数可写为:Q=f〔X1、X2……Xn〕通常假定出产中只使用劳动〔L〕和成本〔K〕两种出产要素,那么出产函数写为:Q=f〔L、K〕注意:出产函数的前提条件是一按时期内既定的出产技术程度,一旦出产技术程度变化,原有出产函数就会变化,从而形成新的出产函数。
二、常见的出产函数〔一〕固定投入比例出产函数固定投入比例出产函数是指在每一个产量程度上任何一对要素投入量之间的比例都是固定的出产函数。
假定出产中只使用劳动〔L〕和成本〔K〕两种出产要素,那么固定投入比例出产函数通常写为:此中,Q暗示一种产物的产量,U和V别离为固定的劳动和成本的出产技术系数,各暗示出产一单元产物所需的固定的劳动的投入量和成本的投入量。
该出产函数暗示:产量Q取决于和这两个比值中较小的一个。
这是因为Q的出产被假定为必需按照L和K之间的固定比例,当一种出产要素数量固按时,另一种出产要素数量再多,也不克不及增加产量。
该出产函数一般又假定劳动〔L〕和成本〔K〕两种出产要素都满足最小的要素投入组合的要求,那么有:,即上式暗示两种出产要素的固定投入比例等于两种出产要素的固定出产技术系数之比。
第四章 生产理论

微观经济学M I C R O E C O N O M I C S生产者行为研究的三个层次投入的生产要素与产量的关系——生产理论即如何在生产要素既定时实现产量最大,或者在产量既定时使投入的生产要素最少。
成本与收益的关系——成本理论要使利润最大化,就是要使扣除成本后的收益达到最大化。
这就要进行成本-收益分析并确定一个利润最大化的原则。
不同市场结构下产品产量与价格的确定——市场结构理论市场有各种结构,即竞争与垄断的程度不同,当厂商处于不同的市场上时,应该如何确定自己产品的产量与价格。
第四章生产理论目录/Contents01 02 03生产与生产函数短期生产理论长期生产理论01生产与生产函数1.厂商定义:市场上商品或劳务的供给者,是购买或雇佣生产要素并将之组织起来生产和销售商品或劳务的经济组织。
目标:利润最大化分类:厂商分为个人企业,合伙制企业和公司制企业。
2.生产生产是对各种生产要素进行组合以制成产品的行为。
所以,生产也就是把投入变为产出的过程。
3.生产要素:生产中所使用的各种资源现代西方经济学认为生产要素包括劳动力、土地、资本、企业家四种4.生产函数Q=f(X1,X2,……X n),Q表示所能生产的最大产量,X1,X2,……X n表示生产要素的投入数量一般简化为:Q=f(L,K),L表示劳动投入数量,K表示资本投入数量。
短期是生产者来不及调整全部生产要素的数量,至少有一种生产要素的投入数量固定不变的生产周期。
长期是生产者可以调整全部生产要素投入数量的生产周期。
5.生产期间的分类一些具体的生产函数0102指在每一个产量水平上任何一对要素投入量之间的比例都是固定的生产函数。
其中,常数u 和v 分别为固定的劳动和资本的生产技术系数,他们分别表示生产一单位产品所需要的固定的劳动投入量和资本投入量。
产量Q 取决于和这两个比值中较小的那一个,即使其中的一个比例数值较大,那也不会提高产量Q 。
固定投入比例生产函数――里昂惕夫生产函数Leontief Production Function(0<α,β <1)其中,A 为技术系数,即给定的技术水平对总产出的效应;L ,K 分别为劳动和资本的投入量;α,β分别为固定的劳动和资本的生产技术系数,它们分别表示生产以单位产品所需要的劳动投入量和固定的资本投入量。
第四章笔记 生产论

第四章生产论重点难点1、重点:边际报酬递减规律;生产的合理投入区;最优的生产要素投入组合;规模报酬。
2、难点:总产量、平均产量和边际产量相互之间的关系;生产的合理投入区和最优的生产要素投入组合;规模报酬的三种类型。
第一节生产函数(production function)一、生产(了解)----厂商投入生产要素到产品产出的过程。
从经济学的角度看,生产就是指一切能够创造或增加效用的人类活动。
1、生产者(或称厂商,企业)—Firm澄清误解——不是老板。
又称生产者或企业,指在市场经济条件下,能够做出统一的生产决策,为了实现最大利润而从事生产的单个经济单位。
2.三种组织形式:个人企业(sole proprietorship)、合伙企业(partnerships)、公司企业(corporations)3.经营目标:利润最大化企业要实现利润最大化必须同时实现两个效率:A、技术效率:是投入的生产要素与产量的关系,即在生产产品的过程中不存在生产要素的浪费。
(生产函数)B、经济效率:如何使在生产要素成本既定时使产量最大(最大产量原则),或在产量既定时使投入的生产要素成本最小。
(最小成本原则)4、生产要素(Factors of Production)劳动(L)、资本(K)、土地(N)、企业家才能(E, entrepreneurship)劳动——工资、资本——利息、土地——地租、企业家才能——正常利润二、生产函数(掌握)1.定义:表示在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最大产量之间的关系。
Q = f(L,K,N,E)--- 生产函数其中N是固定的,E难以估算,所以,Q = f(L,K)称为简化的生产函数。
作用:对比生产函数可以看出技术水平的差距。
注意:(1)一个生产函数表示一定的技术水平;(2)生产函数中的产出是最大产出。
2. 生产函数的类型微观经济学的生产理论:短期生产理论和长期生产理论短期--指生产者来不及调整全部生产要素的数量,至少有一种生产要素(如机器设备、厂房等)是固定不变的时间周期。
第四章 生产理论
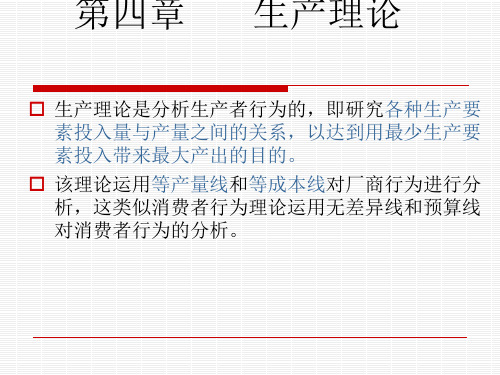
一单位劳动投入量,必须放弃的资本投入量,也即
资本与劳动的替代比例。
2、公式: MRTSLK = -ΔK /ΔL
绝对值,以便于比较。
加负号是为了取
3、几何意义:边际技术替代率,实际上就是等产
量线上点的斜率的绝对值。
在通常情况下,由于劳动和资本的变 化量成反方向变动,为使边际技术替代率 是正值以便于比较,在公式中加了一个负 号。 当 时,则有:
说明等产量曲线上任一点的边际技术替 代率等于等产量曲线在该点的斜率的绝对 值。
对于任意一条给定的的等产量曲线来说,当用 劳动投入去替代资本投入时,在维持产量水平 不变的前提下,由增加劳动投入量所带来的总 产量的增加量和由减少资本投入量所带来的总 产量的减少量必定是相等的。
• 厂商及企业组织
生产者、厂商或企业是指能够做出统一的生产决 策的单个经济单位。 或者市场经济中为达到一定目标而从事生产活 动的经济单位。 ( 厂商不仅生产出有形的商品,还包括提供无 形的服务。) 在经济学中,企业被假定为合乎理性的经济人, 是以营利为目标,能够独立核算和自主经营的经
济单位,或者说,我们假设企业把利润最大化作
劳动的平均产量APL指总产量与 所使用的可变要素劳动的投入量之 比,写为:
劳动的边际产量MPL指增加一 单位可变要素劳动的投入量所增加 的产量,写为:
或:
总产量的导数就是边际产量,边际产量是总产量曲线的 斜率。
二、边际报酬递减规律
1、定义: 在技术水平不变的条件下,在连续等量地把某一种 可变生产要素增加到其他一种或几种数量不变的生 产要素上去的过程中,当这种可变生产要素的投入 量小于某一特定值时,增加该要素投入所带来的边 际产量是递增的;当这种可变要素的投入量连续增 加并超过这个特定值时,增加该要素投入所带来的 边际产量是递减的。这就是边际报酬递减规律。 简单描述:对一种可变生产要素的生产函数来说,边 际产量先上升然后下降。
第四章 生产论

第四章生产论1、边际报酬递减规律:在技术水平不变的条件下,连续等量地把一种可变生产要素增加到一种或几种数量不变的可变要素上去的过程中,当这种生产要素的投入量小于某一特定值时,增加该要素投入所带来的边际产量是递增的;当这种可变要素的投入量大于某一特定值时,增加该生产要素的投入量所带来的边际产量是递减的。
2、试说明理性的生产者应如何组织生产。
答:(1)对于单一可变生产要素的情况,其最优生产投入量应在第二阶段内,即在该可变要素的平均产量下降且边际产量大于零的阶段。
因为,在第一阶段,平均产量递增,若继续增加该要素的投入量,总产量和平均产量会相应增加,因而理性的生产者将不会停留在该阶段;在第三阶段,边际产量为负,若减少该要素的投入量,总产量会相应增加,因而理性的生产者也不会停留在该阶段。
至于生产者究竟在第二阶段的哪一点为最佳,则取决于该要素投入所能带来的收益与其花费的成本的比较。
若它带来的边际收益等于它带来的边际成本,则它的最佳投入数量就达到了,否则需要增加或减少投入量。
(2)对于两种及两种以上的生产要素,其投入比例取决于边际技术替代率和各要素的价格,当RTS=ω/r时,要素的投入比例为最佳。
在等产量线和等成本线上,则是二者相切之处决定最佳比例。
如此确定的比例有无数个,表现为等产量线和等成本线有无数个切点,这些切点构成生产的扩展线。
那么,理性的生产者应选择扩展线的哪一点,取决于产品价格和要素的规模收益情况。
生产规模的确定需由收益情况来定。
如果规模收益呈递增趋势,则生产规模应继续扩大,增加使用各要素的数量;如果规模收益呈递减趋势,则生产规模应缩小,直到处于规模收益不变的阶段。
关于规模与收益之间的具体关系,则涉及产品价格的变化情况,这种变化视不同的市场形态而不同。
但生产者选择最优规模时,其基本原则是MR=MC。
3、等产量曲线:表示在生产技术水平不变的条件下,生产同一产量的两种要素的投入量的所以不同组合的轨迹。
《西方经济学》第四章 生产理论

彭
腾主讲
西方经济学
第四章 生产理论
二、边际收益递减规律
总产量要经历一个逐渐上升加快 增长趋缓 最大不变绝对下降的过程。 边际收益(报酬)递减规 律:在技术和其他生产 要素不变的情况下,追 加一种生产要素,所形 成的产量,最初会增加, 但到一定限度后,增幅 开始递减,最终还会使 产量绝对减少。 Q
2、等产量线的特征
A.等产量线是一条向右下方倾斜的线。
B.等产量线不能相交。 K
C、在同一个平面上可以 有无数条等产量线。 D、凸向原点。
9
Q
0
彭
L
腾主讲
二、等成本线
西方经济学
第四章 生产理论
• 等成本线(企业预算线):指生产要素价格一定 时,既定的成本可购买的两种生产要素(K,L)最 大组合的轨迹。 • 成本方程: TC = PL· + PK· L K
11
K
•成本既定,产 量最大; • 产量既定, 成本最小。 E
Q
L
彭
腾主讲
西方经济学
第四章 生产理论
第三节 全部生产要素的投入 (规模经济)
• 一、规模经济与规模不经济
技术水平不变,生产要素按同样的比例增加即
生产规模扩大,起初量的增加要大于生产规模 的扩大;随生产规模扩大超过一定的限度,产 量的增加将小于生产规模的扩大甚至使产量绝 对地减少,则规模经济走向规模不经济。 规模经济是指生产者在一定的技术条件下,所 有生产要素按相同比例增加而能获得相应的经 济上的收益。
6
彭
腾主讲
西方经济学
第四章 生产理论
三、生产的合理投入区域
•第一阶段,平均产出递 增,因为生产的规模效 益正在表现出来; F TP •第二阶段,平均产出递 减,总产出增长的速度 Ⅱ Ⅲ 放慢; •第三阶段,边际产出为 E 负,总产出绝对下降。 AP 生产合理区域在第二阶 L 段。 A B MP
西方经济学微观部分-第四章_生产论

4.边际报酬递减规律的3阶段
总产量要经历一个逐渐上升加快 增长趋缓 最大不变绝对下降的 过程。
一种生产要素增加所引起的边 际产量变动三阶段:
第一阶段:边际产量递增 总产量增加
第二阶段:边际产量递减 总产量增加
第三阶段:边际产量为负 总产量开始减少
Q
G
B
TP
Ⅰ
O
ⅡⅢ
A E
F AP
L1 L2 L3 MP L
来的全部产量。 TPL f (L, K )
平均产量AP(average product ) :平均每单位要素所生产出来的产
量。 (如劳动力L)
AP = TP/L
APL
f (L, K ) TPL
L
L
边际产量MP(marginal product) :增加一单位要素所增加的产量。
(如劳动力L) MP = TP/ L
技术水平
如果生产技术发生了变化……
“足蒸暑土气,背灼炎天光,力尽不知热,但惜夏日
长”VS“联合收割机伴随音乐,倘佯在诗情画意的田
野上”
一、技术变革 生产过程改进、旧产品革新、新产品发明
二、作用——生产函数发生移动 使用相同数量的投入获得更多的产出 用更少的投入获得相同数量的产出
1.生产函数
在一定时期、一定的生产技术水平下,生产要素投入量与最大 产出量之间的物质数量关系。
金字塔
(1)企业家:顶层 冒着一定风险,在变幻莫测的市场风云中抓 住机会成就事业的人。“四有”+高等教育
(2)管理者:中层 落实企业家的意志和决策。“上传下达”
(3)工人:底层 把原料变成产品的执行者
2.厂商(企业)的本质
(一)大规模生产的经济性 在自己家地下室生产自己所需产品,经济吗?
4第四章 生产论 微观经济学
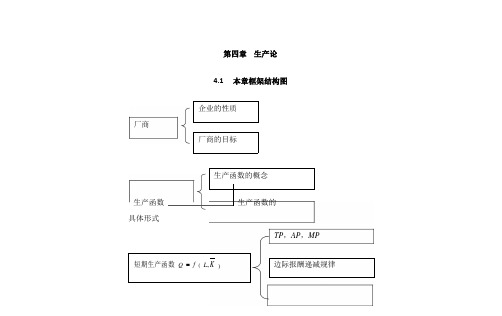
四、长期生产函数:两种可变生产要素的生产函 数1.长期生产函数的形式 在生产理论中,为了简化分析,通常以两种可变生产要素的生产函数来考察长期生产问题。假定生产者使用劳 动和资本两种可变生产要素来生产一种产品,则两种可变生产要素的长期生产函数可以写为:
Q f L,K 2.等产量曲线 等产量曲线(Equal-Product Curves)是在技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不 同组合的轨迹,每一条等产量曲线对应的是特定的产出水平。等产量曲线如图4-2所示。
点的线段的斜率,就是相应的 APL 值。(3)边际产量和平均产量之间 的关系
就平均产量 APL 和边际产量 MPL来说,当 MPL APL 时, APL 曲线是上升的;当MPL APL 时,APL曲
线是下降的;当 MPL APL 时,APL 曲线达极大值。数学证明如下:
dTPL L −TP
d APL d TPL dL
二、生产函数 1.生产函数的概念
劳动、土地、资本和企业家才能
生产函数表示在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最
大产量之间的关系(The production function specifies the maximum output that can be produced with a given quantity of
劳动的平均产量 APL 指平均每一单位可变要素劳动的投入量所生产的产量,即 APL = TPL L,K 。
L
劳动的边际产量 MPL 指增加一单位可变要素劳动投入量所增加的产量,即:
TPL L,K
MP
lim
TP dTPL L,K
L
L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( x1 , x2 ,..., xn ) → Q
Q = f ( x1 , x2 ,..., xn )
若假定只使用劳动和资本两种生产要素, 则有:
Q = f ( L, K )
2012-3-19 5
几种生产函数表达式
• (1)固定替代比例 生产函数,即线性生 产函数:Q=aL+bK, 其中a、b>0 • 表明在每一产量水平 上任何两种生产要素 之间的替代比例都是 固定的。
2012-3-19 26
§4.3 等成本线
一、等成本线的含义
在既定的成本和既定的生产要素价格条件下,生产者 在既定的成本和既定的生产要素价格条件下, 可以购买到的两种生产要素的各种不同数量组合的轨迹。 可以购买到的两种生产要素的各种不同数量组合的轨迹。
可以看出,由于K、L都是 公式、 二、公式、图像 可变的,因此等成本线的斜 率是可变的。
•公式: MRTS = − ∆K 公式: LK ∆L
MRTS LK
2012-3-19
∆K dK = lim ( − )=− ∆L → 0 ∆L dL
24
•边际技术替代率递减规律 在维持产量不变的前提 下,当一种生产要素的投入 量不断增加时, 量不断增加时,每一单位的 这种生产要素所能替代的另 一种生产要素的数量是递减 的。 等产量曲线的斜率的绝对值 是递减的,所以, 是递减的,所以,等产量线 凸向原点
TP AP MP
2012-3-19
L
= 20 L − 0 . 5 L 2 − 50 = TP L 50 = 20 − 0 . 5 L − L L d TP L = = 20 − L dL
L
L
16
(2)关于总产量的最大值: 令
dTPL dTPL = 0,即 = 20 − L = 0, 解得L = 20 dL dL d 2TPL 且 = −1〈0 2 dL
2012-3-19
K 3 2 1 O Q1 Q2 Q3 2 4 6 L
6
• (2)固定投入比例 木桶短板 的生产函数,即里昂 原理 K 惕夫生产函数:
R c b Q3 Q2 L
L K Q = min{ , } u v
其中,常数u、v >0
L K K v Q= = → = u v L u K1 K 2 K 3 v Q= = = = L1 L2 L3 u 2012-3-19
2012-3-19
13
(3)总产量与平均产量
平均产量:平均每一单位可变要素投入所生产的产量。 平均产量:平均每一单位可变要素投入所生产的产量。 Q D
TPL = f ( L, K )
f ( L, K ) APL = L
C
f ( L1 , K )
TPL
★平均产量等于总产 量曲线上的点与原点 连线的斜率
0
资本
C D
R
Q2
Q = f ( L, K ) = Q
•图形:见右 图形: 图形
2
O
Q1
1 2 劳动
22
2012-3-19
• 特征:
∆等产量曲线与坐标原点的距离的大小表示 产量水平的高低,离原点越近的等产量曲 线代表的产量水平越低,反之,代表的产 量水平越高。 ∆同一坐标平面上的任意两条等产量曲线不 会相交。 ∆等产量曲线是凸向原点的。
以L=10代入劳动边际产量函数
MPL = dTPL = 20 − L dL
得到MP=10,显然,当MPL=APL=10时, 时
一定达到最大值。 APL一定达到最大值。
2012-3-19
18
(5)生产的三个阶段
第I阶段
•总产量递增 •平均产量递增 •边际产量先增后减但始终大于平均产 量
短期生产决策区 Q
这一特征与前 文什么曲线特 征相似?
2012-3-19
23
3、边际技术替代率(MRTS) 边际技术替代率(MRTS) •含义:在维持产量水平不变的条件下,增 含义:在维持产量水平不变的条件下,
注意,MRTS与 加一单位某种生产要素投入量时所减少的另
一种要素的数量。 一种要素的数量。
MRS有何含义 差别?
=
1 L
(MP
L
− AP
L
)
E
TPL
可见, 可见,当MPL=APL时,
dAP L 达到最大值。 = 0 ,APL达到最大值。 O dL
2012-3-19
APL
L0 L2 L3 L4
MPL
L
15
习题讲解 • 已知生产函数Q=f(L,K)=2KL-0.5L2-0.5K2,假定厂商目 前处于短期生产,且K=10。(1)写出短期中厂商关于劳 动的总产量函数、平均产量函数和边际产量函数。(2)分 别计算劳动的总产量、平均产量和边际产量各自达到最大 值时厂商的劳动投入量。(3)何时APL=MPL?其值是多少? • 解答:(1)由生产函数Q=f(L,K)=2KL-0.5L2-0.5K2, 且K=10,可得短期生产函数为: Q=20L-0.5L2-50,于是, 关于劳动的总产量函数、平均产量函数和边际产量函数分 别为:
9
2、一种可变生产要素的生产函数
(1)一种可变生产要素的生产函数的形式 (短期生产函数) 短期生产函数) Q = f ( L, K )
Q = f (L, K )
固定生产要素(固定、不变投入) 固定生产要素(固定、不变投入)
在短期内, 在短期内,生产者无法调整的那部分投入
可变生产要素(可变投入) 可变生产要素(可变投入)
K1
O
Q3 Q2 Q1
L
29
MPK MPL ⇒ = r w 2012-3-19
L1
成本最小化问题 ——给定生产产量,实现成本最小化的要素组合。 给定生产产量, 给定生产产量 实现成本最小化的要素组合。
TPL
APL
O
所以第 阶段是短期生产 ★ 所以第II阶段是短期生产 决策区间
2012-3-19
L3 L4 MP L L
19
四、两种可变生产要素的生产函数
1、两种可变生产要素的生产函数的形式 (长期生产函数) 长期生产函数)
Q = f ( L, K )
2012-3-19
20
等产量曲线的来源
• 两种生产要素与产量关 系的曲面图
2012-3-19 3
§4.2
生产函数
一、生产函数所包含的生产要素类型 劳动 资本 土地 企业家才能
2012-3-19
Байду номын сангаас
4
二、生产函数的含义
1、 生产函数 、 在一定时期内,在技术水平不变的情况下, 在一定时期内,在技术水平不变的情况下, 生产中所使用的各种生产要素的数量与所能生 产的最大产量之间的关系。 产的最大产量之间的关系。
劳动投入量 L 0 1 2 3 4 5 6 7 8
2012-3-19
劳动的总产量 TPL 0 3 8 12 15 17 17 16 13
劳动平均产量 APL 0 3 4 4 15/4 17/5 17/6 16/7 13/8
劳动边际产量 MPL 3 5 4 3 2 0 -1 -3
11
总产量与边际产量
D
第II阶段 II阶段
•总产量递增
•平均产量递减 平均产量递减
•边际产量递减但始终大于 边际产量递减但始终大于0 边际产量递减但始终大于
C
第III阶段 III阶段
•总产量递减 总产量递减 •平均产量递减 平均产量递减 •边际产量递减且始终小于 边际产量递减且始终小于0 边际产量递减且始终小于
I
II
III
2012-3-19 25
K
18
Q
A
12 8 6
B E F
O
1
2
3
4
L
小结
• 长期中,两种可变生产要素函数是二元 一次函数,形成一个曲面图象,它们影 响产量是通过二者投入比例的不同而发 生的,由此出现一个等产量曲线。等产 量曲线具有三个特征,其中凸向原点的 特征是由于边际技术替代率递减规律导 致的。等产量曲线是可变生产要素比例 组合的最佳轨迹,是可变生产要素形成 产量的最大约束外界。
2012-3-19
APL
L1 L3 L4
L
14
(4)平均产量与边际产量
APL与MPL相交于 L曲线的最高点。 相交于AP 曲线的最高点。
dAP dL
1 = L
L
d = dL
f (L, K ) Q L
)
B C D
df ( L , K ) f (L, K − dL L
2
• 二、厂商的目标 • 在微观经济学中,一般总是假定厂商 在微观经济学中,一般总是假定厂商 的目标是利润最大化。实际上,厂商还 的目标是利润最大化。实际上,厂商还 追求销售收入最大化、市场占有率最大 化等。 • 厂商中的委托代理关系——资产所有 厂商中的委托代理关系——资产所有 者与经营者分离。
K
C ( L, K ) = wL + rK
C r
C0 = wL + rK C0 w ⇒ K = − L+ r r
2012-3-19
C = wL + rK
O
C w
L
27
• 3、等成本线的变动
K K
A2 A A1 A
绕A旋转
C = wL + rK
O
C = wL + rK
L
B1 B B2
L
O
B1 B B2 A2 A
总产量 Q D
TPL = f ( L, K )
边际产量
MP L ∆ TP L = ∆L
= df ( L , K ) dL
