高中数学-算法初步测试题
新课改高中数学数学必修三《算法初步》单元测试[技巧]
![新课改高中数学数学必修三《算法初步》单元测试[技巧]](https://img.taocdn.com/s3/m/4768975ecc22bcd127ff0c56.png)
结束
三、解答题: (本大题分 4 小题共 56 分) 26.( 1)( I )用辗转相除法求 840 与 1 764 的最大公约数 .
END
A. 3 或 -3
B
. -5 C
.5 或 -3 D .5 或 -5
18.( 2009 江苏卷)上(右)图是一个算法的流程图,最后输出的
W
.
19。如图 1 所示的算法流程图中,第 3 个输出的数是
开始 S=0
I=2
Y S=S+1/I
N 输出 S
I=I+2
结束
20、下图给出的是计算 1 1 1 246
B.11
C.xy=11
D. 出错信息
7.图中程序运行后输出的结果为 ( ) ( A) 3 43 ( B) 43 3 ( C) -18 16
8. 如果下边程序执行后输出的结果是 990,那么在程序中 UNTIL 后面的“条件”应为
A. i>10
B. i<8 C. i<=9 D. i<9
( D) 16 -18 ()
5.用秦九韶算法求多项式 f x 5 x5 4 x4 3x3 2 x2 x 1, 当 x 2 时的值的过程中,做的乘法和加法次
数分别为 ( ) A
、 4, 5 B 、 5,4 C 、 5, 5 D 、 6, 5
6. x=5
y=6 :
PRINT x+y=11
END
上面程序运行时输出的结果是 ( )
A.xy=11
输入 a=1
A.条件
B
.条件语句
C .满足条件时执行的内容 D .不满足条件时执行的内容
4.将两个数 a=2, b= -6 A. a=b B . c=aC
(典型题)高中数学必修三第二章《算法初步》测试题(含答案解析)
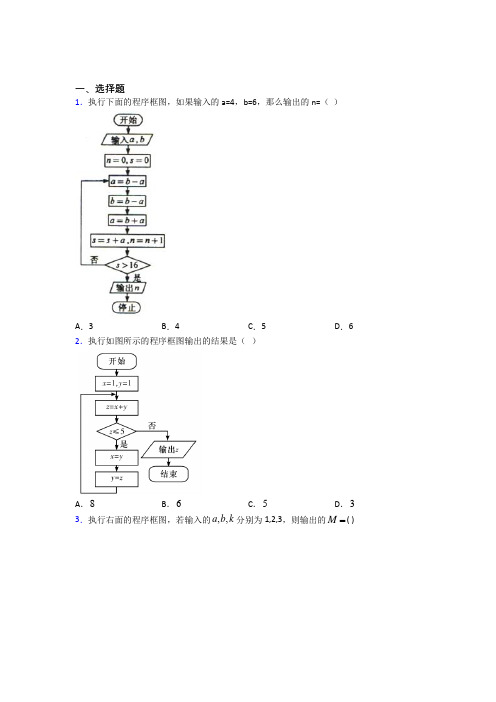
一、选择题1.执行下面的程序框图,如果输入的a=4,b=6,那么输出的n=()A.3 B.4 C.5 D.6 2.执行如图所示的程序框图输出的结果是()A.8B.6C.5D.3a b k分别为1,2,3,则输出的M ( ) 3.执行右面的程序框图,若输入的,,A.203B.72C.165D.1584.执行如图所示的程序框图,则输出的a=()A.-9 B.60 C.71 D.815.执行如图所示的程序框图,若输出S的值为511,则判断框内可填入的条件是()A .4i ≤B .5i ≤C .5i <D .6i ≤6.执行如图所示的程序框图,如果输入x =5,y =1,则输出的结果是( )A .261B .425C .179D .5447.朱世杰是我国元代伟大的数学家,其传世名著《四元玉鉴》中用诗歌的形式记载了下面这样一个问题:我有一壶酒,携着游春走.遇务①添一倍,逢店饮斛九②.店务经四处,没了这壶酒.借问此壶中,当原多少酒?①“务”:旧指收税的关卡所在地;②“斛九”:1.9斛.下图是解决该问题的算法程序框图,若输入的x 值为0,则输出的x 值为( )A.5740B.13380C.5732D.5893208.若执行如图所示的程序框图,输出S的值为511,则输入n的值是()A.7B.6C.5D.4 9.执行如下图的程序框图,如果输入的N的值是7,那么输出的p的值是()A.3 B.15 C.105 D.94510.如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b 分别为10,14,则输出的a =( )A .6B .4C .2D .011.执行如图的程序框图,如果输出a 的值大于100,那么判断框内的条件为()A .5k <?B .5k ≥?C .6k <?D .6k ≥?12.执行如图所示程序框图,当输入的x 为2019时,输出的y (= )A .28B .10C.4D.2二、填空题13.下图所示的算法流程图中,输出的S表达式为__________.14.已知某程序框图如图所示,则该程序运行后输出S的值为__________.15.执行如图所示的程序框图,输出的值为__________.16.如图是一个算法流程图,则输出的S的值为______.17.阅读如图所示的程序框图,运行相应的程序,则输出n的值为___________18.下图程序运行结果是________.19.执行下图所示的程序框图,若输入,则输出的值为_____________.20.执行如图所示的程序框图,输出的T ______.三、解答题21.如图,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,APB△的面积为y,求y与x之间的函数关系式,并画出程序框图.22.有关专家建议预测,在未来几年内,中国的通货膨胀率保持在3%左右,这将对我国经济的稳定有利无害.所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情况下,某种品牌的钢琴2015年的价格是10 000元,试分析其算法并用流程图描述这种钢琴今后四年的价格变化情况,并输出四年后的价格.23.写出一个算法,求底面边长为42,侧棱长为5的正四棱锥的体积.24.设计程序求π的近似值可以用公式:2222π1116123=+++…+21n ,用此公式求2π6,即逐项进行累加,直到21n <0.000 01为止(该项不累加),然后求出π的近似值. 25.古希腊杰出的数学家丢番图的墓碑上有这样一首诗:这是一座古墓,里面安葬着丢番图.请你告诉我,丢番图的寿数几何?他的童年占去了一生的六分之一,接着十二分之一是少年时期,又过了七分之一的时光,他找到了自己的终身伴侣.五年之后,婚姻之神赐给他一个儿子,可是儿子不济,只活到父亲寿数的一半,就匆匆离去.这对父亲是一个沉重的打击,整整四年,为失去爱子而悲伤,终于告别了数学,离开了人世.试用循环结构,写出算法分析和算法程序. 26.已知函数2()32,(3)(5)f x x x f f =--+-求的值,设计一个算法并画出算法的程序框图.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】试题分析:模拟执行程序, 可得4,6,0,0a b n s ====,执行循环体,2,4,6,6,1a b a s n =====,不满足条件16s >,执行循环体,2,6,4,10,2a b a s n =-====, 不满足条件16s >,执行循环体,2,4,6,16,3a b a s n =====, 不满足条件16s >,执行循环体,2,6,4,20,4a b a s n =-====,不满足条件16s >,退出循环, 输出n 的值为4,故选B.考点:1、程序框图;2、循环结构.2.A解析:A【分析】根据程序框图循环结构运算,依次代入求解即可.【详解】根据程序框图和循环结构算法原理,计算过程如下:1,1,x y z x y ===+第一次循环2,1,2z x y ===第二次循环3,2,3z x y ===第三次循环5,3,5z x y ===第四次循环8z =,退出循环输一次8z =.所以选A【点睛】本题考查了程序框图的基本结构和运算,主要是掌握循环结构在何时退出循环结构,属于基础题.3.D解析:D【详解】试题分析:根据题意由13≤成立,则循环,即1331,2,,2222M a b n =+====;又由23≤成立,则循环,即28382,,,33323M a b n =+====;又由33≤成立,则循环,即3315815,,,428838M a b n =+====;又由43≤不成立,则出循环,输出158M =. 考点:算法的循环结构4.C解析:C【分析】根据程序框图,模拟运算即可求解.【详解】第一次执行程序后,1a =-,i=2;第二次执行程序后,9a =-,i=3;第三次执行程序后,a=71,i=4>3,跳出循环,输出a=71.故选:C【点睛】本题主要考查了程序框图,循环结构,条件分支结构,属于中档题.5.B【分析】模拟运行程序1i =,满足条件,1013S =+⨯,2i =,满足条件,进入循环体,反复操作,直到输出511S =,核对满足的条件即可. 【详解】 1i =,满足条件,1013S =+⨯; 2i =,满足条件,111335S =+⨯⨯; 3i =,满足条件,111133557S =++⨯⨯⨯; 4i =,满足条件,111113355779S =+++⨯⨯⨯⨯; 5i =,满足条件,11111115(1)1335577991121111S =++++=-=⨯⨯⨯⨯⨯; 6i =,不满足条件,输出511S =. 故选:B.【点睛】 本题考查了对程序框图的理解与应用,由程序运行结果,补充条件,数列求和的裂项相消法,属于中档题.6.B解析:B【分析】根据循环结构的条件,依次运算求解,即得解.【详解】起始值:5,1,0x y n ===,满足1105<⨯,故:5,0,2x y n ===;满足0105<⨯,故:7,4,4x y n ===;满足4107<⨯,故:11,36,6x y n ===;满足361011<⨯,故:17,144,8x y n ===;满足1441017<⨯,故:25,400,10x y n ===;此时:4001025>⨯,满足输出条件:输出425x y +=故选:B【点睛】本题考查了程序框图的循环结构,考查了学生逻辑推理,数学运算的能力,属于中档题. 7.C【分析】本题首先可以根据题意以及程序框图明确输入的数据为“0x =,0i =”和运算的算式为“119210x x 、1i i =+”,然后进行运算并结合条件“4i ”得出结果。
【高中数学】第一章《算法初步》测试题

【高中数学】第一章《算法初步》测试题一、选择题1.看下面的四段话,其中不是解决问题的算法的是().a.从济南至北京旅游,先坐火车,再坐飞机到达b.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1c.方程存有两个实根d.求1+2+3+4+5的值,先算1+2=3,再算3+3=6,6+4=10,10+5=15,最终结果为15考查目的:考查算法的概念.答案:c.解析:算法通常就是指按照一定的规则化解某一类问题的明晰的非常有限的步骤.2.用秦九韶算法计算多项式在时的值时,的值为().a.-845b.220c.-57d.34考查目的:考查秦九韶算法的基本步骤.答案:d.解析:v0=3,v1=v0×(-4)+5=?7,v2=v1×(-4)+6=34.3.以下得出的赋值语句中恰当的就是().a.3=ab.c.b=a=2d.考查目的:考查赋值语句的格式.答案:b.解析:赋值语句中的“=”叫做赋值号,它和数学中符号不全然一样,格式为:变量=表达式,把“=”右边的表达式的值赋值给“=”左边的变量.4.算法:第一步,输入n.第二步,推论n是否是2,若n=2,则n满足条件,若n>2,则继续执行第三步.第三步,依次从2到n一1检验能不能整除n,若不能整除n,则n满足条件.满足用户上述条件的n就是().a.质数b.奇数c.偶数d.约数考查目的:考查推论一个数与否为质数的算法的设计.答案:a.解析:利用质数的性质.5.如图所示,程序框图(算法流程图)的输出结果是().a.b.c.d.考查目的:考查含条件结构程序框图的应用.答案:b.解析:6.例如图就是排序的值的一个程序框图,其中推论框内应当插入的条件就是().a.i>100b.i<=100c.i>50d.i<=50考查目的:考查循环结构中掌控条件的确认.答案:b.解析:当i<=100时,继续执行循环体;当i>100时,退出程序。
高中数学算法初步综合检测考试试题含答案解析A

算法初步本章达标测评(总分:150分;时间:120分钟)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面对算法的描述正确的一项是( )A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同2.执行如图所示的框图,输入N=5,则输出S的值为( )A.54B.45C.65D.563.下面一段程序执行后的结果是( )A.6B.4C.8D.104.算式1 010(2)+10(2)的值是( )A.1 011(2)B.1 100(2)C.1 101(2)D.1 000(2)5.执行如图所示的程序框图,当输入的值为3时,输出的结果是( )A.3B.8C.12D.206.若如图所示的程序框图的功能是计算1×12×13×14×15的结果,则在空白的执行框中应该填入( )A.T=T·(i+1)B.T=T·iC.T=T·1i+1D.T=T·1i7.已知7 163=209×34+57,209=57×3+38,57=38×1+19,38=19×2.根据上述一系列等式,可确定7 163和209的最大公约数是( )A.57B.3C.19D.348.已知44(k)=36,则把67(k)转化成十进制数为( )A.8B.55C.56D.629.执行如图所示的程序框图,若输出的k=5,则输入的整数p的最大值为( )A.7B.15C.31D.6310.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时的值时,其中v4的值为( )A.-57B.124C.-845D.22011.某程序框图如图所示,若该程序运行后输出的值是9,则( )5A.a=4B.a=5C.a=6D.a=712.执行如图所示的程序框图,则输出的n的值是( )A.29B.31C.61D.63二、填空题(本大题共4小题,每小题4分,共16分,把正确答案填在题中横线上)13.输入8,则下列程序运行后输出的结果是.化成十进制数,结果为,再将该结果化成七进制数,结14.将二进制数110 101(2)果为.15.执行如图所示的程序框图,则输出结果S= .16.阅读下面程序,当输入x的值为3时,输出y的值为.(其中e为自然对数的底数)三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(12分)下面给出一个用循环语句编写的程序:(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;(2)请用另一种循环语句的形式把该程序写出来.18.(12分)输入10个数,找出其中最大的数并输出,画出程序框图,并写出程序.19.(12分)如图所示,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动(不与A、B重合).设点P运动的路程为x,△APB的面积为y,求y与x之间的函数关系式,画出程序框图,写出程序.20.(12分)把区间[0,1]10等分,求函数y=√2x+1+|x-2|在各分点(包括区间端点)的函数值,写出程序.21.(12分)设计一个程序求11×4+13×6+15×8+…+199×102的值.22.(14分)“角谷猜想”是由日本学者角谷静夫首先提出的,所以称为“角谷猜想”.猜想的内容是:对于任意一个大于1的整数n,如果n 为偶数就除以2,如果n 是奇数,就将其乘3再加1,然后将得到的结果再进行以上处理,则最后结果总是1.试设计一个算法的程序框图,对任意输入的整数n(n≥2)进行检验,要求输出每一步的结果,直到结果为1时结束.附加题1.(2015河北石家庄一模,★★☆)执行下面的程序框图,如果输入的依次是1,2,4,8,则输出的S 为( )A.2B.2√2C.4D.62.(2015山西四校联考三,★★☆)执行如图的程序框图,则输出S 的值为( )D.-1 A.2 016 B.2 C.12一、选择题1.C 算法可以用自然语言、图形语言和程序语言来描述;同一个问题可以有不同的算法,但算法的结果相同.2.D 第一次循环,S=0+11×2=12,k=2;第二次循环,S=12+12×3=23,k=3;第三次循环,S=23+13×4=34,k=4;第四次循环,S=34+14×5=45,k=5;第五次循环,S=45+15×6=56,此时k=5不满足判断框内的条件,跳出循环,输出S=56,选D.3.A 由程序知a=2,2×2=4,4+2=6,故最后输出a 的值为6,故选A.4.B 1 010(2)+10(2)=(1×23+0×22+1×21+0×20)+(1×21+0×20)=12=1 100(2).5.B 3<5,执行y=x 2-1,所以输出结果为8.故选B.6.C 程序框图的功能是计算1×12×13×14×15的结果,依次验证选项可得选项C 正确. 7.C 由辗转相除法的思想可得结果. 8.B 由题意得,36=4×k 1+4×k 0,所以k=8. 则67(k)=67(8)=6×81+7×80=55.9.B 由程序框图可知:①S=0,k=1;②S=1,k=2;③S=3,k=3;④S=7,k=4;⑤S=15,k=5,输出k,此时S=15≥p,则p 的最大值为15,故选B. 10.D由已知,得a 0=12,a 1=35,a 2=-8,a 3=79,a 4=6,a 5=5,a 6=3,所以v 0=3,v 1=3×(-4)+5=-7,v 2=(-7)×(-4)+6=34,v 3=34×(-4)+79=-57,v 4=(-57)×(-4)-8=220.11.A 此程序框图的作用是计算S=1+11×2+12×3+…+1a (a+1)的值,由已知得S=95,即S=1+1-12+12-13+…+1a -1a+1=2-1a+1=95,解得a=4.12.D 开始:p=5,n=1;p=9,n=3;p=15,n=7;p=23,n=15;p=31,n=31;p=31,n=63,此时log 3163>1,结束循环,输出n=63. 二、填空题 13.答案 0.7解析 这是一个用条件语句编写的程序,由于输入的数据为8,8<-4不成立,所以c=0.2+0.1×(8-3)=0.7. 14.答案 53;104(7)解析 110 101(2)=1×25+1×24+0×23+1×22+0×21+1×20=53,然后用除7取余法得53=104.(7)15.答案 1 007解析根据程序框图知,S=(-1+2)+(-3+4)+…+(-2 013+2 014)=1 007,故输出的S的值为1 007.16.答案 1.5解析当输入x=3时,由于3>e,故执行y=0.5x,即y=0.5×3=1.5.三、解答题17.解析(1)本程序所用的循环语句是WHILE循环语句,其功能是计算12+22+32+…+92的值.(2)用UNTIL语句改写程序如下:18.解析程序框图如图.程序:19.解析 函数关系式为 y={2x (0<x ≤4),8(4<x ≤8),2(12-x )(8<x <12).程序框图如图所示:程序:20.解析把区间[0,1]10等分,故步长为0.1,∴用“x=x+0.1”表达,y=√2x+1+|x-2|,用“y=SQR(2*x+1)+ABS(x-2)”表达,循环控制条件x≤1.程序如下:21.解析程序:22.解析程序框图如图:附加题1.B 由程序框图可知,S=1,i=1;S=1,i=2;S=√2,i=3;S=2,i=4;S=2√2,i=5,此时跳出循环,输出S=2√2.故选B.2.B 循环前S=2,k=0,第一次循环,得S=11-2=-1,k=1;第二次循环,得S=11-(-1)=12,k=2;第三次循环,得S=11-12=2,k=3;……,由此可知S 的值的变化周期为3,又2 016=672×3,所以输出S 的值为2,故选B.。
高中数学必修三《算法初步》练习题(内含答案)

2、基本算法语句:①输入语句。
输入语句的格式:INPUT “提示内容”;变量②输出语句。
输出语句的一般格式:PRINT“提示内容”;表达式③赋值语句。
赋值语句的一般格式:变量=表达式④条件语句。
(1)“IF—THEN—ELSE”语句格式:IF 条件THEN语句1ELSE语句2END IF⑤循环语句。
(1)当型循环语句当型(WHILE型)语句的一般格式为:WHILE 条件循环体WEND(2)“IF—THEN”语句格式:IF 条件THEN语句END IF(2)直到型循环语句直到型(UNTIL型)语句的一般格式为:DO循环体LOOP UNTIL 条件高中数学必修三《算法初步》练习题一、选择题1.下面对算法描述正确的一项是 ( )A .算法只能用伪代码来描述B .算法只能用流程图来表示C .同一问题可以有不同的算法D .同一问题不同的算法会得到不同的结果2.程序框图中表示计算的是 ( ).A .B CD3将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )A B C D .4. 计算机执行下面的程序段后,输出的结果是( )1a = 3b = a a b =+ b a b =-PRINT a ,b A .1,3 B .4,1 C .0,0 D .6,05.当2=x 时,下面的程序运行后输出的结果是 ( )A .3B .7C .15D .17 6. 给出以下四个问题:①输入一个数x , 输出它的相反数 ②求面积为6的正方形的周长 ③输出三个数,,a b c 中的最大数 ④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值其中不需要用条件语句来描述其算法的有 ( ) A .1个 B .2个 C . 3个 D .4个7.图中程序运行后输出的结果为 ( ) A. 3 43 B. 43 3 C. 18- 16 D. 16 18-8. 如果右边程序执行后输出的结果是990,那么在程序中 UNTIL 后面的“条件”应为 ( )A. i>10B. i<8C. i<=9D. i<99. INPUT 语句的一般格式是( )A. INPUT “提示内容”;表达式B.“提示内容”;变量C. INPUT “提示内容”;变量D. “提示内容”;表达式10.算法共有三种逻辑结构,即顺序结构、条件结构、循环结构,下列说法正确的是( )A . 一个算法只能含有一种逻辑结构 B. 一个算法最多可以包含两种逻辑结构 C. 一个算法必须含有上述三种逻辑结构D. 一个算法可以含有上述三种逻辑结构的任意组合11. 如右图所示的程序是用来 ( )A .计算3×10的值B .计算93的值C .计算103的值D .计算12310⨯⨯⨯⋅⋅⋅⨯的值12. 把88化为五进制数是( )A. 324(5)B. 323(5)C. 233(5)D. 332(5)13.下列判断正确的是 ( )A.条件结构中必有循环结构B.循环结构中必有条件结构C.顺序结构中必有条件结构D.顺序结构中必有循环结构14. 如果执行右边的框图,输入N =5,则输出的数等于( ) A .54B.45C. 65 D.5615.某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是 ( )A .2()f x x =B .1()f x x =C .()ln 26f x x x =+-D . ()f x x =二、填空题: 16.(如右图所示)程序框图能判断任意输入的正整数x 是奇数或是偶数, 其中判断框内的条件是_____________17.执行右边的程序框图, 若0.8p =,则输出的n =18. 读下面程序 , 该程序所表示的函数是19.对任意非零实数a ,b ,若a b ⊗的运算原理如图所示,则21lg1000()2-⊗=________.20.将二进制数101 101(2) 化为八进制数,结果为 .21.用“秦九韶算法”计算多项式12345)(2345+++++=x x x x x x f ,当2x =时的值的过程中,要经过 次乘法运算和 次加法运算,其中3v 的值是 .三、解答题: 22.设计算法求S = 201614121+⋅⋅⋅+++的值, 并画出程序框图.23.(1) 用辗转相除法求840与1785的最大公约数 ;(2) 用更相减损术求612 与468的最大公约数.高中数学必修三《算法初步》练习题-----参考答案一、选择题:CABBC, BADCD, CBBDD二、填空题:16.m = 0?17.4 18.10,00,10.x xy xx x+>⎧⎪==⎨⎪-+<⎩19.1 20.55(8)21.5,5,64三、解答题:22.解:(算法略)程序框图如右图所示.23. 解:(1)105;(2)36.。
高中数学:第1章《算法初步》单元测试(1)(新人教A版必修3)

i=1 s=0 WHILE i<=4 s=s*x+1 i=i+1 WEND PRINT s END第一章 算法初步 单元测试一、选择题1. 用“辗转相除法”求得459和357的最大公约数是( )A. 3B. 9C. 17D. 51 2. 当2=x 时,下面的程序段结果是 ( )A. 3B. 7C. 15D. 173. 利用“直接插入排序法”给8,1,2,3,5,7按从大到小的顺序排序, 当插入第四个数3时,实际是插入哪两个数之间 ( ) A. 8与1 B. 8与2 C. 5与2 D. 5与14. 对赋值语句的描述正确的是 ( )①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A. ①②③ B. ①② C. ②③④ D. ①②④ 5. 在repeat 语句的一般形式中有“until A ”,其中A 是 ( )A. 循环变量B. 循环体C. 终止条件D. 终止条件为真 6. 用冒泡排序法从小到大排列数据 13,5,9,10,7,4需要经过( )趟排序才能完成 A. 4 B. 5 C. 6 D. 7二、填空题1. 根据条件把流程图补充完整,求11000→内所有奇数的和;(1) 处填(2) 处填2. 图中所示的是一个算法的流程图,已知31=a ,输出的7b =,则2a 的值是____________.3. 下列各数)9(85 、 )6(210 、 )4(1000 、 )2(111111中最小的数是____________.4. 右图给出的是计算201614121++++ 的值的一个流程图,其中判断框内应填入的条件是____________.5. 用直接插入排序时对:7,1,3,12,8,4,9,10进行从小到大排序时,第四步得到的一组数为: ___________________________________.三、解答题1. 以下是计算1234...100+++++程序框图,请写出对应的程序开始i:=1,S:=0i<1000(1)(2)输出S结束否是 是否开始 s : = 0 i : = 1is s 21:+= i : = i+1输出s 结束2. 函数⎪⎩⎪⎨⎧≤<-≤<≤≤=128),12(284,840,2x x x x x y ,写出求函数的函数值的程序.3. 用辗转相除法或者更相减损术求三个数324,243,135的最大公约数.4. 意大利数学家菲波拉契,在1202年出版的一书里提出了这样的一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔 问这样下去到年底应有多少对兔子? 试画出解决此问题的程序框图,并编写相应的程序.第一章 算法初步参考答案一、选择题1. D 4593571102,357102351,102512=⨯+=⨯+=⨯51是102和51的最大公约数,也就是459和357的最大公约数 2. C 0211,1213,3217,72115⨯+=⨯+=⨯+=⨯+=3. B 先比较8与1,得8,1;把2插入到8,1,得8,2,1;把3插入到8,2,1,得8,3,2,1;4. A 见课本赋值语句相关部分5. D Until 标志着直到型循环,直到终止条件成就为止6. B 经过第一趟得5,9,10,7,4,13;经过第二趟得5,9,7,4,10,13;经过第三趟得5,7,4,9,10,13;经过第四趟得5,4,7,9,10,13;经过第五趟得4,5,7,9,10,13;二、填空题1. (1)s s i =+(2)2i i =+2. 111227,112a a a +== 3. )2(111111 (9)8589577=⨯+= 、 2(6)2102616078=⨯+⨯+= 、3(4)10001464=⨯= 、 5432(2)1111111212121212163=⨯+⨯+⨯+⨯+⨯+= 4. 10i >5. 1,3,7,8,12,4,9,10 1,7,3,12,8,4,9,10①; 1,3,7,12,8,4,9,10②;1,3,7,12,8,4,9,10③;1,3,7,8,12,4,9,10④三、解答题 1. 解: i=1sum=0WHILE i<=100 sum=sum+i i=i+1 WEND PRINT sum END2. 解:INPUT “x=”;xIF x>=0 and x<=4 THEN y=2*xELSE IF x<=8 THENy=8ELSE y=2*(12-x) END IF END IF PRINT y END3. 解: 324=243×1+81243=81×3+0则 324与 243的最大公约数为 81又 135=81×1+5481=54×1+27 54=27×2+0则 81 与 135的最大公约数为27所以,三个数 324、243、135的最大公约数为 27另法32424381,24381162,1628181;-=-=-=1358154,815427,542727-=-=-=27∴为所求4. 解: 根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N 个月有F 对兔子,第1N -个月有S 对兔子,第2N -个月有Q 对兔子,则有F S Q =+,一个月后,即第1N +个月时,式中变量S 的新值应变第N 个月兔子的对数(F 的旧值),变量Q 的新值应变为第1N -个月兔子的对数(S 的旧值),这样,用S Q +求出变量F 的新值就是1N +个月兔子的数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第×个月的I 从3逐次增加1,一直变化到12,最后一次循环得到的F 就是所求结果 流程图和程序如下:关于数学名言警句大全1、数学家本质上是个着迷者,不迷就没有数学。
(典型题)高中数学必修三第二章《算法初步》测试卷(含答案解析)

一、选择题1.给出一个算法的程序框图如图所示,该程序框图的功能是( )A .求出,,a b c 三数中的最小数B .求出,,a b c 三数中的最大数C .将,,a b c 从小到大排列D .将,,a b c 从大到小排列2.程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.它问世后不久便风行宇内,成为明清之际研习数学者必读的教材,而且传到朝鲜、日本及东南亚地区,对推动汉字文化圈的数学发展起了重要的作用.卷八中第33问是:“今有三角果一垛,底阔每面七个,问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S 为( )A .84B .56C .35D .283.执行如图所示的程序框图,输出S 的值为( )A.1-B.0 C.1 D.2 4.执行如图所示的程序框图,若输入10n=,则输出的结果是()A.11114135717P⎛⎫=-+-++⎪⎝⎭B.11114135719P⎛⎫=-+-+-⎪⎝⎭C.11114135721P⎛⎫=-+-+⋯+⎪⎝⎭D.11114135721P⎛⎫=-+-+-⎪⎝⎭5.执行如图所示的程序框图,若输出的结果为126,则判断框内的条件可以为()A .5n ≤B .6n ≤C .7n ≤D .8n ≤ 6.正整数N 除以正整数m 后的余数为n ,记为()N n MODm ≡,例如()2516MOD ≡.如图所示程序框图的算法源于“中国剩余定理”,若执行该程序框图,当输入49N =时,则输出结果是( )A .58B .61C .66D .767.执行如图所示的程序框图,则输出的k 的值为( )A .3B .4C .5D .68.执行如下图的程序框图,如果输入的N 的值是7,那么输出的p 的值是( )A .3B .15C .105D .945 9.读下面的程序:上面的程序在执行时如果输入6,那么输出的结果为()A.6 B.720 C.120 D.5040 10.执行如图所示的程序框图,则输出的n值是()A.5B.7C.9D.1111.执行如图所示的程序框图,若输出的值为﹣1,则判断框①中可以填入的条件是()A.n≥999B.n≤999C.n<999 D.n>999 12.若执行如图所示的程序框图,则输出S的值为( )A.10072015B.10082017C.10092019D.10102021二、填空题13.如图是一个算法流程图,若输入x的值为2,则输出y的值为_______. .14.执行如图所示的程序框图,输出的值为__________.15.如下图,程序框图中,若输入4,10m n ==,则输出a 的值是________.16.执行如图所示的算法框图,若输入的x 的值为2,则输出的n 的值为__________.17.如图是一个算法的流程图,则输出的a 的值是___________.18.101110(2)转化为十进制数是__________.19.程序如下:以上程序输出的结果是_________________20.如图所示的程序框图输出的值是 .三、解答题21.(1)用辗转相除法求840与1 764的最大公约数;(2)用更相减损术求440 与556的最大公约数.1,2上的近似根的算法.(近似根与精确解的差22.用二分法设计一个求方程230x-=在[]的绝对值不超过0.0005)23.某函数的解析式由如图所示的程序框图给出.(1)写出该函数的解析式;(2)执行该程序框图,若输出的结果为4,求输入的实数x 的值.24.图是求239111112222S =+++++的一个程序框图. (1)在程序框图的①处填上适当的语句;(2)写出相应的程序.25.分别标有1,2,3,4,5,6六个号码的小球,有一个最重,写出挑出最重球的算法,并画出程序框图.26.已知华氏温度与摄氏温度的转换公式是(华氏温度532)9-⨯=摄氏温度.编写一个程序,输入一个华氏温度,输出其相应的摄氏温度.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】对a 、b 、c 赋三个不等的值,并根据程序框图写出输出的结果,可得知该程序的功能.【详解】令2a =,3b =,1c =,则23>不成立,21>成立,则1a =,输出的a 的值为1, 因此,该程序的功能是求出a 、b 、c 三数中的最小数,故选A .【点睛】本题考查程序框图的功能,解题的关键就是根据题意将每个步骤表示出来,考查分析问题的能力,属于中等题.2.A解析:A【分析】按照程序框图运行程序,直到满足7i ≥时输出结果即可.【详解】按照程序框图运行程序,输入0i =,0n =,0S =,则1i =,1n =,1S =,不满足7i ≥,循环;2i =,3n =,4S =,不满足7i ≥,循环;3i =,6n =,10S =,不满足7i ≥,循环;4i =,10n =,20S =,不满足7i ≥,循环;5i =,15n =,35S =,不满足7i ≥,循环;6i =,21n =,56S =,不满足7i ≥,循环;7i =,28n =,84S =,满足7i ≥,输出84S =.故选:A .【点睛】本题考查根据程序框图循环结构计算输出结果的问题,属于基础题.3.C解析:C【分析】由函数()πsin 2x f x =,可求周期为4,()(1)(2)(3)40+++=f f f f ,由题意可知()(1)(2)(2021)=2021(1)1=+++==S f f f f f【详解】 由函数()πsin 2x f x =的周期为2π4π2T ==, ()π1sin 12f ==,()2π2sin 02f ==, ()3π3sin 12f ==-,()4π4sin 02f ==,()(1)(2)(3)40+++=f f f f ()(1)(2)(2021)=2021(1)1∴=+++==S f f f f f .故选:C【点睛】 本题考查了程序框图求和,正弦型三角函数的周期等基本知识,考查了运算求解能力和逻辑推理能力,属于一般题目.4.B解析:B【分析】按照程序框图运行程序,寻找规律,直到i n >输出结果即可.【详解】按照程序框图运行程序,输入10n =,0S =,1i =,则1S =,2i =,不满足i n >,循环;113S =-,3i =,不满足i n >,循环;11135S =-+,4i =,不满足i n >,循环; 以此类推,1111135719S =-+--⋅⋅⋅-,11=i ,满足i n >,则4P S =, 11114135719P ⎛⎫∴=-+--⋅⋅⋅- ⎪⎝⎭. 故选:B .【点睛】本题考查根据程序框图循环结构计算输出结果的问题,属于常考题型.5.B解析:B【分析】根据框图,模拟程序运行即可求解.【详解】根据框图,执行程序,12,2S n ==;1222,3S n =+=;⋯12222,1i S n i =++⋯+=+,令12222126i S =++⋯+=,解得6i =,即7n =时结束程序,所以6n ≤,故选 :B【点睛】本题主要考查了程序框图,循环结构,条件分支结构,等比数列求和,属于中档题.genju 6.B解析:B【分析】该程序框图的作用是求被3和5除后的余数为1的数,根据所给的选项,得出结论.【详解】模拟程序的运行,可得49N =,50N =,不满足条件()13N MOD ≡,51N =;不满足条件()13N MOD ≡,52N =;满足条件()13N MOD ≡,不满足条件()15N MOD ≡,53N =;不满足条件()13N MOD ≡,54N =;不满足条件()13N MOD ≡,55N =; 满足条件()13N MOD ≡,不满足条件()15N MOD ≡,56N =;不满足条件()13N MOD ≡,57N =;不满足条件()13N MOD ≡,58N =; 满足条件()13N MOD ≡,不满足条件()15N MOD ≡,59N =;不满足条件()13N MOD ≡,60N =;不满足条件()13N MOD ≡,61N =; 满足条件()13N MOD ≡,满足条件()15N MOD ≡,输出61N =.故选:B.【点睛】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.7.C解析:C【分析】根据框图模拟程序运算即可.【详解】第一次执行程序,2111S =⨯-=,25S >-,继续循环,第二次执行程序,2k =,2121S =⨯-=-,25S >-,继续循环,第三次执行程序,3k =,2(1)35S =⨯--=-,25S >-,继续循环,第四次执行程序,4k =,2(5)414S =⨯--=-,25S >-,继续循环,第五次执行程序,5k =,2(14)532S =⨯--=-,25S <-,跳出循环,输出5k =,结束.故选C.【点睛】本题主要考查了程序框图,涉及循环结构,解题关键注意何时跳出循环,属于中档题. 8.C解析:C【分析】由已知中的程序框图,得到该程序的功能是利用循环结构计算并输出变量p 的值,模拟程序的运行过程,分析循环中各变量的变化情况,可得答案.【详解】模拟程序的运行,可得:7,1,1N k p ===,满足条件7k <,执行循环体,3,3k p ==;满足条件7k <,执行循环体,5,15k p ==;满足条件7k <,执行循环体,7,105k p ==;此时,不满足条件7k <,推出循环,输出p 的值为105,故选C .【点睛】本题主要考查了程序框图的应用问题,解答中应模拟程序框图的运行过程,逐次计算是解答的关键,着重考查了推理与运算能力,属于基础题.9.B解析:B【解析】【分析】执行程序,逐次计算,根据判断条件终止循环,即可求解输出的结果,得到答案.【详解】由题意,执行程序,可得:第1次循环:满足判断条件,1,2S i ==;第2次循环:满足判断条件,2,3S i ==;第3次循环:满足判断条件,6,4S i ==;第4次循环:满足判断条件,24,5S i ==;第5次循环:满足判断条件,120,6S i ==;第6次循环:满足判断条件,720,7S i ==;不满足判断条件,终止循环,输出720S =,故选B.【点睛】本题主要考查了循环结构的程序框图的计算输出,其中解答中正确理解循环结构的程序框图的计算功能,逐次计算是解答的关键,着重考查了推理与运算能力,属于基础题. 10.C解析:C【分析】根据程序框图列出算法循环的每一步,结合判断条件得出输出的n 的值.【详解】执行如图所示的程序框图如下:409S =≥不成立,11S 133==⨯,123n =+=; 1439S =≥不成立,1123355S =+=⨯,325n =+=; 2459S =≥不成立,2135577S =+=⨯,527n =+=; 3479S =≥不成立,3147799S =+=⨯,729n =+=. 4499S =≥成立,跳出循环体,输出n 的值为9,故选C. 【点睛】本题考查利用程序框图计算输出结果,对于这类问题,通常利用框图列出算法的每一步,考查计算能力,属于中等题.11.C解析:C【分析】分析循环结构中求和式子的特点,可到最终结果:2lg(1)S n =-+,当1S =-时计算n 的值,此时再确定判断框的内容.【详解】由图可得:2lg1lg 2lg 2lg3...lg lg(1)S n n =+-+-++-+,则2lg(1)1S n =-+=-,所以999n =,因为此时需退出循环,所以填写:999n <. 故选C.【点睛】lg lg lg(1)1n n n n =-++,通过将除法变为减法,达到简便运算的目的. 12.C解析:C【解析】【分析】首先确定流程图的功能为计数111113355720172019S =++++⨯⨯⨯⨯的值,然后利用裂项求和的方法即可求得最终结果.【详解】 由题意结合流程图可知流程图输出结果为111113355720172019S =++++⨯⨯⨯⨯, 11(2)111(2)2(2)22n n n n n n n n +-⎛⎫=⨯=- ⎪+++⎝⎭, 111113355720172019S ∴=++++⨯⨯⨯⨯ 11111111123355720172019⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1110091220192019⎛⎫=-= ⎪⎝⎭. 本题选择C 选项.【点睛】识别、运行程序框图和完善程序框图的思路:(1)要明确程序框图的顺序结构、条件结构和循环结构.(2)要识别、运行程序框图,理解框图所解决的实际问题.(3)按照题目的要求完成解答并验证.二、填空题13.5【分析】直接模拟程序即可得结论【详解】输入的值为2不满足所以故答案是:5【点睛】该题考查的是有关程序框图的问题涉及到的知识点有程序框图的输出结果的求解属于简单题目解析:5【分析】直接模拟程序即可得结论.【详解】输入x 的值为2,不满足1x ≤,所以3325y x =+=+=,故答案是:5.【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有程序框图的输出结果的求解,属于简单题目.14.【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到输出的的值【详解】输入第一次循环;第二次循环;第三次循环;第四次循环;第五次循环;第六次循环退出循环输出故答案为解析:42【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的S 的值.【详解】输入0,2,1S a i ===,第一次循环,2,4,2S a i ===;第二次循环,6,6,3S a i ===;第三次循环,12,8,4S a i ===;第四次循环,20,10,5S a i ===;第五次循环,30,12,6S a i ===;第六次循环,42,14,7S a i ===,退出循环,输出42S =,故答案为42.【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可.15.20【解析】模拟执行程序可得:不满足条件整除以不满足条件整除以不满足条件整除以不满足条件整除以满足条件整除以退出循环输出的值为点睛:本题主要考查的程序框图的知识点解题的关键是要读懂程序框图模拟执行程 解析:20【解析】模拟执行程序,可得:4,10m n ==,1i =,4a =不满足条件n 整除以a2i =,8a =不满足条件n 整除以a3i =,12a =不满足条件n 整除以a4i =,16a =不满足条件n 整除以a5i =,20a =满足条件n 整除以a ,退出循环,输出a 的值为20点睛:本题主要考查的程序框图的知识点.解题的关键是要读懂程序框图.模拟执行程序,依次写出每次循环得到的i ,a 的值,当20a =的时候,满足条件n 整除以a ,退出循环,即可得到输出a 的值为20.16.2【解析】当x=2时x2﹣4x+3=﹣1<0满足继续循环的条件故x=3n=1;当x=3时x2﹣4x+3=0满足继续循环的条件故x=4n=2;当x=4时x2﹣4x+3=3>0不满足继续循环的条件故输出解析:2【解析】当x=2时,x 2﹣4x+3=﹣1<0,满足继续循环的条件,故x=3,n=1;当x=3时,x 2﹣4x+3=0,满足继续循环的条件,故x=4,n=2;当x=4时,x 2﹣4x+3=3>0,不满足继续循环的条件,故输出的n 值为2;故答案为2.点睛:算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括顺序结构、条件结构、循环结构,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 17.9【解析】:试题分析:由题意可得a 是在不断变大的b 是在不断变小当程序运行两次时a=9b=5a>b 跳出程序输出a=9;考点:算法的流程图的计算 解析:9【解析】:试题分析:由题意可得,a 是在不断变大的,b 是在不断变小,当程序运行两次时,a=9,b=5,a>b,跳出程序,输出a="9;"考点:算法的流程图的计算18.46【解析】试题分析:考点:进位制间的关系解析:46【解析】试题分析:2345(2)101110121212021246=⨯+⨯+⨯+⨯+⨯=.考点:进位制间的关系. 19.24【解析】考点:程序框图专题:图表型分析:由程序中循环的条件为i≤4我们易得到最后一次循环时i=4又由循环变量i 的初值为2故我们从2开始逐步模拟循环的过程即可得到结论解答:解:模拟程序的运行结果:解析:24【解析】考点:程序框图.专题:图表型.分析:由程序中循环的条件为i≤4,我们易得到最后一次循环时i=4,又由循环变量i 的初值为2,故我们从2开始逐步模拟循环的过程,即可得到结论.解答:解:模拟程序的运行结果:i=2时,t=2,i=3时,t=6,i=4时,t=24,故答案为24点评:本题考查的知识点是程序框图及程序代码,在写程序运行结果时,模拟程序的运行过程是解答此类问题最常用的方法,模拟时要分析循环变量的初值,步长和终值 20.144【分析】直接利用循环结构计算循环各个变量的数值当满足判断框的条件推出循环输出结果【详解】判断前第1次判断循环;第2次判断循环第3次判断循环;第4次判断循环;第5次判断循环;第6次判断循环;第7 解析:144【分析】直接利用循环结构,计算循环各个变量的数值,当10k =满足判断框的条件,推出循环,输出结果.【详解】判断前,2c =,第1次判断循环,1,2,2,3a b k c ====;第2次判断循环,2,3,3,5a b k c ====第3次判断循环,3,5,4,8a b k c ====;第4次判断循环,5,8,5,13a b k c ====;第5次判断循环,8,13,6,21a b k c ====;第6次判断循环,13,21,7,34a b k c ====;第7次判断循环,21,34,8,55a b k c ====;第8次判断循环,34,55,9,89a b k c ====;第9次判断循环,55,89,10,144a b k c ====;第10次判断不满足判断框条件,退出循环,输出144c =,故答案为144.【点睛】本题考查循环结构的应用,注意每一步循环的变量的数值,计算准确是解题的关键.三、解答题21.(1)84;(2)4.【分析】(1)根据辗转相除法,求余数,直至余数为零,(2)根据更相减损术,求减数,直至减数为零.【详解】(1)用辗转相除法求840与1 764 的最大公约数.1 764 = 840×2 + 84 840 = 84×10 +0所以840与1 764 的最大公约数是84.(2)用更相减损术求440 与556的最大公约数.556-440 = 116 440-116 = 324324-116 = 208 208-116 = 92116-92 = 24 92-24 = 6868-24 = 44 44-24 = 2024-20 = 4 20-4 = 1616-4 = 12 12-4 = 88-4 = 4所以440 与556的最大公约数4.【点睛】本题考查辗转相除法与更相减损术,考查基本求解能力.22.见解析【分析】计算(1)0,(2)0f f <>,设121,2x x ==,122x x m +=,判断()f m 的符号,根据零点存在定理得到算法.【详解】第一步:令2()3f x x =-,(1)20,(2)10f f =-<=>,∴设121,2x x ==; 第二步:令122x x m +=,判断()f m 是否为0,若是,则m 为所求;若不是,则继续判断()1()f x f m ⋅大于0还是小于0;第三步:若()1()0f x f m ⋅>,则令1x m =;否则,令2x m =; 第四步:判断120.0005x x -≤是否成立?若是,则12,x x 之间的任意值均为满足条件的近似根;若不是,则返回第二步.【点睛】本题考查了求方程近似根的算法,意在考查学生对于算法的理解和应用.23.(1) 22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩当0x =时,y 无解.(2) 2x =-.【分析】(1)根据框图得到函数解析式;(2)结合第一问得到的函数表达式,分情况得到x 值即可.【详解】(1)函数解析式为22,0log ,042,4x x x y x x x ⎧<⎪=<≤⎨⎪>⎩,当0x =时,y 无解.(2)当0x <时,24x =,2x =-或2(舍).当04x ≤≤时,2log 4x =,解得16x =(舍).当4x >时,24x =,解得2x =(舍)所以2x =-【点睛】这个题目考查了程序框图的应用,以及分段函数的应用;解决分段函数求值问题的策略:(1)在求分段函数的值f (x 0)时,一定要首先判断x 0属于定义域的哪个子集,然后再代入相应的关系式;(2)分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数,分段函数是一个函数,而不是多个函数;分段函数的定义域是各段定义域的并集,值域是各段值域的并集,故解分段函数时要分段解决;(3)求f (f (f (a )))的值时,一般要遵循由里向外逐层计算的原则.24.(1)2T T =;(2)见解析 【解析】【分析】⑴要计算239111112222S =+++++的一个程序框图的值需要用直到型循环结构,利用被累加数列的通项公式求解即可⑵根据框图写出对应得程序语句,即可得解【详解】(1)的意图为表示各累加项,即数列的通项公式,故为2T T =(2)程序如下:【点睛】本题主要考查了程序框图的补全,结合题意运用数列的通项公式求出结果,然后再给出程序,需要熟练掌握各知识点。
高中数学-算法初步_测试练习题

高中数学-算法初步测试练习题1. 下列说法正确的是()A.算法就是某个问题的解题过程B.算法执行后可以产生不同的结果C.解决某一个具体问题算法不同结果不同D.算法执行步骤的次数不可以为很大,否则无法实施2. 将两个数a=2,b=−6交换,使a=−6,b=2,下列语句正确的是()A.a=b,b=aB.c=a,a=b,b=cC.b=a,a=bD.a=c,c=b,b=a3. 算法:S1m=aS2若b<m,则m=bS3若c<m,则m=cS4若d<m,则m=dS5输出m,则输出m表示()A.a,b,c,d中最大值B.a,b,c,d中最小值C.将a,b,c,d由小到大排序D.将a,b,c,d由大到小排序4. 观察下列各式:,则的末四位数为()A.3125B.5624C.0625D.81255. 给出下列问题:(1)求面积为1的正三角形的周长;(2)求键盘所输入的三个数的算术平均数;(3)求键盘所输入两个数的最小数;(4)求函数f(x)={2xx2(x≥3)(x<3)当自变量取相应值时的函数值.其中不需要用条件语句描述的算法的问题有()A.1个B.2个C.3个D.4个6. 执行如下的程序框图,则输出的结果是()A.1 132B.833C.1112D.147. 阅读如图所示的程序框图,若输入m=2020,则输出S为()A.20202B.10092C.10102D.101128. 某程序的框图如图所示,若执行该程序,输出的S值为( )A.45B.36C.25D.169. 图中程序是计算2+3+4+5+6的值的程序.在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是()A.①i>1②i=i−1B.①i>1②i=i+1C.①i>=1②i=i+1D.①i>=1②i=i−110. 如图,程序运行后输出的结果为()A.3B.5C.2D.011. 下面的流程图中,能实现数据A,B互相交换的有________.(要求把符合条件的图形序号全填上)12. 用辗转相除法求324和243的最大公约数为________.13. 下列给出的几个式子中,正确的赋值语句是(填序号)________.①3←A;②M←−M;③B←A←2;④x+y←0.14. 已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均成绩的一个算法为:第一步:取A=89,B=96,C=99;第二步:________;第三步:________;第四步:输出计算的结果.15. 用秦九韶算法计算多项式f(x)=1+8x+7x2+5x4+4x5+3x6在x=5时所对应的v4的值为________.16. 用辗转相除法求294和84的最大公约数时,需要做除法的次数是________.17. 写出下列语句的运行结果:输入aif a<0tℎen输出“是负数”else t=√a输出ta=−4,输出结果为________,a=9,输出结果为________.18. 阅读程序框图,则输出的S=________.19. 若二进制数100y011和八进制数x03相等,则x+y=________.20. 用秦九韶算法求多项式f(x)=4x5+2x4−3x2+1,当x=3时,v3=________.21. 某居民区的物业管理部门每月向居民收取卫生费,计费方法如下:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费只需画出程序框图即可.22. 在程序语言中,下列符号分别表示什么运算*;\;∧;SQR;ABS?23. 执行如图所示的伪代码,则输出的S值为________.24. x的取值范围为[0, 10],给出如图所示程序框图,输入一个数x.求:(1)输出的x(x<6)的概率;(2)输出的x(6<x≤8)的概率.25. 已知10b1(2)=a02(3),求数字a,b的值.参考答案与试题解析高中数学-算法初步测试练习题一、选择题(本题共计 10 小题,每题 3 分,共计30分)1.【答案】B【考点】算法的概念【解析】广义的算法是指完成某项工作的方法和步骤,那么我们可以说洗衣机的使用说明书是操作洗衣机的算法,菜谱是做菜的算法等等.在数学中,现代意义的算法是指可以用计算机来解决的某一类问题的程序和步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成,根据算法的定义进行逐一判定即可.【解答】解:选项A,算法不能等同于解法,故不正确;选项B,判断一个整数是否为偶数,结果为“是偶数”和“不是偶数”两种,故正确;选项C,解决某一个具体问题算法不同结果应该相同,否则算法构造得有问题,故不正确;选项D,算法可以为很多次,但不可以无限次,故不正确.故选B.2.【答案】B【考点】赋值语句【解析】要实现两个变量a,b值的交换,需要借助中间量c,先把a的值赋给中间变量c,这样c=2,再把b的值赋给变量a,这样a=−6,把c的值赋给变量b,这样a=2.问题解决.【解答】解:先把a的值赋给中间变量c,这样c=a,再把b的值赋给变量a,把c的值赋给变量b,故选:B3.【答案】B【考点】算法的概念【解析】逐步分析算法图中的各语句的功能,第二步条件结构是比较a,b的大小,并将a,b中的较小值保存在变量m中,第三步条件结构是比较m,c的大小,并将m,c中的较小值保存在变量m中,第四步条件结构是比较m,d的大小,并将m,d中的较小值保存在变量m中,故变量m的值最终为a,b,c中的最小值.由此不难推断程序的功能.【解答】解:逐步分析框图中的各框语句的功能,第二步条件结构是比较a,b的大小,并将a,b中的较小值保存在变量m中,→第三步条件结构是比较m,c的大小,并将m,c中的较小值保存在变量m中,→第四步条件结构是比较m,d的大小,并将m,d中的较小值保存在变量m中,故变量m的值最终为a,b,c中的最小值.由此程序的功能为求a,b,c三个数的最小数.故选B4.【答案】C【考点】进位制排序问题与算法的多样性用辗转相除计算最大公约数【解析】由54=3125,54=15.5=78.53=390625,55=195312510=97676.562…可以看出这些幂的最后四位是以4为周期进行变化的,因此52016的末四位数0625,故选C.【解答】此题暂无解答5.【答案】B【考点】条件语句算法的概念【解析】由于条件语句适用于不同前提条件下不同处理方式的问题的解决,可依次对四个问题进行分析找出具有不同前提条件下不同处理方式这一特征的问题,即可得到正确选项【解答】解:(1)求面积为1的正三角形的周长用顺序结构即可,故不需要用条件语句描述;(2)求键盘所输入的三个数的算术平均数用顺序结构即可解决问题,不需要用条件语句描述;(3)求键盘所输入两个数的最小数,由于要作出判断,找出最小数,故本问题的解决要用到条件语句描述;(4)求函数f(x)={2xx2(x≥3)(x<3)当自变量取相应值时的函数值,由于此函数是一个分段函数,所以要用条件结构选择相应的函数解析式,需要用条件语句描述.综上,(3)(4)两个问题要用到条件语句描述,(1),(2)不需要用条件语句描述故选B6.【答案】C程序框图循环结构的应用【解析】此题暂无解析【解答】解:开始:T=0,S=0,n=1:T=2,S=12=1−12;n=2:T=2×3,S=12+12×3=12+12−13=1−13;n=3:T=3×4,S=12+12×3+13×4=12+12−13+13−14=1−14;…n=11:T=11×12,S=1−112,此时满足n>10,跳出循环结构,输出S=1112.故选C.7.【答案】D【考点】程序框图【解析】此题暂无解析【解答】解:当输入m=2020时,执行第1次循环,S=1,i<m,i=1+2=3,执行第2次循环,S=1+3=4,i<m,i=3+2=5,执行第3次循环,S=4+5=9,i<m,i=5+2=7,⋯由此可得,当i>m时,i=2021,此时S=0+1+3+⋯+2021=1011(1+2021)2=10112.故选D.8.【答案】D【考点】程序框图【解析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.解:由题意模拟程序的运行,可得k=1,s=0,满足条件k≤8,执行循环体,S=1,k=3;满足条件k≤8,执行循环体,S=4,k=5;满足条件k≤8,执行循环体,S=9,k=7;满足条件k≤8,执行循环体,S=16,k=9;此时,不满足条件k≤8,退出循环,输出S的值为16.故选D.9.【答案】A【考点】循环语句【解析】根据流程图所表示的算法功能可知求2+3+4+5+6的和,从而应该利用累积加的表达式,以及数i是逐一减小的,可得处理框应填的内容.【解答】解:程序框图是计算2+3+4+5+6的和则第一个处理框应为i>1,i是减小1个,i=i−1从而答案为:①i>1②i=i−1.故选A.10.【答案】A【考点】输入、输出语句【解析】分析已知中程序的语句及结构,我们易得本程序的功能是利用循环判断2∼12中,4的倍数的个数,根据约束的定义,即可求出答案.【解答】解:根据伪代码所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是利用循环判断2∼12中,4的倍数的个数,由于2∼12中,4的倍数有4,8,12三个故选A.二、填空题(本题共计 10 小题,每题 3 分,共计30分)11.【答案】①②③【考点】顺序结构的应用【解析】对三个图形的运算过程进行分析,根据运行的顺序检验运算的结果,可判断出正确结果【解答】解:①中引入了一个中间量,先把A记入C,再把B赋给A,然后把C赋给B,实现数据交换;②先把两者的和记到A 里,再用和减去B 赋给B ,此过程把A 记到B 中了,再计算A −B ,此时差为原来的B ,将其赋给A ,可以实现数据交换;③同理可得,③也可以实现数据交换,故①②③都正确故答案为①②③12.【答案】81【考点】辗转相除法【解析】用较大的数字除以较小的数字,得到商和余数,然后再用上一式中的除数和得到的余数中较大的除以较小的,以此类推,当整除时,就得到要求的最大公约数.【解答】解:∵ 324÷243=1⋯⋯81,243÷81=3,∴ 324和243的最大公约数是81.故答案为:81.13.【答案】②【考点】赋值语句【解析】根据赋值语句的功能和格式,逐一分析四个答案中四个赋值语句,根据赋值号左边只能是变量,右边可以是任意表达式,即可得到答案.【解答】解:赋值号的左边是常量,故①错误;赋值语句不能连续赋值,故③错误;x +y =0中,赋值号的左边是表达式,故④错误;只有②是正确的赋值语句,故答案为:②14.【答案】S =A +B +C ,x ¯=A+B+C 3【考点】算法的概念【解析】由题意,第二步,求和,第三步,计算平均成绩.【解答】解:由题意,第二步,求和S =A +B +C ,第三步,计算平均成绩x ¯=A+B+C 3. 故答案为:S =A +B +C ;x ¯=A+B+C 3.15.【答案】2507【考点】秦九韶算法【解析】首先把一个n次多项式f(x)写成(…((a[n]x+a[n−1])x+a[n−2])x+...+a[1])x+ a[0]的形式,然后化简,求n次多项式f(x)的值就转化为求n个一次多项式的值,求出V4的值.【解答】解:∵f(x)=1+8x+7x2+5x4+4x5+3x612+35x−8x2+79x3+6x4+5x5+3x6=(((((3x+4)x+5)x+0)x+7)x+8)x+1,∴v0=a6=3,x=5时,v1=v0x+a5=3×5+4=19,v2=v1x+a4=19×5+5=100,v3=v2x+a3=100×5+0=500,v4=v3x+a4=500×5+7=2507∴V4的值为2507;故答案为:2507.16.【答案】2【考点】用辗转相除计算最大公约数辗转相除法【解析】用大数除以小数,得到商和余数,再用上面的除数除以余数,又得到商和余数,继续做下去,知道刚好能够整除为止,得到两个数的最大公约数,从而得到需要做除法的次数.【解答】解:∵294÷84=3...42,84÷42=2,∴用辗转相除法求294和84的最大公约数时,需要做除法的次数2.故答案为217.【答案】负数,3【考点】条件语句输入、输出语句【解析】根据所给的语句看出运行结果的表达式,根据所写的表达式在两种不同的情况下分别求解,得到结果.【解答】解:由语句可知,这是一个条件语句,对应的输出运行结果的表达式是t ={负数,a <0√a ,a ≥0当输入的值是−4时,选择代入的表达式,输出结果为负数当输入的值是9时,选择代入的表达式,输出结果为√9=3故答案为:负数;3.18.【答案】40【考点】循环结构的应用【解析】写出前5次循环的结果,判断出各次得到的结果是否满足判断框中的条件,直到满足判断框中的条件执行输出结果.【解答】解:经过第一次循环得到的结果为T =2,S =2,i =2,不满足判断框中的条件,执行“否”经过第二次循环得到的结果为T =5,S =7,i =3,不满足判断框中的条件,执行“否” 经过第三次循环得到的结果为T =8,S =15,i =4,不满足判断框中的条件,执行“否”经经过第四次循环得到的结果为T =11,S =26,i =5,不满足判断框中的条件,执行“否”过第五次循环得到的结果为T =14,S =40,i =6,满足判断框中的条件,执行“是”,输出40.故答案为:40.19.【答案】1【考点】进位制【解析】将二进制、八进制转化为十进制,利用两数相等及进制数的性质,即可解得x ,y 的值,从而得解.【解答】解:∵ 100y011(2)=1+1×21+y ×23+1×26=67+8y ,x03(8)=3+x ×82=3+64x ,∴ 由3+64x =67+8y ,解得:8+y =8x ,∵ y ∈{0, 1},x ∈{0, 1, 2, 3, 4, 5, 6, 7, },∴ 解得:x =1,y =0.x +y =1.故答案为:1.20.【答案】【考点】秦九韶算法【解析】此题暂无解析【解答】此题暂无解答三、解答题(本题共计 5 小题,每题 10 分,共计50分)21.【答案】解:依题意得,费用y与人数n之间的关系为:y={5(n≤3)5+1.2(n−3)(n>3).程序框图如图所示:【考点】程序框图的三种基本逻辑结构的应用【解析】本题考查的知识点是设计程序框图解决实际问题,我们根据题目已知中应收取的卫生费计费方法,然后可根据分类标准,设置两个判断框的并设置出判断框中的条件,再由各段的输出,确定判断框的“是”与“否”分支对应的操作,由此即可画出流程图,再编写满足题意的程序.【解答】解:依题意得,费用y与人数n之间的关系为:y={5(n≤3)5+1.2(n−3)(n>3).程序框图如图所示:22.【答案】解:“*”表示乘法运算;“\”表示除法运算;“∧”表示乘方运算;“SQR()”表示求算术平方根运算;“ABS()”表示求绝对值运算.【考点】输入、输出语句【解析】由程序语句中各种运算符表示的意义对题目中的各运算符逐一进行判断,即可得到答案.【解答】解:“*”表示乘法运算;“\”表示除法运算;“∧”表示乘方运算;“SQR()”表示求算术平方根运算;“ABS()”表示求绝对值运算.23.【答案】30【考点】伪代码(算法语句)【解析】此题暂无解析【解答】解:模拟程序的运行过程如下:i=1,S=2;S=2,i=3;S=6,i=5;S=30,i=7;此时不满足循环条件,故输出S=30.故答案为:30.24.【答案】解:(1)由已知中的程序框图可得该程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值, 当x <6时,输出x +1,此时输出的结果满足x +1<6,所以x <5,所以输出的x(x <6)的概率为5−010−0=12;(2)当x ≤7时,输出x +1,此时输出的结果满足6<x +1≤8解得5<x ≤7;当x >7时,输出x −1,此时输出的结果满足6<x −1≤8解得7<x ≤9;综上,输出的x 的范围中5<x ≤9.则使得输出的x 满足6<x ≤8的概率为9−510=25.【考点】程序框图【解析】(1)由已知中的程序框图,我们根据选择结构的功能,可能分析出程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值,输出的x(x <6),可得x <5,即可求出输出的x(x <6)的概率;(2)由输出的结果在区间6<x ≤8上,我们可以分当x ≤7时和x >7时两种情况,分别讨论满足条件的x 的取值范围,得到输出结果的范围,最后根据输入x 的取值范围利用几何概型求出概率即可.【解答】解:(1)由已知中的程序框图可得该程序的功能是计算并输出分段函数y ={x −1,x >7x +1,x ≤7的值, 当x <6时,输出x +1,此时输出的结果满足x +1<6,所以x <5,所以输出的x(x <6)的概率为5−010−0=12;(2)当x ≤7时,输出x +1,此时输出的结果满足6<x +1≤8解得5<x ≤7;当x >7时,输出x −1,此时输出的结果满足6<x −1≤8解得7<x ≤9;综上,输出的x 的范围中5<x ≤9.则使得输出的x 满足6<x ≤8的概率为9−510=25.25.【答案】解:10b1(2)=1×20+b ×21+0×22+1×23=9+2b .a02(3)=2×30+0×31+a×32=9a+2,∵10b1(2)=a02(3),b∈{0, 1},a∈{0, 1, 2},且9+2b=9a+2∴a=b=1.【考点】进位制【解析】把两个数都化为10进制,即可求出结果.【解答】解:10b1(2)=1×20+b×21+0×22+1×23=9+2b.a02(3)=2×30+0×31+a×32=9a+2,∵10b1(2)=a02(3),b∈{0, 1},a∈{0, 1, 2},且9+2b=9a+2∴a=b=1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学-算法初步测试题
检测(A)
(时间:90分钟满分:120分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1下列关于算法的叙述不正确的是()
A.在任何数值计算或非数值计算的过程中所采取的方法和步骤,都可称之为算法
B.计算机解决问题的方法和步骤,就是计算机的算法
C.算法并不给出问题的精确的解,只是说明怎样才能得到解
D.算法中执行的步骤可以是无限次数的,能无休止地执行下去
解析本题主要考查算法的基本概念和特点.算法就是解决问题的步骤,可以是数值或者非数值操作,它必须是有限的步骤,不能无休止地执行下去,必须“有始有终”.
答案D
2“x=4+5”,“x=x-1”是某一程序中先后相邻的两个语句,那么下列说法正确的是()
①x=4+5的意思是x=4+5=9,此式与算术中的式子是一样的;
②x=4+5是将数值9赋给x;
③x=4+5可以写成4+5=x;
④x=x-1语句在执行时,“=”右边x的值是9,执行后左边x的值是8.
A.①③
B.②④
C.①④
D.②③
解析在x=4+5中,是先计算4+5,再用其结果9代替左边的x,由于赋值号“=”左边与右边的含义不一样,因而x=4+5不能写成4+5=x.
答案B
3下列程序运行的结果是()
a=1;
b=2;
c=3;
a=b;
b=c;
c=a;
a
b
c
A.1,2,3
B.2,3,1
C.2,3,2
D.3,2,1
解析由已知得a=1,b=2,c=3⇒a=2⇒b=3⇒c=2,故a,b,c的值分别是2,3,2.
答案C
4对于下列算法,
a=input(“a=”);
if a>5
b=4;
else
if a<3
b=5;
else
b=9;
end
end
print(%io(2),a);
print(%io(2),b);
如果在运行时,输入2,那么输出的结果是()
A.2,5
B.2,4
C.2,3
D.2,9
解析本题主要考查条件语句的应用.输入a的值为2,首先判断是否大于5,显然2不大于5,然后判断2与3的大小,显然2小于3,所以结果是b=5,因此结果应当输出2,5.
答案A
5执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于()
A.[-3,4]
B.[-5,2]
C.[-4,3]
D.[-2,5]
解析当-1≤t<1时,s=3t,则s∈[-3,3).当1≤t≤3时,s=4t-t2.∵该函数的对称轴为t=2,∴该函数在[1,2]上单调递增,在[2,3]上单调递减.∴s max=4,s min=3.
∴s∈[3,4].综上知s∈[-3,4].故选A.
答案A
6两个正整数490和910的最大公约数是()
A.2
B.10
C.30
D.70
解析910=91×10,490=49×10.
∵91=49×1+42,
49=42×1+7,
42=7×6,
∴91与49的最大公约数为7.
故910与490的最大公约数为70.
答案D
7下面的程序框图表示的算法的功能是()
A.计算小于100的奇数的连乘积
B.计算从1开始的连续奇数的连乘积
C.从1开始的连续奇数的连乘积,当乘积大于100时,计算奇数的个数
D.计算1×3×5×…×n≥100时的最小的n值
解析题中程序框图表示的算法是确定使1×3×…×n≥100成立的最小整数n的值.
答案D
8某程序框图如图所示,运行后输出的倒数第二个数是()
A
解析当n=1时,输出a=3;
当n=2时,输出a=2;
当n=3时,输出a
当n=4时,输出a
当n=5时,输出a
故输出的倒数第二个数
答案C
9下面程序执行后输出的结果是()
n=5;
S=0;
while S<15
S=S+n;
n=n-1;
end
n
A.-1
B.0
C.1
D.2
解析∵5+4+3+2+1=15,∴当n=1时进行最后一次循环,最后输出n=n-1=1-1=0.
答案B
10执行两次下图所示的程序框图,若第一次输入的a的值为-1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为()
A.0.2,0.2
B.0.2,0.8
C.0.8,0.2
D.0.8,0.8
解析第一次:a=-1.2<0,a=-1.2+1=-0.2,-0.2<0,a=-0.2+1=0.8>0,a=0.8≥1不成立,输出0.8.
第二次:a=1.2<0不成立,a=1.2≥1成立,a=1.2-1=0.2≥1不成立,输出0.2.
答案C
二、填空题(本大题共5小题,每小题5分,共25分.把答案填在题中的横线上)
11三个数72,120,168的最大公约数是.
解析利用辗转相除法:120=72×1+48,72=48×1+24,48=24×2,所以72和120的最大公约数是24,又168=24×7,所以三个数的最大公约数是24.
答案24
12下面是求S=1+3+5+…+2 015的程序,在横线处填上正确的内容.
S=;
i=1;
for i=1::
S=;
end
print(%io(2),S);
答案0 2 2 015S+i
13阅读某一问题的算法的程序框图(如图所示).此框图反映的算法功能
是.
答案计算任意实数x的绝对值|x|
14执行如图所示的程序框图,如果输入a=1,b=2,则输出的a的值为.
解析输入a=1,b=2,不满足a>8,故a=3;
a=3不满足a>8,故a=5;
a=5不满足a>8,故a=7;
a=7不满足a>8,故a=9,满足a>8,终止循环.输出a=9.
答案9
15用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是.
解析由于f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,
因此需做乘法6次,加法6次.
答案6,6
三、解答题(本大题共5小题,共45分.解答时应写出文字说明、证明过程或演算步骤)
16(8分)分别用更相减损之术与辗转相除法求161与253的最大公约数.
解更相减损之术:
(161,253)→(161,92)→(69,92)→(69,23)→(46,23)→(23,23).
故161与253的最大公约数为23.
辗转相除法:
253÷161=1(余92),161÷92=1(余69),92÷69=1(余23),69÷23=3(余0),
故161与253的最大公约数为23.
17(8分)如图所示的程序框图.
(1)试写出该程序框图的功能;
(2)若输出的值为3,求输入x的值.
解(1)该程序框图的功能是输入自变量x的值,输出函数y.
(2)若输出的值为3,当x<0时,2x2-5=3,解得x=2(舍去)或x=-2;
当x≥0时,x-1=3,解得x=4.
综上所得x=-2或x=4.
18(9分)老师将一次测验的成绩分为3个等级:85~100为“A”;60~84为“B”;60以下为“C”.试用条件分支结构的框图表示某个学生成绩等级的算法.
解程序框图如图所示.
19(10分)已知如图所示的程序框图(未完成).设当箭头a指向①时,输出的结果为s=m,当箭头a 指向②时,输出的结果为s=n,求m+n的值.
解当箭头a 指向①时,s 和i 的结果如下:
s
0+1 0+2 0+3 0+4 0+5 i 2 3 4 5 6
因此,s=m=5.
当箭头a 指向②时,输出s 和i 的结果如下:
s
0+1 0+1+2 0+1+2+3 0+1+2+3+4 0+1+2+3+4
+5 i 2 3 4 5 6
因此,s=n=1+2+3+4+5=15.故m+n=20.
20(10分)相传古代印度国王在奖赏他聪明能干的宰相达依尔(国际象棋发明者)时,问他需要什么,达依尔说:“国王只要在国际象棋棋盘的第一格子上放一粒麦子,第二格子上放二粒,第三格子上放四粒,以后按比例每一格加一倍,一直放到第64格(国际象棋棋盘格数是8×8=64),我就感恩不尽,其他什么也不要了.”国王想:“这才有多少,还不容易!”于是让人扛来一袋小麦,但不到一会儿就用完了,再来一袋很快又没有了,结果全印度的粮食用完还不够,国王很奇怪,怎么也算不清这笔账.请你设计一个程序框图表示其算法,来帮国王计算一下需要多少粒小麦,并用算法语句编写程序.
解程序框图如图所示.
程序如下:
i=0;
S=0;
while i<64
S=S+2^i;
i=i+1; end
print(%io(2),S);。
