建立递阶结构模型的规范方法
系统工程 完整版 汪应洛主编课后题答案
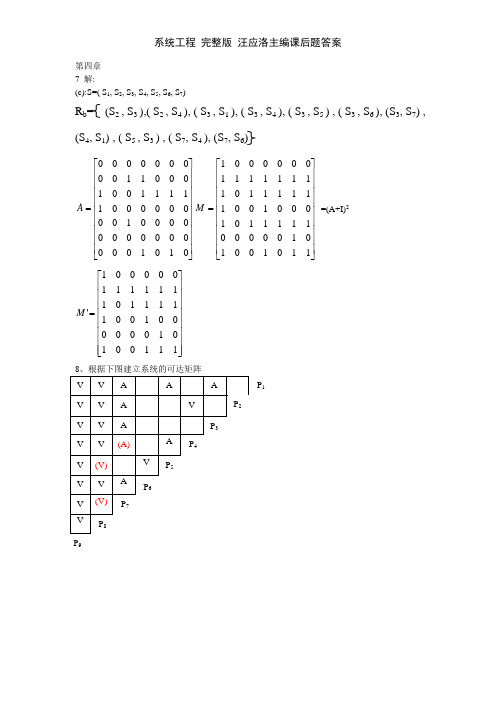
第四章 7 解:(c):S=( S 1, S 2, S 3, S 4, S 5, S 6, S 7)R b= (S 2 , S 3 ),( S 2 , S 4 ), ( S 3 , S 1 ), ( S 3 , S 4 ), ( S 3 , S 5 ) , ( S 3 , S 6 ), (S 3, S 7) , (S 4, S 1) , ( S 5 , S 3 ) , ( S 7, S 4 ), (S 7, S 6)⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=0101000000000000001000000001111100100011000000000A ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1101001010000011111010001001111110111111110000001M =(A+I)2 ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=111001010000001001111101111111000001'M解:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000000110000000111100111110100000110111001110001000110000101110001010110000001M9、(2)解:规范方法:所以设B 中元素Bu=3、Bv=6R(3)={ 1,2,3,4}、R(6)={ 2,4,5,6,7,8}R(3)∩R(6)={ 1,2、3,4} ∩ {2,4,5,6,7,8} ≠φ,故区域不可分解 2将满足C =R 的元素2,8挑出作为第1级 将满足C =R 的元素4挑出作为第2级 将满足C =R 的元素1,5挑出作为第3级 将满足C =R 的元素3,7挑出作为第4级 将满足C =R 的元素6挑出作为第5级 将M 按分级排列:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=110101110101011100101101000101010000110100000101000000100000000167351482M提取骨架矩阵如下:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=010000000001001000001000000001000000010000000001000000000000000067351482'A(1) 实用方法:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=1101100100100100100000000000067351482M建立其递阶结构模型同上。
(完整版)第二章模型化

第二章 系统模型与模型化第一节 概述一、模型及模型化的定义模型可以说是现实系统的替代物。
模型应反映出系统的主要组成部分、各部分的相互作用,以及在运用条件下的因果作用及相互关系。
模型是现实系统的理想化抽象或简洁表示,它描绘了现实系统的某些主要特点,它是为了客观地研究系统而发展起来的。
模型有三个特征:①它是现实世界部分的抽象或模仿;②它是由那些与分析的问题有关的因素构成; ③它表明了有关因素间的相互关系。
模型是描述现实世界的一个抽象。
在构造模型时,要兼顾到它的现实性和易处理性。
考虑到现实性,模型必须包含现实系统中的主要因素。
考虑到易处理性,模型要采取一些理想化的办法,即去掉一些外在的影响并对一些过程作合理的简化。
二、模型化的本质、作用及地位模型化就是为描述系统的构成和行为,对实体系统的各种因素进行适当筛选后,用一定方式(数学、图象等)表达系统实体的方法。
简言之就是构模的过程。
1 本质:利用模型与原型之间某方面的相似关系,在研究过程中用模型来代替原型,通过对于模型的研究得到关于原型的一些信息。
这里的相似关系是指两事物不论其自身结构如何不同,其某些属性是相似的。
2 作用:①模型本身是人们对客体系统一定程度研究结果的表达。
这种表达是简洁的、形式化的。
②模型提供了脱离具体内容的逻辑演绎和计算的基础,这会导致对科学规律、理论、原理的发现。
③利用模型可以进行“思想”试验。
3 地位:模型的本质决定了它的作用的局限性。
它不能代替对客观系统内容的研究,只有在和对客体系统内容研究相配合时,模型的作用才能充分发挥。
模型是对客体的抽象,由它得到的结果,必须再回到现实中去检验。
系统模型(化)的作用与地位如图4-1所示。
图4-1 模型的作用与地位三、模型的分类一般说来,模型可按图4-2所示进行分类。
概念模型是通过人们的经验、知识和直觉形成的。
符号模型用符号来代表系统的各种因素和它们间的相互关系。
这种模型是抽象模型。
它通常采用图示或数学形式,一般分为结构模型和数学模型。
1解释结构模型ISM及其应用

从可达性矩阵各元素是 1 还是 0 很容易进 行关系划分。
关系划分可以表示为:
14
2、区域划分 2 ( S )
区域划分将系统分成若干个相互独立的、 没有直接或间接影响的子系统。
可达集 先行集 底层单元集(初始集,其中元素具有此性质: 不能存在一个单元只指向它而不被它所指向。)
15
对属于初始集B的任意两个元素 t、t′,如果可能指 向相同元素 这种划分对经济区划分、行政区、 R( t )∩R( t′)≠φ 功能和职能范围等划分工作很有 意义。 则元素 t 和 t′属于同一区域; 反之,如果 t、t′不可能指向相同元素 R( t )∩R( t′)=φ 则元素 t 和 t′属于不同区域。 这样可以以底层单元为标准进行区域的划分。 经过上述运算后,系统单元集系统就划分成若干区 域, 可以写成 π2(S)={P1,P2,…,Pm}, 其中m为区域数。
34
7
6
5
4 3
1
2
图4-2
35
1 1 2
2
3
4
5
6
7
1 1 0 0 0 0 1
0 1 0 0 0 0 1
0 0 1 0 0 0 0
0 0 1 1 0 1 0
0 0 1 1 1 1 0
0 0 1 1 0 1 0
0 0 0 0 0 0 1
3
M= 4 5 6 7
36
1.区域划分
为对给出的与图4-5所对应的可达矩阵进行区域划分,可列出任一要 素Si(简记作i,i=1,2,…,7)的可达集R(Si) 、先行集A(Si) 、共同 集C (Si),并据此写出系统要素集合的起始集B(S),如表4-1所示:
18
R(e3 ) ? A(e3 )
系统模型与模型化(结构模型化技术)

✓ 系统构成要素中满足其种二元关系R的要素Si、Sj的要素对 (Si,Sj)的集合,称为S上的二元关系集合,记作Rb,即有: Rb={(Si,Sj)|Si、Sj∈S,SiRSj,i,j=1,2,…,n},且在一般情况下, (Si,Sj)和(Sj,Si)表示不同的要素对。
系统模型与模型化
第一节 概述 第二节 系统结构模型化技术 第三节 主成分分析及聚类分析 第四节 状态空间模型 第五节 系统工程模型技术的新进
2021/2/23
1
2021/2/23
第一节 系统模型与模型化概述
❖ 一切客观存在的事物及其运动形态称为“实体” (即原型)。为便于实验、分析和预测,总是 先把所需研究的系统结构型态或运动形态变成 易于考察的形式,即转化为“模型”。
✓ 2、考虑信息的相关性:只应包括系统中与研究目的有 关的信息;
✓ 3、考虑准确性:收集的用以建模的信息要准确;
✓ 4、考虑结集性:将一些个别的实体组成更大实体的程
度。
用户订货
生产管理部门
原料 采购部门
制造车间
装配车间
成品 装运部门
2021/2/23
13
五、建模一般过程
✓ (1)明确建模目的和要求; ✓ (2)弄清系统或子系统中的主要因素及其相互关系; ✓ (3)选择模型方法; ✓ (4)确定模型结构; ✓ (5)估计模型参数; ✓ (6)模型试运行; ✓ (7)对模型进行实验研究; ✓ (8)对模型进行必要修正。
2021/2/23
19
系统结构分析
✓ 系统结构分析的具体内容:对系统目的—功能的认识;系统构成
要素的选取;对要素间的联系及其层次关系的分析;系统整体结构的确 定及其解释。
系统工程 [完整版] 汪应洛主编课后题答案,DOC
![系统工程 [完整版] 汪应洛主编课后题答案,DOC](https://img.taocdn.com/s3/m/b7cc20eabceb19e8b8f6ba83.png)
0.3 0.40.20.1
0.20.30.40.1
R=
0.10.20.30.4 0.40.40.20
00.40.40.2 (3)解:S5 的权重为 0.24,S6 的权重为 0.16,S7 的权重为 0.4,S8 的权重为 0.14,S9 的权重
为 0.06。
0.30.40.20.1 (4)解:(0.24,0.16,0.4,0.14,0.00.62)0.30.40.1
结果在 i 评审指标下属于第 j 等级的人数)。请写出隶属度 rij 的定义式(i=1,2,…,m,j=1,2,…,
技术水n)平及(隶S5)属度矩技阵术难R。度(S6)
Nij 等级
一
指标
技术水平
3
技术难度 成果 A(2S10)
经济效益
1
社会效益
4
工作量
0
经济效益(S7)
二
4 成果3 B(S11)
2 4 4
8
8
6,7,8
8
将满足 C=R 的元素 2,8 挑出作为第 1 级 将满足 C=R 的元素 4 挑出作为第 2 级 将满足 C=R 的元素 1,5 挑出作为第 3 级 将满足 C=R 的元素 3,7 挑出作为第 4 级 将满足 C=R 的元素 6 挑出作为第 5 级 将 M 按分级排列: 提取骨架矩阵如下:
人口的年自然增长率。
解:(1)因果关系图:
年 新 增 个 体 NS
仅供个人学习参考
服务网点数
+
千人均服务
网点期望差
个体服务 S
流程图:
S(90)
P(100)
第六章:
12、今有一项目建设决策评价问题NS,已经建立S 起层次结N构P 和判断矩阵P如下图、表所示,试用层次分
系统工程大作业资料讲解

系统工程大作业系统工程大作业班级:工程1301姓名:韦天伦学号:201304060123基于ISM/AHP方法的大学生就业难对策研究高校大学生是国家宝贵的人才资源,其就业问题, 关系到我国经济建设、社会稳定和人民群众的根本利益, 关系到高等教育的持续健康协调发展, 是我们党的执政能力建设的重要组成部分。
做好高校大学生的就业工作, 力争让每一名大学生都能及时、充分地将其所学的知识技能应用于社会实践, 既是社会主义现代化建设事业的现实要求, 也是中华民族生存发展的长远需要。
一.大学生就业难的实际情况现实中,中国大学生在数量、质量、结构上的供给均与用人单位的要求存在一定程度上的错位,从而导致大学生就业市场供求关系失去平衡。
从经济学角度上来说,就是供过于求。
每年毕业生的人数比社会上所需要的就业岗位数量多得多,而且这个差距还在逐年的增大。
有关资料表明,从2001年至2006年全国高校毕业生从110万增加到410万,是扩招前的四倍,而2009年更是达到了610万的新高度,然而用人岗位增加比例却远远小于此数目。
不仅在数量上,这种差距在结构和质量上也越来越明显,专业扎堆现象严重,热门专业人才过剩。
2007 年, 我国大学毕业生历史性地超过了495 万人, 随着大学扩招人数的激增, 一提到大学生就业难, 人们很容易把责怪的矛头对准近几年的高校扩招, 然而, 笔者认为, 高校扩招并不是大学大学生就业难的根本原因。
从高校扩招的目的来看扩招在于让更多人受到良好的教育; 从长远来看, 扩招将会制造出更多的高素质人才, 他们将为中国创造出更多的就业机会。
大学生就业难虽然已成为一个社会性问题, 但远没有达到不可救药的程度, 只是一个相对性暂时的难题。
二.解析递阶模型(ISM)的建立①相关因素的确定A 外部原因。
(1)我国整体就业形势的严峻。
(2)高等教育结构的不合理。
(3)学校缺乏对毕业生的有针对性的就业指导。
(4)社会和家人的观念。
《系统工程》结构模型

•
25
西南交大物流学院
SWJTU
1.区域划分
• 系统要素Si的可达集R(Si) 、先行集A(Si) 、共同集C (Si) 之间的关系如图所示:
26
西南交大物流起始集B(S)和终止集E(S)。系统要素集合S的起始集是在S中 只影响(到达)其他要素而不受其他要素影响(不被其他要素到 达)的要素所构成的集合,记为B(S)。 B(S)中的要素在有 向图中只有箭线流出,而无箭线流入,是系统的输入要素。其定 义式为: B(S)= { Si | Si ∈S, C(Si)= A(Si), i= 1,2,…,n } 如在于前有向图所对应的可达矩阵中, B(S)={S3,S7}。 当Si为S的起始集(终止集)要素时,相当于使前图中的阴影部分 C(Si)覆盖到了整个 A(Si)( R(Si))区域。 这样,要区分系统要素集合S是否可分割,只要研究系统起始集B (S)中的要素及其可达集(或系统终止集E(Si)中的要素及其 先行集要素 )能否分割(是否相对独立)就行了。
两两判断认为:S2影响S1,S3影响S4,S4影响S5,S7影 响S2,S4和S6相互影响。这样,该系统的基本结构可用 要素集合S和二元关系集合Rb来表达,其中: • S = {S1,S2,S3,S4,S5,S6,S7}
Rb = {(S2,S1),(S3,S4),(S4,S5),
(S7,S2),(S4,S6),(S6,S4)}
(3)选择模型方法;
(4)确定模型结构; (5)估计模型参数; (6)对模型进行实验研究; (7)对模型进行必要修正。
8
西南交大物流学院
SWJTU
二.解释结构模型(ISM)
(一)系统结构模型化基础
1.概念
结构→结构模型→结构模型化→结构分析
《系统工程》第四版习题解答

系统工程第四版习题解答第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3-16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1111001000011000111011111M ,M M ='}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3-16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111M①区域划分φ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
2020年3月6日11时35
分
16
7
5 4
6 3
1
2
图3-5 例 3-1 有向图
2020年3月6日11时35 分
返回
17
进入“状态空间模型(数学模型)” 退回上一讲
2020年3月6日11时35分18源自L1 5 0 0 0
L2 4 1 0 0
0
A’=M’’(L)- I =
L3 3 0
L1 1
1
0
0
0
0
L2 2
0
L3 7
1 0 0
0 1 0
2020年3月6日11时35
分
12
4.绘制多级递阶有向图D(A’)
根据骨架矩阵A’,绘制出多级递阶有 向图D(A’),即建立系统要素的递阶结 构模型。绘图一般分为如下三步:
某系统由七个要素(S1,S2,…,S7)组 成。经过两两判断认为:S2影响S1、S3影 响S4、S4影响S5、S7影响S2、S4和S6相互 影响。这样,该系统的基本结构可用要 素集合S和二元关系集合Rb来表达,其中:
S = {S1,S2,S3,S4,S5,S6,S7} Rb = {(S2,S1),(S3,S4),(S4,S5),
分
4
系统要素Si的可达集R(Si) 、先行集A(Si) 、 共同集C(Si)之间的关系如图3-7所示:
A(Si)
C (Si)
Si
R(Si)
图3-7 可达集、先行集、共同集关系示意图
2020年3月6日11时35
分
5
④ 起始集B(S)——只影响(到达)其他要素的要素所构成 的集合。
B(S)中的要素在有向图中只有箭线流出,而无箭线流入, 是系统的输入要素。其定义式为:
分
10
②去掉M’(L)中已具有邻接二元关系的要素 间的越级二元关系,得到经进一步简化后的新 矩阵M’’(L)。
如在原例的M’(L)中,将 M’(L)中 3→5和7→1的“1”改为“0”,得:
54 31
27
L1 5 1 0 0
L2 4 1
1
0
0
M’’(L)=
L3 3
0
L1 1
(二)建立递阶结构模型的规范方法
建立反映系统问题要素间层次关系的递阶 结构模型,可在可达矩阵M的基础上进行, 一般要经过区域划分、级位划分、骨架矩 阵提取和多级递阶有向图绘制等四个阶段。 这是建立递阶结构模型的基本方法。
现以例3-1所示问题为例说明:
与图3-5对应的可达矩阵(其中将Si简记为i) 为:
缩检共分三步,即:
①检查各层次中的强连接要素,建立可达矩阵M (L)的缩减矩阵M’(L)(区域下三角矩阵):
54 31
27
L1 5
1
0
0
M’(L)=
L2 4 L3 3
1 1
L1 1
1 1
0 1
1
0
0
0
L2 2
0
L3 7
1
1
0
1
1
1
2020年3月6日11时35
及R(bu)、 R(bv)中的要素属同一区域。若对所有 u和v均有此结果(均不为空集),则区域不可分。 ② 如果R(bu)∩ R(bv)=ψ,则bu、bv及R(bu)、 R (bv)中的要素不属同一区域,系统要素集合S至少可 被划分为两个相对独立的区域。
区域划分的结果可记为: ∏(S)=P1,P2,…,Pk,…,Pm (其中Pk为第k个相对独立区域的要素集合)。经过区 域划分后的可达矩阵为块对角矩阵(记作M(P))。
1. 分区域从上到下逐级排列系统构成要素。
2. 同级加入被删除的与某要素有强连接关系 的要素,及表征它们相互关系的有向弧。
3. 按A’所示的邻接二元关系,用级间有向弧 连接成有向图D(A’)。
2020年3月6日11时35
分
13
原例的递阶结构模型:
S1
S5
S2
S4
S7
S3
第1级
S6
第2级
第3级
以可达矩阵M为基础,以矩阵变换为主线的递阶结构模型的建 立过程:
2020年3月6日11时35
分
7
2.级位划分
区域内的级位划分,即确定某区域内各要素所处 层次地位的过程。这是建立多级递阶结构模型的 关键工作。 设P是由区域划分得到的某区域要素集合,若用 L(1,其L中2,l为…最,大L级l表位示数从)高,到则低级的位各划级分要的素结集果合可写 成:
∏(P)=L1,L2 ,…,Ll • 某系统要素集合的最高级要素即该系统的终止集
2020年3月6日11时35
分
3
① 可达集R(Si)——在可达矩阵或有向图中,由 Si可到达的诸要素所构成的集合,其定义式为:
R(Si)= { Sj | Sj∈S,mij = 1,j = 1,
2,…,n }
i = 1,2,…,n
② 先行集A( Si )——在可达矩阵或有向图中, 可到达Si的诸要素所构成的集合,其定义式为:
2020年3月6日11时35
分
2
1.区域划分
区域划分即将系统的构成要素集合S, 分割成关于给定二元关系R的相互独立的区 域的过程。
首先以可达矩阵M为基础,划分与要 素Si(i = 1,2,…,n)相关联的系统要 素的类型,并找出在整个系统(所有要素 集合S)中有明显特征的要素。
有关要素集合的定义如下:
L2 2
L3
7
00 11 11 11
0
31
0 0 0 1
1 1 1
27
0
0
0
1
0
1
1
经过级位划分后的可达矩阵变为区域块三角 矩阵,记为M(L)。
2020年3月6日11时35
分
9
3.提取骨架矩阵
提取骨架矩阵,是通过对M(L)的缩约和检出, 建立起M(L)的最小实现矩阵,即骨架矩阵A’。
强连接
剔除
去掉
区域
级位
要素
越级
自身
划分
划分
缩减
关系
关系 绘图
M → M(P )→ M(L)→ M’(L) → M’’(L) → A’→ D(A’)
(块对角) (区域
(区域
块三角) 下三角)
2020年3月6日11时35
结束
分
14
“建立递阶结构模型的规范方法”结束
2020年3月6日11时35
分
15
例3-1
A(Si)= { Sj | Sj∈S,mji = 1,j = 1,
2,…,n }
i = 1,2,…,n
③ 共同集C ( Si )——R(Si)∩ A(Si) 其定义式为:
C(Si)= { Sj | Sj∈S,mij = 1, mji = 1, j = 1,2,…,n } i = 1,2,…,n
2020年3月6日11时35
要区分系统要素集合S是否可分割,只要研究系 统起始集B(S)中的要素及其可达集(或系统终 止集E(S)中的要素及其先行集要素 )能否分割 (是否相对独立)就行了。
2020年3月6日11时35
分
6
利用起始集B(S)判断区域能否划分的规则如下:
在B(S)中任取两个要素bu、bv: ① 如果R(bu)∩ R(bv)≠ψ(ψ为空集),则bu、bv
B(S)= { Si | Si ∈S, C(Si)= A(Si) ,i= 1,2,…,n }
终止集E(S)——只受其他要素影响(到达)的要素所构 成的集合。
E(S)中的要素在有向图中只有箭线流入,而无箭线流出, 是系统的输出要素。其定义式为:
E(S)= { Si | Si ∈S, C(Si)= R(Si) ,i= 1,2,…,n }
2020年3月6日11时35
分
1
1 2 3 4 56 7
1 1 0 0 0 0 0 0
2 1 1 0 0 0 0 0
3 0 0 1 1 1 1 0
M = 4 0 0 0 1 1 1 0
5 0 0 0 0 1 0 0
6 0 0 0 1 1 1 0
7 1 1 0 0 0 0 1
1
1
1
0
0
L2 2
0
2020年3月6日11时35
L3 7
1 1 0
0 1 1
分
11
③进一步去掉M’’(L)中自身到达的二元关系, 即减去单位矩阵,将M’’(L)主对角线上的 “1”全变为“0”,得到经简化后具有最小二元 关系个数的骨架矩阵A’。
如对原例有:
54 31
27
要素。级位划分的基本做法是:找出整个系统要 素集合的最高级要素(终止集要素)后,可将它 们去掉,再求剩余要素集合的最高级要素,依次 类推,直到确定出最低一级要素集合(即Ll)。
2020年3月6日11时35
分
8
这时的可达矩阵为:
54 6
L1 L2
M(L)= L3
5 1
4
1
6 1
3
1
L1
1
