二进制与各种类型的数据转换
关于二进制、十进制、八进制、十六进制数据转换计算方法详细总结
在我们接触编程知识时,总会接触有关进制转换的知识,最常见的就是10进制与二进制或十六进制之间的转换,很多时候我们总会遗忘,虽然现在也出现了很多可以直接使用的网络在线的进制转换工具,但考试中,我们就要靠自己通过公式进行运算了。
今天就跟大家分享一下有关进制转换的理论知识,大家可以通过对比从里面发现共同点,这样便于我们理解记忆。
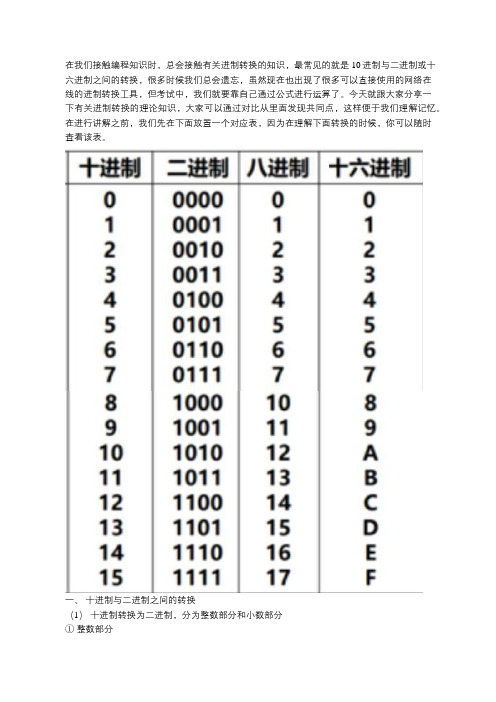
在进行讲解之前,我们先在下面放置一个对应表,因为在理解下面转换的时候,你可以随时查看该表。
一、十进制与二进制之间的转换(1)十进制转换为二进制,分为整数部分和小数部分①整数部分方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
下面举例:例:将十进制的168转换为二进制得出结果将十进制的168转换为二进制,(10101000)2分析:第一步,将168除以2商84余数为0。
第二步,将商84除以2,商42余数为0。
第三步,将商42除以2,商21余数为0。
第四步,将商21除以2,商10余数为1。
第五步,将商10除以2,商5余数为0。
第六步,将商5除以2,商2余数为1。
第七步,将商2除以2,商1余数为0。
第八步,将商1除以2,商0余数为1。
第九步,读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,即10101000②小数部分方法:乘2取整法,即将小数部分乘以2,然后取整数部分,剩下的小数部分继续乘以2,然后取整数部分,剩下的小数部分又乘以2,一直取到小数部分为零为止。
如果永远不能为零,就同十进制数的四舍五入一样,按照要求保留多少位小数时,就根据后面一位是0还是1,取舍,如果是零,舍掉,如果是1,向入一位。
换句话说就是0舍1入。
读数要从前面的整数读到后面的整数,下面举例:例1:将0.125换算为二进制得出结果:将0.125换算为二进制(0.001)2分析:第一步,将0.125乘以2,得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。
各种进制之间的转换方法

各种进制之间的转换方法进制转换是指将数字从一种进制表示转换为另一种进制表示。
常见的进制有二进制、八进制、十进制和十六进制。
下面将详细介绍各种进制之间的转换方法。
1.二进制转换为十进制:二进制数是由0和1组成的数字序列。
转换为十进制的方法是,将二进制数每一位上的数字乘以2的幂次方,然后将得到的结果相加。
例如:将二进制数1101转换为十进制,计算方法为:1*2^3+1*2^2+0*2^1+1*2^0=8+4+0+1=132.八进制转换为十进制:八进制数是由0到7之间的数字组成的数字序列。
转换为十进制的方法与二进制类似,只是要将八进制数每一位上的数字乘以8的幂次方,然后将得到的结果相加。
例如:将八进制数157转换为十进制,计算方法为:1*8^2+5*8^1+7*8^0=64+40+7=1113.十六进制转换为十进制:十六进制数是由0到9和A到F之间的数字和字母组成的数字序列,其中A表示十进制的10,B表示十进制的11,以此类推。
转换为十进制的方法是,将十六进制数每一位上的数字或字母转换为对应的十进制数,然后将得到的结果相加。
例如:将十六进制数1E8转换为十进制,计算方法为:1*16^2+14*16^1+8*16^0=256+224+8=4884.十进制转换为二进制:将十进制数转换为二进制的方法是,使用除2取余法。
即将十进制数连续除以2,将得到的余数从下往上排列,直到商为0为止。
例如:将十进制数43转换为二进制,计算方法为:43÷2=21余121÷2=10余110÷2=5余05÷2=2余12÷2=1余01÷2=0余15.十进制转换为八进制:将十进制数转换为八进制的方法是,使用除8取余法。
即将十进制数连续除以8,将得到的余数从下往上排列,直到商为0为止。
例如:将十进制数145转换为八进制,计算方法为:145÷8=18余118÷8=2余22÷8=0余2从下往上排列得到八进制数2216.十进制转换为十六进制:将十进制数转换为十六进制的方法是,使用除16取余法。
二进制与十进制转换

二进制与十进制转换在计算机科学和信息技术领域,二进制(binary)和十进制(decimal)之间的转换是非常常见且重要的操作。
二进制是一种使用0和1表示数字的数制,而十进制是我们日常生活中常用的十个数字(0-9)的数制。
理解二进制和十进制之间的转换方法,有助于我们更好地理解计算机内部数据的表示和运算。
一、二进制转换为十进制二进制转换为十进制的方法相对简单。
我们可以通过将二进制数从右向左依次乘以2的幂次,然后将结果累加得到对应的十进制数。
以下是转换步骤:1. 将给定的二进制数从右向左从低位到高位编号,用n表示位数;2. 对每一位进行操作,将每位的值乘以2的对应次幂;3. 对每个乘积进行累加;4. 得到所求的十进制数。
举例来说,我们将一个八位的二进制数转换为十进制:```二进制数:10101010第一位(右数第一位)为0,对应的2的0次幂为1;第二位为1,对应的2的1次幂为2;第三位为0,对应的2的2次幂为4;第四位为1,对应的2的3次幂为8;第五位为0,对应的2的4次幂为16;第六位为1,对应的2的5次幂为32;第七位为0,对应的2的6次幂为64;第八位(左数第一位)为1,对应的2的7次幂为128。
将每一位的乘积累加:1 + 2 + 0 + 8 + 0 + 32 + 0 + 128 = 171所以,二进制数10101010转换为十进制数为171。
```二、十进制转换为二进制十进制转换为二进制相对复杂一些,但也有一定的规律可循。
我们可以使用“除2取余”的方法进行转换。
以下是转换步骤:1. 将给定的十进制数进行除以2的操作;2. 将每次除法的余数记录下来,从下往上排列;3. 将每次的商作为下一次除法的被除数,重复以上步骤,直到商为0。
举例来说,我们将一个十进制数转换为二进制:```十进制数:85第一次除以2,商为42,余数为1;第二次除以2,商为21,余数为0;第三次除以2,商为10,余数为1;第四次除以2,商为5,余数为0;第五次除以2,商为2,余数为1;第六次除以2,商为1,余数为1;第七次除以2,商为0,余数为1。
二进制与数值转换

二进制与数值转换二进制与数值转换二进制是计算机中最基本的数字系统,由两个数字0和1组成。
因为它只有两个状态,所以它被广泛应用于数字电子技术和计算机领域。
但是二进制对于人类来说并不方便,因为我们使用的是十进制数字系统。
将二进制转换为十进制和将十进制转换为二进制是很常见的需求,下面将介绍如何进行这些转换。
一、将二进制转换为十进制1.将二进制数按权展开二进制数是按位赋权值展开的,权值是2的幂。
例如,二进制数10011的权值为:1×2^4 + 0×2^3 + 0×2^2 + 1×2^1 + 1×2^0 = 16 + 2 + 1 =19所以,二进制数10011的十进制表示为19。
2.使用加法像算长加法一样,将二进制数位倒过来,将每个数字与其相应的权相乘,然后将它们相加,即可得到十进制值。
例如,将二进制数11101转换为十进制:1×2^4 + 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0 = 16 + 8 + 4 + 0 + 1 = 29所以,二进制数11101的十进制表示为29。
二、将十进制转换为二进制将十进制数转换为二进制数需要用到短除法。
我们用2除以十进制数,得到商和余数。
再用商继续除以2,得到新的商和余数。
重复这个过程直到商为0为止。
最后,我们将余数从下往上排列在一起,这就是十进制数的二进制表示。
例如,将十进制数42转换为二进制:42 ÷ 2 = 21 余021 ÷ 2 = 10 余110 ÷ 2 = 5 余05 ÷ 2 = 2 余12 ÷ 2 = 1 余01 ÷2 = 0 余1所以,十进制数42的二进制表示为101010。
综上所述,二进制与十进制之间的转换是非常简单的。
这种转换对于计算机科学家、程序员和电子工程师来说是非常重要的。
计算机常用数制之间的转换

计算机常用数制之间的转换在计算机科学中,数制是指用来表示数字的符号系统。
计算机常用的数制有二进制、八进制、十进制和十六进制。
这些数制之间的转换是计算机科学中非常重要的基础知识。
本文将介绍这些数制之间的转换方法。
一、二进制转八进制二进制数是由0和1组成的数,八进制数是由0到7组成的数。
将二进制数转换为八进制数的方法是将二进制数从右往左每三位分成一组,然后将每组转换为对应的八进制数。
如果最左边的一组不足三位,则在左边补0。
例如,将二进制数101101101转换为八进制数的过程如下:101 101 101= 5 5 5因此,二进制数101101101转换为八进制数555。
二、二进制转十进制二进制数转换为十进制数的方法是将二进制数从右往左每一位乘以2的幂次方,然后将结果相加。
例如,将二进制数101101101转换为十进制数的过程如下:1×2^8 + 0×2^7 + 1×2^6 + 1×2^5 + 0×2^4 + 1×2^3 + 1×2^2 + 0×2^1 + 1×2^0= 256 + 0 + 64 + 32 + 0 + 8 + 4 + 0 + 1= 365因此,二进制数101101101转换为十进制数365。
三、二进制转十六进制二进制数转换为十六进制数的方法是将二进制数从右往左每四位分成一组,然后将每组转换为对应的十六进制数。
如果最左边的一组不足四位,则在左边补0。
例如,将二进制数101101101转换为十六进制数的过程如下:1011 0110 1= B 6 1因此,二进制数101101101转换为十六进制数B61。
四、八进制转二进制八进制数是由0到7组成的数,二进制数是由0和1组成的数。
将八进制数转换为二进制数的方法是将八进制数的每一位转换为对应的三位二进制数。
例如,将八进制数555转换为二进制数的过程如下:5 5 5= 101 101 101因此,八进制数555转换为二进制数101101101。
各进制之间的转换方法及表格

各进制之间的转换方法及表格1. 介绍在计算机科学和数学领域中,进制是表示数字的一种方式。
常见的进制包括二进制、八进制、十进制和十六进制。
不同进制之间的转换是计算机科学和数学中非常重要的基本知识点。
本文将介绍各种进制之间的转换方法,并提供一个详细的表格以便于查阅。
2. 进制介绍2.1 二进制(Binary)二进制是计算机中最基础也最常用的一种进制,它只有两个数字:0和1。
在二进制中,每一位上的数字称为一个比特(bit)。
2.2 八进制(Octal)八进制使用0到7这8个数字来表示数值。
在八进制中,每一位上的数字相当于三个二进制位。
2.3 十进制(Decimal)十进制是我们日常生活中最常用的一种数字表示方式,它使用0到9这10个数字来表示数值。
2.4 十六进制(Hexadecimal)十六进制使用0到9这10个数字以及A到F这6个字母来表示数值。
在十六进制中,每一位上的数字相当于四个二进制位。
3. 进制转换方法3.1 二进制转换为八进制和十六进制将二进制数转换为八进制和十六进制的方法非常简单。
只需要将二进制数从右往左每三(对于八进制)或四(对于十六进制)个数字分组,并将每组转换为对应的八进制或十六进制数字即可。
示例1:将二进制数10101011转换为八进制和十六进制•八进制:10101011 = (001)(010)(101) = 125•十六进制:10101011 = (0010)(1011) = 2B3.2 八进制转换为二进制和十六进制将八进制数转换为二进制和十六进制的方法也很简单。
只需要将每一位上的数字分别转换为对应的三个(对于二进制)或四个(对于十六禁止)二级禁止即可。
示例2:将八禁止数125转换为二禁止和十禁止•二禁止:125 = (001)(010)(101) = 10101011•十禁止:125 = (2B)3.3 十禁止转换为二禁止和八禁止将十禁止数转换为二禁止和八禁止的方法也很简单。
各个进制数的转换方式

各个进制数的转换方式在计算机科学中,我们经常需要处理不同进制数的转换。
以下是各种进制数之间的转换方式:1.二进制(Binary)转十进制(Decimal):这种转换是通过不断乘以2的幂,然后求和来实现的。
例如,二进制数1101(在8位系统中为1101 0000)可以这样转换:1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 13所以,二进制数1101等于十进制数13。
2.十进制转二进制:这种转换是通过不断除以2,然后记录余数来实现的。
例如,十进制数13可以这样转换:13 / 2 = 6 余 16 / 2 = 3 余 03 / 2 = 1 余 12 / 2 = 1 余 01 /2 = 0 余 1然后,从下往上读取这些余数,得到二进制数1101。
3.二进制转十六进制(Hexadecimal):这种转换和二进制转十进制类似,只不过在每一步中,我们乘以的是16的幂,而不是2的幂。
例如,二进制数1101(在8位系统中为1101 0000)可以这样转换:(1 * 8) + (0 * 4) + (0 * 2) + (0 * 1) = 8所以,二进制数1101等于十六进制数8。
4.十六进制转二进制:这种转换是通过不断除以16,然后记录余数来实现的。
例如,十六进制数8可以这样转换:8 / 16 = 0 余 8所以,十六进制数8等于二进制数1000。
5.十进制转十六进制:这种转换是通过不断除以16,然后记录余数来实现的。
例如,十进制数13可以这样转换:13 / 16 = 0 余 7 (即十六进制的7)所以,十进制数13等于十六进制数7。
6.十六进制转十进制:这种转换是通过不断乘以16的幂,然后求和来实现的。
例如,十六进制数7可以这样转换:7 * 16^0 = 7 (即十进制的7)所以,十六进制数7等于十进制数7。
以上就是各种进制数之间的转换方式。
在实际使用中,我们常常会遇到不同进制数的转换问题,特别是在计算机科学和电子工程领域中。
二进制转long规则-概述说明以及解释

二进制转long规则-概述说明以及解释1.引言1.1 概述在计算机科学中,二进制是一种基础的数字系统,它由0和1两个数字组成。
随着计算机技术的发展,我们经常需要在不同的数据类型之间进行转换,其中之一就是将二进制转换为长整型(long)。
长整型是一种用于表示大范围整数的数据类型,通常由32个二进制位或64个二进制位组成。
本文的主要目的是探讨二进制如何转换为长整型,并介绍相应的规则。
在深入研究二进制转long的基本原理之前,我们将先了解一下本文的结构和目的。
本文将首先介绍二进制转long的基本原理,即如何将一个二进制数值映射到对应的长整型数值。
通过了解这些基本原理,读者将能够更好地理解后面讲解的规则。
随后,我们将详细讨论二进制转long的规则。
这些规则描述了在转换过程中需要遵循的步骤和注意事项。
了解这些规则将帮助读者正确地执行二进制转long的操作。
最后,我们将对本文进行总结,并展望二进制转long的应用前景。
虽然在实际编程中,很少直接进行二进制转long的操作,但了解这一过程对于理解计算机内部数据表示方式以及数据类型转换的机制非常重要。
通过阅读本文,读者将能够全面了解二进制转long的基本原理和规则,进而在实际应用中灵活运用。
希望本文能为读者提供有益的指导和参考。
1.2 文章结构文章结构部分的内容应该对整篇文章的框架进行介绍和概括。
可以根据提供的目录内容,描述文章的整体结构如下:文章结构部分内容:本文主要分为引言、正文和结论三个部分组成。
引言部分中,我们将对二进制转long规则进行概述和介绍文章的结构。
包括对二进制转long的概念进行简要说明,并提出文章编写的目的。
正文部分将重点介绍二进制转long的基本原理和规则。
在2.1节中,我们将详细解释二进制转long的基本原理,包括如何将二进制数转换为十进制数,并且将其转换为长整型数据类型。
在2.2节中,我们将详细介绍二进制转long的规则,包括转换过程中需要注意的细节,如符号位的处理和位数溢出等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二进制与各种类型的数据转换
注:下面所说的都和语言无关,不管是c、c++、c#、java、objective-c,都是一样的。
但是不同的语言定义数组的方式不一样,c、c++是这样的:byte temp[],java、c#是这样的:byte []temp。
下面定义数组统一byte []temp方式;
1.基本知识
byte[] temp= {0,0,0,0,0,0,0,15};
在内存中存的是什么
00000000 00000000 00000000 00000000 00000000 00000000 00000000 00001111
如何把一个整数转换为byte[]数组,以一个int整数为例;
int temp = 0x0F070301;
在内存中存放的16进制数据
0x0f x07 0x03 x01
在内存中存放的10进制数据
15 7 3 1
在内存中存放的2进制数据
00001111 00000111 00000011 00000001
2.整数转byte数组
我要把temp = 0x0F070301;转为byte数组是什么意思呢?先看temp转换为byte数组的结果。
byte[] temp1= {0x0F,0x07,0x03,0x01};
转换方法:
int temp3 = 0x0F070301&0xFF
此时temp3 就等于0x01
int temp3 = (0x0F070301>> 8)&0xFF
此时temp3 就等于0x03
依次类推即可得到数组元素的每个值。
3.byte数组转换为int类型
●c、c++的转换方式:
如何把一个byte数组转换为int类型。
这种转换在c和c++中最方便,当然在objective-c可以使用c的代码也很方便。
例如有数组
byte temp1[]= {0x0F,0x07,0x03,0x01};
因为temp1数组的指针,转换方式如下:
int* p_temp1 = (int*)temp1;
int temp1_value = *p_temp1;
此时temp1_value为0x0F070301
●其他语言的转换方式:
在所有语言(c、c++、c#、java、objective-c)中,通用的转换方式为:
byte temp1[]= {0x0F,0x07,0x03,0x01};
tmp0 =emp1[0]
tmp1= temp1[1]
tmp2 = temp1[2]
tmp3 = temp1[3]
tmp3 <<= 0;
tmp2 <<= 8;
tmp1 <<= 16;
tmp0 <<= 24;
tmp5 = tmp0 | tmp1 | tmp2 | tmp3 = 0x0F070301
4.有符号和无符号的概念
在计算机中,可以区分正负类型的数,成为“有符号数”(signed);无正负类型的数(只有整数类型),成为“无符号数”(unsigned)。
简明的说,无符号说就是其所有的位数都用来表示数值的大小,有符号数除最高位来表示数值的正负外(0表示正数;1表示负数),
首先得知道最高位是哪一位?1个字节的类型,如字符类型,最高位是第7位,2个字节的数,最高位是第15位,4个字节的数,最高位是第31位。
不同长度的数值类型,其最高位也就不同,但总是最左边的那位(如下示意)。
字符类型固定是1个字节,所以最高位总是第7位。
(红色为最高位)
单字节数:11111111
双字节数:11111111 11111111
四字节数:11111111 11111111 11111111 11111111
八字节数:11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111 当我们指定一个数是无符号类型时,那么其最高位的1或0,和其它位一样,用来表示该数的大小。
当我们指定一个数量是有符号类型时,此时,最高数称为“符号位”。
为1时,表示该数为负值,为0时表示为正值。
很多语言(比如上面说到的c、c++、c#、objective-c,甚至java)的基本整数类型,都会有一个“无符号”的概念,但是java的“无符号”的概念用的太少了,因为java的所有整数类型(byte、char、short、int、long),只有char类型是“无符号”的。
而我们平时太少用这个类型去表示整数了。
例如java语言:
java中char(无符号)和short(有符号)都是两个字节的。
他们都可以表示一个整数。
char charvalue = 11111111 11111111
short shortvalue = 11111111 11111111
假如定义一个char类型和一个short类型,在内存中都存入上面的二进制。
那么他们的整数值是多少呢?
charvalue = 65536; (正数)
shortvalue=-1; (负数)
char的值范围是(0 ~ 65535),而short的值范围是(-32768~+32767)
如果其他语言给java传了一个“无符号”整数,java程序员应该怎么处理呢?
例如:
其他语言给了一个两个字节的无符号整数:1111111111111111(65535)
java可以定义三种变量存放该值:
char charvalue= 1111111111111111
int intvalue = 0000000000000000 1111111111111111
long longvalue=0000000000000000 0000000000000000 0000000000000000 1111111111111111 上面3个值都表示65535;虽然charvalue的最高为1,当时因为是无符号的,所以可以表示65535,intvalue和longvalue的最高为是0,当时也可以表示65535.
上面都是基本概念,知道二进制在计算机的表示。
java要把一个无符号整数转换为合适的有符号整数,那么只需要通过移位<<和与&操作,即可得到想要的数值。
当然,如果其他语言给了一个两个字节的有符号整数:1111111111111111,java只能定义short来存放该值。
5.大端小端概念
在写tcp协议的过程中,经常会遇到一个大端小端的问题。
这是什么意思呢?假如我们要存一个int 类型的数据,int类型占4个字节。
大端和小端,存放的方式是这样的:
假如:int temp = 15;
temp大端的存放在内存的中的数据是这样的:
temp :00000000 00000000 00000000 00001111
temp小端的存放在内存的中的数据是这样的:
temp :00001111 00000000 00000000 00000000
所谓的大端模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址中;
所谓的小端模式,是指数据的低位保存在内存的低地址中,而数据的高位保存在内存的高地址中。
我们的机器究竟是大端和小端,这是有操作系统和硬件决定的。
