中考数学复习指导:勾股定理中的分类讨论
中考数学专题复习《勾股定理之折叠问题分类讨论、存在性问题》测试卷(附带答案)

中考数学专题复习《勾股定理之折叠问题分类讨论存在性问题》测试卷(附带答案)学校:___________班级:___________姓名:___________考号:___________一 单选题1.如图 ABC 中 90A ∠= 7AB = 24AC = 点D 为边AC 上一点 将ABC 沿BD 折叠后 点A 的对应点A '恰好落在BC 边上 则线段AD 的长为( )A .407B .214C .16825D .3262.如图是一张直角三角形纸片 已知6AC = 10AB = 将纸片沿AD 折叠 使点C 落在AB 边上的点C '处 则折痕AD 长为( ).A .5B .35C .3D .323.已知2OA = 2OB = 将AOB 沿着某直线CD 折叠后如图所示 CD 与x 轴交于点C 与AB 交于点D 则点C 坐标是( )A .()0.4,0B .()0.5,0C .()0.6,0D .()0.7,04.如图 长方形纸片ABCD 中 6AB = 18AD = 将此长方形纸片折叠 使点D 与点B 重合 点C 落在点H 的位置 折痕为EF 则ABE 的面积为( )A .6B .18C .24D .485.如图 在平行四边形ABCD 中 60B ∠=︒ 4AB = 6AD = E 是AB 边的中点 F 是线段BC 上的动点 将EBF 沿EF 所在直线折叠得到EB F ' 连接B D ' 则B D '的最小值是( )A .4B .6C .2D .26.将长方形纸片ABCD 如图折叠 B C 两点恰好重合在AD 边上的同一点P 处折痕分别是MH NG 若90MPN ∠=︒ 3PM = 5MN = 分别记PHM PNG PMN 的面积为1S 2S 3S 则1S 2S 3S 之间的数量关系是 ( )A .312S S S =+B .312322S S S =+C .32155S S S =-D .2123S S S =-7.如图 直角ABC 中 90C ∠=︒ 3AC = 4BC = 将ABC 沿AB 折叠得ABD △ 点C 的对应点为点D 则点D 到BC 的距离为( )A .125B .245C .9625D .125或245 8.如图 在Rt ABC △纸片中 9043A AB AC ∠=︒==,, 将Rt ABC △纸片按图示方式折叠 使点A 恰好落在斜边BC 上的点E 处 BD 为折痕 则下列四个结论:①BD 平分ABC ∠①AD DE = ①DE EC = ①DEC 的周长为4 其中正确的个数有( )A .1B .2C .3D .4二 填空题9.如图 Rt ABC △中 90ACB ∠=︒ 30B ∠=︒ 4AC = 点P 为AB 上一个动点 以PC 为轴折叠APC △得到QPC 点A 的对应点为点Q 当点Q 落在ABC 内部(不包括边)上时 AP 的取值范围为 .10.如图 在平面直角坐标系中 长方形ABCO 的边OC OA 、分别在x 轴 y 轴上 3AB = 点E 在边BC 上 将长方形ABCO 沿AE 折叠 若点B 的对应点F 恰好是边OC 的三等分点 则点E 的坐标是 .11.如图 有一个直角三角形纸片 两直角边18cm AC = 24cm BC = 现将直角边AC 沿直线AD 折叠 使它落在斜边AB 上 且与AE 重合 则BD = cm .12.已知直线l 为长方形ABCD 的对称轴 5AD = 6AB = 点E 为射线DC 上一个动点 把ADE 沿直线AE 折叠 点D 的对应点D 恰好落在对称轴l 上.则点D 到边CD 的距离是 .13.如图 把长方形ABCD 沿直线BD 向上折叠 使点C 落在C '的位置上 BC '交AD 于E 已知4CD = 8BC = 则EC D '的面积为 .三 解答题14.如图是一张直角三角形ABC 纸片 90C ∠=︒ 6AC = 8BC =.(1)在图1中 将直角边AC 沿AD 折叠 使点C 落在斜边AB 上的点E 处 求CD 的长(2)在图2中 将BFG 沿FG 折叠 使点B 与点A 重合 求BF 的长.15.一数学兴趣小组探究勾股定理在折叠中的应用 如图 将一张长方形纸片ABCD 放在平面直角坐标系中 点A 与原点O 重合 顶点B D 分别在x 轴 y 轴上 P 为边CD 上一动点 连接BP 将BCP 沿BP 折叠 点C 落在点C '处.(1)若4AB = 3AD = 如图1 连接BD 当点C '在线段BD 上时 求点P 的坐标.(2)在(1)的条件下如图2 当点P 与点D 重合时 沿BD 将BCD △折叠得BC D '△ DC '与x 轴交于E 点 求BDE 的面积.(3)若8AB = 4BC = 当ADC '为等腰三角形时 求点P 的坐标.16.如图1 ABC 中 90,BAC AB AC ∠=︒= D E 是直线BC 上两动点 且45DAE =︒∠.探究线段BD DE EC 三条线段之间的数量关系:小明的思路是:如图2 将ABD △沿AD 折叠 得ADF △ 连接EF 看能否将三条线段转化到一个三角形中 …请你参照小明的思路 探究并解决下列问题:(1)猜想BD DE EC 三条线段之间的数量关系 并证明(2)如图3 当动点E 在线段BC 上 动点D 运动在线段CB 延长线上时 其它条件不变 (1)中探究的结论是否发生改变?请说明你的猜想并给予证明.17.已知ABC CDE △≌△ 且90B D ∠=∠=︒ 把ABC 和CDE 拼成如图所示的形状 使点B C D 在同一条直线上 若4AB = 3DE =.(1)求AE 的长(2)将ABC 沿AC 折叠 点B 落在点F 处 延长AF 与CE 相交于点G 求FG 的长.18.如图 在ABC 中 90C ∠=︒ 把ABC 沿直线DE 折叠 使ADE 与BDE 重合.(1)若38A ∠=︒ 则CBD ∠的度数为________(2)若6AC = 4BC = 求AD 的长(3)当(0)AB m m ABC =>,△的面积为24m +时 求BCD △的周长.(用含m 的代数式表示)参考答案:1.B2.B3.B4.C5.C6.C7.C8.C9.234AP <<10.25⎛- ⎝⎭或2⎛- ⎝⎭11.1512.1或9/9或113.614.(1)3CD = (2)254BF15.(1)点P 的坐标为5,32⎛⎫ ⎪⎝⎭ (2)7516(3)当ADC '为等腰三角形时 点P 的坐标为()44,或4⎫⎪⎪⎝⎭.16.(1)222DE BD EC =+(2)不变 222DE BD EC =+17.(1)AE =(2)9418.(1)14︒ (2)133AD =(3)BCD △的周长为4m +.。
中考勾股数知识点总结

中考勾股数知识点总结一、勾股定理在讨论勾股数之前,首先需要了解勾股定理。
勾股定理是古希腊数学家毕达哥拉斯在公元前6世纪提出的一个重要定理,它表明在直角三角形中,直角三角形的斜边的平方等于两条直角边的平方之和,即a² + b² = c²。
这个定理对于解决数学和几何问题都有很大的帮助,也为勾股数的研究奠定了基础。
二、勾股数的性质1. 勾股数的分类根据勾股定理,我们可以将勾股数分为两种情况:(1)素勾股数:如果a、b、c互质(即它们的最大公因数为1),则称这组勾股数为素勾股数。
(2)合成勾股数:如果a、b、c不互质(即它们的最大公因数大于1),则称这组勾股数为合成勾股数。
2. 勾股数的性质勾股数有着一些特殊的性质,这些性质对于中考数学的学习和解题都有一定的帮助:(1)勾股数的性质1:一个数的平方如果是勾股数,那么这个数一定是偶数。
这可以通过反证法来证明:假设一个数n的平方是勾股数,且n是奇数,那么n可以表示为2m+1,其中m是整数。
那么n的平方就可以表示为(2m+1)²=4m²+4m+1=2(2m²+2m)+1,这样n的平方就变成了奇数,与勾股数必为偶数的性质相矛盾。
所以一个数的平方如果是勾股数,那么这个数一定是偶数。
(2)勾股数的性质2:3、4、5是最小的一组勾股数。
根据勾股定理,3²+4²=5²,所以3、4、5就是最小的一组勾股数。
这也是勾股数的一个重要性质。
(3)勾股数的性质3:所有的勾股数都可以表示成m²-n²、2mn、m²+n²的形式。
这是勾股数的三角形形式,通过这个公式,我们可以求得无数个勾股数。
三、勾股数的判定方法判定一个数是否是勾股数是中考数学的重要考点之一,下面将介绍几种判定勾股数的方法:1. 枚举法:对于一个较小的数,可以通过暴力枚举的方法判断它是否是勾股数。
勾股定理知识点总结(经典、实用)

第三章、勾股定理 一、知识要点:1、勾股定理勾股定理:直角三角形两直角边的平方和等于斜边的平方。
也就是说:如果直角三角形的两直角边为a 、b ,斜边为c ,那么 a 2 + b 2= c 2。
公式的变形:a 2 = c 2- b 2, b 2= c 2-a 2 。
符号语言:注意:前提一定是直角三角形.a ,b 也可能是斜边,分清斜边直角边.勾股定理的证明 :勾股定理的证明方法很多,常见的的方法是面积相等---根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理勾股定理的证明方法很多,常见的是拼图的方法 常见方法如下: 方法一:4EFGHS S S ∆+=正方形正方形ABCD ,2214()2ab b a c ⨯+-=,化简可证.方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积.四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=方法三:1()()2S a b a b =+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证勾股定理的适用范围 : 勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征。
2、勾股定理的逆定理如果三角形ABC 的三边长分别是a ,b ,c ,且满足a 2 + b 2= c 2,那么三角形ABC 是直角三角形。
这个定理叫做勾股定理的逆定理.该定理在应用时,同学们要注意处理好如下几个要点: ① 已知的条件:某三角形的三条边的长度.②满足的条件:最大边的平方=最小边的平方+中间边的平方.③得到的结论:这个三角形是直角三角形,并且最大边的对角是直角. ④如果不满足条件,就说明这个三角形不是直角三角形。
cb aHG F EDCB A bacbac cabcab a bcc baED CBA(分类讨论,数形结合)最大边的平方<最小边的平方+中间边的平方是锐角三角形 最大边的平方>最小边的平方+中间边的平方是钝角三角形说明:勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时应注意:(1)首先确定最大边,不妨设最长边长为:c ;(2)分别求出c 2与a 2+b 2,判定c 2与a 2+b 2是否具有相等关系,若c 2=a 2+b 2,则△ABC是以∠C 为直角的直角三角形(若c 2>a 2+b 2,则△ABC 是以∠C 为钝角的钝角三角形;若c 2<a 2+b 2,则△ABC 为锐角三角形)。
专题 分类讨论思想在勾股定理中的应用(四大题型)(原卷版)-2024-2025学年八年级数学上册同步
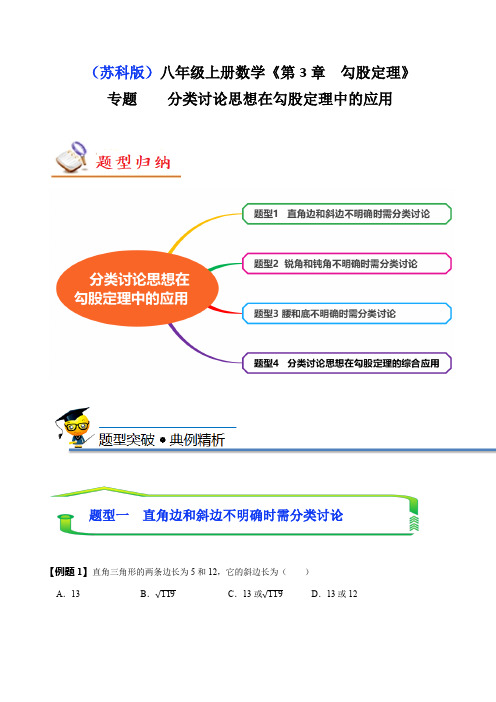
(苏科版)八年级上册数学《第3章 勾股定理》专题 分类讨论思想在勾股定理中的应用【例题1】直角三角形的两条边长为5和12,它的斜边长为( )A .13B .√119 C .13或√119 D .13或12题型一 直角边和斜边不明确时需分类讨论【变式1-1】(2021•滨州模拟)已知直角三角形两边的长分别为3和4,则此三角形的周长为( )A .5B .7+√7C .12D .12或7+√7【变式1-2】(2022秋•肃州区期末)已知直角三角形两边的长分别为3cm ,4cm ,则以第三边为边长的正方形的面积为 .【变式1-3】如图,长方形ABCD 中,AD =BC =6,AB =CD =10.点E 为射线DC 上的一个动点,△ADE 与△AD ′E 关于直线AE 对称,当△AD ′B 为直角三角形时,DE 的长为( )A .2或8B .83或18C .83或2D .2或18【变式1-4】(2022春•绥江县期中)如图,在△ABC 中,AC =5,D 为BC 边上一点,且CD =1,AD =√26,BD =4,点E 是AB 边上的动点,连接DE .(1)求AB 的长;(2)当△BDE 是直角三角形时,求AE 的长.【变式1-5】(2022秋•崇义县月考)在四边形ABCD 中,AB =4,AD =3,BC =12,CD =x ,AB ⊥AD .(1)求BD的长;(2)若△BCD是直角三角形,求x的值.【变式1-6】(2022秋•宛城区校级期末)已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以2cm/s的速度移动,设运动的时间为ts.(1)求BC边的长;(2)当△ABP为直角三角形时,求t的值.题型二锐角和钝角不明确时需分类讨论【例题2】(2022春•兰山区期中)已知△ABC中,AB=17,AC=10,BC边上的高AH=8,则BC的长是()A.21B.15C.6D.21或9【变式2-1】(2021秋•海门市期末)△ABC中,AB=20,AC=13,高AD=12,则△ABC的面积为()A.66B.126C.54或44D.126或66【变式2-2】在△ABC中,AB=17,AC=10,BC边上的高AD=8,求△ABC的周长.【变式2-3】等腰△ABC的腰长AB=AC=10,一腰上的高BD=6,则底边BC=.【变式2-4】△ABC中,AB=AC=5,S△ABC=7.5,则BC的长为.【变式2-5】等腰三角形一腰长为5,一边上的高为3,求底边长.【例题3】(2022秋•南岗区校级期末)在矩形ABCD中,点E在AD边上,△BCE是以BE为一腰的等腰三角形,若AB=4,BC=5,则线段DE的长为.【变式3-1】(2022秋•新昌县校级期中)如图,在等腰△ABC中,AB=CB.AD⊥BC.垂足为D.已知AD=3,CD=1.(1)求AC与AB的长.(2)点P是线段AB上的一动点,当AP为何值时,△ADP为等腰三角形.【变式3-2】(2022秋•禅城区校级月考)已知:如图,有一块Rt△ABC的绿地,量得两直角边AC=8m,BC=6m.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长.题型三腰和底不明确时需分类讨论(1)在图1中,当AB=AD=10m时,求△ABD的周长;(2)在图2中,当BA=BD=10m时,求△ABD的周长;(3)在图3中,当DA=DB时,求△ABD的周长.【变式3-3】(2022秋•大丰区期中)如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC:BC=3:4,动点P从B出发沿射线BC以1cm/s的速度运动,设运动时间为t(s).(1)求BC边的长.(2)当△ABP为等腰三角形时,求t的值.【变式3-4】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.(1)求BC边上的高;(2)若AB=10,①求线段DF的长;②连接AE,当△ABE是等腰三角形时,求a的值.【变式3-5】(2022秋•永春县期末)如图△ABC中,∠ACB=90°,AC=12,BC=5.(1)求AB的长;(2)若动点P从点C开始以每秒1个单位的速度,按C→A→B的路径运动,设运动的时间为t秒,当t为何值时,△BCP为等腰三角形?【变式3-6】(2022春•铁西区期中)如图,△ABC中,∠ABC=90°,AC=20,BC=12.(1)直接写出AB的长度.(2)设点P在AB上,若∠P AC=∠PCA.求AP的长;(3)设点M在AC上,若△MBC为等腰三角形,直接写出AM的长.【变式3-7】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.(1)AC=cm;(2)若点P恰好在AB的垂直平分线上,求此时t的值;(3)在运动过程中,当t为何值时,△ACP是以AC为腰的等腰三角形(直接写出结果)?【变式3-8】(2022春•福田区校级期中)如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B 开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.(1)出发4秒后,求PQ的长;(2)从出发几秒钟后,△PQB第一次能形成等腰三角形?(3)当点Q运动到CA上时,求能使△BCQ是等腰三角形时点Q的运动时间,请直接写出t的值.【变式3-9】(2022秋•南关区校级期末)如图,在△ABC中,∠ABC=90°,AC=13,BA=5,点P从点C出发,以每秒3个单位长度的速度沿折线C﹣A﹣B运动.设点P的运动时间为t(t>0).(1)BC=.(2)求斜边AC上的高线长.(3)①当P在AB上时,AP的长为,t的取值范围是.(用含t的代数式表示)②若点P在∠BCA的角平分线上,则t的值为.(4)在整个运动过程中,直接写出△P AB是以AB为一腰的等腰三角形时t的值.题型四分类讨论思想在勾股定理的综合应用【例题4】(2022春•海淀区校级期中)在Rt△ABC中,∠ACB=90°,AC=BC=1,点Q在直线BC上,且AQ=2,则线段BQ的长为.【变式4-1】(2022秋•南阳期末)如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若动点P 从点A出发,以1cm/s的速度沿折线A﹣C﹣B﹣A运动.设运动时间为t(t>0)s.当点P运动到恰好到点A和点B的距离相等的位置时,t的值为.【变式4-2】(2022春•思明区校级期中)定义:如图,点M、N把线段AB分割成AM、MN、NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.(1)已知M、N把线段AB分割成AM、MN、NB,若AM=1.5,MN=2.5,BN=2,则点M、N是线段AB的勾股分割点吗?请说明理由.(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若AB=24,AM=6,求BN的长.【变式4-3】(2023春•乳山市期末)如图,在△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P 从点B出发沿射线BC以每秒1cm的速度运动,设运动的时间为t秒.(1)若△ABP是以BP为斜边的直角三角形,求t的值;(2)若△ABP是以BP为腰的等腰三角形,求t的值.【变式4-4】如图,△ABC中,∠C=90°,CA=8cm,CB=6cm,D为动点,沿着C→A→B→C的路径运动(再次到达C点则停止运动),点D的运动速度为2cm/秒,设点D运动时间为t秒.(1)当点D在AC上运动时,若DC=BC,则t=;(2)若点D与△ABC某一顶点的连线平分△ABC的周长,求t的值.【变式4-5】(2022秋•姑苏区校级月考)如图1,△ABC中,CD⊥AB于D,且BD;AD:CD=2:3:4.(1)试说明△ABC是等腰三角形;(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时,整个运动都停止,设点M运动的时间为t(秒),若△DMN的边与BC平行,求t的值.【变式4-6】如图,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,AD为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,设点D运动的时间为t秒,速度为每秒2个单位长度.(1)当t为何值时,△CBD是直角三角形;(2)若△CBD是等腰三角形,求t的值.【变式4-7】(2022春•广州期中)在△ABC中,∠ACB=90°,AB=10,BC=6,点P从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C运动.设点P的运动时间为t秒(t>0).(1)求斜边AB 上的高;(2)①当点P 在BC 上时,PC = ;(用含t 的代数式表示)②若点P 在∠BAC 的角平分线上,求t 的值.【变式4-8】(2021秋•青岛期末)已知△ABC 中,∠B =90°,AB =8cm ,BC =6cm ,P 、Q 是△ABC 边上的两个动点,其中点P 从点A 开始沿A →B 方向运动且速度为每秒1cm ,点Q 从点B 开始沿B →C →A 方向运动,在BC 边上的运动速度是每秒2cm ,在AC 边上的运动速度是每秒1.5cm ,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t 秒.(1)出发2秒后,求PQ 的长;(2)当点Q 在边BC 上运动时,t 为何值时,△ACQ 的面积是△ABC 面积的13; (3)当点Q 在边CA 上运动时,t 为何值时,PQ 将△ABC 周长分为23:25两部分.【变式4-9】如图,△ABC 中,BA =BC ,CO ⊥AB 于点O ,AO =4,BO =6.(1)求BC ,AC 的长;(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连接OE.当点D在线段OB上时,若△AOE 是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.。
勾股定理的分类讨论

解析: 由于锐 角三 角 形 的高都 在 形 内 , 钝 角 三角 形 有 的高 在形 外 , 直
角三角 形有 的高与 一条 直角边 重合 ,而 本题 画 出符合 条件 的三 角形 有两
种, 即锐角三 角形 和钝 角三角 形. ( 1 ) 当 D 在 AAB C 的 内部 时 , 如 图3 , 由勾股 定理 ,
高 A D , 则 肋= ÷日 c : 6 , 在R t A A B D q b , 由 勾
C
股定理, 得A D = 、 / , A ' 一 肋々 ‘ = 、 / , 1 一 々 6 ’ = 8 .
( 2 ) 当腰 长 为 1 2 , 底边长为l 0 时, 如 图2 , 在 AA B C中, A B = A C = 1 2 , B C = 1 0 , 作底 边 B C
的 高是 .
解析 : 由于题 中 的 l 0 和1 2 没 有 指 明哪 条边 是腰 、 哪条 边 是底 , 故 需分 两种 情况 讨 论.
( 1 ) 当腰 长 为 1 0 , 底边长为1 2 [ 付, 如 图1 ,
在 AA B C 中, A B - AC = I O , B C = 1 2 , 作底 边 上 的
( 1 ) 当 为斜边 时 , 有3 ‘ + 4 . x = 5 .
( 2 ) 当4 为斜边 时 , 有4 = 3 ‘ 综合 , 得 为5 或、 / 了. 二、 腰、 底 不确 定 时 , 需 分类
. = 、 / 丁.
例2 已知 一个 等 腰 三 角 形 的一 边 长 是 l 0 , 另一 边 长是 l 2 , 则 底边 上
勺 定理
甘
哼江苏 袁 志琴 胡 怀志
分类 讨 论是数 学 中的~种 重要 思 想方 法和 解题 策 略 ,当 一个数 学 问 题 的条件 、 结论不 明确 或会 出现 多种情 况 时 , 就 需 要对 这个 问题 进行 必 要
勾股定理分类讨论思想总结

勾股定理分类讨论思想总结勾股定理分类讨论思想总结勾股定理是几何学中的重要定理之一,也是元代数学家周公瑾发现的。
它表述了在直角三角形中,直角边的平方和等于斜边的平方,即a² + b² = c²。
勾股定理的分类讨论思想是一种运用数学知识进行问题解答的方法,下面我将对其进行总结。
1. 分类思想的基本概念:分类思想是将问题进行分门别类地讨论,运用不同的方法和技巧进行求解。
在勾股定理的分类讨论中,可以根据已知条件的不同进行分类,如根据已知边长的关系、已知角度的关系等。
2. 已知边长的关系:根据已知边长的关系,可以将问题分为已知两直角边求斜边的问题和已知一直角边求另一直角边的问题。
对于已知两直角边求斜边的问题,可以利用勾股定理直接求解,其思路清晰、简单明了。
而对于已知一直角边求另一直角边的问题,则需要运用勾股定理的逆定理,即通过已知边长求出斜边的平方,然后开平方即可得到另一直角边的长度。
3. 已知角度的关系:根据已知角度的关系,可以将问题分为已知一个锐角求另一锐角的问题和已知一个锐角和斜边的关系求其它边长的问题。
对于已知一个锐角求另一锐角的问题,可以利用三角函数的知识,通过求解三角函数值来确定另一锐角的大小。
而对于已知一个锐角和斜边的关系求其它边长的问题,则可以利用勾股定理和三角函数的关系,通过求解三角函数值和代入勾股定理进行计算。
4. 实际问题的应用:勾股定理的分类讨论思想不仅适用于纯粹的数学问题,还可以应用于解决实际问题。
比如在建筑工程中,可以利用勾股定理来确定房屋的斜坡度,计算建筑物的高度和斜边长度等。
在地理测量中,也可以运用勾股定理来测量两点间的距离,确定地图上的位置等。
总之,勾股定理分类讨论思想是一种灵活运用数学知识解决问题的方法。
通过将问题进行分类、分析和讨论,可以选择与问题相适应的解法,提高问题解决的准确性和效率。
同时,勾股定理分类讨论思想的应用也拓宽了勾股定理的实际应用范围,使其成为一种强有力的工具。
勾股定理中的分类讨论

勾股定理中的分类讨论在学习勾股定理时,有时会遇到多种情况,稍不留神就会丢解或造成错解,这就需要我们利用分类讨论思想对各种情况加以分类,并逐类求解,然后综合得解.为帮助同学们解决这类问题,现将勾股定理中需用到分类的问题为同学们分类浅析.一、按直角边、斜边分类例1 如果三条线段的长分别为3cm 、x cm 、5cm ,这三条线段恰好能组成一个直角三角形,那么x 等于________.解:(1)当以3cm 、x cm 为直角边,5cm 为斜边时,有52=32+x 2,x =4;(2)当3cm 、5cm 均为直角边时,有32+52=x 2,x因此,x 为4二、按等腰三角形的腰与底分类例2 在等腰三角形ABC 中,AB =5cm ,BC =6cm ,则△ABC 的面积为________.解:(1)当5cm 为腰,6cm 为底时,则AB =AC =5cm ,如图1.过A 点作AD ⊥BC ,所以CD =3,在Rt △ACD 中,AD 2=AC 2-CD 2,所以AD 2=52-32,AD =4,因此S △ABC =12×6×4=12cm 2. (2)当6cm 为腰,5cm 为底时,则BC =AC =6cm ,如图2.过C 点作CD ⊥AB 于点D ,所以AD =52,在Rt △ACD 中,CD 2=AC 2-AD 2,所以222562CD ⎛⎫=- ⎪⎝⎭,CD ,因此1522ABC S =⨯⨯=△2.所以△ABC 的面积为12cm 2cm 2. 三、按高的位置分类例3 在△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为________.解:(1)当△ABC 的高在三角形内时,如图3.由题意可知,BD 2=AB 2-AD 2,所以BD 2=152-122,BD =9,CD 2=AC 2-AD 2,所以CD 2=132-122,CD =5,所以BC =9+5=14,因此△ABC 的周长为9+5+15+13=42.(2)当△ABC 的高在三角形外时,如图4.由题意可知,BD 2=AB 2-AD 2,所以BD 2=152-122,BD =9,CD 2=AC 2-AD 2,所以CD 2=132-122,CD =5,所以BC =9-5=4,因此△ABC 的周长为4+15+13=32.综上所述△ABC 的周长为32或42.四、按展开方式的不同分类例4 如图5是一个放置雕塑的长方体底座,AB =12米,BC =2米,BB ′=3米,一只蚂蚁从点A 出发,以2厘米/秒的速度沿长方体表面爬到C ′至少需( )A .11052分钟 B .5106分钟 C .1132分钟 D .10分钟 解:2厘米/秒=0.02米/秒.(1)将正面与右面展开,如图6.由两点之间,线段最短及勾股定理可知路径一:AC ′2=AC 2+CC ′2=142+32=205;(2)将左面与上面展开,如图7.由勾股定理知路径二:AC ′2=AD 2+C ′D 2=152+22=229;(3)将正面与上面展开,如图8.由勾股定理知路径三:AC′2=AB2+BC′2=122+52=169.因为229>205>169,所以路径二AC′>路径一AC′>路径三AC′,因此按路径三的方式0.02=650秒,即5106分钟,故应选B.。
勾股定理知识点+对应类型

勾股定理一、勾股定理:1、勾股定理定义:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾:直角三角形较短的直角边股:直角三角形较长的直角边弦:斜边勾股定理的逆定理:如果三角形的三边长a,b,c有下面关系:a2+b2=c2,那么这个三角形是直角三角形。
2. 勾股数:满足a2+b2=c2的三个正整数叫做勾股数(注意:若a,b,c、为勾股数,那么ka,kb,kc同样也是勾股数组。
)*附:常见勾股数:3,4,5; 6,8,10; 9,12,15; 5,12,133. 判断直角三角形:如果三角形的三边长a、b、c满足a2+b2=c2 ,那么这个三角形是直角三角形。
(经典直角三角形:勾三、股四、弦五)其他方法:(1)有一个角为90°的三角形是直角三角形。
(2)有两个角互余的三角形是直角三角形。
用它判断三角形是否为直角三角形的一般步骤是:(1)确定最大边(不妨设为c);(2)若c2=a2+b2,则△ABC是以∠C为直角的三角形;若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)4.注意:(1)直角三角形斜边上的中线等于斜边的一半(2)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
(3)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于30°。
5. 勾股定理的作用:(1)已知直角三角形的两边求第三边。
(2)已知直角三角形的一边,求另两边的关系。
(3)用于证明线段平方关系的问题。
(4)利用勾股定理,作出长为n的线段常见题型(一)结合三角形:1.已知∆ABC 的三边a 、b 、c 满足0)()(22=-+-c b b a ,则∆ABC 为 三角形2.在∆ABC 中,AB=13,AC=15,高AD=12,则BC 的长为(二)、实际应用:1. 梯子滑动问题:(1)一架长2.5m 的梯子,斜立在一竖起的墙上,梯子底端距离墙底0.7m (如图),如果梯子的顶端沿墙下滑0.4m ,那么梯子底端将向左滑动 米(2)如图,一个长为10米的梯子,斜靠在墙面上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离 1米,(填“大于”,“等于”,或“小于”)(3)如图,梯子AB 斜靠在墙面上,AC ⊥BC ,AC=BC ,当梯子的顶端A 沿AC 方向下滑x 米时,梯足B 沿CB 方向滑动y 米,则x 与y 的大小关系是( ) A. y x = B. y x > C. y x < D. 不能确定(4)小明想知道学校旗杆的高度,他发现旗杆上的绳子吹到地面上还多1 m ,当他把绳子的下端拉开5米后,发现绳子下端刚好触到地面,试问旗杆的高度为 米86ACB2. 直角边与斜边和斜边上的高的关系:直角三角形两直角边长为a ,b ,斜边上的高为h ,则下列式子总能成立的是( ) A. 2b ab = B. 2222h b a =+ C. h b a 111=+ D. 222111hb a =+ 3. 爬行距离最短问题:1.如图,一个无盖的正方体盒子的棱长为10cm ,得到1C 处有一只昆虫甲,在盒子的内部有一只昆虫乙(盒壁的 忽略不计)(1)假设昆虫甲在顶点1C 处静止不动,如图a ,在盒子的内部我们先取棱1BB 的中点E ,再连结AE 、1EC ,昆虫乙如果沿途径1C E A →→爬行,那么可以在最短的时间内捕捉到昆虫甲,仔细体会其中的道理,并在图b 中画一条路径,使昆虫乙从顶点A 沿这条路爬行,同样可以在最短的时间内捕捉到昆虫甲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理中的分类讨论
在学习勾股定理时,有时会遇到多种情况,稍不留神就会丢解或造成错解,这就需要我们利用分类讨论思想对各种情况加以分类,并逐类求解,然后综合得解.为帮助同学们解决这类问题,现将勾股定理中需用到分类的问题为同学们分类浅析.
一、按直角边、斜边分类
例1 如果三条线段的长分别为3cm 、x cm 、5cm ,这三条线段恰好能组成一个直角三角形,那么x 等于________.
解:(1)当以3cm 、x cm 为直角边,5cm 为斜边时,有52=32+x 2,x =4;
(2)当3cm 、5cm 均为直角边时,有32+52=x 2,x
因此,x 为4
二、按等腰三角形的腰与底分类
例2 在等腰三角形ABC 中,AB =5cm ,BC =6cm ,则△ABC 的面积为________.
解:(1)当5cm 为腰,6cm 为底时,则AB =AC =5cm ,如图1.过A 点作AD ⊥BC ,所以CD =3,在Rt △ACD 中,AD 2=AC 2-CD 2,所以AD 2=52-32,AD =4,因此S △ABC =12
×6×4=12cm 2. (2)当6cm 为腰,5cm 为底时,则BC =AC =6cm ,如图2.过C 点作CD ⊥AB 于点
D ,所以AD =52,在Rt △ACD 中,CD 2=AC 2-AD 2,所以222562CD ⎛⎫=- ⎪⎝⎭
,CD ,
因此1522ABC S =⨯⨯=△2.
所以△ABC 的面积为12cm 2cm 2. 三、按高的位置分类
例3 在△ABC 中,AB =15,AC =13,高AD =12,则△ABC 的周长为________.
解:(1)当△ABC 的高在三角形内时,如图3.由题意可知,BD 2=AB 2-AD 2,所以BD 2=152-122,BD =9,CD 2=AC 2-AD 2,所以CD 2=132-122,CD =5,所以BC =9+5=14,因此△ABC 的周长为9+5+15+13=42.
(2)当△ABC 的高在三角形外时,如图4.由题意可知,BD 2=AB 2-AD 2,所以BD 2=152-122,BD =9,CD 2=AC 2-AD 2,所以CD 2=132-122,CD =5,所以BC =9-5=4,因此△ABC 的周长为4+15+13=32.
综上所述△ABC 的周长为32或42.
四、按展开方式的不同分类
例4 如图5是一个放置雕塑的长方体底座,AB =12米,
BC =2米,BB ′=3米,一只蚂蚁从点A 出发,以2厘米/秒的
速度沿长方体表面爬到C ′至少需( )
A .1105
2分钟 B .5106分钟 C .1132
分钟 D .10分钟 解:2厘米/秒=0.02米/秒.
(1)将正面与右面展开,如图6.
由两点之间,线段最短及勾股定理可知路径一:AC ′2=AC 2+CC ′2=142+32=205;
(2)将左面与上面展开,如图7.
由勾股定理知路径二:AC ′2=AD 2+C ′D 2=152+22=229;
(3)将正面与上面展开,如图8.
由勾股定理知路径三:AC′2=AB2+BC′2=122+52=169.
因为229>205>169,所以路径二AC′>路径一AC′>路径三AC′,因此按路径三的方式
0.02=650秒,即
5
10
6
分钟,故应选B.。
