安徽省怀远三中2009届第五次月考数学理科试题
安徽省怀远三中2009届高三第二学期第六次月考文科2009.2.8

7 8 994 4 6 4 7 3安徽省怀远三中2009届高三第二学期第六次月考数学(文科)试题2009.2、8注意:1.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),本试卷满分为150分,考试时间为120分钟。
2.考试过程中不得使用计算器。
3.所有答案均须写在答卷纸上,写在试卷上无效。
第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集{}4,3,2,1,0=U ,{}4,3,0=A ,{}3,1=B ,则B A C U ⋃)(=( ▲ ) A .{2} B .{1,2,3} C .{1,3} D .{0,1,2,3,4} 2.要得到函数)3sin(π-=x y 的图象,只需将函数x y sin =的图象( ▲ )A.向左平行移动3π个单位 B.向右平行移动3π个单位 C.向左平行移动6π个单位 D.向右平行移动6π个单位3.若命题“P Q ∨”与“P Q ∧”中一真一假,则可能是( ▲ )A .P 真Q 假B .P 真Q 真C .P ⌝真Q 假 D .P 假Q ⌝真4. "3)(""2"2有两个零点函数是=x mx x f m ++-=的( ▲ )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 5.在三棱锥的六条棱中任意选择两条,则这两条棱是一对异面直线的概率为( ▲ )A .201 B .151 C .51 D .61 6.若双曲线)0,0(12222>>=-b a by a x 的两个顶点三等分焦距,则该双曲线的渐近线方程是( ▲ ) A .x y 22±= B .x y 2±= C .x y 3±= D .x y 22±= 7.某校举行2008年元旦汇演,七位评委为某班的小品打出的分数如下茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为 ( ▲ )A .84,4.84B .84,1.6C .85,1.6D .85,4 8.m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:① 若γαβα//,//,则γβ//; ②若αβα//,m ⊥,则β⊥m ;③ 若βα//,m m ⊥,则βα⊥; ④若α⊂n n m ,//,则α//m .其中真命题的序号是 ( ▲ ) A .①③ B .①④ C .②③ D .②④9. 已知向量a ,b ,c 满足1,2,4===a b c ,且a ,b ,c 两两夹角均为120,则=a +b+c( )A .7B .7C .35D .7或710、 在平面直角坐标系中, 不等式组⎩⎨⎧x +y ≥0x -y +4≥0x ≤a(a ∈[-2,2])表示的平面区域面积是f(a), 那么f(a)的图像可能是( ▲ )A .B .C .D .11、关于x 的不等式22cos lg(1)cos lg(1)x x x x +-<+-的解集为 ( )A .(—1,1)B .(,1)(1,)22ππ--C .(,)22ππ-D .(0,1)12.如果数列}{n a 满足:首项⎩⎨⎧+==+,,2,,2,111为偶数为奇数n a n a a a nn n 那么下列说法正确的是( ▲ )A .该数列的奇数项 ,,,531a a a 成等比数列,偶数项 ,,,642a a a 成等差数列B .该数列的奇数项 ,,,531a a a 成等差数列,偶数项 ,,,642a a a 成等比数列C .该数列的奇数项 ,,,531a a a 分别加4后构成一个公比为2的等比数列D .该数列的偶数项 ,,,642a a a 分别加4后构成一个公比为2的等比数列第Ⅱ卷二、填空题(本大题共7小题,每小题4分,共28分,把答案填在答题纸上)13. 设i 为虚数单位,则41i i +⎛⎫= ⎪⎝⎭__▲__。
安徽省怀远三中2009届高三第一次月考试卷数学理科

安徽省怀远三中2009届高三第一次月考试卷数学(理科)本试卷共22小题,满分150分.考试用时120分钟.第 Ⅰ 卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合{}{}{}1,2,3,4,5,1,2,3,2,3,4U A B ===,则=)(B A C U ( ) A 、{}2,3 B 、{}1,4,5 C 、{}4,5 D 、{}1,52、下列函数中,在其定义域内既是奇函数又是减函数的是( )A 、);()21(R x y x ∈=B 、);0(1≠=x xy C 、y=x (x ∈R ); D 、).(3R x x y ∈-=3、某个命题与正整数有关,若n=k (k ∈N +)时,命题成立,那么可推出当n=k+1时,该命题也成立。
现已知当n=5时,该命题不成立,那么可以推得( )A .当n=6时,该命题不成立B .当n=6时,该命题成立C .当n=4时,该命题不成立D .当n=4时,该命题成立4、若13(1)ln 2ln ln x e a x b x c x -∈===,,,,,则( )A .a <b <cB .c <a <bC . b <a <cD . b <c <a5、函数y=213log (3)x x -的单调递增区间为 。
A 、(3,)+∞B 、3[,)2+∞C 、3(,]2-∞ D 、(,0)-∞6、 “18a =”是“对任意的正数x ,21ax x+≥”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件 7.已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( ) A.(0,11a ) B. (0,12a ) C. (0,31a ) D. (0,32a ) 8、已知函数2,()2,x x f x x x +⎧=⎨-+>≤⎩,则不等式2()f x x ≥的解集是 A 、[1,1]- B 、[2,2]- C 、[2,1]- D 、[1,2]- 9.若121212120,01a a b b a a b b <<<<+=+=,且,则下列代数式中值最大的是A . 1221a b a b +B .1212a a bb +C .1122a b a b +D .1210、命题“0x R ∃∈,3210x x -+>”的否定是A .0x R ∀∈,3210x x -+≤B .0x R ∃∈,3210x x -+<C .0x R ∃∈,3210x x -+≤D .不存在0x R ∈,3210x x -+>11、定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++(x y ∈R ,),(1)2f =,则(3)f -等于( )A .2B .3C .6D .912、已知定义在R 上的函数()f x 的图像关于点304⎛⎫- ⎪⎝⎭,对称,且满足3()()2f x f x =-+,(1)1f -=,(0)2f =-,则(1)(2)(2009)f f f +++ 的值为A .2-B .0C .1D .2二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在各题中的横线上13、已知,,x y z R +∈,230x y z -+=,则2y xz的最小值14、函数2log x y -=的定义域是 .15、已知a ∈R ,若关于x 的方程2104x x a a ++-+=有实根,则a 的取值范围是 .16.若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围 ___三、解答题:本大题共6小题,共74分,解答应写出文字说明、演算步骤或推证过程。
2009年安徽省高考数学试卷(理科)及答案
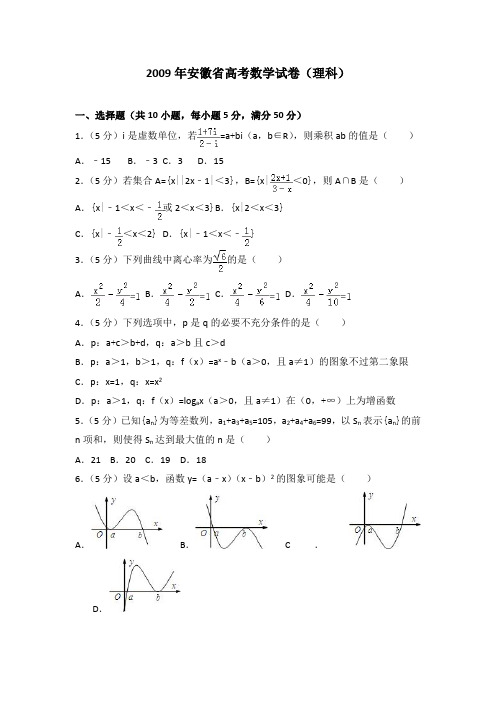
2009年安徽省高考数学试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1.(5分)i是虚数单位,若=a+bi(a,b∈R),则乘积ab的值是()A.﹣15 B.﹣3 C.3 D.152.(5分)若集合A={x||2x﹣1|<3},B={x|<0},则A∩B是()A.{x|﹣1<x<﹣或2<x<3}B.{x|2<x<3}C.{x|﹣<x<2}D.{x|﹣1<x<﹣}3.(5分)下列曲线中离心率为的是()A.B.C.D.4.(5分)下列选项中,p是q的必要不充分条件的是()A.p:a+c>b+d,q:a>b且c>dB.p:a>1,b>1,q:f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限C.p:x=1,q:x=x2D.p:a>1,q:f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数5.(5分)已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以S n表示{a n}的前n项和,则使得S n达到最大值的n是()A.21 B.20 C.19 D.186.(5分)设a<b,函数y=(a﹣x)(x﹣b)2的图象可能是()A.B.C.D.7.(5分)若不等式组所表示的平面区域被直线y=kx+分为面积相等的两部分,则k的值是()A.B.C.D.8.(5分)已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z9.(5分)已知函数f(x)在R上满足f(1+x)=2f(1﹣x)﹣x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是()A.x﹣y﹣2=0 B.x﹣y=0 C.3x+y﹣2=0 D.3x﹣y﹣2=010.(5分)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()A.B.C.D.二、填空题(共5小题,每小题5分,满分20分)11.(5分)若随机变量X~N(μ,σ2),则P(X≤μ)=.12.以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为(ρ∈R),它与曲线(α为参数)相交于两点A和B,则|AB|=.13.(5分)程序框图(即算法流程图)如图所示,其输出结果是.14.(5分)给定两个长度为1的平面向量和,它们的夹角为120°.如图所示,点C在以O为圆心,以1半径的圆弧AB上变动.若=x+y,其中x,y∈R,则x+y的最大值是.15.(5分)对于四面体ABCD,下列命题正确的序号是.①相对棱AB与CD所在的直线异面;②由顶点A作四面体的高,其垂足是△BCD的三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高所在直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.三、解答题(共6小题,满分75分)16.(12分)在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.17.(12分)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A 到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是.同样也假定D受A、B和C感染的概率都是.在这种假定之下,B、C、D中直接受A感染的人数x就是一个随机变量.写出x的分布列(不要求写出计算过程),并求x的均值(即数学期望).18.(13分)如图所示,四棱锥F﹣ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.(1)求二面角B﹣AF﹣D的大小;(2)求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积.19.(12分)已知函数f(x)=x﹣+a(2﹣lnx),(a>0),讨论f(x)的单调性.20.(13分)点P(x0,y0)在椭圆(a>b>0)上,x0=acosβ,y0=bsinβ,0<.直线l2与直线l1:垂直,O为坐标原点,直线OP的倾斜角为α,直线l2的倾斜角为γ(Ⅰ)证明:点P是椭圆与直线l1的唯一交点;(Ⅱ)证明:tanα,tanβ,tanγ构成等比数列.21.(13分)首项为正数的数列{a n}满足a n+1=(a n2+3),n∈N+.(1)证明:若a1为奇数,则对一切n≥2,a n都是奇数;(2)若对一切n∈N+都有a n+1>a n,求a1的取值范围.2009年安徽省高考数学试卷(理科)参考答案与试题解析一、选择题(共10小题,每小题5分,满分50分)1.(5分)(2009•安徽)i是虚数单位,若=a+bi(a,b∈R),则乘积ab的值是()A.﹣15 B.﹣3 C.3 D.15【分析】先根据两个复数相除的除法法则化简,再依据两个复数相等的充要条件求出a和b的值,即得乘积ab的值.【解答】解:∵===﹣1+3i=a+bi,∴a=﹣1,b=3,∴ab=﹣1×3=﹣3.故选B.2.(5分)(2009•安徽)若集合A={x||2x﹣1|<3},B={x|<0},则A∩B 是()A.{x|﹣1<x<﹣或2<x<3}B.{x|2<x<3}C.{x|﹣<x<2}D.{x|﹣1<x<﹣}【分析】集合A中的绝对值不等式可利用讨论2x﹣1的正负得到一个不等式组,求出不等式组的解集即可得到集合A;集合B中的其他不等式可转化为2x+1与x ﹣3同号即同时为正或同时为负得到两个不等式组,分别求出解集即可得到集合B,求出两集合的交集即可.【解答】解:∵|2x﹣1|<3,∴﹣3<2x﹣1<3,即,∴﹣1<x<2,又∵<0,∴(2x+1)(x﹣3)>0,即或,∴x>3或x<﹣,∴A∩B={x|﹣1<x<﹣}.故选D3.(5分)(2009•安徽)下列曲线中离心率为的是()A.B.C.D.【分析】通过验证法可得双曲线的方程为时,.【解答】解:选项A中a=,b=2,c==,e=排除.选项B中a=2,c=,则e=符合题意选项C中a=2,c=,则e=不符合题意选项D中a=2,c=则e=,不符合题意故选B4.(5分)(2009•安徽)下列选项中,p是q的必要不充分条件的是()A.p:a+c>b+d,q:a>b且c>dB.p:a>1,b>1,q:f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限C.p:x=1,q:x=x2D.p:a>1,q:f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数【分析】由题意根据必要条件、充分条件和充要条件的定义对ABCD四个选项进行一一判断,从而求解.【解答】解:A、∵q:a>b且c>d,∴a+c>b+d,∴q⇒p,但p推不出q,p 是q的必要不充分条件,故A正确;B、∵p:a>1,b>1,∴f(x)=a x﹣b(a>0,且a≠1)的图象不过第二象限,但若b=1,a>1时f(x)的图象也不过第二象限,q推不出p,∴p是q的充分不必要条件,故B错误;C、∵x=1,∴x=x2,但当x=0时,x=x2,也成立,q推不出p,∴p是q的充分不必要条件,故C错误;D、∵a>1,∴f(x)=log a x(a>0,且a≠1)在(0,+∞)上为增函数,p是q 的充要条件,故D错误;故选A.5.(5分)(2009•安徽)已知{a n}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以S n表示{a n}的前n项和,则使得S n达到最大值的n是()A.21 B.20 C.19 D.18【分析】写出前n项和的函数解析式,再求此式的最值是最直观的思路,但注意n取正整数这一条件.【解答】解:设{a n}的公差为d,由题意得a1+a3+a5=a1+a1+2d+a1+4d=105,即a1+2d=35,①a2+a4+a6=a1+d+a1+3d+a1+5d=99,即a1+3d=33,②由①②联立得a1=39,d=﹣2,∴S n=39n+×(﹣2)=﹣n2+40n=﹣(n﹣20)2+400,故当n=20时,S n达到最大值400.故选:B.6.(5分)(2009•安徽)设a<b,函数y=(a﹣x)(x﹣b)2的图象可能是()A.B.C.D.【分析】根据所给函数式的特点,知函数值的符号取决于x的值与a的值的大小关系,当x≥a时,y≤0,当x≤a时,y≥0,据此即可解决问题.【解答】解:∵y=(a﹣x)(x﹣b)2∴当x≥a时,y≤0,故可排除A、D;又当x≤a时,y≥0,故可排除C;故选B.7.(5分)(2009•安徽)若不等式组所表示的平面区域被直线y=kx+分为面积相等的两部分,则k的值是()A.B.C.D.【分析】先根据约束条件:,画出可行域,求出可行域顶点的坐标,再利用几何意义求面积即可.【解答】解:满足约束条件:,平面区域如图示:由图可知,直线恒经过点A(0,),当直线再经过BC的中点D (,)时,平面区域被直线分为面积相等的两部分,当x=,y=时,代入直线的方程得:k=,故选A.8.(5分)(2009•安徽)已知函数f(x)=sinwx+coswx(w>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间是()A.[kπ﹣,kπ+],k∈Z B.[kπ+,kπ+],k∈ZC.[kπ﹣,kπ+],k∈Z D.[kπ+,kπ+],k∈Z【分析】先把函数化成y=Asin(ωx+φ)的形式,再根据三角函数单调区间的求法可得答案.【解答】解:f(x)=sinwx+coswx=2sin(wx+),(w>0).∵f(x)的图象与直线y=2的两个相邻交点的距离等于π,恰好是f(x)的一个周期,∴=π,w=2.f(x)=2sin(2x+).故其单调增区间应满足2kπ﹣≤2x+≤2kπ+,k∈Z.kπ﹣≤x≤kπ+,故选C.9.(5分)(2009•安徽)已知函数f(x)在R上满足f(1+x)=2f(1﹣x)﹣x2+3x+1,则曲线y=f(x)在点(1,f(1))处的切线方程是()A.x﹣y﹣2=0 B.x﹣y=0 C.3x+y﹣2=0 D.3x﹣y﹣2=0【分析】对等式两边进行求导数,通过赋值求切线斜率;对等式赋值求切点坐标;据点斜式写出直线方程.【解答】解:∵f(1+x)=2f(1﹣x)﹣x2+3x+1∴f′(1+x)=﹣2f′(1﹣x)﹣2x+3∴f′(1)=﹣2f′(1)+3∴f′(1)=1f(1+x)=2f(1﹣x)﹣x2+3x+1∴f(1)=2f(1)+1∴f(1)=﹣1∴切线方程为:y+1=x﹣1即x﹣y﹣2=0故选A10.(5分)(2009•安徽)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于()A.B.C.D.【分析】先用组合数公式求出甲乙从这6个点中任意选两个点连成直线的条数共有C62,再用分步计数原理求出甲乙从中任选一条共有225种,利用正八面体找出相互平行但不重合共有共12对,代入古典概型的概率公式求解.【解答】解:甲从这6个点中任意选两个点连成直线,共有C62=15条,乙也从这6个点中任意选两个点连成直线,共有C62=15条,甲乙从中任选一条共有15×15=225种不同取法,因正方体6个面的中心构成一个正八面体,有六对相互平行但不重合的直线,则甲乙两人所得直线相互平行但不重合共有12对,这是一个古典概型,所以所求概率为=,故选D.二、填空题(共5小题,每小题5分,满分20分)11.(5分)(2009•安徽)若随机变量X~N(μ,σ2),则P(X≤μ)=.【分析】由正态分布的图象规律知,其在x=μ左侧一半的概率为,故得P(ζ≤μ)的值.【解答】解:∵ζ服从正态分布N(μ,σ2),根据正态密度曲线的对称性可得∴曲线关于x=μ对称,P(X≤μ)=选填:.12.(2009•安徽)以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为(ρ∈R),它与曲线(α为参数)相交于两点A和B,则|AB|=.【分析】把参数方程、极坐标方程化为直角坐标方程,求出弦心距,再利用弦长公式求得弦长|AB|的值.【解答】解:直线的极坐标方程为(ρ∈R),化为直角坐标方程为x﹣y=0.曲线(α为参数)的普通方程为(x﹣1)2+(y﹣2)2=4,表示以(1,2)为圆心,半径等于2的圆.求得弦心距d==,故弦长为2=2=,故答案为.13.(5分)(2009•安徽)程序框图(即算法流程图)如图所示,其输出结果是127.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算a值,并输出满足条件a>100的第一个a值,模拟程序的运行过程,用表格将程序运行过程中变量a的值的变化情况进行分析,不难给出答案.【解答】解:程序在运行过程中各变量的值如下表示:a 是否继续循环循环前1/第一圈 3 是第二圈7 是第三圈15 是第四圈31 是第五圈63 是第六圈127 否故最后输出的a值为:127故答案为:12714.(5分)(2009•安徽)给定两个长度为1的平面向量和,它们的夹角为120°.如图所示,点C在以O为圆心,以1半径的圆弧AB上变动.若=x+y,其中x,y∈R,则x+y的最大值是2.【分析】根据题意,建立坐标系,设出A,B点的坐标,并设∠AOC=α,则向量,且=x+y,由向量相等,得x,y的值,从而求得x+y 的最值.【解答】解:建立如图所示的坐标系,则A(1,0),B(cos120°,sin120°),即B(﹣,).设∠AOC=α,则=(cosα,sinα).∵=x+y=(x,0)+(﹣,y)=(cosα,sinα);则,解得,∴x+y=sinα+cosα=2sin(α+30°).∵0°≤α≤120°.∴30°≤α+30°≤150°.∴x+y有最大值2,当α=60°时取最大值2.答案:215.(5分)(2009•安徽)对于四面体ABCD,下列命题正确的序号是①④⑤.①相对棱AB与CD所在的直线异面;②由顶点A作四面体的高,其垂足是△BCD的三条高线的交点;③若分别作△ABC和△ABD的边AB上的高,则这两条高所在直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点;⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.【分析】①根据三棱锥的结构特征判断.②根据对棱不一定相互垂直判断.③可由正四面体时来判断.④由棱中点两两连接构成平行四边形判断.⑤根据两边之和大于第三边判断.【解答】解:①根据三棱锥的结构特征知正确.②因为只有对棱相互垂直才行,所以不一定,不正确.③若分别作△ABC和△ABD的边AB上的高,若是正四面体时,则两直线相交,不正确.④因为相对棱中点两两连接构成平行四边形,而对棱的中点的连接正是平行四边形的对角线,所以三条线段相交于一点,故正确.⑤设图中CD是最长边.BC+BD>CD,AC+AD>CD若AC+BC≤CD 且AD+BD≤CD则AC+AD+BC+BD≤CD+CD,矛盾则命题成立.故答案为:①④⑤三、解答题(共6小题,满分75分)16.(12分)(2009•安徽)在△ABC中,sin(C﹣A)=1,sinB=.(Ⅰ)求sinA的值;(Ⅱ)设AC=,求△ABC的面积.【分析】(I)利用sin(C﹣A)=1,求出A,C关系,通过三角形内角和结合sinB=,求出sinA的值;(II)通过正弦定理,利用(I)及AC=,求出BC,求出sinC,然后求△ABC 的面积.【解答】解:(Ⅰ)因为sin(C﹣A)=1,所以,且C+A=π﹣B,∴,∴,∴,又sinA>0,∴(Ⅱ)如图,由正弦定理得∴,又sinC=sin(A+B)=sinAcosB+cosAsinB=∴17.(12分)(2009•安徽)某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是.同样也假定D受A、B和C感染的概率都是.在这种假定之下,B、C、D中直接受A感染的人数x 就是一个随机变量.写出x的分布列(不要求写出计算过程),并求x的均值(即数学期望).【分析】由题意知X的可能取值为1,2,3,分别求出相应的概率,由此能求出x的分布列和x的均值.【解答】解:由题意知X的可能取值为1,2,3,随机变量X的分布列是X123PX的均值为EX=1×+2×+3×=.18.(13分)(2009•安徽)如图所示,四棱锥F﹣ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.(1)求二面角B﹣AF﹣D的大小;(2)求四棱锥E﹣ABCD与四棱锥F﹣ABCD公共部分的体积.【分析】(1)连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG,根据定义可知∠BGD为二面角B﹣AF﹣D的平面角,在三角形BGD 中求出此角即可;(2)连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E﹣ABCD 与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD,过H作HP⊥平面ABCD,P•HP求解即可.为垂足,然后求出HP,利用体积公式V=S菱形ABCD【解答】解:(1)解:连接AC、BD交于菱形的中心O,过O作OG⊥AF,G为垂足,连接BG、DG.由BD⊥AC,BD⊥CF得BD⊥平面ACF,故BD⊥AF.于是AF⊥平面BGD,所以BG⊥AF,DG⊥AF,∠BGD为二面角B﹣AF﹣D的平面角.由FC⊥AC,FC=AC=2,得∠FAC=,OG=.由OB⊥OG,OB=OD=,得∠BGD=2∠BGO=.(2)解:连接EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E﹣ABCD与四棱锥F﹣ABCD的公共部分为四棱锥H﹣ABCD.过H作HP⊥平面ABCD,P为垂足.因为EA⊥平面ABCD,FC⊥平面ABCD,所以平面ACEF⊥平面ABCD,从而P∈AC,HP⊥AC.由+=+=1,得HP=.=AC•BD=,又因为S菱形ABCD故四棱锥H﹣ABCD的体积V=S•HP=.菱形ABCD19.(12分)(2009•安徽)已知函数f(x)=x﹣+a(2﹣lnx),(a>0),讨论f (x)的单调性.【分析】先求出函数的定义域,然后求出导函数,设g(x)=x2﹣ax+2,二次方程g(x)=0的判别式△=a2﹣8,然后讨论△的正负,再进一步考虑导函数的符号,从而求出函数的单调区间.【解答】解:f(x)的定义域是(0,+∞),.设g(x)=x2﹣ax+2,二次方程g(x)=0的判别式△=a2﹣8.①当△=a2﹣8<0,即时,对一切x>0都有f′(x)>0,此时f(x)在(0,+∞)上是增函数.②当△=a2﹣8=0,即时,仅对有f′(x)=0,对其余的x>0都有f′(x)>0,此时f(x)在(0,+∞)上也是增函数.③当△=a2﹣8>0,即时,方程g(x)=0有两个不同的实根,,0<x1<x2.x(0,x1)x1(x1,x2)x2(x2,+∞)f'(x)+0_0+f(x)单调递增↗极大单调递减↘极小单调递增此时f(x)在上单调递增,在是上单调递减,在上单调递增.20.(13分)(2009•安徽)点P(x0,y0)在椭圆(a>b>0)上,x0=acosβ,y0=bsinβ,0<.直线l2与直线l1:垂直,O为坐标原点,直线OP的倾斜角为α,直线l2的倾斜角为γ(Ⅰ)证明:点P是椭圆与直线l1的唯一交点;(Ⅱ)证明:tanα,tanβ,tanγ构成等比数列.【分析】(Ⅰ)由,得y=,从而x=acosβ,由此能证明直线l1与椭圆有唯一交点P.(Ⅱ)tanα==tanβ,由此得ta nαtanγ=tan2β≠0,从而能证明tanα,tanβ,tanγ构成等比数列.【解答】解:(Ⅰ)由,得y=,代入椭圆,得,将,代入上式,得x2﹣2acosβx+a2cos2β=0,从而x=acosβ,∴有唯一解,即直线l1与椭圆有唯一交点P.(Ⅱ)tanα==tanβ,l1的斜率为tan=,由此得tanαtanγ=tan2β≠0,∴tanα,tanβ,tanγ构成等比数列.21.(13分)(2009•安徽)首项为正数的数列{a n}满足a n+1=(a n2+3),n∈N+.(1)证明:若a1为奇数,则对一切n≥2,a n都是奇数;(2)若对一切n∈N+都有a n+1>a n,求a1的取值范围.【分析】(1)首先在n=1时,知a1为奇数,再利用归纳法证明对一切n≥2,a n 都是奇数;(2)先求出a n+1﹣a n的表达式,利用函数思想求解不等式a n+1﹣a n>0,求出a n 取值范围,利用归纳法求出a1的取值范围.【解答】(1)证明:已知a1是奇数,假设a k=2m﹣1是奇数,其中m为正整数,则由递推关系得a k+1==m(m﹣1)+1是奇数.根据数学归纳法,对任何n≥2,a n都是奇数.(2)法一:由a n+1﹣a n=(a n﹣1)(a n﹣3)知,a n+1>a n当且仅当a n<1或a n >3.另一方面,若0<a k<1,则0<a k+1<=1;若a k>3,则a k+1>=3.根据数学归纳法得,0<a1<1⇔0<a n<1,∀n∈N+;a1>3⇔a n>3,∀n∈N+.综上所述,对一切n∈N+都有a n+1>a n的充要条件是0<a1<1或a1>3.法二:由a2=>a1,得a12﹣4a1+3>0,于是0<a1<1或a1>3.a n+1﹣a n=﹣=,因为a1>0,a n+1=,所以所有的a n均大于0,因此a n+1﹣a n与a n﹣a n﹣1同号.根据数学归纳法,∀n∈N+,a n+1﹣a n与a2﹣a1同号.因此,对一切n∈N+都有a n+1>a n的充要条件是0<a1<1或a1>3.。
怀远三中数学试卷

怀远三中数学试卷第Ⅰ卷(选择题,共50分)一.选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,选择符合题目要求的选项。
1.已知i R b a ,,∈是虚数单位,若i a -与bi +2互为共轭复数,则=+2)(bi a (A )i 45- (B) i 45+ (C) i 43- (D) i 43+2.设集合},]2,0[,2{},21{∈==<-=x y y B x x A x则=B A(A) [0,2] (B) (1,3) (C) [1,3) (D) (1,4) 3.设0sin 33a =,0cos55b =,0tan 35c =,则( ) A .a b c >> B .b c a >> C .c b a >> D .c a b >> 4.若向量,a b 满足:||1a =,()a b a +⊥,(2)a b b +⊥,则||b =( )A .2B .1 D .25.设,8.0,2,7log 3.33===c b a 则( ) A.c a b << B.b a c << C.a b c << D.b c a <<6. 过点P )(1,3--的直线l 与圆122=+y x 有公共点,则直线l 的倾斜角的取值范围是( )A.]60π,( B.]30π,( C.]60[π, D.]30[π, 7.若将函数x x x f 2cos 2sin )(+=的图像向右平移ϕ个单位,所得图像关于y 轴对称,则ϕ 的最小正值是( ) A.8π B.4π C.83π D.43π8.从正方体六个面的对角线中任取两条作为一对,其中所成的角为60︒的共有 A.24对 B.30对 C.48对 D.60对 9.若函数()|1||2|f x x x a =+++的最小值为3,则实数a 的值为A.5或8B.1-或5C.1-或4-D.4-或8 10.在平面直角坐标系xOy 中,已知向量a 、b ,||||1a b ==,0a b ⋅=,点Q 满足2()OQ a b =+.曲线{|cos sin C P OP a b θθ==+,02}θπ≤<,区域{|0||P r PQ R Ω=<<≤,}r R <.若C Ω为两段分离的曲线,则A.13r R <<<B.13r R <<≤C.13r R ≤<<D.13r R <<<第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共计25分.请把答案填写在答题卡相应位置上......... 11. 从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是 ▲ . 12. 设抽测的树木的底部周长均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有 ▲ 株树木的底部周长小于100cm.13. 在各项均为正数的等比数列}{n a 中,,12=a 4682a a a +=,则6a 的值是 ▲ .14. 在平面直角坐标系xOy 中,直线032=-+y x 被圆4)1()2(22=++-y x 截得的弦长为▲ .15. 若△ABC 的内角满足C B A sin 2sin 2sin =+,则C cos 的最小值是 ▲ .三、解答题:本大题共6小题,共75分.解答应写出文子说明、证明过程或演算步骤.解答写在答题卡上的指定区域内 16. (本小题满分12分)已知数列{n a }的前n 项和为n S ,1a =1,0n a ≠,11n n n a a S λ+=-,其中λ为常数. (Ⅰ)证明:2n n a a λ+-=;(Ⅱ)是否存在λ,使得{n a }为等差数列?并说明理由. 17. (本小题满分12分)设1F ,2F 分别是椭圆C:()222210y x a b a b+=>>的左,右焦点,M 是C 上一点且2MF 与x 轴垂直,直线1MF 与C 的另一个交点为N.(Ⅰ)若直线MN 的斜率为34,求C 的离心率;(Ⅱ)若直线MN 在y 轴上的截距为2,且15MN F N =,求a,b .100 80 90 110 120 底部周长/cm(第6题)18.(12分)如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(Ⅰ)求证:平面ABE⊥B1BCC1;(Ⅱ)求证:C1F∥平面ABE;(Ⅲ)求三棱锥E﹣ABC的体积.19.(13分)(2014•北京)从某校随机抽取100名学生,获得了他们一周课外阅读时间(单12小时的概率;(Ⅱ)求频率分布直方图中的a,b的值;(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写结论)20.(本小题满分13分)如图,已知双曲线)0(1:222>=-a y ax C 的右焦点F,点A,B 分别在C 的两条渐近线上,AF ⊥x 轴,AB ⊥OB,BF ∥OA(O 为坐标原点), (1) 求双曲线C 的方程;(2)过C 上一点P(x 0,y 0)(y 00≠)的直线l :1020=-y y a xx 与直线AF 相交于点M ,与直线23=x 相交于点N 。
安徽省蚌埠市怀远县第三中学高二数学上学期第二次月考

2016-2017年度高二上学期第二次月考数学试卷(理)一. 选择题:1.在△ABC 中,a =10,B=60°,C=45°,则c 等于 ( )A .310+B .()1310-C .13+D .3102. 已知命题p q ,,若命题“p ⌝”与命题“p q ∨”都是真命题,则( ) A .p 为真命题,q 为假命题 B .p 为假命题,q 为真命题 C .p ,q 均为真命题 D .p ,q 均为假命题3. 命题:p 2,11x x ∀∈+≥R ,则p ⌝是( )A .2,11x x ∀∈+<R B .2,11x x ∃∈+≤R C .2,11x x ∃∈+<R D .2,11x x ∃∈+≥R 4.设R c b a ∈,,,且b a >,则( )A .bc ac >B .ba 11< C .22b a > D .33b a > 5.已知点P (x ,y )在不等式组⎩⎪⎨⎪⎧x -2≤0,y -1≤0,x +2y -2≥0表示的平面区域内,则z =x -y 的最小值是( )A .-2B .2C .-1D .16.已知不等式ax 2+bx +2>0的解集为{x |-1<x <2},则不等式2x 2+bx +a <0的解集为( )A.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-1<x <12 B.⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <-1或x >12 C .{x |-2<x <-1} D .{x |x <-2或x >1}7.如果等差数列{}n a 中,34512a a a ++=,那么127...a a a +++=( ) A .14 B . 21 C .28 D . 358.边长为1( )A .60° B.120° C .135° D .150°9.下列函数中,最小值为2的是( )A .y =x +1xB .y =sin x +1sinx ,(0,)2x π∈C .y =42x x +,[0,)x ∈+∞D .y =x 2+3x 2+210. 设a 、b 、c 是ABC ∆的三边长,对任意实数x ,222222()()f x b x b c a x c =++-+有( )A 、()0f x =B 、()0f x >C 、()0f x ≥D 、()0f x <11.已知数列{}n a 满足)(l o g 1l o g313++∈+=N n a a n n ,且9642=++a a a ,则)(l o g 97531a a a ++的值是( )A.51-B.5-C.5D.5112.已知命题p :m >2,命题q :x 2+2x -m >0对[1,2]x ∈恒成立.若p ∧q 为真命题,则实数m 的取值范围是( )A .2<m <3B .m >2C .m <-1或m >2D .m <-1 二.填空题:13.如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D 测得∠BCD =15°,∠BDC =30°,CD =40米,并在点C 测得塔顶A 的仰角为60°, 则塔高AB =________米.14.设x ∈R,则“x >12”是“2x 2+x -1>0”的_________________条件.(填:充分不必要、必要不充分、充要、既不充分也不必要条件) 15.若a >0,b >0,且a+b=2,则ba 91+的最小值为 . 16.已知数列{}n a 的前n 项和21()2n S n kn k *=-+∈N ,且n S 的最大值为8,则=2a ___.40三.解答题:17.(本小题满分10分)解不等式组⎩⎪⎨⎪⎧3x -2x -6≤1,2x 2-x -1>0.18. 在∆ABC 中,sin()1C A -=, sinB=13.(I )求sinA 的值; (II)设,求∆ABC 的面积.19. (本小题满分12分) 已知单调递增的等比数列{}n a 满足:23428a a a ++=,且32a +是2a ,4a 的等差中项.(I )求数列{}n a 的通项公式;(II )设2log n n n b a a =,求数列{}n b 的前n 项和n S .20. (本小题满分12分)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的23倍,且对每个项目的投资不能低于5万元.对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润.该公司如何正确规划投资,才能在这两个项目上共获得的利润最大,最大利润是多少?21.(本小题满分12分)已知044,:2<-+∈∀mx mx R x p 为真命题。
安徽省合肥七中2009届高三第五次月考数学试题理科2009.2

安徽省合肥七中2009届高三第五次月考数学试题(理科)命题人:费忠萍 第Ⅰ卷(选择题 共60分)一、选择题:本大题共12题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合A 、B 均为数集,且{}{}12123,,,,A a a B b b b ==,则集合A B 中元素的个数至 多为( )A .5个B .4个C .3个D .2个2. 若奇函数()()(2)1,(2)()(2),(1)f x x R f f x f x f f ∈=+=+满足则等于( )A .0B .1C .12-D .123. 若复数(a 2-4a +3)+(a -1)i 是纯虚数,则实数a 的值为( )A.1B.3C.1或3D.-14.在边长为1的等边ABC ∆中,设,,BC a CA b AB c a b b c c a ===⋅+⋅+⋅=,则( ) A .32-B .0C .32D .3 5.已知相异直线a ,b 和不重合平面,αβ,则a ∥b 的一个充分条件是A .a ∥α, b ∥αB .a ∥α,b ∥β,α∥βC .a ⊥α,b ⊥β,α∥βD .α⊥β,a ⊥α,b ∥β6. 按如右图所示的程序框图运算,若输入8x =,则输出k = ( )A.2B. 3C.4D. 57. P 是双曲线)0,0(12222>>=-b a bya x 左支上的一点,F 1、F 2分别是左、右焦点,且焦距为2c ,则21F PF ∆的内切圆的圆心的横坐标为( (A )a - (B )b - (C )c - (D )c b a -+8.在等差数列{a n }中,其前n 项和为S n .若a 2,a 10是方程x 2+12x -8=0的两个根, 那么S 11的值为( )A.44B.-44C.66D.-669.设P 为曲线C :223y x x =++上的点,且曲线C 在点P 处的切线的倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦,,则点P 的横坐标的取值范围为( ) A .112⎡⎤--⎢⎥⎣⎦,B .[]10-,C .[]01,D .112⎡⎤⎢⎥⎣⎦,10.函数f (x)的图象是如图所示的折线段OAB ,点A 坐标 为(1,2),点B 坐标为(3,0).定义函数()()(1)g x f x x =⋅-.则函数g (x)最大值为( )A.0B.2C.1D.4 11. 已知集合M 是满足下列条件的函数()f x 的全体; ①当]0,x ⎡∈+∞⎣时,函数值为非负实数;②对于任意的s 、[)∞+∈,0t ,0>λ,都有)1(1)()(λλλλ++≤++ts f t f s f在四个函数x x f =)(1,12)(2-=x x f ,1)(3+=x x f ,x x f 24log )(=中,属于集合M 的函数有( )个A.1B.2C.3D.412. 设0b >,二次函数221y ax bx a =++-的图像为下列之一,则a 的值为( )A .1B .-1C.12- D.12-y xoA321B合肥七中2009届高三第五次月考试题答题卷数学(理科)一、选择题:本大题共12题,每小题5分,共60分。
安徽省宿州市2009届高三五月联考数学试卷理科(附答案)
安徽省宿州市2009届高三五月联考数学试卷(理)一选择题:1.已知集合{})90sin(,0cos 0-= A ,{}02=+=x x x B ,则B A ⋂为( ) {}1,0.-A {}1,1.-B {}1.-C {}0.D 2.i 为虚数单位,则复数=+-)1()1(2i i ( )i A 22.+- i B 22.-- i C 22.+ i D 22.-3.设γβα、、为三个不同的平面,给出下列条件:①b a 、为异面直线,βαβα//,//,,a b b a ≠≠⊂⊂ ②α内有三个不共线的点到β的距离相等 ③γβγα⊥⊥, ④γβγα//,//,则其中能使βα//成立的条件为:( )A ①④B ②③C ①③D ②④4.如图是2008年北京奥运会上男子跳台跳水比赛中, 12位评委为某个运动员打出的分数的茎叶统计图, 去掉一个最高分和一个最低分之后,所剰数据的 平均数和标准差分别为( )16,84.A 4,84.B 16,85.C 4,85.D5.已知变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则2x+y 的最大值是( )A .3B .4C .5D .66.已知21nx x ⎛⎫+ ⎪⎝⎭的二项展开式的各项系数和为32,则二项展开式中x 系数为( )5.A 10.B 20.C 40.D7.设134:≤-x p ;0)1()12(:2≤+++-a a x a x q .若p ⌝是q ⌝的必要而不充分条件, 则实数a 的取值范围是( )⎥⎦⎤⎢⎣⎡21,0.A ⎪⎭⎫ ⎝⎛21,0.B (]⎪⎭⎫⎢⎣⎡+∞⋃∞-,210,.C ()⎪⎭⎫⎝⎛+∞⋃∞-,210,.D8.△ABC 中,AB=AC ,BC=2,则=⋅( )2.-A 2.B 1.-C .D 不确定9.当20π<<x 时,函数xxx x f 2sin sin 82cos 1)(2++=的最小值为( )2.A 32.B 34.C 4.D10.若正四面体SABC 的面ABC 内有一动点P 到平面SAB 、平面SBC 、平面SCA 的距离依次成等差数列,则点P 的轨迹是( ).A 一条线段 .B 一个点 .C 一段圆弧 .D 抛物线的一段11.已知点P 是抛物线x y 42=上一点,设点P 到此抛物线准线的距离为1d ,到直线0102=++y x 的距离为2d ,则21d d +的最小值为( )5.A 4.B 5511.C 511.D12.在数列{}n a 中,对任意*∈N n ,都有k a a a a nn n n =--+++112(k 为常数),则称{}n a 为“等差比数列”,下面对“等差比数列”的判断:①k 不可能为零;②等差数列一定是等差比数列;③等比数列一定是等差比数列;④通项公式为)1,0,0(≠≠+⋅=b a c b a a n n 的数列一定是等差比数列,其中正确的判断为( ) .A ① ② .B ② ③ .C ③ ④ .D ① ④二填空题:13.()202x x e dx -=⎰ .14. 执行右边的程序框图,若4p =,则输出的S =15.设M 、N 分别是曲线0sin 2=+θρ和224sin(=+πθρ上的动点,则M 、N 的最小距离是______16.设定义域为R 的函数⎪⎩⎪⎨⎧=≠-=)1(2)1(44)(x x x x f ,若关于x 的方程0)()(2=++c x bf x f 有三个不同的实数解321,,x x x ,则=++232221x x x ____三解答题:17.在锐角ABC ∆中,C B A ,,的对边分别为c b a ,,且A c B b C a cos ,cos ,cos 成等差数列, (1)求B 的值(2)求)cos(sin 22C A A -+的范围18. (12分)一个多面体的直观图如图所示(其中N M ,分别为BC AF ,的中点) (1)求证://MN 平面CDEF (2)求多面体CDEF A -的体积19.已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为31,某植物研究所分2个小组分别独立开展该种子的发芽试验,每次实验种一粒种子,如果某次没有发芽,则称该次实验是失败的。
安徽怀远县龙亢农场中学2009届高三第五次月考测试理科试卷2009.1.7
安徽怀远县龙亢农场中学2009届高三年级第五次月考测试数 学 试 卷(理)贵在坚持、难在坚持、成在坚持 命题人:崔北祥姓名_________ 班级_________ 学号_________ 2009.01.07本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22-24题为选考题,其它题为必考题.考生作答时,将答案答在答题卡上.在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回. 注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上.2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚.3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效. 4.保持卡面清洁,不折叠,不破损.5.做选考题时,考生按照题目要求作答,并用2B 铅笔在答题卡上把所选题目对应的题号涂黑. 参考公式: 锥体体积公式 V =31Sh 其中S 为底面面积,h 为高 柱体体积公式V =Sh 其中S 为底面面积,h 为高如果事件A 、B 互斥,那么 P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么 P (AB )=P (A )P (B )第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数2211x x y -+-=的定义域为( )A .}11|{-≤≥x x x 或B .}11|{≤≤-x xC .{1}D .{-1,1}2.已知等比数列{n a }中,n a >0,955,a a 为方程016102=+-x x 的两根,则805020a a a ⋅⋅的值为( ) A .32 B .64 C .256 D .±64 3.已知一个空间几何体的三视图如图所示,其中 正视图、侧视图都是由半圆和矩形组成,根据图中标 出的尺寸(单位:cm),可得这个几何体的体积是( ) A .π B .π34C .π35D .2π俯视图4.如图所示,墙上挂有边长为a 的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为2a的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )A .1-4πB .4πC .1-8πD .与a 的取值有关5.如图给出了计算401614121++++ 的值的程序框图,其中①②分别是( ) A .i<20,n=n+2 B .i=20,n=n+2 C .i>20,n=n+2 D .i>20,n=n+16.在各项均为正数的数列{n a }中,n S 为前n 项和,1221)1(++++=n n n n a a a n na 且π=3a ,则4tan S =( )A .-33 B .3 C .-3 D .33 7.若函数)10)(12(log 32≠>++-=a a a x x y a 且的图象沿向量)2,1(-=a 平移后所得图象恒过定点A ,且点A 在直线01=-+ny mx )0(>mn 上,则nm 12+的最小值为( ) A .5+22 B .9 C .8 D .168.若函数)0(cos sin )(>+=a ax ax x f 的最小正周期为1,则它的图象的一条对称轴方程为( )A .8π=x B .8π-=x C .81-=x D .81=x 9.已知函数))((R x x f y ∈=满足)1()3(+=+x f x f 且,时||)(,]1,1[x x f x =-∈则)(x f y =与x y 5log =的图象的交点个数是( )A .3B .4C .5D .610.对于集合N M 、定义)()(},|{M M N N M N M N x M x x N -⋃-=+∉∈=-且,设},2|{},,3|{2R x y y N R x x x y y M x ∈-==∈-==,则=+N M ( )A .(-49,0) B .[-49,0) C .(-∞,-49)∪[0,+∞) D .(-∞,-49]∪(0,+∞)甲 乙 7 9 8 0 7 8 5 5 79 1 1 1 3 3 4 6 2 2 0 2 3 1 01411.如图,在平面直角坐标系中,Ω是一个 与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成区域(含边界),A 、B 、C 、D 是该圆的 四等分点,若点P (x ,y )、P 0(x 0,y 0)满足x ≤x 0 且y ≥y 0, 则称P 优于P 0,如果Ω中的点Q 满足:不存在Ω中的其 它点优于Q ,那么所有这样的点Q 组成的集合是劣弧( )A .弧AB B .弧BCC .弧CDD .弧DA12.已知R b a ∈,,若关于x 的方程02=+-b ax x 的实根1x 和2x 满足-1≤1x ≤1,1≤2x ≤2,则在平面直角坐标系aob 中,点(b a ,)所表示的区域内的点P 到曲线1)2()3(22=-++b a 上的点Q 的距离|PQ|的最小值为( )A .32-1B .22-1C .32+1D .22+1第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分. 13.某赛季,甲、乙两名篮球运动员都参加了 11场比赛,他们每场比赛得分的情况用如图所 示的茎叶图表示,则甲、乙两名运动员比赛得分 的中位数分别是14.如图,在平行四边形ABCD 中,)2,3(),2,1(-==BD AC则=⋅AC AD _______________。
怀远县第三中学校2018-2019学年高三上学期11月月考数学试卷含答案
若设 AC=BC=a,则由 根据题意,∠ACD=60°,∠DCF=30°; ∴ 即 解得 故选:A. 【点评】考查当满足 ,平面向量基本定理,余弦函数的定义. 12.【答案】C 【解析】解:∵S16<0,S17>0, ∴ ∴a8<0,a9>0, ∴公差 d>0. ∴Sn 中最小的是 S8. 故选:C. =8(a8+a9)<0, . ; ;
第 7 页,共 16 页
f (11) f (3) f (1 4) f (1) f (1) ,
又∵奇函数 f ( x) 在区间 [0, 2] 上是增函数,∴ f ( x) 在区间 [ 2, 2] 上是增函数, ∴ f ( 25) f (80) f (11) ,故选 D. 10.【答案】B 【解析】解:由于反证法是命题的否定的一个运用,故用反证法证明命题时,可以设其否定成立进行推证. 命题“a,b∈N,如果 ab 可被 5 整除,那么 a,b 至少有 1 个能被 5 整除”的否定是“a,b 都不能被 5 整除”. 故选:B. 11.【答案】A 【解析】解:如图,根据题意知,D 在线段 AB 上,过 D 作 DE⊥AC,垂足为 E,作 DF⊥BC,垂足为 F;
得,CE=ta,CF=(1﹣t)a;
时,便说明 D,A,B 三点共线,以及向量加法的平行四边形法则
=17a9>0,
第 1 页,共 16 页
A.
B.
C.
D.
9. 已知定义在 R 上的奇函数 f ( x) ,满足 f ( x 4) f ( x) ,且在区间 [0, 2] 上是增函数,则 A、 f ( 25) f (11) f (80) C、 f (11) f (80) f ( 25) 设的内容应为( ) D.a 不能被 5 整除 =t +(1﹣t) D. ) ,若∠ACD=60°,则 t 的值为( ) B、 f (80) f (11) f ( 25) D、 f ( 25) f (80) f (11)
安徽省怀远三中2009届第五次月考数学理科试题
安徽省怀远三中2009届第五次月考数学(理科)试题第Ⅰ卷(选择题 共60分)一.选择题(每小题5分,共8小题,共40分),把答案涂在答题卡上. 1.已知b a s 2+=,12++=b a t ,则s 和t 的大小关系中正确的是A .s <tB .t s ≤C .s >tD .t s ≥2.已知平面向量),2(),2,1(m b a -==,且∥,则32+= A .(-2,-4)B .(-3,-6)C .(-4,-8)D .(-5,-10)3.已知集合2{|log 1},{|1}M x x N x x =<=<,则M N =A .{|01}x x <<B .{|02}x x <<C .{|1}x x <D .∅4.已知α,β是平面,m ,n 是直线,给出下列命题①若α⊥m ,β⊂m ,则βα⊥.②若α⊂m ,α⊂n ,β//m ,β//n ,则βα//. ③如果m n m ,,αα⊄⊂.n 是异面直线,那么α与n 相交. ④若m αβ=,n ∥m ,且βα⊄⊄n n ,,则n ∥α且n ∥β.其中正确命题的个数是A .4 B .3 C .2 D .15.将函数1)(+=x x x f 图象上每一点的横坐标变为原来的21倍,纵坐标不变,然后再将图象向左平移1个单位,所得图象的函数表达式为A .3222)(++=x x x fB .31)(++=x x x f C .1222)(--=x x x fD .11)(+-=x x x f6.设函数)(x f 定义如下表,数列}{n x 满足50=x ,且对任意自然数n 都有)(1n n x f x =+,则=2008xA .1B .2C .4D .57.已知函数xxx f ln )(=,b a e <<,无理数e 是自然对数的底,则 A .1)()(>b f a fB .)()(b f a f =C .)()(b f a f >D .)()(b f a f <8.如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦函数)0)(sin()(>+=w wx A x f ϕ半个周期的图象,这部分图象与正方形的一边围成图中的阴影区域.某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影区域的概率等于 A .π1B .π21C .31 D .41 第Ⅱ卷(非选择题 共100分)二.填空题:(本大题共6小题;每小题5分,共30分) 9.数列{}n a 中,n n a a 31=+,271321=++a a a ,则=++654a a a . 10.已知22=+y x ,则yx42+的最小值等于 .11.已知nx x ⎪⎪⎭⎫⎝⎛-3251展开式中所有项的二项式系数的和等于32,则其展开式中的常数项为 . 12.已知26cos sin =+αα,)4,0(πα∈,则45sin(πα-= . 13.已知()f x 是以2为周期的偶函数,且当[0,1]x ∈时,()f x x =,若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围是 .14.下图是一个物体的三视图,根据图中尺寸(单位:cm ),可求得该物体的体积为 cm 3.三.解答题.解答应写出文字说明,证明过程或演算步骤.(共6小题,共80分) 15.(本小题满分12分)在△ABC 中,角A .B .C 的对边分别为a .b .c ,且满足C b B c a cos cos )2(=-. (Ⅰ)求角B 的大小;(Ⅱ)设)1,1(),1,(sin -==A ,求⋅的最小值.16.(本小题满分12分) 某地区试行高考考试改革:在高三学年中举行4次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不再参加其余的测试,而每个学生最多也只能参加4次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立.(I ) 求该学生在前两次测试中至少有一次通过的概率;(II )如果考上大学或参加完4次测试,那么测试就结束.记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.17. (本题满分14分)如图所示的几何体是由以正三角形ABC 为底面的直棱柱(侧棱垂直于底面的棱柱)被平面DEF 所截而得.AB=2,BD=1,CE=3,AF=a ,O 为AB 的中点. (I )当5=a 时,求证:OC//平面DEF ;(II )当4=a 时,求平面DEF 与平面ABC 相交所成且为锐角的二面角的余弦值;(III )当a 为何值时,在DE 上存在点P ,使CP ⊥平面DEF ?18.(本小题满分14分)某工厂生产了一批产品共有100件,尺寸大小属于区间3[,)5.3或4[,)5.4的为合格品,属于区间5.3[,)4的为优等品.根据尺寸大小按如下区间进行分组:5.2[,)3.3[,)5.3.5.3[,)4.4[,)5.4.5.4[,]5,得到这批产品的频率分布直方图如图所示(单位:cm ). (I ) 求这批产品中合格品与优等品共有多少件?(II )只有合格品与优等品才可以在市场上销售,且优等品的售价每件不超过31元,优等品的售价不低于合格品的售价.当合格品的售价为每件x 元,优等品的售价每件y 元时,合格品的销售量为y x 5.05.1+件,优等品的销售量为x y 5.05.1-件,那么x .y 分别为多少时,这批产品的销售总量最大,最大销售总量是多少件?OPFEDCBA2.53.54.5 5尺寸(cm )0.1 3 419.(本题满分14分).等差数列{}n a 中,*)(1N n a a n n ∈>+,42,a a 为方程021102=+-x x 的两根,前n 项和为n S .等比数列{}n b 的前n 项和c T n n +=3(c 为常数).(I )求c ;(II )证明:对任意*N n ∈,1<-n n T S ;(III )证明:对任意*N n ∈,)!(log 4)1(3n n n >+.20.(本小题满分14分)已知函数),()(23R b a b ax x x f ∈++-=.(I )当0>a 时,求函数)(x f y =的极值;(II ) 若函数)(x f y =的图象上任意不同的两点连线的斜率都小于2,求证:66<<-a ;(III )对任意],1,0[0∈x )(x f y =的图像在0x x =处的切线的斜率为k ,求证:31≤≤a 是1||≤k 成立的充要条件.参考答案一.选择题(5⨯8=40) BCAC ACDA 二.填空题(5⨯6=30)9.1 10.4 11.2 12.21 13.10,4⎛⎤⎥⎝⎦14.256+64π 三.解答题:(共6小题,共80分) 15.(本小题满分12分)在△ABC 中,角A .B .C 的对边分别为a .b .c ,且满足C b B c a cos cos )2(=-. (Ⅰ)求角B 的大小;(Ⅱ)设)1,1(),1,(sin -==A ,求⋅的最小值.解:(I )由正弦定理R BbC c A a 2sin sin sin ===,有 A R a sin 2=, B R b s i n 2=,C R c sin 2=代入(2a -c)cosB=bcosC ,得(2sinA -sinC )cosB=sinBcosC .…………………4分即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)∵A+B+C=π,∴2sinAcosB=sinA .…………………6分 ∵0<A<π,∴sinA≠0.∴cosB=21.……………………………………7分 ∵0<B<π,∴B=3π.……………………………8分(II )⋅=-sinA+1 …………………………10分由B=3π得A ∈(0,32π) ……………………11分所以,当2π=A 时,⋅取得最小值0.………12分16.(本小题满分12分) 某地区试行高考考试改革:在高三学年中举行4次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不再参加其余的测试,而每个学生最多也只能参加4次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立.OPFEDCB A(I ) 求该学生在前两次测试中至少有一次通过的概率;(II )如果考上大学或参加完4次测试,那么测试就结束.记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.解:(I )记“该生在前两次测试中至少有一次通过”的事件为事件A ,则P(A)=9531112=⎪⎭⎫ ⎝⎛-- ---4分答:该生在前两次测试中至少有一次通过的概率为95 ---5分(II )参加测试次数ξ的可能取值为2,3,4, ---6分P(ξ=2)=91312=⎪⎭⎫ ⎝⎛, P(ξ=3)=C 27431.32.31.12= ,P(ξ=4)=27203232.313213=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛C , -----9分 故ξ的分布列为:Eξ=2×91+3×274+4×2720=2798-----12分17. (本题满分14分)如图所示的几何体是由以正三角形ABC 为底面的直棱柱(侧棱垂直于底面的棱柱)被平面DEF 所截而得.AB=2,BD=1,CE=3,AF=a ,O 为AB 的中点. (I )当5=a 时,求证:OC//平面DEF ;(II )当4=a 时,求平面DEF 与平面ABC 相交所成且为锐角的二面角的余弦值; (III )当a 为何值时,在DE 上存在点P ,使CP ⊥平面DEF ?(I )证:取DF 的中点G ,连结GE .由三棱柱得,AF//BD//CE , 而BD=1,AF=5, ∴ 四边形ABDF 为梯形, ∵OG 为梯形ABDF 的中位线 ∴OG//AF ,且OG=3y而CE//AF ,且CE=3 ∴OG //CE∴四边形OCEG 为平行四边形∴GE//OC 3分 又OC ⊄平面DEF ,GE ⊂平面DEF∴ OC//平面DEF 4分(II )以直线OB .OC 分别为x 轴.y 轴建立如图所示的空间直角坐标系, AF=4=a ,则D .E .F的坐标分别为:D (1,0,1).E (0,3,3).F (-1,0,4), ∴DE =(-1,3,2),DF =(-2,0,3) 5分 设平面DEF 的法向量),,(z y x n =, 由⎪⎩⎪⎨⎧=+-=⋅=++-=⋅032023z x z y x 得 z y z x 63,23-==可取)1,63,23(-= 6分 平面ABC 的法向量可以取)1,0,0(=7分∴10301121491=++==8分 ∴平面DEF 与平面ABC 所成的锐二面角的余弦值为1030. 9分 (III )在(II )的坐标系中,AF=a ,=(-1,3,2),DF =(-2,0,a -1).因P 在DE 上,设λ=,则)12,3,1()2,3,1()1,0,1(+-=-+=+=λλλλ∴)12),1(3,1()0,3,0()12,3,1(+--=-+-=-=λλλλλλ 11分 于是CP ⊥平面DEF 的充要条件就为⎪⎩⎪⎨⎧=+-+--=⋅=++-+-=⋅0)12)(1()1(20)12(2)1(31λλλλλa DF CP 12分 由此解得,2,41==a λ 13分 即当a =2时,在DE 上存在靠近D 的第一个四等分点P ,使CP ⊥平面DEF . 14分18.(本小题满分14分)某工厂生产了一批产品共有100件,尺寸大小属于区间3[,)5.3或4[,)5.4的为合格品,属于区间5.3[,)4的为优等品.根据尺寸大小按如下区间进行分组:5.2[,)3.3[,)5.3.5.3[,)4.4[,)5.4.5.4[,]5,得到这批产品的频率分布直方图如图所示(单位:cm ). (I ) 求这批产品中合格品与优等品共有多少件?(II )只有合格品与优等品才可以在市场上销售,且优等品的售价每件不超过31元,优等品的售价不低于合格品的售价.当合格品的售价为每件x 元,优等品的售价每件y 元时,合格品的销售量为y x 5.05.1+件,优等品的销售量为x y 5.05.1-件,那么x .y 分别为多少时,这批产品的销售总量最大,最大销售总量是多少件?解:(I )组距等于0.5,得到合格品与优等品的频率之和为9.0)8.05.02(5.0=+⨯⨯909.0100=⨯所以,合格品与优等品共有90件. 4分(II )由(I )可得,这批产品中,合格品有50件,优等品40件,则x .y 满足的约束条件为⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-≤+≥≤>405.05.1505.05.1310x y y x xy y x 即⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥-≤+≥≤>8031003310y x y x x y y x 7分 据此作出可行域如图中的阴影所示2.53.54. 5 尺寸(cm )410分销售总量为y x x y y x z 2)5.05.1()5.05.1(+=-++= 11分 作出直线0l :02=+y x ,平移直线0l 过点)31,23(A 时,z 取得最大值85, 12分 此时,合格品的销售件数为50315.0235.15.05.1=⨯+⨯=+y x 件优等品的销售件数为35235.0315.15.05.1=⨯-⨯=-x y 件 13分所以,当合格品的销价为每件23元且优等品的销售价为每件31元时,这批产品的销售总量最大,最大销售总量为85件. 14分 19.(本题满分14分).等差数列{}n a 中,*)(1N n a a n n ∈>+,42,a a 为方程021102=+-x x 的两根,前n 项和为n S .等比数列{}n b 的前n 项和c T n n +=3(c 为常数).(I )求c ;(II )证明:对任意*N n ∈,1<-n n T S ;(III )证明:对任意*N n ∈,)!(log 4)1(3n n n >+. (I )解:由c T n n +=3得,c b T +==311 c b b T +=+=9212 c b b b T +=++=273213∴c b +=31,62=b 183=b ∵{}n b 为等比数列∴231=+=c b ,∴c =1- 3分 (II )证明:方程021102=+-x x 的两根为3.7,由*)(1N n a a n n ∈>+知,42a a < ∴7,342==a a∴等差数列{}n a 的公差22372424=-=--=a a d∴12321=-=-=d a a ∴21)1(2)1(n n n n d n n na S n =-+=-+= 6分 要证1<-n n T S , 只要证明1+<n n T S 即nn 32<下面用数学归纳法证明nn 32<成立 (i )当1=n ,2,3时,不等式显然成立,(ii )假设当k n =(3≥k )时,不等式成立,即kk 32< 当k n =+1时,22221)1(12)2(223333+=++>-++=>⋅=+k k k k k k k k k k即123)1(+<+k k ,此时不等式也成立.由(i )(ii )知,对任意*N n ∈,nn 32<成立.所以,对任意*N n ∈,1<-n n T S . 10分 (III )证明:由(II )已证nn 32<成立,两边取以3为底的对数得,n n <3log 2 ∴n n +++<+++ 21log 22log 21log 2333 ∴2)1()321(log 23nn n +<⨯⨯⨯⨯ ∴)!(log 4)1(3n n n >+ 14分 20.(本小题满分14分)已知函数),()(23R b a b ax x x f ∈++-=.(I )当0>a 时,求函数)(x f y =的极值;(II ) 若函数)(x f y =的图象上任意不同的两点连线的斜率都小于2,求证:66<<-a ;(III )对任意],1,0[0∈x )(x f y =的图像在0x x =处的切线的斜率为k ,求证:31≤≤a 是1||≤k 成立的充要条件.20.解:(I ))32(323)(2ax x ax x x f --=+-=' 1分 由0)(='x f 得,0=x 或32a x = 而0>a ,列出下表)所以,当0=x 时,)(x f 取得极小值,极小值等于b ;当32ax =时,)(x f 取得极大值,极大值等于b a +2743; 5分 (II )设函数),()(111y x P x f y 点的图象上任意不同的两=.),(222y x P , 不妨设,21x x >66060)8(12408230)2(4)(02)(:2))(())((,22222222222222221122212212121212221212121223221312121<<-∴<-<+--=∆∴∈>+--<+---=∆∴∈>+-+-+<-+-+++--∴<--++-<--a a a a R x a ax x ax x a x R x ax x x a x x x x x x x x a x x x x x x x x ax x ax x x x y y 即即整理得即则(注:若直接用2)('<x f 来证明至少扣1分) 9分 (III )]1,0[,23)(00200∈+-='=x ax x x f k 则当时,12311||020≤+-≤-⇔≤ax x k.311||,31:10)0('123)1(0310)0('123)1(1313)3('10)0('123)1('1302≤≤≤≤≤⎪⎪⎩⎪⎪⎨⎧≤=-≥+-='<⎪⎪⎩⎪⎪⎨⎧-≥=≤+-='>⎪⎪⎪⎩⎪⎪⎪⎨⎧≤=-≥=-≥+-=≤≤⇔a k a f a f a f a f a a a f f a f a 成立的充要条件是故解得或或 14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省怀远三中2009届第五次月考数学(理科)试题第Ⅰ卷(选择题 共60分)一.选择题(每小题5分,共8小题,共40分),把答案涂在答题卡上.1.已知b a s 2+=,12++=b a t ,则s 和t 的大小关系中正确的是A .s <tB .t s ≤C .s >tD .t s ≥2.已知平面向量),2(),2,1(m b a -==,且a ∥b ,则b a 32+= A .(-2,-4)B .(-3,-6)C .(-4,-8)D .(-5,-10)3.已知集合2{|log 1},{|1}M x x N x x =<=<,则M N =A .{|01}x x <<B .{|02}x x <<C .{|1}x x <D .∅4.已知α,β是平面,m ,n 是直线,给出下列命题①若α⊥m ,β⊂m ,则βα⊥.②若α⊂m ,α⊂n ,β//m ,β//n ,则βα//. ③如果m n m ,,αα⊄⊂.n 是异面直线,那么α与n 相交. ④若m αβ=,n ∥m ,且βα⊄⊄n n ,,则n ∥α且n ∥β.其中正确命题的个数是A .4 B .3 C .2 D .15.将函数1)(+=x x x f 图象上每一点的横坐标变为原来的21倍,纵坐标不变,然后再将图象向左平移1个单位,所得图象的函数表达式为A .3222)(++=x x x fB .31)(++=x x x f C .1222)(--=x x x fD .11)(+-=x x x f6.设函数)(x f 定义如下表,数列}{n x 满足50=x ,且对任意自然数n 都有)(1n n x f x =+,则=2008xA .1B .2C .4D .57.已知函数xxx f ln )(=,b a e <<,无理数e 是自然对数的底,则 A .1)()(>b f a fB .)()(b f a f =C .)()(b f a f >D .)()(b f a f <8.如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦函数)0)(sin()(>+=w wx A x f ϕ半个周期的图象,这部分图象与正方形的一边围成图中的阴影区域.某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影区域的概率等于 A .π1B .π21C .31 D .41 第Ⅱ卷(非选择题 共100分)二.填空题:(本大题共6小题;每小题5分,共30分) 9.数列{}n a 中,n n a a 31=+,271321=++a a a ,则=++654a a a . 10.已知22=+y x ,则yx42+的最小值等于 .11.已知nx x ⎪⎪⎭⎫⎝⎛-3251展开式中所有项的二项式系数的和等于32,则其展开式中的常数项为 . 12.已知26cos sin =+αα,)4,0(πα∈,则)45sin(πα-= . 13.已知()f x 是以2为周期的偶函数,且当[0,1]x ∈时,()f x x =,若在区间[1,3]-内,函数()()g x f x kx k =--有4个零点,则实数k 的取值范围是 .14.下图是一个物体的三视图,根据图中尺寸(单位:cm ),可求得该物体的体积为 cm 3.三.解答题.解答应写出文字说明,证明过程或演算步骤.(共6小题,共80分) 15.(本小题满分12分)在△ABC 中,角A .B .C 的对边分别为a .b .c ,且满足C b B c a cos cos )2(=-. (Ⅰ)求角B 的大小;(Ⅱ)设)1,1(),1,(sin -==A ,求⋅的最小值.16.(本小题满分12分) 某地区试行高考考试改革:在高三学年中举行4次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不再参加其余的测试,而每个学生最多也只能参加4次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立.(I ) 求该学生在前两次测试中至少有一次通过的概率;(II )如果考上大学或参加完4次测试,那么测试就结束.记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.17. (本题满分14分)如图所示的几何体是由以正三角形ABC 为底面的直棱柱(侧棱垂直于底面的棱柱)被平面DEF 所截而得.AB=2,BD=1,CE=3,AF=a ,O 为AB 的中点. (I )当5=a 时,求证:OC//平面DEF ;(II )当4=a 时,求平面DEF 与平面ABC 相交所成且为锐角的二面角的余弦值;(III )当a 为何值时,在DE 上存在点P ,使CP ⊥平面DEF ?18.(本小题满分14分)某工厂生产了一批产品共有100件,尺寸大小属于区间3[,)5.3或4[,)5.4的为合格品,属于区间5.3[,)4的为优等品.根据尺寸大小按如下区间进行分组:5.2[,)3.3[,)5.3.5.3[,)4.4[,)5.4.5.4[,]5,得到这批产品的频率分布直方图如图所示(单位:cm ). (I ) 求这批产品中合格品与优等品共有多少件?(II )只有合格品与优等品才可以在市场上销售,且优等品的售价每件不超过31元,优等品的售价不低于合格品的售价.当合格品的售价为每件x 元,优等品的售价每件y 元时,合格品的销售量为y x 5.05.1+件,优等品的销售量为x y 5.05.1-件,那么x .y 分别为多少时,这批产品的销售总量最大,最大销售总量是多少件?OPFEDCBA2.53.54.5 5尺寸(cm )0.1 3 419.(本题满分14分).等差数列{}n a 中,*)(1N n a a n n ∈>+,42,a a 为方程021102=+-x x 的两根,前n 项和为n S .等比数列{}n b 的前n 项和c T n n +=3(c 为常数). (I )求c ;(II )证明:对任意*N n ∈,1<-n n T S ;(III )证明:对任意*N n ∈,)!(log 4)1(3n n n >+.20.(本小题满分14分)已知函数),()(23R b a b ax x x f ∈++-=. (I )当0>a 时,求函数)(x f y =的极值;(II ) 若函数)(x f y =的图象上任意不同的两点连线的斜率都小于2,求证:66<<-a ;(III )对任意],1,0[0∈x )(x f y =的图像在0x x =处的切线的斜率为k ,求证:31≤≤a 是1||≤k 成立的充要条件.参考答案一.选择题(5⨯8=40) BCAC ACDA 二.填空题(5⨯6=30)9.1 10.4 11.2 12.21 13.10,4⎛⎤⎥⎝⎦14.256+64π 三.解答题:(共6小题,共80分) 15.(本小题满分12分)在△ABC 中,角A .B .C 的对边分别为a .b .c ,且满足C b B c a cos cos )2(=-. (Ⅰ)求角B 的大小;(Ⅱ)设)1,1(),1,(sin -==A ,求⋅的最小值.解:(I )由正弦定理R BbC c A a 2sin sin sin ===,有 A R a sin 2=, B R b s i n 2=,C R c sin 2=代入(2a -c)cosB=bcosC ,得(2sinA -sinC )cosB=sinBcosC .…………………4分即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)∵A+B+C=π,∴2sinAcosB=sinA .…………………6分 ∵0<A<π,∴sinA≠0. ∴cosB=21.……………………………………7分 ∵0<B<π,∴B=3π.……………………………8分 (II )n m ⋅=-sinA+1 …………………………10分由B=3π得A ∈(0,32π) ……………………11分所以,当2π=A 时,⋅取得最小值0.………12分16.(本小题满分12分) 某地区试行高考考试改革:在高三学年中举行4次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不再参加其余的测试,而每个学生最多也只能参加4次测试.假设某学生每次通过测试的概率都是31,每次测试时间间隔恰当,每次测试通过与否互相独立.OPFEDCB A(I ) 求该学生在前两次测试中至少有一次通过的概率;(II )如果考上大学或参加完4次测试,那么测试就结束.记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.解:(I )记“该生在前两次测试中至少有一次通过”的事件为事件A ,则P(A)=9531112=⎪⎭⎫ ⎝⎛-- ---4分答:该生在前两次测试中至少有一次通过的概率为95 ---5分(II )参加测试次数ξ的可能取值为2,3,4, ---6分P(ξ=2)=91312=⎪⎭⎫ ⎝⎛, P(ξ=3)=C 27431.32.31.12= ,P(ξ=4)=27203232.313213=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛C , -----9分 故ξ的分布列为:Eξ=2×91+3×274+4×2720=2798-----12分17. (本题满分14分)如图所示的几何体是由以正三角形ABC 为底面的直棱柱(侧棱垂直于底面的棱柱)被平面DEF 所截而得.AB=2,BD=1,CE=3,AF=a ,O 为AB 的中点. (I )当5=a 时,求证:OC//平面DEF ;(II )当4=a 时,求平面DEF 与平面ABC 相交所成且为锐角的二面角的余弦值; (III )当a 为何值时,在DE 上存在点P ,使CP ⊥平面DEF ?(I )证:取DF 的中点G ,连结GE .由三棱柱得,AF//BD//CE , 而BD=1,AF=5, ∴ 四边形ABDF 为梯形, ∵OG 为梯形ABDF 的中位线 ∴OG//AF ,且OG=3y而CE//AF ,且CE=3 ∴OG //CE∴四边形OCEG 为平行四边形∴GE//OC 3分 又OC ⊄平面DEF ,GE ⊂平面DEF∴ OC//平面DEF 4分(II )以直线OB .OC 分别为x 轴.y 轴建立如图所示的空间直角坐标系, AF=4=a ,则D .E .F的坐标分别为:D (1,0,1).E (0,3,3).F (-1,0,4), ∴DE =(-1,3,2),DF =(-2,0,3) 5分 设平面DEF 的法向量),,(z y x n =, 由⎪⎩⎪⎨⎧=+-=⋅=++-=⋅032023z x z y x 得 z y z x 63,23-==可取)1,63,23(-=n 6分 平面ABC 的法向量可以取)1,0,0(=7分∴10301121491=++==8分 ∴平面DEF 与平面ABC 所成的锐二面角的余弦值为1030. 9分 (III )在(II )的坐标系中,AF=a ,DE =(-1,3,2),DF =(-2,0,a -1).因P 在DE 上,设λ=,则)12,3,1()2,3,1()1,0,1(+-=-+=+=λλλλ∴)12),1(3,1()0,3,0()12,3,1(+--=-+-=-=λλλλλλ 11分 于是CP ⊥平面DEF 的充要条件就为⎪⎩⎪⎨⎧=+-+--=⋅=++-+-=⋅0)12)(1()1(20)12(2)1(31λλλλλa DF CP 12分 由此解得,2,41==a λ 13分 即当a =2时,在DE 上存在靠近D 的第一个四等分点P ,使CP ⊥平面DEF . 14分18.(本小题满分14分)某工厂生产了一批产品共有100件,尺寸大小属于区间3[,)5.3或4[,)5.4的为合格品,属于区间5.3[,)4的为优等品.根据尺寸大小按如下区间进行分组:5.2[,)3.3[,)5.3.5.3[,)4.4[,)5.4.5.4[,]5,得到这批产品的频率分布直方图如图所示(单位:cm ). (I ) 求这批产品中合格品与优等品共有多少件?(II )只有合格品与优等品才可以在市场上销售,且优等品的售价每件不超过31元,优等品的售价不低于合格品的售价.当合格品的售价为每件x 元,优等品的售价每件y 元时,合格品的销售量为y x 5.05.1+件,优等品的销售量为x y 5.05.1-件,那么x .y 分别为多少时,这批产品的销售总量最大,最大销售总量是多少件?解:(I )组距等于0.5,得到合格品与优等品的频率之和为9.0)8.05.02(5.0=+⨯⨯ 909.0100=⨯所以,合格品与优等品共有90件. 4分(II )由(I )可得,这批产品中,合格品有50件,优等品40件,则x .y 满足的约束条件为⎪⎪⎪⎩⎪⎪⎪⎨⎧≤-≤+≥≤>405.05.1505.05.1310x y y x xy y x 即⎪⎪⎪⎩⎪⎪⎪⎨⎧-≥-≤+≥≤>8031003310y x y x x y y x 7分 据此作出可行域如图中的阴影所示2.53.54. 5 尺寸(cm )410分销售总量为y x x y y x z 2)5.05.1()5.05.1(+=-++= 11分 作出直线0l :02=+y x ,平移直线0l 过点)31,23(A 时,z 取得最大值85, 12分 此时,合格品的销售件数为50315.0235.15.05.1=⨯+⨯=+y x 件优等品的销售件数为35235.0315.15.05.1=⨯-⨯=-x y 件 13分所以,当合格品的销价为每件23元且优等品的销售价为每件31元时,这批产品的销售总量最大,最大销售总量为85件. 14分 19.(本题满分14分).等差数列{}n a 中,*)(1N n a a n n ∈>+,42,a a 为方程021102=+-x x 的两根,前n 项和为n S .等比数列{}n b 的前n 项和c T n n +=3(c 为常数). (I )求c ;(II )证明:对任意*N n ∈,1<-n n T S ;(III )证明:对任意*N n ∈,)!(log 4)1(3n n n >+. (I )解:由c T n n +=3得,c b T +==311 c b b T +=+=9212 c b b b T +=++=273213∴c b +=31,62=b 183=b ∵{}n b 为等比数列∴231=+=c b ,∴c =1- 3分 (II )证明:方程021102=+-x x 的两根为3.7,由*)(1N n a a n n ∈>+知,42a a < ∴7,342==a a∴等差数列{}n a 的公差22372424=-=--=a a d∴12321=-=-=d a a ∴21)1(2)1(n n n n d n n na S n =-+=-+= 6分 要证1<-n n T S , 只要证明1+<n n T S 即nn 32<下面用数学归纳法证明nn 32<成立 (i )当1=n ,2,3时,不等式显然成立,(ii )假设当k n =(3≥k )时,不等式成立,即kk 32<当k n =+1时,22221)1(12)2(223333+=++>-++=>⋅=+k k k k k k k k k k即123)1(+<+k k ,此时不等式也成立.由(i )(ii )知,对任意*N n ∈,nn 32<成立.所以,对任意*N n ∈,1<-n n T S . 10分 (III )证明:由(II )已证nn 32<成立,两边取以3为底的对数得,n n <3log 2 ∴n n +++<+++ 21log 22log 21log 2333 ∴2)1()321(log 23nn n +<⨯⨯⨯⨯ ∴)!(log 4)1(3n n n >+ 14分 20.(本小题满分14分)已知函数),()(23R b a b ax x x f ∈++-=. (I )当0>a 时,求函数)(x f y =的极值;(II ) 若函数)(x f y =的图象上任意不同的两点连线的斜率都小于2,求证:66<<-a ;(III )对任意],1,0[0∈x )(x f y =的图像在0x x =处的切线的斜率为k ,求证:31≤≤a 是1||≤k 成立的充要条件.20.解:(I ))32(323)(2ax x ax x x f --=+-=' 1分 由0)(='x f 得,0=x 或32a x = 而0>a ,列出下表)所以,当0=x 时,)(x f 取得极小值,极小值等于b ;当32a x =时,)(x f 取得极大值,极大值等于b a +2743; 5分 (II )设函数),()(111y x P x f y 点的图象上任意不同的两=.),(222y x P , 不妨设,21x x >66060)8(12408230)2(4)(02)(:2))(())((,22222222222222221122212212121212221212121223221312121<<-∴<-<+--=∆∴∈>+--<+---=∆∴∈>+-+-+<-+-+++--∴<--++-<--a a a a R x a ax x ax x a x R x ax x x a x x x x x x x x a x x x x x x x x ax x ax x x x y y 即即整理得即则(注:若直接用2)('<x f 来证明至少扣1分) 9分 (III )]1,0[,23)(00200∈+-='=x ax x x f k 则当时,12311||020≤+-≤-⇔≤ax x k.311||,31:10)0('123)1(0310)0('123)1(1313)3('10)0('123)1('1302≤≤≤≤≤⎪⎪⎩⎪⎪⎨⎧≤=-≥+-='<⎪⎪⎩⎪⎪⎨⎧-≥=≤+-='>⎪⎪⎪⎩⎪⎪⎪⎨⎧≤=-≥=-≥+-=≤≤⇔a k a f a f a f a f a a a f f a f a 成立的充要条件是故解得或或 14分。
