灰色关联度分析word版
灰色关联分析与统计分析法

灰關聯分析的原理: 灰關聯分析的原理:
1. 原理與方法簡介 關聯度分析一般包括下列計算和步驟:(1) 原始資料變換;(2) 計算關聯係數;(3) 求關聯度; (3) 排關聯序;(4) 列關聯矩陣。在應用中是否進 行所有步驟,可視具體情況而定。
★它們的理論基礎不同。關聯度分析基於灰色系統的灰色過程,
而相關分析則基於概率論的隨機過程。 ★分析方法不同。關聯分析是進行因素間時間序列的比較,而 相關分析是因素間陣列的比較。 ★資料量要求不同。關聯分析不要求資料太多,而相關分析則 需有足夠的資料量。 ★研究重點不同。關聯度分析主要研究動態過程,而相關分析 則以靜態研究爲主。 因此,關聯度分析適應性更廣,在用 於社會經濟系統中的應用更有其獨到之處。
馬爾可夫─主要貢獻
主要貢獻: 馬爾可夫主要貢獻在概率論、數論、函數逼近 論和微分方程等方面。在概率論中,他發展了 「矩法」,擴大了大數律和中心極限定理的應 用範圍。在1906~1912年間,他提出並研究了一 種能用數學分析方法研究自然過程的一般圖 式——馬爾可夫鏈(Markov Chain)。
馬爾可夫─隨機過程
複習:相關係數(r)的計算公式:
隨機過程
隨機過程是指一變數隨時間的經過,而 隨機過程 呈不確定方向變化的行為。
馬爾可夫─生平事蹟
生平事蹟: 蘇聯數學家。1856年6月14日生於梁贊。1922年 7月20日卒於彼得堡(今列寧格勒)。1878年畢業 於聖彼得堡大學,並以<<用連分數求微分方程 的積分>>一文獲金質獎章。1884年取得物理— 數學博士學位,1886年任該校教授。1896年被 選為聖彼得堡科學院院士。1905年被授予功勛 教授的稱號。
灰色关联分析详解+结果解读

灰色关联分析1、作用对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
因此,灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度。
2、输入输出描述输入:特征序列为至少两项或以上的定量变量,母序列(关联对象)为 1 项定量变量。
输出:反应考核指标与母序列的关联程度。
3、案例示例案例:分析 09-18 年内,影院数量,观影人数,票价、电影上线数量这些因素对全年电影票房的影响。
其中电影票房是母序列,影院数量,观影人数,票价、电影上线数量是特征序列。
4、案例数据灰色关联分析案例数据5、案例操作Step1:新建分析;Step2:上传数据;Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;step4:选择【灰色关联分析】;step5:查看对应的数据数据格式,【灰色关联分析】要求特征序列为定量变量,且至少有一项;要求母序列为定量变量,且只有一项。
step6:设置量纲处理方式(包括初值化、均值化、无处理)、分辨系数(ρ越小,分辨力越大,一般ρ的取值区间为 ( 0 ,1 ),具体取值可视情况而定。
当ρ≤ 0.5463 时,分辨力最好,通常取ρ = 0.5 )step7:点击【开始分析】,完成全部操作。
6、输出结果分析输出结果 1:灰色关联系数图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值(数字越大,代表关联性越强)。
输出结果 2:关联系数图分析:输出结果 1 和输出结果 2 是一样的,输出结果 1 用了表格形式来呈现关联系数,输出结果 2 用了图表形式来呈现关联系数。
图表很直观地展现了,大多数年份的银幕数量和电影上线数量对票房影响更大。
健康险影响因素灰色关联分析(含代码)

健康险影响因素灰色关联分析灰色关联分析(Grey Relational Analysis, GRA)的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密,曲线越接近,相应序列之间的关联度就越大,反之就越小。
应用灰色关联分析方法对受多种因素影响的事物和现象从整体观念出发进行综合评价是一个被广为接受的方法。
一、灰色关联分析步骤(1)确定参考数据列和比较数据列。
参考数据列是能反映系统行为特征的数据序列,比较数据列是影响系统行为的因素组成的数据序列。
(2)对指标数据进行无量纲化。
由于指标数据的性质不一样,导致他们涉及的数值有的很大有的很小,这不代表数值晓的指标不重要,因此为了减少指标数据绝对值的差异,我们需要先对指标数据进行无量纲化。
常用的无量纲化方法有均值化法和初值化法。
均值化法:xi (k)= x′i(k)1m∑x′i(k)mk=1初值化法:xi (k)= x′i(k)x′i(1)i=0,1,…,n;k=1,2,…,m无量纲化后的数据序列形成如下的矩阵:(X0,X1,…,Xn)=(x0(1)x1(1)⋯x n(1) x0(2)x1(2)⋯x n(2)⋮⋮⋮⋮x0(m)x1(m)⋯x n(m))(3)逐个计算每个比较数据列与参考数据列对应元素的绝对差值。
绝对差值:|x0(k)-xi(k)|(i=0,1,…,n;k=1,2,…,m)(4)确定两级最小差和两级最大差。
两级最小差:mini mink|x0(k)−x i(k)|两级最大差:maxi maxk|x0(k)−x i(k)|(5)计算关联系数。
ζi(k)=minimink|x0(k)−x i(k)|+ρ∙maximaxk|x0(k)−x i(k)||x0(k)−x i(k)|+ρ∙maximaxk|x0(k)−x i(k)|(i=1,2,…,n;k=1,2,…,m)其中,ρ为分辨系数,取值在0-1之间,ρ越小,关联系数间差异越大,区分能力越强,本文中ρ取0.5。
灰色关联度分析
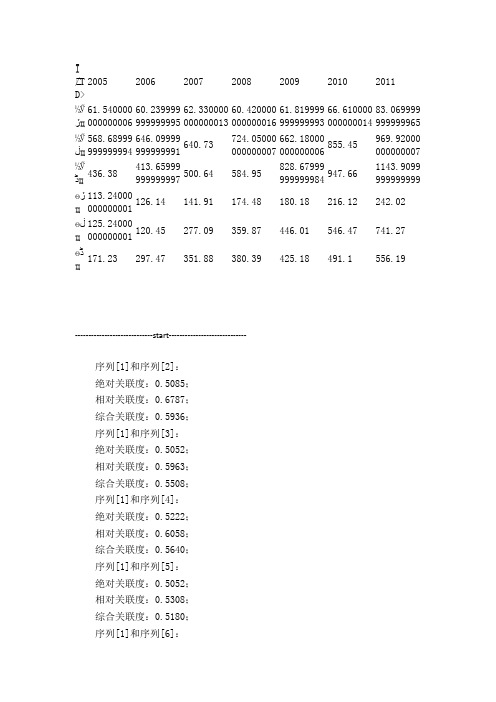
Īݼ/TD>2005 2006 2007 2008 2009 2010 2011½Ӳڒҵ61.54000000000000660.23999999999999562.33000000000001360.42000000000001661.81999999999999366.61000000000001483.069999999999965½Ӳڶҵ568.68999999999994646.09999999999991640.73724.05000000000007662.18000000000006855.45969.92000000000007½Ӳڈҵ436.38413.65999999999997500.64 584.95828.67999999999984947.661143.9099999999999ѳڒҵ113.24000000000001126.14 141.91 174.48 180.18 216.12 242.02ѳڶҵ125.24000000000001120.45 277.09 359.87 446.01 546.47 741.27ѳڈҵ171.23 297.47 351.88 380.39 425.18 491.1 556.19-----------------------------start-----------------------------序列[1]和序列[2]:绝对关联度:0.5085;相对关联度:0.6787;综合关联度:0.5936;序列[1]和序列[3]:绝对关联度:0.5052;相对关联度:0.5963;综合关联度:0.5508;序列[1]和序列[4]:绝对关联度:0.5222;相对关联度:0.6058;综合关联度:0.5640;序列[1]和序列[5]:绝对关联度:0.5052;相对关联度:0.5308;综合关联度:0.5180;序列[1]和序列[6]:绝对关联度:0.5058;相对关联度:0.5460;综合关联度:0.5259;序列[2]和序列[3]:绝对关联度:0.8060;相对关联度:0.7695;综合关联度:0.7878;序列[2]和序列[4]:绝对关联度:0.6904;相对关联度:0.7959;综合关联度:0.7432;序列[2]和序列[5]:绝对关联度:0.8094;相对关联度:0.5862;综合关联度:0.6978;序列[2]和序列[6]:绝对关联度:0.8454;相对关联度:0.6288;综合关联度:0.7371;序列[3]和序列[4]:绝对关联度:0.6166;相对关联度:0.9553;综合关联度:0.7859;序列[3]和序列[5]:绝对关联度:0.9946;相对关联度:0.6600;综合关联度:0.8273;序列[3]和序列[6]:绝对关联度:0.9430;相对关联度:0.7389;综合关联度:0.8409;序列[4]和序列[5]:绝对关联度:0.6178;相对关联度:0.6457;综合关联度:0.6317;序列[4]和序列[6]:绝对关联度:0.6316;相对关联度:0.7176;综合关联度:0.6746;序列[5]和序列[6]:绝对关联度:0.9479;相对关联度:0.8348;综合关联度:0.8913;-----------------------------the end----------------------------- 详细计算过程:-----------------------------start----------------------------- 初始化操作(整理为等长度1-时距序列)序列[1]:61.54,60.24,62.33,60.42,61.82,66.61,83.07,序列[2]:568.69,646.1,640.73,724.05,662.18,855.45,969.92,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-1.3000,0.7900,-1.1200,0.2800,5.0700,21.5300,序列[2]:0.0000,77.4100,72.0400,155.3600,93.4900,286.7600,401.2300,2、计算|s0|,|s1|,|s1-s0||s0|=14.485;|s1|=885.675;|s1-s0|=871.19序列[1]和序列[2]的绝对关联度=0.5085计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9789,1.0128,0.9818,1.0045,1.0824,1.3499, 序列[2]:1.0000,1.1361,1.1267,1.2732,1.1644,1.5042,1.7055, 2、序列的始点零化像:序列[1]:0.0000,-0.0211,0.0128,-0.0182,0.0045,0.0824,0.3499, 序列[2]:0.0000,0.1361,0.1267,0.2732,0.1644,0.5042,0.7055, 3、计算|s0|,|s1|,|s1-s0||s0|=0.23535;|s1|=1.55735;|s1-s0|=1.322结论:序列[1]和序列[2]的相对关联度=0.6787序列[1]和序列[2]:绝对关联度:0.5085;相对关联度:0.6787;综合关联度:0.5936;初始化操作(整理为等长度1-时距序列)序列[1]:61.54,60.24,62.33,60.42,61.82,66.61,83.07,序列[2]:436.38,413.66,500.64,584.95,828.68,947.66,1143.91,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-1.3000,0.7900,-1.1200,0.2800,5.0700,21.5300,序列[2]:0.0000,-22.7200,64.2600,148.5700,392.3000,511.2800,707.5300,2、计算|s0|,|s1|,|s1-s0||s0|=14.485;|s1|=1447.455;|s1-s0|=1432.97序列[1]和序列[3]的绝对关联度=0.5052计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9789,1.0128,0.9818,1.0045,1.0824,1.3499,序列[2]:1.0000,0.9479,1.1473,1.3405,1.8990,2.1716,2.6214,2、序列的始点零化像:序列[1]:0.0000,-0.0211,0.0128,-0.0182,0.0045,0.0824,0.3499, 序列[2]:0.0000,-0.0521,0.1473,0.3405,0.8990,1.1716,1.6214,3、计算|s0|,|s1|,|s1-s0||s0|=0.23535;|s1|=3.317;|s1-s0|=3.08165结论:序列[1]和序列[3]的相对关联度=0.5963序列[1]和序列[3]:绝对关联度:0.5052;相对关联度:0.5963;综合关联度:0.5508;初始化操作(整理为等长度1-时距序列)序列[1]:61.54,60.24,62.33,60.42,61.82,66.61,83.07,序列[2]:113.24,126.14,141.91,174.48,180.18,216.12,242.02,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-1.3000,0.7900,-1.1200,0.2800,5.0700,21.5300,序列[2]:0.0000,12.9000,28.6700,61.2400,66.9400,102.8800,128.7800, 2、计算|s0|,|s1|,|s1-s0||s0|=14.485;|s1|=337.02;|s1-s0|=322.535序列[1]和序列[4]的绝对关联度=0.5222计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9789,1.0128,0.9818,1.0045,1.0824,1.3499, 序列[2]:1.0000,1.1139,1.2532,1.5408,1.5911,1.9085,2.1372, 2、序列的始点零化像:序列[1]:0.0000,-0.0211,0.0128,-0.0182,0.0045,0.0824,0.3499, 序列[2]:0.0000,0.1139,0.2532,0.5408,0.5911,0.9085,1.1372, 3、计算|s0|,|s1|,|s1-s0||s0|=0.23535;|s1|=2.9761;|s1-s0|=2.74075结论:序列[1]和序列[4]的相对关联度=0.6058序列[1]和序列[4]:绝对关联度:0.5222;相对关联度:0.6058;综合关联度:0.5640;初始化操作(整理为等长度1-时距序列)序列[1]:61.54,60.24,62.33,60.42,61.82,66.61,83.07,序列[2]:125.24,120.45,277.09,359.87,446.01,546.47,741.27, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-1.3000,0.7900,-1.1200,0.2800,5.0700,21.5300,序列[2]:0.0000,-4.7900,151.8500,234.6300,320.7700,421.2300,616.0300,2、计算|s0|,|s1|,|s1-s0||s0|=14.485;|s1|=1431.705;|s1-s0|=1417.22序列[1]和序列[5]的绝对关联度=0.5052计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9789,1.0128,0.9818,1.0045,1.0824,1.3499,序列[2]:1.0000,0.9618,2.2125,2.8734,3.5612,4.3634,5.9188,2、序列的始点零化像:序列[1]:0.0000,-0.0211,0.0128,-0.0182,0.0045,0.0824,0.3499, 序列[2]:0.0000,-0.0382,1.2125,1.8734,2.5612,3.3634,4.9188,3、计算|s0|,|s1|,|s1-s0||s0|=0.23535;|s1|=11.4317;|s1-s0|=11.19635结论:序列[1]和序列[5]的相对关联度=0.5308序列[1]和序列[5]:绝对关联度:0.5052;相对关联度:0.5308;综合关联度:0.5180;初始化操作(整理为等长度1-时距序列)序列[1]:61.54,60.24,62.33,60.42,61.82,66.61,83.07,序列[2]:171.23,297.47,351.88,380.39,425.18,491.1,556.19,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-1.3000,0.7900,-1.1200,0.2800,5.0700,21.5300,序列[2]:0.0000,126.2400,180.6500,209.1600,253.9500,319.8700,384.9600,2、计算|s0|,|s1|,|s1-s0||s0|=14.485;|s1|=1282.35;|s1-s0|=1267.865序列[1]和序列[6]的绝对关联度=0.5058计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9789,1.0128,0.9818,1.0045,1.0824,1.3499,序列[2]:1.0000,1.7373,2.0550,2.2215,2.4831,2.8681,3.2482,2、序列的始点零化像:序列[1]:0.0000,-0.0211,0.0128,-0.0182,0.0045,0.0824,0.3499, 序列[2]:0.0000,0.7373,1.0550,1.2215,1.4831,1.8681,2.2482,3、计算|s0|,|s1|,|s1-s0||s0|=0.23535;|s1|=7.4891;|s1-s0|=7.25375结论:序列[1]和序列[6]的相对关联度=0.5460序列[1]和序列[6]:绝对关联度:0.5058;相对关联度:0.5460;综合关联度:0.5259;初始化操作(整理为等长度1-时距序列)序列[1]:568.69,646.1,640.73,724.05,662.18,855.45,969.92,序列[2]:436.38,413.66,500.64,584.95,828.68,947.66,1143.91, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,77.4100,72.0400,155.3600,93.4900,286.7600,401.2300,序列[2]:0.0000,-22.7200,64.2600,148.5700,392.3000,511.2800,707.5300,2、计算|s0|,|s1|,|s1-s0||s0|=885.675;|s1|=1447.455;|s1-s0|=561.78序列[2]和序列[3]的绝对关联度=0.8060计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1361,1.1267,1.2732,1.1644,1.5042,1.7055, 序列[2]:1.0000,0.9479,1.1473,1.3405,1.8990,2.1716,2.6214,2、序列的始点零化像:序列[1]:0.0000,0.1361,0.1267,0.2732,0.1644,0.5042,0.7055, 序列[2]:0.0000,-0.0521,0.1473,0.3405,0.8990,1.1716,1.6214,3、计算|s0|,|s1|,|s1-s0||s0|=1.55735;|s1|=3.317;|s1-s0|=1.75965结论:序列[2]和序列[3]的相对关联度=0.7695序列[2]和序列[3]:绝对关联度:0.8060;相对关联度:0.7695;综合关联度:0.7878;初始化操作(整理为等长度1-时距序列)序列[1]:568.69,646.1,640.73,724.05,662.18,855.45,969.92,序列[2]:113.24,126.14,141.91,174.48,180.18,216.12,242.02,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,77.4100,72.0400,155.3600,93.4900,286.7600,401.2300,序列[2]:0.0000,12.9000,28.6700,61.2400,66.9400,102.8800,128.7800,2、计算|s0|,|s1|,|s1-s0||s0|=885.675;|s1|=337.02;|s1-s0|=548.655序列[2]和序列[4]的绝对关联度=0.6904计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1361,1.1267,1.2732,1.1644,1.5042,1.7055,序列[2]:1.0000,1.1139,1.2532,1.5408,1.5911,1.9085,2.1372,2、序列的始点零化像:序列[1]:0.0000,0.1361,0.1267,0.2732,0.1644,0.5042,0.7055,序列[2]:0.0000,0.1139,0.2532,0.5408,0.5911,0.9085,1.1372,3、计算|s0|,|s1|,|s1-s0||s0|=1.55735;|s1|=2.9761;|s1-s0|=1.41875结论:序列[2]和序列[4]的相对关联度=0.7959序列[2]和序列[4]:绝对关联度:0.6904;相对关联度:0.7959;综合关联度:0.7432;初始化操作(整理为等长度1-时距序列)序列[1]:568.69,646.1,640.73,724.05,662.18,855.45,969.92, 序列[2]:125.24,120.45,277.09,359.87,446.01,546.47,741.27, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,77.4100,72.0400,155.3600,93.4900,286.7600,401.2300,序列[2]:0.0000,-4.7900,151.8500,234.6300,320.7700,421.2300,616.0300,2、计算|s0|,|s1|,|s1-s0||s0|=885.675;|s1|=1431.705;|s1-s0|=546.03序列[2]和序列[5]的绝对关联度=0.8094计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1361,1.1267,1.2732,1.1644,1.5042,1.7055, 序列[2]:1.0000,0.9618,2.2125,2.8734,3.5612,4.3634,5.9188, 2、序列的始点零化像:序列[1]:0.0000,0.1361,0.1267,0.2732,0.1644,0.5042,0.7055, 序列[2]:0.0000,-0.0382,1.2125,1.8734,2.5612,3.3634,4.9188, 3、计算|s0|,|s1|,|s1-s0||s0|=1.55735;|s1|=11.4317;|s1-s0|=9.87435结论:序列[2]和序列[5]的相对关联度=0.5862序列[2]和序列[5]:绝对关联度:0.8094;相对关联度:0.5862;综合关联度:0.6978;初始化操作(整理为等长度1-时距序列)序列[1]:568.69,646.1,640.73,724.05,662.18,855.45,969.92, 序列[2]:171.23,297.47,351.88,380.39,425.18,491.1,556.19, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,77.4100,72.0400,155.3600,93.4900,286.7600,401.2300,序列[2]:0.0000,126.2400,180.6500,209.1600,253.9500,319.8700,384.9600,2、计算|s0|,|s1|,|s1-s0||s0|=885.675;|s1|=1282.35;|s1-s0|=396.675序列[2]和序列[6]的绝对关联度=0.8454计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1361,1.1267,1.2732,1.1644,1.5042,1.7055, 序列[2]:1.0000,1.7373,2.0550,2.2215,2.4831,2.8681,3.2482,2、序列的始点零化像:序列[1]:0.0000,0.1361,0.1267,0.2732,0.1644,0.5042,0.7055, 序列[2]:0.0000,0.7373,1.0550,1.2215,1.4831,1.8681,2.2482,3、计算|s0|,|s1|,|s1-s0||s0|=1.55735;|s1|=7.4891;|s1-s0|=5.93175结论:序列[2]和序列[6]的相对关联度=0.6288序列[2]和序列[6]:绝对关联度:0.8454;相对关联度:0.6288;综合关联度:0.7371;初始化操作(整理为等长度1-时距序列)序列[1]:436.38,413.66,500.64,584.95,828.68,947.66,1143.91,序列[2]:113.24,126.14,141.91,174.48,180.18,216.12,242.02,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-22.7200,64.2600,148.5700,392.3000,511.2800,707.5300,序列[2]:0.0000,12.9000,28.6700,61.2400,66.9400,102.8800,128.7800,2、计算|s0|,|s1|,|s1-s0||s0|=1447.455;|s1|=337.02;|s1-s0|=1110.435序列[3]和序列[4]的绝对关联度=0.6166计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9479,1.1473,1.3405,1.8990,2.1716,2.6214, 序列[2]:1.0000,1.1139,1.2532,1.5408,1.5911,1.9085,2.1372, 2、序列的始点零化像:序列[1]:0.0000,-0.0521,0.1473,0.3405,0.8990,1.1716,1.6214, 序列[2]:0.0000,0.1139,0.2532,0.5408,0.5911,0.9085,1.1372, 3、计算|s0|,|s1|,|s1-s0||s0|=3.317;|s1|=2.9761;|s1-s0|=0.3409结论:序列[3]和序列[4]的相对关联度=0.9553序列[3]和序列[4]:绝对关联度:0.6166;相对关联度:0.9553;综合关联度:0.7859;初始化操作(整理为等长度1-时距序列)序列[1]:436.38,413.66,500.64,584.95,828.68,947.66,1143.91,序列[2]:125.24,120.45,277.09,359.87,446.01,546.47,741.27, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-22.7200,64.2600,148.5700,392.3000,511.2800,707.5300,序列[2]:0.0000,-4.7900,151.8500,234.6300,320.7700,421.2300,616.0300,2、计算|s0|,|s1|,|s1-s0||s0|=1447.455;|s1|=1431.705;|s1-s0|=15.75序列[3]和序列[5]的绝对关联度=0.9946计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9479,1.1473,1.3405,1.8990,2.1716,2.6214, 序列[2]:1.0000,0.9618,2.2125,2.8734,3.5612,4.3634,5.9188,2、序列的始点零化像:序列[1]:0.0000,-0.0521,0.1473,0.3405,0.8990,1.1716,1.6214, 序列[2]:0.0000,-0.0382,1.2125,1.8734,2.5612,3.3634,4.9188,3、计算|s0|,|s1|,|s1-s0||s0|=3.317;|s1|=11.4317;|s1-s0|=8.1147结论:序列[3]和序列[5]的相对关联度=0.6600序列[3]和序列[5]:绝对关联度:0.9946;相对关联度:0.6600;综合关联度:0.8273;初始化操作(整理为等长度1-时距序列)序列[1]:436.38,413.66,500.64,584.95,828.68,947.66,1143.91, 序列[2]:171.23,297.47,351.88,380.39,425.18,491.1,556.19, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-22.7200,64.2600,148.5700,392.3000,511.2800,707.5300,序列[2]:0.0000,126.2400,180.6500,209.1600,253.9500,319.8700,384.9600,2、计算|s0|,|s1|,|s1-s0||s0|=1447.455;|s1|=1282.35;|s1-s0|=165.105序列[3]和序列[6]的绝对关联度=0.9430计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9479,1.1473,1.3405,1.8990,2.1716,2.6214, 序列[2]:1.0000,1.7373,2.0550,2.2215,2.4831,2.8681,3.2482, 2、序列的始点零化像:序列[1]:0.0000,-0.0521,0.1473,0.3405,0.8990,1.1716,1.6214, 序列[2]:0.0000,0.7373,1.0550,1.2215,1.4831,1.8681,2.2482, 3、计算|s0|,|s1|,|s1-s0||s0|=3.317;|s1|=7.4891;|s1-s0|=4.1721结论:序列[3]和序列[6]的相对关联度=0.7389序列[3]和序列[6]:绝对关联度:0.9430;相对关联度:0.7389;综合关联度:0.8409;初始化操作(整理为等长度1-时距序列)序列[1]:113.24,126.14,141.91,174.48,180.18,216.12,242.02, 序列[2]:125.24,120.45,277.09,359.87,446.01,546.47,741.27,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,12.9000,28.6700,61.2400,66.9400,102.8800,128.7800,序列[2]:0.0000,-4.7900,151.8500,234.6300,320.7700,421.2300,616.0300,2、计算|s0|,|s1|,|s1-s0||s0|=337.02;|s1|=1431.705;|s1-s0|=1094.685序列[4]和序列[5]的绝对关联度=0.6178计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1139,1.2532,1.5408,1.5911,1.9085,2.1372,序列[2]:1.0000,0.9618,2.2125,2.8734,3.5612,4.3634,5.9188,2、序列的始点零化像:序列[1]:0.0000,0.1139,0.2532,0.5408,0.5911,0.9085,1.1372,序列[2]:0.0000,-0.0382,1.2125,1.8734,2.5612,3.3634,4.9188,3、计算|s0|,|s1|,|s1-s0||s0|=2.9761;|s1|=11.4317;|s1-s0|=8.4556结论:序列[4]和序列[5]的相对关联度=0.6457序列[4]和序列[5]:绝对关联度:0.6178;相对关联度:0.6457;综合关联度:0.6317;初始化操作(整理为等长度1-时距序列)序列[1]:113.24,126.14,141.91,174.48,180.18,216.12,242.02,序列[2]:171.23,297.47,351.88,380.39,425.18,491.1,556.19,计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,12.9000,28.6700,61.2400,66.9400,102.8800,128.7800,序列[2]:0.0000,126.2400,180.6500,209.1600,253.9500,319.8700,384.9600,2、计算|s0|,|s1|,|s1-s0||s0|=337.02;|s1|=1282.35;|s1-s0|=945.33序列[4]和序列[6]的绝对关联度=0.6316计算相对关联度:1、序列的初值像:序列[1]:1.0000,1.1139,1.2532,1.5408,1.5911,1.9085,2.1372, 序列[2]:1.0000,1.7373,2.0550,2.2215,2.4831,2.8681,3.2482, 2、序列的始点零化像:序列[1]:0.0000,0.1139,0.2532,0.5408,0.5911,0.9085,1.1372, 序列[2]:0.0000,0.7373,1.0550,1.2215,1.4831,1.8681,2.2482, 3、计算|s0|,|s1|,|s1-s0||s0|=2.9761;|s1|=7.4891;|s1-s0|=4.513结论:序列[4]和序列[6]的相对关联度=0.7176序列[4]和序列[6]:绝对关联度:0.6316;相对关联度:0.7176;综合关联度:0.6746;初始化操作(整理为等长度1-时距序列)序列[1]:125.24,120.45,277.09,359.87,446.01,546.47,741.27, 序列[2]:171.23,297.47,351.88,380.39,425.18,491.1,556.19, 计算绝对关联度:1、序列的始点零化像:序列[1]:0.0000,-4.7900,151.8500,234.6300,320.7700,421.2300,616.0300,序列[2]:0.0000,126.2400,180.6500,209.1600,253.9500,319.8700,384.9600,2、计算|s0|,|s1|,|s1-s0||s0|=1431.705;|s1|=1282.35;|s1-s0|=149.355序列[5]和序列[6]的绝对关联度=0.9479计算相对关联度:1、序列的初值像:序列[1]:1.0000,0.9618,2.2125,2.8734,3.5612,4.3634,5.9188, 序列[2]:1.0000,1.7373,2.0550,2.2215,2.4831,2.8681,3.2482,2、序列的始点零化像:序列[1]:0.0000,-0.0382,1.2125,1.8734,2.5612,3.3634,4.9188, 序列[2]:0.0000,0.7373,1.0550,1.2215,1.4831,1.8681,2.2482,3、计算|s0|,|s1|,|s1-s0||s0|=11.4317;|s1|=7.4891;|s1-s0|=3.9426结论:序列[5]和序列[6]的相对关联度=0.8348序列[5]和序列[6]:绝对关联度:0.9479;相对关联度:0.8348;综合关联度:0.8913;-----------------------------the end-----------------------------。
灰色关联分析

灰色关联分析简介灰色关联分析是一种用于评估多个因素之间相关性的统计分析方法。
它可以帮助我们理解一组因素对于某个指标的影响程度,并且可以用来预测未来的趋势。
原理灰色关联分析基于灰色理论,其核心思想是将样本数据转化为灰色数列,然后通过计算灰色相关度来评估因素之间的关联性。
在灰色关联分析中,我们首先需要确定一个参考数列和一个比较数列,然后根据数列的发展趋势和规律性对它们进行排序。
最后,通过计算两个数列之间的关联度来评估它们之间的关联程度。
灰色关联度的计算方法灰色关联度可以通过以下公式计算:$$ \\rho(i,j) = \\frac{{\\min(\\Delta^*+(k-1)\\Delta^*,\\Delta^*+\\delta^*+(k-1)\\Delta^*,\\Delta^*-\\delta^*+(k-1)\\Delta^*)}}{{\\max(\\Delta^*+(k-1)\\Delta^*,\\Delta^*+\\delta^*+(k-1)\\Delta^*,\\Delta^*-\\delta^*+(k-1)\\Delta^*)}} $$其中,$\\Delta^*$表示相邻数据的差值绝对值的最大值,$\\delta^*$表示数列中数据的最大值与最小值之差。
灰色关联分析步骤1.数据预处理:将原始数据进行标准化处理,使其具有可比性。
2.建立关联矩阵:根据参考数列和比较数列计算灰色关联度,并构建关联矩阵。
3.确定权重:根据关联矩阵的行列和大小确定各因素的权重,权重越大表示因素对目标的影响越大。
4.计算综合关联度:将灰色关联度与权重相乘并求和,得到各个因素的综合关联度。
5.分析结果:根据综合关联度的大小对因素进行排序和评估,得出各因素对目标的贡献程度。
适用领域灰色关联分析在许多领域都有广泛的应用,包括经济、环境、工程等。
它可以用于评估多个因素对某个现象的影响程度,帮助决策者制定合理的决策和策略。
优势与局限灰色关联分析具有以下优势:•可以在样本数据不完整或不完全的情况下进行分析。
灰色关联度+层次分析法
计算结果表明,运输业和工业的关联程度大于农业、商业和工业的关联程度。
k
1 0.595
2 0.082 0.236 0.682 3.002 0.001
3 0.429 0.429 0.142 3 0
4 0.634 0.192 0.174 3.009 0.005
5 0.166 0.166 0.668 3 0
( )
0.264 0.476 0.054 0.098 0.109
( )
1,0.9476,0.9236,0.9148 X1
1,0.9706,1.0294,1.0294 X3
1,1.0639,1.1228,1.1483 X2 1,1.0149,0.8060,0.7015 X4
2nd Step:求序列差
2 0,0.1163,0.1992,0.2335 4 0,0.0673,0.1176,0.2134
灰色关联度分析法灰色关联分析法层次分析法ahp层次分析法层次分析法原理层次分析法案例层次分析法软件模糊层次分析法层次分析法步骤层次分析法确定权重
#2 层次分析法 选择旅游地
解: C1、C2、C3、C4、C5 分别表示景色、费用、居住、饮食、旅途; P1、P2、P3 分别表示桂林、黄山、北戴河。 (1)构造成对比较矩阵:
1 2 A 1 4 1 3 1 3
12 4 1 7 17 1 15 2 15 3
3 5 5 1 2 1 3 1 1 1 1 3
2 5 1 C1 1 2 1 2 1 5 1 2 1 1 3 4 C4 1 3 1 1 1 4 1 1
0.264
76
0.054
0.098
0.109
灰色关联度(讲稿)

(6.7)
min 0i (k ) (min)
(6.8)
4.计算关联系数 对绝对差值阵中数据作如下变换:
首 页 上 页 下 页 尾 页
这样的问题很有实际意义,一个自然的想法就是分 别将三次产业产值的时间序列与GDP的时间序列 进行比较,为了能够比较,先对各序列进行无量纲化, 这里采用均值化法.各序列的均值分别为:2716, 461.5,1228.83,1025.67,上表中每列数据除以其均值 可得均值化序列(如表6-2所示)
尾 页
最后分别对各产业与GDP的关联系数序列求算术 平均可得
1 r01 (0.4191 0.3796 0.5808 0.7055 6 0.3696 0.2881) 0.4571 1 r02 (0.6067 0.5178 0.4903 0.8761 6 0.6141 0.3510) 0.5760 1 r03 (0.8687 0.7257 0.5213 0.7338 6 1.000 0.4758) 0.7209
首 页
上 页 下 页
尾 页
上式可变形为
(min) (max) 0i (t ) 0i (t ) (max) i 1, 2,3; t 2000,, 2005
(6.1)
0i (t )称为序列xi和序列x0在第t期的灰色关联系 数(或简称为关联系数). 由(6.1)式可以看出, 取值的大小可以控制(max) 对数据转化的影响, 取较小的值,可以提高关联 系数间差异的显著性,因而称 为分辨系数. 利用(6.1)对表6-3中绝对差值0i (t ) 进行规范化,取 0.4, 结果见表6-4,以01 (2000)计算为例:
01 (t )
灰色关联分析

灰色关联分析关联分析实际上是动态过程发展态势的量化比较分析,所谓发展态势比较,就是系统各时期有关统计数据的几何关系比较例如,某地区1977~1983年总收入与养猪、养兔收入如下表根据上表做散点图如下:显然,曲线A与曲线B发展趋势比较接近,而与曲线C相差较大,因此可以判断,该地区对总收入影响较直接的是养猪业,而不是养兔业。
很显然,几何形状越接近,关联程度也就越大。
当然,直观分析对于稍微复杂的问题则显得难以进行。
因此需要给出一种计算方法来衡量因素间关联程度的大小。
关联分析定义 选取参考数列00000{()|1,2,...}((1),(2),...,())x x k k n x x x n ===假设有m 个比较数列{()|1,2,...}((1),(2),...,())i i i i i x x k k n x x x n ===则称0000min min |()()|max max |()()|()|()()|max max |()()|s s ststi i s stx t x t x t x t k x t x t x t x t ρξρ-+-=-+-(1)为比较数列i x 对参考数列0x 在k 时刻的关联系数,其中[0,1]ρ∈称为分辨系数。
(1)中0min min |()()|s stx t x t -、0max max |()()|s stx t x t -分别称为两级最小差及两级最大差。
一般,分辨系数ρ越大,分辨率越大;ρ越小,分辨率越小。
(1)式定义的关联系数是描述比较数列与参考数列在某时刻关联程度得一种指标,由于各个时刻都有一个关联数,因此信息显得过于分散,不便比较,为此给出如下定义。
定义:称11()ni i i r k n ξ==∑ 为数列i x 对参考数列0x 的关联度。
因此,关联度就是把各个时刻的关联系数集中为一个平均值,从而把分散的信息集中处理。
利用关联度这个概念,我们可以对各种问题进行因素分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章灰色关联度分析目录壹、何谓灰色关联度分析 ------------------------- 5-2贰、灰色联度分析实例详说与练习 ----------------- 5-8负责组员工教行政硕士班二年级周世杰591701017陶虹沅591701020林炎莹591701025第五章灰色关联度分析壹、何谓灰色关联度分析一.关联度分析灰色系统分析方法针对不同问题性质有几种不同做法,灰色关联度分析(Grey Relational Analysis)是其中的一种。
基本上灰色关联度分析是依据各因素数列曲线形状的接近程度做发展态势的分析。
灰色系统理论提出了对各子系统进行灰色关联度分析的概念,意图透过一定的方法,去寻求系统中各子系统(或因素)之间的数值关系。
简言之,灰色关联度分析的意义是指在系统发展过程中,如果两个因素变化的态势是一致的,即同步变化程度较高,则可以认为两者关联较大;反之,则两者关联度较小。
因此,灰色关联度分析对于一个系统发展变化态势提供了量化的度量,非常适合动态(Dynamic)的历程分析。
灰色关联度可分成「局部性灰色关联度」与「整体性灰色关联度」两类。
主要的差别在于「局部性灰色关联度」有一参考序列,而「整体性灰色关联度」是任一序列均可为参考序列。
二.直观分析依据因素数列绘制曲线图,由曲线图直接观察因素列间的接近程度及数值关系,表一某老师给学生的评分表数据数据为例,绘制曲线图如图一所示,由曲线图大约可直接观察出该老师给分总成绩主要与考试成绩关联度较高。
表一某一老师给学生的评分表单位:分/ %由曲线图直观分析,是可大略分析因素数列关联度,可看出考试成绩与总成绩曲线形状较接近,故较具关联度,但若能以量化分析予以左证,将使分析结果更具有说服力。
三. 量化分析量化分析四步曲:1. 标准化(无量纲化):以参照数列(取最大数的数列)为基准点,将各数据标准化成介于0至1之间的数据最佳。
2. 应公式需要值,产生对应差数列表,内容包括:与参考数列值差(绝对值)、最大差、最小差、ζ(Zeta )为分辨系数,0<ζ<1,可设ζ = 0.5(采取数字最终务必使关联系数计算:ξi (k )小于1为原则,至于分辨系数之设定值对关联度并没影响,请参考p14例)3. 关联系数ξi (k )计算:应用公式 maxoi(k)maxmin )(∆+∆∆+∆=ζζξk i 计算比较数列X i 上各点k 与参考数列X 0 参照点的关联系数,最后求各系数的平均值即是X i 与X 0 的关联度r i 。
4. 比较各关联度大小,值愈大,关联度越高。
实例参考(一):根据某一老师给学生成绩的数据数据,依灰色关联度分析法,计算出考试成绩及出席率与学生成绩的关联度。
设分辨系数:ζ=0.5表一某一老师成绩表单位:分/%1、标准化2、对应差数列表()k Nr iNk iξ11=∑=()708.035.0625.01311311=++=∑==k r k ξ3、关联系数计算:ξi (k )ζ=0.5、最大差 0.20、 最小差0(一)、求比较数列X 1对参考数列X 0之关联系数ξ1(k )625.02.05.006.02.05.00m ax )2(m ax m in )2(011=⨯+⨯+=∆+∆∆+∆=ζζξ(二)、求比较数列X 2对参考数列X 0之关联系数ξ2(k )4、求关联度 :即求比较数列所有数关联度的平均值(一)、比较数列X 1对参考数列X 0之关联度(二)、比较数列X 2对参考数列X 0之关联度12.05.002.05.00m ax )1(m ax m in )1(011=⨯+⨯+=∆+∆∆+∆=ζζξ5.02.05.01.02.05.00m ax )3(m ax m in )3(011=⨯+⨯+=∆+∆∆+∆=ζζξ667.02.05.005.02.05.00m ax )2(m ax m in )2(022=⨯+⨯+=∆+∆∆+∆=ζζξ333.02.05.02.02.05.00m ax )3(m ax m in )3(022=⨯+⨯+=∆+∆∆+∆=ζζξ12.05.002.05.00m ax )1(m ax m in )1(022=⨯+⨯+=∆+∆∆+∆=ζζξ()667.03333.0667.01312312=++=∑==k r k ξ1r 2r> 故该教授给的总成绩主要与考试成绩关联度较高。
量化分析公式内容说明:(一)、标准化(无量纲化)由于系统中各因素列中的数据,可能因计算单位的不同,不便于比较,或在比较时难以得到正确的结论。
因此在进行灰色关联度分析时,一般都要进行标准化(无量纲化)的数据处理。
(二)、关联系数:ξ(Xi )所谓关联程度,实质上是曲线间几何形状的差别程度。
因此曲线间差值大小,可做为关联程度的衡量尺度。
对于一个参考数列X 0有若干个比较数列X 1, X 2,…, X n 。
各比较数列与参考数列在各个时刻(即曲线中的各点)的关联系数ξ(Xi )可由下列公式算出:()()()()()()()()()||max max ||||max max ||min min 0000k X k X k X k X k X k X k X k X k i kii i kii kii -+--+-=ζζξ其中 ζ(Zeta )为分辨系数,0<ζ<1()()||min min 0k X k X i ki- 为两层式取绝对差值中最小值计算,第一层为先分别由各比较数列X i曲线上的每一个点与参考数列X0曲线上的每一个点之绝对差值中取最小值,再由这些最小值当中选取最小值。
简记为Δmin。
()()||max max 0k X k X i ki-为两层式取绝对差值中最大值计算,第一层为先分别由各比较数列X i 曲线上的每一个点与参考数列X 0曲线上的每一个点之绝对差值取最大值,再由这些最大值当中选取最大值。
简记为Δmax 。
()()||0k X k X i -为各比较数列X i 曲线上的每一个点与参考数列X 0曲线上的每一个点之绝对差值。
记为Δoi(k)。
所以关联系数ξ(Xi )也可简化如下列公式:m axoi(k)m axm in )(∆+∆∆+∆=ζζξk i(三)、关联度 :r i因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而讯息过于分散不便于进行整体性比较。
因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,也就是求其平均值,做为比较数列与参考数列间关联程度的数量表示,关联度r i 公式如下:()k N r i Nk i ξ11=∑=貳、 灰色联度分析实例详说如表一某家庭收入来源数据数据为例:表一某家庭 1998 ~ 2000年收入单位:十万元绘制曲线图如图二所示:【关联度分析】一.标准化(无量纲化)以1998年收入为基准,将表一进行标准化(无量纲化)处理后得表二:表二标准化后的数列表二. 求最大差值()()||max max 0k X k X i ki-与最小差值()()||min min 0k X k X i ki-为求得()()||min min 0k X k X i ki-及()()||max max 0k X k X i ki-值,必须先求出各比较数列与参考数列之「对应差数列表」如表三: 表三 对应差数列表由表三对应差数列表得知各比较数列对参考数列各点对应差值中之最小值:()()0||min min 0=-k X k X i ki,即Δmin=0各比较数列对参考数列各点对应差值中之最大值:()()3.0||max max 0=-k X k X i ki,即Δmax=0.3三. 关联系数计算:ξi (k ) 设分辨系数:ζ=0.5(一)、求比较数列X 1对参考数列X 0之关联系数ξ1(k )1、13.05.003.05.00m ax )1(m ax m in )1(011=⨯+⨯+=∆+∆∆+∆=ζζξ2、375.03.05.025.03.05.00m ax )2(m ax m in )2(011=⨯+⨯+=∆+∆∆+∆=ζζξ3、667.03.05.0075.03.05.00m ax )3(m ax m in )3(011=⨯+⨯+=∆+∆∆+∆=ζζξ(二)、求比较数列X 2对参考数列X 0之关联系数ξ2(k )1、13.05.003.05.00m ax )1(m ax m in )1(022=⨯+⨯+=∆+∆∆+∆=ζζξ2、333.03.05.03.03.05.00m ax )2(m ax m in )2(022=⨯+⨯+=∆+∆∆+∆=ζζξ3、429.03.05.02.03.05.00m ax )3(m ax m in )3(022=⨯+⨯+=∆+∆∆+∆=ζζξ四. 求关联度 :()k Nr i Nk i ξ11=∑= (一)、比较数列X 1对参考数列X 0之关联度()68.03667.0375.01311311=++=∑==k r k ξ(二)、比较数列X 2对参考数列X 0之关联度()587.03429.0333.01312312=++=∑==k r k ξ五. 结论由上列运算得知:比较数列X 1对参考数列X 0之关联度68.01=r比较数列X 2对参考数列X 0之关联度587.02 r1r >2r故该家庭总收入主要与薪资收入关联度较高。
六、练习:公路建设招标中取最接近标准者得标,请问何者得标?设分辨系数:ζ=0.5厂商及指标 标准标X0 A 厂 X1 B 厂 X2 C 厂 X3 造价(亿) 1.1 1.1 1.2 1.5 建设期限(年) 1.3 1.8 1.5 1.3 车流(百辆) 5 4 3 5 车速(公里/时)11080110100解题: 一、标准化厂商及指标 标准标X0A 厂 X1B 厂 X2C 厂 X3 造价 1 1.00 1.09 1.36 建设期限 1 1.38 1.15 1.00 车流 1 0.80 0.60 1.00 车速10.731.000.91二、对应差数列表指标 ()()||10k X k X - ()()||20k X k X - ()()||30k X k X -kminkmax造价 0.00 0.09 0.36 0.00 0.36 建设期限 0.38 0.15 0.00 0.00 0.38 车流 0.20 0.40 0.00 0.00 0.40 车速0.270.000.09 0.000.27三、关联系数与关联度关联系数ξi (k )ξ1(k )ξ2(k )ξ3(k )造价 1.00 0.69 0.35 建设期限 0.34 0.57 1.00 车流 0.50 0.33 1.00 车速 0.42 1.00 0.69 关联度 r i0.570.650.76r 3 > r 2 > r 1答: C 厂得标为暸解分辨系数的设定对关联度是否造成影响?以下将分辨系数分别以0.2、0.4、0.6、0.8来计算,由以下的结果得知:分辨系数并不影响关联度的判别,但以分辨系数为 0.2 时关联度曲线倾斜角最大最具判断性。
