灰色关联度分析
(整理)灰色关联度分析法
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。
作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。
因此, 进行科学全面的供应商评价就显得十分必要。
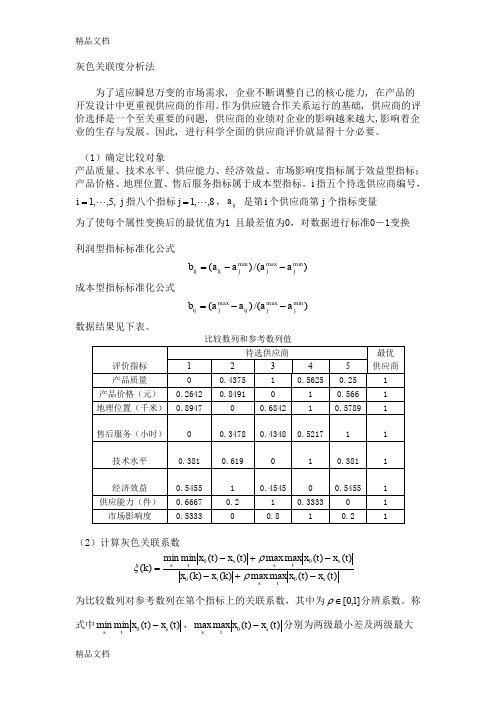
（1）确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标；产品价格、地理位置、售后服务指标属于成本型指标。
i 指五个待选供应商编号，,5,,1 =i j 指八个指标8,,1j =，ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0，对数据进行标准0－1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。
（2）计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数，其中为]1,0[∈ρ分辨系数。
称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。
一般来讲，分辨系数ρ越大，分辨率越大；ρ越小，分辨率越小。
在这里ρ取0.5。
（3）计算灰色加权关联度 灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。
关联系数和关联度值（4）评价分析根据灰色加权关联度的大小，对各评价对象进行排序，可建立评价对象的关联序，关联度越大其评价结果越好。
灰色关联度分析
1.灰色关联理论
1982年，华中理工大学邓聚龙教 授首先提出灰色系统的概念，并建立了 灰色系统理论。 灰色系统理论认为，人们对客观 事物的认识具有广泛的灰色性，就是信 息的不完全性和不确定性，因而有客观 事物所形成的是一种灰色系统，即部分 信息已知、部分信息未知的系统。例如： 社会系统、经济系统、生态系统等都可 以看作是灰色系统。
\\
(min) (max) 0i (k ) 0i (k ) (max)
最后分别对各产业与GDP的关联系数求 平均可得： r01= （0.4191+0.3796+0.5808+0.7055+0.3696 +0.2881）/6 =0.4571 同样求出： r02=0.5760， r03=0.7209 r0i称为序列x0和xi（i=1，2，3）的灰 色关联。由于r03˃r02˃ r01，因而第三 产业产值与GDP的关联度最大，其次是 第二产业，第一次去农业。
5.用GRA进行综合评价
灰色关联分析的目的是揭示因素间 关系的强弱，其操作对象是因素的时间 序列，最终的结果表现为通过关联度对 各比较序列做出排列。综合评价的对象 也可以看作是时间序列（每个被评价事 物对应的各项指标值），并且往往需要 对这些时间序列做出排序，因而也可以 借助灰色关联分心来进行。
01 (1) 02 (1) ... 0 n (1) (2) (2) ... (2) 01 02 0n ... ... ... 01 ( N ) 02 ( N ) ... 0 n ( N ) N n 其中 0i (k ) x0 (k ) xi (k ) (05式) i 1,2,...n; k 1,2,..., N 绝对差矩阵中最大数和 最小数就是最大差和最 小差： max 0i (k ) (max)( 式) 06
灰色关联分析详解+结果解读
灰色关联分析1、作用对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度，称为关联度。
在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。
因此，灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。
2、输入输出描述输入:特征序列为至少两项或以上的定量变量，母序列（关联对象）为 1 项定量变量。
输出:反应考核指标与母序列的关联程度。
3、案例示例案例:分析 09-18 年内，影院数量，观影人数，票价、电影上线数量这些因素对全年电影票房的影响。
其中电影票房是母序列，影院数量，观影人数，票价、电影上线数量是特征序列。
4、案例数据灰色关联分析案例数据5、案例操作Step1：新建分析；Step2：上传数据；Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；step4：选择【灰色关联分析】；step5：查看对应的数据数据格式，【灰色关联分析】要求特征序列为定量变量，且至少有一项；要求母序列为定量变量，且只有一项。
step6：设置量纲处理方式（包括初值化、均值化、无处理）、分辨系数（ρ越小，分辨力越大，一般ρ的取值区间为 ( 0 ，1 )，具体取值可视情况而定。
当ρ≤ 0.5463 时，分辨力最好，通常取ρ = 0.5 ）step7：点击【开始分析】，完成全部操作。
6、输出结果分析输出结果 1：灰色关联系数图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值（数字越大，代表关联性越强）。
输出结果 2：关联系数图分析：输出结果 1 和输出结果 2 是一样的，输出结果 1 用了表格形式来呈现关联系数，输出结果 2 用了图表形式来呈现关联系数。
图表很直观地展现了，大多数年份的银幕数量和电影上线数量对票房影响更大。
灰色关联度分析
灰色关联度分析一、 灰色关联分析及理论对于两系统之间的因素，其随时间或不同对象而变化的关联性的大小的量度，称为关联度。
在系统发展过程中，若两个因素变化的趋势具有一致性，即变化程度较高，即可谓二者的关联度较高；反之，则较低。
因此，灰色关联度分析方法，是根据因素之间发展趋势的相似或相异程度，即“灰色关联度”作为衡量因素之间关联程度的一种方法。
灰色系统理论提出了对各子系统进行灰色关联度分析的概念，意图透过一定方法，去寻求系统各子系统（或因素）之间数值的关系。
因此，灰色关联度分析对于一个系统的发展变化态势提供了量化的度量，非常适合动态历程分析。
灰色关联度分析方法模型灰色综合评价主要是依据以下模型：R=Y×W式中，R 为M 个被评价对象的综合评价结果向量；W 为N 个评价指标的权重向量；E 为各指标的评判矩阵，（矩阵略）)(k i ξ为第i 个被评价对象的第K 个指标与第K 个最优指标的关联系数。
根据R 的数值，进行排序。
（1）确定最优指标集设],,[**2*1n j j j F =,式中*k j 为第k 个指标的最优值。
此最优序列的每个指标值可以是诸评价对象的最优值，也可以是评估者公认的最优值。
选定最优指标集后，可构造矩阵D （矩阵略）式中ikj 为第i 个期货公司第k 个指标的原始数值。
（2）指标的规范化处理由于评判指标间通常是有不同的量纲和数量级，故不能直接进行比较，为了保证结果的可靠性，因此需要对原始指标进行规范处理。
设第k 个指标的变化区间为],[21k k j j ,1k j 为第k 个指标在所有被评价对象中的最小值，2k j 为第k 个指标在所有被评价对象中的最大值，则可以用下式将上式中的原始数值变成无量纲值)1,0(∈ikC 。
ikk k i ki k j j j j C --=21，m i,2,1=，n k ,,2,1 =（矩阵略）（3）计算综合评判结果 根据灰色系统理论，将],,,[}{**2*1*n C C C C=作为参考数列，将],,,[}{21i n i i C C C C =作为被比较数列，则用关联分析法分别求得第i 个被评价对象的第k 个指标与第k 个指标最优指标的关联系数，即i kkkii kki k k k ii k k kiCC C C C C C C k -+--+-=****i max max max max min min )ρρξ（式中)1,0(∈ρ，一般取5.0=ρ。
灰色关联分析
灰色关联分析灰色关联分析是一种常用于研究和预测多个影响因素之间关联程度的方法。
该分析方法可以通过对各个因素的数值进行比较，得出它们之间的关联强度，从而为决策提供依据。
下面将详细介绍灰色关联分析的原理、应用以及优势。
灰色关联分析的原理基于灰色系统理论，该理论是中国科学家陈纳德于1982年提出的一种对部分已知和部分未知信息进行分析的数学方法。
灰色关联分析将各个影响因素的数据进行标准化处理，然后计算各个因素之间的关联度。
通过对关联度进行排序，即可得出影响因素之间的关联程度大小。
灰色关联分析在各个领域都有广泛的应用，比如经济学、管理学、环境科学等。
在经济学领域，可以使用灰色关联分析来研究不同经济指标之间的关联程度，从而预测未来的经济趋势。
在管理学中，可以利用灰色关联分析来研究不同管理指标之间的关联程度，进而指导管理决策。
在环境科学领域，可以运用灰色关联分析来分析各个环境因素对生态系统的影响程度，以及控制污染等。
灰色关联分析相对于其他分析方法有一些独特的优势。
首先，它不要求数据分布满足正态分布等数学假设，可以对数据进行较好的处理。
其次，灰色关联分析可以处理样本量较小的情况，对于样本量不足的数据分析也有较好的适用性。
此外，由于灰色关联分析能够捕捉到数据之间的内在联系，因此对于某些非线性关系的分析，其结果可能更加准确。
然而，灰色关联分析也存在一些限制和不足之处。
首先，该分析方法依赖于数据的稳定性，对于非稳态的数据可能会导致分析结果不准确。
其次，灰色关联分析无法处理存在时间滞后效应的数据。
此外，该方法对数据的标准化要求较高，如果数据质量较差或者存在异常值，也会影响分析结果。
综上所述，灰色关联分析是一种研究和预测多个影响因素之间关联程度的有效方法。
它的原理基于灰色系统理论，可以在各个领域中广泛应用。
灰色关联分析相对于其他分析方法有一些独特的优势，但也存在一定限制。
在实际应用中，我们应该结合具体情况，合理选择分析方法，并充分考虑其适用性和局限性，以提高分析和决策的准确性。
灰色关联分析
灰色关联分析简介灰色关联分析是一种用于评估多个因素之间相关性的统计分析方法。
它可以帮助我们理解一组因素对于某个指标的影响程度，并且可以用来预测未来的趋势。
原理灰色关联分析基于灰色理论，其核心思想是将样本数据转化为灰色数列，然后通过计算灰色相关度来评估因素之间的关联性。
在灰色关联分析中，我们首先需要确定一个参考数列和一个比较数列，然后根据数列的发展趋势和规律性对它们进行排序。
最后，通过计算两个数列之间的关联度来评估它们之间的关联程度。
灰色关联度的计算方法灰色关联度可以通过以下公式计算：$$ \\rho(i,j) = \\frac{{\\min(\\Delta^*+(k-1)\\Delta^*,\\Delta^*+\\delta^*+(k-1)\\Delta^*,\\Delta^*-\\delta^*+(k-1)\\Delta^*)}}{{\\max(\\Delta^*+(k-1)\\Delta^*,\\Delta^*+\\delta^*+(k-1)\\Delta^*,\\Delta^*-\\delta^*+(k-1)\\Delta^*)}} $$其中，$\\Delta^*$表示相邻数据的差值绝对值的最大值，$\\delta^*$表示数列中数据的最大值与最小值之差。
灰色关联分析步骤1.数据预处理：将原始数据进行标准化处理，使其具有可比性。
2.建立关联矩阵：根据参考数列和比较数列计算灰色关联度，并构建关联矩阵。
3.确定权重：根据关联矩阵的行列和大小确定各因素的权重，权重越大表示因素对目标的影响越大。
4.计算综合关联度：将灰色关联度与权重相乘并求和，得到各个因素的综合关联度。
5.分析结果：根据综合关联度的大小对因素进行排序和评估，得出各因素对目标的贡献程度。
适用领域灰色关联分析在许多领域都有广泛的应用，包括经济、环境、工程等。
它可以用于评估多个因素对某个现象的影响程度，帮助决策者制定合理的决策和策略。
优势与局限灰色关联分析具有以下优势：•可以在样本数据不完整或不完全的情况下进行分析。
灰色关联度分析GreyRelationalAnalysis是其中的一种
（ X0 ） 考試成績 考 詴 成 績 出席率 （ X1 ） 出 席 （ X2 ） 率
評分項
實例參考 ( 一 ) 六、綀習題
Hale Waihona Puke 周世傑 周阿舍 100 100 90 100% 90
100%
說明 劉阿華 蕭阿薔 蕭阿薔 劉阿華
95 95 80 90% 80
90%
60 以周阿 60 50 舍為基 80% 50
80% 準點
1、標準化
姓名 評分項目
周阿舍 1 1 1
劉阿華 0.95 0.89 0.90
蕭阿薔 0.60 0.50 0.80
總成績（X0） 考詴成績（X1） 出席率（X2）
2、對應差數列表
差值 姓名 差式
周阿舍 0 0
劉阿華 0.06 0.05
蕭阿薔 0.1 0.2
min
k
max
k
| X 0 k X 1 k |
灰色關聯度可分成「局部性灰色關 聯度」與「整體性灰色關聯度」兩 類。主要的差別在於「局部性灰色 關聯度」有一參考序列，而「整體 性灰色關聯度」是任一序列均可為 參考序列。
二.直觀分析
依據因素數列繪製曲線圖，由曲 線圖直接觀察因素列間的接近程 度及數值關係，表一某老師給學 生的評分表數據資料為例，繪製 曲線圖如圖一所示，由曲線圖大 約可直接觀察出該老師給分總成 績主要與考詴成績關聯度較高。
第五章 灰色關聯度分析
目錄
壹、何謂灰色關聯度分析 5-2 貳、灰色聯度分析實例詳說與練習 5-8
負責組員 工教行政碩士班二年級 周世傑591701017 陶虹沅591701020 林炎瑩591701025
壹、何謂灰色關聯度分析
灰色关联分析方法
灰色关联分析方法灰色关联分析方法（Grey Relational Analysis，GRA）是一种多指标决策方法，它用于研究因素之间的关联程度。
与传统的关联分析方法相比，灰色关联分析方法具有较强的适用性和灵活性。
它可以用于分析多个指标之间的关联程度，对于复杂决策问题具有较强的应用能力。
灰色关联分析方法的基本思想是将系统的各个指标转化为灰色数列，再利用灰色关联度来评估指标之间的关联程度。
该方法可以对多个指标进行综合评价，找出各个指标之间的关联程度，并根据关联程度来进行排序和决策。
灰色关联分析方法的具体步骤如下：1. 数据预处理：将原始数据进行标准化处理，以确保各指标在同一数量级上进行比较。
2. 构建灰色数列：将标准化后的数据转化为灰色数列，通过建立灰色微分方程来描述数据序列的发展趋势。
3. 确定关联度测度：根据灰色数列的特点，选择适当的关联度测度方法来计算指标之间的关联程度。
4. 计算关联度：根据所选择的关联度测度方法，计算每个指标与其他指标之间的关联度。
5. 排序和决策：根据计算得到的关联度值进行排序，并作出相应的决策。
灰色关联分析方法的优点有以下几个方面：1. 适用性广泛：灰色关联分析方法适用于各种类型的指标数据，包括定量指标和定性指标。
2. 考虑了指标之间的时序关系：灰色关联分析方法考虑了指标数据的时序性，能够更好地反映指标之间的演变趋势。
3. 简单易行：灰色关联分析方法不需要过多的统计方法和复杂的计算过程，容易被理解和操作。
4. 提供了多指标综合评价的能力：灰色关联分析方法可以将多个指标之间的关联程度综合考虑，对于决策问题的综合评价有着较好的效果。
然而，灰色关联分析方法也存在一些限制和局限性：1. 灵敏度不高：由于灰色关联分析方法只考虑了指标之间的线性关联程度，对于非线性关系的刻画较为困难，灵敏度较低。
2. 依赖于初始数据：灰色关联分析方法对初始数据的选取较为敏感，不同的初始数据可能导致不同的关联度结果。
灰色关联分析法(灰色综合评价法)
灰色关联分析法对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度，称为关联度。
在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。
因此，灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法。
应用于综合评价（灰色综合评价）步骤：（1） 确定比较对象（评价对象）和参考数列（评价标准）。
设评价对象有m 个，评价指标有n 个，参考数列为{}00()|1,2,,x x k k n ==⋅⋅⋅，比较数列为{}()|1,2,,,1,2,,i i x x k k n i m ==⋅⋅⋅=⋅⋅⋅。
（2） 对参考数列和比较数列进行无量纲化处理由于系统中各因素的物理意义不同，导致数据的量纲也不一定相同，不便于比较，或在比较时难以得到正确的结论。
因此在进行灰色关联度分析时，一般都要进行无量纲化的数据处理。
设无量纲化后参考数列为{}00()|1,2,,x x k k n ''==⋅⋅⋅，无量纲化后比较数列为{}()|1,2,,,i i x x k k n ''==⋅⋅⋅1,2,,i m =⋅⋅⋅。
（3） 确定各指标值对应的权重。
可用层次分析法等确定各指标对应的权重[]12,,,n w w w w =⋅⋅⋅，其中(1,2,,)k w k n =⋅⋅⋅为第k 个评价指标对应的权重。
（4） 计算灰色关联系数：0000min min ()()max max ()()()()()max max ()()s s s t s t i i s s tx t x t x t x t k x k x k x t x t ρξρ''''-+-=''''-+- 为比较数列i x 对参考数列0x 在第k 个指标上的关联系数，其中[]0,1ρ∈为分辨系数，称0min min ()()s s t x t x t ''-、0max max ()()s s tx t x t ''-分别为两级最小差及两级最大差。
灰色关联度分析法
灰色关联度分析法引言灰色关联度分析法是一种用于揭示变量之间关联程度的方法。
它可以在缺乏足够数据的情况下，通过对变量之间的相关性进行评估，帮助分析人员做出决策。
在本文中，我们将介绍灰色关联度分析法的原理和应用，并探讨其在实际问题中的价值和局限性。
一、灰色关联度分析法的原理灰色关联度分析法是在灰色系统理论基础上发展起来的一种关联性分析方法。
灰色关联度分析法的核心思想是通过模糊度量的方法，将样本数据的数量化描述量和次序特征结合起来，通过计算变量间的关联度，得出它们之间的相关性。
具体而言，灰色关联度分析法的步骤主要包括以下几个方面：1. 数据标准化：将原始数据进行归一化处理，以消除变量之间的量纲差异，使其具有可比性。
2. 确定参考序列：在给定的多个序列中，根据研究目标和实际需求，选择一个作为参考序列，其他序列将与之进行比较。
3. 计算关联度指数：通过计算每个序列与参考序列之间的关联度指数，来评估它们之间的关联程度。
关联度指数的计算通常有多种方法，如灰色关联度、相对系数法等。
4. 判别等级：根据关联度指数的大小，将序列划分为几个等级，以便更直观地评估变量之间的关联程度。
二、灰色关联度分析法的应用灰色关联度分析法在许多领域和问题中都有广泛的应用。
下面将介绍一些典型的应用情况：1. 经济领域：灰色关联度分析法可以用于评估经济指标之间的关联性，识别影响经济发展的主要因素，帮助政府和企业做出相应的调整和决策。
2. 工业制造业：在工业制造领域，灰色关联度分析法可以用于优化生产工艺，提高产品质量，降低成本。
通过分析不同因素对产品质量的影响程度，可以找出关键因素，并制定相应的改进措施。
3. 市场调研：在市场调研中，灰色关联度分析法可以用于分析消费者行为和市场趋势，预测产品的需求量和销售额。
通过对多个变量之间的关联性进行评估，可以为企业的市场营销决策提供有价值的参考和支持。
4. 环境管理：在环境管理领域，灰色关联度分析法可以用于评估各种环境因素对生态系统的影响程度，为环境保护和可持续发展提供科学依据。
灰色关联度分析 简介
4、计算 绝对值差
5、确定 极大差值与 极小差值
灰色关联综合评价
6、计算关 联系数
7、确计算 关联序
8、计算综 合评价值
i
()
min i
min x k
x0 (k)
0(k)
xi (k)
max max
i
k
x0 (k)
xi
xi (k)
max max
i
k
x0 (k)
xi (k )
灰色关联分析与回归分析区别
问题：对该地区总收入影响较直接的是养猪业还是养 兔业？
灰色关联综合评价
1、收集 分析数据
2、确定 参考数据列
3、无量纲化 处理
X1, X 2
,
X n
x1 1 x1 2
x1 m
x2 1 x2 2
x2 m
(k)
（12 5)
k 1, , m
r0i
1 m
m
i (k )
k 1
r0i
1 m
m
Wk
k 1
i (k)
（k=1,
式中Wk为各指标权重。
, m）
应用
例1：利用灰色关联分析对6位教师工作 状况进行综合分析
1．分析指标包括：专业素质、外语水平 、教学工作量、科研成果、论文、著作 与出勤．
应用
7．分别计算每个人各指标关联系数的均
值（关联序）：
r01
0.778 1.000
0.778
0.636 7
灰色关联度分析法
灰色关联度分析法
灰色关联度分析法（Grey Relational Analysis，GRA）是一种多属性
决策分析的统计方法，是一个在变量未知情况下实现系统模型和控制
不确定性的有用工具。
灰色关联度分析法主要用于研究和分析影响多
维度多属性数据测量结果的各种因素之间的相关关系。
它对模糊数据
进行综合处理，可以把多维评价分解成基本的准则来实现。
灰色关联度分析法的原理是利用灰色关联度的基本定义来衡量某种系
统的相关程度，灰色关联度通过确定系统的相似度和差异度来计算相
关程度，以此作为最终判断结果。
首先，将所有系统样本的信息表示
成一维度序列，并计算各时间点的灰色关联度。
其次，将灰色关联度
转化成定量指标，以此确定每一种系统的相关程度。
最后，根据定量
指标的值，把每一种系统分成几个类，以便于进一步分析和研究。
灰色关联度分析法可以应用于多种领域，例如工程设计、产品设计、
资源调配等。
例如，当进行工程设计时，可以利用灰色关联度分析法，通过灰色关联度来考虑多种参数和因素，以便最大限度地满足工程项
目的要求。
总之，灰色关联度分析法是一种有效的多属性决策分析方法，在许多
领域得到了广泛的应用，对于多维度和多属性问题具有显著优势。
有
效地利用灰色关联度分析法，能够更好地实现系统模型和控制不确定性，有助于优化效率和提高决策水平。
灰色关联度分析
就可求得两级最大差Δ(max)和两级最小差Δ(min) 计算关联系数
计算第i 个被评价对象与最优参考序列间的关联 系数。
计算关联度
对各评价对象分别计算其p个指标与参考序列对应元素的关联系数的
均值，以反映各评价对象与参考序列的关联关系，称其为关联度，
记为 0i
1
P
(k)
P 0i k1
i1,2,..n.,
第六步 排关联序 由关联度数值可看出，r03＞r01＞r02。这表明，三种工资对工资总 额的关联程度的排列顺序为：承包工资、计时工资、档案工资。即该 公路施工企业的工资发展方向是以承包工资为主导，计时工资和档案 工资对工资总额的影响属于同一水平。
综合评价
基本思路是： 从样本中确定一个理想化的最优样本，以此为参考数列，通过计 算各样本序列与该参考序列的关联度，对被评价对象做出综合比 较和排序。
灰色关联度分析的运用
➢因 素 分 析 ➢综 合 评 价
因素分析
第一步 对数据做均值化处理
第二步 计算各比较数列同参考数列在同一时期的绝对差 再分别计算出其余4年的各绝对差
第三步 找出两极最大差与最小差
第四步 计算关联系数，取分辨系数
，则计算公式为：
第五步 计算关联度。
利用表4，分别求各个数列每个时期的关联系数的平均值即得关联度：
一般地，三种方法不宜混合、重叠作用，在进行系统因素分析时， 可根据实际情况选用其中一个。
若系统 因素 X i 与系统主行为 X
可以将其逆化或倒数化后进行计算。
0
呈负相关关系，我们
逆化
倒数化
关联系数的计算
设经过数据处理后的参考数列为：
比较数列为：
从几何角度看，关联程度实质上是参考数列与比较数列曲线形状的相似程度。凡 比较数列与参考数列的曲线形状接近，则两者间的关联度较大；反之，如果曲线 形状相差较大，则两者间的关联度较小。因此，可用曲线间的差值大小作为关联 度的衡量标准。 则：
灰色关联度分析
灰色关联度分析灰色关联度分析是一种常用的多指标决策方法，它可以用于相关性较强但不易被直接比较的指标之间的关联度分析。
该方法最早由中国工程师陶行知在20世纪50年代提出，并在实践中得到广泛应用。
灰色关联度分析的基本思想是将研究对象的各个指标进行数值标准化处理，以消除量纲和单位的差异。
然后，根据数据序列中的变化趋势，寻找出存在的关联规律。
通过计算不同指标之间的关联度，可以确定其相关性的强弱程度。
具体而言，灰色关联度分析的步骤如下：首先，将各个指标的原始数据进行正态化处理，将其限制在0-1之间。
然后，根据数据的发展趋势，构建关联数列，并计算相邻数据之间的差值。
接下来，通过计算累加生成序列的绝对值来确定各个指标的权重。
最后，根据权重值计算出不同指标之间的关联度。
灰色关联度分析的优点是能够充分考虑不同指标之间的相关程度，避免了单指标评价所带来的不足之处。
它对于数据规模较小、数据质量较差的情况下仍能有效分析，并且可以通过调整权重值来考虑不同指标的重要性。
此外，灰色关联度分析方法简单易行，不需要大量数据和复杂的运算，适用范围广泛。
然而，灰色关联度分析也存在一些限制和不足之处。
首先，该方法对于数据的处理比较敏感，一旦数据质量较差或者变化趋势不明显，分析结果可能受到较大影响。
其次，该方法不能直接评估指标的具体表现，只能提供关联度的大小，对于指标的具体意义和解释需要结合实际情况进行判断。
此外，灰色关联度分析所得到的关联度结果不能作为因果关系的证据，只能作为参考依据。
综上所述，灰色关联度分析是一种常用的多指标决策方法，通过对指标间关联度的计算，帮助决策者进行综合评价。
虽然该方法存在一些局限性，但在实际应用中却有着广泛的应用前景。
随着大数据时代的到来，灰色关联度分析方法也得到了进一步的发展和完善，为决策提供更准确、科学的依据。
经济统计学中的灰色关联度分析方法
经济统计学中的灰色关联度分析方法引言：经济统计学是一门研究经济现象的科学，通过收集、整理和分析经济数据，揭示经济规律和趋势，为经济决策提供科学依据。
在经济统计学中，灰色关联度分析方法是一种重要的分析工具，能够帮助我们揭示经济指标之间的内在联系和相互影响。
本文将介绍灰色关联度分析方法的基本原理和应用。
一、灰色关联度分析方法的基本原理灰色关联度分析方法是由我国学者陈纳德于1981年提出的，它是一种基于灰色系统理论的分析方法。
灰色系统理论是一种研究不确定性问题的数学理论，它将不确定性问题分为已知信息和未知信息两部分，通过建立灰色关联度模型，揭示已知信息对未知信息的影响程度。
灰色关联度分析方法的基本原理是通过建立关联度函数，衡量不同经济指标之间的关联程度。
关联度函数是一个表示相似程度的函数，数值越大表示两个经济指标之间的关联程度越高，反之则越低。
通过计算不同经济指标之间的关联度，我们可以找出对某一经济指标影响最大的指标，从而揭示经济指标之间的内在联系。
二、灰色关联度分析方法的应用灰色关联度分析方法在经济统计学中具有广泛的应用价值。
以下将介绍几个典型的应用场景。
1. 经济增长与产业结构调整的关联度分析经济增长和产业结构调整是经济发展的两个重要方面。
通过灰色关联度分析方法，我们可以计算经济增长与产业结构调整之间的关联度，从而揭示二者之间的内在联系。
例如，我们可以计算不同产业的增加值与GDP增长率之间的关联度，找出对经济增长影响最大的产业，为产业政策的制定提供科学依据。
2. 消费者支出与收入增长的关联度分析消费者支出和收入增长是经济发展中的重要指标。
通过灰色关联度分析方法，我们可以计算消费者支出与收入增长之间的关联度，从而揭示二者之间的内在联系。
例如，我们可以计算不同消费品类的销售额与居民收入增长率之间的关联度，找出消费者支出的主要驱动因素，为消费政策的制定提供科学依据。
3. 出口与汇率波动的关联度分析出口和汇率波动是国际贸易中的重要因素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章灰色关联度分析目录壹、何谓灰色关联度分析 ------------------------- 5-2 贰、灰色联度分析实例详说与练习 ----------------- 5-8负责组员工教行政硕士班二年级周世杰591701017陶虹沅591701020林炎莹591701025第五章灰色关联度分析壹、何谓灰色关联度分析一.关联度分析灰色系统分析方法针对不同问题性质有几种不同做法，灰色关联度分析(Grey Relational Analysis)是其中的一种。
基本上灰色关联度分析是依据各因素数列曲线形状的接近程度做发展态势的分析。
灰色系统理论提出了对各子系统进行灰色关联度分析的概念，意图透过一定的方法，去寻求系统中各子系统(或因素)之间的数值关系。
简言之，灰色关联度分析的意义是指在系统发展过程中，如果两个因素变化的态势是一致的，即同步变化程度较高，则可以认为两者关联较大；反之，则两者关联度较小。
因此，灰色关联度分析对于一个系统发展变化态势提供了量化的度量，非常适合动态(Dynamic)的历程分析。
灰色关联度可分成「局部性灰色关联度」与「整体性灰色关联度」两类。
主要的差别在于「局部性灰色关联度」有一参考序列，而「整体性灰色关联度」是任一序列均可为参考序列。
二.直观分析依据因素数列绘制曲线图，由曲线图直接观察因素列间的接近程度及数值关系，表一某老师给学生的评分表数据数据为例，绘制曲线图如图一所示，由曲线图大约可直接观察出该老师给分总成绩主要与考试成绩关联度较高。
表一某一老师给学生的评分表单位：分/ %由曲线图直观分析，是可大略分析因素数列关联度，可看出考试成绩与总成绩曲线形状较接近，故较具关联度，但若能以量化分析予以左证，将使分析结果更具有说服力。
三. 量化分析量化分析四步曲：1. 标准化(无量纲化)：以参照数列(取最大数的数列)为基准点，将各数据标准化成介于0至1之间的数据最佳。
2. 应公式需要值，产生对应差数列表，内容包括：与参考数列值差(绝对值)、最大差、最小差、ζ（Zeta ）为分辨系数，0＜ζ＜1，可设ζ = 0.5(采取数字最终务必使关联系数计算：ξi （k ）小于1为原则，至于分辨系数之设定值对关联度并没影响，请参考p14例) 3. 关联系数ξi （k ）计算：应用公式 maxoi(k)maxmin )(∆+∆∆+∆=ζζξk i 计算比较数列X i 上各点k 与参考数列X 0 参照点的关联系数，最后求各系数的平均值即是X i 与X 0 的关联度r i 。
4. 比较各关联度大小，值愈大，关联度越高。
实例参考(一)：根据某一老师给学生成绩的数据数据，依灰色关联度分析法，计算出考试成绩及出席率与学生成绩的关联度。
设分辨系数：ζ=0.5表一某一老师成绩表单位：分/%1、标准化2、对应差数列表()k Nr iN k iξ11=∑=3、关联系数计算：ξi （k ）ζ=0.5、最大差 0.20、 最小差0(一)、求比较数列X 1对参考数列X 0之关联系数ξ1（k ）625.02.05.006.02.05.00m ax )2(m ax m in )2(011=⨯+⨯+=∆+∆∆+∆=ζζξ(二)、求比较数列X 2对参考数列X 0之关联系数ξ2（k ）4、求关联度 ：即求比较数列所有数关联度的平均值 (一)、比较数列X 1对参考数列X 0之关联度12.05.002.05.00m ax )1(m ax m in )1(011=⨯+⨯+=∆+∆∆+∆=ζζξ5.02.05.01.02.05.00m ax )3(m ax m in )3(011=⨯+⨯+=∆+∆∆+∆=ζζξ667.02.05.005.02.05.00m ax )2(m ax m in )2(022=⨯+⨯+=∆+∆∆+∆=ζζξ333.02.05.02.02.05.00m ax )3(m ax m in )3(022=⨯+⨯+=∆+∆∆+∆=ζζξ12.05.002.05.00m ax )1(m ax m in )1(022=⨯+⨯+=∆+∆∆+∆=ζζξ()708.035.0625.01311311=++=∑==k r k ξ()667.03333.0667.01312312=++=∑==k r k ξ1r 2r(二)、比较数列X 2对参考数列X 0之关联度＞ 故该教授给的总成绩主要与考试成绩关联度较高。
量化分析公式内容说明：(一)、标准化（无量纲化）由于系统中各因素列中的数据，可能因计算单位的不同，不便于比较，或在比较时难以得到正确的结论。
因此在进行灰色关联度分析时，一般都要进行标准化（无量纲化）的数据处理。
(二)、关联系数：ξ（Xi ）所谓关联程度，实质上是曲线间几何形状的差别程度。
因此曲线间差值大小，可做为关联程度的衡量尺度。
对于一个参考数列X 0有若干个比较数列X 1, X 2,…, X n 。
各比较数列与参考数列在各个时刻（即曲线中的各点）的关联系数ξ（Xi ）可由下列公式算出：()()()()()()()()()||max max ||||max max ||min min 0000k X k X k X k X k X k X k X k X k i kii i kii kii -+--+-=ζζξ其中 ζ（Zeta ）为分辨系数，0＜ζ＜1()()||min min 0k X k X i ki- 为两层式取绝对差值中最小值计算，第一层为先分别由各比较数列X i 曲线上的每一个点与参考数列X 0曲线上的每一个点之绝对差值中取最小值，再由这些最小值当中选取最小值。
简记为Δmin 。
()()||max max 0k X k X i ki-为两层式取绝对差值中最大值计算，第一层为先分别由各比较数列X i 曲线上的每一个点与参考数列X 0曲线上的每一个点之绝对差值取最大值，再由这些最大值当中选取最大值。
简记为Δmax 。
()()||0k X k X i -为各比较数列X i 曲线上的每一个点与参考数列X 0曲线上的每一个点之绝对差值。
记为Δoi(k)。
所以关联系数ξ（Xi ）也可简化如下列公式：m axoi(k)m axm in )(∆+∆∆+∆=ζζξk i(三)、关联度 ：r i因为关联系数是比较数列与参考数列在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，而讯息过于分散不便于进行整体性比较。
因此有必要将各个时刻（即曲线中的各点）的关联系数集中为一个值，也就是求其平均值，做为比较数列与参考数列间关联程度的数量表示，关联度r i 公式如下：()k N r i Nk i ξ11=∑=貳、 灰色联度分析实例详说如表一某家庭收入来源数据数据为例：表一 某家庭 1998 ~ 2000年收入 单位：十万元绘制曲线图如图二所示：【关联度分析】一. 标准化（无量纲化）以1998年收入为基准，将表一进行标准化（无量纲化）处理后得表二：表二 标准化后的数列表二. 求最大差值()()||max max 0k X k X i ki-与最小差值()()||min min 0k X k X i ki-为求得()()||min min 0k X k X i ki-及()()||max max 0k X k X i ki-值，必须先求出各比较数列与参考数列之「对应差数列表」如表三： 表三 对应差数列表由表三对应差数列表得知各比较数列对参考数列各点对应差值中之最小值：()()0||min min 0=-k X k X i ki，即Δmin=0各比较数列对参考数列各点对应差值中之最大值：()()3.0||max max 0=-k X k X i ki，即Δmax=0.3三. 关联系数计算：ξi （k ） 设分辨系数：ζ=0.5(一)、求比较数列X 1对参考数列X 0之关联系数ξ1（k ）1、13.05.003.05.00m ax )1(m ax m in )1(011=⨯+⨯+=∆+∆∆+∆=ζζξ2、375.03.05.025.03.05.00m ax )2(m ax m in )2(011=⨯+⨯+=∆+∆∆+∆=ζζξ3、667.03.05.0075.03.05.00m ax )3(m ax m in )3(011=⨯+⨯+=∆+∆∆+∆=ζζξ(二)、求比较数列X 2对参考数列X 0之关联系数ξ2（k ）1、13.05.003.05.00m ax )1(m ax m in )1(022=⨯+⨯+=∆+∆∆+∆=ζζξ2、333.03.05.03.03.05.00m ax )2(m ax m in )2(022=⨯+⨯+=∆+∆∆+∆=ζζξ3、429.03.05.02.03.05.00m ax )3(m ax m in )3(022=⨯+⨯+=∆+∆∆+∆=ζζξ四. 求关联度 ：()k N r i Nk i ξ11=∑= (一)、比较数列X 1对参考数列X 0之关联度()68.03667.0375.01311311=++=∑==k r k ξ(二)、比较数列X 2对参考数列X 0之关联度()587.03429.0333.01312312=++=∑==k r k ξ五. 结论由上列运算得知：比较数列X 1对参考数列X 0之关联度68.01=r 比较数列X 2对参考数列X 0之关联度587.02=r1r ＞2r故该家庭总收入主要与薪资收入关联度较高。
六、练习：公路建设招标中取最接近标准者得标，请问何者得标？设分辨系数：ζ=0.5厂商及指标 标准标Ｘ０ A 厂 Ｘ１ B 厂 Ｘ２ C 厂 Ｘ３ 造价(亿) 1.1 1.1 1.2 1.5 建设期限(年) 1.3 1.8 1.5 1.3 车流(百辆) 5 4 3 5 车速(公里/时)11080110100解题： 一、标准化厂商及指标 标准标Ｘ０A 厂 Ｘ１B 厂 Ｘ２C 厂 Ｘ３ 造价 11.00 1.09 1.36 建设期限 1 1.38 1.15 1.00 车流 1 0.80 0.60 1.00 车速10.731.000.91二、对应差数列表指标 ()()||10k X k X - ()()||20k X k X - ()()||30k X k X -kminkmax造价 0.00 0.09 0.36 0.00 0.36 建设期限 0.38 0.15 0.00 0.00 0.38 车流 0.20 0.40 0.00 0.00 0.40 车速0.270.000.090.000.27三、关联系数与关联度关联系数ξi （k ）ξ1（k ）ξ2（k ）ξ3（k ）造价 1.00 0.69 0.35 建设期限 0.34 0.57 1.00 车流 0.50 0.33 1.00 车速 0.42 1.00 0.69 关联度 r i0.570.650.76r 3 ＞ r 2 ＞ r 1答： C 厂得标为暸解分辨系数的设定对关联度是否造成影响？以下将分辨系数分别以0.2、0.4、0.6、0.8来计算，由以下的结果得知：分辨系数并不影响关联度的判别，但以分辨系数为 0.2 时关联度曲线倾斜角最大最具判断性。