五年级奥数寒假讲义
五年级奥数寒假讲义
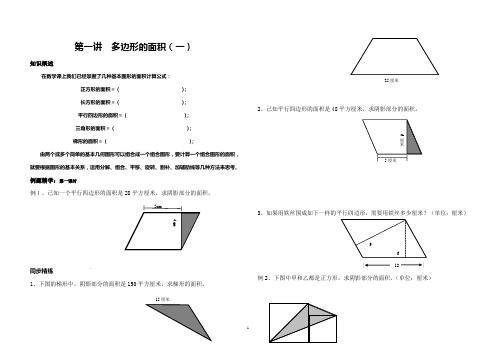
第一讲多边形的面积(一)知识概述在数学课上我们已经掌握了几种基本图形的面积计算公式:正方形的面积=();长方形的面积=();平行四边形的面积=();三角形的面积=();梯形的面积=();由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。
例题精学:第一课时例1、已知一个平行四边形的面积是28平方厘米,求阴影部分的面积。
同步精练1、下图的梯形中,阴影部分的面积是150平方厘米,求梯形的面积。
2、已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)| 12|例2、下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5cm4cm 15厘米25厘米5厘米6厘米96 6 4甲乙同步精练1、求右图中阴影部分的面积。
(单位:厘米)2、求右图中的阴影部分的面积。
(单位:厘米)3、如图所示,四边形ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例题精学 第二课时:例3、如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
同步精练1、四边形ABCD 是一个长为10厘米,宽为6厘米的长方形,三角形ADE 的面积比三角形CEF 的面积大10平方厘米。
求CF 的长是多少厘米?4厘米3厘米DCAB8厘米5厘米甲A 乙 CB EDF4 厘米 4厘米FEADC B2、平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长为8厘米,已知阴影部分三角形ABG 和三角形CDF 的面积和比三角形EFG 的面积大10平方厘米。
求CF 的长。
3、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,求: (1)三角形DEF 的面积; (2)CF 的长。
例4、两条对角线把梯形ABCD 分割成四个三角形。
小学数学五年级思维奥数寒假讲义-第8讲 牛吃草问题进阶(学生版)

第8讲牛吃草问题进阶【知识梳理】1、英国科学家牛顿在他的《普通算术》一书中,有一道关于牛在牧场上吃草的问题,即牛在牧场上吃草,牧场上的草在不断的、均匀的生长。
后人把这类问题称为牛吃草问题或叫做“牛顿问题”。
2、“牛吃草”问题主要涉及三个量:草的数量、牛的头数、时间.难点在于随着时间的增长,草也在按不变的速度均匀生长,所以草的总量不定。
“牛吃草”问题是小学应用题中的难点。
3、解“牛吃草”问题的主要依据:草的每天生长量不变每头牛每天的食草量不变草的总量=草场原有的草量+新生的草量,其中草场原有的草量是一个固定值新生的草量=每天生长量⨯天数4、同一片牧场中的“牛吃草”问题,一般的解法可总结为:⑴设定1头牛1天吃草量为“1”⑵草的生长速度=(对应牛的头数⨯较多天数-对应牛的头数⨯较少天数)÷(较多天数-较少天数)⑶原来的草量=对应牛的头数⨯吃的天数-草的生长速度⨯吃的天数⑷吃的天数=原来的草量÷(牛的头数-草的生长速度)⑸牛的头数=原来的草量÷吃的天数+草的生长速度5、“牛吃草”问题有很多的变例,像抽水问题、检票口检票问题等等,只有理解了“牛吃草”问题的本质和解题思路,才能以不变应万变,轻松解决此类问题。
【典例精讲】一牧场长满青草,27头牛6个星期可以吃完,或者23头牛9个星期可以吃完。
若是21头牛,要几个星期才可以吃完?(注:牧场的草每天都在生长)牧场上长满牧草,每天牧草都匀速生长.这片牧场可供10头牛吃20天,可供15头牛吃10天.供25头牛可吃几天?由于天气逐渐变冷,牧场上的草每天以均匀的速度减少.经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天.那么,可供11头牛吃几天?由于天气逐渐冷起来,牧场上的草不仅不长,反而以固定的速度在减少。
如果某块草地上的草可供25头牛吃4天,或可供16头牛吃6天,那么可供10头牛吃多少天?一水库原有存水量一定,河水每天均匀入库.5台抽水机连续20天可抽干;6台同样的抽水机连续15天可抽干.若要求6天抽干,需要多少台同样的抽水机?北京密云水库建有10个泄洪洞,现在水库的水位已经超过安全线,并且水量还在以一个不变的速度增加,为了防洪,需要调节泄洪的速度,假设每个闸门泄洪的速度相同,经测算,若打开一个泄洪闸,30个小时以后水位降至安全线;若同时打开两个泄洪闸,10个小时后水位降至安全线.根据抗洪形势,需要用2个小时使水位降至安全线以下,则至少需要同时打开泄洪闸的数目为多少个?画展8:30开门,但早有人来排队入场,从第一个观众来到时起,若每分钟来的观众一样多,如果开3个入场口,9点就不再有人排队;如果开5个入场口,8点45分就没有人排队。
五年级寒假奥数培优讲义——5-04-典型问题3-讲义-学生

第4讲典型问题【学习目标】1、巩固数论专题、计数原理、排列组合、容斥原理和抽屉原理;2、深入研究各专题。
【知识梳理】1、整除:被除数、除数、商都得是整数,而且没有余数;2、特殊数的倍数:尾数系、和系、差系;3、分解质因数:短除法;4、余数问题:和的余数等于余数的和、差的余数等于余数的差、积的余数等于余数的积;5、加法原理(或者或者):分类计数,类类独立;6、乘法原理(先……再……又……):分步计数;7、容斥原理(都……,都不……):不重不漏;8、抽屉原理:最不利原则。
【典例精析】【例1】一个五位数37y5x能被72整除,求这个数除以72的商。
【趁热打铁-1】一个六位数13y75x能被24整除,求这个六位数所有可能的情况。
【例2】已知a是质数,b是偶数,且a2+b=2008,则a+b+1=_____。
【趁热打铁-2】已知a是质数,b是偶数,且a2+b=2020,则a×b=_____。
【例3】在乘积1×2×3×…×98×99×100中,末尾有_____个零。
【趁热打铁-3】如果1×2×3×…×(n-2)×(n-1)×n的积末尾有25个0,则n最大是___。
【例4】一堆新书不超过500本,3本3本地数,5本5本地数,7本7本地数都恰好合适,这堆书最多有本。
【趁热打铁-4】一堆新书,2本2本地数,5本5本地数,9本9本地数都恰好合适,这堆书最少有本。
【例5】电视台要播出一部30集电视连续剧,若要每天安排播出的集数互不相等,则该电视【趁热打铁-5】把20个球放入若干个盒子中,每个盒子中的球的个数都不相同,则最多可以放个盒子。
【例6】房管员不小心把11个房间的11把钥匙放混了,若每把钥匙恰好能开启一个房间,则【趁热打铁-6】房管员不小心把10个房间的10把钥匙放混了,若每把钥匙恰好能开启一个房不同的装束。
小学五年级奥数讲义(60页)

第1讲 巧求周长和面积几何是研究现实世界的空间形式与数量关系的一门科学,是日常生活和进一步学习必不可少的基础和工具。
几何问题非常直观、有趣,但是仍然有的同学对解几何问题的基本方法掌握不好。
之前已经学习了长方形和正方形的周长和面积公式,利用公式可以解决一些简单的标准图形的周长和面积问题,对于一些复杂的不规则图形的周长和面积问题,我们可以采用平移、转化、分割、添补、合并等方法,将问题转化为我们熟悉的、简单的图形问题,从而顺利的解决。
本讲掌握长度与面积的概念和基本计算方法。
学会运用平移、标方向等方法处理某些长度计算问题;运用平移、旋转、对称等方法处理某些面积计算问题。
学海导航巧求周长(三年级秋季) 巧求周长与面积(四年级暑假) 等积变换(四年级春季) 巧求周长与面积(本讲) 直线型面积(一)(五年级秋季) 直线型面积(二)(五年级秋季) 直线型面积(三)(五年级寒假)知识要点周长:围成一个图形的所有边长的总和就是这个图形的周长。
长方形周长公式:()()22a b =+⨯=+⨯长方形长方形周长长宽,记作:C 正方形周长公式:44a =⨯=⨯正方形正方形周长边长,记作:C 方法:公式法、平移线段法、标向法面积:物体的表面或围成的平面图形的大小,叫做它们的面积。
长方形面积公式:a b =⨯=⨯长方形长方形面积长宽,记作:S 正方形面积公式:2a a a =⨯=⨯=正方形正方形面积边长边长,记作:S三角形面积公式:1122a h =⨯⨯=⨯⨯三角形三角形面积底高,记作:S平行四边形面积公式:a h =⨯=⨯平行四边形平行四边形面积底高,记作:S梯形面积公式:()()1122a b h =⨯⨯=⨯+⨯梯形梯形面积上底+下底高,记作:S方法:公式法、割补法(将图形平移、对称、旋转)例题详解【例1】 用若干个边长都是2厘米的平行四边形与三角形(如图所示)拼接成一个大的平行四边形,已知大平行四边形的周长是236厘米,那么平行四边形和三角形各有多少个?【例2】如图,这个多边形任意相邻的两条边都互相垂直。
五年级寒假奥数培优讲义——5-01-图形综合训练1-讲义-学生

第1讲图形综合训练【学习目标】1、复习基本图形的相关知识;2、熟悉小升初常见题型。
【知识梳理】1、三角形的面积公式:;2、平行四边形的面积公式:;3、梯形的面积公式:;4、学过的五种模型:、、、、。
【综合训练】1、如下图,长方形 ABCD 的面积为100平方厘米,E、F、G 分别是 AB、BC、CD 的中点,H 为AD边上的任意一点。
求阴影部分的面积是多少平方厘米?2、已知四边形 ABCD 的对角线被 E、F、G 三点四等分,且阴影部分面积为 15 平方厘米。
求四边形 ABCD 的面积。
3、如图所示,长方形 ABCD 内的阴影部分的面积之和为 70,AB=8 ,AD=15 ,四边形 EFGO的面积为多少?4、如图,正方形 ABCD 面积为3平方厘米, M 是 AD 边上的中点。
求图中阴影部分的面积。
5、如下图,在三角形 ABC 中,CD=3BD,AE=DE。
如果三角形 ABC 的面积是 5.6 平方厘米,那么阴影部分的面积是多少平方厘米?6、如图,E为AC的中点,BD=2CD,三角形DGC的面积为4,求三角形ABC的面积?7、如图,正方形ABCD和正方形CEFG,且正方形ABCD的边长是1厘米,图中阴影部分的面积是多少平方厘米?8、把两个长方形叠放在一起,小长方形的宽是2米,A点是大长方形一边的中点。
图中阴影部分的面积是多少平方米?9、用22张同样大小的长方形小纸片摆成一个大长方形,已知小纸片的宽是12厘米,那么图中阴影部分的面积一共是多少平方厘米?10、如图,两个一样的直角三角形重叠在一起,按照图上标出的数,计算阴影部分的面积。
(单位:厘米)11、如图,在直角三角形ABC中,四边形BEDF为正方形,AD=15厘米,CD=20厘米。
图中阴影部分的面积是多少平方厘米?12、如图,大正方形边长为4厘米,阴影部分面积为14平方厘米,小正方形的边长为多少厘米?13、如图,三角形ABC的面积是36平方厘米,AC长8厘米,DE长3厘米(四边形ADFC不是正方形)。
五年级寒假奥数培训教程

五年级寒假奥数培训教程新世纪奥数五年级寒假奥数五年级寒假奥数培训教程目录第一讲数图形第二讲平均数第三讲等差数列第四讲巧算(一)第五讲巧算(二)第六讲平面图形面积(一) 第七讲平面图形面积(二) 第八讲平面图形面积(三) 第九讲流水问题第十讲周期问题第十一讲加法原理第十二讲乘法原理第十三讲尾数和余数1新世纪奥数五年级寒假奥数第一讲数图形专题简析:我们在数数的时候,遵循不重复、不遗漏的原则,能使数出的结果准确。
但是在数图形的个数的时候,往往就不容易了。
分类数图形的方法能够帮助我们找到图形的规律,从而有秩序、有条理并且正确地数出图形的个数。
【例题1】下面图形中有多少个长方形,多少个正方形,【思路导航】图中的正方形的个数可以分类数,如由一个小正方形组成的有6×3=18个,2×2的正方形有5×2=10个,3×3的正方形有4×1=4个。
因此图中共有18,10,4=32个正方形。
练习一1、下图中共有多少个正方形,2、下图中共有多少个正方形,多少个三角形,2新世纪奥数五年级寒假奥数【例题2】下图中共有多少个三角形,【思路导航】为了保证不漏数又不重复,我们可以分类来数三角形,然后再把数出的各类三角形的个数相加。
(1)图中共有6个小三角形;(2)由两个小三角形组合的三角形有3个;(3)由三个小三角形组合的三角形有4个;(4)由六个小三角形组合的三角形有1个。
所以共有6,3,4,1=14个三角形。
练习二1、下面图中共有多少个三角形,2、数一数,图中共有多少个三角形。
3、数一数,图中共有多少个三角形,【例题3】数出下图中所有三角形的个数。
3新世纪奥数五年级寒假奥数【思路导航】和三角形AFG一样形状的三角形有5个;和三角形ABF一样形状的三角形有10个;和三角形ABG一样形状的三角形有5个;和三角形ABE一样形的三角形有5个;和三角形AMD一样形状的三角形有5个,共35个三角形。
小学奥数模块教程时钟问题(五年级提尖寒假)

时钟问题本章知识1、简单的钟面角度问题2、钟表中的相遇与追及问题3、坏钟问题前铺知识1、相遇问题2、追及问题课前加油站1、请默写出直线相遇与追及问题的两个公式。
2、甲、乙两人同时同地同向在400米长的环形跑道上跑步,甲的速度为6米/秒,乙的速度为4米/秒。
(1)开始后多长时间,甲乙第一次处于跑道的某直径的两端?(2)开始后多长时间,甲第一次超过乙?(3)开始后多长时间,甲乙第一次处于起点所在的直径对称的位置?要研究时钟某个时刻时针与分针成什么角度,我们首先要知道时针与分针行走的速度。
它们的速度有两种表达形式:以小格/分钟为单位或以角度/分钟为单位。
格 度 时钟一圈 60格360度时针速度 121格/分钟 21度/分钟 分针速度 1格/分钟6度/分钟时针速度:分针速度=1:12。
牢记它有助于我们记忆时针和分针的速度。
1、已知:钟表上60小格,一圈是360度,则分针1小时转多少度?时针1小时转多少度?分针速度是时针速度的多少倍?【演练】分针1分转多少度?时针1分转多少度?时针速度是分针速度的几分之几?2、3:00时,分针落后时针 度,15分钟内,分针走 度,时针走 度,因此3:15时,时针与分针的夹角是 度。
模块1简单的钟面角度问题【演练】在下表中仿照第二行的例子填入适当的算式。
X :Y (X 点Y 分) X 点时两针的角度 Y 分时时针走的度数 Y 分时分针走的度数 X 点Y 分时两针的度数 4:16 4×30=120 16×6=96 16×0.5=8 120-96+8=32 8:12 3:40 9:10【演练】当时钟表示1点45分时,时针和分针所成的钝角是多少度?【演练】在16点16分这个时刻,钟表盘面上时针和分针的夹角是多少度?3、小明家的时钟正对着衣柜上的镜子,某天早上起床时,小明看到镜子中的时钟两针指向5点20分的位置,那么现在真正的时钟显示的时间是?题型一 重合问题公式:分针到时针相差的格数÷(1-121)=重合分钟数分针到时针相差的度数÷(6-0.5)=重合分钟数1、现在是2点,从现在开始,分针与时针什么时刻第一次重合在一起?第二次呢?模块2钟表中的相遇与追及问题【演练】现在是7点40分,从现在开始过多长时间时针与分针第一次重合?【演练】有一座时钟现在显示10时整。
五年级奥数能力提升寒假讲义

第一节定义新运算【知识要点】说起运算,同学们马上就会想到我们课堂上学过的加、减、乘、除四则运算,并且还能熟练地说出这些运算的一些运算性质和运算定律。
当然,对于什么样的问题该用加法或减法、乘法还是除法计算更是烂熟于胸。
其实,在加、减、乘、除四则运算之外,还有其他多种法则的运算。
我们这一讲里将要学习的“新运算”,就是用*、△、☆、⊙等多种符号,按照一定的关系,临时规定的一种新的运算程序(新运算)。
学习“定义新运算”,关键是要深刻理解运算符号的新规定,严格按照规定的法则运算,最后达到解决问题的目的。
【典型例题】例1 设a,b都表示数,规定是a△b表示a的3倍减去b的2倍,a△b=a×3-b×2。
试计算:5△6;(7△6)△4的值。
例2 有两个数是A 、B ,A △B 表A 与B 的平均数。
、(1)已知A △6=17,求A 。
(2)如果已知4△B=2,求B 。
例3 规定△=x+,那么3△4= 。
例4 如果2*3=2+3+4,5*4=5+6+7+8,按此规律计算:3*5;5*3x y 32y x yx ⨯+【小试锋芒】1.设a,b都表示数,规定a△b=6×a-2×b。
试计算3△42.设a,b都表示数,规定a△b=3×a+2×b 试计算:(5△6)△7;5△(6△7)3. 规定:6*2=6+66=72,2*3=2+22+222=246,1*4=1+11+111+1111=1234。
求:7*54.如果2*4=24÷(2+4),按此规律计算3*6;6*3;历届竞赛中的定义新运算:1.观察5*2=5+55=60,7*4=7+77+777+7777=8638,推知9*5的值是?(第一届小学“希望杯”全国数学邀请赛五年级 第1试)2.规定:A*B=3A+2B,如4*5=3×4+2×5,那么,B*A=________。
(第四届小学“希望杯”全国数学邀请赛五年级 第1试)3.“△”是一种新运算,规定:a△b=a×c+b×d(其中c,d为常数),如5△7=5×c+7×d。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲多边形的面积(一)知识概述在数学课上我们已经掌握了几种基本图形的面积计算公式:正方形的面积=();长方形的面积=();平行四边形的面积=();三角形的面积=();梯形的面积=();由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、加辅助线等几种方法来思考。
例题精学:第一课时例1、已知一个平行四边形的面积是28平方厘米,求阴影部分的面积。
同步精练1、下图的梯形中,阴影部分的面积是150平方厘米,求梯形的面积。
2、已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3、如果用铁丝围成如下一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)| 12|例2、下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)5cm4cm 15厘米25厘米5厘米6厘米96 6 4甲乙同步精练1、求右图中阴影部分的面积。
(单位:厘米)2、求右图中的阴影部分的面积。
(单位:厘米)3、如图所示,四边形ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例题精学 第二课时:例3、如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE 的长度。
同步精练1、四边形ABCD 是一个长为10厘米,宽为6厘米的长方形,三角形ADE 的面积比三角形CEF 的面积大10平方厘米。
求CF 的长是多少厘米?4厘米3厘米DCAB8厘米5厘米甲A 乙 CB EDF4 厘米 4厘米FEADC B2、平行四边形ABCD 的边长BC=10厘米,直角三角形BCE 的直角边EC 长为8厘米,已知阴影部分三角形ABG 和三角形CDF 的面积和比三角形EFG 的面积大10平方厘米。
求CF 的长。
3、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,求: (1)三角形DEF 的面积; (2)CF 的长。
例4、两条对角线把梯形ABCD 分割成四个三角形。
已知两个三角形的面积如图所示,求另两个三角形的面积各是多少?(单位:厘米)同步精练1、如下图,图中BO =2DO ,阴影部分三角形BCO 的面积是4平方厘米,求梯形的面积是多少平方厘米?2、下图的梯形ABCD 中,下底是上底的2倍,E 是AB 的中点,求梯形ABCD 的面积是三角形EDB 面积的多少倍?3、下图梯形ABCD 中,AD =7厘米,BC=12厘米,梯形的高是8厘米,求三角形BOC 的面积比三角形AOD 的面积大多少平方厘米?EDCBAGF FADCB122OADCB6 DBBDOCAE CAOCDAB练 习 卷第三课时 时间: 分数:1、正方形ABCD 的面积是100平方厘米,AE=8厘米,CF=6厘米,求阴影部分BFDE的面积。
2、下图长方形中,E 、F 分别是AD 和DC 的中点,已知AB=10厘米,BC=8厘米,那么阴影部分的面积是多少平方厘米?3、求下面图形中梯形ABCD 的面积。
(单位:厘米)4、求出下图中阴影甲的面积比阴影乙的面积大多少?(单位:厘米)5、下图中平行四边形ABCD 的边BC 长10厘米,直角三角形BCE 的直角边EC 长10厘米,已知阴影部分三角形ABG 、三角形CDF 的面积和比三角形EFG 的面积小10平方厘米,求CF 的长是多少?6、下图是一块长方形的草地,长方形的长为16米,宽为12米,中间有一条宽为2米的小路,求草地的面积。
BDCAFBFE D CAEBA 3DC4 858甲乙66DBCAEFG7、下图中,乙三角形的面积比甲三角形的面积大4平方厘米,求a 的长度。
8、如图,已知三角形ABC 的周长是20厘米,三角形内一点到三角形三条边的距离都是3厘米,求三角形的面积。
9、如图,已知四边形ABCD ,AB 垂直BC ,BC =7厘米,AD 垂直DC ,AD =3厘米,角BCD =450,求四边形ABCD 的面积。
10、如图,梯形ABCD 的面积是45平方厘米,高6厘米,三角形AED 的面积是5平方厘米,BC =10厘米,求阴影部分三角形BEC 的面积。
第二讲 多边形的面积(等积变形)知识概述:三角形面积的公式是( ),两个三角形只要是底和高分别相等,它们的面积就相等;而这两个三角形的形状不一定完全相等,例如下面两个三角形的面积就是相等的,但是形状却完全不一样。
等底等高的三角形面积相等;高相等的三角形,底边的倍数关系和它们的面积的倍数关系相等。
例题精学例1、四边形ABCD 中,M 为AB 的中点,N 为CD 的中点,如果四边形ABCD 的面积是80平方厘米,求阴影部分BNDM 的面积是多少?同步精练第四课时1、如下图,六边形ABCDEF 的面积是16平方厘米,M 、N 、P 、Q 分别是AB 、CD 、DE 、AF 的中点,求图中阴影部分的面积。
4甲乙5aCBPA A BCD45度BADCE6厘米6厘米4厘米 4厘米BMADN CDACBEPNFQ M2、如图,平行四边行的面积为50平方厘米,P 是其中任意一点,求阴影部分的面积。
3、如图,正方形的边长是6厘米,E 、H 是所在边的二等分点,F 、G 、L 、M 是所在边的三等分点,求阴影部分的面积和。
例2、如下图,三角形ABC 为等边三角形, D 为AB 边上的中点,已知三角形BDE 的面积为5平方厘米,求等边三角形ABC 的面积。
同步精练1、如图,平行四边形ABCD 中AE =EF =FB ,AG =2CG ,三角形GEF 的面积是6平方厘米,平行四边形的面积是多少平方厘米?2、如图,长方形ABCD ,三角形ABG 的面积为20平方厘米,三角形CDQ 的面积为35平方厘米,求阴影部分的面积是多少平方厘米?3、如图,在一个等边三角形中任意取一点P ,连接PA 、PB 、PC ,过P 点作三角形三边的垂线,E 、F 、G 分别为垂足。
三角形ABC 被分成6个三角形。
已知三角形的面积为40平方厘米,求图中阴影部分的面积。
PEAF PPGLBH CACBDEGDEAFCBADB G FGC EFEP GBAC例3、下图中正方形ABCD 的边长是4厘米,长方形DEFG 的长DG=5厘米,问长方形的宽DE 为多少厘米?同步精练1、如图,两个相同的直角三角形叠放在一起,求阴影部分的面积。
(单位:分米)2、如图,ABCD 为长方形,AB =10厘米,BC =6厘米,E 、F 分别为AB 、AD 的中点,且FG =2GE ,求阴影部分的面积。
3、如图,ABCD 是直角梯形,其中AD=12厘米,AB =8厘米,BC =15厘米,且三角形ADE 、四边DEBF 及三角形CDF 的面积相等,三角形EBF 的面积是多少?例4、下图是两个正方形的拼成的图形,其中小正方形的边长是4厘米,求阴影部分的面积。
同步精练1、如果下图中大正方形的边长是6分米,求阴影部分的面积。
BAFEDGCAGD BCEF583GFECDA BBFECDA2、如图,AD=2AB,CF=3AC,BE=4BC,已知三角形ABC的面积是5平方厘米,求三角形DEF的面积。
3、如图,AE=ED,AF=FC,已知三角形ABC的面积为100平方厘米,求阴影部分的面积。
练习卷时间:分数:1、如图,在平行四边形ABCD中,EF与AC平行,如果三角形BFC的面积是35平方厘米,那么三角形AEB的面积能不能确定?如果能确定,它的面积是多少?2、在三角形ABC中,AD垂直于BC,CE垂直于AB,AD=8厘米,CE=7厘米,AB+BC =21厘米,求三角形ABC的面积。
3、如图,AB=4厘米,BC=6厘米,AC=2CD,BE=BD,求三角形ADE的面积。
4、如图,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长ED长的2倍,求三角形CDE的面积。
5、三角形ABC的面积是180平方厘米,D是BC的中点,AD的长是AE的长的3倍,EF的长是BF的3倍,求三角形AEF的面积。
6、下图中,正方形ABCD的边长是12厘米,P是AB边上任意一点,M、N、I、H分别是BC、AD的三等分点,E、F、G是CD的四等分点,求图中阴影部分的面积。
7、正三角形ABC的边长是12厘米,BD、DE、EF、GF四条线段把它的面积5等分,求AF、FD、DC、AG、GE、EB的长。
8、下图中,BD=2DC,AE=BE,已知三角形ABC的面积是18平方厘米,求四边形AEDC的面积等于多少平方厘米?9、两个边长为2厘米的正方形,其中一个的顶点在另一个的中心上,如下图,求两个正方形的不重合的部分的面积和。
10、在下面的正方形中,A、B、C分别是所在边的中点,三角形CDO的面积是三角形ABO的面积的几倍?第三讲观察物体(排列与组合)知识概述:在日常生活和生产实践中,我们经常要用到排列与组合的一些知识。
计数时常用到这两个原理:加法原理,做一件事时,有几类不同的方法,而每类方法中,又有几种不同的方法,那么,完成这件事共有多少种方法,就要用到加法原理;乘法原理,做一件事时,要分几个步骤才能完成,而在完成每一步时,又有几种不同的方法,完成这件事一共有几种方法,就要用到乘法原理。
例题精学例1、把12支圆珠笔分级三个人,每个人都得到偶数枝,且每人到少得到2枝的分法一共有多少种?同步精练1、学校组织读书活动,要求每个同学读一本书,小丹到图书室借书时,图书室里有不同的书科技书150本,不同的故事书200本,不同的外语书75本,小丹借一本书可以有多少种不同的选法?2、有1角、2角、5角的人民币各一张,可以组成多少种不同币值的人民币?3、有一个三位数,它的各位上的数字的各等于24,这样的三位数一共有多少个?例2、用数字1,2,3,4,5这五个数字,可以组成多少个没有重复数字的三位数?同步精练1、书架上层有6本不同的故事书,中层有5本不同的历史书,下层有10本不同的连环画,如果要从书架的上、中、下层各取一本书,一共有多少种不同的选书方法?2、用数字4,5,6,7可以组成多少个没有重复数字的四位数?多少个没有重复数字的三位数?3、用数字0,1,2,3,4可以组成多少个没有重复数字的四位数?例3、由6支篮球队组成的篮球比赛,采取单循环积分赛制确定比赛名次,即每两支队伍都要比赛一场,问一共要安排多少场比赛?同步精练:1、某班有60人,现在要选出两人当升旗手,假设每个人都有可能被选到,一共有多少种不同的选法?2、从南京到北京的往返列车有途还要停靠8个车站,问铁路部门要为这趟列车准备多少种不同的列车票?3、有6名同学和一名老师要照张合影,要求老师必须站在中间,这样他们一共有多少种不同的站法?例4、这是一个小棋盘,将每个白子和一个黑子放在棋盘交叉的地方,但不能放在同一条棋盘线上,问一共有多少种不同的放法?同步精练:1、在下图所示的方格纸中的方格里放上黑棋子和白棋子各一枚,要求两枚棋子不能在同一行也不能在同一列,问一共有多少种不同的放法?2、用四种不同的颜色对下图的A 、B 、C 、D 、E 五个区域染色,要求相邻的区域染不同的颜色,问:一共有多少种不同的染色方法?3、将下图中的分别涂成红色、黄色、绿色,要求有线段相连的两个相邻 涂的颜色不能相同,问:一共有多少种不同的涂法?练 习 卷时间: 分数:1、从A 城到B 城,可以乘汽车、火车、轮船和飞机,一天有汽车有6班,火车有3班,轮船有2班,飞机有4班,问这一天中从A 城到B 城共有多少种不同的走法?2、如图所示,从甲到乙有1条路可走,从乙到丙有3条路可走,从甲到丁和从丁到丙地分别有2条路,问:从甲地到丙地一共有多少种不同的走法?3、一把钥匙只能开一把锁,现在有8把锁都标混了,最多要试验多少次才能把钥匙和锁全部配好?BCDEA甲丙丁乙4、用7,8,9,0四个数字可以组成多少个没有重复数字的四位数呢?5、南京到上海的一趟往返列车,中途还要停靠镇江、常州、无锡、苏州四站,铁路部门要为这趟列车准备多少种不同的车票?6、下图在一共有多少个正方形?7、用四种颜色对下图的A、B、C、D、E五个区域染色,要求相邻的区域染不同的颜色。
