偏振分束器pbs简单画法
基于亚波长光栅辅助定向耦合器的集成铌酸锂偏振分束器

transmission capacity of photonic communication systems. In recent years, PBS has been successfully implemented based on
various structures. Among them, the PBS based on subwavelength grating-assisted directional coupling structure stands out due
heterogeneous integration. Simulation results show that the device achieves a polarization extinction ratio greater than 24. 49 dB
in the wavelength range of 1 500 nm to 1 600 nm. Experimental data further confirms that the polarization extinction ratio of
基金项目:甘肃省自然科学基金重点项目(23JRRA1026) ;甘肃省自然科学基金在站博士后专项项目(23JRRA1126)
作者简介:陈 力(1998—) ,男,浙江省人,硕士研究生。 E-mail:lchen2021@ lzu. edu. cn
通信作者:田永辉,博士,教授。 E-mail:siphoton@ lzu. edu. cn
the device is greater than 18. 06 dB in the wavelength range of 1 500 nm to 1 580 nm.
pbs偏振分束器工作原理

pbs偏振分束器工作原理PBS偏振分束器是一种常用的光学器件,它能将入射光线按照垂直和水平方向的偏振方向分离出来。
它的工作原理是基于菲涅尔衍射原理以及偏振分光器的原理。
首先,我们来了解一下偏振分光器的工作原理。
偏振分光器是一种利用光的偏振特性将光线分离的器件。
一个典型的偏振分光器包括一个玻璃棱镜以及一些偏振片。
当入射光线经过玻璃棱镜时,因为不同偏振方向的光在玻璃棱镜中传播速度不同,导致不同偏振方向的光线会被分离出来。
这一分离效果可以通过添加偏振片来进一步增强。
PBS偏振分束器则是在偏振分光器的基础上进行改进而得到的一种光学器件。
它通常由两个平面后面的偏振片和一个玻璃棱镜组成。
玻璃棱镜用来将入射光线在垂直方向上分离,而两个后面的偏振片则用来将垂直方向上的光线按照偏振方向分离开来。
具体而言,偏振片的偏振方向应该与玻璃棱镜折射后的光线垂直方向相同。
这样,在光线经过偏振片时,偏振片只能透过和其偏振方向相同的光线,而无法透过垂直方向上的光线。
通过这种设计,PBS偏振分束器能够将光线按照垂直和水平方向的偏振方向分离出来。
这一性质使得PBS偏振分束器在许多光学应用中都得到了广泛的应用。
比如,在液晶显示器中,PBS偏振分束器能够将白光分离成红、绿、蓝三种光线,以便于显示不同的颜色。
在激光器中,PBS偏振分束器能够将激光器输出的光线按照垂直和水平方向进行分离,以便于进行精密加工和焊接等工艺。
总之,PBS偏振分束器是一种非常重要的光学器件,它能够实现光线的偏振分离,具有广泛的应用前景。
对其工作原理的深入理解,不仅可以帮助我们更好的了解光学器件的原理,也能够为光学应用领域的发展提供有益的参考。
轨道角动量模式识别方法综述

轨道角动量模式识别方法综述冯文艳;付栋之;王云龙;张沛【摘要】光子轨道角动量具有涡旋和高维特性,在经典和量子领域有巨大应用潜力,目前在光学系统中有多种轨道角动量识别方法,常见的方法有以下8种:干涉仪法、镜像干涉法、平面波干涉法、角双缝干涉法、三角孔衍射法、计算全息光栅法、光学几何变换法和旋转多普勒效应法.本文详细介绍了8种方法的实验原理、实验装置、实验结果及现阶段的研究成果.【期刊名称】《物理实验》【年(卷),期】2019(039)002【总页数】12页(P1-12)【关键词】拉盖尔-高斯模式;轨道角动量;分束器;干涉;衍射【作者】冯文艳;付栋之;王云龙;张沛【作者单位】西安交通大学陕西省量子信息与光电量子器件重点实验室大学物理国家级实验教学示范中心 ,陕西西安710049;西安交通大学陕西省量子信息与光电量子器件重点实验室大学物理国家级实验教学示范中心 ,陕西西安710049;西安交通大学陕西省量子信息与光电量子器件重点实验室大学物理国家级实验教学示范中心 ,陕西西安710049;西安交通大学陕西省量子信息与光电量子器件重点实验室大学物理国家级实验教学示范中心 ,陕西西安710049【正文语种】中文【中图分类】O431.2光子除了具有自旋角动量外还具有轨道角动量. 1909年,在爱因斯坦的光量子理论[1]提出几年之后,Poynting发现了光子具有自旋角动量[2],然而,直到1992年光子的轨道角动量才被Allen等人发现,而且揭示了拉盖尔-高斯模式的角向指数l和光子的轨道角动量之间存在对应关系[3]. 光子的自旋角动量和偏振有关,若1束光是圆偏振光,则光束中每个光子都携带了σħ的自旋角动量. 由于电磁场的横波性,σ只能取±1,分别对应于左旋圆偏振和右旋圆偏振. 这2个态是量子力学中自旋算符的本征态, 因此光的自旋角动量态(偏振态)是二维量子态. 光子的轨道角动量和复电场相位有关,轨道角动量来源于绕传播方向的相位波前. 携带轨道角动量lħ的涡旋光束具有螺旋形等相位面,螺旋相位项为exp (ilφ),l为轨道角动量量子数,其正负代表旋转方向不同,φ是角坐标[3]. 由于波前是螺旋形等相位面,这会导致在传播轴上有相位奇点,即横向光强分布的中心是暗点. 由于l可以是任意整数,所以光子有无数个轨道角动量正交本征态,即光子轨道角动量具有高维特性.光子轨道角动量的发现,除了让人们更进一步理解光的本质外,还拓展了光的应用范围,有着十分重要的科学意义和应用价值. 近年来, 科学家在量子信息的研究中发现高维量子态相比于二维量子态体现出更加特殊和优越的性质, 如在基础量子理论的验证方面,高维量子体系相比于二维量子体系更大程度地违背了贝尔不等式[4-5],这使得寻找高维量子态很有必要,而光子轨道角动量具有高维特性. 由于光子又是很好的量子系统和信息载体,近年来基于光子轨道角动量的高维量子态的研究,引起了人们的广泛兴趣[6-7]. 目前,由于光子轨道角动量的涡旋特性和高维特性,轨道角动量模式被应用在多个领域中,如光镊[8-9]、显微操作[10-11]、探测旋转微粒或旋转物体的角速度[12-13]、量子信息[14-15]、量子计算[16-19]、光通信[20-21]和量子密码学[22]等. 对光子轨道角动量的区分显得尤为重要,如在量子信息处理中,若利用光子轨道角动量进行编码信息,最后解码信息时,必然要求对光子轨道角动量进行识别. 目前已有多种探测轨道角动量模式的方法,本文针对目前在光学系统中已有的对轨道角动量模式识别的方法以分类的方式给予综述. 具有螺旋相位结构最常见的形式之一是拉盖尔-高斯模式. 拉盖尔-高斯模式是在傍轴近似条件下波动方程在柱坐标系下的解. 拉盖尔-高斯模式有2个指数,其中角向指数l与螺旋相位有关,径向指数p与拉盖尔多项式控制的振幅变化有关. 角向指数l也被称为轨道角动量量子数或轨道角动量拓扑荷,携带轨道角动量的光束也被称为涡旋光束. 本文以拉盖尔-高斯模式为例来阐述识别轨道角动量模式的方法.1 干涉仪法Padgett等人提出利用两臂加入Dove棱镜的 Mach-Zehnder干涉仪来测量拉盖尔-高斯模式的轨道角动量量子数l[23]. 其中一臂的Dove棱镜是旋转的,另一臂的Dove 棱镜是静止的,如图1所示. SPP为螺旋相位板;HWP为半波片;PBS 为偏振分束器;M为反射镜. 当Dove棱镜沿长轴方向旋转α/2时,经过Dove棱镜的光束将被旋转α. 当携带轨道角动量lħ的拉盖尔-高斯光束经过图1中的Mach-Zehnder干涉仪时,两臂间将产生Δφ= lα的相位差,当旋转的Dove棱镜旋转1周时,在探测端口将产生明暗交替变化的干涉图样. 在入射不同拉盖尔-高斯模式的情况下,干涉图样的光强随旋转角α的变化如图2所示,α/2表示Dove棱镜的旋转角,α表示拉盖尔-高斯光束的旋转角. 干涉图样光强变化的周期等于入射的拉盖尔-高斯光束的轨道角动量量子数l的大小,因此,通过测量干涉图样光强的变化周期就可以得到入射的拉盖尔-高斯模式的轨道角动量量子数l.图1 两臂插有Dove棱镜的Mach-Zehnder干涉仪(a)l=0 (b)l=1(c)l=2 (d)l=3图2 携带不同轨道角动量的拉盖尔-高斯模式入射Mach-Zehnder 干涉仪得到的干涉图样的光强随旋转角α的变化2002年,Leach等人提出基于Mach-Zehnder干涉仪在单光子水平下有效区分不同轨道角动量模式的方法[24]. 如图3所示(图中BS为分束器; DP为Dove棱镜),在 Mach-Zehnder干涉仪一臂中插入无旋转的 Dove棱镜,另一臂中插入旋转角度为α/2的 Dove 棱镜,这将会在通过两臂的涡旋光束中引起依赖于轨道角动量量子数l的相位差Δφ=lα. 对于l和α特定的组合,不同的拉盖尔-高斯模式将会在不同的端口出现干涉相长或干涉相消. 例如,当α=π时,即其中一臂的Dove棱镜被旋转α/2=π/2时,奇数和偶数l将分别被分离在端口A1和B1. 理论上,N个轨道角动量模式可以通过级联N-1个Mach-Zehnder干涉仪进行分离,在每一级中旋转的Dove棱镜的旋转角度不同,原理图如图4所示. 此方法可以在单光子水平下探测轨道角动量模式,但是,对于测量多个轨道角动量模式,需要级联多个Mach-Zehnder干涉仪,这对目前现有的技术来说是很大的挑战.图3 两臂中插入Dove棱镜的Mach-Zehnder干涉仪图4 级联3级干涉仪分离8个轨道角动量模式的原理图(从l=0到l=7,第1级、第2级和第3级光束旋转的角度分别为π,π/2和π/4)除此之外,还有许多基于干涉仪识别轨道角动量模式的方法[25-29],如利用稳定性较好的Sagnac干涉仪代替Mach-Zehnder干涉仪来区分轨道角动量模式[27,29]、利用Mach-Zehnder干涉仪或Sagnac 干涉仪将轨道角动量和偏振耦合起来的方法探测轨道角动量模式[28-29].2 镜像干涉通过观察轨道角动量模式与其镜像模式(携带的轨道角动量大小相等,正负相反)的干涉图样可以探测轨道角动量模式[30-32]. 众所周知,如果携带轨道角动量为lħ的涡旋光束被镜子反射之后,其旋转方向反转,即轨道角动量变为-lħ. 现在考虑2个具有相反螺旋性的轨道角动量光束沿与z轴成角度α和-α的方向传播,如图5所示(红色和蓝色实线分别表示轨道角动量量子数为l和-l的涡旋光束的波矢量. 红色虚线和蓝色虚线分别表示轨道角动量量子数为l和-l的涡旋光束的波前). 入射的轨道角动量光束和它的镜像模式光束的电场表达式为El=u0exp [iφ1(x)]exp (ilφ),E-l=u0exp [iφ2(x)]exp (-ilφ),(1)其中u0是轨道角动量光束的振幅. 由图5可知,在z=0的平面上,φ1(x)=kxcos α+φ10=kxx+φ10,φ2(x)=kxcos (π-α)+φ20=-kxx+φ20,(2)其中φ10(x)和φ20(x)分别是入射的轨道角动量光束和其镜像模式光束在坐标原点O的初始相位. 从而得到2束光干涉图样的强度分布为I=|El+E-l|2=2I0[1+cos (2lφ-2kxx+Δφ0)].(3)图5 轨道角动量模式与其镜像模式干涉原理图其中I0是入射的轨道角动量光束或其镜像模式光束的光强,Δφ0=φ10-φ20是入射的轨道角动量光束与其镜像模式光束的初始相位差. 从式(3)可以看出,干涉图样的强度分布类似于中心有2l个错位条纹的振幅全息图,因此,可以根据干涉图样中条纹错位的个数来确定入射的轨道角动量模式. 如图6所示,因为入射的2个轨道角动量光束的波前具有相反的螺旋性,且沿与z轴角度α的方向传播,因此,干涉图样的下半部分的条纹相对于上半部分额外多了2l个.(a)l=1 (b)l=2 (c)l=3图6 轨道角动量量子数为1,2,3的涡旋光束与其镜像模式干涉图样(干涉图样底部分别有2条、4条、6条额外的条纹)当然,如果轨道角动量光束与其镜像模式进行同轴干涉,即α=0,则它们的干涉图样类似于2个具有相反符号的轨道角动量光束的叠加的结果,即干涉图样中含有2l个花瓣,如图7所示. 由于l和-l互为镜像,因此,此方法只能探测涡旋光束的轨道角动量量子数l的大小,无法探测其正负.(a)l=1 (b)l=2 (c)l=3图7 轨道角动量量子数为1,2,3的涡旋光束与其镜像模式同轴干涉图样(干涉图样分别有2,4,6个花瓣)3 平面波干涉1束涡旋光和1束平面波干涉,由于涡旋光束的螺旋相位结构exp (ilφ),干涉图样是l条螺旋形条纹,因此,可以通过干涉图样中的螺旋条纹的个数有效地识别轨道角动量模式[32-34]. 平面波与轨道角动量模式的电场可分别表达为E0=u0(r)exp [iφ1(r)],El=ul(r)exp [iφ2(r)]exp (ilφ).(4)其中u0和ul分别是平面波和涡旋光束的振幅. 涡旋光束和平面波之间的同轴干涉可以用Mach-Zehnder干涉仪来实现,如图8所示,在 Mach-Zehnder干涉仪其中一臂用螺旋相位板(SPP)产生待测的携带轨道角动量的涡旋光束,另一臂中加入扩束器用来产生平面波. 当涡旋光束和平面波进行同轴干涉时,将会得到带有螺旋条纹的干涉图样. 在z=0平面上干涉图样的光强分布为I= |E0+El|2=|u0|2+|ul|2+2|u0||ul|cos (Δφ),(5)其中Δφ为涡旋光束和平面波之间的相位差. 考虑同轴干涉,且干涉发生在z=0的平面上,则涡旋光束和平面波间的相位差表达式为Δφ=lφ-θ,其中θ在干涉平面上为常数. 如果Δφ=2nπ(其中n为整数),则涡旋光束和平面波干涉将得到相干相长的干涉图样,此时即在此处发生干涉相长. 从式(5)可以看出,在任何情况下,干涉图样条纹的个数等于入射涡旋光束的轨道角动量量子数l,即干涉图样是从中心向外呈扇形发散的干涉条纹,且干涉条纹的个数为l条. 由于依赖坐标的古伊相位和球面相位的存在,在z≠0的平面上干涉图样中的条纹是成螺旋状的,如图9所示,图9中干涉条纹的个数等于入射涡旋光束的轨道角动量量子数l. 另外,从图9(a)和(b)中可以看出,干涉条纹的旋转方向和轨道角动量量子数l的正负有关,当l为负时,干涉图8 涡旋光束与平面波干涉的示意图(a)l=-3 (b)l=3 (c)l=5图9 轨道角动量量子数为-3,3,5的涡旋光束与平面波干涉的干涉图样(干涉图样中条纹的个数分别为3条,3条,5条,干涉条纹的旋转方向分别为顺时针、逆时针、逆时针)条纹呈顺时针旋转;当l为正时,干涉条纹呈逆时针旋转. 因此,这种方法可以同时测量待测涡旋光束的轨道角动量量子数l的大小和符号.4 角双缝干涉图10 角双缝干涉原理图当1束具有螺旋相位项exp (ilφ) 的涡旋光束经过动态角双缝,由于螺旋相位项和角双缝到观察平面的光程差的存在,在观察平面上将会出现明暗相间的干涉图样,通过观察干涉图样光强的变化可以得到入射光束轨道角动量信息[35-38]. 如图10所示,其中,α是每个角缝的缝宽,φ是角双缝之间的夹角,q1和q2和q3是动态角双缝平面上的3个点,oq3是角双缝夹角∠q1oq2的角平分线,p是远场衍射图样上的点,θ代表附加相位. 2个缝在观察平面p点的电场分别为E1(p)=u0(p)exp [iφ1(p)],E2(p)=u0(p)exp [iφ2(p)],(6)其中u0(p)和φ(p)分别是振幅和相位. 因此,角双缝在点p的干涉光强分布为I(p)=|E1(p)+E2(p)|2∝1+cos (Δφ),(7)其中,Δφ是角双缝到点p的相位差,由图10可知等号右边第一项lφ是由涡旋光束的螺旋相位项引起的相位差,等号右边第二项是由几何光程差引起的相位差. 如果角双缝是关于o′p轴对称的,那么角双缝到点p 的几何光程差为零,则角双缝到点p的相位差只依赖于由螺旋相位项引起的相位差,即Δφ=lφ,此时干涉光强的分布为I∝1+cos (lφ),当角双缝间的夹角φ 由0变化到2π时,光强变化的周期等于l,如图11所示. 由于余弦函数是偶函数,因此l的正负无法从光强变化中识别. 为解决该问题,在角双缝的其中1个角缝上加附加相位θ. 那么角双缝在点p的相位差变为Δφ=lφ+θ, 则干涉图样的光强分布为I∝1+cos (lφ+θ).(8)(a)l=6 (b)l=10 (c)l=15图11 强度随双缝间夹角的变化而变化的数值模拟(a)l=3,ΔΨ=30° (b)l=-3,ΔΨ=30°(c)l=6,ΔΨ=15° (d)l=-6,ΔΨ=15°(e)l=10,ΔΨ=9° (f)l=-10,ΔΨ=9°图12 携带不同轨道角动量的涡旋光束经过角双缝后,干涉图样中心区域的光强随角双缝旋转的变化(φ-I曲线)在这种情况下,附加相位会引起随角双缝夹角变化的光强分布曲线的旋转,旋转的方向和轨道角动量量子数l的正负有关. 因此,通过对光强变化曲线的分析可以得到轨道角动量量子l的大小与正负,如图12所示. 图12是干涉图样中心区域的光强随角双缝夹角的变化而变化的曲线(φ-I曲线),其中绿色的φ-I曲线是在没有加附加相位(θ=0)时得到的实验结果,因此,只能从中得到轨道角动量量子数l的大小,不能得到其正负的信息;蓝色的φ-I曲线是在有附加相位(θ=π/2)时得到的实验结果,从中可以看出,相对于绿色的φ-I曲线,蓝色的φ-I曲线有旋转. 通过对比绿色和蓝色的φ-I曲线可以得知:当轨道角动量量子数l为正时,蓝色的φ-I曲线沿顺时针旋转;当轨道角动量量子数l为负时,蓝色的φ-I曲线沿逆时针旋转. 因此,利用角双缝干涉,在有附加相位的条件下,可以很好地识别轨道角动量量子数l的大小和正负.5 三角孔衍射涡旋光束经过等边三角孔在远场的衍射图样可以折射出涡旋光束的轨道角动量量子数l的信息[39-41]. 当1束涡旋光束经过三角孔衍射,由夫琅禾费衍射积分得在远场的电场分布为∬(9)其中El(x,y,z=0)和τ(x, y)分别是入射涡旋光束的电场和三角孔平面的透射率函数. 通过数值求解式(9),得到不同轨道角动量模式经过三角孔夫琅禾费衍射图样的数值模拟结果,如图13所示,图13(a)中的插图为三角孔的方向. 从图13中可以看出,衍射图样呈三角形晶格阵列,而入射涡旋光束的轨道角动量量子数为l=N-1,其中N为衍射图样中三角形晶格阵列任意一边上晶格点的个数. 而l的正负可由三角形衍射图样的旋转方向来判断,如果入射的涡旋光束的轨道角动量量子数l的符号是相反的,则对应的衍射图样的旋转方向也是相反的. 另外,入射的涡旋光束的轨道角动量量子数l为负值的衍射图样相对于l为正值的衍射图样旋转了180°.(a)模拟结果(b)实验结果图13 不同轨道角动量模式经过三角孔衍射图样的数值模拟结果和实验结果由于涡旋光束经过三角孔的衍射图样是经过三角孔三边的场相互干涉的结果,因此,接下来分析涡旋光束经过三角孔时,三角孔边缘对光束的影响. 如图14所示,假设入射的涡旋光束落在三角孔径的中心O点所在的区域,则沿三角形孔径任意一条边缝的相位为(10)其中a是三角形孔径每条边的边长. 现考虑三角形孔径的每条缝近似为无限小的缝,且忽略了场振幅的变化,则可以将缝视为狄拉克函数. 在这种情况下,涡旋光束通过三角孔其中一边时相应的电场为exp (-ik·r)dxdy=(11)其中x和y是三角形孔径平面上横向笛卡尔坐标,kx和ky是傅里叶平面上的横向坐标. 由式(11)可知,三角孔衍射图样的大小和l成正比,且和三角形孔径边长a成反比,另外也可以看出,当入射的涡旋光束的轨道角动量量子数l的符号相反时,衍射图样的旋转方向是也是相反的.图14 三角孔示意图6 计算全息光栅法携带轨道角动量的涡旋光束可以用衍射光学元件(类似地,可以用螺旋相位板、Q-plate代替衍射光学元件)或计算全息光栅来产生[42-44]. 叉形光栅可以表示为(12)图15 1束轨道角动量量子数l=3的涡旋光束经过含有Δl=-3的叉形计算全息光栅其中l是轨道角动量量子数,φ是方位角,Λ=2π/kx是沿x方向的光栅周期. 从激光器或者单模光纤输出的光束(基模高斯光束)经过含有l个错位的叉形衍射光栅,在衍射1级处的光束携带了lħ的轨道角动量. 反之亦然,如图15所示,当1束具有轨道角动量量子数l=3的涡旋光束入射具有3个错位的叉形光栅(Δl=-3),此叉形光栅可以将入射光束中携带轨道角动量为3ħ的涡旋光束变成基模高斯光束,即将其螺旋相位消除掉,然后基模高斯光束可以耦合进单模光纤中. 在这种情况下,全息光栅结合单模光纤可作为特殊的轨道角动量模式探测器,这个探测器在单光子水平下仍然工作[14,45-46]. 但该方法只允许对光子的特定轨道角动量模式进行检测,若待测光束中含有多个轨道角动量模式,则需一系列的全息光栅对其进行探测,用不同l值的全息光栅就可测出待测光束中是否含有相应的轨道角动量模式. 此外,用该方法来探测N个模式时,至少需N个光子,并会受到全息光栅和单模光纤(或小孔)过滤系统传输效率低的影响. 之后,更复杂的全息光栅被提出来,此全息光栅可探测几种不同的轨道角动量模式[47-49]. 如图16(a)所示的计算全息光栅是由2个正交叉形衍射光栅组成,水平放置的衍射光栅中心错位为1,竖直放置的衍射光栅中心错位为3. 水平和竖直叉形全息光栅可表示为(13)其中a的取值范围从0到2π. 这2个全息光栅相结合组成了3 × 3的阵列,当1束平面波入射此光栅时,可以产生轨道角动量量子数从l=-4到l=4的轨道角动量模式. 反之亦然,当1束具有轨道角动量量子数l∈[-4,4]的轨道角动量模式通过此计算全息光栅时,高斯模式的光束将出现在3 × 3阵列中相应的位置,此位置与入射涡旋光束的轨道角动量量子数l一一对应,如图16中(b),(c)和(d)所示. 因此,这种全息光栅可以测量9种轨道角动量模式中的任意一模式,但其效率近似等于模式个数的倒数. 另一种利用衍射光栅探测轨道角动量模式的方法是通过分析衍射图样的位置特征来确定待测光束的轨道角动量量子数l的大小和正负[50]. 此外,基于计算全息光栅和单模光纤的投影技术——量子态层析是有效测量轨道角动量模式的方法[51-52].(a)二维叉形衍射光栅 (b)l=0(c)l=1 (d)l=2图16 经过叉形光栅后得到的实验结果7 光学几何变换法光波可以分解成不同方向的平面波的叠加,透镜可以将这些平面波聚焦到其局部平面上的不同的位置,其横向位置取决于平面波的传播方向. 基于这一特性,Berkhout等人提出利用2种衍射光学元件对轨道角动量模式进行分离的有效方法[53-55]. 此方法中,其中一个衍射光学元件用于几何变换,即将轨道角动量模式对应的笛卡尔坐标中的方位位置转换为横向动量态对应的对数极坐标中的横向位置;另一个衍射光学元件用于矫正经过几何变换时引入的相位畸变. 相位校正后,利用透镜将每个依赖于输入轨道角动量模式的横向动量态聚焦到1个平面的不同横向位置.如图17所示,空间光调制器(SLM1)用于产生待测的轨道角动量模式,SLM2和SLM3分别用于产生所需的相位剖面φ1(x, y)和φ2(u v),(x,y)和(u,v)分别是输入平面和输出平面的笛卡尔坐标系. 如图18所示,φ1(x,y)和φ2(u,v)表达式为(14)其中λ是入射涡旋光束波长,f是傅里叶透镜的焦距,a与转换后光束的长度d有关,b与输出平面的坐标有关(a和b是缩放常数). 由于φ1(x,y)和φ2(u,v) 分别实现了笛卡尔坐标与对数极坐标的变换和相位校正,因此由同心圆组成的输入图像(x,y)将会转变成平行线的输出图像(u,v). 经过相位校正元件后,利用透镜将转换后的态分离到观察平面指定的横向位置,聚焦点的横向位置取决于输入的轨道角动量模式,其关系为图17 实验装置示意图(a)几何变换 (b)相位矫正图18 光学元件的相位剖面(15)根据探测平面的强度分布,待测光束中所含的轨道角动量模式可以被识别出来,如图19所示,第1列是待测涡旋光束经过几何变换元件(SLM2)之前的相位和光强分布,第2列是待测涡旋光束经过相位校正元件(SLM3)之后的相位和光强分布,最后2列分别是在探测平面上的数值模拟结果和实验结果. 此外,此方法可以用来识别轨道角动量的叠加态,如图19最后1行所示. 但是,由于衍射极限的存在,2个相邻的轨道角动量模式产生的光斑略有重叠. 为了解决这一问题,Boyd等人提出利用光束复制装置来增强转换后的轨道角动量模式分离的方案[55-56]. 另外,他们利用光学几何变换结合光束复制技术,通过对轨道角动量的弱测量和角位置的强测量,得到了不同轨道角动量模式的复振幅[57]. 此外,由于空间光调制器的衍射效率有限,可以用折射率元件将其代替来执行笛卡尔坐标到对数坐标的变换[58-59].图19 数值模拟结果和实验结果8 旋转多普勒效应法旋转多普勒效应类似于传统的多普勒效应,是在角动量的基础之上发生的多普勒效应. 如图20所示, 当1束携带轨道角动量量子数l、频率为f的涡旋光束入射到旋转物体表面,其转速为Ω,则在散射光中会发现旋转多普勒效应,频移量为Δf=(l-m)Ω/2π,其中m表示散射光中的轨道角动量量子数. 若旋转物体的转速已知,则通过测量散射光中特殊模式的频移量就可以得到入射光束携带的轨道角动量[60-61].图20 旋转多普勒效应示意图旋转物体对入射涡旋光束的作用是进行了相位和振幅调制,将旋转考虑进去,则物体的调制函数用傅里叶展开可表达为M(r,φ)=∑An(r)exp (inφ)exp (-inΩt),其中n为整数,An(r)为n阶谐波复振幅,满足∑ |An(r)|2=1. 若入射光束是携带多个轨道角动量叠加态的涡旋光束,即含有N个未知的轨道角动量模式,可将入射的涡旋光束表示为(16)其中ls是轨道角动量量子数,取值范围为l1到lN,f是入射涡旋光束的初始频率,Bs表示入射涡旋光束的相应模式的复振幅. 引入参考光γB0exp (-i2πtf)exp (il0φ),参考光和待测的涡旋光束一起入射到旋转物体上,其中γ是用来调节参考光光强的参数. 那么从旋转物体上散射的光束的复振幅的表达式为B1exp (-2iπtf)Am-l1exp (imφ)exp [-i(m-l1)Ωt]+B2exp (-2iπtf)Am-l2exp (imφ)exp [-i(m-l2)Ωt]+…BNexp (-2iπtf)Am-lNexp (imφ)exp [-i(m-lN)Ωt],(17)由式(17)可知,所有的入射模式经过旋转物体后均转换成一系列相同的轨道角动量模式,这意味着散射光束经历了和入射涡旋光束的轨道角动量量子数ls成线性关系的多普勒频移. 当散射光束传播一定距离后,利用模式滤波器选择其中1个模式,假设该模式为OAMm,一般情况下m=0,即OAM0模式,然后利用光电探测器对该模式进行探测. 由于拍频效应,则收集到的光强分布可表示为Im(γ)=,(18)。
模数、数模转换及其应用论文

模数、数模转换及其应用摘要:随着电子技术的迅速发展以及计算机在自动检测和自动控制系统中的广泛应用,利用电子系统处理模拟信号的情况变得更加普遍。
数字电子计算机所处理的都是不连续的数字信号,而实际遇到的大都是连续的模拟量,模拟量经过传感器转换成电信号的模拟量后,需经过模/数转换变成数字信号后才可输入到数字系统中进行处理和控制。
同时,往往还要求将处理后得到的数字信号再经过数/模转换成相应的模拟信号,作为最后的输出。
模数、数模转换建立在各种转换电路的基础上,并且不断改进模数、数模转换器的转换精度与转换速度。
模数、数模转换技术在工业中有着重要的应用。
关键字:电子系统模数转换器数模转换器转换技术的应用Digital to analog、digital to analog conversion and its application Abstract: With the rapid development of electronic technology and computer in the automatic detection and automatic control system in the broad application, the use of electronic system for processing analog signal conditions become more common. Digital electronic computer processing are not continuous digital signal, but actually encountered mostly continuous analog, analog quantity sensor is converted into electrical signals by analog, after A / D conversion into digital signal can be input to a digital system for processing and control. At the same time, also often seek treatment received digital signals through D / A conversion into a corresponding analog signal, as the final output. ADC, DAC based on conversion circuit based on continuous improvement, and module, digital to analog converter conversion precision and conversion rate. ADC,DAC technology in industry has important applications.Key words: electronic system;analog to digital converter;digital to analog converter;conversion technology application1引言作为把模拟电量转换成数字量或数字量转换成模拟电量输出的接口电路,转换器是现实世界中模拟信号通向数字信号的桥梁,是电子技术发展的关键和瓶颈所在。
基于氧化镁晶体中级联四波混频过程的紫外飞秒光脉冲产生

基于氧化镁晶体中级联四波混频过程的紫外飞秒光脉冲产生*陈忠1)2) 华林强1)2)† 张津1)2) 龚成1)2) 柳晓军1)2)‡1) (中国科学院精密测量科学与技术创新研究院, 波谱与原子分子物理国家重点实验室, 武汉 430071)2) (中国科学院大学, 北京 100080)(2020 年9 月22日收到; 2020 年11 月11日收到修改稿)紫外波段飞秒激光脉冲是研究超快化学和超快物理相关过程的重要工具, 实现波长可调谐的宽带紫外飞秒光脉冲将有助于推动超快动力学及相关领域的研究. 本文报道了以两束400 nm的飞秒光脉冲作为级联四波混频的抽运源, 在氧化镁晶体中产生9阶频率上转换和5阶频率下转换边带信号的实验结果. 边带波长范围从350 nm到450 nm连续可调谐, 这些边带信号的发散角和波长与级联四波混频理论预测结果吻合. 紫外边带相对于入射光的整体转化效率约为1.2%. 同时, 高阶边带的光谱形状呈现高斯型, 其谱宽理论上支持傅里叶转换极限脉宽为20—50 fs. 本文展示了一种高效产生波长可连续调谐的紫外飞秒光脉冲的便捷方法,为基于紫外超短脉冲的相关研究提供了有效工具.关键词:紫外飞秒光脉冲, 级联四波混频, 氧化镁晶体PACS:42.65.–k, 42.65.Re, 42.65.Ky DOI: 10.7498/aps.70.202015731 引 言紫外飞秒激光脉冲在超快化学和超快物理研究领域有着十分重要的作用. 在超快化学研究中,大量分子体系的成键轨道到反键轨道的跃迁位于紫外波段, 紫外波段飞秒光脉冲结合时间分辨光谱技术, 能够让人们直接观察极短时间尺度内分子的形成或解离过程[1]; 在超快物理研究中, 紫外波段飞秒脉冲结合多维相干光谱技术[2], 能够研究半导体内激子动力学过程. 产生宽带可调谐的紫外飞秒光脉冲将有助于推动上述领域的研究.受限于激光工作介质, 目前大部分商用飞秒激光器的基频波长都在近红外波段, 采用一种便捷的方式将激光器输出波长拓展到紫外波段无疑具有重要的科学意义和应用前景. 目前, 基于非线性晶体将基频飞秒光脉冲的波长转换到紫外波段的主要方法包括: 倍频与和频[3]、光学参量放大[4]、级联四波混频[5−7]等. 其中级联四波混频由于其转化效率高、产生的边带波段范围宽、可调谐以及能够合成超短飞秒(甚至阿秒)脉冲等优点, 成为近年来的研究热点[8−33]. 例如: Crespo小组[8]利用级联四波混频在玻璃片中观察到了11阶边带的产生, 并且将光谱从近红外延伸到了紫外波段. 另外他们还利用可调谐染料飞秒激光器输出的两种频率的激光, 在熔融石英中实现了更高的20阶的频率上转换边带, 最短波长为209 nm, 并利用这些边带合成了2.2 fs的近单光学周期超短脉冲[9]. 文献[10−17]将级联四波混频方法扩展到了BBO[10,11]、蓝宝石[12−14]、石英[15,16]、氟化钙[17]等各向异性材料中.* 国家自然科学基金(批准号: 11674356, 11527807)和中国科学院战略性先导科技专项(B类)(批准号: XDB21010400)资助的课题.† 通信作者. E-mail: hualq@‡ 通信作者. E-mail: xjliu@© 2021 中国物理学会 Chinese Physical Society 他们通过拓展抽运光的光谱并引入适量的啁啾, 使产生的紫外脉冲输出能量稳定、波长可调谐, 提高了级联四波混频输出的多色飞秒光脉冲的实用性. Fang等[18,19]还发展了和频级联四波混频技术, 他们利用一束800 nm基频脉冲和一束红外超连续白光脉冲, 在BBO晶体中实现了倍频与四波混频之间的级联效应, 拓展了紫外波段的光谱范围. 文献[20−33]则选择具有拉曼活性的晶体, 实现了更高的边带转化效率并且产生了更高的阶次. 这些研究工作推动了基于级联四波混频技术产生宽带紫外飞秒光脉冲的发展. 然而, 这些级联四波混频研究所采用的驱动光源都在近红外或者可见波段, 所产生的紫外飞秒光脉冲对应很高的阶次. 在级联四波混频中, 每一阶信号光由上一阶信号光和两束抽运光共同产生, 边带阶次越高, 产生效率越低. 因此, 利用短波长的驱动光进行级联四波混频, 将降低紫外波段边带对应的阶次, 有助于提高紫外边带的产生效率[9,12,13,16].本文报道了采用两束400 nm的飞秒激光作为级联四波混频的抽运源来产生波长可调谐的紫外飞秒光脉冲的研究成果. 利用紫外脉冲驱动晶体介质产生级联四波混频要求所用晶体具有紫外波段透射率高、3阶非线性极化率大和带隙宽度宽等特性. 本实验选取氧化镁(MgO)晶体作为工作介质, MgO晶体的紫外波段透射率为92%, 3阶非线性极化率为c(3) = 7.3×10–15 cm3·erg[34], 是紫外波段透射率大于90%的晶体材料中, 3阶非线性极化率最大的一种. 此外, 其带隙宽度为7.8 eV, 有较高的损伤阈值. 实验中级联四波混频产生的飞秒光脉冲覆盖了350—450 nm波段, 实现了直接倍频难以达到的光谱范围. 紫外边带相对于入射光的整体转化效率约为1.2%, 优于已有报道结果[9,12,16],其中390 nm的紫外边带效率约为0.7%, 高于已有实验中同波长边带的产生效率[9]. 本方案为高效产生波长可连续调谐的紫外飞秒光脉冲提供了一种有效途径.2 实验装置实验装置如图1所示. 实验中所使用的飞秒激光器(Legend HE+, Coherent Inc.)由一个振荡器和一个再生放大器组成, 它输出的光脉冲参数如下: 最大能量为4.8 mJ, 中心波长为792 nm, 重复频率为1 kHz, 脉宽约为35 fs. 激光器输出的脉冲经分束镜后被分为两束, 其中反射的部分经透镜聚焦后入射到0.6 mm厚的第Ⅰ类相位匹配BBO 中. 通过优化基频光的入射角度和晶体的光轴方向, 获得了功率约为180 mW的倍频脉冲, 其脉宽估算约为140 fs. 倍频光经过透镜准直后, 平行入射至透800 nm反400 nm的二色镜上. 二色镜滤掉基频成分, 以排除基频对级联四波混频实验的影响. 400 nm光经过偏振方向调节后, 被分光棱镜(PBS)分成两路: 一路经过f = 20 cm的透镜后,聚焦在MgO晶体上; 另一路则经过恰当的偏振调节和延时调节, 同样被f = 20 cm的透镜聚焦于MgO晶体上. 两束光的焦点以非共线方式在MgOFemtosecondlaser BBODichroicbeamsplitterPBSDelay stageSpectrometerMgOBS3=20 cm12图 1 实验装置图(PBS为偏振分束器; 1, 2, 3为半波片; BS为分光镜)Fig. 1. Schematic diagram of the experimental setup (PBS represents polarization beam splitter; 1, 2, 3 represent half wave plates; BS represents beam splitter).⟨100⟩晶体中重合, 通过调节两束光在f = 20 cm 透镜上的间距对其夹角进行精密控制, 两束光的偏振方向由透镜前的半波片(图1中编号为3)控制. 实验采用的MgO 晶体的厚度为0.2 mm, 晶向为 ,两面抛光. 实验产生的四波混频边带信号通过宽波段的光谱仪(QE65pro 和Maya2000pro, Ocean Optics)进行测量, 并实时记录到电脑中, 以便于实验条件的实时优化和后期数据处理.3 实验结果与分析实验首先测量了钛宝石激光器输出的基频光的光谱, 如图2(a)所示, 其中心波长为792 nm, 光谱范围为760—820 nm. BBO 晶体作为倍频介质,通过调节其光轴角度, 可以实现倍频光的中心波长连续调谐. 这种方式产生的倍频光的光谱范围约为380—410 nm, 如图2(b)所示. 本文将倍频效率最高时的光轴角度设为0°, 可产生倍频的光轴角度范围为±10°. 注意到图中光谱在395 nm 附近出现干涉条纹, 它可能来源于BBO 晶体中倍频光与和频光之间的干涉.在级联四波混频实验中, 使用的两束400 nm 抽运光的功率分别为14 mW 和9 mW, 偏振为s 偏振. 经过透镜聚焦后, 光斑直径约为170 µm,0.2 mm 厚的MgO 基片被放置于焦点附近, 两束光在MgO 晶体中实现时间和空间上的重合. 实验发现, 两束抽运光在空气中的夹角为0.9°—2.8°时,均有四波混频信号产生. 相对延迟为零时, 发生比较明显的自衍射[20], 当两束抽运光的夹角为1.3°、相对延迟为80 fs 左右时, 级联四波混频产生的边带数量最多, 且边带信号强度最强. 在上述条件下产生了9阶频率上转换边带和5阶频率下转换边带, 抽运光的左侧为频率下转换边带, 右侧为频率上转换边带, 从左到右波长依次减小. 实验结果表明斯托克斯一侧的边带数目较少, 这是由于当阶数增加时, 产生级联四波混频信号所需的波矢量|k (m )|在反斯托克斯和斯托克斯侧都会增大[7], 对于反斯托克斯光束, 波长随阶数的增加而减小, 与|k (m )|长度增大的要求相一致. 在此情形下, 高阶边带也可以满足一定的相位匹配条件. 与此相对,斯托克斯光束的波长随阶数的增加而增大, 红移波长不满足增大|k (m )|长度的要求. 因此, 斯托克斯信号的相位失配随阶数的增加而迅速增加, 使得斯托克斯侧的边带数量比反斯托克斯侧的少. 本文将第m 阶的频率上(下)转换的边带命名为AS m (S m ). 其中, AS2到AS7投影到白色纸片上的照片如图3(a)所示. 这些边带沿着不同的散射角发散, 利用光谱仪在不同位置对边带信号进行收集和测量, 得到每一阶边带的归一化光谱, 如图3(b)和图3(c)所示, 它们的波长范围为350—450 nm. 其中, 高阶边带在400 nm 左右的次峰来自于抽运光的杂散信号. 同时, 注意到四波混频信号在空间上并非绝对分离, 这使得在信号的主峰旁边产生了其他信号的小峰.级联四波混频过程产生边带的中心波长和发散角满足频率对应关系和相位匹配关系[7]:其中, w 1, w 2, k 1, k 2分别为两束抽运光各自的角频率和波矢量; w As m , k As m 分别为AS m 边带的角频74076078080082084000.20.40.60.81.0归一化光强波长/nm波长/nm(a)3803904004100.20.40.60.81.0归一化光谱10O 3O 0O -10O(b)图 2 (a) 钛宝石激光器输出的基频光光谱; (b) BBO 在不同光轴角度下的倍频光光谱Fig. 2. (a) Output spectrum of Ti-Sapphire laser; (b) spectra of the second harmonic generation under different BBO orientations.率和波矢量. 利用抽运光的作用波长: 395.0 nm 和400.6 nm 及抽运光之间的夹角, 通过(1a )式和(1b )式及MgO 的Sellmeier 方程, 计算得到AS1到AS9的理论中心波长分别为: 390, 384, 379,374, 369, 364, 359, 355和350 nm, 这和实验测量的结果吻合, 如图4(a)所示, 其中低阶的差异来源于自相位调制和交叉相位调制[35]. 同样, 计算得到AS1到AS7的理论散射角度分别为: 2.54°, 3.76°,4.93°, 6.08°, 7.18°, 8.25°和9.29°. 图4(b)为其与实验测量结果的对比, 可以看到散射角度和理论预测的结果在低阶时符合得很好, 在高阶的情况下有少量偏移. 此外, 产生的边带在平面上也有小的弯曲, 波长越短的边带越往上偏移. 这是因为实验中晶体的光轴与入射光所在平面存在微小夹角, 对于MgO 样品, 波长越短对应的折射率越大, 当不同波长的边带以不同角度出射时, 波长越短、出射角度越大的光束将产生更明显的折射, 这导致了高阶边带的偏移并且散射角度比预测角度大. 类似现象也出现在以钨酸铅和金刚石为介质的实验中[20−22].为考察此方案产生的紫外飞秒光脉冲的特征,本实验测量了400 nm 光激发MgO 晶体所产生边3403603804000.20.40.60.81.0归一化光谱波长/nm波长/nmAS9AS8AS7AS6AS5AS4AS3AS2AS1(b)38040042044046000.20.40.60.81.0归一化光谱S1S2S3S4S5(c)图 3 (a) AS2到AS7边带的照片; (b) AS1至AS9边带的光谱; (c) S1至S5边带的光谱Fig. 3. (a) Photographs of AS2 to AS7; (b) spectra of sidebands from AS1 to AS9; (c) spectra of sidebands from S1 to S5.波长/n m阶次散射角度/(O )阶次图 4 (a) AS1到AS9边带的理论计算中心波长(红色圆圈)和实验测量(黑色方块)之间的比对; (b) AS1到AS7边带的理论计算散射角(红色圆圈)和实验测量(黑色方块)之间的比对Fig. 4. (a) Comparison of calculated results (red circles) and experimental data (black squares) of central wavelengths of AS1 to AS9; (b) comparison of calculated results (red circles) and experimental data (black squares) of scattering angle of AS1 to AS7.带的功率. 测量得到AS1到AS7的功率分别为169.3, 85.7, 17.8, 5.2, 1.6, 0.2和0.032 µW. 紫外边带相对于入射光的整体转化效率约为1.2%, 其中, 390 nm (AS1)紫外边带的产生效率约为0.7%.在红外光或可见光驱动级联四波混频产生宽带紫外飞秒光脉冲的实验中[9,12,16], 已见报道的紫外波段整体转化效率最高约为0.7%, 390 nm 边带产生效率约为0.3%[9]. 但注意到本实验中高阶边带效率偏低, 边带的整体带宽有限, 如何进一步提升高阶边带的转换效率、扩展边带的整体带宽有待进一步研究. 同时, 实验中还测量了边带的谱宽, 通过对每一阶边带的光谱进行高斯拟合, 发现AS3到AS9的光谱形状十分接近高斯线型, 图5(a)为AS3边带高斯拟合的结果. 拟合AS3至AS9边带得到的光谱半高全宽分别为5.1, 5.7, 5.6, 6.7, 5.6, 4.6和6.5 nm. 根据计算, AS3到AS9对应的傅里叶转换极限脉宽分别为42, 36, 35, 28, 33, 39, 27 fs.此外, 通过在驱动光脉冲中引入合适啁啾, 利用改变脉冲到达样品的延迟时间能够改变两个脉冲相互作用波长的原理, 可以实现以调节延时的方式来便捷地调谐产生边带的中心波长. 在本实验中, 通过调节钛宝石激光器的脉冲压缩光栅引入约–400 fs 2的啁啾, 结合对两束抽运光的延时控制实现了对边带中心波长的有效调控. 以AS4为例, 本文给出了几个特定延迟时间条件下的该边带波长的相对变化, 如图5(b)所示. 可以看出, 在两束脉冲相互作用产生边带信号的时间范围内, AS4边带的中心波长可以从373 nm 到385 nm 之间连续调谐. 利用产生的全部边带, 可以实现波长从350 nm 到450 nm 全覆盖.4 结 论本文以两束400 nm 的飞秒光脉冲作为级联四波混频的驱动光源, 在0.2 mm 的MgO 介质中产生了一系列频率上转换和频率下转换的飞秒脉冲. 这些边带的波长和散射角符合理论预测, 光谱范围从350 nm 到450 nm 全覆盖. 其中, 紫外边带的产生效率约为1.2%, 高于用近红外光或者可见光驱动产生紫外边带的效率. 通过调控两束400 nm 脉冲的相对延时, 可实现波长宽带调谐. 同时, AS3到AS9边带的光谱形状呈现高斯型, 这些脉冲支持的理论极限宽度为20—50 fs. 本文为高效产生波长连续可调谐的紫外飞秒光脉冲提供了一种有效途径, 有助于推动超快化学与超快物理方面的相关研究.参考文献D emtroder W (translated by Ji Y) 2012 Laser Spectroscopy(Vol.2): Experimental Techniques (Beijing: Science Press)pp466–468 (in Chinese) [戴姆特瑞德W 著 (姬扬 译) 2012 激光光谱学(第2卷): 实验技术 (北京: 科学出版社) 第466—468页][1]B ruder L, Bangert U, Binz M, Uhl D, Vexiau R, Bouloufa MN, Dulieu O, Stienkemeier F 2018 Nat. Commun. 9 2519[2]Y ao J Q 1995 Nonlinear Optical Frequency Conversion andTunable Lasers (Beijing: Science Press) pp146–148 (in Chinese) [姚建铨 1995 非线性光学频率变换及激光调谐技术(北京: 科学出版社) 第146—148页][3]Y e P X 2007 Nonlinear Optical Physics (Beijing: PekingUniversity Press) pp99–103 (in Chinese) [叶佩弦 2007 非线性光学物理 (北京: 北京大学出版社) 第99—103页][4]H e J P, Liu J, Kobayashi T 2014 Appl. Sci. 4 444[5]W eigand R, Crespo H M 2015 Appl. Sci. 5 485[6]L iu J, Kobayashi T 2010 Sensors 10 4296[7]C respo H M, Mendonça J T, Dos S A 2000 Opt. Lett. 25 829[8]3753803853900.20.40.60.81.01.2归一化强度Guassian fit(a)3653703753803853900.20.40.60.81.0归一化强度波长/nm波长/nm20 fs 40 fs 60 fs 80 fs 100 fs(b)图 5 (a) AS3边带光谱(实线)及其高斯拟合(虚线);(b)不同延时下AS4边带的光谱, 图中的光谱对应的延时分别为20, 40, 60, 80, 100 fsFig. 5. (a) Spectra of the AS3 sideband (solid curve) and its Gaussian fitting (dashed curve); (b) spectra of the AS4 sideband at several specific time delays, i.e. 20, 40, 60,80, and 100 fs.W eigand R, Mendon J T, Crespo H M 2009 Phys. Rev. A 79063838[9]L iu J, Zhang J, Kobayashi T 2008 Opt. Lett. 33 1494[10]W ang P, Shen X, Zeng Z N, Liu J, Li R X, Xu Z Z 2019 Opt.Lett. 44 3952[11]L iu J, Kobayashi T 2008 Opt. Express 16 22119[12]L iu J, Kobayashi T, Wang Z 2009 Opt. Express 17 9226[13]W ang P, Liu J, Li F J, Shen X, Li R X 2014 Appl. Phys.Lett. 105 201901[14]L iu J, Kobayashi T 2010 Opt. Commun. 283 1114[15]W ang P, Liu J, Li F J, Shen X, Li R X 2015 Photon. Res. 3210[16]L iu Q F, Li F J, Liu J 2014 Acta Phys. Sin. 63 094209 (inChinese) [刘奇福, 李方家, 刘军 2014 物理学报 63 094209][17]L iu W M, Zhu L D, Fang C 2012 Opt. Lett. 37 3783[18]L iu W M, Zhu L D, Wang L, Fang C 2013 Opt. Lett. 38 1772[19]Z hi M C, Sokolov A V 2008 New J. Phys. 10 025032[20]Z hi M C, Sokolov A V 2007 Opt. Lett. 32 2251[21]W ang K, Zhi M C, Hua X, Strohaber J, Sokolov A V 2014Appl. Opt. 53 2866[22]W ang K, Alexandra Z, Zhi M C, Hua X, Sokolov A V 2015Appl. Sci. 5 145[23]S hutova M, Shutov A D, Zhdanova A A, Thompson J V,Sokolov A V 2019 Sci. Rep. 9 1565[24]T akahashi J I, Matsubara E, Arima T, Hanamura E 2003Phys. Rev. B 68 155102[25]T akahashi J I, Kawabe Y, Hanamura E 2004 Opt. Express 121185[26]M atsubara E, Inoue K, Hanamura E 2005 Phys. Rev. B 72134101[27]M atsuki H, Inoue K, Hanamura E 2007 Phys. Rev. B 75024102[28]I noue K, Kato J, Hanamura E, Matsuki H, Matsubara E 2007Phys. Rev. B 76 041101(R)[29]T akahashi J I, Keisuke M, Toshirou Y 2006 Opt. Lett. 311501[30]M atsubara E, Sekikawa T, Yamashita M 2008 Appl. Phys.Lett. 92 071104[31]S okolov A V, Harris S E 2003 J. Opt. B 5 R1[32]Z hi M C, Wang X, Sokolov A V 2008 Opt. Express 16 12139[33]S hea J J 2004 IEEE Electri. Insul. M. 20 46[34]D harmadhikari J A, Dota K, Kritkika D, Mathur D,Dharmadhikari A K 2016 Appl. Phys. B 122 140[35]Generation of tunable ultraviolet femtosecond pulse in MgO crystal by cascaded four wave mixing*Chen Zhong 1)2) Hua Lin -Qiang 1)2)† Zhang Jin 1)2)Gong Cheng 1)2) Liu Xiao -Jun 1)2)‡1) (State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Innovation Academy forPrecision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China)2) (University of Chinese Academy of Sciences, Beijing 100080, China)( Received 22 September 2020; revised manuscript received 11 November 2020 )AbstractUltraviolet femtosecond laser pulse is an important tool in studying ultrafast chemical and physical processes. Realizing broadband ultraviolet laser pluses with a wide tunable range would significantly facilitate the study of ultrafast processes. As an effective and convenient method, the cascaded four-wave mixing (CFWM) has been widely adopted to generate broadband and tunable ultraviolet femtosecond laser pulses. In this work, we carry out CFWM in MgO crystal by using two 400-nm pulses to generate tunable ultraviolet femtosecond pulse. The MgO crystal is chosen due to its high third-order nonlinear susceptibility, large band gap and high transmittance in the ultraviolet region. In the experiment, nine frequency up-converted and five frequency down-converted sidebands are observed. The measured wavelength and scattering angle of each sideband are consistent with the CFWM theory predictions. The wavelength range of the sidebands covers 350–450 nm. The total conversion efficiency of the ultraviolet sidebands is 1.2%, which is higher than the reported values with visible/near infrared driven lasers. Meanwhile, the spectra of the high-order sidebands present a Gaussian profile and can support a Fourier-transform-limited pulse duration of less than 50 fs. Besides, the central wavelengths of the sidebands can be effectively tuned by adjusting the time-delay between the two pre-chirped pump pulses. Our study provides an efficient and convenient scheme to generate short ultraviolet femtosecond pulses with a wide tunable range.Keywords: ultraviolet femtosecond pulse, cascaded four wave mixing, MgO crystalPACS: 42.65.–k, 42.65.Re, 42.65.Ky DOI: 10.7498/aps.70.20201573* Project supported by the National Natural Science Foundation of China (Grant Nos. 11674356, 11527807) and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences, China (Grant No. XDB21010400).† Corresponding author. E-mail: hualq@‡ Corresponding author. E-mail: xjliu@。
偏振分束器pbs简单画法

偏振分束器(PBS)简单画法一、介绍在光学领域中,偏振分束器(Polarizing Beam Splitter,PBS)是一种能够将入射光分成两个具有不同偏振状态的光束的器件。
它广泛应用于激光系统、显微镜、光学仪器等领域。
二、PBS的工作原理PBS的工作原理基于偏振光的性质。
偏振光是指光波中的电场沿特定方向振动的光。
偏振光可以沿任意方向传播,但当它遇到一个偏振分束器时,只有与特定偏振方向相匹配的光可以通过。
PBS通常由一个玻璃体和一层金属或薄膜组成。
玻璃体可以是一段棱镜或一个平板,它用于引导和分束光。
金属或薄膜层用于实现对不同偏振状态光的分离。
当未偏振光正入射到PBS上时,它会被分成两个彼此垂直方向振动的偏振光。
一个偏振光沿着入射角的方向传播,被称为s偏振光(或TE波),而另一个偏振光则沿着与入射角垂直的方向传播,被称为p偏振光(或TM波)。
三、PBS的简单画法1. 步骤1: 准备材料•一个玻璃体(可以是棱镜或平板)•金属或薄膜(用于制作PBS的分束层)•一台激光器或光源•光学工具(如反射镜、透镜等)2. 步骤2: 精确定位将玻璃体放置在光路上,并使用光学工具将其固定在适当的位置。
确保入射光能够与玻璃体相交。
3. 步骤3: 制作分束层在玻璃体的一侧涂覆金属或薄膜,用于将偏振光分离成s偏振光和p偏振光。
这一步需要精确的工艺来确保分束层的质量和性能。
4. 步骤4: 调整角度旋转玻璃体,调整入射光的角度,以便能够正确地分离出偏振光。
通常需要通过试错的方法来找到最佳的角度。
5. 步骤5: 测试和优化使用激光器或光源照射PBS,观察光束的分离效果。
如果分离效果不理想,可以尝试调整角度或修改分束层的制作工艺。
四、PBS的应用1. 激光系统PBS广泛应用于激光系统中。
在激光器的输出端,PBS可以将激光分成两个偏振方向垂直的光束,用于实现不同的激光功率分配或激光束控制。
2. 显微镜在共聚焦激光扫描显微镜(Confocal Laser Scanning Microscopy,CLSM)中,PBS常用于分离和选择特定偏振方向的激光束。
光学pbs的原理

光学pbs的原理光学PBS(偏振分束器,Polarizing Beam Splitter)是一种常用的光学元件,其原理是利用特殊的材料和构造,将入射光按照偏振方向分成两束,其中一束透射,另一束反射。
PBS常用于光学仪器和设备中,用于分离或合并不同偏振方向的光线。
光学PBS的基本构造是由两个折射率不同的介质组成的复合结构。
其中一个介质具有较高的折射率,另一个介质折射率较低。
这两个介质的界面通过抛光或涂覆等方法使得界面较为平坦,减小反射和散射。
在光学PBS的结构中,一束入射光线从一个介质(通常是玻璃)射入另一个介质(通常是偏振材料或薄膜)。
由于两个介质的折射率不同,入射光线在其中一个介质与另一个介质的界面上会产生反射和折射。
反射光线和折射光线的偏振方向根据入射光线的偏振方向和两个介质的折射率确定。
当入射光线的偏振方向与PBS的结构中的边界平行时,入射光线只会发生反射,折射光线几乎不存在。
这是因为在这个边界上,两个介质的折射率差异最大,反射光线的偏振方向与入射光线的偏振方向相同。
当入射光线的偏振方向与PBS的结构中的边界垂直时,入射光线只会发生折射,反射光线几乎不存在。
这是因为在这个边界上,两个介质的折射率差异最小,折射光线几乎与入射光线的偏振方向相同。
当入射光线的偏振方向介于平行和垂直于结构边界之间时,入射光线会发生部分反射和部分折射。
这是因为在这种情况下,折射光线和反射光线的偏振方向分别是沿入射面与法线之间的偏振方向和垂直于入射面的偏振方向。
通过以上原理,光学PBS将入射光线按照偏振方向分成两束光线,其中一束光线透射通过PBS,另一束光线反射回去。
透过率和反射率取决于入射光线的偏振方向与PBS结构边界之间的夹角。
在设计PBS时,我们可以根据具体需求选择合适的材料和结构参数,来实现不同的分束比例和偏振特性。
总结来说,光学PBS是一种通过利用折射率不同的介质和特殊结构,将入射光线按照偏振方向分成两束光线的光学元件。
偏振的图画,动画讲解
n1 n2
i0
i0 90
n2 tan i0 n1
布儒斯特角(polarizting angle ):
玻璃堆
布儒斯特角
i0
线偏振光
应用举例: 激光器谐振腔
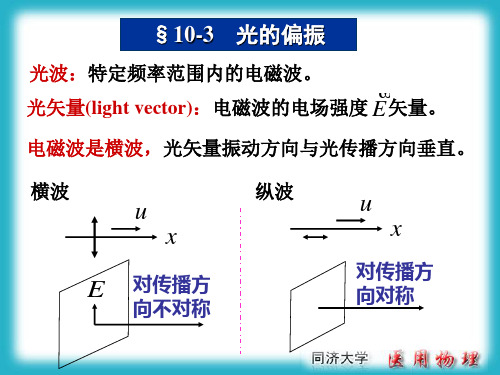
圆偏振光 (circularly polarized light)) 光矢量端点在垂直于 光传播方向的截面内描绘 出圆形轨迹。检偏器旋转 一周,光强无变化。
点击图片放大
2. 波片
x y 2 xy 2 cos( ) sin ( 2 1 ) 2 1 2 2 A1 A2 A1 A2
x y 2 xy 2 2 cos( 2 1 ) sin ( 2 1 ) 2 A1 A2 A1 A2
2
2
o e
光轴
光轴
o e
问题:自然光垂直入射双折射晶体表面,投射后 为何不能产生椭圆偏振光?
自 然 光
偏 振 光 A o
Ae
x ye Ae cos (t ) ve
检偏
偏振光
(1) 自然光强 I0 线偏振光强 :
I0 I 2
光强不变无消光
(2) 线偏振光强 I0 线偏振光强 有两次消光现象
(3)部分偏振光(混合) 线偏振光 有两次极大极小
马吕斯定律(Malus law)
A0
A2
I0
A1
I
光强为I0的线偏振光,透过偏振片后,透射强度为:
I I 0 cos
白云石 1.6811
正晶体:石英、冰 负晶体:方解石、电气石、白云石、硝酸钠 正晶体 负晶体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
偏振分束器pbs简单画法
偏振分束器PBS简单画法
一、什么是偏振分束器PBS?
偏振分束器PBS(Polarizing Beam Splitter)是一种光学元件,能够将入射的光线按照其偏振方向进行分离,将其中一个方向的光线反射出去,另一个方向的光线则透过去。
它通常由两个三棱镜组成,其中一个是玻璃三棱镜,另一个是由特殊材料制成的棱镜。
二、PBS的简单画法
1. 画出玻璃三棱镜
首先,在纸上画出一个三角形,表示玻璃三棱镜。
然后在三角形中心处画出一条垂直于底边的直线,表示入射光线。
接着,在底边中心处画出一条与底边垂直的虚线,表示反射光线。
2. 画出特殊材料制成的棱镜
在纸上画出另一个三角形,表示特殊材料制成的棱镜。
与玻璃三棱镜
类似,在三角形中心处也要画出一条垂直于底边的直线,表示入射光线。
但不同的是,在底边中心处画出两条虚线,分别表示反射光线和透射光线。
3. 组合两个三棱镜
将两个三棱镜组合在一起,使它们的入射光线重合。
玻璃三棱镜的反射光线和特殊材料制成的棱镜的透射光线重合,而玻璃三棱镜的透射光线和特殊材料制成的棱镜的反射光线重合。
这样,入射光线就被分成了两个方向,一个方向是反射方向,另一个方向是透射方向。
4. 标注偏振方向
在玻璃三棱镜和特殊材料制成的棱镜上标注偏振方向。
通常用箭头表示偏振方向,箭头所指的方向为偏振面。
在玻璃三棱镜上标注垂直于底边的箭头表示s偏振(即电场垂直于纸面),在特殊材料制成的棱镜上标注平行于底边的箭头表示p偏振(即电场平行于纸面)。
5. 完整画法
将以上步骤综合起来,就可以画出一个完整的偏振分束器PBS。
在画图时,要注意比例和标注清晰,以便更好地理解PBS的工作原理和应用。
