19 全因子实验设计
全因子试验设计概述

复杂系统试验设计
随着产品复杂性的增加,未来全因子试验设计将 面临更多的挑战,需要更加注重复杂系统的试验 设计和优化方法的研究。
跨学科合作与创新
未来全因子试验设计需要更加注重跨学科的合作 与创新,融合多个学科的理论和方法,推动全因 子试验设计的不断发展和完善。
THANKS FOR WATCHING
感谢您的观看
响应变量
试验中因因子的变化而变化的量,通常是试验指标的具体数值表现。例如,抗拉强度的具体数值就是 响应变量。
重复试验和随机化
重复试验
为了获得更可靠的结果,通常会在相同的条件下重复进行试验。重复试验可以减少随机误差的影响,提高结果的 稳定性。
随机化
在试验设计中,随机化是一种重要的原则。它要求试验的安排不应受到任何系统性偏好的影响。例如,在安排试 验顺序时,应采用随机方法,以避免因时间、环境等因素引起的系统性误差。随机化可以提高试验结果的客观性 和可重复性。
制定试验计划
根据选定的试验设计方法,制定详细的试验 计划,包括试验的时间、地点、人员、仪器
、试剂等具体安排。
实施试验并收集数据
实施试验
按照试验计划进行试验操作,确保试验过程 的准确性和可重复性。
收集数据
在试验过程中及时记录试验数据,包括因子 的实际取值和相应的试验结果。
分析试验结果并得出结论
数据处理
全因子试验设计考虑了 所有因子的所有水平组 合,因此可以获得最全 面的试验信息。
通过合理安排试验顺序 和组合方式,可以在较 短时间内完成大量试验 ,提高试验效率。
由于考虑了所有可能的 组合情况,因此全因子 试验设计的结果具有较 高的可重复性和稳定性 。
全因子试验设计适用于 多因子、多水平的研究 场景,广泛应用于农业 、工业、医学等领域。
全因子实验及部分因子实验设计-精品文档

小组的试验设计策划如下
DOE 试验计划表
项目负责人: 张军 项目 冰箱服务请求问题改善
部门: 工程部 日期: 2019.3.15
DOE目标:确定不同供应商的压缩机对冰箱寿命的影响
相关背景:现在公司冰箱的市场服务求升为10起/天,且有增高之势
输出特性指标
关键特性
如何测量
规格
MTBF
常温下运转至出现故 障
目前水 目标水
平
平
△
否
◎
是
如非试验因素
如何固定其为常量,在 何种水平上
滚珠10的角度 ◎
◎
是
滚珠压力
◎
◎
是
Y装配速度
○
◎
否
注: ◎代表有重大影响,容易改变
○有中等影响,相对容易改变
△代表影响很少,很难改变
使用现在装配速度
噪声因素表
噪声因素
对输 出的 影响
试验 时改 变难 易度
要否 做为 实验 因素
相关背景:现在市场上此款滑轨的潜动力超规格,经小组调查分析,决定施实DOE进 行改善
输出特性指标
关键特性 测量什么/如何测量
规格
是否用于DOE
滑动力
用测力计测
22~172N
否
配合间隙
内外滑轨尺寸差异
-0.01~0.03mm
否
内轨的外部尺寸
19.07± 0.1mm
否
滑轨尺寸
外轨的内部尺寸
19.07± 0.15mm
确定影响因素XS
从可控因素表各噪声因素表可知,确定为试验因素的 胡三个,分别是: 1.滚珠固定座的位置. 2.滚珠10的角度. 3.滚珠压力.
本试验设计围绕滚珠成型机器,试验3个因素的水 平的测量指标如下表
全因子DOE实验设计方法论

820 112 40 144 140 132 138.667820 120 50 125 127 140 130.667810 116 45 92 136 83 103.667810 116 45 129 119 87 111.667800 112 50 91 79 94 88.000820 120 40 116 121 94 110.333800 120 50 118 98 90 102.000820 112 50 135 149 137 140.333820 112 50 131 140 142 137.667820 112 40 113 110 136 119.667800 120 40 82 116 113 103.667820 120 50 99 159 118 125.333800 112 40 82 101 87 90.000800 120 40 107 126 116 116.333820 120 40 159 118 108 128.333800 112 40 114 92 109 105.000800 120 50 116 111 71 99.333810 116 45 134 132 130 132.0002。
第二阶段;分析因子设计。
目的:得到Y=f(x),确定哪些因子值得存在函式内。
结果: 第1次实验MINITAB路径:统计-DOE-因子-因子分析设计拟合因子: Y 与压力, 密度, 温度Y 的效应和系数的估计(已编码单位)系数标项效应系数准误 T P常量 114.211 2.179 52.42 0.000压力 29.917 14.958 2.374 6.30 0.000密度 1.167 0.583 2.374 0.25 0.810温度 -0.167 -0.083 2.374 -0.04 0.973压力*密度 -11.583 -5.792 2.374 -2.44 0.033(P0.05,接受HO:交互作用对Y没有影响)压力*温度 9.417 4.708 2.374 1.98 0.073(P0.05,接受HO:交互作用对Y 没有影响)密度*温度 -0.167 -0.083 2.374 -0.04 0.973(P0.05,接受HO:交互作用对Y没有影响)压力*密度*温度 -0.417 -0.208 2.374 -0.09 0.932(P0.05,接受HO:交互作用对Y没有影响)S = 9.49770 PRESS = 2630.73R-Sq = 81.86% R-Sq(预测)= 51.91% R-Sq(调整)= 70.32%对于Y 方差分析(已编码单位)来源自由度 Seq SS Adj SS Adj MS F P主效应 3 3585.58 3585.58 1195.19 13.25 0.0012因子交互作用 3 891.50 891.50 297.17 3.29 0.0623因子交互作用 1 0.69 0.69 0.69 0.01 0.932残差误差 11 992.27 992.27 90.21弯曲 1 8.75 8.75 8.75 0.09 0.772纯误差 10 983.52 983.52 98.35合计 18 5470.05从上图可以看出,P0.05,接受HO:交互作用对Y没有影响,可以通过缩减再观察P值Y 的效应和系数的估计(已编码单位)系数标项效应系数准误 T P常量 114.211 2.571 44.42 0.000压力 29.917 14.958 2.802 5.34 0.000密度 1.167 0.583 2.802 0.21 0.838(P0.1,接受HO:因子对Y没有影响)温度 -0.167 -0.083 2.802 -0.03 0.977(P0.1,接受HO:因子对Y没有影响)S = 11.2085 PRESS = 2995.55R-Sq = 65.55% R-Sq(预测) = 45.24% R-Sq(调整) = 58.66%对于 Y 方差分析(已编码单位)来源自由度 Seq SS Adj SS Adj MS F P主效应 3 3585.58 3585.58 1195.19 9.51 0.001 残差误差 15 1884.46 1884.46 125.63弯曲 1 8.75 8.75 8.75 0.07 0.802失拟 4 892.19 892.19 223.05 2.27 0.134纯误差 10 983.52 983.52 98.35合计 18 5470.05通过上图可以看出,密度和温度P值0.1,接受HO:因子对Y没有影响。
DOE 全因子设计

All terms are free from aliasing
( Worksheet的内容 )
Improve- 完全要因实验 - 20
3阶段: 实施实验输入DATA
Improve- 完全要因实验 - 21
利用Minitab的分析
4 阶段: 关于完全模型(Full Model)的ANOVA表作成
Step 2
在ANOVA表中看p值时,消除没有影响的效果( p值 > 0.05 ), (“Selected Terms”中不包括无影响的项)从新实行Analyze Stat > DOE > Analyze Factorial Design
Improve- 完全要因实验 - 29
Step 3
实行Analyze Factorial Design时,为了残差分析把
Analysis of Variance for 数率 (coded units) Source DF Seq SS Adj SS Adj MS Main Effects 3 1112.50 1112.50 370.833 2-Way Interactions 2 204.50 204.50 102.250 Residual Error 2 0.50 0.50 0.250 Total 7 1317.50 F 1E+03 409.00 P 0.001 0.002
显示可能的实验设计 Menu
Click
因子数
Improve- 完全要因实验 - 14
Step 2
确认可能的实验设计及根据被选取设计的实验数
实验数
因子数
Click
上表只能看出可能的实验设计。 在这个例中要做3因子完全要因实验(Full Factorial Design),所以对应因子 3 的实验数为8
《全因子试验设计》课件

全因子试验设计应尽可能全面地考察各因子之间的交互作用,以便更 好地了解试验系统的性能和特点。
03 全因子试验设计 的方法与步骤
确定因子与水平
因子
全因子试验设计的核心是选择试验因子 ,即影响试验结果的主要变量。在选择 因子时,需要考虑与研究目标相关的所 有重要变量。
VS
水平
每个因子都有不同的水平,即该因子的不 同取值。选择合适的水平数,确保能够全 面探索因子与试验结果之间的关系。
01
Design Expert专注于试验设计领域,提供了多种试
验设计方法和数据分析工具。
用户友好的界面
02 软件界面简洁明了,易于使用,适合初学者快速入门
。
全面的数据分析
03
Design Expert不仅提供了基础的统计分析,还支持
高级数据分析方法,如响应曲面设计和混合模型等。
06 全因子试验设计 的案例分析
详细描述
在软件开发与测试过程中,全因子试验设计 可以对软件的各项功能和性能进行全面的测 试。通过全面考虑各种可能的输入和条件, 设计出完整的测试用例,可以对软件的各项 功能进行细致的测试和分析。这种方法有助 于发现潜在的问题和缺陷,提高软件的质量 和稳定性,确保软件能够满足用户的需求。
05 全因子试验设计 的软件工具
多重比较
对试验结果进行多重比较,以确定各因子水平之 间的差异。
ABCD
回归分析
通过回归分析,可以建立因子与试验结果之间的 数学模型,预测不同因子水平下的结果。
可重复性检验
对试验结果进行可重复性检验,确保结果的稳定 性和可靠性。
04 全因子试验设计 的实际应用
工业生产优化
总结词
全因子试验设计在工业生产优化中应用广泛 ,通过全面考虑各种因素,可以找到最优的 生产条件,提高生产效率和产品质量。
全因子实验和部分因子实验设计说明书

高
全因子试验表如下
试验
A
B
C
1
-
-
-
2
+
-
-
3
-
+
-
4
+
+
-
5
-
-
+
6
+
-
+
7
-
+
+
8
+
+
+
上表包含了3因素2水平的所有可能组合
小组对试验设计策划如下
试验规划表如下
试验 1 2 3 4 5 6 7 8
A
B
C 样品1 样品2 样品3
-
-
- 19.18 19.02 19.09
+
-
-
-
+
-
+
+
-
-
-
+
确定影响因素XS
从可控因素表各噪声因素表可知,确定为试验因素的 胡三个,分别是: 1.滚珠固定座的位置. 2.滚珠10的角度. 3.滚珠压力.
本试验设计围绕滚珠成型机器,试验3个因素的水 平的测量指标如下表
测量指标:外滑轨的内部尺寸.
小组对试验设计策划如下
因素 滚珠固定座的位置
滚珠10的角度
水平1 位置1
是
是否通过对单一输出关键特性的测量可以代表 以上所有关键特性呢,是的,因为SPC图显示内轨 的外部尺寸已十分稳定.通过降低外轨内部尺寸 的偏差可以同时发送滑动力和内外轨的配合间 隙.
可控因素
对输 出的 影响
材料硬度
○
滚珠固定座的 位置
Minitab 19 DOE 设计范例 3因子2水平
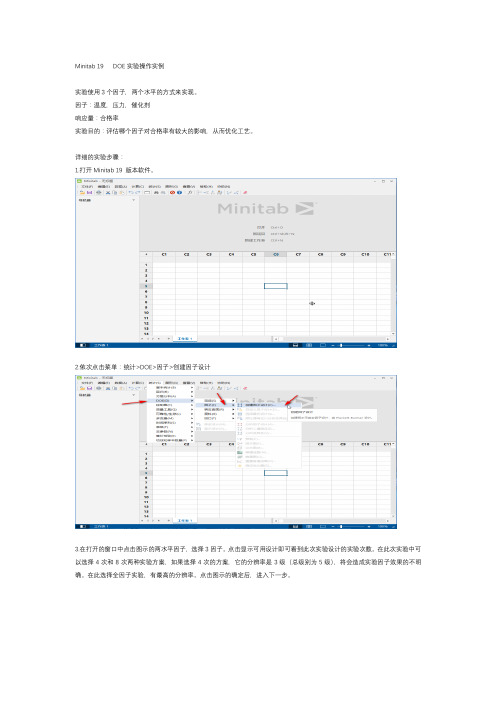
Minitab 19 DOE实验操作实例实验使用3个因子,两个水平的方式来实现。
因子:温度,压力,催化剂响应量:合格率实验目的:评估哪个因子对合格率有较大的影响,从而优化工艺。
详细的实验步骤:1.打开Minitab 19 版本软件。
2.依次点击菜单:统计>DOE>因子>创建因子设计3.在打开的窗口中点击图示的两水平因子,选择3因子。
点击显示可用设计即可看到此次实验设计的实验次数。
在此次实验中可以选择4次和8次两种实验方案,如果选择4次的方案,它的分辨率是3级(总级别为5级),将会造成实验因子效果的不明确。
在此选择全因子实验,有最高的分辨率。
点击图示的确定后,进入下一步。
4.点击设计菜单,按照图示点击设置相关参数之后,点击确定。
角点的仿行数设置为2,表示给实验参数重复两次。
中心点数0表示:没有设置高和低水平之间的中间水平或者理解为当前现实参数。
区组数1:只有一组实验。
5.点击因子菜单,即可对因子及水平具体的输入:按照图示样式输入实验参数后,点击确定。
6.在图示的选项及结果菜单中,默认参数即可。
7.点击确定之后,即可看到软件自动生成的实验方案,详细的实验次数,因子分组,实验顺序等,如右图所示。
保存实验方案,待实验后输入数据。
8.按照上述方案完成实验后,打开上次的实验表格,输入合格率数据如图示。
9. 依次点击菜单:统计>DOE>因子>分析因子设计10.在响应栏中选择合格率,再点击图形,在打开的菜单中,按照图示设置参数后,依次点击两次确定。
11. 在效应图中我们可以看到图示显示红色的ABC 的交互作用和C因子的作用是有明显的影响,即是我们需要重点关注的因子。
12.经过上一步分析得出ABC和C是我们的重要因子,现在继续对重要因子分析,列出因子图更加直观的看到因子对合格率影响效果。
依次点击菜单:统计>DOE>因子>因子图13.在打开的因子窗口中,如图所示设置,点击确定。
全因子实验设计

谢谢观看
其二,因素对定量观测结果的影响是地位平等的,即在专业上没有充分的证据认为哪些因素对定量观测结果的 影响大、而另一些影响小(注:若实验因素对观测结果的影响在专业上能排出主、次顺序,一般就被称为"系统分组 或嵌套设计");
其三,可以准确地估计各因素及其各级交互作用的效应大小(注:若某些交互作用的效应不能准确估计,就属于 非正规的析因设计了,如分式析因设计、正交设计、均匀设计,等等).
设计特点
最大缺点
最大优点
明显特点
是所获得的信息量很多,可以准ห้องสมุดไป่ตู้地估计各实验因素的主效应的大小,还可估计因素之间各级交互作用效应的 大小;
是所需要的实验次数最多,因此耗费的人力、物力和时间也较多,当所考察的实验因素和水平较多时,研究者 很难承受.
其一,它要求实验时全部因素同时施加,即每次做实验都将涉及到每个因素的一个特定水平(注:若实验因素施 加时有"先后顺序"之分,一般被称为"分割或裂区设计");
全因子实验设计
析因设计
目录
01 实验设计
02 设计特点
全因子实验设计( DOE)是指所有因子的所有水平的所有组合都至少进行一次实验,可以估计所有的主效应和 所有的各阶交互效应。
实验设计
(design of experimental,DOE)是一种安排实验和分析实验数据的数理统计方法;实验设计主要对实验进 行合理安排,以较小的实验规模(实验次数)、较短的实验周期和较低的实验成本,获得理想的实验结果以及得出 科学的结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MSD 23 案例
做试验:
MSD 案例
分析试验:
MSD 案例
Pg 9
试验设计的全因子方法
同时改变几个因子(变量),而不是一次一个
开始时,只对每个因子使用2个水平
考虑所有可能的因子条件组合
容易处理随机(普通原因)变差,使用它确定哪些因子是重要的
鼓励仿行试验 (对相同的组合进行仿行试验) ,以协助测量普通原因
Pg 33
案例:MSD数据的残差图
输入
1 2
输出图
统计>DOE>分析因子设计>…
Pg 34
残差的假设检验-续
四合一图
Pg 35
步骤6 : 识别影响大的因子
两类影响 主要因子影响(主效应) 每个因子对响应的总体影响
1.
2.
交互作用影响
因子高低水平间的协同作用
Pg 36
确定哪些因子的影响大 (显著)
表示为加号 (+)
运行 1 2
速度 20 40
压力 2.0 2.5
辛烷值 93 97
运行 1 2
速度 +
压力 +
辛烷值 +
运行1 为试验所有因子的“低”水平 (-); 运行2 为试验所有因子的“高”水平,其他组合将是高低水平的 混合
Pg 12
三个因子: 23全因子设计
标准顺序 因子1 因子2 因子3
仿行会增加试验的自由度
Pg 26
步骤 4 – 设计试验
4. 背景:
继续前边的MSD试验设计 输入因子名称和水平:
选择
“因子” 按钮 >
(输入因子名称和水平)
Pg 27
步骤5 随机化运行
5. 观察试验设计: OK > OK Minitab 在工作 表中自动存储设 计
有16次运行,因为 23= 8, 仿行2= 16
因变差)下运行的试验间的变化量
为了更清楚地知道一个因子是否显著—结果的差别是由于因子
条件的变差呢Special Causes(一种诱导的特殊原因),还是 由于普通原因Common Causes变差?
如果需要的话,不仅从平均响应上看改变的因子条件的结果,
还要从响应变化上看(可以分析两个响应:均值和方差)
– 这些来源对结果的影响最大
量化重要的X对Y的影响,包括其交互作用 得出一个量化的X和Y关系的方程
– 从中可以预测过程条件变化时会带来多大的收益或损失
Pg 3
根本原因的分析方法
观察过程(被动式)
使用历史数据观察研究过程
(或不打断正常的生产秩序)
控制图,方差分析等 用回归分析进行相关性研究
练习案例:速度:20或40,压力:2.0或2.5;辛烷值:
93 或97
运行次数 Run
也叫做试验 在试验中所尝试或运行的一组因子条件
Pg 11
试验设计中的因子概念和术语-续
使用 “+ “和 “-“ 表示每个因子的两个水平
也叫做高水平和低水平(代码化) 如果存在标准条件,通常表示为 减号(-),新条件通常
先从这部分开始
特性研究 Characteristic
Full Factorials 全因子设计
最佳化研究 Optimization
Response Surface Methods 响应曲面方法
Pg 5
试验设计方法
试错法(Trial and Error )
每次改变一个因子( One-Factor-at-a-Time (OFAT) ) 部分因子试验( Fractional Factorials ) 全因子试验( Full Factorials ) 响应曲面方法( Response Surface Methods (RSM))
1. 识别响应 2. 识别因子 试验设计 3. 选择因子水平 4. 选择设计 5. 随机化运行
6. 执行试验,收集数据
7. 分析数据 试验分析 8. 得出结论 9. 验证结果
Pg 30
用Minitab:寻找问题-续
时间序列图 MSD 案例 1.
对Y做一个响应 时间序列图
图形
25
> 时序图>
弯曲
15
5 5
指标
10
15
Pg 31
残差 Residual
定义
残差 = (观察到的 Y值) – (拟合的Y值)
残差是响应结果同我们所“预期”的值之间的差别(期望值
是给定因子设置组合的所有仿行的平均值)。 排的变化来解释
我们希望Y的大部分变差都可以用我们在因子设定中故意安 所有变化的剩余项都是残差项
minitab‘s 的 缺省项是随 机化运行并 按运行顺序 列举出来。
给出标准顺序号作以 参考
本列给出了运行的顺序
暂时忽略
Pg 28
试验设计内容
试验设计介绍 设计试验的全因子方法 设计试验:
MSD 23 案例
做试验:
MSD 案例
分析试验:
MSD 案例
Pg 29
我们处于什么位置?
主效应图
正交试验
1 2 3 4 5 6 7 8
– + – + – + – +
– – + + – – + +
– – – – + + + +
全因子试验包括了所有可能的因子组合
Pg 13
全因子试验
问题: 每升汽油所行驶的里程 12 公里
速度 辛烷值 轮胎压力 公里数 9.2 11.6 14.8 9.2 14.8 9.6 12 14.4
定义
仿行意味着两次或者多次重复所有的试验条件
这并不是说对一个试验单位重复测量两次
这意味着在某种试验条件下重复做并测量新输出值
一次仿行实际上意味着没有仿行
H H
L H
H L
L H L H
L H
H L
L L
Pg 25
为什么要仿行?
为了测量纯误差Pure Error,即在相同试验条件(这代表普通原
变差
容易分析 使用这些方法处理在试验中无法控制的其他因子(比如随机化和区组
化)- 噪声,使结论仍然有效
Pg 10
术语和概念
因子 (X) Factors
要研究的输入或过程变量 案例:速度,压力,辛烷值
因子水平 Level
要试验的每个因子的设置或水平
现在,我们只对每个因子考虑两个水平
确定影响显著性的三种方式:
每个影响的P-值 Pareto影响图 正态分布影响图
我们将通过
Minitab 案例来看每一个方法的结果
Pg 37
用Minitab : 主效应和交互作用
背景: 继续前面做的关于MSD数据样本的分析。 数据: MSD.mpj 说明: 生成图形 统计>DOE>分析因子设计>图形> (选择 Normal 和 Pareto,设定Alpha水平为0.05)
Pg 7
每次改变一个因子的传统方法
问题: 每升汽油所行驶的里程 12公里(假设有4个重要因子)
从某个条件的基本组合开始
改变一个因子 如果更好,保持这个因子, 并尝试改变下一个因子 如果结果没有改进,尝试改变下 一个因子水平…
Pg 8
试验设计内容
试验设计介绍
设计试验的全因子方法 设计试验:
大
购买代理
管理总成本
供货商 质量
差
型号
小
人
质量
材料
步骤3,选择设计-全因子试验设计
Pg 21
案例: 步骤 3 – 选择因子水平
步骤3: 分析 建立MSD材料的购买规格,我们需要确定三 个因子对MSD使用寿命的影响
设计试验: 因子
供货商 型号 热处理
设定
1,2 4,10 100度,500度
Pg 22
环境
日期
步骤 2: 分析
原因 效果
便宜 购买
没有规格
类型
程序
类型
加工
温度 批量
清洁
库存
时间 方法
热处理
检查
日期
湿度 时间
一致
化工
类型
检查
属性
包装
原材料
质量供货商
规格
过期 库存时间
供货商 Abel
使用寿命 短的问题
要求者
详细情况 信息 低投标 个性 高 缺少
原材料
仓库
供货商 Noesting
好
库存 成本
Pg 38
主效应和交互作用 (步骤 6B)–续
MSD案例的Pareto影响图
标准影响的Pareto图 (响应是使用寿命, Alpha = .05)
C AB AC ABC BC B A 0 1 2 3 4 A: 供货商 B: 型号 C: 热处理
P值= .05
可以看到交互影响 哪些影响较大或者显著?
– 假设残差变差反映的是试验中的普通原差符合以下条件,则试验结果就是有效的:
我们假设残差:
分布: 钟形的正态分布,均值为 0
常量: 残差不随拟合值的增减而增减
稳定:不随时间变化
同 X(连续因子)不相关
随机:代表变化的普通原因
0
独立
20
40 20 40 20 40 20 40
93
93 97 97 93 93 97 97
2
2 2 2 2.5 2.5 2.5 2.5
