4.5 关系的闭包
合集下载
闭包和等价关系

例:分析前述例子是否具有传递性 传递性: 传递性:若R是传递的,则RoR ⊆ R 是传递的,
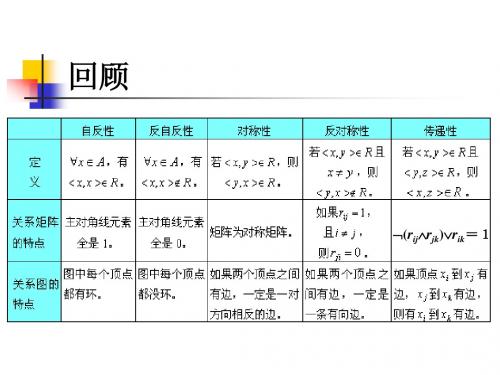
R具性质 自反性
定义
∀x∊A,有〈x,x〉∊R
关系矩阵的特 点
关系图的特点
主对角线元素全是 图中每个顶点都是 环 1 主对角线元素全是 图中每个顶点都没 有环 0 如果, 如果,两个顶点之 间有边, 间有边,一定是 一对方向相反的 边 如果, 如果,两个顶点之 间有边, 间有边,一定是 一条有向边 如果顶点x到y有边, 如果顶点x 有边, y到z有边,则从x 有边,则从x 到y有边
传递性
内容回顾: 内容回顾:关系的性质 A上的关系R={〈1,1〉 上的关系R={ 例:A={1,2,3}, A上的关系R={〈1,1〉, 1,2〉 2,2〉 2,3〉 〈1,2〉, 〈2,2〉, 〈2,3〉}
1
反对称性
2
3
有时候我们希望R具有一些有用的性质,例如, 自反性(对称性或传递性) 为此,需要在R中添加一些有序对而构成新的 关系,使得新关系具所需要的性质 希望添加的有序对尽可能的少 —即不希望新关系变得太”大” 满足这些要求的新关系就是R的闭包
t (R ) = R ∪ R2 ∪ R3 {<a,a>,<a,b>, <a,c>,<a,d>, <b,a>, ={<a,a>,<a,b>, <a,c>,<a,d>, <b,a>, <b,b>, <b,c>, <b,b>, <b,c>,<b,d>, <c,d>}
②、关系矩阵法
自反闭包的关系矩阵: 自反闭包的关系矩阵: Mr(R)=MR+E 对称闭包的关系矩阵: 对称闭包的关系矩阵: Ms(R)=MR+MR’ 传递闭包的关系矩阵: 传递闭包的关系矩阵: Mt(R)=MR+MR2+MR3…….. +MRn-1 .. 利用关系矩阵求R的幂,最后将各个幂的 利用关系矩阵求R的幂, 矩阵逻辑加
离散数学课件-第4章-5

M R3 M R 2 M R
0 0 1 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1
M t ( R ) M R M R 2 M R3
二、有向图的路径
使用有向图表示关系有助于构造关系的传递闭包 。为此引入 一些需要用到的术语。
通过沿有向图的边(按照这条边的箭头指示的相同方向)移动有 向图就得到一条有向图中的路径。
定义1:在有向图G中从a到b的一条路径是G中一条或多条
边的序列(x0,x1),(x1, x2),(x2, x3),„,(xn-1, xn),其中 x0=a, xn=b. 即一个边的序列,其中一天的终点和路径中下一条边 的起点相同。这条路径记为x0, x1,„, xn-1, xn,长度为n 。在同一定点开始和结束的路径叫做回路或圈。 注:有向图的一条路径可以多次通过一个顶点。此外,有 向图的一条边也可以多次出现在一条路径中。
定理1:设R是集合A上的关系。从a到b存在一条长为1的路径, 当且仅当(a,b)∈Rn。 Proof: 使用数学归纳法证明。 根据定义,从a到b存在一条长为1的路径,当且仅当 (a,b)∈R。因此当n=1时定理为真。
假定对于正整数n定理为真,这是归纳假设。从a到b存 在一条长为n+1的路径,当且仅当存在元素c ∈A使得从a 到c存在一条长为1的路径,即(a,c) ∈R,以及一条从c到b
由引理1,我们看出R的传递闭包是R,R2,R3,…,Rn的并。这是 由于在R*的两个顶点之间存在一条路径,当且仅当对某个正整 数i(i ≤ n)在Ri的这些顶点之间存在一条路径。因为
R*=R ∪R2 ∪R3 ∪… ∪Rn
并且表示关系的并的0-1矩阵式这些关系的0-1矩阵的联合。 因此传递闭包的0-1矩阵是R的0-1矩阵的前n次幂的0-1矩阵 的联合。
关系的闭包
1 0 0 0
0 0 1 0 1 0 0 0
2014-10-14
关系的闭包
28
例8(续4)
解(续4):
b a
c d
1 1 . 1 0
1 1 M (t ( R)) M ( R) M ( R 2 ) M ( R 3 ) 0 0
问题: (1) r( R ) = R ?
(2) s( R ) = R ?
(3) t( R ) = R ?
2014-10-14
关系的闭包
19
定理7.10
定理7.10 : 设 RAA 且 A, 则
r( R ) = RIA; s( R ) = RR-1; t( R ) = RR2R3….
a
2014-10-14
d
关系的闭包
0 1 0 0 1 0 1 0 . M ( s ( R )) 0 1 0 1 0 0 1 0
26
例8(续2)
解(续2):
b a
c dபைடு நூலகம்
1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 0 1 0 0 0
关系的闭包
0 1 M (R 2 ) 0 0 0 1 3 M (R ) 0 0
2014-10-14
1 0 0 0 0 1 0 0
0 1 M ( R) 0 0 0 0 1 0 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0
G( R ) G(s( R ))
关系的闭包 12
离散数学及其应用 第2版课件第4章 关系

2021/4/1
第4章 关系
定义4.7 A×B的任意子集R称为A到B的二元关系。特 别当A=B时,称R为A上的二元关系。其中称为空关系, A×B称为全关系。
关系可以推广到n元关系,我们主要讨论二元关系。 在计算机领域中,关系的概念也是到处存在的。如数据 结构中的线性关系和非线性关系,数据库中的表关系等。 例如,若A={1,2,3,4,5},B={a,b,c},则R= {<1,a>,<1,b>,<2,b>,<3,a>}是A到B的关系,S={<a, 2>,<c,4>,<c,5>}是B到A的关系。
第4章 关系
4.2 关系及其表示
4.2.1 关系
世界上存在着各种各样的关系。人和人之间有“同志”关 系、“师生”关系、“上下级”关系;两个数之间有“大于” 关系、“等于”关系、“小于”关系;两个变量之间有“函数” 关系;程序之间有“调用”关系等。所以,对关系进行深刻的 研究,对数学和计算机都有很大的用处。
定义4.6 令R为二元关系,DR={x|y(xRy)}和RR= {y|x(xRy)}分别称为R的定义域(或前域)和值域。关系R的域记 为FR=DR∪RR。
例如,设H={<1,2>,<1,4>,<2,4>,<3,4>}是一个 二元关系,则DH={1,2,3},RH={2,4},FR={1,2,3,4}。
2021/4/1
第4章 关系
定义4.8 若IA是A上的二元关系,且满足IA={<x, x>|x∈A},则称IA为A上的恒等关系。
定理4.5 若R和S是集合A到B的两个二元关系,则: (1)DR∪S=DR∪DS。 (2)DR∩SDR∩DS。 (3)DR-DSDR-S。 (4)RR∪S=RR∪RS。 (5)RR∩SRR∩RS。 (6)RR-RSRR-S。
第4章 关系
定义4.7 A×B的任意子集R称为A到B的二元关系。特 别当A=B时,称R为A上的二元关系。其中称为空关系, A×B称为全关系。
关系可以推广到n元关系,我们主要讨论二元关系。 在计算机领域中,关系的概念也是到处存在的。如数据 结构中的线性关系和非线性关系,数据库中的表关系等。 例如,若A={1,2,3,4,5},B={a,b,c},则R= {<1,a>,<1,b>,<2,b>,<3,a>}是A到B的关系,S={<a, 2>,<c,4>,<c,5>}是B到A的关系。
第4章 关系
4.2 关系及其表示
4.2.1 关系
世界上存在着各种各样的关系。人和人之间有“同志”关 系、“师生”关系、“上下级”关系;两个数之间有“大于” 关系、“等于”关系、“小于”关系;两个变量之间有“函数” 关系;程序之间有“调用”关系等。所以,对关系进行深刻的 研究,对数学和计算机都有很大的用处。
定义4.6 令R为二元关系,DR={x|y(xRy)}和RR= {y|x(xRy)}分别称为R的定义域(或前域)和值域。关系R的域记 为FR=DR∪RR。
例如,设H={<1,2>,<1,4>,<2,4>,<3,4>}是一个 二元关系,则DH={1,2,3},RH={2,4},FR={1,2,3,4}。
2021/4/1
第4章 关系
定义4.8 若IA是A上的二元关系,且满足IA={<x, x>|x∈A},则称IA为A上的恒等关系。
定理4.5 若R和S是集合A到B的两个二元关系,则: (1)DR∪S=DR∪DS。 (2)DR∩SDR∩DS。 (3)DR-DSDR-S。 (4)RR∪S=RR∪RS。 (5)RR∩SRR∩RS。 (6)RR-RSRR-S。
关系的性质闭包和

对n>=1用数学归纳法:n=1, trivial. 奠基n=2,直接由关系复合的定义可 得;归纳基于:Rn=Rn-1 ◦R
集合A上的关系R是传递关系 R2R
必要性: 任取(a,b) R2 ,根据上述命题以及R的传递性可得(a,b)R
充分性: 若(a,b)R, (b,c)R, 则(a,c)R2, 由R2R可得: (a,c)R,则 R 是传递关系
1 1 0 1
关系的性质:自反性
8
集合A上的关系 R 是:
自反的 reflexive:定义为:对所有的 aA, (a,a)R 反自反的 irreflexive:定义为:对所有的aA, (a,a)R
注意区分”非”与”反”
设 A={1,2,3}, RAA
利用公式证明闭包相等
证明:r(s(R)) = s(r(R))
r(s(R))
= r(RR-1) = (RR-1)IA = (RIA)(R-1IA-1) = (RIA)(RIA)-1 = s ( R IA ) = s(r(R)) 注意:r(s(R))一般省略为rs(R)
(注意:IA=IA-1, 并用等幂率)
1
关系的性质、闭包和 等价
回顾
2
概率论 贝叶斯定理 期望与方差
提要
关系的性质
闭包的定义与计算
传递闭包的Warshall算法
等价关系、等价类、划分
回顾:关系的定义
4
若A, B是集合, 从A到B的一个关系是AB的一个 子集.
集合,
可以是空集 集合的元素是有序对
关系的闭包教学课件

03
关系闭包的计算方法
BIG DATA EMPOWERS TO CREATE A NEW
ERA
自反闭包
总结词
自反闭包是关系的一种扩展,它使得每个元素都与自己有关系。
详细描述
自反闭包是通过将所有自反关系(即关系中元素与自身相关)扩展到整个关系 而得到的。如果关系中存在元素A与自身相关,则自反闭包中一定包含该关系。
要点二
详细描述
在推荐系统中,闭包关系可以帮助理解用户的行为和兴趣 ,从而为用户提供更加准确的推荐。例如,通过分析用户 行为路径和物品间的闭包关系,可以发现用户可能感兴趣 的潜在物品或服务,从而为用户提供更加丰富的推荐内容 。同时,利用闭包关系还可以提高推荐系统的多样性,避 免用户陷入信息过载和推荐疲劳的问题。
函数依赖
一种特殊的数据依赖,表示一个属性决定另一个属性 的值。
范式转换
将关系模式从低范式向高范式转换,以消除数据冗余 和异常。
关系闭包与数据库设计
关系闭包
通过计算关系模式的闭包,可以确定关系模式满足的范式级别,从 而指导数据库设计。
闭包计算
通过计算属性集合的闭包,可以确定属性之间的函数依赖关系。
数据库设计优化
提高代码复用
闭包可以用于实现高阶函数、回调函数、观察者 模式等高级编程技术,提高代码复用性和可维护 性。
实现封装和隐藏
通过闭包,可以将数据封装在内部,对外只暴露 必要的接口,实现数据的隐藏和封装,提高代码 的安全性和模块化。
02
什么是关系的闭包?
BIG DATA EMPOWERS TO CREATE A NEW
闭包在数据库系统、知识表示、推理等领域有着广泛的应用。例如,在关系数据库中,闭包 可以用于查询优化和数据更新;在自然语言处理中,闭包可以用于语义分析和文本处理;在 人工智能和机器学习中,闭包可以用于知识表示和推理。
离散-8-2-关系闭包

i 1
n
证明: t (R ) R
i 1
i
R t (R )
i i 1
n
下面证明:t (R ) R i
i 1
n
x, y t (R ) R i , 有正整数k, 使得<x,y>Rk
有x a 0 , a1 ,, a k 1 , a k y, 使 a i , a i1 R(a i A)(0 i k 1)
主要内容:
关系的闭包
求关系闭包的方法 关系闭包的性质 定义 等价类
等价关系
1
§4.3 关系的运算
5. 关系的闭包(1)
«定理7 证明a) 证明c
定义:设A为集合, RAA,若R’AA,并且满足:
R’是最小扩充
(1) R’是自反的(对称的、传递的); (2) RR’;
R’是R的扩充
(3) 对任何自反(对称,传递)的关系R’’AA ;若RR’’,必有R’R’’, 则称R’是R的自反(对称、传递)闭包,记作r(R)(s(R),t(R))。 例1:A={a,b,c,d}, R={<a,a>,<a,b>,<b,a>,<c,d>},
r(R)={<a,a>,<a,b>,<b,a>,<c,d>,<b,b>,<c,c>,<d,d>},
8
§4.4 等价关系与集合的划分
1. 等价关系(1)
等价类»
等价关系:设A是集合,RAA,若R是自反的、对称的和传递的, 则称R为A上的等价关系。 若aRb,则称a与b等价。
n
证明: t (R ) R
i 1
i
R t (R )
i i 1
n
下面证明:t (R ) R i
i 1
n
x, y t (R ) R i , 有正整数k, 使得<x,y>Rk
有x a 0 , a1 ,, a k 1 , a k y, 使 a i , a i1 R(a i A)(0 i k 1)
主要内容:
关系的闭包
求关系闭包的方法 关系闭包的性质 定义 等价类
等价关系
1
§4.3 关系的运算
5. 关系的闭包(1)
«定理7 证明a) 证明c
定义:设A为集合, RAA,若R’AA,并且满足:
R’是最小扩充
(1) R’是自反的(对称的、传递的); (2) RR’;
R’是R的扩充
(3) 对任何自反(对称,传递)的关系R’’AA ;若RR’’,必有R’R’’, 则称R’是R的自反(对称、传递)闭包,记作r(R)(s(R),t(R))。 例1:A={a,b,c,d}, R={<a,a>,<a,b>,<b,a>,<c,d>},
r(R)={<a,a>,<a,b>,<b,a>,<c,d>,<b,b>,<c,c>,<d,d>},
8
§4.4 等价关系与集合的划分
1. 等价关系(1)
等价类»
等价关系:设A是集合,RAA,若R是自反的、对称的和传递的, 则称R为A上的等价关系。 若aRb,则称a与b等价。
关系的闭包教学-PPT精品.ppt

关系R, r(R), s(R), t(R)的关系图的顶点集相等。 为了得到r(R)的关系图,在R的关系图中,考察每
个顶点, 如果没有环就加上一个环; 为了得到s(R)的关系图,在R的关系图中,考察每
条边, 如果有一条 xi 到 xj 的单向边, i≠j, 则在G中加 一条 xj 到 xi 的反方向边;
例5:A = {a1,a2,a3,a4,a5}, R = {<a1,a2>,<a2,a3>,<a3,a3>,<a3,a4>,
<a5,a1>,<a5,a4>},求R的传递闭包。
解:先写出R的关系矩阵
0 1 0 0 0
考察第1列,m51=1,于
0
0
1
0
0
M 0 0 1 1 0
是应将第1行元素加到第
R也不具备对称性,增加有序对<1,,1>,<1,2>},具有对称性。 闭包运算即:添加最少的有序对,使得原关系具 有某种性质的运算。
2020/12/30
2
一、闭包定义
定义:设R是A上的二元关系,R的自反(对称、 传递)闭包是关系R1,则 ① R1是自反的(对称的、传递的) ② RR1 ③ 对A上的任何自反的(对称的、传递的)关系 R2,若RR2,则R1R2。
<b,c> R1,<c,b> R1,而<b,b> R1 <c,a> R1, <a,c> R1,而<c,c> R1
R2 ={<a,b>,<b,c>,<c,a>,<a,c>,<b,a>,<c,b>, <a,a>,<b,b>,<c,c>}
个顶点, 如果没有环就加上一个环; 为了得到s(R)的关系图,在R的关系图中,考察每
条边, 如果有一条 xi 到 xj 的单向边, i≠j, 则在G中加 一条 xj 到 xi 的反方向边;
例5:A = {a1,a2,a3,a4,a5}, R = {<a1,a2>,<a2,a3>,<a3,a3>,<a3,a4>,
<a5,a1>,<a5,a4>},求R的传递闭包。
解:先写出R的关系矩阵
0 1 0 0 0
考察第1列,m51=1,于
0
0
1
0
0
M 0 0 1 1 0
是应将第1行元素加到第
R也不具备对称性,增加有序对<1,,1>,<1,2>},具有对称性。 闭包运算即:添加最少的有序对,使得原关系具 有某种性质的运算。
2020/12/30
2
一、闭包定义
定义:设R是A上的二元关系,R的自反(对称、 传递)闭包是关系R1,则 ① R1是自反的(对称的、传递的) ② RR1 ③ 对A上的任何自反的(对称的、传递的)关系 R2,若RR2,则R1R2。
<b,c> R1,<c,b> R1,而<b,b> R1 <c,a> R1, <a,c> R1,而<c,c> R1
R2 ={<a,b>,<b,c>,<c,a>,<a,c>,<b,a>,<c,b>, <a,a>,<b,b>,<c,c>}
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
是整数集Z上 (小于)关系, 例4.5.5 设R是整数集 上<(小于)关系,因R是传 是整数集 是传 递的, 关系, 递的,于是 st ( R) = s ( R) 是 Z上 ≠ 关系, 上 上的全关系, 但 ts( R) = t (Z上 ≠ 关系) 是 Z上的全关系, 上的全关系 s 故 st ( R) ⊆ ts( R) 且 st ( R) ≠ ts( R)。 特别地, 设 A = {1, 2,3} , R是 A上<(小于)关系,则 特别地 是 上 (小于)关系, R = {(1, 2), (1,3), (2,3)}是传递的,于是 是传递的,
整数集Z <(小于 小于) 例4.5.2 整数集Z上<(小于)关系的对称闭包 是≠(不等于)关系; (不等于)关系; ≤(小于等于)关系的对称闭包是全关系。 (小于等于)关系的对称闭传递闭包的结构) 上的关系, 上的关系,则 t(R) = RU R2 U R3 UL
定理4.5.5 (有限集上的传递闭包的结构)设A是 定理 有限集上的传递闭包的结构) n个元素的集合,R是其上的关系,则 个元素的集合, 是其上的关系,
t(R) = RU R2 ULU Rn
个元素的集合时, 当A是n个元素的集合时,结合关系矩阵的定 闭包所对应的矩阵: 义可得关系R闭包所对应的矩阵:
二.闭包的结构
定理4.5.2 (自反闭包的结构)设R是非空集合A上 自反闭包的结构) 定理 的关系, 的关系,则 r(R) = RU IA 证. 记 R′ = RU IA,则 R′满足定义 满足定义4.5.1的(1)( ), )(2), 的 )( 是自反的, 设 R′′ 是自反的,且 R ⊆ R′′ ,往证 R′ ⊆ R′′ (3), 有二个情形: 对 (a, b) ∈R′,有二个情形: 一、若 (a, b) ∈R,则 (a, b) ∈R′′ ; 二、若 (a, b) ∈IA,即 a = b,则 (a, a) ∈R′′ 总之, 总之,(a, b) ∈R′′ 因此 R′ ⊆ R′′ , 。
定理4.5.3 (对称闭包的结构)设R是非空集合A 对称闭包的结构) 定理 上的关系,则 s(R) = RU R−1 上的关系, 满足定义2.5.1中的条件 证. 记 R′ = RUR−1,则 R′ 满足定义 中的条件 (1) (2)。设 R′′ 是对称的,下面证明 R′ ⊆ R′′ ) ) 是对称的, ′ 则有二种情形: 若 (a, b) ∈R,则有二种情形: ( 情形1, 情形 , a, b) ∈R ,则 (a, b) ∈R′′, (a,b) ∈R−1,则 (b, a) ∈R ,于是 (b, a) ∈R′′ 情形2, 情形 , 故 (a, b) ∈R′′ 。 综合得, 满足条件( ) 综合得,R′ ⊆ R′′ ,于是 R′ 满足条件(3)从而 R′ 就 的对称闭包。 是R的对称闭包。
例4.5.1 整数集Z上<(小于)关系的自反闭包 整数集Z <(小于) 小于 是≤(小于等于)关系; (小于等于)关系; 关系的自反闭包是全关系; ≠ 关系的自反闭包是全关系; 空关系的自反闭包是恒等关系; 空关系的自反闭包是恒等关系; 上定义关系: Z上定义关系:R ={(x, y)| x + y = 2} ,则R的自 反闭包 r(R) ={(x, y)| x + y = 2或x = y}。
用集合形式表示为
t ( R) = {(a , b),(a , c ),(a , d ),(b, c ),(b, d ),(c , c ),(c , d ),(d , c ),(d , d )}。
三、闭包的性质
定理4.5.6 设R是非空集合A上的关系,则 定理 是非空集合 上的关系, 是自反的,那么 也是自反的; (1)如果 是自反的 那么 )如果R是自反的 那么s(R)和t(R)也是自反的; 和 也是自反的 是对称的,那么 也是对称的; (2)如果 是对称的 那么 )如果R是对称的 那么r(R)和t(R)也是对称的; 和 也是对称的 是传递的,那么 是传递的。 (3)如果 是传递的 那么 )如果R是传递的 那么r(R)是传递的。 是传递的
上的全关系。 是 A上的全关系。 上的全关系
′ = RU R2 U R3 L,则 R′满足定义 满足定义2.5.1中 证. 记 R 中 的条件( ) 的条件(1)。 ′ 设 (a, b),(b, c) ∈R,则存在正整数 i, j ,使 (a, b) ∈Ri 且 (b, c) ∈Rj,于是 (a, c) ∈Ri o Rj = Ri+ j ⊆ R′ ,满足条 件(2), ) 再设 (a, b) ∈R′,则存在 k 使 (a,b) ∈Rk ,于是存在 a1, a2,L, ak−1,使 (ai−1, ai ) ∈R 其中 a0 = a, ak = b ,则有 , (ai−1, ai ) ∈R′′ ,从而 (a, b) ∈R′′
M r (R) = M R ∨ E
Τ M s(R) = M R ∨ M R
2 n M t (R) = M R ∨ M R ∨ L ∨ M R
例4.5.3 设 A = {a, b, c, d } , A 上的二元关系R为 R = {(a, b), (b, c), (c, d ), (d , c)} , 求 t ( R ) 解 R的关系矩阵 的关系矩阵
是对称的; 于是 r(R)是对称的; 是对称的 则存在k 对于 t(R) , 若 (a, b) ∈ t ( R) , 则存在 使 (a, b) ∈ R k , 而 (b, a) ∈ ( R k ) −1 = ( R −1 ) k = R k ,于是 于是t(R)是对称的。 是对称的。 于是 是对称的 (3)因R是传递的,故R 2 ⊆ R ,而 因 是传递的 是传递的,
自反, 证. (1)因R自反 故 I A ⊆ R ⊆ s( R) , 于是s(R)是自反的 因 自反 是自反的 也是自反的。 同理 t(R) 也是自反的。 −1 (2)因R是对称的 故 R = R , 而 是对称的, 因 是对称的
− r −1 ( R ) = ( R U I A ) −1 = R −1 U I A1 = R U I A = r ( A)
(3)证.注意到一个事实,若关系 R1 ⊆ R2 ,则有 (3)证 注意到一个事实, t ( R1 ) ⊆ t ( R2 ) 和 s ( R1 ) ⊆ s ( R2 ) 由 R ⊆ s( R) 知 t ( R) ⊆ ts( R) ,进而 st ( R) ⊆ sts ( R) 是对称的, 也是对称的, 再由 s( R) 是对称的,可知 ts( R) 也是对称的, 故 sts( R) = ts( R) ,于是 st ( R) ⊆ ts( R)
0 0 MR = 0 0 1 0 0 0 1 0 , 0 0 1 0 1 0
及
M t ( R ) = M R ∨ M R 2 ∨ M R3 ∨ M R 4
0 0 = 0 0
1 1 1 0 1 1 , 0 1 1 0 1 1
st ( R ) = s ( R) = {(1, 2), (1,3), (2,3), (3, 2), (3,1), (2,1)}
关系, 是 A上≠关系,但 上 关系
ts ( R) = {(1, 2), (1,3), (2,3), (3, 2), (3,1), (2,1), (1,1), (2, 2), (3,3)}
r 2 ( R) = ( R U I A ) 2 = R 2 U I A ⊆ R U I A = r ( R)
于是r(R)是传递的。 是传递的。 于是 是传递的
定理4.5.7 设R是非空集合A上的关系,则 定理 是非空集合 上的关系,
(1) rs(R) = sr(R); (2) rt(R) = tr(R); (3) st(R) ⊆ts(R)。
4.5 关系的闭包
它往往不具有4.4节中讨 集合A上的关系R,它往往不具有 节中讨 论过的某些性质,考虑适当扩大R以使其满足要 论过的某些性质, 这一想法就导致闭包概念的引入。 求,这一想法就导致闭包概念的引入。
一、闭包的定义
定义4.5.1 设R是非空集合A上的关系,若A上 定义 上的关系, 的关系′ 满足下列条件: R 满足下列条件: (1) R ⊆ R′, ) (2) R′是自反的(对称的、传递的), ) 是自反的(对称的、传递的) 是自反的(对称的、传递的) (3)若 R′′是自反的(对称的、传递的)且 R ⊆ R′′ ) , 就有 R′ ⊆ R′′ 。 的自反(对称、传递)闭包, 则称 R′是R的自反(对称、传递)闭包,记为 r(R) t )。 ( s(R)、 (R))。 并且具有自反(对称、传递) • 闭包是包含R并且具有自反(对称、传递)性质的 最小关系, 是自反(对称、传递) 最小关系,并且关系R是自反(对称、传递)的当 的自反(对称、传递) 本身。 且仅当R的自反(对称、传递)闭包就是R本身。
