内模控制.ppt
合集下载
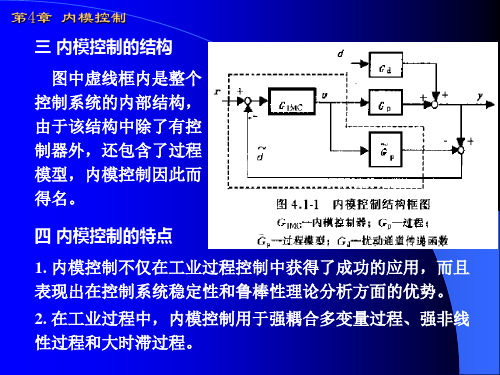
6.内模控制

这里 f 为IMC滤波器。选择滤波器的形式,以保证 内模控制器为真分式。
对于阶跃输入信号,可以确定Ⅰ型IMC滤波器的形式
1 f ( s) (Tf s 1)r
对于斜坡输入信号,可以确定Ⅱ型IMC滤波器的形式为
rTf s 1 f ( s) (Tf s 1)r
Tf ——滤波器时间常数。
4.采用理想控制器构成的系统,对模型误差极为敏感,鲁棒性、 稳定性变差。
2. 内模控制器的设计
步骤1 因式分解过程模型
ˆ G ˆ G ˆ G p p pˆ 包含了所有的纯滞后和右半平面的零点,并 式中,G p ˆ 为过程模型的最小相位部分。 规定其静态增益为1。G p
步骤2 设计控制器
GIMC ( s ) 1 ˆ ( s) G p f ( s)
过程无扰动Leabharlann 图6-3过程有扰动
例3-2 考虑实际过程为
R( s)
D( s)
10s 1 5s 1
1 G( s) e 10 s 10s 1
1 10 s 1
e
10 s
Y (s)
1 e 8s 10s 1
内部模型为
ˆ ( s) G 1 e8 s 10s 1
讨论(1)当 K 1 , T 2 , 1 时,滤波时间常数取不同值 时,系统的输出情况。(2)当 K 1 , T 2 ,由于外界干扰 使 由1变为1.3,取 Tf 不同值时,系统的输出情况。
1~4曲线分别为 Tf 取0.1、0.5、1.2、2.5时,系统的输 出曲线。
图6-2
2.若对象含有s平面右半平面( RHP)零点,
ˆ 1 ( s) 中含有RHP极点,控制器本身不稳定,闭 则 GIMC (s) G p 环系统不稳定。
内模控制
然后在反馈和输人通道上增加反馈滤波器
和输人滤波器
,通过调整滤波器的结构和参数,使系统获得所期望的性能。 下面就对开环稳定过程进行离散内模控制器设计。
考虑一般情况,令被控对象为有纯滞后的非最小相位过程,则过
程模型可分解为两部分:
控制器取为: 设计时为保持闭环系统零稳态偏差特性,需满足:
可实现因子可取为:
经输人滤波器
后再送至控制器。
经柔化后的输人参考轨迹的一般形式为:
即
第4章 内模控制 4.6 简化模型预测控制(SMPC) 内模控制是一种极具理论价值的基于模型的控制策略,但其工程实
现因涉及模型求逆和滤波器合理设计等问题,设计过程较为复杂,尤
其是对于多输人多输出过程,实施难度更大。 1987年以后,Arulalan等人提出了一种简化模型预测控制(SMPC),其
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
第4章 内模控制
对于模型无差,即 em (s) 的 0特殊情况,上式可简化为:
以上两式表明:对于无模型失配的情形,闭环传递函数
除了
中必须包含所有的滞后和右半
平面零点,且 必须有足够的阶次来避免物理上的不可实
现外,其他都是可以任意选择的。因此,闭环响应可以直接设
第4章 内模控制 4.3.3 设计示例
4.3.3.1 一阶加纯滞后过程
4.3.3.2 高阶过程
情形A.无右半平面(RHP)零点
情形B.具有右半平面(RHP)零点
第4章 内模控制
4.4 内模控制器设计——离散过程
当过程模型采用离散脉冲传递函数形式时,内模控制系统的性质仍
然成立。在离散时间条件下,设计内模控制器也仍然分为两步进行: 首先是设计一个稳定的理想控制器;
模板工程施工工艺图解PPT课件

L=构件尺寸
L=构件尺寸
L=构件尺寸+1模板厚 度
L=构件尺寸+1模板厚度 L=构件尺寸+2模板厚度
L=构件尺寸
柱墙模板配模原则:长边包短边,模板尽量采用横配,尺寸必须 准确。
效果图1
•背方间距200mm •螺杆离阴角间距
200mm •螺杆离封头间距
200mm •第一道加固离楼
面200mm
效果图2
四、模板工程施工工艺
模板体系 施工准备 柱墙模板施工 梁板模板施工 支撑体系 模板拆除
测量放线\施工缝处理
一
柱、墙钢筋竖焊、绑扎 满堂架搭设
般
柱墙安装配管及施工缝清洁 标高抄测
标 准
下 一
层层
柱、墙钢筋垫块 柱、墙钢筋验收
梁底模 梁侧模、板模
结施 构工 施
梁钢筋安装、梁垫块
标高、模板开间复测及梁板模清洁
拆模作业不得野蛮施工。不得损坏混凝土构件棱角 。严格按文明施工要求作业。
模板拆除后应及时清理、涂刷脱模剂。不得将模板 吊运至作业楼层后再清理涂刷脱模剂。
拆模作业管理人员必须巡视,检查卸料平台使用情 况、塔吊指挥到位情况、临边防护情况及作业行为 ,应杜绝高空坠物及其他安全事故发生。
吊模拆模后效果
不烂根、不漏 浆
楼梯施工
楼梯模板施工步骤
标高复核并弹出 底模线
1、结构复核
净空尺寸复核
板底模线
挂线找平支 撑体系
支撑体系间 距600
2、支撑体系搭设
连接件
板底方间距200mm,用铁 钉与支撑架固定
3、摆板底方
板底模
4、板底模安装
反复梯基
5、反扶梯基安装
顶撑木方固定
L=构件尺寸
L=构件尺寸+1模板厚 度
L=构件尺寸+1模板厚度 L=构件尺寸+2模板厚度
L=构件尺寸
柱墙模板配模原则:长边包短边,模板尽量采用横配,尺寸必须 准确。
效果图1
•背方间距200mm •螺杆离阴角间距
200mm •螺杆离封头间距
200mm •第一道加固离楼
面200mm
效果图2
四、模板工程施工工艺
模板体系 施工准备 柱墙模板施工 梁板模板施工 支撑体系 模板拆除
测量放线\施工缝处理
一
柱、墙钢筋竖焊、绑扎 满堂架搭设
般
柱墙安装配管及施工缝清洁 标高抄测
标 准
下 一
层层
柱、墙钢筋垫块 柱、墙钢筋验收
梁底模 梁侧模、板模
结施 构工 施
梁钢筋安装、梁垫块
标高、模板开间复测及梁板模清洁
拆模作业不得野蛮施工。不得损坏混凝土构件棱角 。严格按文明施工要求作业。
模板拆除后应及时清理、涂刷脱模剂。不得将模板 吊运至作业楼层后再清理涂刷脱模剂。
拆模作业管理人员必须巡视,检查卸料平台使用情 况、塔吊指挥到位情况、临边防护情况及作业行为 ,应杜绝高空坠物及其他安全事故发生。
吊模拆模后效果
不烂根、不漏 浆
楼梯施工
楼梯模板施工步骤
标高复核并弹出 底模线
1、结构复核
净空尺寸复核
板底模线
挂线找平支 撑体系
支撑体系间 距600
2、支撑体系搭设
连接件
板底方间距200mm,用铁 钉与支撑架固定
3、摆板底方
板底模
4、板底模安装
反复梯基
5、反扶梯基安装
顶撑木方固定
神经网络控制

习调整网络的权值,使反馈控制输入趋近于零,
从而使神经网络控制器逐渐在控制作用中占据主
导地位,最终取消反馈控制器的作用;
✓
一旦系统出现干扰,反馈控制器重新起作用。
✓
可确保控制系统的稳定性和鲁棒性,有效提高系
统的精度和自适应能力。
神经网络
控制器
期望输出
()
−1
()
+
-
()
传统控
网络实现;可进行离线辨识,也可进行在线辨识。
+
-
逆向建模
一般而言,建立逆模型对神经网络控制意义重大。
直接逆建模简化结构图:
可用于离线辨识,也可
用于在线辨识。
对 象
+
神经网络
逆模型
缺点:不是目标导向的,系统输入也不可能预先定义。
实际常采用正-逆建模结构。
正-逆建模
神经网络
逆模型
对 象
第3章 神经网络控制
第2部分 控制基础
3.5 神经网络控制基础
3.5.1 神经网络控制的优越性
神经网络可以处理那些难以用模型或规则描述的过
程或系统。
神经网络采用并行分布式信息处理,具有很强的容
错性。
神经网络是本质非线性系统,可实现任意非线性映
射。
神经网络具有很强的信息综合能力,能同时处理大
期望输出
()
稳定的参
考模型
参考模
型输入
()
+
()
()
+
-
神经网络
控制器
()
对象
()
从而使神经网络控制器逐渐在控制作用中占据主
导地位,最终取消反馈控制器的作用;
✓
一旦系统出现干扰,反馈控制器重新起作用。
✓
可确保控制系统的稳定性和鲁棒性,有效提高系
统的精度和自适应能力。
神经网络
控制器
期望输出
()
−1
()
+
-
()
传统控
网络实现;可进行离线辨识,也可进行在线辨识。
+
-
逆向建模
一般而言,建立逆模型对神经网络控制意义重大。
直接逆建模简化结构图:
可用于离线辨识,也可
用于在线辨识。
对 象
+
神经网络
逆模型
缺点:不是目标导向的,系统输入也不可能预先定义。
实际常采用正-逆建模结构。
正-逆建模
神经网络
逆模型
对 象
第3章 神经网络控制
第2部分 控制基础
3.5 神经网络控制基础
3.5.1 神经网络控制的优越性
神经网络可以处理那些难以用模型或规则描述的过
程或系统。
神经网络采用并行分布式信息处理,具有很强的容
错性。
神经网络是本质非线性系统,可实现任意非线性映
射。
神经网络具有很强的信息综合能力,能同时处理大
期望输出
()
稳定的参
考模型
参考模
型输入
()
+
()
()
+
-
神经网络
控制器
()
对象
()
神经网络内模控制 PPT课件

7
内部模型辨识目标函数
8
内模控制过程及结果2
(2) 系统输入:
r (k ) 是周期 k 100 的方波
9
控制系统输入、输出:r、y
112
内部模型辨识目标函数
13
结束
14
例3 神经非线性 内模控制
1
一阶 SISO 可逆、具有一阶时延的非线性系统,仿真模型:
y (k 1) 0.8 sin( y (k )) 1.2u (k )
(1) 系统输入:
r (k ) 1(k )
输出端干扰: ( k 50) 0.1( k ) (2) 系统统输入:
r (k ) 是周期 k 100 的方波
P( z )
y ˆ y
内部模型 e1
ˆ ( z) P
0.5
内模控制结构
3
内模控制过程及结果1
(1) 系统输入: 输出端干扰:
r (k ) 1(k )
(k 50) 0.1(k )
4
控制系统输入、输出、扰动:r、y、v
5
内模控制器输出:u
6
内模控制器、内部模型调整
2
内模控制设计
• 神经模型辨识器结构 1 BP网络N1,3,1 +两个 z • 内模控制器设计 取具有一阶时延对象逆模型 结构与例2逆模型辨识器同 • 滤波器设计 取滤波器:
F ( z) 1 , 0 1 1 z 1
r e
_
滤波器
F ( z)
g
内模 控制器
D( z )
u
对象
直流锅炉汽温控制ppt课件
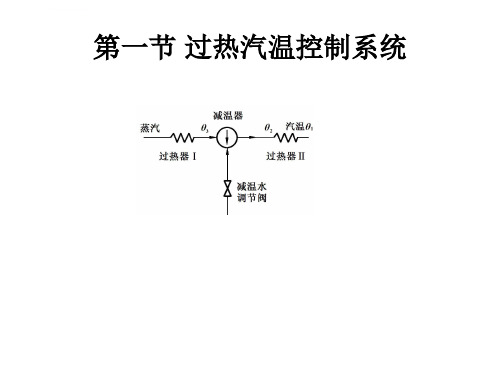
由于再热器是纯对流布置,再热器入口工质状况取决 于汽轮机高压缸排汽工况,因而再热汽温的变化幅度较过 热汽温大的多。
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
在各种扰动下,再热汽温的动态响应特性与 过热汽温相类似,共有的特点为有迟延、有惯性、 有自平衡能力。
-
G’(s) +
D
G(s)
Y
YSP
+
-
Gc(s)
D
Y G(s)
内模控制系统
单回路反馈控制系统
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
YSP
+-
+ - Gc1(s)
Gc2(s)
G2(s)
- +
G’1(s)
G1(s)
D Y
串级控制系统的内模控制
YSP
+-
KP1
+- Gc2(s)
+
G2(s)
G’1(s)
G1(s)
D Y
一种内模控制形式
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
Y Y S P ( ( s s ) ) 1 K P 1 G C 2 ( s ) G 2 ( s ) K G 1 P ( 1 G s ) C 2 ( G s ) C G 2 ( 2 s ( ) s G ) G 2 ( 1 s ( ) s ) G C 2 ( s ) G 2 ( s ) G ˆ 1 ( s )
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
在各种扰动下,再热汽温的动态响应特性与 过热汽温相类似,共有的特点为有迟延、有惯性、 有自平衡能力。
-
G’(s) +
D
G(s)
Y
YSP
+
-
Gc(s)
D
Y G(s)
内模控制系统
单回路反馈控制系统
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
YSP
+-
+ - Gc1(s)
Gc2(s)
G2(s)
- +
G’1(s)
G1(s)
D Y
串级控制系统的内模控制
YSP
+-
KP1
+- Gc2(s)
+
G2(s)
G’1(s)
G1(s)
D Y
一种内模控制形式
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
Y Y S P ( ( s s ) ) 1 K P 1 G C 2 ( s ) G 2 ( s ) K G 1 P ( 1 G s ) C 2 ( G s ) C G 2 ( 2 s ( ) s G ) G 2 ( 1 s ( ) s ) G C 2 ( s ) G 2 ( s ) G ˆ 1 ( s )
基于内模原理的PID控制器参数整定

1 f (0) , Gm (0) D(0) (18) [Gm ' (0) D(0) Gm (0) D' (0)] , f ' (0) 2 [Gm (0) D(0)] Gm ' ' (0) D(0) 2Gm ' (0) D' (0) Gm (0) D' ' (0) f ' ' (0) f ' (0) 2 f ' (0) / f (0) , Gm ' (0) D(0) Gm (0) D' (0)
1s1??从以上内模pid整定步骤可以看出整个整定过程中只有滤波器时间常数是需要调整的参数所以控制器的参数比例增益积分时间和微分时间都与滤波器时间常数有关而且随着的增大kc和td都将趋向于零而积分时间ti将接近于过程模型时间常数tp这些可有上面得到的公式看出
基于内模原理的PID控制器参数整定
导师:朱翔鸥教授 报告人:邱伟 专业:电气装备信息化 学号:16451187196
简介
内模控制方法是Garcia和Morari于1982年首先正式提出,以其简 单、跟踪调节性能好、鲁棒性强、能消除不可测干扰等优点,为控 制理论界和工程界所重视。1989年Morari透彻研究了内模控制的鲁 棒性和稳定性,并且由其他学者推广到非线性系统,蓬勃发展中的 神经网络也引入到内模控制中。内模控制还和许多其它控制方式相 结合,如内模控制与模糊控制、内模控制和自适应控制、内模控制 和最优控制、预测控制的结合使内模控制不断得到改进并广泛应用 于工程实践中,取得了良好的效果。
+
+ +
d1(s)
y(s)
-
内模控制的基本结构框图如图 所示。GIMC内模控制器;Gp为过 程;Gm为过程模型;Gd为扰动 通道传递函数。通过求取参考输 入量r和扰动输入d与过程输出y之 间的传递函数,易得出系统的闭 环响应为:
1s1??从以上内模pid整定步骤可以看出整个整定过程中只有滤波器时间常数是需要调整的参数所以控制器的参数比例增益积分时间和微分时间都与滤波器时间常数有关而且随着的增大kc和td都将趋向于零而积分时间ti将接近于过程模型时间常数tp这些可有上面得到的公式看出
基于内模原理的PID控制器参数整定
导师:朱翔鸥教授 报告人:邱伟 专业:电气装备信息化 学号:16451187196
简介
内模控制方法是Garcia和Morari于1982年首先正式提出,以其简 单、跟踪调节性能好、鲁棒性强、能消除不可测干扰等优点,为控 制理论界和工程界所重视。1989年Morari透彻研究了内模控制的鲁 棒性和稳定性,并且由其他学者推广到非线性系统,蓬勃发展中的 神经网络也引入到内模控制中。内模控制还和许多其它控制方式相 结合,如内模控制与模糊控制、内模控制和自适应控制、内模控制 和最优控制、预测控制的结合使内模控制不断得到改进并广泛应用 于工程实践中,取得了良好的效果。
+
+ +
d1(s)
y(s)
-
内模控制的基本结构框图如图 所示。GIMC内模控制器;Gp为过 程;Gm为过程模型;Gd为扰动 通道传递函数。通过求取参考输 入量r和扰动输入d与过程输出y之 间的传递函数,易得出系统的闭 环响应为:
模型预测控制 PPT课件

现代典型过程对象的控制系统层次图
Unit1 为 传 统 结构 Unit2 为 MPC 结构
模型预测控制的基本特点
预测控制算法的核心内容:
建立内部模型 确定参考轨迹 设计控制算法 实行在线优化
预测控制算法的三要素为:
预测模型 滚动优化 反馈校正
模型预测控制的三要素
预测模型
对未来一段时间内的输出进行预测
工业自动化工具的发展(仪表)
年代 1950
1960
工业发展状况
仪表技术
化工、钢铁、纺织、造纸等,规 气动仪表,标准信号:20~100kPa
模较小;电子管时代
采用真空电子管;自动平衡型
记录仪
半导体技术;石油化工;计算机; 电动仪表,标准信号:0~10mA
大型电站;过程工业大型化
仪表控制室;模拟流程图;DDC
反馈校正
y (k+j|k)= ym(k+j|k) +e(k+j|k) e (k+j|k)= y (k|k) - ym (k|k)
反馈校正
2 3 y
u
4
yˆ(k 1) ym (k
e(k 1) yˆ(k
1
k k+1
t/T
1─k时刻的预测输出ym(k)
2─k+1时刻实际输出y (k+1)
3─预测误差e(k+1)
预测模型形式
➢ 参数模型:如微分方程、差分方程、状态方程、 传递函数等
➢ 非参数模型:如脉冲响应、阶跃响应、模糊模型、 智能模型等
预测模型
基于模型的预测示意图(P=M)
过去
未来
3
y
4
1u2ຫໍສະໝຸດ k 时刻1—控制策略Ⅰ 2—控制策略Ⅱ 3—对应于控制 策略Ⅰ的输出 4—对应于控制策略Ⅱ的输出
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前将其稳定。
内模控制的主要性质
2.理想控制器特性
当模型是准确的,且模型稳定,若设计控制器
使
GIMC
(s)
1 Gp (s)
,且 1 存在并可实现
Gp (s)
则,控制器具有理想控制器特性,即在所有时间 内和任何干扰作用下,系统输出都等于输入设定 值,保证对参考输入的无偏差跟踪。
内模控制的主要性质
3.零稳态偏差特性
Gˆ p Gˆ pGˆ p-
式中,Gˆ p 包含了所有的纯滞后和右半平面的零点,并 规定其静态增益为1。Gˆ p 为过程模型的最小相位部分。
步骤2 设计控制器
1 GIMC(s) Gˆ p (s) f (s)
这里 f 为IMC滤波器。选择滤波器的形式,以保证
内模控制器为真分式。
对于阶跃输入信号,可以确定Ⅰ型IMC滤波器的形式
其反馈信号
Dˆ (s) [Gp(s) Gˆp(s)]U(s) D(s) 0 ——内模控制系统具有开环结构。
内模控制的主要性质
1.对偶稳定性 若模型是准确的,则IMC系统内部稳定的充要
条件是过程与控制器都是稳定的。 所以,IMC系统闭环稳定性只取决于前向通
道的各环节自身的稳定性。 结论:对于开环不稳定系统,在使用IMC之
R(s)
GIMC(s) U(s)
Dˆ (s)
Gp (s)
D(s)
Y (s)
Gˆ p ( s)
Ym (s)
图6-1 内模控制结构框图
Gp (s) ——实际对象; Gˆ p(s) ——对象模型;
R(s) ——给定值;
Y (s) ——系统输出;
内模控制器的设计思路是从 理想控制器出发,然后考虑 了某些实际存在的约束,再 回到实际控制器的。
表明控制器是Y (s) 跟踪 R(s) 变化的 理想控制器。
1 Y (s) GIMC(s)Gp (s)R(s) Gˆ p (s) Gp (s)R (s) R(s)
Y (s) GIMC(s)Gp (s)R (s) [1 GIMC(s)Gp (s)]D (s) 当模型没有误差,且没有外界扰动时
第六章 内模控制
内模控制(Internal Model Control——IMC) 是一种基于过程数学模型进行控制器设计的新型 控制策略。
它与史密斯预估控制很相似,有一个被称为 内部模型的过程模型,控制器设计可由过程模型 直接求取。设计简单、控制性能好、鲁棒性强, 并且便于系统分析。
1.什么是内模控制?
f
(s)
(Tf
1 s
1)r
对于斜坡输入信号,可以确定Ⅱ型IMC滤波器的形式为
f
(s)
rTf s 1 (Tf s 1)r
Tf ——滤波器时间常数。
r ——整数,选择原则是使 GIMC(s)成为有理传递函数。
因此,假设模型没有误差,可得
Y (s) Gˆp (s) f (s)R(s) [1 f (s)Gˆp (s)]D(s)
D(s) ——在控制对象输出上叠加的扰动。
讨论两种不同输入情况下,系统的输出情况:
(1)当 R(s) 0, D (s) 0 时:
假若模型准确,即 GˆP(s) Gp(s)
由图可见 Dˆ (s) D (s)
Y (s) D(s)[1 GIMC(s)Gp(s)] D(s)[1 GIMC(s)Gˆp(s)]
设 D(s) 0 时
Y (s) R(s)
Gˆ p
(s)
f
(s)
表明:滤波器 f (s) 与闭环性能有非常直接的关系。
滤波器中的时间常数 Tf 是个可调整的参数。时间 常数越小,Y (s) 对 R(s)的跟踪滞后越小。
事实上,滤波器在内模控制中还有另一重要作 用,即利用它可以调整系统的鲁棒性。其规律 是,时间常数 Tf 越大,系统鲁棒性越好。
假若“模型可倒”,即Gˆp1(s) 可以实现
则令
1 GIMC(s) Gˆ p (s)
可得 Y (s) 0
不管 D(s) 如何变化,对 Y (s)的 影响为零。表明控制器是克服
外界扰动的理想控制器。
(2)当 D (s) 0, R(s) 0 时:
假若模型准确,即 GˆP(s) Gp(s)
又因为 D (s) 0 ,则 Dˆ (s) 0
外部扰动的情况)。
Gˆ p (s)
Gp (s)
Ke s Ts 1
Dˆ (s) 0
则
Gˆ P1(s)
Ts K
1
e
s
在单位阶跃信号作用下,设计IMC控制器为
• 计,且设计步骤比常规反馈控制器要清楚很多。
(i): (ii): 对于最小相位系统:
4.3.2 滤波器设计
f(s)p(s)q(s)
取如下形式:
满足上式的滤波器最简单形式为:
滤波器可以采取其他形式,甚至可获得更快的响应。例如r=2,滤波器可取为:
例3-1 过程工业中的一阶加纯滞后过程(无模型失配和无
s
)GIMC
(s)]
s
0
0
)
对于所有斜坡输入和常值干扰均不存在稳态误差。
IMC系统本身具有偏差积分作用。
内模控制的实现问题
1.若对象含有滞后特性
则 GIMC(s) Gˆ p1(s中) 含有纯超前项,物理上难以实现。 2.若对象含有s平面右半平面( RHP)零点,
则 GIMC(s) Gˆ p1(s) 中含有RHP极点,控制器本身不稳定,闭 环系统不稳定。
I型系统(模型存在偏差,闭环系统稳定,只要设 计控制器满足 GIMC(0) Gˆ p1(0) 即控制器的稳态增益等于 模型稳态增益的倒数。)对于阶跃输入和常值干扰均 不存在稳态误差。
II型系统(模型存在偏差,闭环系统稳定,只要设
计控制器满足 GIMC(0) Gˆ p1(0)
,且
d ds
[Gˆ
p
(
3.若对象模型严格有理,
lim 则
GIMC(s) Gˆ p1(s) 非有理,即
GIMC(s)
s0
GIMC(s) 中将出现N阶微分器,对过程测量信号中的噪声极
为敏感,不切实际。
4.采用理想控制器构成的系统,对模型误差极为敏感,鲁棒性、 稳定性变差。
2. 内模控制器的设计
步骤1 因式分解过程模型
二、内模控制器对闭环 系统的影响:
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
对于模型无差,即em (s) 0的特殊情况,上式可简化为:
•
以上两式表明:对于无模型失配的情形,闭环传递函数
•
除了
中必须包含所有的滞后和右半
• 平面零点,且 必须有足够的阶次来避免物理上的不可实
• 现外,其他
内模控制的主要性质
2.理想控制器特性
当模型是准确的,且模型稳定,若设计控制器
使
GIMC
(s)
1 Gp (s)
,且 1 存在并可实现
Gp (s)
则,控制器具有理想控制器特性,即在所有时间 内和任何干扰作用下,系统输出都等于输入设定 值,保证对参考输入的无偏差跟踪。
内模控制的主要性质
3.零稳态偏差特性
Gˆ p Gˆ pGˆ p-
式中,Gˆ p 包含了所有的纯滞后和右半平面的零点,并 规定其静态增益为1。Gˆ p 为过程模型的最小相位部分。
步骤2 设计控制器
1 GIMC(s) Gˆ p (s) f (s)
这里 f 为IMC滤波器。选择滤波器的形式,以保证
内模控制器为真分式。
对于阶跃输入信号,可以确定Ⅰ型IMC滤波器的形式
其反馈信号
Dˆ (s) [Gp(s) Gˆp(s)]U(s) D(s) 0 ——内模控制系统具有开环结构。
内模控制的主要性质
1.对偶稳定性 若模型是准确的,则IMC系统内部稳定的充要
条件是过程与控制器都是稳定的。 所以,IMC系统闭环稳定性只取决于前向通
道的各环节自身的稳定性。 结论:对于开环不稳定系统,在使用IMC之
R(s)
GIMC(s) U(s)
Dˆ (s)
Gp (s)
D(s)
Y (s)
Gˆ p ( s)
Ym (s)
图6-1 内模控制结构框图
Gp (s) ——实际对象; Gˆ p(s) ——对象模型;
R(s) ——给定值;
Y (s) ——系统输出;
内模控制器的设计思路是从 理想控制器出发,然后考虑 了某些实际存在的约束,再 回到实际控制器的。
表明控制器是Y (s) 跟踪 R(s) 变化的 理想控制器。
1 Y (s) GIMC(s)Gp (s)R(s) Gˆ p (s) Gp (s)R (s) R(s)
Y (s) GIMC(s)Gp (s)R (s) [1 GIMC(s)Gp (s)]D (s) 当模型没有误差,且没有外界扰动时
第六章 内模控制
内模控制(Internal Model Control——IMC) 是一种基于过程数学模型进行控制器设计的新型 控制策略。
它与史密斯预估控制很相似,有一个被称为 内部模型的过程模型,控制器设计可由过程模型 直接求取。设计简单、控制性能好、鲁棒性强, 并且便于系统分析。
1.什么是内模控制?
f
(s)
(Tf
1 s
1)r
对于斜坡输入信号,可以确定Ⅱ型IMC滤波器的形式为
f
(s)
rTf s 1 (Tf s 1)r
Tf ——滤波器时间常数。
r ——整数,选择原则是使 GIMC(s)成为有理传递函数。
因此,假设模型没有误差,可得
Y (s) Gˆp (s) f (s)R(s) [1 f (s)Gˆp (s)]D(s)
D(s) ——在控制对象输出上叠加的扰动。
讨论两种不同输入情况下,系统的输出情况:
(1)当 R(s) 0, D (s) 0 时:
假若模型准确,即 GˆP(s) Gp(s)
由图可见 Dˆ (s) D (s)
Y (s) D(s)[1 GIMC(s)Gp(s)] D(s)[1 GIMC(s)Gˆp(s)]
设 D(s) 0 时
Y (s) R(s)
Gˆ p
(s)
f
(s)
表明:滤波器 f (s) 与闭环性能有非常直接的关系。
滤波器中的时间常数 Tf 是个可调整的参数。时间 常数越小,Y (s) 对 R(s)的跟踪滞后越小。
事实上,滤波器在内模控制中还有另一重要作 用,即利用它可以调整系统的鲁棒性。其规律 是,时间常数 Tf 越大,系统鲁棒性越好。
假若“模型可倒”,即Gˆp1(s) 可以实现
则令
1 GIMC(s) Gˆ p (s)
可得 Y (s) 0
不管 D(s) 如何变化,对 Y (s)的 影响为零。表明控制器是克服
外界扰动的理想控制器。
(2)当 D (s) 0, R(s) 0 时:
假若模型准确,即 GˆP(s) Gp(s)
又因为 D (s) 0 ,则 Dˆ (s) 0
外部扰动的情况)。
Gˆ p (s)
Gp (s)
Ke s Ts 1
Dˆ (s) 0
则
Gˆ P1(s)
Ts K
1
e
s
在单位阶跃信号作用下,设计IMC控制器为
• 计,且设计步骤比常规反馈控制器要清楚很多。
(i): (ii): 对于最小相位系统:
4.3.2 滤波器设计
f(s)p(s)q(s)
取如下形式:
满足上式的滤波器最简单形式为:
滤波器可以采取其他形式,甚至可获得更快的响应。例如r=2,滤波器可取为:
例3-1 过程工业中的一阶加纯滞后过程(无模型失配和无
s
)GIMC
(s)]
s
0
0
)
对于所有斜坡输入和常值干扰均不存在稳态误差。
IMC系统本身具有偏差积分作用。
内模控制的实现问题
1.若对象含有滞后特性
则 GIMC(s) Gˆ p1(s中) 含有纯超前项,物理上难以实现。 2.若对象含有s平面右半平面( RHP)零点,
则 GIMC(s) Gˆ p1(s) 中含有RHP极点,控制器本身不稳定,闭 环系统不稳定。
I型系统(模型存在偏差,闭环系统稳定,只要设 计控制器满足 GIMC(0) Gˆ p1(0) 即控制器的稳态增益等于 模型稳态增益的倒数。)对于阶跃输入和常值干扰均 不存在稳态误差。
II型系统(模型存在偏差,闭环系统稳定,只要设
计控制器满足 GIMC(0) Gˆ p1(0)
,且
d ds
[Gˆ
p
(
3.若对象模型严格有理,
lim 则
GIMC(s) Gˆ p1(s) 非有理,即
GIMC(s)
s0
GIMC(s) 中将出现N阶微分器,对过程测量信号中的噪声极
为敏感,不切实际。
4.采用理想控制器构成的系统,对模型误差极为敏感,鲁棒性、 稳定性变差。
2. 内模控制器的设计
步骤1 因式分解过程模型
二、内模控制器对闭环 系统的影响:
对象输入为:
闭环系统输出为:
闭环系统误差为:
其中:
对于模型无差,即em (s) 0的特殊情况,上式可简化为:
•
以上两式表明:对于无模型失配的情形,闭环传递函数
•
除了
中必须包含所有的滞后和右半
• 平面零点,且 必须有足够的阶次来避免物理上的不可实
• 现外,其他
