线性代数B(A卷)
线性代数试题A及答案
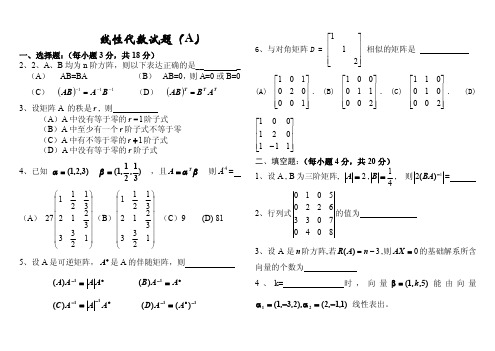
线性代数试题(A )一、选择题:(每小题3分,共18分)2、2、A 、B 均为n 阶方阵,则以下表达正确的是__ _ (A ) AB=BA (B ) AB=0,则A=0或B=0 (C ) ()111---=B A AB (D ) ()T T TA B AB =3、设矩阵A 的秩是r , 则(A )A 中没有等于零的1-r 阶子式 (B )A 中至少有一个r 阶子式不等于零 (C )A 中有不等于零的1+r 阶子式 (D )A 中没有等于零的r 阶子式4、已知 )3,2,1(=a )31,21,1(=b ,且b a T A = 则4A =(A ) 27÷÷÷÷÷÷øöççççççèæ1233321231211(B )÷÷÷÷÷÷øöççççççèæ1233321231211 (C )9 (D) 81 5、设A 是可逆矩阵,*A 是A 的伴随矩阵,则*-=A A A A 1)( *-=A A B 1)( *--=A AA C 11)( 11)()(-*-=A A D6、与对角矩阵D = úúúûùêêêëé211 相似的矩阵是 (A) úúúûùêêêëé100020101. (B) úúúûùêêêëé200110001. (C) úúúûùêêêëé200010011. (D) úúúûùêêêëé-111021001 二、填空题:(每小题4分,共20分)1、设A , B 为三阶矩阵, 2=A ,41=B , 则12-)(BA = 2、行列式8040703362205010的值为 3、设A 是n 阶方阵,若3-=n A R )(,则0=AX 的基础解系所含向量的个数为4、k= 时,向量)5,,1(k =b 能由向量)1,1,2(),2,3,1(21-=a -=a 线性表出。
同济大学2010-11线性代数B期末考试试卷_A卷_

同济大学课程考核试卷(A 卷)2010—2011学年第一学期命题教师签名: 审核教师签名: 课号:122009 课名:线性代数B 考试考查:考试此卷选为:期中考试( )、期终考试( √ )、重修( )试卷年级 专业 学号 姓名 任课教师题号 一 二 三 四 五 六 七 总分 得分(注意:本试卷共七大题,三大张,满分100分.考试时间为120分钟. 要求写出解题过程,否则不予计分)一、填空与选择题(均为单选题)(27分)1、 已知4阶方阵123456789054a b A c d ⎛⎞⎜⎟⎜⎟=⎜⎟⎜⎟⎝⎠,函数()||f x xE A =−,这里E 为4阶单位阵,则函数()f x 中3x 项的系数为_______a+b+c+d____________.2、 设12312,,,,αααββ均为4维列向量,已知4阶行列式1231,,,m αααβ=,又1223,,,n ααβα=,则4阶行列式32112,,,αααββ+=______n m −_______________.3、 已知3阶方阵A 满足320A E A E A E +=−=−=,其伴随矩阵为*A ,则行列式*A =_____36_________.4、 已知α是3维实列向量,且111111111Tαα−⎛⎞⎜⎟=−−⎜⎟⎜⎟−⎝⎠,则α=5、设α是3R 空间中的某一向量,它在基123,,εεε下的坐标为()123,,Tx x x ,则α在基1323,,k εεεε+下的坐标是_________1231(,,)T x x x kx −________________.6、 下列关于矩阵乘法的结论中错误的是____________B_________.1(). ).(). ().n A A A A B C n cE c D −若矩阵可逆,则与可交换(可逆阵必与初等矩阵可交换任一个阶方阵均与可交换,这里为任意常数 初等矩阵与初等矩阵乘法未必可交换7、 设A B 、均为n 阶方阵,且()2AB E =,则下列式子中成立的是_____D_______.()222(). (). (). ().A AB E B AB E C A B E D BA E==−==8、 设Ax b =为n 元非齐次线性方程组,则下面说法中正确的是_____C____(). 0 (). 0(). 0().() A Ax Ax b B Ax Ax b C Ax b Ax D Ax b R A n =======⇔=若只有零解,则有唯一解若有无穷多个解,则有无穷多个解若有两个不同的解,则有无穷多个解 有唯一解9、 下列向量组中线性无关的是_______C__________.()()()()()()()()()()()()()()(). 1,1,0,20,1,1,10,0,0,0). ,,,,,,,,,,, (). ,1,,0,0,,0,,1,0,,0,,0,1().1,2,1,5,1,2,1,6,1,2,3,7,0,0,0,1A B a b c b c d c d a d a b C a b c d e f D −−,, (二、(10分) 已知n 阶行列式12312001030100n n D n="""###%#",求第一行各元素的代数余子式之和.三、(10分)参数,a b 满足什么条件的时侯,线性方程组1234512345234512345132322635433x x x x x x x x x x a x x x x x x x x x b ++++=⎧⎪+++−=⎪⎨+++=⎪⎪+++−=⎩有解?并在有解的情况下,求出它的通解.四、(15分)已知3阶方阵3221423A k k −⎛⎞⎜⎟=−−⎜⎟⎜⎟−⎝⎠,问参数k 满足什么条件的时候A 可以对角化?并求出可逆阵P 及对角阵Λ,使得1P AP −=Λ.五、(12分)设向量组12341111,,1,4115k k k αααα−−⎛⎞⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟⎜⎟====⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟−⎝⎠⎝⎠⎝⎠⎝⎠,问: (1) 参数k 为何值时,123,,ααα为向量组的一个最大线性无关组?(2) 参数k 为何值时,12,αα为向量组的一个最大线性无关组?并在此时,求出34,αα由最大线性无关组表出的线性表达式.六、(12分)设V 为实数域R 上全体2阶方阵关于矩阵的加法和数乘运算所成的线性空间,在V中定义映射:()a b T T X X c d ⎛⎞=⎜⎟⎝⎠,(1) 证明T 是V 中的线性变换,(2) 求线性变换T 在自然基11122122,,,E E E E 下的矩阵,(3) 若1,2,3,4a b c d ====,试求线性变换T 的核ker T 与像空间Im T .七、(1)(7分)已知A 为3阶方阵,123,,λλλ为A 的三个不同的特征值,123,,ααα分别为相应的特征向量,又123βααα=++,试证:2,,A A βββ线性无关.(2) (7分)设A 为3阶实对称阵,且220A A +=,又()2R A =,试求出A 的全体特征值,并问参数k 为何值时,矩阵A kE +为正定阵?。
线性代数试卷

12008-2009-1年秋线性代数期末试卷(A)一、单项选择题(每小题3分,共15分)1.设A 中有2n n -个以上元素为零,则A 的值为( ) A.大于零; B. 等于零; C. 小于零; D. 不能确定.2.设n 阶方阵A 有一个特征值为零,则下列说法正确的是( )A. 0;A =B. ();R A n =;C.A 可逆;D. A 的列向量组线性无关. 3. 设A 为n 阶方阵,若A 与n 阶单位矩阵等价,则方程组Ax b =有( )A. 无解;B. 有唯一解;C. 有无穷多解;D. 解的情况不能确定。
4. 设,A B 为三阶方阵,若A 可逆,()2R B =,则()R AB =( ) A. 0; B. 1; C. 2; D. 3。
5. 同阶方阵A 与B 相似的充要条件是( )A. 存在两个可逆矩阵P 与Q ,使得PAQ B =;B. 存在可逆矩阵P ,使得1P AP B -=;C. 存在可逆矩阵P ,使得T P AP B =;D. ()()R A R B =。
二、填空题(每小题3分,共15分)6.行列式1234003209156412a a a a 中4a 的代数余子式的值等于 。
7.若2λ=是可逆方阵A 的一个特征值,则方阵1212A -⎛⎫⎪⎝⎭必有一个特征值为 。
8.当t = 时,下列向量组()123(2,1,0),(3,2,5),10,6,a a a t ===线性相关。
9.设A 是三阶方阵,*A 是A 的伴随矩阵,已知12A =,则()1*32A A --= 。
10.二次型121323222f x x x x x x =++的秩等于 。
三、计算题(每小题10分,共50分)11. 若111121()11x x f x n x++=+,求(0)f 。
12.设矩阵111111111A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,矩阵X 满足*12A X A X -=+,求X 。
13. 问,a b 取何值时,向量()1,2,T b β=可由向量组()11,1,2T α=,()22,3,3Tα=,()33,6,Ta α=(1)唯一的线性表示, (2)无穷多的线性表示, (3)不能线性表示。
2007级线性代数试题和答案 A卷

2007级线性代数试题和答案 A 卷2007级线性代数期末试题答案一、填空题(每小题4分、本题共28分)1.设A *是n 阶方阵A 的伴随矩阵,行列式2A =,则*2A = .2n n n 12 2|=22222n -=⨯=n-1**n-1n-1解应填因为行列式|2A |A |=|A|2.设4阶方阵A 和B 的伴随矩阵为A *和B *,且它们的秩分别为3)(=A r ,4)(=B r ,则秩=)(**B A r .()()()()****** 1.14 1.r A r B B r A B r A ====解应填由题设可知,,的可逆矩阵,故 3.设n 维向量(,0,,0,)T x x α=,其中0x <;又设矩阵T A E αα=-,且11T A E xαα-=+,则x = .()()()()()2-1-12 -12111- --111----21 -1-201111-22-12-11012T T T T T T TT T T T T T TT T x AA E E E x x x E E x x x x E x x AA E x x x x x x x x x x αααααααααααααααααααααααααααααααα=⎛⎫=+=+ ⎪⎝⎭=+=+⎛⎫=+ ⎪⎝⎭=≠+=+=+==解应填 因为,而 由及可知 故或-10-1x x =<=,又由可得4.已知n 阶方阵()ij n nA a ⨯=,12,,n ααα⋅⋅⋅,是A 的列向量组,行列式0A =,伴随矩阵*O A ≠,则齐次线性方程组*0A x =的通解为 .解 应填α =111221...n i i n i k k k ααα--+++ ,其中 121n i i i ααα⋅⋅⋅- 是向量组 12n ααα⋅⋅⋅的极大线性无关组, 121n k k k ⋅⋅⋅- 是任意常数。
因为|A|=0,A *≠0 所以秩r(A)=n-1,因此,向量组12n ααα⋅⋅⋅的秩r(12n ααα⋅⋅⋅)=n-1,由此又可知线性方程组A *x=0的基础解系含n-1个解,12n ααα⋅⋅⋅的极大线性无关组含n-1个向量,而A *A= A *(12n ααα⋅⋅⋅)=|A|E=0即A *=0(j=1 n) ,亦即12n ααα 都是A *x=0 的解,故12n ααα的极大线性无关组可作为A *x=0 的基础解系。
(完整版)线性代数试卷及答案详解

《线性代数A 》试题(A 卷)试卷类别:闭卷考试时间:120分钟考试科目:线性代数考试时间:学号:姓名:3的一组标准正交基,=___________《线性代数A》参考答案(A卷)一、单项选择题(每小题3分,共30分)二、填空题(每小题3分,共18分)1、 256;2、 132465798⎛⎫ ⎪--- ⎪ ⎪⎝⎭; 3、112211221122000⎛⎫⎪- ⎪ ⎪-⎝⎭; 4、; 5、 4; 6、 2 。
三. 解:因为矩阵A 的行列式不为零,则A 可逆,因此1X A B -=.为了求1A B -,可利用下列初等行变换的方法:231211201012010*******121011411033110331023211027210027810027801141010144010144001103001103001103---⎛⎫⎛⎫⎛⎫⎪⎪⎪-−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫⎛⎫⎪⎪⎪−−→--−−→-−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭―――――(6分)所以1278144103X A B -⎛⎫ ⎪==-- ⎪ ⎪⎝⎭.―――――(8分)四.解:对向量组12345,,,,ααααα作如下的初等行变换可得:1234511143111431132102262(,,,,)21355011313156702262ααααα--⎛⎫⎛⎫⎪ ⎪----- ⎪ ⎪=→ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭111431212011310113100000000000000000000--⎛⎫⎛⎫⎪⎪---- ⎪ ⎪→→⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭――――(5分)从而12345,,,,ααααα的一个极大线性无关组为12,αα,故秩12345{,,,,}ααααα=2(8分)且3122ααα=-,4123ααα=+,5122ααα=--――――(10分) 五.解:对方程组的增广矩阵进行如下初等行变换:221121121121110113011311101112002421120113400(2)(1)42p p p p p p p p p p p p p p p p p p p p p ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪−−→--−−→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--+--+⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪−−→------- ⎪ ⎪-+-+⎝⎭(分)(1) 当10,(2)(1)0,p p p -≠-+-≠且时即1,2,p p ≠≠-且时系数矩阵与增广矩阵的秩均为3,此时方程组有唯一解.――――(5分) (2) 当1,p =时系数矩阵的秩为1,增广矩阵的秩为2,此时方程组无解.――――(6分)(3) 当2,p =-时此时方程组有无穷多组解. 方程组的增广矩阵进行初等行变换可化为1122112211221211033301112111033300001011011180000------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-−−→-−−→-- ⎪ ⎪ ⎪⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭--⎛⎫⎪−−→------ ⎪ ⎪⎝⎭(分)故原方程组与下列方程组同解:132311x x x x -=-⎧⎨-=-⎩ 令30,x =可得上述非齐次线性方程组的一个特解0(1,1,0)Tξ=--;它对应的齐次线性方程组13230x x x x -=⎧⎨-=⎩的基础解系含有一个元素,令31,x =可得1(1,1,1)T ξ=为该齐次线性方程组的一个解,它构成该齐次线性方程组的基础解系.此时原方程组的通解为001101,,.k k k k ξξ+这里为任意常数――――(12分)六.解:(1)由于A的特征多项式2124||222(3)(6)421I A λλλλλλ----=-+-=+----故A 的特征值为13λ=-(二重特征值),36λ=。
2007-2008学年第1学期线性代数B期终考试试卷A
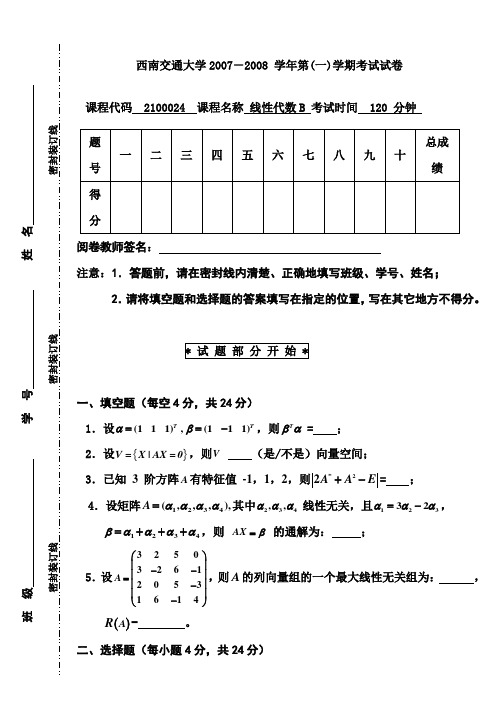
西南交通大学2007-2008 学年第(一)学期考试试卷课程代码 2100024 课程名称 线性代数B 考试时间 120 分钟阅卷教师签名:注意:1.答题前,请在密封线内清楚、正确地填写班级、学号、姓名;2.请将填空题和选择题的答案填写在指定的位置,写在其它地方不得分。
一、填空题(每空4分,共24分)1.设(111),(111)T T αβ==-,则T βα= ; 2.设{}V =X |AX =0,则V (是/不是)向量空间; 3.已知 3 阶方阵A 有特征值 -1,1,2,则2*2A A E +-= ; 4.设矩阵1234(,,,),A =αααα其中234,,ααα线性无关,且12332ααα=-,1234=+++βαααα,则 AX β= 的通解为: ;5.设3250326120531614A ⎛⎫⎪-- ⎪= ⎪- ⎪-⎝⎭,则A 的列向量组的一个最大线性无关组为: , ()A R = 。
二、选择题(每小题4分,共24分)班 级 学 号 姓 名密封装订线 密封装订线 密封装订线6.行列式 001100010020100003A ⎛⎫⎛⎫⎪⎪= ⎪⎪ ⎪⎪⎝⎭⎝⎭求1A -=( )(A ) 100010121⎛⎫ ⎪ ⎪ ⎪⎝⎭ (B )1001002103⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ (C ) 001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭ (D ) 00110021003⎛⎫ ⎪ ⎪⎪⎪ ⎪⎝⎭7.设 21201123()132013x x x f x x x x--=,则()f x 中3x 的系数为( )。
(A) -1 ; (B) 1 ; (C) -17 ; (D) 17 。
8.设 A B 、 均为 n 阶可逆方阵,下列各式正确的是( )。
(A) ||||A A λλ=; (B) 111()AB B A ---=; (C) ()T T T AB A B =; (D)||||||A B A B +=+。
线性代数试卷及答案3套

《线性代数》(A 卷 共四页)一.填空或选择填空(共30分,每小题3分)1.设],,,[A 432γγγα=,],,,[B 432γγγβ=,其中432,,,,γγγβα均为四维列向量. 已知4|A |=,1|B |=,则_____|B A |=+.2.设A 为)(m n m n >⨯矩阵,S 为n 阶可逆矩阵,且r r =)A (,)SA (r 1r =,则( ). A r r m >>1B m r r >>1C m r =1D r r =13.四维列向量组 T1]4,2,1,1[-=α,T2]2,1,3,0[=α,T3]14,7,0,3[=α,T 4]0,2,1,1[-=α的秩为_______,一个极大无关组为_____________.4.齐次线性方程组0=AX 有非零解的充分必要条件是( ). A A 的列向量组线性无关 B A 的行向量组线性无关 C A 的列向量组线性相关 D A 的行向量组线性相关5.设T1]0,2,1[=α,T2]1,0,1[=α都是三阶方阵A 的属于特征值12=λ的特征向量,而T]2,2,1[--=β,则______________=βA .6.设2=λ为可逆矩阵A 的一个特征值,则12A 31-⎪⎭⎫⎝⎛有一个特征值为_____=μ.78.下列矩阵中不与对角矩阵相似的是( ).A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡600540321B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡653542321C ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200020012D ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡200010012 9.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=001010100A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100010001B ,则A 与B ( ). A 合同但不相似 B 合同且相似 C 不合同但相似D 不合同且不相似10.设实二次型312322213212),,(x cx ax bx ax x x x f +++=,当( )时,该二次型为正定二次型.A 0,0>+>c b aB 0,0>>b aC 0|,|>>b c aD 0,||>>b c a 二.计算下列行列式(共12分,每小题6分)1.67412120603115124-----=D ;2.111122111n nn a a a a a a D ---=+(空白处元素全为0).三.计算(共20分,每小题10分) 1.设A 为可逆矩阵,且B AB A +=-1*.1) 求证B 为可逆矩阵;2) 当⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=200620062A 时,求矩阵B . 2.求解如下线性方程组;若有无穷多解,请用其特解与导出组的基础解系联合表出通解.四.(18分)求一个正交替换SY X =,将如下实二次型化为标准形.32312123222132184422),,(x x x x x x x x x x x x f ++---=.五.(5分)求证秩为r 的实对称矩阵可以写成r 个秩为1的实对称矩阵之和.《线性代数》(B 卷)一.填空与选择(30分,每小题3分)1.设d a a a a a a a a a =333231232221131211,则=------333232213123222221211312121111432432432a a a a a a a a a a a a a a a ________.2.=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10057002311003200______________________.3.设B A ,均为n 阶方阵,则有( ).A )B ()A ()B A (r r r +=+ B )B ()A ()AB (r r r =C )B ()A (B O O A r r r +=⎥⎦⎤⎢⎣⎡D )B ()A (B O O A r r r =⎥⎦⎤⎢⎣⎡ 4.设向量组4321,,,αααα线性无关,则14433221,,,αααααααα++++的秩为______.5.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----13222123a 与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡λ00020002相似,则=λ______,=a ______. 6.设33⨯A 的全体特征值为3,2,1-,则( )为可逆矩阵.A A E -B E A 2+C E A 2-DE A 3-7.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=100110111A 为线性变换σ在基321,,:(I)ξξξ下的矩阵,则σ在基321211,,:(II)ξξξξξξ+++下的矩阵为=B _______________.8.设T ]2,1[是实对称矩阵A 的特征向量,且0|A |<,则( )也是A 的特征向量.A R ∈k k ,]2,1[T B R ∈-k k ,]1,2[T 非零 C R ∈-+21T2T 1,,]1,2[]2,1[k k k k 不全为零D R ∈-+21T2T 1,,]1,2[]2,1[k k k k 全不为零9.实二此型32312123222132182292),,(x x x x x x x x x x x x f +++++=有标准形( ).A 23222192y y y ++ B 23222192y y y -+ C 23222192y y y -- D 2221y y +10.设B A ,均为n 阶正定矩阵,则( )不一定是正定矩阵.A B A + B BA AB + C ABA D ⎥⎦⎤⎢⎣⎡B O O A 二.(28分,前3小题各6分,第4小题10分)1.计算n 阶行列式(3≥n )0221202122011110 =n D .2.设n 阶方阵A 满足O E A A A =+--43223,求证E A 2-可逆,并求1)2(--E A .3.求向量组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=6211α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=2102α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3013α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=4234α的一个极大无关组,并用该极大无关组线性表示向量组中其他向量.。
全校各专业《线性代数》课程试卷及答案A卷

全校各专业《线性代数》课程试卷及答案A 卷试卷 A 考试方式 闭卷 考试时间(120分钟)一、选择题(本题共4小题,每小题4分,满分16分。
每小题给出的四个选项中,只有一项符合题目要求) 1、设A ,B 为n 阶方阵,满足等式0=AB,则必有( ) (A)0=A 或0=B ; (B)0=+B A ; (C )0=A 或0=B ; (D)0=+B A 。
2、A 和B 均为n 阶矩阵,且222()2A B A AB B +=++,则必有( ) (A) A E =; (B)B E =; (C ) A B =. (D) AB BA =。
3、设A 为n m ⨯矩阵,齐次方程组0=Ax 仅有零解的充要条件是( )(A) A 的列向量线性无关; (B) A 的列向量线性相关; (C ) A 的行向量线性无关; (D) A 的行向量线性相关. 4、 n 阶矩阵A 为奇异矩阵的充要条件是( ) (A) A 的秩小于n ; (B) 0A ≠;(C) A 的特征值都等于零; (D) A 的特征值都不等于零; 二、填空题(本题共4小题,每题4分,满分16分)5、若4阶矩阵A 的行列式5A =-,A *是A 的伴随矩阵,则*A = 。
6、A 为n n ⨯阶矩阵,且220A A E --=,则1(2)A E -+= 。
7、已知方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-+43121232121321x x x a a 无解,则a = 。
8、二次型2221231231213(,,)2322f x x x x x tx x x x x =++++是正定的,则t 的取值范围是 。
三、计算题(本题共2小题,每题8分,满分16分)9、计算行列式1111111111111111x x D y y+-=+-10、计算n 阶行列式121212333n n n n x x x x x x D x x x ++=+四、证明题(本题共2小题,每小题8分,满分16分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江理工大学2013—2014学年第一学期 《线性代数B 》期末试卷(A 卷)
本人郑重承诺:本人已阅读并且透彻地理解《浙江理工大学考场规则》,愿意在考试中自觉遵守这些规定,保证按规定的程序和要求参加考试,如有违反,自愿按《浙江理工大学学生违纪处分规定》有关条款接受处理。
承诺人签名: 学号: 班级:
一、选择题(每小题4分,共24分)
1.设A 为3阶矩阵,把A 按列分块为),,(321αααA =,矩阵),2,2(1213ααααB -=,若
2-=A ,则=||B ( ).
(A )4 (B ) 4- (C )8 (D ) 8-
2. 设3阶矩阵⎪⎪⎪⎭
⎫
⎝⎛=a b b b a b b b a A ,已知伴随矩阵*
A 的秩为1,则必有( ).
(A )b a ≠且02≠+b a (B ) b a ≠且02=+b a
(C )b a =或02≠+b a (D ) b a =或02=+b a 3.矩阵A ( )时,可能改变其秩.
(A )转置 (B )初等变换 (C )乘以奇异矩阵 (D )乘以非奇异矩阵 4.设321,,ααα线性相关,则以下结论正确的是( ).
(A )21,αα一定线性相关 (B )31,αα一定线性相关 (C )21,αα一定线性无关 (D )存在不全为零的数321,,k k k 使0ααα=++332211k k k 5. 若A 为正交矩阵,则下列命题正确的是( ).
(A )1=A (B ) 1-=A (C )A 为对称阵 (D ) T
A 与A 为可交换矩阵 6. 设0λ是n 阶矩阵A 的特征值,且齐次线性方程组0X E A =-)(0λ的基础解系为21,ηη,则A 的对应于0λ的全部特征向量是( ).
(A )1η和2η (B )1η或2η
(C )2211ηηk k +(21,k k 全不为0) (D )2211ηηk k +(21,k k 不全为0) 二、填空题(每小题4分,共24分)
1. 三阶行列式=16
94432
1
1
1 . 2. 设)3,2,1(=α,)3,2,1(=β,则=k T )(βα .
3. 设矩阵⎪⎪⎭
⎫ ⎝⎛-=3211A ,E A A B 232
+-=,则=B .
4. 设⎪⎪⎪
⎭
⎫ ⎝⎛--=t 27121103121301A ,若齐次线性方程组0AX =的基础解系含有3个解向量 ,
则=t .
5. 已知线性方程组⎪⎩⎪
⎨⎧=++=+-=-+d
cx bx ax x x x x x x 321321321,22,12的两个解⎪⎪⎪⎭
⎫ ⎝⎛=323112η和⎪⎪
⎪⎭⎫ ⎝⎛--=13412η,则方程组的通解为 .
6. 已知三阶矩阵A 的三个特征值为3,2,1,则=A ,1
-A 的特征值为 . 三、计算题(共46分)
1. 若⎪⎪⎪⎭⎫ ⎝⎛=110011101A ,⎪⎪⎪
⎭
⎫
⎝⎛=521234311B ,求矩阵X ,使得B AX =.(8分)
2. 已知⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=32011α,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=53112α,⎪⎪⎪
⎪⎪⎭⎫ ⎝⎛+-=12113a α,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+=84214a α,及⎪⎪⎪⎪
⎪⎭
⎫ ⎝⎛+=5311b β, (1)b a ,为何值时,β不能表示成4321,,,αααα的线性组合?
(2)b a ,为何值时,β有4321,,,αααα的唯一线性表达式? 并写出该表示式. (10分)
3. 在3维空间V 中,已知从基321,,ααα到基321,,βββ的过渡矩阵⎪⎪⎪
⎭⎫ ⎝⎛----=321421311P ,
(1)若向量β在基321,,ααα下的坐标为⎪⎪⎪
⎭
⎫
⎝⎛111,求β在基321,,βββ下的坐标.
(2)求一个向量α,使其在基321,,ααα和基321,,βββ下的坐标相同. (8分)
4. 设矩阵⎪⎪⎪
⎭
⎫ ⎝⎛=112121211A ,求一个正交矩阵Q ,使得AQ Q T 为对角阵.(10分)
5. 已知⎪⎪⎪⎭⎫ ⎝⎛-=111p 是矩阵⎪⎪⎪
⎭
⎫ ⎝⎛---=2100
212b a A 的特征向量, (1)求b a ,的值;(2)问A 能否相似对角化,并说明理由. (10分)
四、证明题(共6分)
1.设A 为n m ⨯矩阵,B 为s n ⨯矩阵,证明:如果0AB =,那么n R R ≤+)()(B A .。
