带通滤波器
带通滤波器

带通滤波器带通滤波器是一种常见的电子元件,用于去除电子信号中的特定频率范围之外的信号。
它在各种电子设备和通信系统中发挥着重要的作用。
本文将从基本原理、应用领域和未来发展等方面进行阐述。
带通滤波器适用于那些需要选择特定频率范围内信号的电路。
它可以通过阻碍或通过特定频率范围内的信号来实现这一目的。
带通滤波器主要由一个输入端、一个输出端和一个中心频率组成。
中心频率是带通滤波器允许通过的信号的频率范围的中间值。
带通滤波器的基本原理取决于其类型。
常见的有主动滤波器和被动滤波器。
主动滤波器利用放大器来增强信号,以实现滤波效果。
被动滤波器则主要依靠电容器、电感器和电阻器等被动元件来实现滤波。
无论是主动滤波器还是被动滤波器,它们的工作原理都是基于电路中的共振现象,选择性地通过或阻碍特定频率范围的信号。
带通滤波器在很多领域都有广泛的应用。
在音频设备中,带通滤波器被用于隔离和增强特定频率范围内的声音信号,以实现音效调节和噪音消除。
在无线通信系统中,带通滤波器被用于选择所需的频率范围内的信号进行接收或传输,以实现可靠的通讯。
在雷达系统中,带通滤波器被用于去除杂波和干扰信号,以提高目标检测的准确性。
此外,带通滤波器还被广泛应用于医疗设备、图像处理、仪器仪表等领域。
随着科技的不断发展,带通滤波器也在不断演进。
新的滤波器设计和材料的发展使得滤波器的性能不断提升。
例如,有源滤波器采用了新型放大器和控制电路,使得滤波器的频率范围更广,滤波效果更好。
此外,尺寸更小、功耗更低的滤波器也正在被广泛研发,以适应无线通信设备的小型化和便携化需求。
未来,带通滤波器将继续在各个领域发挥重要的作用,并随着技术的进步不断演化。
随着5G通信技术的发展,对高频滤波器的需求将进一步增加,以实现更高的数据传输速率和更可靠的通讯。
同时,对功耗更低、尺寸更小的滤波器的需求也将持续增长,以适应便携设备的需求。
总之,带通滤波器作为一种常见的电子元件,在各种电子设备和通信系统中发挥着重要作用。
带通滤波器工作原理与带通滤波器原理图详解

带通滤波器工作原理与带通滤波器原理图详解带通滤波器(band-pass filter)是一个允许特定频段的波通过同时屏蔽其他频段的设备。
比如RLC振荡回路就是一个模拟带通滤波器。
带通滤波器是指能通过某一频率范围内的频率分量、但将其他范围的频率分量衰减到极低水平的滤波器,与带阻滤波器的概念相对。
一个模拟带通滤波器的例子是电阻-电感-电容电路(RLC circuit)。
这些滤波器也可以用低通滤波器同高通滤波器组合来产生。
工作原理一个理想的带通滤波器应该有一个完全平坦的通带,在通带内没有放大或者衰减,并且在通带之外所有频率都被完全衰减掉,另外,通带外的转换在极小的频率范围完成。
实际上,并不存在理想的带通滤波器。
滤波器并不能够将期望频率范围外的所有频率完全衰减掉,尤其是在所要的通带外还有一个被衰减但是没有被隔离的范围。
这通常称为滤波器的滚降现象,并且使用每十倍频的衰减幅度的dB数来表示。
通常,滤波器的设计尽量保证滚降范围越窄越好,这样滤波器的性能就与设计更加接近。
然而,随着滚降范围越来越小,通带就变得不再平坦,开始出现“波纹”。
这种现象在通带的边缘处尤其明显,这种效应称为吉布斯现象。
除了电子学和信号处理领域之外,带通滤波器应用的一个例子是在大气科学领域,很常见的例子是使用带通滤波器过滤最近3到10天时间范围内的天气数据,这样在数据域中就只保留了作为扰动的气旋。
在频带较低的剪切频率f1和较高的剪切频率f2之间是共振频率,这里滤波器的增益最大,滤波器的带宽就是f2和f1之间的差值。
典型应用许多音响装置的频谱分析器均使用此电路作为带通滤波器,以选出各个不同频段的信号,在显示上利用发光二极管点亮的多少来指示出信号幅度的大小。
这种有源带通滤波器的中。
一、带通滤波器(BandpassFilter)
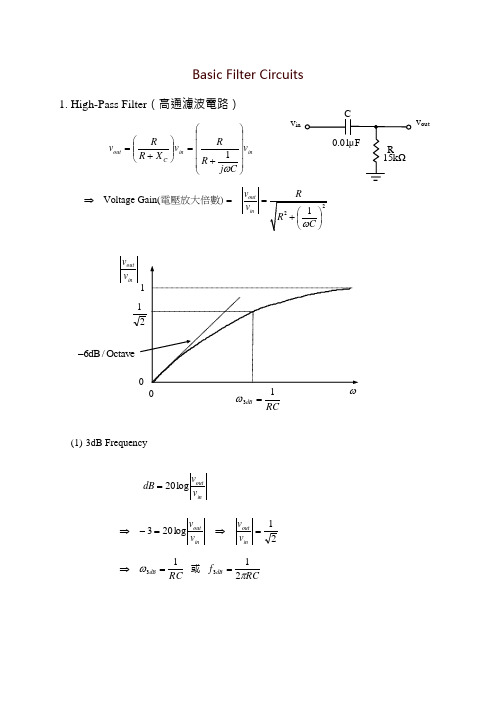
Basic Filter Circuits1. High-Pass Filter (高通濾波電路)inin C outv C j R R v X R R v ⎪⎪⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=ω1Voltage Gain(outinv v ⇒==電壓放大倍數)(1) 3dB Frequencyinoutv v dB log20= 21log203=⇒=-⇒in out inoutv v v v RC dB 13=⇒ω 或 RCf dB π213=6dB/-0ω31dB RC=C.0v outv in(2) Roll-off Attenuation (衰減斜率) At low frequencies, dB RC31ωω=<<,dBin out RC v v 3ωωω=≈ ⎪⎪⎭⎫ ⎝⎛=⇒dB in outdB v v 3log 20)(log20ωω or ()dB 3log log 20ωω-At dB 321ωω=(called “Octave ” (八度音)), )(621log 20log 20log203dB -===dB in out v v ωω ⇒Roll-off Attenuation (衰減斜率) 6dB/octave =0.1 110)/log(3dB ωωdB /6+or dB /20+At dB 3101ωω=(called “decade ” ), )(20101log 20log20dB -==in out v v ⇒Roll-off Attenuation (衰減斜率) 20dB/decade =(3) Phase Shift (相移)22111⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=+=C R C j R R C j R R v v inout ωωωThe output voltage, v out , leads ahead of the input voltage, v in , by the angle θ, where 31/tan dBC R ωωθω==. At 3110dB ωω=, 8410tan ≈⇒=θθAt 310dB ωω=, 61.0tan ≈⇒=θθdB 3θ90045002. Low-Pass Filter (低通濾波電路)in in C C outv C j R C j v X R X v ⎪⎪⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+=ωω11Voltage Gain out in v v ⇒==(1) 3dB Frequencyinoutv v dB log20= 21log203=⇒=-⇒in out inoutv v v v RC dB 13=⇒ω or RCf dB π213=ω3dB RC=v in v out 0.01μF(2) Roll-off Attenuation (衰減斜率) At high frequencies, dB RC31ωω=>>,ωωωdB in out RC v v 31=≈ ⎪⎭⎫⎝⎛=⇒ωωdB in out dB v v 3log 20)(log20 or ()ωωlog log 203-dBAt dB 32ωω=(Octave(八度音),)(621log 20log 20log203dB -===ωωdB in out v v ⇒Roll-off Attenuation(衰減斜率)6dB/octave =-At dB 310ωω=,)(20101log 20log20dB -==in out v v ⇒Roll-off Attenuation (衰減斜率) 20dB/decade =-20log outin v v 0-10 -20 -300.1 110102 )/log(3dB ωω(3) Phase Shift (相移)2211111⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛-=+=C R jR C C C j R C j v v inout ωωωωωThe output voltage, v out , lags behind the input voltage, v in , by the angle θ,where 3tan 1/dBR C ωθωω=-=-.dB 3101ωω=當, 61.0tan -≈⇒-=θθdB 310ωω=當, 8410tan -≈⇒-=θθθ-90-45000dB 3ω3. Band-Pass Filter (帶通濾波器)CL LC Z Z Z 111+= Cj Lj ωω111+=⎪⎭⎫ ⎝⎛-=L C j ωω1111111)(+⎪⎭⎫ ⎝⎛-=+⎪⎪⎭⎫ ⎝⎛=+==L C jR R Z Z R Z v v T LC LC LC in out ωωω 111)(22+⎪⎭⎫ ⎝⎛-=⇒L C R T ωωωResonant Frequency (共振頻率): LCf π210=,or LC 001ωω=∞=⇒LC Z ,1=inoutv vQuality factor (品質因數)dBf f 30∆≡(sharpness of the bell-shape curve) v outv inR(ωT 1ω12ωo =LC1At 3dB point ,21)(=ωT1122=⎪⎭⎫ ⎝⎛-⇒L C R ωωRL C 11±=-⇒ωωRC120±=-⇒ωωωThere are two 3dB points: ω1 and ω2⇒ RC 11201-=-ωωω )(10ωω> RC12202=-ωωω )(20ωω<⇒ RC112=-ωω 2021ωωω=⇒ LCRRC f f Q dB ==-=∆=012030ωωωω4. Band-Reject Filter (or called Notch Filter) (帶拒濾波器)inout v v T =)(ω⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=C L j R C L j ωωωω112211)(⎪⎭⎫ ⎝⎛-+-=⇒C L R CL T ωωωωω2021ωωω=LR =-12ωω CLR R L f f Q dB 1012030==-=∆=⇒ωωωω)(ωT0.70ω1 2v outv in。
1到30赫兹的带通滤波器-概述说明以及解释

1到30赫兹的带通滤波器-概述说明以及解释1.引言1.1 概述在撰写本文中,我们将重点介绍1到30赫兹的带通滤波器。
带通滤波器是一种常见的电子滤波器,用于选择特定范围内的频率信号。
在本文中,我们将探讨其概念、工作原理和应用。
带通滤波器的基本原理是通过阻止或放行特定频率范围内的信号来实现滤波效果。
比如在1到30赫兹的频率范围内,滤波器可以过滤掉低于1赫兹和高于30赫兹的信号,只保留在这个范围内的信号。
这就使得滤波器非常适用于许多应用,如声音处理、通信系统和医学设备等。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联而成。
低通滤波器可以将低于截止频率的信号通过,而高通滤波器可以将高于截止频率的信号通过。
当这两个滤波器结合在一起时,就形成了一个带通滤波器。
带通滤波器在各个领域都有广泛的应用。
在音频处理中,它可以用于消除噪音,提升音频质量。
在通信系统中,带通滤波器可以用来选择特定频段的信号,以便传输和接收。
在医学设备中,它可以用于识别和分析特定频率范围内的生物信号,如心电图和脑电图等。
综上所述,本文将详细介绍1到30赫兹的带通滤波器的概念、工作原理和应用。
通过阅读本文,读者将能够更好地理解带通滤波器的作用和重要性,并在相关领域中应用其知识。
接下来的章节将进一步探讨带通滤波器的细节和实际应用案例。
1.2文章结构1.2 文章结构本文将按照以下结构进行阐述:2.1 赫兹与频率的关系首先,我们将介绍赫兹与频率之间的关系。
赫兹是表示每秒周期性事件发生次数的单位,常用于描述声波、电磁波等波动现象的频率。
频率则是指每单位时间内所发生的周期性事件的次数,通常以赫兹为单位进行衡量。
我们将详细探讨赫兹与频率之间的转换关系,以便读者能够更好地理解本文涉及到的带通滤波器的工作原理。
2.2 带通滤波器的定义与原理在这一部分,我们将详细介绍带通滤波器的定义和原理。
带通滤波器是一种能够通过特定频率范围内的信号,而削弱或排除其他频率范围内的信号的设备。
带通滤波器在信号处理中的作用

带通滤波器在信号处理中的作用带通滤波器是一种常见的信号处理工具,用于提取特定频率范围内的信号,并削弱或滤除其他频率范围的噪声或无用信号。
它在信号处理中起到非常重要的作用,被广泛应用于各个领域。
本文将详细介绍带通滤波器的原理、应用场景以及作用。
一、带通滤波器的原理带通滤波器是一种频率选择性滤波器,只允许特定频率范围内的信号通过,削弱或消除其他频率的信号。
其原理基于滤波器的频率响应曲线,通常以振幅-频率图或相位-频率图的形式展示。
带通滤波器通常由低截止频率、高截止频率和中心频率三个参数决定。
低截止频率是指滤波器开始对信号进行削弱的频率,高截止频率是指滤波器完全阻断信号的频率,而中心频率则是带通滤波器希望保留的信号频率。
带通滤波器可以采用各种形式的实现,包括电子滤波器、数字滤波器以及其他形式的滤波器。
不同的滤波器实现方式有不同的特点和应用场景,可以根据实际需求选择合适的滤波器。
二、带通滤波器的应用场景带通滤波器在信号处理中的应用非常广泛,以下列举了一些常见的应用场景:1. 语音处理:在语音识别、语音合成等领域,带通滤波器被用于去除背景噪声或削弱频率范围外的信号,以提高语音质量和准确性。
2. 音频处理:在音频信号处理中,带通滤波器可以用来增强或削弱特定频率的音频信号,以改善音质、减少噪声或实现特定音效。
3. 图像处理:在图像处理中,带通滤波器可以用于图像增强、边缘检测和图像分割等任务。
通过选择适当的带通滤波器参数,可以提取出特定频率范围内的图像细节。
4. 信号分析:在信号分析领域,带通滤波器被广泛用于频谱分析、频域特征提取等任务。
它可以帮助分析人员集中关注感兴趣的频段,提取有用信息。
5. 无线通信:在无线通信系统中,带通滤波器被用于频带分配、信号调制解调以及射频前端信号处理。
它可以帮助实现信号的频率选择和抑制干扰信号。
三、带通滤波器的作用带通滤波器在信号处理中具有以下几个重要的作用:1. 滤波作用:带通滤波器可以提取特定频率范围内的信号,并削弱或滤除其他频率的噪声或无用信号。
常见低通高通带通三种滤波器的工作原理

常见低通高通带通三种滤波器的工作原理低通滤波器的工作原理:低通滤波器是一种能够通过低频信号而抑制高频信号的滤波器。
其工作原理基于信号的频谱特征,将高频成分滤除,只保留低频成分。
最常见的低通滤波器是RC低通滤波器。
它由电阻(R)和电容(C)组成。
当输入信号通过电容时,高频信号会受到电容的阻碍,直流或低频信号则可以通过电容。
由于电阻连接在电容的后面,它可以通过将电流引入接地来吸收高频信号。
因此,该滤波器能够通过电容器传递直流或低频信号,并在一定程度上削弱高频信号。
另一种常见的低通滤波器是巴特沃斯低通滤波器。
巴特沃斯滤波器是一种理想的滤波器,可以将部分高频信号完全剔除而不影响低频信号。
它的原理是将输入信号传递到一个多级滤波器网络中,其中每个级别都由电容、电感和电阻组成。
每个级别的电容和电感与频率有特定的关系,以实现对信号频谱的精确调控。
通过调整这些参数,可以实现不同级别的频率削弱和通带的增益。
高通滤波器的工作原理:高通滤波器是一种能够通过高频信号而抑制低频信号的滤波器。
其原理与低通滤波器相反,在信号频谱中只保留高频成分。
常见的高通滤波器有RC高通滤波器和巴特沃斯高通滤波器。
RC高通滤波器由电容和电阻组成,其工作原理与RC低通滤波器相似,只是电容和电阻的位置调换。
电容呈现出对高频信号的阻碍,而电阻则通过允许低频信号传递。
巴特沃斯高通滤波器与巴特沃斯低通滤波器类似,通过将输入信号传递到多级滤波器网络中,每个级别由电容、电感和电阻组成。
但是,在巴特沃斯高通滤波器中,电容和电感与频率的关系是相反的,可以精确控制信号频谱的通带和削弱。
带通滤波器的工作原理:带通滤波器是一种能够通过一定频率范围内的信号而抑制其他频率信号的滤波器。
其原理是选择性地通过带内信号,同时削弱带外信号。
最常见的带通滤波器是由一个低通滤波器和一个高通滤波器级联组成的。
低通滤波器负责削弱高频信号,高通滤波器负责削弱低频信号,而带通滤波器则保留两者之间的频率范围内的信号。
带通滤波器

摘要滤波器的功能是让一定频率范围内的信号通过,而将此频率范围之外的信号加以抑制或使其急剧衰减。
当干扰信号与有用信号不在同一频率范围之内,可使用滤波器有效的抑制干扰。
用LC网络组成的无源滤波器在低频范围内有体积重量大,价格昂贵和衰减大等缺点,而用集成运放和RC网络组成的有源滤波器则比较适用于低频,此外,它还具有一定的增益,且因输入与输出之间有良好的隔离而便于级联。
由于大多数反映生理信息的光电信号具有频率低、幅度小、易受干扰等特点,因而RC有源滤波器普遍应用于光电弱信号检测电路中。
关键字:滤波器;集成运放;RC网络;有源滤波器The function of the filter is to make certain frequency within the scope of the signal, and the frequency by outside the scope curbed the signal or sharp attenuation. When the disturbance signal and the useful signal not in the same frequency range, can use filter to suppress the interference effectively.With LC network consisting of passive filter in the low frequency within the area, volume weight expensive and attenuation shortcomings, but with integrated op-amp and RC network consisting of active filter is more applicable to low frequency, in addition, it also has some of the gain, and because between the input and output has good isolation and facilitate cascade. Since most reflect the photoelectric signal has a physical information low frequency and amplitude small, vulnerable to interference, and characteristics of the RC active filters widely applied electric light weak signal detection circuit.Filter;integrated op-amp;RC network;active filter引言滤波器的功能是让一定频率范围内的信号通过,而将此频率范围之外的信号加以抑制或使其急剧衰减。
带通滤波器的特点与应用案例

带通滤波器的特点与应用案例一、引言在现代电子通信和信号处理领域中,滤波器是一种非常重要的设备,它可以根据特定的频率范围对信号进行处理。
带通滤波器是滤波器的一种常见形式,它具有许多独特的特点和广泛的应用。
本文将详细介绍带通滤波器的特点,并结合实际应用案例进行说明。
二、带通滤波器的特点1. 频率选择性:带通滤波器可以选择特定的频率范围通过,而将其他频率范围的信号削弱或者完全阻断。
这种特点使得它可以用来消除噪声、提取特定频率的信号等。
2. 幅频响应曲线:带通滤波器的幅频响应曲线可以清楚地显示出其工作的频率范围,有助于我们理解滤波器的工作原理和选择合适的参数。
通常情况下,带通滤波器在其通带内有较大的增益,并在截止频率处呈现出明显的衰减。
3. 相频响应曲线:带通滤波器的相频响应曲线则表示信号传输延迟与频率之间的关系。
在某些特定应用场景中,对于信号的相位信息要求非常严格,因此带通滤波器的相频响应曲线也是需要关注的重要因素。
4. 传递函数:带通滤波器的传递函数可以用来描述输入信号和输出信号之间的关系。
我们可以通过对传递函数进行分析,来了解滤波器对于不同频率的信号的处理情况,从而根据需要进行参数的调整。
5. 滤波器的类型:带通滤波器有很多不同的类型,比如无源滤波器和有源滤波器、模拟滤波器和数字滤波器等。
每种类型的滤波器都有其独特的特点和适用范围,需要根据具体的应用需求进行选择。
三、带通滤波器的应用案例1. 语音信号处理:在语音信号处理中,带通滤波器常被用于语音信号的前端处理,以提取出特定频段的语音信号。
例如,在电话通信中,通过带通滤波器可以提取出人声的频率范围,减少环境噪声的干扰,从而提高通信质量。
2. 音频设备:在音频设备中,带通滤波器常被用于音频信号的调节和增强。
例如,在音响系统中,通过带通滤波器可以选择特定的频率范围,增加低频或高频的音响效果,使音乐更加丰富和逼真。
3. 图像处理:在图像处理中,带通滤波器可以用于图像增强和噪声去除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选频网络
放大电路
(+)
R C + Z2 R C + A - R1
F V
Rf
A V
V O
断开环路某一点,用瞬时 极性法判断可知,电路满足相 位平衡条件: a f 2nπ
V V i f
= -
此时若放大电路的电压增益为 AV 1 Rf 3 R1 则振荡电路满足振幅平衡条件 AV FV 3 1 1 3
GS
AV
AV 3
RDS
可变电阻区, 斜率随vGS不同 而变化
0.3 F
T CS146
R2 2.4k
C21
C22
C23
iD
AV FV 1 稳幅
vGS=0V -1V -2V -3V vDS
4. 稳幅措施
采用非线性元件
二极管 起振时
R2 R3 AV 1 3 R1
是R3、D1和D2并 其 中R3 联支路的等效电阻
反馈网络 F
9.6 RC正弦波振荡电路
1. 电路组成 2. RC串并联选频网络的选频特性 3. 振荡电路工作原理 4. 稳幅措施 5. 移相式正弦波振荡电路
1. 电路组成
RC桥式振荡电路 反馈网络兼做选频 网络
选频网络 放大电路
Z1
R C
F V
Rf + + A - R1
A V
V O
Z2
例题分析
例题分析
滤波器设计:1、电容的选取
fc(Hz) C 1~10 20~1 μF 10~102 1~0.1 μF 102~103 103~104 104~105 105~106 0.1~0.01 104~103 103~102 102~10 μF pF pF pF
2、由 取 R3=R4=R 则可由设计要求的fn选取 C ,并求得R; 再由设计要求的Avp求得R1;由设计要求的Q求得R2。 由上面的公式可以看出,调整C,可以单独调整fn, 对Avp和Q无引响;调整R1可以单独调整 Avp ;调整 R2可以单独调整 Q。这是该类滤波器的优点。
补充:无源滤波器
无源滤波器(即仅由R、L、C等元件组成而无放大器的滤波器)
补充:理想滤波器
理想滤波器的传递函数:
n的阶次即滤波器的阶次,阶次越高,越逼近理想 。分子分母都可以分解为若干个二次多项式(和一个 一次多项式, n为奇数)之积的形式。所以,只要会 设计一阶、二阶滤波器,串联起来就是多阶滤波器。
稳幅环节
稳幅原理
V o
R3
AV
AV 3
AV FV 1 稳幅
讨论
不符合相位条件
不符合幅值条件
1)是否可用共射放大电路? 2)是否可用共集放大电路? 3)是否可用共基放大电路? 4)是否可用两级共射放大电路?
输入电阻小、输出 电阻大,影响f0 可引入电压串联负反馈,使 电压放大倍数大于3,且Ri大、 Ro小,对f0影响小
# 振荡电路是单口网络,无须输入信号就能起振,起振的 信号源来自何处? 电路器件内部噪声以及电源接通扰动 噪声中,满足相位平衡条件的某一频率 0的噪声信号被 放大,成为振荡电路的输出信号。 当输出信号幅值增加到一定程度时,就要限制它继续增 加,否则波形将出现失真。
稳幅的作用就是,当输出信号幅值增加到一定程度时, 使振幅平衡条件从 AF 1 回到 AF 1 。
9.5 正弦波振荡电路的振荡条件
1. 振荡条件
正反馈放大 电路框图 (注意与负 反馈方框图 的差别)
X X X a i f X , 仍有稳定的输出。 ,X F 1 则 X 去掉 X 若环路增益 A a f o i
F F A AF 又A a f a f
1 的正弦波 2 πRC
Av
电路可以输出频率为 f 0
RC正弦波振荡电路一般用于产生频率低于 1 MHz 的正弦波
4. 稳幅措施
4. 稳幅措施
选频网络
热敏电阻
放大电路
采用非线性元件 热敏元件
Z1 R C + Z2 R C + A - R1
F V
Rf
A V
Rf 起振时, AV 1 3 R1 即 AV FV 1
o
C11 0.003 F Rp2 27k C12
Rp1 27k R1 2.4k
0.003 F
C13 0.3 F + A - Rp3 6.8 k R3 1k RP4 2.4k R5 10 k C3 10 F + vO D 稳幅环节
2CP11 R4 1 k
0.003 F
0.03 F
2 o
补充:关于Q与通频带宽度的关系
AVP K ( j ) n 2 2 2f 2 2 1 Q ( ) 1 Q ( ) fo n 在截止频率f L与f H 点, AVP AVP K ( j0.7 ) 2 2 2f 0.7 2 1 Q ( ) fo 2f 0.7 Q 1, fo 2f 0.7 fo Q
3
f
90 60 30 0 0.1 1 -30 -60 -90 (b) 10
当 0 1 或 f f0 1 RC 2πRC 幅频响应有最大值
FVmax 1 3
/ 0
相频响应 f 0
3. 振荡电路工作原理
1 当 0 时, f 0 RC
热敏电阻的作用
V o I o
V O
V V i f
= -
Rf 功耗 AV 3
Rf 温度
Rf 阻值
AV
AV FV 1 稳幅
4. 稳幅措施
采用非线性元件
场效应管(JFET) D 、R4 、C 3 整流滤波 T 为压控电阻 Rp3 AV 1 3 R3 RDS 稳幅原理 V V (负值)
9.5 正弦波振荡电路的振荡条件
a ( ) f ( ) 2nπ
9.5 正弦波振荡电路的振荡条件
3. 振荡电路基本组成部分
放大电路(包括负反馈放大电路) 反馈网络(构成正反馈的)
选频网络(选择满足相位平衡条件的一个频率。经常与反 馈网络合二为一。)
稳幅环节
Xa + Xf 放大电路 A Xo
相频响应 f arctg
0 ( 0) 0
3
2. RC串并联选频网络的选频特性
FV 1
f arctg
0 2 3 ( ) 0 0 ( ) 0
2
FV 0.4 0.3 0.2 0.1 0.1 0 1 (a)
1 3
10
/ 0
补充:按滤波器性能分类
补充:按滤波器性能分类
补充:关于Q与通频带宽度的关系
f0
补充:关于Q与通频带宽度的关系
( n )( n ) n n n n
2 2 n
在通带内,与n相比, ( n )很小,所以
n 2o,n , n n 2 o 2 2f 2 n o o fo
AVP
补充
• 在实际应用中滤波器的问题分为“分析”与“设 计” • 分析时,根据电路求出传递函数,归纳为“通式 ”的形式。与标准“通式”对比,便可知是哪种 滤波器(低通?…?);通带增益是多少;特征频率 是多少;是哪种性能(巴特沃思?…?) • 设计时,先选中滤波器电路形式(无限增益多路 反馈型?…?),再选电容器参数,然后根据 题目要 求的 参数,依其公式便可设计出其它电 路参数。
应为RC 串并联网路配一个电压放大倍数略大于3、输入电 阻趋于无穷大、输出电阻趋于0的放大电路。
9 信号处理与信号产生电路
9.1 滤波电路的基本概念与分类 9.2 一阶有源滤波电路 9.3 高阶有源滤波电路 *9.4 开关电容滤波器 9.5 正弦波振荡电路的振荡条件 9.6 RC正弦波振荡电路 9.7 LC正弦波振荡电路 9.8 非正弦信号产生电路
补充:电子信息系统框图
电子信息系统
第七章 传感器 接收器 隔离、滤 波、放大 第九章 运算、转 换、比较 信号的产生 A/D转换 功放 第八章 执行机构
作业
证明如图所示电路为带通滤波器。设计这个滤 波器,使其中心频率为1KHz,通频带宽度为 100Hz,通带内放大倍数为10。要求计算出各 个电阻与电容参数。图中运放选用μA741是否 可行?为什么?
9 信号处理与信号产生电路
9.1 滤波电路的基本概念与分类 9.2 一阶有源滤波电路 9.3 高阶有源滤波电路 *9.4 开关电容滤波器 9.5 正弦波振荡电路的振荡条件 9.6 RC正弦波振荡电路 9.7 LC正弦波振荡电路 9.8 非正弦信号产生电路
所以振荡条件为
A( ) F ( ) 1
振幅平衡条件
a ( ) f ( ) 2nπ 相位平衡条件
9.5 正弦波振荡电路的振荡条件
2. 起振和稳幅
起振条件
A( ) F ( ) 1
+ Xf Xa 放大电路 A Xo
a ( ) f ( ) 2nπ
反馈网络 F
补充:二阶滤波器的通式
其中Q为品质因数;α=1/ Q称为阻尼系数; ωn为特征角频率,对于带通和带阻滤波器是 中心频率; Avp是通带增益。
•对于实际频率来说S=jω 。 •对于低通、高通,其通式很容易理解。 •对于带通和带阻:Q=ω 0/B
f0
f0
补充:按滤波器性能分类
按滤波性能分类,滤波器又可分为:
通带截止频率
复习
3、理想滤波器的幅频特性
高通滤波器(HPF)
阻容耦合
带通滤波器(BPF)
通信电路
带阻滤波器(BEF))
抗已知频率的干扰
全通滤波器(APF))
f-φ转换
