相似多边形导学案
《相似多边形》导学案
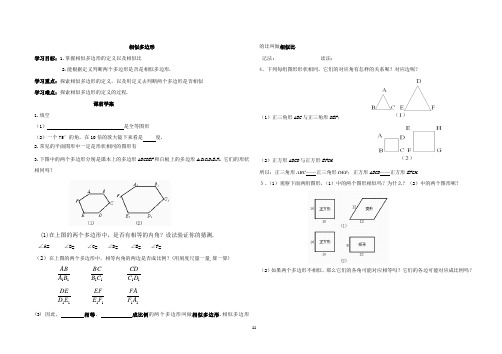
相似多边形学习目标:1.掌握相似多边形的定义以及相似比2.能根据定义判断两个多边形是否是相似多边形.学习重点:探索相似多边形的定义,以及用定义去判断两个多边形是否相似 学习难点:探索相似多边形的定义的过程. 课前学案 1.填空(1) 是全等图形. (2)一个75°的角,在10倍的放大镜下来看是 度. 2.常见的平面图形中一定是形状相同的图形有3.下图中的两个多边形分别是课本上的多边形ABCDEF 和白板上的多边形A 1B 1C 1D 1E 1F 1,它们的形状相同吗?(1)在上图的两个多边形中,是否有相等的内角?设法验证你的猜测. ∠A= ∠B= ∠C= ∠D= ∠E= ∠F=(2)在上图的两个多边形中,相等内角的两边是否成比例?(用刻度尺量一量,算一算)(3) 因此, 相等, 成比例的两个多边形叫做相似多边形.相似多边形 的比叫做相似比.记法: 读法:4、下列每组图形形状相同,它们的对应角有怎样的关系呢?对应边呢?(1)正三角形ABC 与正三角形DEF ;(2)正方形ABCD 与正方形EFGH.所以:正三角形ABC ——正三角形DEF ;正方形ABCD ——正方形EFGH .5、(1)观察下面两组图形,(1)中的两个图形相似吗?为什么?(2)中的两个图形呢?(2)如果两个多边形不相似,那么它们的各角可能对应相等吗?它们的各边可能对应成比例吗?111111111111A F FA F E EF E D DE D C CD C B BC B A AB课中案相关定义:1.六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的图形;它们的六个角都分别相等,称为____;六条边的比都相等,称为_____.2.(1)多边形相似需满足几个条件?(2)相似多边形的记法有什么要求?(3)什么叫相似比?求相似比要注意什么?题组一1.两个多边形相似的条件是()A.对应角相等 B.对应边相等C.对应角相等,对应边相等 D.对应角相等,对应边成比例2.在四边形ABCD与四边形A′B′C′D′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,•∠D=∠D′,且2''''''''3AB BC CD DAA B B C C D D A====,则四边形________∽四边形________,且它们的相似比是________.注意:相似比与顺序有关。
九年级数学浙教版上册4-6相似多边形导学案

1.以下几个命题:①四条边相等的四边形都相似;②四个角都相等的四边形都相似;③三条边相等的三角形都相似;④所有的正方形都相似.其中正确的有〔〕
A. 1个B. 2个C. 3个D. 4个
2.两个正方形的边长之比为1∶2,那么它们的周长之比是,面积之比是.
4.如图四边形ABCD∽四边形A'B'C'D',∠A=110°,∠B=95°,∠C=45°,AB=10cm,BC=14cm,A'B'=5cm,那么∠D'=°,B'C'=cm.
三、当堂练习
P153页作业题1、5、6
四、小结:
1、相似多边形的概念及性质
2、相似多边形的证明,性质的应用
当堂训练
课后作业
反思
相似多边形的概念及性质:
相似多边形的证明,性质的应用:
附件1:律师事务所反盗版维权声明
附件 2 : 独家资源交换签约 学校名录〔放大查看〕
学校 名录参 见: :// zx xk /wxt/l i s t. aspx ClassID=3060
课题
4.6相似多边形
学习目标
1、了解相似多边形的概念和性质
2、在简单情形下,能根据定义判断两个多边形相似
3、会用相似多边形的性质解决简单的几何问题
重点难点
重点相似多边形的定义与性质
难点相似多边形的判断.
【课前自学 课堂交流】
【课前自学】
一、仔细阅读P149~150页的内容,完成以下作业
1、一般地,两个多边形中做相似多边形。相似多边形
叫相似比。四边形ABCD与四边形EDFH相似记为
2、完成课内练习1、2、3
二、课中交流1、模仿Βιβλιοθήκη 150页例1,完成作业题3例题
4.6《相似多边形》导学案
4.6 相似多边形
学习目标:
了解相似多边形的概念和性质;在简单情形下,能根据定义判断两个多边形相似;会用相似多边形的性质解决简单的几何问题.
学习重难点:
重点是相似多边形的定义和性质;难点是判断两个多边形是否相似.
导学过程:
一、合作学习
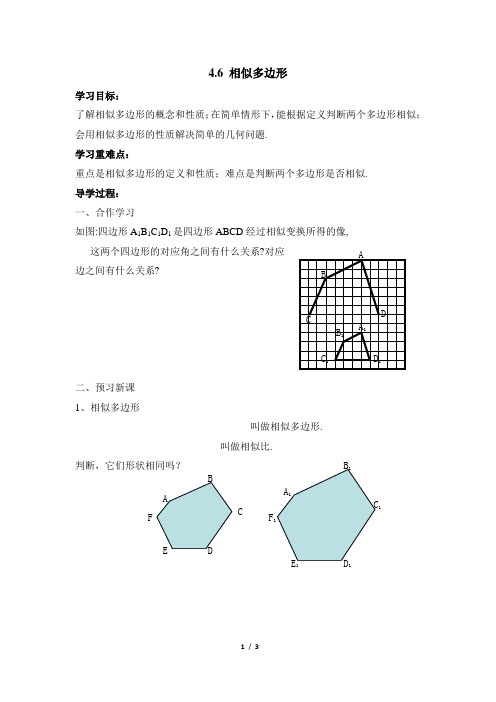
如图:四边形A1B1C1D1是四边形ABCD经过相似变换所得的像,
这两个四边形的对应角之间有什么关系?对应
边之间有什么关系?
二、预习新课
1、相似多边形
___________________________________叫做相似多边形. _____________________________叫做相似比.
判断,它们形状相同吗?A
B
C
D
A
1
B
1
C
1
D
1
C 1
1
1
F
1 / 3
2 / 3
2、练习
(1)它们相似吗? (2)它们呢?
3、相似多边形的性质
问题:如果两个多边形相似,那么它们的对应角有什么关系?对应边呢? 相似多边形的性质:
相似多边形的________相等,_________成比例.
相似多边形的__________等于相似比;__________等于相似比的平方. 4、例题学习
矩形纸张的长与宽的比为 2 ,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.
5、课内练习
(1)右面两个矩形相似,求它们对应边的比.
8
A
B
C
D
E
F
2
3。
北师大版九年级数学上册相似多边形导学案4.4
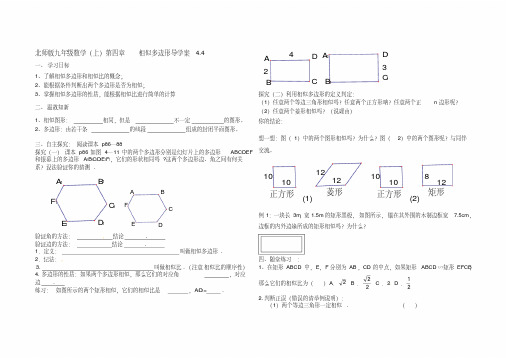
n 边形呢?
1、相似图形: 2、多边形:由若干条
相同,但是 的线段
不一定
的图形。
组成的封闭平面图形。
你的结论:
三、自主探究: 阅读课本 p86—88 探究(一) 课本 p86 如图 4— 11 中的两个多边形分别是幻灯片上的多边形 ABCDEF 和银幕上的多边形 A1B1C1D1E1F1,它们的形状相同吗 ?这两个多边形边、角之间有何关 系?设法验证你的猜测 .
△△ A1B1C1 与△ ABC 的相似比是 ( )
A. 5∶4
B. 4∶5
C. 5∶2
D. 2 ∶5
3.以下的结论中:①所有的正方形都相似;②所有的矩形都相似;③所有的三角形
都相似;④所有的等腰三角形都相似;⑤所有的直角三角形都相似;⑥所有的等腰
直角三角形都相似;⑦所有的等边三角形都相似;⑧所有的正五边形都相似;其中
验证角的方法:
结论
.
验证边的方法:
结论
.
1.定义:
叫做相似多边形 .
2.记法:
3.
叫做相似比 . (注意 相似比的顺序性)
4. 多边形的性质:如果两个多边形相似,那么它们的对应角
,对应
边.
练习: 如图所示的两个矩形相似,它们的相似比是
, A1D1=
.
四、随堂练习 : 1、在矩形 ABCD 中, E, F 分别为 AB ,CD 的中点,如果矩形 ABCD ∽矩形 EFCB,
那么它们的相似比为( ) A. 2 B . 2 C . 2 D . 1
2
2
2. 判断正误(错误的请举例说明): (1)两个等边三角形一定相似 .
()
( 2)两个全等多边形一定相似 . ( 3)各边对应成比例的两个四边形一定相似 . ( 4)各角对应相等的两个四边形一定相似 .
相似多边形导学案1

《4.5相似多边形》导学案学习目标:探索相似多边形的性质并会运用性质解决有关问题。
课中导学【一】自学新知:阅读教材118-119页例题之前,完成下列填空。
1、的两个多边形叫做相似多边形。
如图六边形ABCDEF与六边形A1B1C1D1E1F1相似记为_____________________2、相似多边形的________________________比叫做它们的相似比。
3、在记两个多边形相似时,要注意___________________________。
4、如图,四边形ABCD∽四边形A1B1C1D1,且11BAAB=k(1)由定义可知,相似多边形的对应角对应边。
(2)的周长四边形的周长四边形1111DCBAABCD=(3)将两个四边形对应的分割为两个三角形①△ABC与△A1B1C1相似吗?为什么?②S△ABC与S△A1B1C1有什么关系?S△ACD与S△A1C1D1呢?③S四边形ABCD︰S四边形A1B1C1D1=___5、对于一般的相似多边形也有相同的结论吗?小结:相似多边形的对应角,对应边,周长比等于它们的,面积比等于它们的。
【三】新知应用:1、如果四边形ABCD∽四边形EFGH相似,且∠A=68°,则∠E= ________ 。
2、一个多边形的边长分别是2、3、4、5、6,另一个和它相似的多边形的最短边长为6,则这个多边形的最长边为____________ 。
3、下列说法中正确的是()A、所有的矩形都相似B、所有的正方形都相似C、所有的菱形都相似D、所有的等腰梯形都相似E、所有的正多边形都相似F、所有的直角三角形都相似G、所有的等腰直角三角形都相似【四】例题解析:例.矩形纸张的长与宽的比为2,对开后所得的矩形纸张是否与原来的矩形纸相似?请说明理由.思考:某种纸张有以下特征:每次对折后,所得到的长方形均与原长方形相似。
这种纸张的长与宽满足什么条件?达标测评1、两个多边形相似的条件是()A 对应角相等B 对应边成比例C 对应角相等或对应边成比例D 对应角相等且对应边成比例2、两个相似六边形的周长分别是l1,l2,面积分别是S1,S2,若 l1:l2=2︰3,S2-S1=30,则S1=_________,S2=___________.3、在一张比例尺为1︰3000的地图上,一块多边形区域的周长是4㎝,面积是1㎝2,这个区域的实际周长为__________,面积为__________。
北师大八下数学相似多边形导学案

相似多边形学习目标、重点、难点【学习目标】1、 相似多边形的定义;2、 相似多边形的特征;【重点难点】相似多边形的定义和特征.知识概览图相似多边形⎩⎨⎧相似多边形的特征相似多边形的定义 新课导引观察下图所示的图形.【问题探究】观察上述三组图形,每组图形的对应角和对应边之间有什么关系?【点拨】每组图形的对应角相等,对应边的比相等.教材精华知识点 相似多边形各角对应相等、各边对应成比例的两个多边形叫做相似多边形.拓展 这个定义跟其他定义一样,有两个功能:一方面,如果两个多边形的角都对应相等,且边都对应成比例,那么我们就可以判定这两个多边形是相似的;另一方面,如果已知两个多边形相似,那么它们的对应角一定相等,对应边一定成比例,这是相似多边形的本质特征,用它可以解决有关的问题.相似多边形的表示方法:若五边形ABCDE 与五边形E D C B A '''''相似,记作:五边形ABCDE ∽五边形E D C B A '''''.相似多边形对应边的比叫做相似比.拓展 (1)“多边形”的“多”字包含3或3以上的所有自然数,所以有了相似多边形的定义,就不必再重新定义“相似三角形”“相似四边形”…….(2)前面我们学过图形的全等,全等其实是相似的一个特例,全等图形是相似比为l 的相似图形. 多边形相似的判定:(1)边数相同;(2)对应角相等;(3)对应边成比例.拓展 (1)判定两个多边形相似,这三个条件缺一不可.(2)两个边数不相同的多边形一定不相似.相似多边形的特征:如果两个边数相同的多边形相似,那么这两个多边形的对应角相等,对应边成比例.相似多边形特征的应用:应用相似多边形的特征,可以证明角相等、线段成比例. 课堂检测基础知识应用题 1、(1)正三角形ABC 与正三角形DEF 相似吗?(2)正方形ABCD 与正方形EFGH 相似吗?综合应用题2、如图4-33所示,梯形ABCD 与梯形D C B A ''''相似,求未知边x ,y ,z 的长度和角α,β的度数.探索创新题3、小强将一张报纸对折后,发现对折后的半张报纸与整张报纸相似,则整张报纸的长和宽的比是 ( )A .2∶lB .4∶1C .2∶1D .∶l体验中考1、如图4-35所示,若△ABC ∽△DEF ,则∠D 的度数为 .学后反思附: 课堂检测及体验中考答案课堂检测1、分析 根据相似多边形的定义和等边三角形、正方形的性质来判定.解:(1)由于正三角形的每个内角都等于60°,所以∠A =∠D =60°,∠B =∠E =60°,∠C =∠F =60°.由于正三角形的三条边都相等,所以FD CA EF BC DE AB ==.所以正三角形ABC 与正三角形DEF 相似. (2)由于正方形的每个内角都是直角,所以∠A =∠E =90°,∠B =∠F =90°,∠C =∠G =90°,∠D =∠H =90°.由于正方形的四条边都相等,所以EHAD GH CD FG BC EF AB ===, 所以正方形ABCD 与正方形EFGH 相似.【解题策略】 根据相似多边形的定义来确定.2、分析 解题中要充分利用相似多边形的特征和梯形的性质.解:由于梯形ABCD 与梯形D C B A ''''相似,所以对应边成比例,所以 4.5 4.8324 3.22x y z ====, 所以x =3,y =6,z =3.由于对应角相等,所以α=∠D =180°-∠A =180°-62°=118°,β=∠B =180°-∠C =180°- 110°=70°.【解题策略】 准确掌握相似多边形的特征及梯形上、下底平行这一条件是解决此题的关键.3、分析 抓住题中的关键:整张报纸和半张报纸相似,设原报纸的长为x ,宽为y ,则对折后得到的半张报纸的长为y ,宽为x 21,如图4-34所示,由相似多边形的定义知AB AD AE AB =,所以y 2=x ·x 21,所以2122=x y ,所以2x y=. 故选A.体验中考1、分析 本题考查相似三角形的性质.∵△ABC ∽△DEF ,∴∠A =∠D .又∵∠A =30°,∴∠D =30°.故填30°.【解题策略】 相似多边形(包括三角形)的对应角相等.。
最新北师大版初中八年级数学《4.4 相似多边形》导学案

ACB(2)(1)(3)A DCBA DECBFED HGFEA1E1D1C1B1北师大版初中八年级数学《4.4 相似多边形》导学案一、学习目标: 1.经历探索相似多边形概念的过程,知道相似多边形的对应角相等,对应边成比例。
2.在探索相似多边形的过程中,进一步发展归纳、类比、反思、交流等方面的能力,提高数学思维水平,体会反例的作用。
二、教学重难点:重点: “相似多边形定义”的理解与应用.难点:“对应边成比例”的理解与正确运用.三、教学过程(一)、复习引入1、全等图形的定义?2、全等三角形的边、角各有什么特点?(二)、初步探究1、你能发现每一对图形中有什么共同特征吗?2、观察下列三组图形有什么共同特征?CFD EB A 3、下面两个图形之间,角有什么关系?边有什么联系?4、在小组合作、班内交流的基础上,类比全等给出: ①相似多边形的定义 ②表示法 ③相似比的定义(三)、议一议:它们是相似多边形吗? 1、任意两个等边三角形; 2、任意两个正方形;的两个正多边形一定相似。
3、任意两个菱形;的两个菱形一定相似。
4、任意两个矩形;的两个矩形一定相似。
5、如图,点E 、F 分别是等腰梯形ABCD 两腰的中点, 梯形AEFD 和梯形EBCF 相似吗? (四)、想一想1、只满足各角对应相等的两个多边形一定相似吗?2、只满足各边对应成比例的两个多边形一定相似吗?3、如果两个多边形要相似,需要满足哪些条件? 反过来会怎样?1、如果两个多边形相似,那么它们的对应角有什么关系? 对应边呢?2、如果两个多边形不相似,那么它们的角有可能对应相等吗? 它们的各边可能对应成比例吗?3、多边形相似和多边形全等有什么关系?A 1E 1D 1C 1B 1ADECBE AD F BC(五)、应用与延伸1、如图,五边形ABCDE ∽五边形A ´B ´C ´D ´E ´。
则∠ E = ,∠ A ´= ,C ´D ´= ;五边形A ´B ´C ´D ´E ´与五边形ABCDE 的相似比为 。
相似多边形的性质导学案

相似多边形的性质导学案一、导学1.课题导入:问题1:形状相同的两个多边形相似吗?问题2:怎样从数学的角度刻画“形状相同”呢?这节课我们一起来探究相似多边形.2.学习目标:(1)知道相似多边形的性质,并能判定两个多边形是否是相似的.(2)知道相似比,能根据相似多边形的性质进行相关的计算.3.学习重点,难点:重点:相似多边形的性质.难点:相关的计算.二、分层学习第一层次学习1.自学指导(1)自学内容:相似多边形.(2)自学时间:6分钟.(3)自学方法:阅读教材并完成自学参考提纲,然后同桌之间交流.(4)自学参考提纲:①相似多边形的定义:如果两个多边形的边数______,角______,边_____,那么这两个多边形相似.②相似比:相似多边形________的比称为相似比,全等的两个图形的相似比为______.③如图,△ABC与△DEF中,∠ACB=∠DFE=90°,∠A=∠D,则△ABC与△DEF相似吗?为什么?④如图所示的两个三角形相似吗?为什么?2.自学:学生参考自学指导进行自学.3.助学:(1)师助生:①明了学情:关注学生对定义的理解.②差异指导:根据学情进行指导.(2)生助生:小组间相互合作,共同研讨.4.强化:(1)相似多边形的定义.(2)点两名学生口答第③、④题,并点评.第二层次学习1.自学指导(1)自学内容:P26例题.(2)自学时间:6分钟.ABC53FD E21.5(3)自学方法:自主探究后合作交流.(4)自学参考提纲:①相似多边形的性质:相似多边形的对应角______,对应边______.②如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.由已知四边形ABCD和EFGH相似,结合图形可确定:α与是对应角,直接求α,∠A与是对应角,再根据四边形的内角和求β= °.由18,24是对应边,21与x是对应边,在根据对应边成比例,可得方程,解方程得x= .③如图所示的两个五边形相似,求a,b,c,d的值.2.自学:学生参考自学指导进行自学..3.助学(1)师助生:①明了学情:观察学生能否利用相似多边形的性质解决问题.②差异指导:指导学困生寻找对应元素.(2)生助生:小组合作交流.4.强化:(1)多边形相似的性质.(2)最大边(角)与最大边(角);最小边(角)与最小边(角)是对应边(角).(3)方程思想的运用.三、评价1.学生学习的自我评价:这节课你有哪些收获?还有哪些方面的不足?2.教师对学生的评价:(1)表现性评价:从学习态度、注意力状况小组合作等方面评价.(2)纸笔评价:课堂评价检测.3.教师的自我评价(教学反思).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1相似多边形
一、学习目标
1通过实例认识图形的相似;知道全等形与相似形的联系与区别,了解相似多边形和相
似比。
2、能识别两个相似多边形的对应顶点、对应角和对应边,会求相似多边形的相似比。
3、会用符号表示相似多边形及它们的对应元素,写出对应边之间的比例式,发展学生的
符号意识。
二、导学精练
1两个矩形一定相似。
()2 .两个正方形一定相似.()3 .任意两个菱形都相似.()4 .有一
个角相等的两个菱形相似.()5 .边数不同的多边形一定不相似. ()
三、规律与技巧
若两个多边形相似,则它们的对应角相等,对应边成比例。
相似形必须满足的两个条件:对应角相等,对应边成比例。
四、当堂达标
1.下列说法正确的是()
A.所有的三角形都相似
B.所有的正方形都相似
C.所有的菱形都相似
D.所有的矩形都相似
2•下列四组图形中必相似的是()
A.有一组邻边相等的两个平行四边形
B.有一个角相等的两个等腰梯形
C.对角线互相垂直的两个矩形 D .对角线互相垂直且相等的两个四边形相似
3.若五边形ABCDE s五边形MNOPQ,且AB=12, MN =6, AE=7,贝U MQ= _____________ .
4.一个六边形六边长分别为3, 4, 5, 6, 7, 8,另一个与它相似的六边形的最短边
为6,则其周长为 _______ .
5 .矩形ABCD 与矩形EFGH 中,AB=4, BC=2, EF=2, FG=1,则矩形ABCD 与矩
形EFGH _________ 相似(填一定”或不一定”)
6.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之
比为__________ .
7 .如图,图(1 )是一个正六边形ABCDEF,使线段BC、FE的长增加相等的数,
得图(2),将图(1)中的点A、D分别向两边拉长相等的量,得图(3).那么
【MeiWei 81重点借鉴文档】
图(1)与图(2)相似吗?图(1)与图(3)相似吗?图(2)与图(3)呢?为什 AD=5cm,试求梯形 ABCD 的各角的度数与 A 'D B 'C '的长. 21 •世纪R 教育网
[MeiWei 81重点借鉴文档】
A'B'C'D 相似, / A ' =65 °A B ' =J3n, AB=8cm
,
8 •如图,等腰梯形 ABCD 与等腰梯形。
