三棱柱的展开图
展开与折叠(3种题型)-2023年新七年级数学核心知识点与常见题型(北师大版)(解析版)

展开与折叠(3种题型)【知识梳理】一.几何体的展开图(1)多数立体图形是由平面图形围成的.沿着棱剪开就得到平面图形,这样的平面图形就是相应立体图形的展开图.同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,同时也可看出,立体图形的展开图是平面图形.(2)常见几何体的侧面展开图:①圆柱的侧面展开图是长方形.②圆锥的侧面展开图是扇形.③正方体的侧面展开图是长方形.④三棱柱的侧面展开图是长方形.(3)立体图形的侧面展开图,体现了平面图形与立体图形的联系.立体图形问题可以转化为平面图形问题解决.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.二.展开图折叠成几何体通过结合立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.三.专题:正方体相对两个面上的文字(1)对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想象.(2)从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.(3)正方体的展开图有11种情况,分析平面展开图的各种情况后再认真确定哪两个面的对面.【考点剖析】一.几何体的展开图(共9小题)1.(2022秋•江汉区期末)下列平面图形中,是棱柱的展开图的是()A.B.C.D.【分析】依据棱柱的所有的面的形状以及位置,即可得到棱柱的表面展开图.【解答】解:A.该平面图形不能围成棱柱,故本选项错误;B.该图是棱柱表面展开图,故本选项正确;C.该平面图形不能围成棱柱,故本选项错误;D.该平面图形不能围成棱柱,能围成圆柱,故本选项错误.故选:B.【点评】本题考查了几何体的展开图以及棱柱的结构特征,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.2.(2022秋•南京期末)如图是一个正方体的表面展开图,在这个正方体中,与点B重合的点为()A.点C和点D B.点A和点E C.点C和点E D.点A和点D【分析】根据图形,把正方体展开图折叠成正方体,观察得到重合的点.【解答】解:在这个正方体中,与点B重合的点为点C和点D.故选:A.【点评】本题考查了几何体的展开图,掌握折叠后的正方体的图形是关键.3.(2022秋•莲湖区期末)诗语同学周末帮妈妈拆完快递后,将包装盒展开,进行了测量,结果如图所示.已知长方体盒子的长比宽多3cm,高是2cm.(1)求长方体盒子的长和宽.(2)求这个包装盒的体积.【分析】(1)利用图中关系首先求出宽,然后求出长;(2)用体积公式即可.【解答】解:(1)宽为:(14﹣2×2)÷2=5(cm),长为:5+3=8(cm);(2)8×5×2=80(cm3).【点评】本题考查的是几何体的展开图,解题的关键是求出长和宽.4.(2022秋•鹤壁期末)如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.(1)制作这样的包装盒需要多少平方厘米的硬纸板?(2)若1平方米硬纸板价格为元,则制作10个这样的包装盒需花费多少钱?(不考虑边角损耗)【分析】(1)根据长方体的表面积公式计算即可;(2)根据题意列式计算即可.【解答】解:(1)由题意得,2×(12×6+12×6+6×6)=360cm2;答:制作这样的包装盒需要360平方厘米的硬纸板;(2)360÷10000×5×10=1.8元,答:制作10个这样的包装盒需花费1.8元钱.【点评】本题考查了几何体的表面积,正确的计算出长方体的表面积是解题的关键.5.(2022秋•和平区期末)某校积极开展文明校园的创建活动,七年级学生设计了正方体废纸回收盒,如图所示,将写有“收”字的正方形添加到图中,使它们构成完整的正方体展开图,共有种添加方式.【分析】根据正方体表面展开图的特征进行判断即可.【解答】解:“收”字分别放在“垃”“圾”“分”“类”下方均可成完整的正方体展开图,所以有4种添加方式.故答案为:4.【点评】本题主要考查了正方体的展开图特点,掌握正方体表面展开图的特征是正确判断的关键.6.(2022秋•江阴市期末)如图是一个正方体纸盒,下面哪一个可能是它的表面展开图()A.B.C.D.【分析】正方体的空间图形,从相对面入手,分析及解答问题.B,D与此不符,所以错误;再观察3个图案所在的位置,而选项C不符,正确的是A.故选:A.【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.7.(2022秋•二道区校级期末)图①,图②,图③均为5×5的正方形网格,在网格中选择2个空白的正方形涂上阴影,使它们与图中四个有阴影的正方形一起构成一个正方体的表面展开图,并且3种方法得到的展开图不相同.【分析】依据正方体展开图的特征进行判断,即可得到3种不同的正方体展开图.【解答】解:如图所示:(答案不唯一)【点评】此题主要考查了几何体的展开图,关键是掌握正方体展开图的结构特点.8.(2022秋•伊川县期末)如图,是一个几何体的表面展开图:(1)请说出该几何体的名称;(2)求该几何体的表面积;(3)求该几何体的体积.【分析】(1(2)依据长方体的表面积等于六个面面积之和即可得出结论;(3)依据体积计算公式,即可得到该几何体的体积.【解答】解:(1)该几何体的名称是长方体;(2)该几何体的表面积为:2×(2×3+2×1+1×3)=22(平方米);(3)该几何体的体积为:2×3×1=6(立方米).【点评】本题考查了几何体的展开图,掌握立体图形与平面图形的转化,建立空间观念是关键.9.(2022秋•仪征市期末)将一个无盖正方体展开成平面图形的过程中,需要剪开条棱.【分析】根据无盖正方体的棱的条数以及展开后平面之间应有棱连着,即可得出答案.【解答】解:∵无盖正方体有5个表面,两个面共一条棱,共8条棱,要展成如图所示图形必须4条棱连接,∴要剪8﹣4=4条棱,故答案为:4.【点评】此题主要考查了正方体的展开图的性质,根据展开图的性质得出要展成如图所示图形必须4条棱连接,是解题关键.二.展开图折叠成几何体(共9小题)10.(2022秋•沈河区期末)如图,如果裁掉一个正方形后能折叠成正方体,那么能裁掉的是()A.①B.②和③C.③和④D.②或③或④【分析】根据正方体的展开图得出结论即可.【解答】解:由正方体的展开图可知,去掉②或③或④原图都可以折叠成正方形,故选:D.11.(2022秋•高新区期末)下列图形经过折叠不能成为一个封闭的正方体的是()A.B.C.D.【分析】根据正方体的展开图得出结论即可.【解答】解:由题意知,图形不能折叠成正方体,故选:D.【点评】本题主要考查正方体的展开图,熟练掌握正方体的展开图是解题的关键.12.(2022秋•青秀区校级期末)如图平面图形不能折成无盖长方体盒子的是()A.B.C.D.【分析】根据长方体展开图得出结论即可.【解答】解:由题意知,图形不能折成无盖长方体盒子,故选:C.【点评】本题主要考查长方体展开图的知识,熟练掌握长方体展开图的知识是解题的关键.13.(2022秋•晋江市期末)图①是正方体的表面展开图,该正方体从图①所示的位置折叠成图②的正方体,在图①标注的顶点A、B、C、D中,与点P重合的顶点是()A.点A B.点B C.点C D.点D【分析】先找出下面,然后折叠,找出正方形ABCD位于正方体的哪个面上,点P所在正方形位于正方体的哪个面上,即可找出与点P重合的顶点.【解答】解:如图:以正方形1为下面,将正方体从图①所示的位置折叠成图②的正方体时,正方形ABCD位于正方形的上面,点P所在正方形在前面,点B与点P重合.故选:B.【点评】本题考查正方形的展开图和空间想象能力,关键是找出或想象出折叠前后图形的关系.14.(2022秋•秦淮区期末)下列图形中,能通过折叠围成一个三棱柱的是()A.B.C.D.【分析】根据三棱柱及其表面展开图的特点对各选项分析判断即可得解.【解答】解:A、折叠后两侧面重叠,不能围成三棱柱,故本选项错误;B、折叠后能围成三棱柱,故本选项正确;C、底面有2个三角形,不能折叠围成一个三棱柱,故本选项错误;D、展开图有3个底面,不能围成三棱柱,故本选项错误.故选:B.【点评】本题考查了三棱柱表面展开图,上、下两底面应在侧面展开图长方形的两侧,且是全等的三角形,15.(2022秋•姜堰区期末)小明在学习了《展开与折叠》这一课后,掌握了长方体盒子的制作方法.如图是他制作的一个半成品的平面图:(1)在中补充一个长方形,使该平面图能折叠成一个长方体盒子;(2)已知小明制作长方体的盒子长是宽的2倍,宽是高的2倍,且长方体所有棱长的和为56cm,求这个长方体盒子的体积.【分析】(1)根据长方体的展开图补充图形即可求解;(2)根据题意,设长方体的高为a,则宽为2a,长为4a,根据长方体所有棱长的和为56cm,列出方程,进而根据体积公式即可求解.【解答】解:(1)如图所示,(2)设长方体的高为acm,则宽为2acm,长为4acm,根据题意得,4(a+2a+4a)=56(cm),解得:a=2,∴这个长方体的高为2cm,宽为4cm,长为8cm,∴这个长方体盒子的体积为:2×4×8=64(cm3).【点评】本题考查了长方体的展开图,一元一次方程的应用,掌握以上知识是解题的关键.16.(2022秋•宛城区校级期末)某“综合实践”小组开展了“长方体纸盒的制作”实践活动,他们利用边长为a(cm)的正方形纸板制作出两种不同方案的长方体盒子(图1为无盖的长方体纸盒,图2为有盖的长方体纸盒).【操作一】根据图1方式制作一个无盖的长方体盒子.方法:先在纸板四角剪去四个同样大小边长为b (cm)的小正方形,再沿虚线折合起来.【问题解决】(1)若a=12cm,b=3cm,则长方体纸盒的底面积为;【操作二】根据图2方式制作一个有盖的长方体纸盒.方法:先在纸板四角剪去两个同样大小边长为b (cm)的小正方形和两个同样大小的小长方形,再沿虚线折合起来.【拓展延伸】(2)若a=12cm,b=2cm,该长方体纸盒的体积为;(3)现有两张边长a均为30cm的正方形纸板,分别按图1、图2的要求制作无盖和有盖的两个长方体盒子,若b=5cm,求无盖盒子的体积是有盖盒子体积的多少倍?【分析】(1)由折叠可得底面是边长为6cm的正方形,进而求出底面积即可;(2)由展开与折叠可知,折叠成长方体的长、宽、高分别为a﹣2b,,b,根据体积公式进行计算即可;(3)当a=30cm,b=5cm时,分别求出按图1,图2的折叠方式所得到的长方体的体积即可.【解答】解:(1)如图1,若a=12cm,b=3cm,则长方体纸盒的底面是边长为12﹣3×2=6(cm)的正方形,因此面积为6×6=36(cm2),故答案为:36cm2;(2)如图2,先在纸板四角剪去两个同样大小边长为b(cm)的小正方形和两个同样大小的小长方形,再沿虚线折合起来可得到长为a﹣2b,宽为,高为b的长方体,当a=12cm,b=2cm,该长方体纸盒长为12﹣2×2=8(cm),宽为=4(cm),高为2cm,所以体积为8×4×2=64(cm3),故答案为:64cm3;(3)当a=30cm,b=5cm时,按图1作无盖的长方体的纸盒的体积为(30﹣5×2)(30﹣5×2)×5=2000(cm3),按图2作的长方体的纸盒的体积为(30﹣5×2)()×5=1000(cm3),2000÷1000=2(倍),答:无盖盒子的体积是有盖盒子体积的2倍.【点评】本题考查展开图折叠成几何体,掌握棱柱的展开图的特征是正确解答的前提,根据展开图得出折叠后长方体的长、宽、高是解决问题的关键.17.(2022秋•昆明期末)图(1)和图(2)中所有的正方形都相同,将图(1)的正方形放在图(2)中的①②③④⑤某一位置,所组成的图形不能围成正方体的位置是()A.①②B.②③C.③④D.②⑤【分析】由平面图形的折叠及正方体的表面展开图的特点解题.【解答】解:将图1的正方形放在图2中的②⑤的位置出现重叠的面,所以不能围成正方体.故选:D.【点评】本题考查了展开图折叠成几何体,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意:只要有“田”字格的展开图都不是正方体的表面展开图.熟记正方体的11种展开图是解题的关键.18.(2022秋•阳泉期末)小明在学习了正方体的展开图后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀剪开了一个长方体纸盒,可是一不小心多剪开了一条棱,把纸盒剪成了两部分,如图1、图2所示.请根据你所学的知识,回答下列问题:观察判断:小明共剪开了条棱;动手操作:现在小明想将剪断的图2重新粘贴到图1上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒(如图3),请你帮助小明在图1中补全图形;解决问题:经过测量,小明发现这个纸盒的底面是一个正方形,其边长是长方体的高的5倍,并且纸盒所有棱长的和是880cm,求这个纸盒的体积.【分析】(1)根据平面图形得出剪开棱的条数,(2)根据长方体的展开图的情况可知有四种情况,(3)设最短的棱长高为acm,则长与宽相等为5acm,根据棱长的和是880cm,列出方程可求出长宽高,即可求出长方体纸盒的体积.【解答】解(1)小明共剪了8故答案为:8.(2)如图,四种情况.(3)∵长方体纸盒的底面是一个正方形,∴设最短的棱长高为acm,则长与宽相等为5acm,∵长方体纸盒所有棱长的和是880cm,∴4(a+5a+5a)=880,解得a=20,∴这个长方体纸盒的体积为20×100×100=200000(立方厘米).【点评】本题主要考查了几何展开图,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.三.专题:正方体相对两个面上的文字(共7小题)19.(2022秋•泗阳县期末)动手操作:做一个正方体木块,在正方体的各面分别写上1,2,3,4,5,6这6个不同的数字,若它可以摆放成如图所示的两种不同位置,请你判断数字5对面的数字是()A.1B.2C.3D.6【分析】根据图形以及数字的摆放,第一图可得6的下面为1,1的右边为4,第二个图可知4的下面是5,5的右边是2【解答】解:根据图形以及数字的摆放,第一图可得6的下面为1,1的右边为4,第二个图可知4的下面是5,5的右边是2,将正方形展开如图所示,∴5的对面是6,故选:D.【点评】本题考查了正方体展开图,相对面上的字,注意数字的摆放是解题的关键.20.(2022秋•溧水区期末)如图是一个正方体的平面展开图,若该正方体相对两个面上的数相等,则a+b+c =.【分析】利用正方体及其表面展开图的特点解题.【解答】解:由图可知,c+1=3,1+b=1,a=﹣2,所以a=﹣2,b=0,c=2,所以a+b+c=0.故答案为:0.【点评】本题考查了正方体相对两个面上的文字,解答本题的关键在于注意正方体的空间图形,从相对面入手,分析及解答问题.21.(2022秋•高邮市期末)一个正方体的6个面上分别标有字母a、b、c、d、e、f.若甲、乙两位同学分别在f、e朝上时,看到的另两个字母如图,则b对面的是.【分析】根据第一个图形和第二个图形中都含有d的面,即可判断.【解答】解:由题意可知d字母所在面相邻的面上的字母分别为a、c、e、f,则d的对面是b.即b对面的是d.故答案为:d.【点评】本题考查了正方体相对两个面上的文字,同时也考查了空间想象能力和推理能力.正确记忆立方体的特点是解题关键.22.(2022秋•川汇区期末)党的二十大报告提出,要以中国式现代化全面推进中华民族伟大复兴.将“中国式现代化”这六个字分别写在一个正方体的六个表面上,如图是它的一种展开图,则与“式”相对的字是()A.中B.国C.现D.代【分析】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此作答.【解答】解:∵正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,∴在此正方体上与“式”字相对的面上的汉字是“中”.故选:A.【点评】本题考查了正方体的展开图形,掌握相对面进行分析及解答是关键.23.(2022秋•青神县期末)如果一个骰子相对两面的点数之和为7,它的表面展开图如图所示,则下面判断正确的是()A.A代表B.B代表C.C代表D.B代表【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点对各选项分析判断后利用排除法求解.【解答】解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,A与点数是1的对面,B与点数是2的对面,C与点数是4的对面,∵骰子相对两面的点数之和为7,∴A代表的点数是6,B代表的点数是5,C代表的点数是3.故选:A.【点评】本题考查了正方体相对两个面上的文字,掌握从相对面入手是关键.24.(2022秋•汉台区期末)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数之和为7,求x﹣y+z的值.【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端是对面判断即可.【解答】解:由图可知:z与4相对,y与﹣2相对,x与12相对,由题意得:z+4=7,y+(﹣2)=7,x+12=7,∴z=3,y=9,x=﹣5,∴x﹣y+z=﹣5﹣9+3=﹣11,∴x﹣y+z的值为﹣11.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.25.(2022秋•青神县期末)一个立方体的六个面上分别标上一至六点(一个小圆表示一点,每个面上的点数不同),然后将完全一样的四个立方体摆放成如图样式的一个长方体,我们能看到的面上的点数如图所示,则长方体底面上的点数之和是.【分析】先判断出相对的面的点数,再进行计算即可.【解答】解:由题意可知,“3点”的面的邻面有“2点、6点、4点、5点”,所以与“3点”相对的面的点数为“1点”;因为“4点”的面的邻面有“6点、5点、3点、1点”,所以与“4点”相对的面的点数为“2点”;因为“6点”的面的邻面有“3点、1点、4点、2点”,所以与“6点”相对的面的点数为“5点”;所以长方体底面上的点数之和是:4+1+5+2=12.故答案为:12.【点评】本题考查了正方体相对两个面上的文字,关键是弄清每个骰子六面点数之和是几,每个骰子看见面的点数之和是几.【过关检测】一.选择题(共4小题)1.(2022•河南三模)某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“豫”字所在面相对的面上的汉字是()A.老B.南C.河D.家【分析】根据正方体的平面展开图找相对面的方法,同层隔一面判断即可.【解答】解:在原正方体中,与“豫”字所在面相对的面上的汉字是“家”,故选:D.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的平面展开图找相对面的方法是解题的关键.2.(2022•金坛区二模)某几何体的表面展开图如图所示,这个几何体是()A.圆柱B.长方体C.四棱锥D.五棱锥【分析】根据四棱锥的侧面展开图得出答案.【解答】解:这个几何体由四个三角形和一个正方形围成,故这个几何体为四棱锥.故选:C.【点评】此题主要考查了几何体的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.3.(2022•梧州模拟)下列在立体图形中,它的侧面展开图是扇形的是()A.正方体B.长方体C.圆柱D.圆锥【分析】根据常见立体图形的侧面展开图判断即可得出答案.【解答】解:A选项,正方体的侧面展开图是长方形,故该选项不符合题意;B选项,长方体的侧面展开图是长方形,故该选项不符合题意;C选项,圆柱的侧面展开图是长方形,故该选项不符合题意;D选项,圆锥的侧面展开图是扇形,故该选项符合题意;故选:D.【点评】本题考查了几何体的展开图,掌握常见几何体的侧面展开图:①圆柱的侧面展开图是长方形.②圆锥的侧面展开图是扇形.③正方体的侧面展开图是长方形是解题的关键.4.(2022•丰台区二模)如图,下列水平放置的几何体中,侧面展开图是扇形的是()A.B.C.D.【分析】根据几何体的展开图:三棱柱的侧面展开图是三个长方形;四棱柱的侧面展开图是四个长方形;圆柱的侧面展开图是矩形;圆锥的侧面展开图是扇形;可得答案.【解答】解:AB、侧面展开图是四个长方形,故此选项不符合题意;C、侧面展开图是一个长方形,故此选项不符合题意;D、侧面展开图是扇形,故此选项符合题意.故选:D.【点评】本题考查了几何体的展开图,记住常用几何体的侧面展开图是解题的关键.二.填空题(共3小题)5.(2022•晋中一模)“双奥之城”指既举办过夏季奥运会又举办过冬季奥运会的城市.2008年北京夏季奥会之后,2022年北京冬季奥运会成功举办,使北京成为世界上首座“双奥之城”.下列正方体展开图的每个面上都标有一个汉字,把它们折成正方体后,与“双”字相对面上的汉字是.【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端是对面,判断即可.【解答】解:与“双”字相对面上的汉字是城,故答案为:城.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.6.(2021秋•息县期末)根据表面展开图依次写出立体图形的名称:、、.【分析】根据表面展开图的形状判断即可.【解答】解:圆锥的表面展开图是一个扇形和圆,四棱锥的表面展开是一个四边形和四个三角形,三棱柱的表面展开是三个长方形和两个三角形.【点评】本题考查立体图形的表面展开,熟悉各几何体表面展开的形状是求解本题的关键.7.(2021秋•绵阳期末)如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“y”一面与相对面上的代数式相等,则有“xy2”一面与相对面上的代数式的和等于0(用数字作答).【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端对面,判断即可.【解答】解:由图可知:y与2y﹣3相对,xy2与﹣3xy相对,由题意得:y=2y﹣3,∴y=3,∴xy2+(﹣3xy)=9x+(﹣9x)=0,∴有“xy2”一面与相对面上的代数式的和等于0,故答案为:0.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.三.解答题(共5小题)8.(2021秋•武功县期末)如图是正方体的平面展开图,若将图中的平面展开图折叠成正方体后,相对面上的两个数之和为7,求x﹣y+z的值.【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端是对面判断即可.【解答】解:由图可知:z与4相对,y与﹣2相对,x与12相对,由题意得:z+4=7,y+(﹣2)=7,x+12=7,∴z=3,y=9,x=﹣5,∴x﹣y+z=﹣5﹣9+3=﹣11,∴x﹣y+z的值为﹣11.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据正方体的表面展开图找相对面的方法是解题的关键.9.(2021秋•临汾期末)阅读与思考请阅读下列材料,并完成相应的任务:任务:(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置是;A.字母B B.字母A C.字母R D.字母T(2)若在图③中,网格中每个小正方形的边长为1,求包装盒的表面积.【分析】(1)根据长方体的表面展开图找相对面的方法,同层隔一面,判断即可;(2)根据长方体的表面积公式进行计算即可解答.【解答】解:(1)在图②中,若字母Q表示包装盒的上表面,字母P表示包装盒的侧面,则下表面在包装盒表面展开图中的位置:字母B,故答案为:A;(2)由题意得:2×3×2+2×3×1+2×2×1=12+6+4=22,∴包装盒的表面积为22.【点评】本题考查了正方体相对两个面上的文字,熟练掌握根据长方体的表面展开图找相对面的方法是解题的关键.10.(2021秋•渠县期末)如图,是底面为正方形的长方体的表面展开图,折叠成一个长方体,那么:(1)与N重合的点是哪几个?(2)若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?【分析】(1)把展开图折叠即可得出答案;。
第5讲 直棱柱及表面展开图

第5讲直棱柱及表面展开图【知识要点】1.由若干个平面围成的几何体叫多面体;多面体上相邻两个面之间的交线叫多面体的棱;几个面的公共顶点叫多面体的顶点。
2.棱柱的上下底面平行且全等,每个侧面都是平行四边形。
3.根据侧棱与底面是否垂直,棱柱分为直棱柱和斜棱柱,直棱柱的每个侧面都是长方形(含正方形)。
4.根据底面多边形的边数,直棱柱可分为直三棱柱、直四棱柱……长方体和正方体都是直四棱柱。
5.欧拉公式:V+F-E=2(V:顶点数,F: 面数,E: 棱数)。
6.几何体的表面积=侧面积+底面积(上、下底的面积和)7.常见的几种几何体的表面积的计算公式①圆柱体表面积:2πR2+2πRh (R为圆柱体上下底圆半径,h为圆柱体高)②长方体表面积:2(ab+ah+bh)(a为长方体的长,b为长方体的宽,h为长方体的高③正方体表面积:6a2(a为正方体棱长)8.几何体的展开图:(1)同一个立体图形按不同的方式展开,得到的平面展开图是不一样的,立体图形的展开图是平面图形。
(2)常见几何体的侧面展开图:①圆柱的侧面展开图是长方形.②圆锥的侧面展开图是扇形.③正方体的侧面展开图是长方形.④三棱柱的侧面展开图是长方形.从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.9.正方体相对两个面上文字:(1)对于此类问题一般方法是用纸按图的样子折叠后可以解决,或是在对展开图理解的基础上直接想像。
(2)正方体的展开图有11种情况,分析平面展开图的各种情况后再认真确定哪两个面的对面.【典型例题】〖讨论1〗在长、宽都是3,高是8的长方体纸箱的外部,一只蚂蚁从顶点A沿纸箱表面爬到顶点B点,那么它所行的最短路线的长是____________.〖讨论2〗如图是一个正方体纸盒的展开图,当折叠成正方体纸盒时,A点与_______点重合,C点与_______点重合.〖讨论3〗一个简单多面体的各个面都是三角形,请你说明它的顶点数V和面数F之间的关系为F=2V-4.学力训练一.选择题(共15小题)1.下列各几何体中,直棱柱的个数是()A.5B.4C.3D.22.七棱柱的侧面是()第3题A.长方形B.七边形C.三角形D.正方形3.如图所示,在长方体中,与棱AB平行的棱有()A.1条B.2条C.3条D.4条4.下列关于棱柱的说法:①棱柱的所有面都是平面;②棱柱的所有棱长都相等;③棱柱的所以侧面都是长方形或正方形;④棱柱的侧面个数与底面边数相等;⑤棱柱的上、下底面形状、大小相等其中正确的有()A.2个B.3个C.4个D.5个5.一个直棱柱有12个顶点,那么它的面的个数是()A.10个B.9个C.8个D.7个6.一个棱柱有18条棱,那么它的底面一定是()A.十八边形B.八边形C.六边形D.四边形7.(2012•台湾)如图1为图2中三角柱ABCEFG的展开图,其中AE、BF、CG、DH是三角柱的边.若图1中,AD=10,CD=2,则下列何者可为AB长度?()A. 2B. 3C. 4D. 5第7题第8题第9题8.(2012•佛山)一个几何体的展开图如图所示,这个几何体是()A.三棱柱B.三棱锥C.四棱柱D.四棱锥9.(2011•台湾)若下列只有一个图形不是右图的展开图,则此图为何?()A.B.C.D.10.(2011•呼和浩特)将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是()A.B.C.D.11. (2012•德州)如图给定的是纸盒的外表面,下面能由它折叠而成的是()A.B.C.D.12.(2011•河北)将图1围成图2的正方体,则图1中的红心“”标志所在的正方形是正方体中的()A.面CDHE B.面BCEF C.面ABFG D.面ADHG13.(2010•宁波)骰子是一种特的数字立方体(见图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是()A.B.C.D.二.填空题(共2小题)14.已知三棱柱有5个面6个顶点9条棱,四棱柱有6个面8个顶点12条棱,五棱柱有7个面10个顶点15条棱,…,由此可以推测n 棱柱有_________个面,_________个顶点,棱有_________条.15.一个直棱柱有7个面,则它有________个顶点,________条棱,表面上至少有______个直角.三.解答题(共6小题)16.(2010•宁波)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:(1)根据上面多面体模型,完成表格中的空格:多面体顶点数(V)面数(F)棱数(E)四面体 4 4长方体8 6 12正八面体8 12正十二面体20 12 30你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_________.(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是_________.(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.17..下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.图号顶点数x 棱数y 面数z(a)8 12 6(b)(c)(d)(e)(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表;(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.18.如图1所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图2所示.已知展开图中每个正方形的边长为1.(1)求在该展开图中可画出最长线段的长度这样的线段可画几条?(2)试比较立体图中∠BAC与平面展开图中∠B′A′C′的大小关系?19.如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整.(请画出三种)20.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)21.如图是一个正方体的展开图,标注了字母“a”的面是正方体的正面,如果正方体相对两个面上的代数式的值相等,求x、y的值.22.一个简单多面体的各个面都是五边形,请你说明它的顶点数V和面数F满足以下关系式:2V=3F+4。
人教版七年级数学上册4.1.3展开图

Zx.xk
-2
3 -4 1
A 3x-2
有一个正方体,在它的各个面上分别涂了白、 红、黄、兰、绿、黑六种颜色。甲、乙、丙三 位同学从三个不同的角度去观察此正方体,结 果如下图,问这个正方体各个面的对面的颜色 是什么?
黑 红兰
甲
白 黄红
乙
绿 兰黄 丙
1、学会了从不同方向观察立体图形。
第三类,中间二连方,两侧各有二个,只有一种。“222”型
第四类,两排各三个,只有一种。“33”型
Zx.xk
结果:共有种1情1况
注意:不能有:"z"型,“田字”型,“缺口”型,“一五”型,“六”型,
试一试
1.下面六个正方形连在一起的图形,经折叠后 能围成正方体的图形有哪几个?(动手试试)
A
B
C
D
正方体
Zx.xk
长方体
四棱锥
三棱柱
2.下列图形能折叠成什么立体图形?
圆
五
柱
棱
1
柱
2
圆
三
锥
棱
柱
4 3
5 三棱柱
223465
用剪刀把正方体纸盒按任意方式沿棱 展开,你能得到哪些不同的展开图?
第一类,中间四连方,两侧各一个, 共六种。"141"型
1
2
3
4
5
6
第二类,中间三连方,两侧各有一、二个,共三种。“231”型
初中数学课件
金戈铁骑整理制作
4.三棱柱展开图
三棱柱
立体图形和平面图形有何关系?
展开 立体图形平面图形 Z.x.x.K
围成
利用你手中所制作的卡片模型,观察这些 平面展开图可以分为几类,每一类展开图 及其原来的几何图形有什么特点?
棱柱PPT教学课件

直平行六面体
平
行
长 正方体 方
体
六 面 体
四棱柱
柱体的体积公式:V柱体 =Sh
全面积公式=底面积+侧面积
长方体的对角线性质:
长方体一条对角线的长的平方等于 一个顶点上三条棱的长的平方和.
练习
正三棱柱ABC A1B1C1底边边长为10,过底边一边AB, 作与底面ABC成60的截面交CC1于D,求截面面积
这刻不知道下刻的命, 它有泪只往心里咽, 眼里飘来一道鞭影, 它抬起头望望前面。
臧克家其人
• 臧克家(1905~ ) 现代诗人。山东诸 城人。有诗集《烙印》(1933)、《罪恶的 黑手》(1934) 。代表作《有的人》 。
• 前期诗歌以经过锤练的诗句,抒写旧中 国农民的苦难与不幸,勤劳与坚忍,具 有真实、精练、含蓄的艺术风格,能让 读者从咀嚼和回味中体会诗人深沉的感 情A1源自B1C1EA
D
B
C
一个斜三棱柱ABC A1B1C1底面边长为4的正三角形, 侧 棱 长 为5, 若 侧 棱 和 底 面 三 角 形相 邻 两 边 都 成45 ,
求这个三棱柱的体积
A1
B1
C1
A
O
B
E
C
正三棱柱
A
C
B
正三棱柱的侧面展开图
A'
C'
B'
A
C
B
A
A'
C'
B'
A'
老马
总得叫大车装个够, 它横竖不说一句话, 背上的压力往肉里扣, 它把头沉重地垂下!
第2节,写扬鞭出发
• 前两句是虚写,刻画老 马的悲愤而又无望的心 理。后两句写实,“一 道鞭影”,活现出主人 的凶狠、无情。在这样 严酷的压迫下,在“前 面”等待老马的又是什 么呢?诗人给读者留下 了无限的想象空间。
2022年中考数学真题分项汇编(全国通用) :视图与投影、尺规作图、命题与定理(解析版)

专题16 视图与投影、尺规作图、命题与定理一.选择题1.(2022·山东临沂)如图所示的三棱柱的展开图不可能...是()A.B.C.D.【答案】D【分析】三棱柱的表面展开图的特点,由三个长方形的侧面和上下两个三角形的底面组成.从而可得答案.【详解】解:选项A、B、C均可能是该三棱柱展开图,不符合题意,而选项D中的两个底面会重叠,不可能是它的表面展开图,符合题意,故选:D.【点睛】考查了几何体的展开图,动手折叠一下,有助于空间想象力的培养.2.(2022·江苏常州)如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是()A.垂线段最短B.两点确定一条直线C.过一点有且只有一条直线与已知直线垂直D.过直线外一点有且只有一条直线与已知直线平行【答案】A【分析】根据垂线段最短解答即可.【详解】解:行人沿垂直马路的方向走过斑马线,体现的数学依据是垂线段最短,故选:A.【点睛】本题考查垂线段最短,熟知垂线段最短是解答的关键.3.(2022·广西贵港)下列命题为真命题的是()A a=B.同位角相等C.三角形的内心到三边的距离相等D.正多边形都是中心对称图形【答案】C【分析】根据判断命题真假的方法即可求解.【详解】解:当0a<a-,故A为假命题,故A选项错误;当两直线平行时,同位角才相等,故B为假命题,故B选项错误;三角形的内心为三角形内切圆的圆心,故到三边的距离相等,故C为真命题,故C选项正确;三角形不是中心对称图形,故D为假命题,故D选项错误,故选:C.【点睛】本题考查了真假命题的判断,熟练掌握其判断方法是解题的关键.4.(2022·湖南邵阳)下列四个图形中,圆柱体的俯视图是()A.B.C.D.【答案】D【分析】根据俯视图是从上面看到的视图进而得出答案即可.【详解】解:竖直放置的圆柱体,从上面看是圆,所以俯视图是圆.故选∶D.【点睛】此题考查了简单几何体的三视图,解题的关键是熟练掌握圆柱体的三视图.5.(2022·湖北鄂州)如图所示的几何体是由5个完全相同的小正方体组成,它的主视图是()A.B.C.D.【答案】A【分析】根据从正面看到的图形是主视图,即可得.【详解】解:从前面看,第一层是两个小正方形,第二层左边一个小正方形,第三层左边1个小正方形,故选A.【点睛】本题考查了简单几何体的三视图,解题的关键是掌握从正面看到的图形是主视图.6.(2022·辽宁锦州)下列命题不正确...的是()A.经过直线外一点,有且只有一条直线与这条直线平行B.负数的立方根是负数C.对角线互相垂直的四边形是菱形D.五边形的外角和是360︒【答案】C【分析】由平行线公理、立方根的定义、菱形的判定定理、多边形的外角和,分别进行判断,即可得到答案.【详解】解:A、经过直线外一点,有且只有一条直线与这条直线平行;故A正确;B、负数的立方根是负数;故B正确;C、对角线互相垂直的平行四边形是菱形,故C错误;D、五边形的外角和是360︒,故D正确;故选:C【点睛】本题考查了判断命题的真假,以及考查了平行线公理、立方根的定义、菱形的判定定理、多边形的外角和,解题的关键是掌握所学的知识,正确的进行判断.7.(2022·内蒙古通辽)下列命题:①()3235m n m n⋅=;②数据1,3,3,5的方差为2;③因式分解()()3x x x x x-=+-;④平分弦的直径垂直于弦;则1 422x.其≥中假命题的个数是()A.1B.3C.2D.4【答案】C【分析】根据积的乘方,方差的计算,多项的因式分解,垂径定理的推论,二次根式有意义的条件,逐项判断即可求解.【详解】解:①()3362m n m n ⋅=,故原命题是假命题; ②数据1,3,3,5的平均数为()1133534+++= ,所以方差为()()()()222211333335324⎡⎤-+-+-+-=⎣⎦,是真命题; ③()()()324422x x x x x x x -=-=+-,是真命题;④平分弦(不是直径)的直径垂直于弦,故原命题是假命题;10x -≥,即1≥x ,是真命题;∴假命题的个数是2.故选:C【点睛】本题主要考查了积的乘方,方差的计算,多项的因式分解,垂径定理的推论,二次根式有意义的条件,熟练掌握相关知识点是解题的关键.8.(2022·山东威海)过直线l 外一点P 作直线l 的垂线PQ .下列尺规作图错误的是( )A .B .C .D .【答案】C【分析】根据线段垂直平分线的逆定理及两点确定一条直线一一判断即可.【详解】A 、如图,连接AP 、AQ 、BP 、BQ ,AP=BP,AQ=BQ,∴点P在线段AB的垂直平分线上,点Q在线段AB的垂直平分线上,∴直线PQ垂直平分线线段AB,即直线l垂直平分线线段PQ,本选项不符合题意;B、如图,连接AP、AQ、BP、BQ,AP= AQ,BP =BQ,∴点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,∴直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,本选项不符合题意;C、C项无法判定直线PQ垂直直线l,本选项符合题意;D、如图,连接AP、AQ、BP、BQ,AP= AQ,BP =BQ,∴点A在线段PQ的垂直平分线上,点B在线段PQ的垂直平分线上,∴直线AB垂直平分线线段PQ,即直线l垂直平分线线段PQ,本选项不符合题意;故选:C.【点睛】本题考查作图-复杂作图,线段垂直平分线的逆定理及两点确定一条直线等知识,读懂图像信息是解题的关键,属于中考常考题型.9.(2022·湖南长沙)如图,在ABC中,按以下步骤作图:①分别过点A 、B 为圆心,大于12AB 的长为半径画弧,两弧交于P 、Q 两点; ②作直线PQ 交AB 于点D ;③以点D 为圆心,AD 长为半径画弧交PQ 于点M 、连接AM 、BM .若AB =AM 的长为( )A .4B .2 CD【答案】B 【分析】根据作图可知PM 垂直平分AB ,12DM AB =,ABM 是等腰直角三角形,据此即可求解.【详解】解:由作图可得PM 垂直平分AB ,12AD DM AB ===则ADM 是等腰直角三角形∴由勾股定理得:2AM =故选:B .【点睛】本题考查了作垂线,等腰直角三角形的性质,勾股定理,掌握基本作图理解题意是解题的关键.11.(2022·贵州毕节)在ABC 中,用尺规作图,分别以点A 和C 为圆心,以大于12AC 的长为半径作弧,两弧相交于点M 和N .作直线MN 交AC 于点D ,交BC 于点E ,连接AE .则下列结论不一定正确的是( )A .AB AE =B .AD CD =C .AE CE =D .ADE CDE ∠=∠【答案】A【分析】根据作图可知AM =CM ,AN =CN ,所以MN 是AC 的垂直平分线,根据垂直平分线的性质,线段垂直平分线上的点到线段两端的距离相等,且平分此点到线段两端构成的夹角,分别对各选项进行判断.【详解】由题意得,MN 垂直平分线段AC ,∴AD CD =,AE CE =,ADE CDE ∠=∠所以B 、C 、D 正确,因为点B 的位置不确定,所以不能确定AB =AE ,故选 A【点睛】本题考查了线段垂直平分线,熟练掌握线段垂直平分线的作图方法和性质是解题的关键. 10.(2022·四川广安)下列说法正确的是( )A .对角线相等的四边形是矩形.B .相似三角形的面积的比等于相似比.C .方差越大,数据的波动越大;方差越小,数据的波动越小.D .过一点有且只有一条直线与已知直线平行.【答案】C【分析】根据矩形的判定,相似三角形的性质,方差的意义,平行公理逐项分析判断即可求解.【详解】解:A. 对角线相等的平行四边形是矩形,故该选项不正确,不符合题意;B. 相似三角形的面积的比等于相似比的平方,故该选项不正确,不符合题意;C. 方差越大,数据的波动越大;方差越小,数据的波动越小,故该选项正确,符合题意;D. 同一平面内,过直线外一点有且只有一条直线与已知直线平行,故该选项不正确,不符合题意; 故选C【点睛】本题考查了矩形的判定,相似三角形的性质,方差的意义,平行公理,掌握相关知识是解题的关键.12.(2022·山东烟台)如图,是一个正方体截去一个角后得到的几何体,则该几何体的左视图是( )A .B .C .D .【答案】A【分析】根据左视图是从左面看到的图形判定则可.【详解】解:从左边看,可得如下图形:故选:A.【点睛】本题考查三视图、熟练掌握三视图的定义是解决问题的关键.13.(2022·山东聊城)如图,该几何图形是沿着圆锥体的轴切割后得到的“半个”圆锥体,它的左视图是()A.B.C.D.【答案】B【分析】根据左视图的定义及画法即可判定.【详解】解:从左边看该几何体是一个斜边在左侧的直角三角形,故选:B.【点睛】本题考查画简单几何的三视图,熟练掌握和运用简单几何三视图的画法是解决本题的关键.14.(2022·内蒙古赤峰)下面几何体的俯视图是()A.B.C.D.【答案】B【分析】俯视图是从物体的上面看得到的视图.【详解】圆台的俯视图是一个同心圆环.故选:B.【点睛】本题考查几何体的三视图,主要考查学生空间想象能力及对立体图形的认知能力.15.(2022·黑龙江)如图是由若干个相同的小正方体搭成的一个几何体的左视图和俯视图,则所需的小正方体的个数最多是()A.7B.8C.9D.10【答案】B【分析】这个几何体共有2层,由俯视图可得第一层小正方体的个数,由左视图可得第二层小正方体的最多个数,再相加即可.【详解】由俯视图可知最底层有5个小正方体,由左视图可知这个几何体有两层,其中第二层最多有3个,+=个.那么搭成这个几何体所需小正方体最多有538故选:B.【点睛】本题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.16.(2022·广西贵港)一个圆锥如右图所示放置,对于它的三视图,下列说法正确的是()A.主视图与俯视图相同B.主视图与左视图相同C.左视图与俯视图相同D.三个视图完全相同【答案】B【分析】根据三视图的定义即可求解.【详解】解:主视图为等腰三角形,左视图为等腰三角形,俯视图为有圆心的圆,故主视图和左视图相同,主视图俯视图和左视图与俯视图都不相同,故选:B.【点睛】本题考查了几何体的三视图,掌握三视图的定义,会看得出三视图是解题的关键.17.(2022·山东青岛)如图①.用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.图②“堑堵”的俯视图是()A.B.C.D.【答案】C【分析】根据几何体的俯视图是从上面看进行判断解答即可.【详解】解:由图可知,该“堑堵”的俯视图是,故选:C.【点睛】本题考查几何体的俯视图,理解俯视图的概念是解答的关键.18.(2022·辽宁)如图所示的几何体是由4个完全相同的小正方体搭成的,它的主视图是()A.B.C.D.【答案】C【分析】根据几何体的三视图可直接进行排除选项.【详解】解:由题意得:该几何体的主视图为;故选C.【点睛】本题主要考查三视图,熟练掌握几何体的三视图是解题的关键.19.(2022·辽宁营口)如图是由五个相同的正方体搭成的几何体,这个几何体的左视图是()A.B.C.D.【答案】B【分析】左视图是从物体的左边观察得到的图形,结合选项进行判断即可.【详解】解:从左边看,有两列,从左到右第一列是两个正方形,第二列底层是一个正方形.故选:B.【点睛】本题考查了简单组合体的三视图,属于基础题,解答本题的关键是掌握左视图的定义.20.(2022·广西玉林)如图是由4个相同的小正方体组成的几何体,它的主视图是()A.B.C.D.【答案】B【分析】根据几何体的三视图可进行求解.【详解】解:由题意可知该几何体的主视图为;故选B.【点睛】本题主要考查三视图,熟练掌握三视图是解题的关键.21.(2022·四川广安)如图所示,几何体的左视图是()A.B.C.D.【答案】B【分析】根据从正面看的图形是主视图,从左面看到的图形是左视图,从上面看到的图形是俯视图判断即可.【详解】解:几何体的左视图是故选:B.【点睛】本题考查了几何体的三视图的知识,从正面看的图形是主视图,从左面看到的图形是左视图,从上面看到的图形是俯视图.掌握以上知识是解题的关键.22.(2022·内蒙古呼和浩特)图中几何体的三视图是()A.B.C.D.【答案】C【分析】根据图示确定几何体的三视图即可得到答案.【详解】由几何体可知,该几何体的三视图为故选C【点睛】本题考查了简单几何体的三视图,掌握三视图的视图方位及画法是解题的关键,注意实际存在又没有被其他棱所挡,在所在方向看不到的棱应用虚线表示.23.(2022·贵州遵义)如图是《九章算术》中“堑堵”的立体图形,它的左视图为()A.B.C.D.【答案】A【分析】根据左视图的意义和画法可以得出答案.【详解】解:∵该几何体为放倒的三棱柱,∴根据左视图的画法,从左往右看,看到的是一个直角在左边的直角三角形,故选:A.【点睛】本题考查简单几何体的三视图,熟练掌握简单几何体的三视图是解答本题的关键.从正面、上面和左面三个不同的方向看一个物体,并描绘出所看到的三个图形,即几何体的三视图.24.(2022·黑龙江哈尔滨)六个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.【答案】D【分析】根据从左边看得到的图形是左视图,可得答案.【详解】解:从左边看下面一层是两个小正方形,上面一层左边一个小正方形,故选:D.【点睛】本题主要考查左视图,掌握三视图是解题的关键.25.(2022·吉林)吉林松花石有“石中之宝”的美誉,用它制作的砚台叫松花砚,能与中国四大名砚媲美.下图是一款松花砚的示意图,其俯视图为()A.B.C.D.【答案】C【分析】根据俯视图的定义(从上面观察物体所得到的视图)即可得.【详解】解:其俯视图是由两个同心圆(不含圆心)组成,即为,故选:C.【点睛】本题考查了俯视图,熟记定义是解题关键.26.(2022·江苏泰州)如图为一个几何体的表面展开图,则该几何体是()A.三棱锥B.四棱锥C.四棱柱D.圆锥【答案】B【分析】底面为四边形,侧面为三角形可以折叠成四棱锥.【详解】解:由图可知,底面为四边形,侧面为三角形,∴该几何体是四棱锥,故选:B.【点睛】本题主要考查的是几何体的展开图,熟记常见立体图形的展开图特征是解题的关键.27.(2022·贵州贵阳)如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是()A.B.C.D.【答案】B【分析】根据圆锥体的立体图形判断即可.【详解】用平行底面的平面截圆锥体,截面是圆形,故选:B.【点睛】本题考查了截面图形的判断,具有一定的空间想象力是解答本题的关键.28.(2022·江苏常州)下列图形中,为圆柱的侧面展开图的是()A.B.C.D.【答案】D【分析】根据题意,注意其按圆柱的侧面沿它的一条母线剪开,分析得到图形的性质,易得答案.【详解】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,得到其侧面展开图是对边平行且相等的四边形;又有母线垂直于上下底面,故可得是矩形.故选:D.【点睛】本题考查的是圆柱的展开图,解题的关键是需要对圆柱有充分的理解;难度不大.29.(2022·四川内江)如图是正方体的表面展开图,则与“话”字相对的字是()A.跟B.党C.走D.听【答案】C【分析】根据正方体表面展开图的特征进行判断即可.【详解】解:由正方体表面展开图的“相间、Z端是对面”可知,“话”与“走”是对面,故答案为:C.【点睛】本题考查正方体相对两个面上的文字,掌握正方体表面展开图的特征是正确判断的前提.30.(2022·北京)下面几何体中,是圆锥的为()A.B.C.D.【答案】B【分析】观察所给几何体,可以直接得出答案.【详解】解:A选项为圆柱,不合题意;B选项为圆锥,符合题意;C选项为三棱柱,不合题意;D选项为球,不合题意;故选B.【点睛】本题考查常见几何体的识别,熟练掌握常见几何体的特征是解题的关键.圆锥面和一个截它的平面,组成的空间几何图形叫圆锥.31.(2022·广西)下列几何体中,主视图为矩形的是()A.B.C.D.【答案】C【分析】根据常见几何体的主视图,依次判断即可.【详解】A.该三棱锥的主视图为中间有条线段的三角形,故不符合题意;B.该圆锥的主视图为三角形,故不符合题意;C.该圆柱的主视图为矩形,故符合题意;D.该圆台的主视图为梯形,故不符合题意;故选:C.【点睛】本题考查常见几何体的三视图,掌握常见几何体的三视图是解答本题的关键.32.(2022·湖北恩施)下图是一个正方体纸盒的展开图,将其折叠成一个正方体后,有“振”字一面的相对面上的字是()A.“恩”B.“乡”C.“村”D.“兴”【答案】D【分析】根据正方体的平面展开图的特点即可得.【详解】解:由正方体的平面展开图的特点得:“恩”字与“乡”字在相对面上,“施”字与“村”字在相对面上,“振”字与“兴”字在相对面上,故选:D.【点睛】本题考查了正方体的平面展开图,熟练掌握正方体的平面展开图的特点是解题关键.33.(2022·四川广元)如图是某几何体的展开图,该几何体是()A.长方体B.圆柱C.圆锥D.三棱柱【答案】B【分析】根据几何体的展开图可直接进行排除选项.【详解】解:由图形可得该几何体是圆柱;故选B.【点睛】本题主要考查几何体的展开图,熟练掌握几何体的展开图是解题的关键.34.(2022·湖北武汉)如图是由4个相同的小正方体组成的几何体,它的主视图是()A.B.C.D.【答案】A【分析】根据从正面所看得到的图形为主视图,据此解答即可.【详解】解:从正面可发现有两层,底层三个正方形,上层的左边是一个正方形.故选:A.【点睛】本题主要考查了三视图的知识,掌握主视图是从物体的正面看得到的视图成为解答本题的关键.35.(2022·四川凉山)如图所示的几何体的主视图是()A.B.C.D.【分析】根据主视图的定义(从正面观察物体所得到的视图叫主视图)即可得.【详解】解:这个几何体的主视图是故选:C.【点睛】本题考查了主视图,熟记定义是解题关键.36.(2022·四川泸州)如图是一个由6个大小相同的正方体组成的几何体,它的俯视图是()A.B.C.D.【答案】C【分析】观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形即可判定.【详解】解:由俯视图的定义可知:从上往下观察发现∶故选C.【点睛】本题考查三视图,解题的关键是熟练掌握俯视图是从物体上面看所得到的图形.37.(2022·浙江湖州)如图是由四个相同的小正方体组成的几何体,它的主视图是()A.B.C.D.【答案】D【分析】主视图就是从主视方向看到的正面的图形,也可以理解为该物体的正投影,据此求解即可.【详解】解:观察该几何体发现:从正面看到的应该是三个正方形,上面左边1个,下面2个,【点睛】本题考查了简单组合体的三视图,解题的关键是了解主视图的定义,属于基础题,难度不大.38.(2022·四川眉山)下列立体图形中,俯视图是三角形的是()A.B.C.D.【答案】B【分析】俯视图是从物体上面看所得到的图形,据此判断得出物体的俯视图.【详解】解:A、圆锥体的俯视图是圆,故此选项不合题意;B、三棱柱的俯视图是三角形,故此选项符合题意;C、球的俯视图是圆,故此选项不合题意;D、圆柱体的俯视图是圆,故此选项不合题意;故选:B.【点睛】本题考查了几何体的三视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.39.(2022·浙江台州)如图是由四个相同的正方体搭成的立体图形,其主视图是()A.B.C.D.【答案】A【分析】找到几何体的正面看所得到的图形即可.【详解】解:从几何体的正面看可得如下图形,故选:A.【点睛】此题主要考查了简单几何体的三视图,关键是掌握主视图是从正面所看到的图形.40.(2022·黑龙江绥化)下列命题中是假命题的是()A.三角形的中位线平行于三角形的第三边,并且等于第三边的一半B.如果两个角互为邻补角,那么这两个角一定相等C.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D.直角三角形斜边上的中线等于斜边的一半【答案】B【分析】利用三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质分别判断后即可确定正确的选项.【详解】解:A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半,是真命题,故此选项不符合题意;B. 如果两个角互为邻补角,那么这两个角不一定相等,故此选项是假命题,符合题意;C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,是真命题,故此选项不符合题意;D. 直角三角形斜边上的中线等于斜边的一半,是真命题,故此选项不符合题意;故选:B【点睛】考查了命题与定理的知识,解题的关键是了解三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质.41.(2022·广西河池)下列几何体中,三视图的三个视图完全相同的几何体是()A.B.C.D.【答案】D【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可.【详解】解:A.三棱柱的俯视图与主视图和左视图都不同,故此选项错误;B.圆柱的俯视图与主视图和左视图不同,故此选项错误;C.圆锥的俯视图与主视图和左视图不同,故此选项错误;D.球的三视图完全相同,都是圆,故此选项正确.故选:D.【点睛】本题主要考查了三视图的有关知识,注意三视图都相同的常见的几何体有球和正方体.42.(2022·辽宁锦州)如图是某几何体的三视图,该几何体是( )A .B .C .D .【答案】C【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.【详解】解:主视图和左视图都是等腰三角形,那么此几何体为锥体,由俯视图为圆,可得此几何体是圆锥.故选:C .【点睛】本题考查了由三视图判断几何体,主视图和左视图的大致轮廓为三角形的几何体为锥体. 43.(2022·内蒙古呼和浩特)以下命题:①面包店某种面包售价a 元/个,因原材料涨价,面包价格上涨10%,会员优惠从打八五折调整为打九折,则会员购买一个面包比涨价前多花了0.14a 元;②等边三角形ABC 中,D 是BC 边上一点,E 是AC 边上一点,若AD AE =,则3∠=∠BAD EDC ;③两边及第三边上的中线对应相等的两个三角形全等;④一列自然数0,1,2,3,55,依次将该列数中的每一个数平方后除以100,得到一列新数,则原数与对应新数的差,随着原数的增大而增大.其中真命题的个数有( )A .1个B .2个C .3个D .4个【答案】C【分析】根据全等三角形的判定与性质、二次函数的性质等知识逐项判断即可,【详解】解:①项,会员原来购买一个面包需要0.85a 元,现在需要a ×(1+10%)×0.9=0.99a ,则会员购买一个面包比涨价前多花了0.99a -0.85a =0.14a 元,故①项正确;②项,如图,∵△ABC是等边三角形,∴∠B=∠C=60°,∵∠B+∠BAD=∠ADE+∠EDC,∠C+∠EDC=∠AED,又∵AD=AE,∴∠ADE=∠AED,∴∠B+∠BAD=∠ADE+∠EDC=∠C+∠EDC+∠EDC,∴∠BAD=∠EDC+∠EDC=2∠EDC,故②项错误;③项,如图,△ABC和△DEF,AB=DE,AC=DF,AM是△ABC的BC边上的中线,DN是△DEF的边EF上的中线,AM=DN,即有△ABC≌△DEF,理由如下:延长AM至G点,使得AM=GM,连接GC,延长DN至H点,使得DN=NH,连接HF,∵AM是中线,∴BM=MC,∵AM=MG,∠AMB=∠GMC,∴△AMB≌△GMC,∴AB=GC,同理可证DE=HF,∵AM=DN,∴AG=2AM=2DN=DH,∵AB =DE ,∴GC =HF ,∴结合AC =DF 可得△ACG ≌△DFH ,∴∠GAC =∠HDF ,同理可证∠GAB =∠HDE ,∴∠BAC =∠GAB +∠GAC =∠HDF +∠HDE =∠EDF ,∵AB =DE ,AC =DF ,∴△ABC ≌△DEF ,故③正确;④设原数为x ,则新数为21100x ,设原数与新数之差为y , 即21100y x x =-,变形为:21(50)25100y x =--+, 将x 等于0、1、2、3、55分别代入可知,y 随着x 的增大而增大,故④正确;即正确的有三个,故选:C ,【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质、二次函数的应用等知识,掌握全等三角形的判定与性质是解答本题的关键.44.(2022·吉林长春)如图,在ABC 中,根据尺规作图痕迹,下列说法不一定正确的是( )A .AF BF =B .12AE AC = C .90DBF DFB ∠+∠=︒D .BAF EBC ∠=∠【答案】B 【分析】根据尺规作图痕迹,可得DF 垂直平分AB ,BE 是ABC ∠的角平分线,根据垂直平分线的性质和角平分线的定义,直角三角形两锐角互余,等边对等角的性质进行判断即可.【详解】根据尺规作图痕迹,可得DF 垂直平分AB ,BE 是ABC ∠的角平分线,,90,AF BF BDF ABF CBE ∴=∠=︒∠=∠,。
1.2 第2课时 棱柱、圆柱、圆锥的展开与折叠 (课件)北师大版(2024)数学七年级上册)

探究新知
展开 四棱锥的平面展开图
探究新知
展开 五棱锥的平面展开图
巩固练习
想一想: 下面几个图形是一些常见几何体的展开图,
你能正确说出这些几何体的名字么?
圆锥
三棱锥
四棱锥
六棱锥
长方体
三棱柱
三棱柱
圆柱
当堂检测
1.一个棱柱的侧面展开图如图所示,
则该棱柱底面的形状是( B )
A
B
C
D
当堂检测
2.有一种包装盒如图所示,若不考虑粘贴 处的重叠部分,将下面展开图沿虚线折叠,
颜色
红黄蓝白紫绿
花的朵数 1 2 3 4 5 6
现将上述大小相同、颜色、花朵分布完全一样的
四个正方体拼成一个水平旋转的长方体,如图所示,
那么长方体的下底面共有 17 朵花.
综合运用 例1 如图所示是一个五棱柱,它的底面 边长都是4 cm,侧棱长都是6 cm.
(1)这个五棱柱共有多少个面?它们分别是什么形状? 哪些面的形状、面积完全相同? 解:这个五棱柱共有7个面,其中上、下两个底面,5个侧面.上、 下底面都是五边形,侧面都是长方形,上、下底面的形状、面积完 全相同.5个侧面的形状、面积完全相同.
探究新知
知识点 3 圆柱、圆锥的展开图
1.把圆柱的侧面展开,会得到什么图形?
探究新知
思考2 圆柱展开后的平面图形是什么样的?
结论:圆柱展开图是由两个等圆 和一个长方形组成,其中侧面展 开图的一边的长是底面圆的周长, 另一边的长是圆柱的高.
探究新知 2.把圆锥的侧面展开,会得到什么图形?
探究新知
第一章 丰富的图形世界 1.2 从立体图形到平面图形
第2课时 棱柱、圆柱、圆锥的展开与折叠
北师大版数学七年级上册:1.2 第2课时 棱柱、圆锥、圆柱的展开与折叠 课件

1.2.2 棱柱、圆柱、圆锥的展开与折叠
情境导入 例题讲解 课堂小结
获取新知 随堂演练
ห้องสมุดไป่ตู้
情境导入
将图中的棱柱沿某些棱剪开,展开成一个平面图 形,你能得到哪些形状的平面图形?
获取新知
展开
展开
展开
归纳总结
1.棱柱的表面展开图是由两个相同的多边形和一些长方形 组成的. 2.棱柱的展开图中上、下底面的边数与侧面长方形的个数 相等. 3.棱柱的上、下底面分别在侧面展开图的上、下两端. 4.底面多边形的各边长分别与侧面的各边长相等.
课堂小结
2. 把圆锥的侧面展开,会得到什么图形?
例题讲解 例2 [教材补充例题]图1-2-9中所示的图形是某些立体图形 的表面展开图,请写出这些立体图形的名称.
图1-2-9 解:(1)长方体.(2)五棱柱.(3)圆柱.(4)圆锥.(5)三棱柱.
归纳总结
名称 长方体 五棱柱 圆柱 圆锥
立体图形
表面展开图 底面形状 侧面形状 长方形 长方形
侧面展开 图的形状
长方形
五边形 长方形
长方形
圆
曲面
长方形
圆
曲面
扇形
随堂演练
1. 如图是一个长方体包装盒,则它的平面展开图是( A )
2.下列图形中可以作为一个三棱柱的展开图的是( A )
3. 如图所示的平面图形不可能围成圆锥的是( D ) 导引:圆锥的侧面展开图是扇形,底面为圆.
4.将图①的正四棱锥ABCDE沿着其中的四个边剪开后, 形成的展开图为图②,判断下列哪一个选项中的四个边可 为此四个边?( A ) A.AC,AD,BC,DE B.AB,BE,DE,CD C.AC,BC,AE,DE D.AC,AD,AE,BC
视图知识梳理
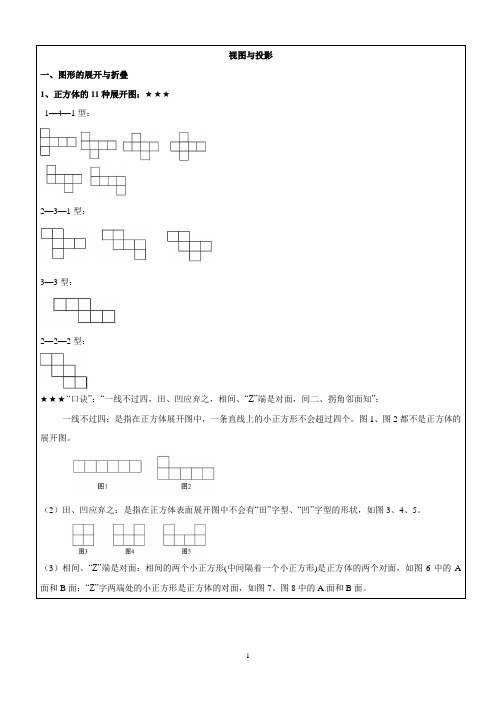
视图与投影一、图形的展开与折叠1、正方体的11种展开图:★★★1—4—1型:2—3—1型:3—3型:2—2—2型:★★★“口诀”:“一线不过四,田、凹应弃之,相间、“Z”端是对面,间二、拐角邻面知”:一线不过四:是指在正方体展开图中,一条直线上的小正方形不会超过四个。
图1、图2都不是正方体的展开图。
(2)田、凹应弃之:是指在正方体表面展开图中不会有“田”字型、“凹”字型的形状,如图3、4、5。
(3)相间、“Z”端是对面:相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,如图6中的A 面和B面;“Z”字两端处的小正方形是正方体的对面,如图7、图8中的A面和B面。
(4)间二、拐角邻面知:中间隔着两个小正方形或拐角型的三个面是正方体的邻面。
2、三棱柱和三棱锥的展开图:3、圆柱、圆锥、正三棱锥、正四棱锥、正五棱锥、正三棱柱的展开图:二、截面用一个平面去截一个几何体,截出的面叫做截面1、用一个平面截正方体:技巧:正方体的截面(1)截面经过正方体的几个面,截面就是几边形(2)截一个n棱柱截面最多是(n+2)边形(3)正方体切去一个角,截面形状可以是一般的锐角三角形、锐角的等腰三角形、等边三角形,不能截出直角三角形和钝角三角形2、圆柱、圆锥的截面3、用平面截球:注:用平面去截球体,只能出现一种形状的截面——___________.★归纳:用一个平面去截某一几何体,若截面是圆,则原来的几何体可能是:圆柱,圆锥,球,圆台三、从三个方向看物体1、从三个方向看物体在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.2、常见几何体的三视图几何体主视图左视图俯视图3.画三视图的原则(1)位置:俯视图在主视图的正下方,左视图在主视图的正右方;(2)尺寸:主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等.温馨提示:画三视图时,看得见部分的轮廓线通常画成实线;看不见部分的轮廓线通常画成虚线. 4.由三视图还原几何体由三视图描述几何体,一般先根据各视图想象从各个方向看到的几何体的形状,然后综合起来确定几何体的形状,再根据“长对正、高平齐、宽相等”的关系,确定轮廓线的位置以及各个面的尺寸,最后画出还原的几何体.例1:如图是由几个小正方体所搭成的几何体上面看到的图形,小正方形中的数字表示该位置的小正方体的个数,请你画出从正面、左面可以看到的图形.例2:某几何体的三视图如图所示,则组成该几何体的小正方体的个数是__________四、投影1、投影现象物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是_____________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三棱柱的展开图
三棱柱的展开图有三类(只考虑直三棱柱):
1、将矩形的侧面完全展开可以得如下
2、选择一个三角形的面展开,如果不是正三菱柱可以有三种,是正三菱柱只有一种。
3、选取一个矩形侧面为中心,三个方向展开。
扩展资料:
三棱柱是一种柱体,底面为三角形。
正三棱柱是半正多面体、均匀多面体的一种。
三棱柱是一种五面体,且有一组平行面,即两个面互相平行,而其他三个表面的法线在同一平面上(不一定是平行的面)。
这三个面可以是平行四边形。
所有平行于底面的横截面都是相同的三角形。
由于三棱柱也可以视为三面体截去2个顶点,故又称截角三面体,另外,因为正三棱柱具有对称性,且由2种正多边形组成,因此有人称正三棱柱为半正五面体。
一般三棱柱有5个面、9个边和6个顶点。
