2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级(下)期末数学试卷
吉林省长春市南关区东北师大附中明珠校区2021-2022学年七年级上学期期末数学试卷
2021-2022学年吉林省长春市南关区东北师大附中明珠校区七年级（上）期末数学试卷一、选择题（每小题3分，共24分）1．﹣3的相反数是（）A．3B．﹣3C．D．﹣2．将多项式﹣9+x3+3xy2﹣x2y按x的降幂排列的结果为（）A．x3+x2y﹣3xy2﹣9B．﹣9+3xy2﹣x2y+x3C．﹣9﹣3xy2+x2y+x3D．x3﹣x2y+3xy2﹣93．如图，AB＝8cm，AD＝BC＝5cm，则CD的长度为（）A．1cm B．2cm C．3cm D．4cm4．有理数a，b，c在数轴上的对应点的位置如图所示，若b与c互为相反数，则a，b，c 三个数中绝对值最大的数是（）A．a B．b C．c D．无法确定5．下列几何体的展开图中，能围成圆柱的是（）A．B．C．D．6．如图，将一副直角三角尺按不同方式摆放，则图中∠α与∠β互余的是（）A．B．C．D．7．根据等式的性质，若等式m＝n可以变形得到m+a＝n﹣b，则a、b应满足的条件是（）A．相等B．互为倒数C．互为相反数D．a＝0，b＝0 8．如图①，在长方形ABCD中，点E在AD上，且∠AEB＝60°，分别以BE：CE为折痕进行折叠并压平，如图②，若∠AED＝10°，则∠DEC的度数为（）A．25°B．30°C．35°D．40°二、填空题（每小题3分，共18分）9．单项式3x3y的次数是．10．国家电影专资办数据显示，截至2021年1月25日，国产电影《长津湖》票房达到人民币5700000000元，成为中国影史上的票房冠军．将5700000000这个数用科学记数法表示为．11．若一个角的大小为35°18'，则这个角的补角的大小为．12．某种商品每件的进价为m元，标价为n元，后来由于该商品积压，于是将此商品按标价的70%销售，则该商品每件利润为元．13．如图，直线AB和CD相交点O，CO⊥OE，OF平分∠AOE，∠EOF＝64°，则∠BOD 的大小为．14．如图，已知BC⊥AE，DE⊥AB，∠2+∠3＝180°．若∠1＝66°，BC平分∠ABD，则∠ACF＝°．三、解答题（共78分）15．计算：（1）13+（﹣5）﹣（﹣21）﹣19；（2）（﹣2）2+[18﹣（﹣3）×2]÷4．16．计算：（1）3a2﹣2a+4a2﹣7a；（2）（3x2+x﹣5）﹣（4﹣x+7x2）．17．解下列方程：（1）10x+9＝12x﹣1；（2）x﹣3（x﹣2）＝4；（3）5（x﹣1）＝8x﹣2（x+1）；（4）＝1．18．先化简，再求值：7x2+3（x2﹣6y）﹣2（3x2﹣y），其中x＝2，y＝﹣1．19．如图是由6个边长为1的相同小正方体组成的几何体，请在边长为1的网格中画出它的三视图．20．在下列解题过程的空白处填上恰当的内容（推理的理由或数学表达式）．已知：如图，∠1+∠2＝180°，∠3＝∠4．求证：EF∥GH．证明：∵∠1+∠2＝180°（已知），∠AEG＝∠1（），∴∠AEG+∠＝180°，∴AB∥CD（）∴∠AEG＝∠EGD（）∴∠3＝∠4（已知），∴∠3+∠AEG＝∠4+（等式的性质），即∠FEG＝∠，∴EF∥GH（）21．为了在中小学生中进行爱国主义教育，我校初一年级开展了“纪念一二•九”红领巾知识竞赛活动，并设立了一、二、三等奖．根据需要购买了100件奖品，其中二等奖的奖品件数比一等奖奖品的件数的3倍多10，各种奖品的单价如表所示：一等奖奖品二等奖奖品三等奖奖品单价（单位：元）22155数量（单位：件）x（1）请用含x的代数式把表格补全；（2）求购买100件奖品所需的总费用（用含x的代数式表示）；（3）若一等奖奖品购买了10件，求共需花费的钱数．22．以直线AB上一点O为端点作射线OC，使∠BOC＝40°，将一个直角三角板的直角顶点放在O处，即∠DOE＝90°．（1）如图1，若直角三角板DOE的一边OB放在射线OA上，则∠COD＝°；（2）如图2，将直角三角板DOE绕点O顺时针转动到某个位置，若OE恰好平分∠AOC，求∠COD的度数；（3）在图1中，将直角三角板DOE绕点O顺时针转动（OD与OB重合时停止）的过程中，恰好有∠COD＝∠AOE，则∠BOD的大小为．23．【问题背景】同学们，我们一起观察小猪的猪蹄，你会发现一个我们熟悉的几何图形，我们就把这个图形形象的称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．（1）如图①，AB∥CD，E为AB，CD之间一点，连接BE，DE，得到∠BED．试探究∠BED与∠B、∠D之间的数量关系，并说明理由．（2）请你利用上述“猪蹄模型”得到的结论或解题方法，完成下面的问题：【类比探究】如图②，AB∥CD，线段AD与线段BC相交于点E，∠BAD＝36°，∠BCD ＝80°，EF平分∠BED交直线AB于点F，则∠BEF＝°．【拓展延伸】如图③，AB∥CD，线段AD与线段BC相交于点E，∠BAD＝36°，∠BCD ＝80°，过点D作DG∥CB交直线AB于点G，AH平分∠BAD，DH平分∠CDG，则∠AHD＝°．24．如图，数轴上有A、B、C三个点，分别表示数﹣18、﹣10、20，有两条动线段PQ和MN（点Q与点A重合，点N与点B重合，且点P总在点Q的左边，点M总在点N的左边），PQ＝2，MN＝5，线段MN以每秒1个单位的速度从点B开始一直向右匀速运动，同时线段PQ以每秒3个单位的速度从点A开始向右匀速运动．当点Q运动到点C时，线段PQ立即以相同的速度返回；当点P运动到点A时，线段PQ、MN立即同时停止运动．设运动时间为t秒（整个运动过程中，线段PQ和MN保持长度不变）．（1）当t＝2时，点Q表示的数为，点M表示的数为．（2）当开始运动后，t＝秒时，点Q和点C重合．（3）在整个运动过程中，求点O和点N重合时t的值．（4）在整个运动过程中，当线段PQ和MN重合部分长度为1时，请直接写出此时t的值．。
吉林省长春市东北师大附中明珠学校2017-2018学年七年级下学期期末英语试题
吉林省长春市东北师大附中明珠学校2017-2018学年七年级下学期期末英语试题注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I卷（选择题)请点击修改第I卷的文字说明一、单选题1．It is ______ very interesting job to be a police artist.A．a B．an C．the D．/2．There ______ a sports meeting in our school last Wednesday.A．were B．is C．are D．was3．I saw Li Ming ______ near the river on my way home.A．plays B．playing C．to play D．played4．______ there, I usually walk out and turn right on Bridge Road.A．Get B．Gets C．To get D．Got 5．Students helped each other to ______ a tent a moment ago.A．cut up B．cut down C．put up D．put down 6．---- Do you take exercise every day?----Yes. I always thirty minutes after supper.A．spend B．cost C．take D．pay7．I’d like a bowl of dumplings ______ meat and cabbage.A．in B．to C．of D．with 8．—______ was your trip to Jingyue Park?—It was great! We had a good time there.A．What B．How C．Where D．When 9．TFBOYS are very ______ with boys and girls.A．strict B．special C．friendly D．popular 10．—I hear you run for half an hour at school every morning.—Right, we have to. It is one of the ______ in our class.A．messages B．rules C．problems D．persons 11．I ______ a surprise when I saw a big snake near our tent.A．gets B．get C．got D．getting 12．—Mom, must I come back before 6 o’clock?—No, you ______.A．must B．mustn’t C．need D．needn’t 13．______ good weather! Let’s go to the park to fly a kite, OK?A．What a B．What C．How D．How a 14．—Would you like some green tea?—______.A．Green tea, please B．Yes, I would C．Yes, please D．No, I wouldn’t 15．—I’m going to Hainan with my uncle tomorrow.—______!A．Have a good time B．Let’s go C．Thanks D．Sounds good二、补全对话6选5根据对话内容及方框中所给的句子补全对话。
吉林省长春市东北师大附中明珠学校2018-2019学年七年级下学期期末考试试卷及参考答案
吉林省长春市东北师大附中明珠学校2018-2019学年七年级下学期期末考试试卷一、选择题1. 下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是A .B .C .D .2. 如图，将沿BC方向平移1 得到，若的周长为8cm，则四边形ABFD的周长为（）A . 8B . 9C . 10D . 113. 如图， ,，则的大小是（）A . 25°B . 35°C . 45°D . 65°4. 小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可能是（）A . 正三角形B . 正方形C . 正五边形D . 正六边形5. 如图，将绕点按逆时针方向旋转后得到，若，则的度数为( )A .B .C .D .6. 已知一个三角形的两边长分别为2、5，则第三边的长可以为（）A . 2B . 3C . 5D . 77. 如图，已知AB＝DE，∠B＝∠DEF，下列条件中不能判定△ABC≌△DEF的是（）A . ∠A＝∠DB . AC∥DFC . BE＝CFD . AC＝DF8. 如图，在中，，的垂直平分线交于点．交于点，且与的比为4：1，则的度数为（）A . 20°B . 22.5°C . 25°D . 30°二、填空题9. 在中，，则 ________度．10. 东北师大附中校团委组织了职业微体验活动，初一（3）班52名学生分别去科技馆和图书馆参观，去科技馆的人数比去图书馆人数的2倍少5人，设去图书馆的人数为人，则可列方程：________．11. 如图所示，五角星的顶点是一个正五边形的五个顶点，这个五角星绕中心至少旋转________度能和自身重合．12. 已知等腰三角形的周长为29，一边长为7，则此等腰三角形的腰长为________．13. 若不等式组，恰有两个整数解，则的取值范围是________．14. 如图，在△ABC中，BF⊥AC 于点F，AD⊥BC 于点D，BF 与AD 相交于点E．若AD=BD，BC=8cm，DC=3cm．则 AE=________cm ．三、综合题15. 解下列方程（组）：（1）（2）16. 解下列不等式（组）：（1）（2）17. 如图，点是的边的延长线上一点，于点，，，求的度数．18. 五月份的第二个星期天是母亲节．如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒，根其图中提供信息，求每束鲜花和每个礼盒的价格．19. 如图，在正方形网格中，的三个顶点都在格点上，点也在格点上．（1）画，使与关于直线成轴对称．（2）画，使与关于点成中心对称．20. 如图：点、、、在一条直线上，、，，求证：．21. 如图，是等边三角形，点，分别在、边上，且．（1）求证：．（2）求的度数．22. 小明到某服装商场进行社会调查，了解到该商场为了激励营业员的工作积极性，实行“月总收入=基本工资+计件奖金”的方法，并获得如下信息：营业员：月销售件数100件，月总收入2400元；营业员：月销售件数150件，月总收入2700元；假设营业员的月基本工资为元，销售每件服装奖励元．（1）求、的值．（2）若某营业员的月总收入不低于3200元，则她当月至少要卖出服装多少件？23. 直角三角形中，，直线过点．（1）当时，如图①，分别过点、作于点，于点．求证：．（2）当，时，如图②，点与点关于直线对称，连接、，动点从点出发，以每秒1个单位长度的速度沿边向终点运动，同时动点从点出发，以每秒3个单位的速度沿向终点运动，点、到达相应的终点时停止运动，过点作于点，过点作于点，设运动时间为秒．①用含的代数式表示．②直接写出当与全等时的值．24. 已知和都是等腰三角形，，，．（1）（初步感知）特殊情形：如图①，若点，分别在边，上，则 ;．（填＞、＜或=）（2）发现证明：如图②，将图①中的绕点旋转，当点在外部，点在内部时，求证：．（3）（深入研究）如图③，和都是等边三角形，点，，在同一条直线上，则的度数为；线段，之间的数量关系为．（4）如图④，和都是等腰直角三角形，，点、、在同一直线上，为中边上的高，则的度数为；线段，，之间的数量关系为．（5）（拓展提升）如图⑤，和都是等腰直角三角形，，将绕点逆时针旋转，连结、．当，时，在旋转过程中，与的面积和的最大值为．参考答案1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.。
2022-2023学年吉林省长春市南关区东北师大附中明珠校区七年级(上)期末数学试卷(含详细答案)
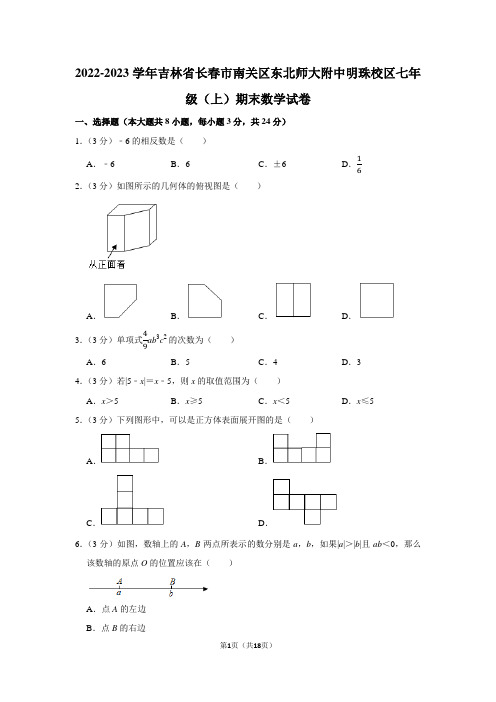
2022-2023学年吉林省长春市南关区东北师大附中明珠校区七年级（上）期末数学试卷一、选择题（本大题共8小题，每小题3分，共24分） 1．（3分）﹣6的相反数是（ ） A ．﹣6B ．6C ．±6D ．162．（3分）如图所示的几何体的俯视图是（ ）A ．B ．C ．D ．3．（3分）单项式49ab 3c 2的次数为（ ） A ．6B ．5C ．4D ．34．（3分）若|5﹣x |＝x ﹣5，则x 的取值范围为（ ） A ．x ＞5B ．x ≥5C ．x ＜5D ．x ≤55．（3分）下列图形中，可以是正方体表面展开图的是（ ）A ．B ．C ．D ．6．（3分）如图，数轴上的A ，B 两点所表示的数分别是a ，b ，如果|a |＞|b |且ab ＜0，那么该数轴的原点O 的位置应该在（ ）A ．点A 的左边B ．点B 的右边C ．点A 与点B 之间且靠近点AD ．点A 与点B 之间且靠近点B7．（3分）下列各式进行的变形中，不正确的是（ ） A ．若3a ＝2b ，则3a +2＝2b +2 B ．若3a ＝2b ，则9a ＝4bC ．若3a ＝2b ，则3a ﹣5＝2b ﹣5D ．若3a ＝2b ，则a2=b38．（3分）已知∠A ＝36°，∠B 的补角是∠A 余角的2倍，则∠B 的度数为（ ） A ．128°B ．108°C ．72°D ．52°二、填空题（本大题共6小题，每小题3分，共18分）9．（3分）将多项式2﹣4ab +3a 2b 2﹣b 3按字母b 降幂排列后，则从左边数第三项为 ． 10．（3分）2022年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”，在制动捕获过程中，探测器距离地球的距离为1920000000公里．数字1920000000用科学记数法表示为 ．11．（3分）如图，计划把池中的水引到C 处，可过点C 作CD ⊥AB ，垂足为点D ，然后沿CD 挖渠，可使所挖的渠道最短，这种设计的依据是 ．12．（3分）如图，直线AB 、CD 、EF 相交于点O ，则∠1+∠2+∠3＝ °．13．（3分）设某数为x ，用含x 的代数式表示“比某数的2倍多3的数”： ． 14．（3分）如图，△ABC 是一块直角三角板，∠BAC ＝90°，∠B ＝30°，现将三角板叠放在一把直尺上，使得点A 落在直尺的一边上，AB 与直尺的另一边交于点D ，BC 与直尺的两边分别交于点E ，F ．若∠CAF ＝20°，则∠BED 的度数为 °．三、解答题（本大题共15小题，共78分）（每题拍一张照片上传） 15．（3分）计算：33÷12−(−2)×4． 16．（3分）计算：(−2)×(56−14)÷(−6)． 17．（3分）化简：﹣a +（2a ﹣2）﹣（3a +5）． 18．（3分）3x 2﹣[7x ﹣（4x ﹣3）﹣2x 2] 19．（6分）解方程：4x ﹣3＝3x +1． 20．解方程：3x +7＝32﹣2x ．21．（6分）解方程：2（3x ﹣2）+1＝8x ． 22．解方程：2x−12−10x+14=3．23．（6分）先化简，再求值：5（3a 2b ﹣ab 2）﹣4（﹣ab 2+3a 2b ），其中a ＝﹣2，b ＝3． 24．（7分）已知：C 为线段AB 的中点，D 在线段BC 上，且AD ＝7，BD ＝5，求：线段CD 的长度．25．（7分）如图是小强用九块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出这个几何体的三视图．26．（8分）如图，已知∠BHF＝∠BDC，∠AED＝∠ACB．求证：∠EDC＝∠BFH．请补全下列解题过程．解：∵∠AED＝∠ACB（已知），∴DE∥BC（）．∴∠EDC＝（）．∵∠BHF＝∠BDC（已知），∴FH∥CD（）．∴∠BFH＝（两直线平行，同位角相等），∴∠EDC＝∠BFH（）．27．（8分）如图，直线AB、CD相交于点O，OM⊥AB．（1）若∠1＝∠2，求∠CON的度数．（2）若OC平分∠AOM，求∠AOC与∠MOD的度数．28．（8分）【阅读理解】定义：数轴上给定不重合两点A、B，若数轴上存在一点M，使得点M到点A的距离等于点M到点B的距离的2倍，则称点M为点A与点B的“双倍绝对点”．请解答下列问题：（1）【特例探究】若点A表示的数为﹣5，点B表示的数为1，点M为点A与点B的“双倍绝对点”，则点M表示的数为．（2）【抽象探究】若点A表示的数为a，点B表示的数为a﹣3，则点A与点B的“双倍绝对点”M表示的数为（用含a的代数式表示）．（3）【拓展应用】点A表示的数为﹣5，点C、D表示的数分别是﹣2、1，点B为线段CD上一点．设点M表示的数为m，且点M在A、B两点之间，若点M可以为点A与点B的“双倍绝对点”，直接写出m的取值范围．29．（10分）如图，∠AOB＝40°，OC平分∠AOB，点E在射线OC上，ED⊥OA，垂足为点D，DF平分∠ODE，交射线OC于点F，动点P从点O出发沿射线OC运动，连结DP．（1）当PD平分∠ODF时，∠PDE＝°．（2）当DP∥OB时，求∠PDE的度数．（3）当DP⊥FD时，∠ADP＝°．（4）当∠PDF=23∠EDF时，直接写出此时∠PDE的度数．2022-2023学年吉林省长春市南关区东北师大附中明珠校区七年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分） 1．（3分）﹣6的相反数是（ ） A ．﹣6B ．6C ．±6D ．16【分析】根据一个数的相反数就是在这个数前面添上“﹣”号，求解即可． 【解答】解：﹣（﹣6）＝6，则﹣6的相反数是6． 故选：B ．2．（3分）如图所示的几何体的俯视图是（ ）A ．B ．C ．D ．【分析】根据视图的意义，从上面看该几何体，所得到的图形进行判断即可． 【解答】解：从上面看该几何体，所看到的图形如下：故选：A ．3．（3分）单项式49ab 3c 2的次数为（ ）A ．6B ．5C ．4D ．3【分析】根据单项式次数的定义解答即可． 【解答】解：1+3+2＝6． 故选：A ．4．（3分）若|5﹣x |＝x ﹣5，则x 的取值范围为（ ） A ．x ＞5B ．x ≥5C ．x ＜5D ．x ≤5【分析】根据绝对值的定义得到5﹣x≤0即可．【解答】解：∵|5﹣x|＝x﹣5，∴5﹣x≤0，即x≥5，故选：B．5．（3分）下列图形中，可以是正方体表面展开图的是（）A．B．C．D．【分析】观察选项中的图形，确定出作为正方体表面展开图的即可．【解答】解：下列图形中，可以是正方体表面展开图的是，故选：D．6．（3分）如图，数轴上的A，B两点所表示的数分别是a，b，如果|a|＞|b|且ab＜0，那么该数轴的原点O的位置应该在（）A．点A的左边B．点B的右边C．点A与点B之间且靠近点AD．点A与点B之间且靠近点B【分析】ab＜0，a、b异号，处在原点的两侧，根据|a|＞|b|，得出a离原点远，b离原点近，得出判断．【解答】解：∵ab＜0，∴a、b异号，∵|a|＞|b|，∵数轴表示a的点离原点的距离大于表示b的点离原点的距离，即：a 、b 在原点的两侧，且a 到原点远，b 到原点近， 故选：D ．7．（3分）下列各式进行的变形中，不正确的是（ ） A ．若3a ＝2b ，则3a +2＝2b +2 B ．若3a ＝2b ，则9a ＝4bC ．若3a ＝2b ，则3a ﹣5＝2b ﹣5D ．若3a ＝2b ，则a2=b3【分析】根据等式的性质逐个判断即可． 【解答】解：A ．∵3a ＝2b ，∴3a +2＝2b +2，故本选项不符合题意； B ．∵3a ＝2b ，∴9a ＝6b ≠4b ，故本选项符合题意； C ．∵3a ＝2b ，∴3a ﹣5＝2b ﹣5，故本选项不符合题意； C ．∵3a ＝2b ，∴a2=b3（等式两边都除以6），故本选项不符合题意；D ．当a ＝0时，由a 2＝6a 不能推出a ＝6，故本选项不符合题意； 故选：B ．8．（3分）已知∠A ＝36°，∠B 的补角是∠A 余角的2倍，则∠B 的度数为（ ） A ．128°B ．108°C ．72°D ．52°【分析】根据题意得出∠A 与∠B 的关系式，即可解得∠B 的度数． 【解答】解：∵∠A ＝36°，∠B 的补角是∠A 余角的2倍， ∴180°﹣∠B ＝2（90﹣∠A ），即180°﹣∠B ＝2（90﹣36°）， 解得∠B ＝72°， 故选：C ．二、填空题（本大题共6小题，每小题3分，共18分）9．（3分）将多项式2﹣4ab +3a 2b 2﹣b 3按字母b 降幂排列后，则从左边数第三项为 ﹣4ab ． 【分析】根据多项式中降幂排序的定义：把一个多项式的各项按照某个字母的指数从大到小的顺序排列即可求解．【解答】解：多项式2﹣4ab +3a 2b 2﹣b 3按字母b 降幂排列为：﹣b 3+3a 2b 2﹣4ab +2， 则从左边数第三项为﹣4ab ，故答案为：﹣4ab．10．（3分）2022年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”，在制动捕获过程中，探测器距离地球的距离为1920000000公里．数字1920000000用科学记数法表示为 1.92×109．【分析】用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，且n比原来的整数位数少1，据此判断即可．【解答】解：1920000000＝1.92×109．故答案为：1.92×109．11．（3分）如图，计划把池中的水引到C处，可过点C作CD⊥AB，垂足为点D，然后沿CD挖渠，可使所挖的渠道最短，这种设计的依据是垂线段最短．【分析】由垂线的性质：垂线段最短，即可得到答案．【解答】解：把池中的水引到C处，可过点C作CD⊥AB，垂足为点D，然后沿CD挖渠，可使所挖的渠道最短，这种设计的依据是：垂线段最短．故答案为：垂线段最短．12．（3分）如图，直线AB、CD、EF相交于点O，则∠1+∠2+∠3＝180°．【分析】根据对顶角相等得∠DOE＝∠2，所以∠1+∠2+∠3＝∠1+∠DOE+∠3＝180°【解答】解：由对顶角相等得：∠DOE＝∠2，∴∠1+∠2+∠3＝1+∠DOE+∠3＝180°．13．（3分）设某数为x，用含x的代数式表示“比某数的2倍多3的数”：2x+3．【分析】要求的数＝某数×2+3，依此即可求解．【解答】解：根据题意得，“比某数的2倍多3的数“为2x+3．故答案为：2x+3．14．（3分）如图，△ABC 是一块直角三角板，∠BAC ＝90°，∠B ＝30°，现将三角板叠放在一把直尺上，使得点A 落在直尺的一边上，AB 与直尺的另一边交于点D ，BC 与直尺的两边分别交于点E ，F ．若∠CAF ＝20°，则∠BED 的度数为 80 °．【分析】依据DE ∥AF ，可得∠BED ＝∠BF A ，再根据三角形外角性质，即可得到∠BF A ＝20°+60°＝80°，进而得出∠BED ＝80°． 【解答】解：如图所示，∵DE ∥AF ， ∴∠BED ＝∠BF A ，又∵∠CAF ＝20°，∠C ＝60°， ∴∠BF A ＝20°+60°＝80°， ∴∠BED ＝80°， 故答案为：80．三、解答题（本大题共15小题，共78分）（每题拍一张照片上传） 15．（3分）计算：33÷12−(−2)×4．【分析】原式先算乘方运算，再算乘除运算，最后算加法运算即可求出值． 【解答】解：原式＝27÷12+2×4 ＝27×2+2×4 ＝54+8 ＝62．16．（3分）计算：(−2)×(56−14)÷(−6)．【分析】先算括号内的式子，同时将除法转化为乘法，然后根据乘法法则计算即可． 【解答】解：(−2)×(56−14)÷(−6) ＝（﹣2）×（1012−312）×（−16）＝（﹣2）×712×（−16）=736．17．（3分）化简：﹣a+（2a﹣2）﹣（3a+5）．【分析】根据整式的加减运算法则即可求出答案．【解答】解：原式＝﹣a+2a﹣2﹣3a﹣5＝﹣2a﹣7．18．（3分）3x2﹣[7x﹣（4x﹣3）﹣2x2]【分析】本题考查整式的加法运算，要先去括号，然后合并同类项．去括号时，当括号前面是负号，括号内各项都要变号；合并同类项时把系数相加减，字母与字母的指数不变．【解答】解：原式＝3x2﹣[7x﹣4x+3﹣2x2]＝3x2﹣7x+4x﹣3+2x2＝5x2﹣3x﹣319．（6分）解方程：4x﹣3＝3x+1．【分析】方程移项，合并同类项，把x系数化为1，即可求出解．【解答】解：移项得：4x﹣3x＝1+3，合并同类项得：x＝4．20．解方程：3x+7＝32﹣2x．【分析】将方程移项，合并同类项，化成ax＝b的形式，再把系数化为1即可．【解答】解：移项得：3x+2x＝32﹣7，合并同类项得：5x＝25，∴x＝5．21．（6分）解方程：2（3x﹣2）+1＝8x．【分析】方程去括号，移项，合并同类项，把x系数化为1，即可求出解．【解答】解：去括号得：6x﹣4+1＝8x，移项得：6x﹣8x＝4﹣1，合并同类项得：﹣2x＝3，解得：x＝﹣1.5．22．解方程：2x−12−10x+14=3．【分析】去分母、去括号、移项、合并同类项、系数化为1，据此求出方程的解即可．【解答】解：去分母，可得：2（2x ﹣1）﹣（10x +1）＝12，去括号，可得：4x ﹣2﹣10x ﹣1＝12，移项，可得：4x ﹣10x ＝12+2+1，合并同类项，可得：﹣6x ＝15，系数化为1，可得：x ＝﹣2.5．23．（6分）先化简，再求值：5（3a 2b ﹣ab 2）﹣4（﹣ab 2+3a 2b ），其中a ＝﹣2，b ＝3．【分析】原式去括号合并得到最简结果，把a 与b 的值代入计算即可求出值．【解答】解：5（3a 2b ﹣ab 2）﹣4（﹣ab 2+3a 2b ）＝15a 2b ﹣5ab 2+4ab 2﹣12a 2b ＝3a 2b ﹣ab 2 ， 把a ＝﹣2，b ＝3代入上式得：原式＝3×（﹣2）2×3﹣（﹣2）×32＝54．24．（7分）已知：C 为线段AB 的中点，D 在线段BC 上，且AD ＝7，BD ＝5，求：线段CD的长度．【分析】根据已知可求得AB 的长，从而可求得AC 的长，已知AD 的长则不难求得CD 的长．【解答】解：∵AD ＝7，BD ＝5∴AB ＝AD +BD ＝12∵C 是AB 的中点∴AC =12AB ＝6∴CD ＝AD ﹣AC ＝7﹣6＝1．25．（7分）如图是小强用九块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出这个几何体的三视图．【分析】读图可得，从正面看有3列，每列小正方形数目分别为2，2，1；从左面看有3列，每列小正方形数目分别为3，1，2；从上面看有3列，每列小正方形数目分别为2，2，2，依此画出图形即可．【解答】解：三视图如下：26．（8分）如图，已知∠BHF＝∠BDC，∠AED＝∠ACB．求证：∠EDC＝∠BFH．请补全下列解题过程．解：∵∠AED＝∠ACB（已知），∴DE∥BC（同位角相等，两直线平行）．∴∠EDC＝∠BCD（两直线平行，内错角相等）．∵∠BHF＝∠BDC（已知），∴FH∥CD（同位角相等，两直线平行）．∴∠BFH＝∠BCD（两直线平行，同位角相等），∴∠EDC＝∠BFH（等量代换）．【分析】由平行线的判定得出DE∥BC，根据两直线平行，内错角相等，可得出∠BHF ＝∠BDC，再由平行线的判定得出FH∥CD，根据两直线平行，同位角相等，可得出∠BFH＝∠BCD，最后根据等量代换可得∠EDC＝∠BFH．【解答】解：∵∠AED＝∠ACB（已知），∴DE∥BC（同位角相等，两直线平行）．∴∠EDC＝∠BCD（两直线平行，内错角相等）．∵∠BHF＝∠BDC（已知），∴FH∥CD（同位角相等，两直线平行）．∴∠BFH＝∠BCD（两直线平行，同位角相等），∴∠EDC＝∠BFH（等量代换）．故答案为：同位角相等，两直线平行；∠BCD；两直线平行，内错角相等；同位角相等，两直线平行；∠BCD；等量代换．27．（8分）如图，直线AB、CD相交于点O，OM⊥AB．（1）若∠1＝∠2，求∠CON的度数．（2）若OC平分∠AOM，求∠AOC与∠MOD的度数．【分析】（1）分析题意，根据垂直的定义可得∠AOC+∠1＝90°，结合∠1＝∠2可求解；（2）根据角的平分线的定义可求得∠AOC＝∠1＝45°，再利用邻补角的定义可求解．【解答】解：（1）∵OM⊥AB，∴∠AOM＝∠AOC+∠1＝90°，∵∠1＝∠2，∴∠CON＝∠AOC+∠1＝90°；（2）∵OC平分∠AOM，∴∠AOC＝∠1=12∠AOM＝45°，∵∠DOC＝180°，∴∠1+∠MOD＝180°，∴∠MOD＝180°﹣45°＝135°．28．（8分）【阅读理解】定义：数轴上给定不重合两点A、B，若数轴上存在一点M，使得点M到点A的距离等于点M到点B的距离的2倍，则称点M为点A与点B的“双倍绝对点”．请解答下列问题：（1）【特例探究】若点A表示的数为﹣5，点B表示的数为1，点M为点A与点B的“双倍绝对点”，则点M表示的数为﹣1或7．（2）【抽象探究】若点A表示的数为a，点B表示的数为a﹣3，则点A与点B的“双倍绝对点”M表示的数为a﹣2或a﹣6（用含a的代数式表示）．（3）【拓展应用】点A表示的数为﹣5，点C、D表示的数分别是﹣2、1，点B为线段CD上一点．设点M表示的数为m，且点M在A、B两点之间，若点M可以为点A与点B的“双倍绝对点”，直接写出m的取值范围．【分析】（1）分点M位于点A、B之间和点B右侧两种情况，根据题意列式求解；（2）也是分点M位于点A、B之间和点B右侧两种情况，根据题意列式求解；（3）先设点B表示的数是b，用含b的式子表示m后进行整理、求解．【解答】解：（1）设点M表示的数为m，当点M位于点A、B之间时，得m﹣（﹣5）＝2（1﹣m），解得m＝﹣1；点M位于点B右侧时，得m﹣（﹣5）＝2（m﹣1），解得m＝7，故答案为：﹣1或7；（2）同样设点M表示的数为m，当点M 位于点A 、B 之间时，得2[m ﹣（a ﹣3）]＝a ﹣m ，解得m ＝a ﹣2；点M 位于点B 左侧时，得2[（a ﹣3）﹣m ]＝a ﹣m ，解得m ＝a ﹣6，故答案为：a ﹣2或a ﹣6；（3）设点B 表示的数是b ，则﹣2≤b ≤1，由题意得，m ﹣（﹣5）＝2（b ﹣m ），解得m =2b−53， 即2×(−2)−53≤m ≤2×1−53， 解得﹣3≤m ≤﹣1，∴m 的取值范围﹣3≤m ≤﹣1．29．（10分）如图，∠AOB ＝40°，OC 平分∠AOB ，点E 在射线OC 上，ED ⊥OA ，垂足为点D ，DF 平分∠ODE ，交射线OC 于点F ，动点P 从点O 出发沿射线OC 运动，连结DP ．（1）当PD 平分∠ODF 时，∠PDE ＝ 67.5 °．（2）当DP ∥OB 时，求∠PDE 的度数．（3）当DP ⊥FD 时，∠ADP ＝ 45 °．（4）当∠PDF =23∠EDF 时，直接写出此时∠PDE 的度数．【分析】（1）根据题意可得∠ODE ＝90°，根据角平分线的性质可得∠ODF ＝∠EDF ＝45°，∠PDF ＝22.5°，以此即可得到∠PDE ＝∠PDF +∠EDF ＝67.5°．（2）根据平行线的性质可得∠AOB +∠ODP ＝180°，由∠AOB ＝40°得∠ODP ＝140°，根据∠PDE ＝∠ODP ﹣∠ODE 即可求解．（3）根据题意得∠PDF ＝90°，则∠ADP ＝180°﹣∠ODF ﹣∠PDF ，以此即可求解．（4）由∠PDF =23∠EDF 得∠PDF ＝30°，再分两种情况：①当∠PDF 在∠EDF 内部时，∠PDE ＝∠PDF +∠EDF ；②当∠PDF 在∠EDF 内部时，∠PDE ＝∠EDF ﹣∠PDF °；以此即可解答．【解答】解：（1）∵ED ⊥OA ，∴∠ODE ＝90°，∵DF 平分∠ODE ，∴∠ODF ＝∠EDF =12∠ODE =45°，∵PD 平分∠ODF ，∴∠PDF ＝∠12∠ODE =22.5°， ∴∠PDE ＝∠PDF +∠EDF ＝67.5°．故答案为：67.5．（2）如图，DP ∥OB ，∵DP ∥OB ，∴∠AOB +∠ODP ＝180°，∵∠AOB ＝40°，∴∠ODP ＝140°，∴∠PDE ＝∠ODP ﹣∠ODE ＝50°．（3）如图，DP ⊥FD ，∵DP ⊥FD ，∴∠PDF ＝90°，∴∠ADP ＝180°﹣∠ODF ﹣∠PDF ＝45°．故答案为：45．（4）∵∠PDF=23∠EDF，∴∠PDF＝30°，①当∠PDF在∠ODF内部时，如图，此时，∠PDE＝∠PDF+∠EDF＝75°；②当∠PDF在∠EDF内部时，如图，此时，∠PDE＝∠EDF﹣∠PDF＝15°；综上，当∠PDF=23∠EDF时，∠PDE的度数为75°或15°．。
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级(上)期末数学试卷含答案解析
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（上）期末数学试卷一、选择题1．﹣5的绝对值是（）A．5B．C．﹣5D．2．实数a，b，c，d在数轴上对应的点的位置如图所示，这四个数中最大的是（）A．a B．b C．c D．d3．如图是一个由两个小正方体和一个圆锥组成的几何体，它的主视图是（）A．B．C．D．4．下列说法正确的是（）A．的系数是﹣2B．x2+x﹣1的常数项为1C．22ab3的次数是6次D．2x﹣5x2+7是二次三项式5．下列四个图形中，是三棱柱的平面展开图的是（）A．B．C．D．6．已知等式3a＝2b+5，则下列等式不一定成立的是（）A．3a﹣5＝2b B．3a+1＝2b+6C．3ac＝2bc D．a7．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A．B．C．D．8．如图，直线AB、CD相交于点O，OE平分∠BOC，∠FOD＝90°，若∠BOD：∠BOE ＝1：2，则∠AOF的度数为（）A．70°B．75°C．60°D．54°二、填空题9．把多项式2m2﹣4m4+2m﹣1按m的升幂排列．10．长春市奥林匹克公园于2018年年底建成，它的总占地面积约为528000平方米，528000这个数字用科学记数法表示为．11．如图，∠AOB＝72°32′，射线OC在∠AOB内，∠BOC＝30°40′，则∠AOC＝．12．今年十一小长假期间，迟老师一家三口开着一辆轿车去长春市净月潭森林公园度假，若门票每人a元，进入园区的轿车每辆收费40元，则迟老师一家开车进入净月潭森林公园园区所需费用是元（用含a的代数式表示）．13．如图，能与∠1构成同位角的角有个．14．如图，在三角形ABC中，AB⊥AC于点A，AB＝6，AC＝8，BC＝10，点P是线段BC 上的一点，则线段AP的最小值为．三、计算题15．计算：（1）（）×（﹣48）（2）（﹣5）3×（）+32÷（﹣2）216．计算：（1）3x+2（x）﹣（x+1）（2）5（2a2b ab2）（6a2b﹣3ab2）四、解答题17．解下列一元一次方程：（1）4x+7＝32﹣x（2）8x﹣3（3x+2）＝1（3）2（y）（3y﹣2）（4）118．先化简，再求值：2（a2+2a﹣1）﹣3（a2﹣2a﹣3），其中a＝﹣2．19．如图，点P是∠AOB的边OB上的一点，点M是∠AOB内部的一点，按下述要求画图，并回答问题：（1）过点M画OA的平行线MN；（2）过点P画OB的垂线PC，交OA于点C；（3）点C到直线OB的距离是线段的长度．20．如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG相交于点H，∠C＝∠EFG，∠BFG＝∠AEM，求证：AB∥CD．（完成下列填空）证明：∵∠BFG＝∠AEM（已知）且∠AEM＝∠BEC（）∴∠BEC＝∠BFG（等量代换）∴MC∥（）∴∠C＝∠FGD（）∵∠C＝∠EFG（已知）∴∠＝∠EFG，（等量代换）∴AB∥CD（）21．如图已知点C为AB上一点，AC＝12cm，CB AC，D、E分别为AC、AB的中点，求DE的长．22．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．23．如图，直线AB、CD相交于点O，OF平分∠AOE，OF⊥CD，垂足为O．（1）写出图中所有与∠AOD互补的角；（2）若∠AOE＝110°，求∠BOD的度数．24．感知：如图①，若AB∥CD，点P在AB、CD内部，则∠P、∠A、∠C满足的数量关系是．探究：如图②，若AB∥CD，点P在AB、CD外部，则∠APC、∠A、∠C满足的数量关系是．请补全以下证明过程：证明：如图③，过点P作PQ∥AB∴∠A＝∵AB∥CD，PQ∥AB∴∥CD∴∠C＝∠∵∠APC＝∠﹣∠∴∠APC＝应用：（1）如图④，为北斗七星的位置图，如图⑤，将北斗七星分别标为A、B、C、D、E、F、G，其中B、C、D三点在一条直线上，AB∥EF，则∠B、∠D、∠E满足的数量关系是．（2）如图⑥，在（1）问的条件下，延长AB到点M，延长FE到点N，过点B和点E 分别作射线BP和EP，交于点P，使得BD平分∠MBP，EN平分∠DEP，若∠MBD＝25°，则∠D﹣∠P＝°．2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（上）期末数学试卷参考答案与试题解析一、选择题1．﹣5的绝对值是（）A．5B．C．﹣5D．【解答】解：﹣5的绝对值是5．故选：A．2．实数a，b，c，d在数轴上对应的点的位置如图所示，这四个数中最大的是（）A．a B．b C．c D．d【解答】解：由数轴可得：a＜b＜c＜d，故选：D．3．如图是一个由两个小正方体和一个圆锥组成的几何体，它的主视图是（）A．B．C．D．【解答】解：由两个小正方体和一个圆锥组成的几何体，它的主视图是，故选：B．4．下列说法正确的是（）A．的系数是﹣2B．x2+x﹣1的常数项为1C．22ab3的次数是6次D．2x﹣5x2+7是二次三项式【解答】解：A．的系数是，此选项错误；B．x2+x﹣1的常数项为﹣1，此选项错误；C．22ab3的次数是4次，此选项错误；D．2x﹣5x2+7是二次三项式，此选项正确；故选：D．5．下列四个图形中，是三棱柱的平面展开图的是（）A．B．C．D．【解答】A、是三棱锥的展开图，故选项错误；B、是三棱柱的平面展开图，故选项正确；C、两底有4个三角形，不是三棱锥的展开图，故选项错误；D、是四棱锥的展开图，故选项错误．故选：B．6．已知等式3a＝2b+5，则下列等式不一定成立的是（）A．3a﹣5＝2b B．3a+1＝2b+6C．3ac＝2bc D．a【解答】解：A.3a＝2b+5，等式两边同时减去5得：3a﹣5＝2b，即A项正确，B.3a＝2b+5，等式两边同时加上1得：3a+1＝2b+6，即B项正确，C.3a＝2b+5，等式两边同时乘以c得：3ac＝2bc+5c，即C项错误，D.3a＝2b+5，等式两边同时除以3得：a，即D项正确，故选：C．7．下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A．B．C．D．【解答】解：A、图中的∠AOB不能用∠O表示，故本选项错误；B、图中的∠1和∠AOB不是表示同一个角，故本选项错误；C、图中的∠1和∠AOB不是表示同一个角，故本选项错误；D、图中∠1、∠AOB、∠O表示同一个角，故本选项正确；故选：D．8．如图，直线AB、CD相交于点O，OE平分∠BOC，∠FOD＝90°，若∠BOD：∠BOE ＝1：2，则∠AOF的度数为（）A．70°B．75°C．60°D．54°【解答】解：∵∠BOD：∠BOE＝1：2，OE平分∠BOC，∴∠BOD：∠BOE：∠EOC＝1：2：2，∴∠BOD＝36°，∴∠AOC＝36°，又∵∠COF＝∠DOF＝90°，∴∠AOF＝90°﹣36°＝54°．故选：D．二、填空题9．把多项式2m2﹣4m4+2m﹣1按m的升幂排列﹣1+2m+2m2﹣4m4．【解答】解：多项式2m2﹣4m4+2m﹣1按m的升幂排列为﹣1+2m+2m2﹣4m4，故答案为：﹣1+2m+2m2﹣4m4．10．长春市奥林匹克公园于2018年年底建成，它的总占地面积约为528000平方米，528000这个数字用科学记数法表示为 5.28×105．【解答】解：528000＝5.28×105，故答案为：5.28×105．11．如图，∠AOB＝72°32′，射线OC在∠AOB内，∠BOC＝30°40′，则∠AOC＝41°52′．【解答】解：∠AOC＝∠AOB﹣∠BOC＝72°32′﹣30°40′＝41°52′，故答案为：41°52′．12．今年十一小长假期间，迟老师一家三口开着一辆轿车去长春市净月潭森林公园度假，若门票每人a元，进入园区的轿车每辆收费40元，则迟老师一家开车进入净月潭森林公园园区所需费用是（40+3a）元（用含a的代数式表示）．【解答】解：根据题意得：（40+3a），故答案为：（40+3a）13．如图，能与∠1构成同位角的角有2个．【解答】解：由同位角的定义知，能与∠1构成同位角的角有∠2、∠3共2个．故答案为214．如图，在三角形ABC中，AB⊥AC于点A，AB＝6，AC＝8，BC＝10，点P是线段BC 上的一点，则线段AP的最小值为．【解答】解：∵AB⊥AC，∴∠BAC＝90°，当AP⊥BC时，AP的值最短，∴AP，∴线段AP的最小值为，故答案为：．三、计算题15．计算：（1）（）×（﹣48）（2）（﹣5）3×（）+32÷（﹣2）2【解答】解：（1）（）×（﹣48）（﹣48）（﹣48）（﹣48）＝﹣40﹣42+46＝﹣36；（2）（﹣5）3×（）+32÷（﹣2）2＝（﹣125）×（）+32÷4＝75+8＝75﹣10＝65．16．计算：（1）3x+2（x）﹣（x+1）（2）5（2a2b ab2）（6a2b﹣3ab2）【解答】解：（1）3x+2（x）﹣（x+1）＝3x+2x﹣1﹣x﹣1＝4x﹣2；（2）5（2a2b ab2）（6a2b﹣3ab2）＝10a2b﹣2ab2﹣4a2b+2ab2＝6a2b．四、解答题17．解下列一元一次方程：（1）4x+7＝32﹣x（2）8x﹣3（3x+2）＝1（3）2（y）（3y﹣2）（4）1【解答】解：（1）4x+7＝32﹣x，4x+x＝32﹣7，5x＝﹣25，x＝﹣5；（2）8x﹣9x﹣6＝1，8x﹣9x＝1+6，﹣x＝7，x＝﹣7；（3）2y﹣3y﹣4，2y y＝﹣4+3，y＝﹣1，y＝2．（4）3（5y﹣1）﹣4（2y+6）＝12，15y﹣3﹣8y﹣24＝12，15y﹣8y＝12+3+24，7y＝39，y．18．先化简，再求值：2（a2+2a﹣1）﹣3（a2﹣2a﹣3），其中a＝﹣2．【解答】解：原式＝2a2+4a﹣2﹣3a2+6a+9＝﹣a2+10a+7，当a＝﹣2时，原式＝﹣4﹣20+7＝﹣24+7＝﹣17．19．如图，点P是∠AOB的边OB上的一点，点M是∠AOB内部的一点，按下述要求画图，并回答问题：（1）过点M画OA的平行线MN；（2）过点P画OB的垂线PC，交OA于点C；（3）点C到直线OB的距离是线段PC的长度．【解答】解：（1）如图所示：（2）如图所示：（3）点C到直线OB的距离是线段PC的长度；故答案为：PC．20．如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG相交于点H，∠C＝∠EFG，∠BFG＝∠AEM，求证：AB∥CD．（完成下列填空）证明：∵∠BFG＝∠AEM（已知）且∠AEM＝∠BEC（对顶角相等）∴∠BEC＝∠BFG（等量代换）∴MC∥GF（同位角相等，两直线平行）∴∠C＝∠FGD（两直线平行，同位角相等）∵∠C＝∠EFG（已知）∴∠FGD＝∠EFG，（等量代换）∴AB∥CD（内错角相等，两直线平行）【解答】证明：∵∠BFG＝∠AEM（已知）且∠AEM＝∠BEC（对顶角相等）∴∠BEC＝∠BFG（等量代换）∴MC∥GF（同位角相等，两直线平行）∴∠C＝∠FGD（两直线平行，同位角相等）∵∠C＝∠EFG（已知）∴∠FGD＝∠EFG，（等量代换）∴AB∥CD（内错角相等，两直线平行）．故答案是：对顶角相等；GF；同位角相等，两直线平行；FGD；内错角相等，两直线平行．21．如图已知点C为AB上一点，AC＝12cm，CB AC，D、E分别为AC、AB的中点，求DE的长．【解答】解：根据题意，AC＝12cm，CB AC，所以CB＝8cm，所以AB＝AC+CB＝20cm，又D、E分别为AC、AB的中点，所以DE＝AE﹣AD（AB﹣AC）＝4cm．即DE＝4cm．故答案为4cm．22．如图，已知∠ABC+∠ECB＝180°，∠P＝∠Q．求证：∠1＝∠2．【解答】证明：∵∠ABC+∠ECB＝180°，∴AB∥DE，∴∠ABC＝∠BCD，∵∠P＝∠Q，∴PB∥CQ，∴∠PBC＝∠BCQ，∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，∴∠1＝∠2．23．如图，直线AB、CD相交于点O，OF平分∠AOE，OF⊥CD，垂足为O．（1）写出图中所有与∠AOD互补的角；（2）若∠AOE＝110°，求∠BOD的度数．【解答】解：（1）与∠AOD互补的角：∠BOD与∠AOC；（2）∵∠AOE＝110°，∴∠BOE＝180°﹣∠AOE＝180°﹣110°＝70°，∵OF平分∠AOE，∴∠FOE∠AOE，∵OF⊥CD，∴∠FOD＝90°，∴∠EOD＝∠FOD﹣∠FOE＝90°﹣55°＝35°，∴∠BOD＝∠BOE﹣∠EOD＝70°﹣35°＝35°．24．感知：如图①，若AB∥CD，点P在AB、CD内部，则∠P、∠A、∠C满足的数量关系是∠P＝∠A+∠C；．探究：如图②，若AB∥CD，点P在AB、CD外部，则∠APC、∠A、∠C满足的数量关系是∠APC＝∠A﹣∠C．请补全以下证明过程：证明：如图③，过点P作PQ∥AB∴∠A＝∠APQ∵AB∥CD，PQ∥AB∴PQ∥CD∴∠C＝∠∠CPQ∵∠APC＝∠APQ﹣∠CPQ∴∠APC＝∠A﹣∠C应用：（1）如图④，为北斗七星的位置图，如图⑤，将北斗七星分别标为A、B、C、D、E、F、G，其中B、C、D三点在一条直线上，AB∥EF，则∠B、∠D、∠E满足的数量关系是∠B+∠D﹣∠E＝180°．（2）如图⑥，在（1）问的条件下，延长AB到点M，延长FE到点N，过点B和点E 分别作射线BP和EP，交于点P，使得BD平分∠MBP，EN平分∠DEP，若∠MBD＝25°，则∠D﹣∠P＝75°．【解答】解：感知：如图①，过点P作PQ∥AB∴∠A＝∠APQ，∵AB∥CD，PQ∥AB∴PQ∥CD，∴∠C＝∠QPC，∴∠APQ+∠QPC＝∠A+∠C，∠APC＝∠A+∠C．故答案为∠P＝∠A+∠C；探究：证明：如图③，过点P作PQ∥AB∴∠A＝∠APQ∵AB∥CD，PQ∥AB∴PQ∥CD∴∠C＝∠CPQ∵∠APC＝∠APQ﹣∠CPQ∴∠APC＝∠A﹣∠C．故答案为：∠APC＝∠A﹣∠C，∠APQ，PQ，∠CPQ，∠APQ，∠CPQ，∠A﹣∠C．应用：（1）如图⑤，过点D作DH∥EF，∴∠HDE＝∠E，∵AB∥EF，DH∥EF∴AB∥DH，∴∠B+∠BDH＝180°，即∠BDH＝180°﹣∠B，∴∠HDE+∠BDH＝∠E+180°﹣∠B，即∠BDE+∠B﹣∠E＝180°，故答案为∠D+∠B﹣∠E＝180°，（2）如图⑥，过点P作PH∥EF，∴∠EPH＝∠NEP，∵AB∥EF，PH∥EF，∴AB∥PH，∴∠MBP+∠BPH＝180°，∵BD平分∠MBP，∠MBD＝25°，∠MBP＝2∠MBD＝2×25°＝50°，∠BPH＝180°﹣50°＝130°，∵EN平分∠DEP，∴∠NEP＝∠DEN∴∠BPE＝∠BPH﹣∠EPH＝∠BPH﹣∠NEP＝∠BPH﹣∠DEN＝130°﹣（180°﹣∠DEF）＝∠DEF﹣50°由①∠D+∠ABD﹣∠DEF＝180°，∵∠MBD＝25°，∴∠ABD＝155°，∴∠D+∠155°﹣∠DEF＝180°，∴∠DEF＝∠D﹣25°∴∠BPE＝∠DEF﹣50°＝∠D﹣25°﹣50°＝∠D﹣75°∠D﹣∠BPE＝75°即∠D﹣∠P＝75°，故答案75．。
长春市东北师大附中明珠学校2018-2019学年下初一英语Unit4大练习无答案
东北师大附中明珠学校2017-2018学年(下)初一年级英语学科大练习(四) Unit 4 Don't eat in class满分120分命题人: 张燕霞审题人:罗焱峰 2018-4-4一、听力部分(共20分)I.听句子，选择与对话内容相符的图片。
(5分)II.听五段对话，根据每段对话内容及问题，选择正确选项。
(5分)6.What can the boy Not do in class?A.Listen 1o music.B.Eat. C Talk with friends.7.Where is the boy's basketball?A. On the desk.B.Under the desk.C.Under the chair.8.What does the boy like doing on the computer?A.Playing games.B.Having classes. C Making friends.9.What does the girl often do after she gets up?A.Makes her bed.B.Goes to school.C.Has breakfast.10.What is the boy good at?A.Doing homework.B.Playing basketball.C.Playing soccer.Ⅲ.听长对话，选择正确选项。
(5分)11.What subject does Bob NOT learn at school?A.Math. B Music. C.History.12.How many lessons does Bob have every afternoon?A.3.B.5C.213.What time does the first lesson begin?A.At8:30.B.At 8 :OO.C.At 7:30.14.When does Bob do outdoor activities(户外活动)?A In the morning. B.In the evening C.In the afternoon.5.What does Bob think of his school life?A.BoringC.InterestingB.RelaxingIV.听短文，选择正确答案。
吉林省长春市南关区东北师大附中明珠学校2023-2024学年七年级上学期期末数学试题
吉林省长春市南关区东北师大附中明珠学校2023-2024学年七年级上学期期末数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在数轴上对应的数互为相反数的两个点是（）A ．点A 和点CB ．点B 和点C C ．点A 和点BD ．点B 和点D 2．杭州第19届亚运会公众售票官方网站8日上午上线开放注册，首批上架比赛项目包括举重、克柔术、网球、花样游泳、击剑、摔跤、蹦床、高尔夫球、跳水、游泳、软式网球、攀岩等12个项目，总计预售113700张门票，数据113700用科学记数法可表示为（）A ．60.113710⨯B ．51.13710⨯C ．61.13710⨯D ．411.3710⨯3．下列四个生活中的现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要确定两棵树的位置，就能确定这一行树所在的直线；③从A 地到B 地架设电线，总是尽可能沿着线段AB 方向架设；④把弯曲的公路改直，就能缩短路程．其中可以用基本事实“两点确定一条直线”来解释的有（）A ．①②B ．①③C ．②③D ．③④4．如图，图（1）和图（2）中所有的正方形都完全相同，将图（1）的正方形放在图（2）中的某一位置，其中所组成的图形不能围成正方体的是（）A ．①B ．②C ．③D ．④5．若单项式213n ax y +与42m ax y -是同类项，则()2023m n -的值是（）A ．0B ．1C ．1-D ．20236．“盈不足问题”作为我国数学的古典问题，在2000多年前的《九章算术》一书中就有很详尽而深刻的阐述．书中记载：今有人买鸡，人出九，盈十一；人出六，不足十六．问人数、物价各几何？意思是：有若干人一起买鸡，如果每人出9文钱，就多出11文钱；A ．911x +7．如图，直线度数是（）A ．15︒B ．8．如图，将矩形ABCD 沿若∠AGE =32°，则∠GHC 等于（A ．112°B ．110°二、填空题9．比较大小：34--10．近似数4.50万精确到11．如图，一把长方形直尺沿直线断开并错位摆放，若131ADE =︒∠，则DBC ∠12．计算：6136'︒=°．13．若244x x +=，则2782x x --的值为14．如图所示，未来公园的广场背景墙上有一系列用灰砖和白砖铺成的图案，图①有块灰砖，8块白砖；图②有4块灰砖，砖，则此图案中有块白砖．三、解答题15．计算：(1)()511110.5626⎛⎫⎛⎫+----+ ⎪ ⎪⎝⎭⎝⎭；(2)1422379⎛⎫⎛⎫-⨯÷- ⎪ ⎪⎝⎭⎝⎭；(3)()()2321162332-÷-⨯-⨯+-．16．解方程：(1)4363x x -=+；(2)()()21213x x --=-+；(3)4172136x x +--=．17．先化简，再求值()(22252334a a a a -++-18．在2023年空军航空开放活动·长春航空展中，某飞机起飞5千米后的高度变化情况如下表所示，按要求解答下列问题：(1)过点A 作直线BC 的垂线，垂足为点(2)作线段AE BC ∥．且AE =(3)若点F 在线段AC 上，连结并说明此时DF EF +的长度最小的理由：20．已知线段AB ，延长AB 到AB 的长．21．已知，如图，点A ，O ，(1)求证：OC 是∠BOE 的平分线，证明：∵90COD ∠=︒，∴DOE ∠+____________90=又∵OD 平分AOE ∠，∴AOD ∠=__________．（________________∴COE ∠=__________．（________________∴OC 是∠BOE 的平分线．(2)图中COE ∠的补角是____________22．随着《某市生活垃圾分类管理条例》正式实施，某市垃圾分类工作进入强制实施阶段，某小区物业管理负责人提出了购买分类垃圾桶的方案．方案一：买A 型号分类垃圾桶，-，b，c，24．已知数轴上A，B，C三个点表示的数分别是10动点P从点A出发，以每秒2个单位长度的速度沿数轴向终点t秒．(1)b=_________，c=__________；(2)点P在数轴上表示的数为___________（用含t的代数式表示）(3)另一动点Q也从点A出发，沿数轴运动至点C后，立刻以原来的速度返回到止，①若P、Q两点同时出发，点Q的速度为每秒4个单位长度，当t=时，PQ②若点P运动到点B时，点Q再从点A出发，当7运动速度．。
2019-2020学年吉林省长春市南关区七年级(下)期末数学试卷(附答案详解)
2019-2020学年吉林省长春市南关区七年级（下）期末数学试卷1. 下列方程的变形，正确的是( )A. 由3x +9=21，得3x =21−9B. 由−2(x −1)=3，得−2x −2=3C. 由x5−1=2，得x −1=10 D. 由7x +4=7，得x +4=12. 下列二元一次方程组中，的解是{x =1y =−1.( )A. {x +y =0x −y =1 B. {x +y =0x −y =−1 C. {x +y =0x −y =2 D. {x +y =0x −y =−2 3. 若代数式2x −3的值为非负数，则x 的取值范围是( )A. x <32B. x ≤32C. x >32D. x ≥324. 如图，在钝角△ABC 中，画AC 边上的高，正确的是( )A.B.C.D.5. 下列正多边形的组合中，能够铺满地面的是( )A. 正六边形和正三角形B. 正五边形和正八边形C. 正八边形和正六边形D. 正五边形和正六边形6. 下列事件中，属于随机事件的有( )①买一张体育彩票会中奖；②掷一枚普通的正方体骰子，掷得的点数小于7； ③掷一枚硬币，有国徽的一面朝下； ④打开电视机，它正在播广告．A. ①②③B. ①③④C. ①②④D. ②③④7. 下列四个图形中，是轴对称图形的是( )A.B.C.D.8. 如图，∠B =25∘，∠A =∠C =90∘，则∠D 的度数是( )A. 65∘B. 35∘C. 25∘D. 15∘9. 如图，△ABC 、△ADE 、△EFG 都是等边三角形，点D和G 分别为AC 和AE 的中点．若AB =8cm ，则图形ABCDEFG 的周长是( )A. 34cmB. 30cmC. 26cmD. 24cm10. 如图，长方形纸片ABCD 中，点E 是AB 的中点，点G是BC 上的一点，∠BEG =70∘.现沿直线EG 将纸片折叠，使点B 落在纸片上的点H 处，连结AH ，则∠HAE 的度数是( )A. 20∘B. 40∘C. 70∘D. 80∘11. 方程3x −6=0的解为x =______ .12. 已知方程组{2x +y =9x +2y =10，则x −y =______.13. 若x −y >0，则x 与y 的大小关系是x ______y.(填“<”或“>”).14. 不透明的袋子中装有4个红球、3个黄球和5个白球，每个球除颜色不同外其它都相同，从中任意摸出一个球，则摸出______球的可能性最大． 15. 如图，直线GH 与正六边形ABCDEF 的边AB 、EF 分别交于点G 、H ，若∠FHG =70∘，则∠AGH =______度．16. 如图，在△ABC 中，∠B =90∘，AB =6cm ，BC =8cm.将△ABC 折叠，使点C 与A 重合，得折痕DE.则△ABE 的周长为______cm.17. 解方程：x+43−x−35=1.18. 解方程组：{3x +4y =19x −y =4.19. 解不等式：2x−13−x >1.20. 解不等式组{2x −1>1x −2≤x−12.21. 已知两条线段a 、b ，其长度分别为15cm 与25cm.另有长度分别为10cm 、20cm 、30cm 、40cm 、50cm 的5条线段，其中能够与线段a 、b 一起组成三角形的有哪几条？ 22. 若一个多边形的内角和比外角和多540∘，求这个多边形的边数．23. 如图，在4×4的正方形网格中，有两个小正方形被涂黑．请你在图①、图②中，分别再将两个空白的小正方形涂黑，使每个图都成为轴对称图形．(要求：图①、图②涂法不同).24. 如图，已知∠AOB =90∘，点E 、F 位于∠AOB 的内部．请在∠AOB 的内部画一点P ，使点P 到点E 、F 的距离相等，且到∠AOB 的两边距离相等．(要求：对画图过程简要说明)25. 如图，在△ABC 中，AB =AC ，点D 在AC 上，且BD =BC =AD ，求△ABC 各角的度数．26. 如图，在直角△ABC 中，∠BAC =90∘，AD ⊥BC 于D ，∠ABC 的平分线BF 交AC 于点F 、交AD 于点E.△AEF 是什么三角形？为什么？请用推理格式写出推理过程．27.学校组织春游，每人车费6元．下面是一班的班长小明与二班的班长小红的对话．小明：我们两班共有91人．小红：我们二班比你们一班多5人．根据上面对话，求一班、二班分别交多少车费．28.如图，在△ABC中，∠DBC=2∠ABD，∠DCB=2∠ACD.(1)若∠ABD=18∘，∠ACD=22∘，求∠A、∠D的度数．(2)若∠ABD=α，∠ACD=β，求∠A、∠D的度数．(用含α、β的代数式表示).(3)∠A与∠D之间的关系是______.答案和解析1.【答案】A【解析】解：A.由3x +9=21，得3x =21−9，故选项A 符合题意； B .由−2(x −1)=3，得−2x +2=3，故选项不B 符合题意； C .由x5−1=2，得x −5=10，故选项C 不符合题意； D .由7x +4=7，得x +47=1，故选项D 不符合题意．故选：A.根据等式的性质进行判断即可．本题考查解一元一次方程，解题关键是熟知解一元一次方程的基本步骤：去分母，去括号，移项，合并同类项，系数化为1.2.【答案】C【解析】解：A 、{x +y =0①x −y =1②，①+②得， 2x =1， 解得：x =12， 故y =−12，故方程组的解为：{x =12y =−12，故此选项错误；B 、{x +y =0①x −y =−1②，①+②得，2x =−1，解得：x =−12，故y =12，故方程组的解为：{x =−12y =12，故此选项错误；C 、{x +y =0①x −y =2②，①+②得，2x =2，解得：x =1， 故y =−1，故方程组的解为：{x =1y =−1，故此选项正确；D 、{x +y =0①x −y =−2②，①+②得，2x =−2，解得：x =−1， 故y =1，故方程组的解为：{x =−1y =1，故此选项错误．故选：C.利用加减消元法分别解出二元一次方程组，进而得出答案．此题主要考查了二元一次方程组的解法，正确掌握解题方法是解题关键．3.【答案】D【解析】解：∵代数式2x −3的值为非负数， ∴2x −3≥0， ∴2x ≥3， 则x ≥32，故选：D.先根据题意列出不等式，再求解即可．本题主要考查解一元一次不等式，解题的关键是掌握解一元一次不等式的基本步骤和依据．4.【答案】B【解析】解：根据三角形高线的定义，AC 边上的高是过点B 向AC 作垂线垂足为E ， 纵观各图形，A 、C 、D 都不符合高线的定义， B 符合高线的定义． 故选：B.根据高的定义对各个图形观察后解答即可．本题主要考查了三角形的高线的定义，是基础题，熟练掌握概念是解题的关键，三角形的高线初学者出错率较高，需正确区分，严格按照定义作图．5.【答案】A【解析】解：A 、正六形和正三角形内角分别为120∘、60∘，因为120∘×2+60∘×2=360∘或120∘+60∘×4=360∘，能构成360∘周角，故能铺满，故此选项符合题意； B 、正五边形和正八边形内角分别为108∘、135∘，不能构成360∘的周角，故不能铺满，故此选项不符合题意；C 、正八边形和正六边形内角分别为135∘、120∘，不能构成360∘的周角，故不能铺满，故此选项不符合题意；D 、正五边形和正六边形内角分别为108∘、120∘，不能构成360∘的周角，故不能铺满，故此选项不符合题意．故选：A.正多边形的组合能否铺满地面，关键是看位于同一顶点处的几个角之和能否为360∘.若能，则说明能铺满；反之，则说明不能铺满．此题主要考查了平面镶嵌，两种或两种以上几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．6.【答案】B【解析】解：①买一张体育彩票会中奖是随机事件；②掷一枚普通的正方体骰子，掷得的点数小于7是必然事件；③掷一枚硬币，有国徽的一面朝下是随机事件；④打开电视机，它正在播广告是随机事件．故属于随机事件的有①③④．故选：B.随机事件就是可能发生，也可能不发生的事件，根据定义即可判断．本题考查的是随机事件，事件分为确定事件和不确定事件(随机事件)，确定事件又分为必然事件和不可能事件，其中，①必然事件发生的概率为1，即P(必然事件)=1；②不可能事件发生的概率为0，即P(不可能事件)=0；③如果A为不确定事件(随机事件)，那么0<P(A)<1.7.【答案】D【解析】解：A.不是轴对称图形，不符合题意；B.不是轴对称图形，不符合题意；C.不是轴对称图形，不符合题意；D.是轴对称图形，符合题意．故选：D.根据轴对称图形的概念，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线(成轴)对称，逐项判定即可．本题主要考查了轴对称图形的概念，判断轴对称图形的关键是寻找对称轴且图形沿对称轴折叠后完全重合．8.【答案】C【解析】解：∵∠C=∠A=90∘，∠AOB=∠COD，∴∠D=∠B=25∘，故选：C.根据三角形的内角和定理计算即可．本题考查三角形内角和定理，解题的关键是熟练掌握基本知识，属于中考常考题型．9.【答案】B【解析】解：∵ABC、△ADE、△EFG都是等边三角形，AB=8cm，∴CB=AC=AB=8cm，∵点D和G分别为AC和AE的中点，∴AD=DE=EA=12AC=4cm，EG=GF=EF=12AE=2cm，∴图形ABCDEFG的周长为8+8+8+2+2+2=30(cm)，故选：B.根据等边三角形的性质进一步可求出图形ABCDEFG的周长．本题考查了等边三角形的性质，熟练掌握等边三角形的性质是解题的关键．10.【答案】C【解析】解：如图，连接BH交EG于O.∵EA=EB=EH，∴∠AHB=90∘，∵EH=EB，GB=GH，∴EG⊥BH，∴∠BOE=90∘，∵∠BEG=70∘，∴∠ABH=20∘，∴∠BAH=70∘，则∠HAE的度数是70∘.故选：C.连接BH交EG于O.首先证明∠AHB=90∘，想办法求出∠BAH即可解决问题．本题考查翻折变换，矩形的性质，直角三角形的判定和性质，三角形内角和定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．11.【答案】2【解析】解：方程3x−6=0，移项得：3x=6，解得：x=2.故答案为：2.方程移项后，将x 系数化为1，即可求出解．此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．12.【答案】−1【解析】解：将2x +y =9记作①，x +2y =10记作②． ∴①-②，得x −y =−1. 故答案为：−1.根据等式的基本性质解决此题．本题主要考查等式的基本性质，熟练掌握等式的基本性质是解决本题的关键．13.【答案】>【解析】解：∵x −y >0， ∴x >y ， 故答案为：>.根据不等式的性质，进行计算即可解答．本题考查了不等式的性质，熟练掌握不等式的性质是解题的关键．14.【答案】白【解析】解：因为袋子中有4个红球、3个黄球和5个白球，从中任意摸出一个球， ①为红球的概率是412=13；②为黄球的概率是312=14； ③为蓝球的概率是512. 可见摸出白球的概率最大． 故答案为：白．分别求出摸出各种颜色球的概率，即可比较出摸出何种颜色球的可能性最小． 本题考查了可能性的大小，要求可能性的大小，只需求出各自所占的比例大小即可，求比例时，应注意记清各自的数目．15.【答案】50【解析】解：∵正六边形的每个内角=(6−2)×180∘6=120∘，∴∠A =∠F =120∘，∵∠A +∠F +∠AGH +∠FHG =360∘， ∴∠AGH =360∘−120∘−120∘−70∘=50∘， 故答案为：50.根据多边形的内角和公式求出正六边形的每个内角是120∘，再根据四边形的内角和是360∘即可求解．本题考查了多边形的内角与外角，考查方程思想，掌握多边形的内角和公式：(n −2)⋅180∘是解题的关键．16.【答案】14【解析】解：∵将△ABC 折叠，使点C 与A 重合，得折痕DE ， ∴AE =EC ，∴△ABE 的周长=AB +BE +AE =AB +BE +EC =AB +BC =6+8=14(cm). 故答案为：14.根据折叠的性质可以得到AE =EC ，则△ABE 的周长=AB +BC ，即可求解． 本题考查了折叠的性质，正确理解折叠中相等的线段是解题的关键．17.【答案】解：x+43−x−35=1，两边同时乘15，得：5(x +4)−3(x −3)=15， 去括号，得：5x +20−3x +9=15， 移项，合并同类项，得：2x =−14， 系数化为1，得：x =−7.【解析】根据解一元一次方程的步骤进行求解即可．本题主要考查解一元一次方程，解答的关键是对解一元一次方程的方法的掌握．18.【答案】解：{3x +4y =19①x −y =4②，将②变形得，x =y +4③ 将其代入①式得， 3(y +4)+4y =19， 解得，y =1， 代入②得，x =5， 故方程组的解为：{x =5y =1.【解析】先将第二个式子变形为用y 的代数式表现x ，再代入第一个式子求出y ，将y 的值代入第二个式子求出x 的值．本题考查用代入法解二元一次方程组：从方程组中选一个系数比较简单的方程，将这个方程组中的一个未知数用含另一个未知数的代数式表示出来，将变形后的关系式代入另一个方程，消去一个未知数，得到一个一元一次方程，解这个一元一次方程，求出x(或y)的值，再求另一个未知数的值．19.【答案】解：∵2x−13−x>1，∴2x−1−3x>3，∴2x−3x>3+1，∴−x>4，则x<−4.【解析】根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得本题主要考查解一元一次不等式，解题的关键是掌握解一元一次不等式的基本步骤和依据．20.【答案】解：{2x−1>1①x−2⩽x−12②，解①得x>1，解②得x≤3，所以不等式组的解集为1<x≤3.【解析】分别解两个不等式得到x>1和x≤3，然后根据大于小的小于大的取中间确定不等式组的解集．本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．21.【答案】解：设第三边为c，∵两条线段a、b，其长度分别为15cm与25cm.∴第三边的取值范围为：10cm<c<40cm，∵20cm、30cm在10cm<c<40cm范围内，所以能够与线段a、b一起组成三角形的有20cm、30cm两条线段．【解析】根据三角形的三边关系得出第三边的取值范围，进而解答即可．此题考查三角形三边关系，关键是根据三角形的三边关系得出第三边的取值范围解答．22.【答案】解：设这个多边形是n边形．则180∘⋅(n−2)=540∘+360∘，解得n=7.【解析】本题考查多边形的内角和与外角和、方程的思想．关键是记住内角和的公式与外角和的特征．此题较难，要结合多边形的内角和公式与外角和的关系来寻求等量关系，构建方程即可求解．23.【答案】解：如图所示：.【解析】直接利用轴对称图形的性质分别得出符合题意的答案．此题主要考查了利用轴对称设计图案，正确掌握轴对称图形的性质是解题关键．24.【答案】解：画出∠AOB的平分线和EF的垂直平分线，它们的交点为P点．如图，【解析】根据角平分线的性质和线段垂直平分线的性质画图．本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了线段垂直平分线的性质．25.【答案】解：设∠A=x.∵AD=BD，∴∠ABD=∠A=x；∵BD=BC，∴∠BCD=∠BDC=∠ABD+∠A=2x；∵AB=AC，∴∠ABC=∠BCD=2x，∴∠DBC=x；∵x+2x+2x=180∘，∴x=36∘，∴∠A=36∘，∠ABC=∠ACB=72∘.【解析】设∠A=x，利用等腰三角形的性质和三角形内角和定理即可求得各角的度数．本题考查等腰三角形的性质；利用了三角形的内角和定理得到相等关系，通过列方程求解是正确解答本题的关键．26.【答案】解：△AEF 是等腰三角形，理由：∵BF 平分∠ABC ，∴∠ABF =∠CBF ，∵∠BAC =90∘，∴∠ABF +∠AFB =90∘，∵AD ⊥BC ，∴∠ADB =90∘，∴∠CBF +∠BED =90∘，∴∠AFB =∠BED ，∵∠BED =∠AEF ，∴∠AEF =∠AFB ，∴AE =AF ，∴△AEF 是等腰三角形．【解析】根据角平分线的定义可得∠ABF =∠CBF ，然后利用直角三角形的两个锐角互余可得∠ABF +∠AFB =90∘，∠CBF +∠BED =90∘，再利用等角的余角相等可得∠AFB =∠BED ，最后结合对顶角相等可得∠AEF =∠AFB ，从而利用等角对等边，即可解答．本题考查了等腰三角形的判定，直角三角形的性质，熟练掌握等腰三角形的判定，以及直角三角形的性质是解题的关键．27.【答案】解：设一班有x 人，二班有y 人，依题意得：{x +y =91y −x =5， 解得：{x =43y =48， ∴6x =6×43=258，6y =6×48=288.答：一班需交258元车费，二班需交288元车费．【解析】设一班有x 人，二班有y 人，根据“两班共有91人，二班比你们一班多5人”，即可得出关于x ，y 的二元一次方程组，解之即可得出x ，y 的值，再将其分别代入6x ，6y 中即可求出结论．本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．28.【答案】∠D =60∘+23∠A【解析】解：(1)∵∠DBC =2∠ABD ，∠DCB =2∠ACD ，∠ABD =18∘，∠ACD =22∘， ∴∠DBC =2∠ABD =36∘，∠DCB =2∠ACD =44∘.∴∠ABC=∠ABD+∠DBC=18∘+36∘=54∘，∠ACB=∠ACD+∠DCB=22∘+44∘=66∘，在△ABC中，∠A=180∘−∠ABC−∠ACB=180∘−54∘−66∘=60∘，在△DBC中，∠D=180∘−∠DBC−∠DCB=180∘−36∘−44∘=100∘，答：∠A=60∘，∠D=100∘；(2)∵∠DBC=2∠ABD，∠DCB=2∠ACD，∠ABD=α，∠ACD=β，∴∠DBC=2∠ABD=2α，∠DCB=2∠ACD=2β.∴∠ABC=∠ABD+∠DBC=α+2α=3α，∠ACB=∠ACD+∠DCB=β+2β=3β，在△ABC中，∠A=180∘−∠ABC−∠ACB=180∘−3α−3β，在△DBC中，∠D=180∘−∠DBC−∠DCB=180∘−2α−2β，答：∠A=180∘−3α−3β，∠D=180∘−2α−2β；(3)由(2)得，α+β=180∘−∠A3=180∘−∠D2，∴3∠D=180∘+2∠A，即∠D=60∘+23∠A，故答案为：∠D=60∘+23∠A..(1)利用角的倍数关系看得出∠DBC=36∘，∠DCB=44∘.进而得出∠ABC=54∘，∠ACB= 66∘，再利用三角形的内角和求出答案即可；(2)利用角的倍数关系看得出∠DBC=2α，∠DCB=2β.进而得出∠ABC=3α，∠ACB= 3β，再利用三角形的内角和求出答案即可；(3)由(2)的结论．得出α+β=180∘−∠A3=180∘−∠D2，再进一步变形即可．本题考查三角形内角和定理，掌握三角形内角和是180∘是正确解答的前提．。
吉林省长春市东北师大附中明珠学校2018-2019学年七年级下学期3月月考英语试题
二、根据句意填空三、用所给单词的正确形式填空1. 找出下列各组划线部分发音与其它三个不同的单词。
【小题1】A ．br eakfast B ．br ead C ．h ealthy D ．dr eam 【小题2】A ．sh e B ．ch ess C ．evening D ．th ese 【小题3】A ．p ut B ．b us C ．br ush D ．h undred 【小题4】A ．ph oto B ．s ofa C ．s ome D ．old 【小题5】A ．b ikeB ．r ideC ．l ifeD ．sw im2. 在横线上填入适当的单词,使句子意思完整,语法准确。
【小题1】Next week, we are going to Shanghai ___________ train.【小题2】I can speak English and I can ___________ speak Japanese.【小题3】Mary ___________ very well so she wants to be a singer one day.【小题4】—Don't be ___________ to ask questions in class.You should be brave(勇敢).—OK.I will try.【小题5】It's my ___________ to be a musician.I hope I can make it come true.一、语音题吉林初一月考134次吉林省长春市东北师大附中明珠学校2018-2019学年七年级下学期3月月考英语试题2-19四、单选题4. My brother Jack can play_________drums.but he can't play_________basketball.A ．/; theB ．the; aC ．the; theD ．the;/5. —Is your uncle good_________children?—Yes.He can always make them happy.A ．atB ．forC ．inD ．with6. Linda is a very nice girl.She always helps_________with_________math.A ．me; meB ．me; myC ．my; myD ．my; me7. I can't sing_________dance,_________I can swim.A ．or; butB ．and; butC ．but; orD ．or; and8. —_________is it from your home to our school?—About five kilometers.A ．How muchB ．How oldC ．How farD ．How long【小题5】It takes Lucy 20 minutes ___________ to the train station by bus.(get)【小题4】John doesn't have much time so he eats breakfast ___________.(quick)【小题3】It's bad for our ___________ to eat too much ice—cream. (tooth)【小题2】I usually get ___________ at 6: 00 and then I have a good break fast. (dress)【小题1】Freddy ___________ us English this term.I think he is my best foreign teacher. (teach)用括号内所给单词的适当形式填空。
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级(下)期末数学试卷
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（下）期末数学试卷一、选择题（本大题共有8道小题．每小题3分，共24分）1．（3分）下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（）A．B．C．D．2．（3分）如图，将△ABC沿BC方向平移1cm得到△DEF，若△ABC的周长为8cm，则四边形ABFD的周长为（）A．8cm B．9cm C．10cm D．11cm3．（3分）如图，∠ACD＝105°．∠A＝70°，则∠B的大小是（）A．25°B．35°C．45°D．65°4．（3分）小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，瓷砖形状不可以是（）A．正三角形B．正四边形C．正五边形D．正六边形5．（3分）如图，将△ABC就点C按逆时针方向旋转75°后得到△A′B′C，若∠ACB＝25°，则∠BCA′的度数为（）A．50°B．40°C．25°D．60°6．（3分）如果一个三角形的两边长分别为2和5，则第三边长可能是（）A．2B．3C．5D．87．（3分）如图，已知AB＝DE，∠B＝∠DEF，下列条件中不能判定△ABC≌△DEF的是（）A．∠A＝∠D B．AC∥DF C．BE＝CF D．AC＝DF8．（3分）如图，在△ABC中，∠B＝45°，AC的垂直平分线交AC于点D．交BC于点E，且∠BAE与∠EAC的比为4：1，则∠C的度数为（）A．20°B．22.5°C．25°D．30°二、填空题（本大题共有6道小题，每小题3分，共18分）9．（3分）在△ABC中，∠A：∠B：∠C＝4：3：2．则∠A＝度．10．（3分）东北师大附中校团委组织了职业微体验活动，初一（3）班52名学生分别去科技细和图书馆参观，去科技馆的人数比去图书馆人数的2倍少5人，去图书馆的人数为x人，则可列方程：11．（3分）如图所示，五角星的顶点是一个正五边形的五个顶点．这个五角星绕中心O至少旋转度能和自身重合．12．（3分）已知等腰三角形的周长为29，一边长为7，则此等腰三角形的腰长为．13．（3分）若不等式组恰有两个整数解，则m的取值范围是．14．（3分）如图，在△ABC中，BF⊥AC于F，AD⊥BC于D，BF与AD相交于E．若AD＝BD，BC＝8cm，DC ＝3cm，则AE＝cm．三、解答题（共10小题，满分78分）15．（8分）解下列方程（组）；（1）；（2）；16．（8分）解下列不等式（组）；（1）3（x﹣1）＞5x+1；（2）；17．（6分）如图，点F是△ABC的边BC的延长线上一点，FD⊥AB于点D．∠A＝30°，∠F＝40°，求∠ACB 的度数．18．（6分）五月份的第二个星期天是母亲节．如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒，根据图中提供信息，求每束鲜花和每个礼的价格．19．（6分）如图，在正方形网格中，△ABC的三个顶点都在格点上，点O也在格点上．（1）画A′B′C′．使△A′B′C′与△ABC关于直线OP成轴对称．（2）画△A''B''C''，使△A''B''C''与△A′B′C′关于点O成中心对称．20．（6分）如图，点B，F，C，E在同一直线上，AB＝DE，BF＝CE，AB∥DE，求证，AC＝DF．21．（8分）如图，△ABC是等边三角形，点D，E分别在AB，AC边上，且AE＝BD．（1）求证：△ABE≌BCD．（2）求∠EFC的度数．22．（8分）小明到某服装商场进行社会调查，了解到该商场为了激励营业员的工作积极性，实行“月总收入＝基本工资+计件奖金”的方法，并获得如下信息：营业员A：月销售件数100件，月总收入2400元；营业员B：月销售件数150件，月总收入2700元；假设营业员的月基本工资为x元，销售每件服装奖励y元．（1）求x、y的值；（2）若某营业员的月总收入不低于3000元，则她当月至少要卖出服装多少件？23．（10分）直角三角形ABC中．∠ACB＝90°，直线l过点C（1）当AC＝BC时，如图①，分别过点A、B作AD⊥l于点E．求证：△ACD≌△CBE．（2）当AC＝8，AC＝6时，如图②，点B与点F关于直线l对称，连接BF，CF．动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动．同时动点N从点F出发．以每秒3个单位的速度沿F→C→B→C→F向终点F运动．点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作l于点E，设运动时间为t秒．①用含t的代数式表示CN．②直接写出当△MDC与△CEN全等时t的值．24．（12分）已知△ABC和△ADE都是等腰三角形，AB＝AC，AD＝AE．∠DAE＝∠BAC．【初步感知】（1）特殊情形：如图①．若点D，E分别在边AB，AC上，则DB EC．（填“＞”、“＜”或“＝”）（2）发现证明：如图②，将图①中的△ADE绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC．【深入探究】（1）如图③，△ABC和△ADE都是等边三角形，点C，E，D在同一条直线上，则∠CDB的度数为线段CE，BD之间的数量关系为；（2）如图④，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，AM 为△ADE中DE边上的高．则∠CDB的度数为；线段AM．BD，CD之间的数量关系为；【拓展提升】如图⑤，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，将△ADE绕点A逆时针旋转，连结BE、CD．当AB＝5．AD＝2时，在旋转过程中，△ABE与△ADC的面积和的最大值为．2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共有8道小题．每小题3分，共24分）1．【解答】解：A、不是轴对称图形，本选项错误；B、不是轴对称图形，本选项错误；C、不是轴对称图形，本选项错误；D、是轴对称图形，本选项正确．故选：D．2．【解答】解：∵△ABC沿BC方向平移1cm得到△DEF，∴AD＝CF＝1，AC＝DF，∴四边形ABFD的周长＝AB+（BC+CF）+DF+AD＝AB+BC+AC+AD+CF，∵△ABC的周长＝8，∴AB+BC+AC＝8，∴四边形ABFD的周长＝8+1+1＝10cm．故选：C．3．【解答】解：∵∠ACD＝∠B+∠A，∠ACD＝105°，∠A＝70°，∴∠B＝105°﹣70°＝35°，故选：B．4．【解答】解：∵用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案，∴小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可以是正五边形．故选：C．5．【解答】解：根据旋转的定义可知旋转角∠ACA′＝75°，∴∠BCA′＝∠ACA′﹣∠ACB＝75°﹣25°＝50°．故选：A．6．【解答】解：设第三边长为x，则由三角形三边关系定理得5﹣2＜x＜5+2，即3＜x＜7．故选：C．7．【解答】解：A、根据ASA判定两个三角形全等；B、根据AAS可以判定两个三角形全等；C、BE＝CF则BC＝FE，根据SAS即可判定两个三角形全等；D、SSA，不能判定三角形全等．故选：D．8．【解答】解：∵ED是AC的垂直平分线，∴AE＝CE，∴∠C＝∠EAC，∵∠B＝45°，∴∠BAC+∠C＝135°，∵∠BAE与∠EAC的比为4：1，∴∠C+∠C+4∠C＝135°，∴∠C＝22.5°，故选：B．二、填空题（本大题共有6道小题，每小题3分，共18分）9．【解答】解：∵∠A：∠B：∠C＝4：3：2，∴可以假设∠A＝4x，∠B＝3x，∠C＝2x，∵∠A+∠B+∠C＝180°，∴4x+3x+2x＝180°，∴x＝20°，∴∠A＝80°，故答案为8010．【解答】解：已知去图书馆人数x人，则去科技馆人数为（2x﹣5）人，根据总人数为52人，可列方程x+（2x﹣5）＝52．故答案为x+（2x﹣5）＝52．11．【解答】解：根据题意，五角星的顶点是一个正五边形的五个顶点，这个五角星可以由一个基本图形（图中的阴影部分）绕中心O至少经过4次旋转而得到，每次旋转的度数为360°除以5，为72度．故答案为：7212．【解答】解：若腰长为7，则底边＝29﹣2×7＝15，∵7+7＜15∴不能组成三角形若底边为7，则腰长＝（29﹣7）÷2＝11故答案为1113．【解答】解：∵不等式组，∴该不等式组的解集为m≤x＜2，∵不等式组恰有两个整数解，∴﹣1＜m≤0，故答案为：﹣1＜m≤0．14．【解答】解：∵BF⊥AC于F，AD⊥BC于D，∴∠CAD+∠C＝90°，∠CBF+∠C＝90°，∴∠CAD＝∠CBF，∵在△ACD和△BED中，，∴△ACD≌△BED，（ASA）∴DE＝CD，∴AE＝AD﹣DE＝BD﹣CD＝BC﹣CD﹣CD＝2；故答案为2．三、解答题（共10小题，满分78分）15．【解答】解：（1）去分母得：2x+1＝3x﹣6，解得：x＝7；（2），①×3+②得：7x＝14，解得：x＝2，把x＝2代入①得：y＝3，则方程组的解为．16．【解答】解：（1）3x﹣3＞5x+1，3x﹣5x＞1+3，﹣2x＞4，x＜﹣2；（2）解不等式x+1≥0，得：x≥﹣1，解不等式5x﹣2＜3（x+2），得：x＜4，则不等式组的解集为﹣1≤x＜4．17．【解答】解：在△DFB中，∵FD⊥AB，∴∠FDB＝90°，∵∠F＝40°，∠F+∠B＝90°，∴∠B＝90°﹣40°＝50°．在△ABC中，∵∠A＝30°，∠B＝50°，∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣30°﹣50°＝100°．18．【解答】解：设每束鲜花x元，每个礼盒y元，根据题意得：，解得：．答：每束鲜花12元，每个礼盒20元．19．【解答】解：（1）如图△A′B′C′即为所求．（2）如图△A''B''C''即为所求．20．【解答】证明：∵AB∥DE，∴∠B＝∠E．∵BF＝CE，∴BF+FC＝CE+FC，即BC＝EF．又AB＝DE，∴△ABC≌△DEF（SAS）．∴AC＝DF．21．【解答】证明：（1）∵△ABC是等边三角形，∴AB＝AC，∠A＝∠DBC＝60°，AE＝BD．∴△ABE≌△BCD（SAS）；（2）∵△ABE≌△BCD，∴∠ABE＝∠BCD．∴∠EFC＝∠FBC+∠FCB＝∠FBC+∠ABE＝∠ABC＝60°．22．【解答】解：（1）由题意，得，解得即x的值为1800，y的值为6；（2）设某营业员当月卖服装m件，由题意得，1800+6m≥3000，解得，m≥200，∵m只能为正整数，∴m最小为200，即某营业员当月至少要卖200件．23．【解答】（1）证明：△ACD与△CBE全等．理由如下：∵AD⊥直线l，∴∠DAC+∠ACD＝90°，∵∠ACB＝90°，∴∠BCE+∠ACD＝90°，∴∠DAC＝∠ECB，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS）；（2）解：①由题意得，AM＝t，FN＝3t，则CM＝8﹣t，由折叠的性质可知，CF＝CB＝6，∴CN＝6﹣3t；②由折叠的性质可知，∠BCE＝∠FCE，∵∠MCD+∠CMD＝90°，∠MCD+∠BCE＝90°，∴∠NCE＝∠CMD，∴当CM＝CN时，△MDC与△CEN全等，当点F沿F→C路径运动时，8﹣t＝6﹣3t，解得，t＝﹣1（不合题意），当点F沿C→B路径运动时，8﹣t═3t﹣6，解得，t＝3.5，当点F沿B→C路径运动时，由题意得，8﹣t＝18﹣3t，解得，t＝5，当点F沿C→F路径运动时，由题意得，8﹣t＝3t﹣18，解得，t＝6.5，综上所述，当t＝3.5秒或5秒或6.5秒时，△MDC与△CEN全等．24．【解答】解：【初步感知】（1）∵DE∥BC，∴＝，∵AB＝AC，∴DB＝EC，故答案为：＝，（2）成立．理由：由旋转性质可知∠DAB＝∠EAC，在△DAB和△EAC中，∴△DAB≌△EAC（SAS），∴DB＝CE；【深入探究】（1）如图③，设AB，CD交于O，∵△ABC和△ADE都是等边三角形，∴AD＝AE，AB＝AC，∠DAE＝∠BAC＝60°，∴∠DAB＝∠EAC，在△DABDAB和△EAC中，∴△DAB≌△EAC（SAS），∴DB＝CE，∠ABD＝∠ACE，∵∠BOD＝∠AOC，∴∠BDC＝∠BAC＝60°；（2）∵△DAE是等腰直角三角形，∴∠AED＝45°，∴∠AEC＝135°，在△DAB和△EAC中，∴△DAB≌△EAC（SAS），∴∠ADB＝∠AEC＝135°，BD＝CE，∵∠ADE＝45°，∴∠BDC＝∠ADB﹣∠ADE＝90°，∵△ADE都是等腰直角三角形，AM为△ADE中DE边上的高，∴AM＝EM＝MD，∴AM+BD＝CM；故答案为：90°，AM+BD＝CM；【拓展提升】如图，由旋转可知，在旋转的过程中△ADE的面积始终保持不变，∴△ABE与△ADC面积的和达到的最大，∴△ADC面积最大，∵在旋转的过程中，AC始终保持不变，∴要△ADC面积最大，∴点D到AC的距离最大，∴DA⊥AC，∴△ABE与△ADC面积的和达到的最大为2××AC×AD＝5×2＝10，故答案为10．。
吉林省长春市东北师大附中明珠学校2024年英语七年级第二学期期末调研试题含答案
吉林省长春市东北师大附中明珠学校2024年英语七年级第二学期期末调研试题满分120分，时间90分钟一、完形填空(10分)1、阅读下面短文，然后从各题所给的四个选项中选出一个最佳答案。
Jack Hunt-Broersma is a 47-year-old woman from South Africa. She finished 102 marathons (马拉松) in 102 days last year. She ____1____ a new world record (纪录) for women.When she was young, she didn’t like ____2____. Jacky lost her left leg because of cancer (癌症) in 2002 when she was only 26 years old. She had to use an artificial limb (假肢). She learned ____3____ to walk again in the next years. To bring her back to ____4____, she started to run after that.“I wanted to run marathons, and it might help ____5____ more. When I told my doctor about it, he didn’t think it was a____6____ idea,” she says. “ But I thought it could help me a lot. So I did that ____7____.” In 2016, she finished her first marathon.“Running really changes (改变) my ____8____,” she says. “I feel like a healthy person when running. I love the sport. It lets me know how strong I am. I hope more people ____9____ artificial limbs can love running. They don’t have to run a marathon, ____10____ I just want to see them make their bodies active (活跃的) and feel free. In fact, you can do what you want.”1. A. answered B. lost C. missed D. made2. A. jumping B. swimming C. running D. shouting3. A. how B. where C. why D. when4. A. school B. health C. study D. work5. A. you B. them C. us D. me6. A. relaxing B. difficult C. good D. funny7. A. quickly B. easily C. freely D. lazily8. A. age B. family C. time D. life9. A. for B. with C. from D. on10. A. but B. so C. because D. or二、阅读理解（40分）2、1. eyes##two big eyes2. (He can speak) English and Chinese.3. He has two big eyes./He has one nose and one mouth./He has ten fingers./He has long arms and small hands /He has two long legs and two big feet.（任意两点即可）。
2019-2020学年吉林省长春市南关区东北师大附中明珠校区七年级(上)期末数学试卷(附答案详解)
2019-2020学年吉林省长春市南关区东北师大附中明珠校区七年级（上）期末数学试卷1.单项式−35ab2的系数是()A. −35B. 35C. −3D. 32.在数轴上，表示−2的点与原点的距离是()A. −2B. 0C. 2D. 不能确定3.如图，水杯的主视图是()A.B.C.D.4.下列各式中正确的是()A. −|5|=|−5|B. |−5|=5C. |−5|=−5D. |−1.3|<05.由下面正方体的平面展开图可知，原正方体“我”字所在的面的对面的汉字是()A. 中B. 国C. 的D. 梦6.下列图形中，∠1与∠2不是互补关系的是()A. B.C. D.7.x、y、c是有理数，则下列判断错误的是()A. 若x=y，则x+2c=y+2cB. 若x=y，则a−cx=a−cyC. 若x=y，则xc =ycD. 若xc=yc，则x=y8.如图，将一副三角尺按不同的位置摆放，下列各图中，∠α与∠β互余的是()A. B.C. D.9.将多项式x2+2−3x3按字母x的降幂排列为______ ．10.2018年10月23日，世界上最长的跨海大桥一港珠澳大桥正式开通，这座海底隧道于一身，全长约55000米．其中55000用科学记数法可表示为______．11.已知∠α=60°32′，则∠α的余角是______ ．12.某商品原价为a元，因销量下滑，经营者连续两次降价，每次降价10%，问现在这种商品的价格是______ 元.13.如图，AB//CD，DB⊥BC，∠1=40°，则∠2的度数是______．14.欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB//CD，∠BAE=92°，∠DCE=115°，则∠E的度数是______°.15.计算：(1)−13+28−77；(2)4−4×(−3)×(−1 3 ).16.计算：(1)3a3+a2−2a3−a2；(2)(2x2−12+3x)−3(x−x2+12).17.解方程：(1)14x=2x−6；(2)x−1=13x+1；(3)4x−x=2(x−1)+5；(4)6x−18=34+x．18.先化简，再求值：(5xy−8x3)−(−12x2+4xy)，其中x=1，y=2．219.如图是由6个边长为1的相同小正方体组成的几何体，请在边长为1的网格中画出它的三视图．20.如图，延长线段AB至点D，使点B为线段AD的中点，点C在线段BD上，CD=2BC，若BC=3，求AD的长．21.如图，某花园的护栏是用一些半圆形造型的钢条围成的，半圆的直径为80厘米，且每增加一个半圆形条钢，护栏长度就增加a厘米(a>0)，设半圆形条钢的总个数为x个(x为正整数)，护栏总长度为y厘米．(1)当a=60时，用含x的代数式表示护栏总长度y(结果要求化简)；(2)用含a、x的代数式表示护栏的总长度y(结果要求化简)，并求a=50，x=41时，护栏长度y的值．22.推理填空已知：如图，AB//CD，∠1=∠2求证：∠BEF=∠EFC证明：连接BC∵AB//CD(已知)∴∠ABC=______(______)∵∠1=∠2∴∠ABC−∠1=______−∠2∴∠EBC=______∴______//______(______)∴∠BEF=∠EFC(______)23.如图，直线AB与直线MN相交，交点为O，OC⊥AB，OA平分∠MOD，若∠BON=20°，求∠COD的度数．24.数轴上任意三个点，如点A、点B、点C，如果满足：点A在点B的左侧，且AC=kBC(k>0)，我们称点C为AB的k阶好点，比如点A、B、C在数轴上表示的数分别是−2，4，2，则AC=2BC，则称点C为AB的2阶好点．(1)若点A、点B、点C表示的数分别是−2，3，8，则点C是AB的______ 阶好点；(2)若点A、点B、点C表示的数分别是−2，3，1，则点C是AB的______ 阶好点；2(3)若点D、点E表示的数分别是−5和−3，动点M从点D出发，以每秒1个单位的速度向左运动，同时，动点N从点E出发，以每秒2个单位的速度向右运动，设运动时间为t，①点M表示的数为______ ，点N表示的数为______ (用含字母t的代数式表示)；②原点为线段MN的2阶好点时，求t的值；③设MN的1阶好点为点P，3阶好点为点Q，直接写出点P、点Q到原点的距离相等时t的值．25.把两个三角尺ABC与DEF按如图所示那样拼在一起，其中点D在BC上，DM为∠CDE的平分线，DN为∠BDF的平分线，则∠MDN的度数是______ ．26.如图，点C是线段AB上的一点，点D是线段CB的中点，已知图中所有线段的长度之和为23，线段AC的长度与线段CB的长度都是正整数，则线段AC的长度是______ ．27.小明学习了《有理数》后，对运算非常感兴趣，于是定义了一种新运算“△”规则．如下：对于两个有理数m，n，m△n=|m−n|+m+n2(1)计算：1△(−2)=______ ；(2)这个运算中，交换m、n两数的位置，计算结果是否会受到影响，请结合整式的计算，说明理由．(3)若a1=|x|，a2=|x−1|，若a1△a2=3，直接写出x的值．28.如图(1)，用两个等腰直角三角形的三角板拼成正方形ABCD，含有30°角的三角板AEF的顶点A与正方形的顶点A重合，边AE与正方形的边AB在同一直线上，∠FAE=30°，∠AEF=90°，将三角形AEF绕点A逆时针旋转，旋转的速度为每秒5°.设运动时间为t秒(0≤t≤18)．(1)如图(2)，当正方形的顶点C在△AEF的内部时，AE、AF与正方形ABCD的边交于点H、G(设AE、AF足够长)；①求此时t的范围；②∠FGC与∠CHE度数的和是否变化？若不变，直接写出∠FGC与∠CHE度数和，若变化，请说明理由；∠FGC．③当t=______ 时，∠CHE=75(2)如图(3)，在整个运动过程中，过点D作DP//EF交正方形ABCD的边于点P，直接写出DP将∠ADC分成的两部分角度之比为1：2时，t的值．答案和解析1.【答案】A【知识点】单项式【解析】解：单项式−35ab2的系数是−35．故选：A．单项式中数字因数叫做单项式的系数．考查了单项式，解答此题关键是构造单项式的系数，把一个单项式分解成数字因数和字母因式的积，是找准单项式的系数关键．2.【答案】C【知识点】数轴【解析】解：如图，在数轴上，表示−2的点与原点的距离为2，故选：C．结合数轴可直接得出答案．本题主要考查数轴，解题的关键是掌握数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．3.【答案】B【知识点】简单组合体的三视图【解析】解：从正面看，圆柱体的部分看到的是长方形，再加上把手即可，故选：B．从正面看，圆柱体的部分看到的是长方形，再加上把手即可，考查简单几何体的三视图，主视图是从正面看到的图形，左视图是从左面看到的图形，俯视图是从上面看到的图形．4.【答案】B【知识点】绝对值、非负数的性质：绝对值【解析】解：A、∵−|5|≠|−5|，∴选项A不符合题意；B、∵|−5|=5，∴选项B符合题意；B、∵|−5|=5，∴选项C不符合题意；D、∵|−1.3|>0，∴选项D不符合题意．故选：B．根据有理数大小比较的方法，以及绝对值的含义和求法，逐项判断即可．此题主要考查了有理数大小比较的方法，以及绝对值的含义和求法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．5.【答案】B【知识点】正方体相对两个面上的文字【解析】解：根据正方体相对的面的特点，“我”字所在的面的对面的汉字是“国”，故选：B．正方体的展开图有11种情况，分析平面展开图的各种情况后再认真确定哪两个面是对面．本题考查了正方体侧面展开图，熟记正方体侧面展开图对面和相邻的面是解题的关键．6.【答案】C【知识点】对顶角、邻补角【解析】解：A.∠1与∠2是互补关系，故本选项不合题意；B.由平行线的性质可知∠1与∠2是互补关系，故本选项不合题意；C.由对顶角的定义可知∠1与∠2是对顶角，不一定具有互补关系，故本选项符合题意；D.∠1+∠2=180°，即∠1与∠2是互补关系，故本选项不合题意．故选：C．根据互补的两个角的和为180°判定即可．本题主要考查了补角的定义，熟记定义是解答本题的关键．7.【答案】C【知识点】等式的概念及其基本性质【解析】解：A、根据等式的性质1可得出，若x=y，则x+2c=y+2c，原变形正确，故此选项不符合题意；B、根据等式的性质1和2得出，若x=y，则a−cx=a−cy，原变形正确，故此选项不符合题意；C、由x=y得出xc =yc必须c≠0，当c=0时不成立，故本选项符合题意；D、根据等式的性质2可得出，若xc =yc，则x=y，原变形正确，故此选项不符合题意；故选：C．根据等式的性质一一判断即可．本题考查等式的性质，解题的关键是记住等式的性质：性质1、等式两边加同一个数(或式子)结果仍得等式；性质2、等式两边乘同一个数或除以一个不为零的数，结果仍得等式．8.【答案】D【知识点】余角和补角、对顶角、邻补角【解析】解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β不互余，故本选项错误；C、∠α与∠β不互余，故本选项错误；D、∠α与∠β互余，故本选项正确．故选：D．根据图形，结合互余的定义判断即可．本题考查了对余角和补角的应用，主要考查学生的观察图形的能力和理解能力．9.【答案】−3x3+x2+2【知识点】多项式【解析】解：多项式x2+2−3x3的项为x2，2，−3x3，按字母x降幂排列为−3x3+x2+2，故答案为：−3x3+x2+2．先分清多项式的各项，然后按多项式降幂排列的定义排列．本题考查了多项式，我们把一个多项式的各项按照某个字母的指数从大到小或从小到大的顺序排列，称为按这个字母的降幂或升幂排列．要注意，在排列多项式各项时，要保持其原有的符号．10.【答案】5.5×104【知识点】科学记数法-绝对值较大的数【解析】解：将55000用科学记数法表示为：5.5×104．故答案为：5.5×104．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值<1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．11.【答案】29°28′【知识点】度分秒的换算、余角和补角【解析】解：∵∠α=60°32′，∴∠α的余角是：90°−60°32′=29°28′，故答案为：29°28′．根据余角的概念进行计算即可．本题考查余角的概念和度分秒的换算．解题的关键是掌握余角和补角的定义，如果两个角的和等于90°，就说这两个角互为余角．如果两个角的和等于180°，就说这两个角互为补角．12.【答案】0.81a【知识点】列代数式【解析】解：根据题意得：设现在的商品价格为s元，则s=a×(1−10%)×(1−10%)=0.81a，故答案为：0.81a．根据题意在原价a的基础上连续两次降价列出代数式，即可求解．本题考查了列代数式，解决本题得关键是正确理解题意．13.【答案】50°【知识点】平行线的性质【解析】解：∵AB//CD，∴∠1=∠BCD=40°，∵DB⊥BC，∴∠CBD=90°，∴∠2=90°−40°=50°．故答案为50°．根据平行线性质由AB//CD得到∠1=∠BCD=40°，再根据垂直的定义得∠CBD=90°，然后利用三角形内角和定理计算∠2的度数．本题考查了平行线性质：两直线平行，同位角相等．14.【答案】23【知识点】三角形的外角性质、平行线的性质【解析】解：如图，延长DC交AE于F，∵AB//CD，∠BAE=92°，∴∠CFE=92°，又∵∠DCE=115°，∴∠E=∠DCE−∠CFE=115°−92°=23°．故答案为：23．延长DC交AE于F，依据AB//CD，∠BAE=92°，可得∠CFE=92°，再根据三角形外角性质，即可得到∠E=∠DCE−∠CFE．本题主要考查了平行线的性质，三角形外角的性质，解决问题的关键是掌握：两直线平行，同位角相等．15.【答案】解：(1)原式=−13−77+28=−90+28=−62；(2)原式=4−4×3×13=4−4=0．【知识点】有理数的混合运算【解析】(1)原式结合后，相加即可求出值；(2)原式先计算乘法运算，再计算减法运算即可求出值．此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．16.【答案】解：(1)原式=a3；(2)原式=2x2−12+3x−3x+3x2−32=5x2−2．【知识点】整式的加减【解析】(1)原式合并同类项即可得到结果；(2)原式去括号合并即可得到结果．此题考查了整式的加减，熟练掌握运算法则是解本题的关键．17.【答案】解：(1)14x=2x−6，移项得：14x−2x=−6，合并同类项得：12x=−6，解得：x=−12；(2)x−1=13x+1，移项得：x−13x=1+1，合并同类项得：23x=2，解得：x=3；(3)4x−x=2(x−1)+5，去括号得：4x−x=2x−2+5，移项得：4x−x−2x=−2+5，合并同类项得：x=3；(4)6x−18=34+x，去分母得：6x−1=6+8x，移项得：6x−8x=6+1，合并得：−2x=7，解得：x=−72．【知识点】一元一次方程的解法【解析】(1)移项，合并同类项，系数化为1即可求解；(2)移项，合并同类项，系数化为1即可求解；(3)去括号，移项，合并同类项，系数化为1即可求解；(4)去分母，移项，合并同类项，系数化为1即可求解．本题考查了解一元一次方程，熟练掌握等式的性质是解题的关键．18.【答案】解：(5xy−8x3)−(−12x2+4xy)=5xy−8x3+12x2−4xy=xy−8x3+12x2，当x=12，y=2时，原式=12×2−8×(12)3+12×(12)2=1−8×18+12×14=1−1+3=3．【知识点】整式的加减【解析】根据去括号、合并同类项化简后再代入求值即可．本题考查整式的加减，掌握去括号、合并同类项法则是正确计算的前提．19.【答案】解：如图所示：【知识点】简单几何体的三视图【解析】由几何体可得从正面看有4列，每列小正方形数目分别为1，2，1，1；从左面看有2列，每列小正方形数目分别为2，1；从上面看有4列，每行小正方形数目分别为1，2，1，1，进而得出答案．本题考查作图−三视图．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．∴CD=6，∴BD=BC+CD=3+6=9，∵点B为线段AD的中点，∴AD=2BD=18．【知识点】两点间的距离【解析】先由CD=2BC，BC=3，求得CD=6，进而得BD，再由点B为线段AD的中点，得AD．本题主要考查了线段的和差计算，线段的中点定义，关键是弄清各线段之间的关系，正确运用线段和差和线段中点，进行解答．21.【答案】解：(1)y=80+a(x−1)，当a=60时，y=80+60(x−1)=60x+20．(2)y=80+a(x−1)，当a=50，x=41时，y=80+50(41−1)=2080．【知识点】列代数式、代数式求值【解析】本题根据每增加一个半圆形护栏长度就增加a，列出代数式，代入值即可．本题考查了根据图形规律列出代数式，能够把数值代入代数式求值的能力．22.【答案】∠DCB；两直线平行，内错角相等；∠DCB；∠FCB；BE；FC；内错角相等，两直线平行；两直线平行，内错角相等【知识点】平行线的判定与性质【解析】证明：连接BC∵AB//CD(已知)∴∠ABC=∠DCB(两直线平行，内错角相等)∵∠1=∠2∴∠ABC−∠1=∠DCB−∠2∴∠EBC=∠FCB∴BE//FC(内错角相等，两直线平行)∴∠BEF=∠EFC(两直线平行，内错角相等)两直线平行，两直线平行，内错角相等．依据两直线平行，内错角相等，可得∠ABC =∠DCB ，进而得出∠EBC =∠FCB ，依据内错角相等，两直线平行，可得BE//FC ，进而得到∠BEF =∠EFC ．本题考查了平行线的判定与性质，熟记性质与判定方法是解题的关键，难点在于作辅助线．23.【答案】解：∵∠BON =20°，∴∠AOM =20°，∵OA 平分∠MOD ，∴∠AOD =∠MOA =20°，∵OC ⊥AB ，∴∠AOC =90°，∴∠COD =90°−20°=70°．【知识点】角的平分线、垂线的相关概念及表示【解析】利用对顶角相等可得∠AOM 的度数，再利用角平分线的定义和垂线定义进行计算即可．此题主要考查了垂线，关键是掌握对顶角相等，当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线． 24.【答案】2 1 −5−t 2t −3【知识点】列代数式、数轴、一元一次方程的应用【解析】解：(1)∵AC =10，BC =5，∴AC =2BC ，∴C 为AB 的2阶好点．故答案为：2．(2)∵AC =52，BC =52∴AC =BC ，∴C 为AB 的1阶好点．故答案为：1．(3)①M 表示的数为−5−t ，N 表示的数为2t −3，故答案为：−5−t ，2t −3；∴OM =2ON ，∴|−5−t|=2|2t −3|，即5+t =−4t +6或5+t =4t −6，解得：t =15或113；③∵MN 的1阶好点为P ，∴MP =NP ，即P 为MN 中点，∴P 表示的数为−5−t+2t−32=12t −4， 又∵Q 为MN 的3阶好点，设表示的数为m ，∴QM =3QN ，|m +t +5|=3|m −2t +3|，解得m =72t −2或54t −72，即|12t −4|=|72t −2|，解得t =32或−23(舍)，|12t 一4|=|54t −72|， 解得t =307或−23， 综上所述，P 、Q 到原点距离相等时t =32或307．(1)分别计算出AC 与BC 的长度，可得结论；(2)分别计算出AC 与BC 的长度，可得结论；(3)①根据两个点的运动速度和方向可得答案；②根据2阶好点的定义列方程可解决问题，注意分情况；③先用含t 的式子表示出P 和Q ，再列方程即可．考查了一元一次方程的应用，此题比较复杂，读题是难点，所以解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解． 25.【答案】135°【知识点】角的平分线【解析】解：∵∠EDF=90°，∴∠CDE+∠BDF=90°，∵DM为∠CDE的平分线，DN为∠BDF的平分线，∴∠MDE=12∠CDE，∠FDN=12∠BDF，∴∠CDM+∠BDF=12(∠CDE+∠BDF)=12×90°=45°，∴∠MDN=180°−45°=135°，故答案为135°．根据∠EDF=90°，可得出∠CDE+∠BDF=90°，再根据DM为∠CDE的平分线，DN为∠BDF的平分线，可得出∠CDM+∠BDF=45°，从而得出∠MDN的度数．本题考查了角平分线的定义，求得∠CDE+∠BDF=90°是解题的关键．26.【答案】3【知识点】两点间的距离【解析】解：设AC=y，CD=BD=12x，则AC+CD+DB+AD+AB+CB=23，即：y+12x+12x+(12x+y)+(x+y)+x=23，得：7x+6y=46，因为线段AC的长度与线段CB的长度都是正整数，所以可知x最大为6，可知：x=6，y为小数，不符合；x=5，y为小数，不符合；x=4，y=3，符合题意；x=3，y为小数，不符合；x=2，y为小数，不符合；x=1，y为小数，不符合．故答案为：3．可以设出AC和CD的长，再根据图中所有线段的长度之和为23，即可列出等式，再根据线段AC的长度与线段CB的长度都是正整数，即可求出答案．本题考查了两点间的距离，有一定难度，根据题意列出方程式，并探讨解的合理性是关键．27.【答案】1【知识点】有理数的混合运算【解析】解：(1)1△(−2)=|1−(−2)|+1+(−2)2=3+1−22=1，故答案为：1；(2)∵m△n=|m−n|+m+n2，n△m=|n−m|+n+m2．而|m−n|=|n−m|，∴m△n=n△m，因此交换m、n两数的位置，计算结果不会受到影响；(3)∵a1△a2=3，∴|a1−a2|+a1+a22=3，∴|a1−a2|+a1+a2=6，①当a1>a2时，|a1−a2|+a1+a2=6，即a1−a2+a1+a2=6，∴a1=3，又∵a1=|x|，∴x=3或x=−3，当x=−3时，a2=|x−1|=4>a1(舍去)，②当a1<a2时，|a1−a2|+a1+a2=6，即−a1+a2+a1+a2=6，∴a2=3，又∵a2=|x−1|，∴x=4或x=−2，当x=4时，a1=|x|=4>a2(舍去)，因此x=3或x=−2．(1)根据“新定义”的运算进行计算即可；(2)求出“m△n”和“n△m”的结果，比较得出结论；(3)求出a1、a2的值，再求出x的值即可．本题考查有理数的混合运算，解答本题的关键是明确有理数混合运算的计算方法．28.【答案】4【知识点】四边形综合【解析】解：(1)①当∠FAB=∠CAB=45°时，点C落在AF上，∴∠EAB=∠FAB−∠FAE=5t=45°−30°=15°，∴t=3，当点C落在AE上时，∠EAB=∠CAB=5t=45°，解得t=9，∴3<t<9．②∠FGC与∠CHE度数的和不变，理由如下：∵CD//AB，∴∠FGC=∠FAB=∠FAE+∠EAB=30°+5t，∠EHC=∠AHB=90°−∠EAB=90°−5t，∴∠FGC+∠CHE=30°+5t+90°−5t=120°．③由②得∠CHE=90°−5t，∠FGC=30°+5t，当∠CHE=75∠FGC时，90°−5t=75(30°+5t)，解得t=4，故答案为：4．(2)∵∠ADC=90°，DP将∠ADC分成的两部分角度之比为1：2，∴∠ADP=13∠ADC=30°，∠CDP=23∠ADC=60°或∠ADP=23∠ADC=60°，∠CDP=13∠ADC=30°，设DP交AE于点M，∵DP//EF，∴∠DMA=∠E=90°，∴∠ADP=90°−∠DAM，又∵∠EAB=90°−∠DAM，∴∠ADP=∠EAB=5t，当5t=30°时，t=6，当5t=60°时，t=12，∴t=6或12．(1)①分别求出点C在AF与AE上的值．②用含t代数式分别表示出∠FGC与∠CHE，再表示出∠FGC与∠CHE度数的和．∠FGC求解．③用含t代数式表示∠CHE=75(2)由DP将∠ADC分成的两部分角度之比为1：2，求出∠ADP的度数为30°或60°，然后由含t代数式分别求解．本题考查动角问题，解题关键是熟练掌握平行线的性质并注意分类讨论．。
吉林市长春市东北师范大学附属中学明珠学校2017-2018学年七年级(下)Unit4大练习试卷及解析
吉林市长春市东北师范大学附属中学明珠学校2017-2018学年七年级(下)Unit4大练习英语试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上第I卷（选择题）一、单选题A. TellB. To tellC. TellingD. Tells2.I can't play with my friends after school___homework comes first.A. andB. butC. becauseD. so3.-Can you play football with us?-Sorry.I have____homework to do.A. so manyB. much tooC. too muchD. too many4.Tom,you can't______late for school.A. isB. beC. arrivesD. was5.I can go out_____school nights,but I have to be back____9 o' lock.A. at; beforeB. on; beforeC. at; afterD. on; for6.My father always likes ______ a newspaper before going to bed.A. watchingB. seeingC. lookingD. reading第II卷（非选择题）二、用所给单词的正确形式填空7.Mary practices____(speak) English every day.so her oral English 口语)is very good.8.Remember_______(call)me when you get to Shanghai.9.Eating______(much) fruit and vegetables is good for our health.10.It's so_____(noise)in the hallways that I can’t go to sleep.11.To grow taller it's____(importance) to rise(起床)early and sleep early.三、单词拼写12.We have a talent show tomorrow. ______your guitar to school and show us!13.It's too cold _____today. Put on your coat if you go out.14.-Why does he______late for class? -Because his bike is broken.15.Everyone needs to be _______in the reading room.16.-I have a math test this afternoon.-Good ______to you.参考答案1.A【解析】1.句意：告诉你妈妈开车带你去学校。
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级(下)第一次月考数学试卷(解析版)
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（下）第一次月考数学试卷一、选择题（本大题共8小题，共24.0分）1.下列方程中，解为x=-1的是（）A. B. C. D.2.x=1是关于x的方程2x-a=0的解，则a的值是（）A. B. 2 C. D. 13.根据“x的3倍与5的和比x的少3”可列方程（）A. B. C. D.4.方程组的解是（）A. B. C. D.5.若二元一次方程组的解为，则a-b=（）A. 1B. 3C.D.6.一个长方形的周长为30cm，若这个长方形的长减少1cm，宽增加2cm就可成为一个正方形，设长方形的长为xcm，可列方程为（）A. B. C. D.7.小明到商店购买“五四青年节”活动奖品，购买20只铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元，设每支铅笔x元，每本笔记本y元，则可列方程组（）A. B. C. D.8.已知某座桥长800米，现有一列火车从桥上通过，测得火车从开始上桥到完全通过共用了1分钟，这列火车完全在桥上的时间为40秒，则火车的速度和车长分别是（）A. 20米秒，200米B. 18米秒，180米C. 16米秒，160米D. 15米秒，150米二、填空题（本大题共6小题，共18.0分）9.当x=______时，代数式4x-5与3x-6的值互为相反数．10.在y=x-4中，如果x=1.5，那么y=______．11.某商品按定价的八折出售，售价14.8元，则原定价是______元．12.某煤矿预计今年比去年增产15%，达到年产煤60万吨，设去年产煤x万吨，则可列方程______．13.若关于x、y的二元一次方程组的解是，则a b的值为______．14.《孙子算经》是中国古代重要的数学著作，其中有一段文字的大意是：甲、乙两人各有若干钱．如果甲得到乙所有钱的一半，那么甲共有钱48文；如果乙得到甲所有钱的，那么乙也共有钱48文．甲、乙两人原来各有多少钱？设甲原有x文钱，乙原有y文钱，可列方程组是______．三、计算题（本大题共3小题，共26.0分）15.解方程组：（1）（用代入消元法解）；（2）（用加减消元法解）；（3）；（4）16.甲、乙两人在400米的环形跑道上进行早锻炼，甲慢跑速度为105米/分，乙步行速度为25米/分，两人同时同地同向出发，经过多少时间，两人第一次相遇？（请列一元一次方程求解）17.民航规定：乘坐飞机普通舱旅客一人最多可免费携带20千克行李，超过部分每千克按飞机票价的1.5%购买行李票．一名旅客带了35千克行李乘机，机票连同行李费共付了1323元，求该旅客的机票票价．四、解答题（本大题共4小题，共32.0分）18.解方程：（1）4x+3=2（x-1）+1；（2）x；（3）；（4）x-+2．19.小明作业本中有一页被墨水污染了，已知他所列的方程组是正确的．写出题中被墨水污染的条件，并求解这道应用题．20.据电力部门统计，每天8：00至21：00是用电的高峰期，简称“峰时”，21：00至次日8：00是用电的低谷时期，简称“谷时”，为了缓解供电需求紧张矛盾，某市电力部门于本月初统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：（1）小张家上月“峰时”用电50度，“谷时”用电20度，若上月初换表，则相对于换表前小张家的电费是增多了还是减少了？增多或减少了多少元？请说明理由．（2）小张家这个月用电95度，经测算比换表前使用95度电节省了5.9元，问小张家这个月使用“峰时电”和“谷时电”分别是多少度？21.[背景资料]一棉花种植区的农民研制出采摘棉花的单人便携式采棉机，采摘效率高，能耗低，绿色环保，经测试，一个人操作该采棉机的采摘效率为35公斤/时，大约是一个人手工采摘的3.5倍，购买一台采棉机需900元，雇人采摘棉花，按每采摘1公斤棉花a元的标准支付雇工工钱，雇工每天工作8小时．[问题解决]（1）一个雇工手工采摘棉花，一天能采摘多少公斤？（2）一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机，求a的值；（3）在（2）的前提下，种植棉花的专业户张家和王家均雇人采摘棉花，王家雇佣的人数是张家的2倍，张家雇人手工采摘，王家所雇的人中有的人自带采棉机采摘，的人手工采摘，两家采摘完毕，采摘的天数刚好一样，张家付给雇工工钱总额为14400元，王家这次采摘棉花的总重量是多少？答案和解析1.【答案】B【解析】解：把x=-1代入题目的四个选项得：A、左边=x-1=-2≠右边=-1，所以，A错误；B、左边=-2x-1=-2×（-1）-1=1=右边，所以，B正确；C、左边=-2x=-2×（-1）=2≠，所以，C错误；D、左边=x=×（-1）=-≠右边=-2，所以，D错误；故选：B．本题考查了方程解的定义：使方程左右两边都相等的未知数的值，叫做方程的解．将x=-1代入四个选项，等式成立者，即为正确答案．本题除了代入法外，还可将选项中的四个方程分别解出来，再进行选择．2.【答案】B【解析】解：将x=1代入2x-a=0中，∴2-a=0，∴a=2故选：B．根据方程的解的概念即可求出a的值．本题考查一元一次方程的解，解题的关键是正确理解方程的解的概念，本题属于基础题型．3.【答案】D【解析】解：依题意，得：3x+5=-3．故选：D．由“x的3倍与5的和比x 的少3”，可得出关于x的一元一次方程，此题得解．本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键．4.【答案】D【解析】解：，①代入②得，3x+2x=15，解得x=3，将x=3代入①得，y=2×3=6，所以，方程组的解是．故选：D．利用代入法求解即可．本题考查的是二元一次方程组的解法，方程组中未知数的系数较小时可用代入法，当未知数的系数相等或互为相反数时用加减消元法较简单．5.【答案】D【解析】解：∵x+y=3，3x-5y=4，∴两式相加可得：（x+y）+（3x-5y）=3+4，∴4x-4y=7，∴x-y=，∵x=a，y=b，∴a-b=x-y=故选：D．将两式相加即可求出a-b的值．本题考查二元一次方程组的解，解题的关键是观察两方程的系数，从而求出a-b的值，本题属于基础题型．6.【答案】D【解析】解：∵长方形的长为xcm，长方形的周长为30cm，∴长方形的宽为（15-x）cm，∵这个长方形的长减少1cm，宽增加2cm就可成为一个正方形，∴x-1=15-x+2，故选：D．根据长方形的周长公式，表示出长方形的宽，再由正方形的四条边都相等得出等式即可．本题考查了有实际问题抽象出一元一次方程，解题的关键是表示出长方形的宽．7.【答案】B【解析】解：设每支铅笔x元，每本笔记本y元，根据题意得．故选：B．设每支铅笔x元，每本笔记本y元，根据购买20只铅笔和10本笔记本共需110元，但购买30支铅笔和5本笔记本只需85元可列出方程组．本题考查了由实际问题抽象出二元一次方程组，根据实际问题中的条件列方程组时，要注意抓住题目中的一些关键性词语，找出等量关系，列出方程组．8.【答案】C【解析】解：设火车的速度是x米/秒，根据题意得：800-40x=60x-800，解得：x=16，即火车的速度是16米/秒，火车的车长是：60×16-800=160（米），故选：C．设火车的速度是x米/秒，根据“已知某座桥长800米，现有一列火车从桥上通过，测得火车从开始上桥到完全通过共用了1分钟，这列火车完全在桥上的时间为40秒”，列出关于x的一元一次方程，解之，即可得到火车的速度，根据车长=火车的速度×火车从开始上桥到完全通过所用的时间-桥长，即可得到火车的车长．本题考查了一元一次方程的应用，正确找出等量关系，列出一元一次方程，是解题的关键．9.【答案】【解析】解：由题意可得：（4x-5）+（3x-6）=0，解得：x=，所以当x=时，代数式4x-5与3x-6的值互为相反数．故答案为：．因为互为相反数的和为0，据此列方程求解即可．此题主要考查了解一元一次方程，关键是明确：互为相反数的和为0．10.【答案】-3【解析】解：把x=1.5代入得：y=×1.5-4=1-4=-3．直接代入计算y即可．此题较简单代入求值即可．11.【答案】18.5【解析】解：设原定价为x，则x×80%=14.8解得x=18.5元，故原定价为18.5元．依据题意得等量关系：原定价×80%=14.8，可列方程式．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．12.【答案】x（1+15%）=60【解析】解：设去年产煤x万吨，由题意得，x（1+15%）=60．故答案为：x（1+15%）=60．设去年产煤x万吨，根据今年比去年增产15%，达到年产煤60万吨，列方程即可．本题考查了由实际问题抽象出一元一次方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．13.【答案】1【解析】解：∵关于x、y的二元一次方程组的解是，∴，解得a=-1，b=2，∴a b=（-1）2=1．故答案为1．将方程组的解代入方程组，就可得到关于a、b的二元一次方程组，解得a、b 的值，即可求a b的值．此题主要考查了二元一次方程组的解的定义：一般地，二元一次方程组的两个方程的公共解，叫做二元一次方程组的解．也考查了解二元一次方程组．14.【答案】【解析】解：由题意可得，，故答案为：．根据甲、乙两人各有若干钱，如果甲得到乙所有钱的一半，那么甲共有钱48文；如果乙得到甲所有钱的，那么乙也共有钱48文，可以列出方程组，从而可以解答本题．本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程组．15.【答案】解：（1）把①代入②得：3x+2（2x-3）=8解得：x=2把x=2代入①，得：y=2×2-3=1∴原方程组的解为（2）①+②得：x+3x=9+（-1）解得：x=2把x=2代入①，得：2+2y=9解得：y=∴原方程组的解为（3）整理方程组得：①×2得：8x-2y=10③②+③得：3x+8x=12+10解得：x=2把x=2代入①得：4×2-y=5解得：y=3（4）①②③①+②得：5x+2y=16④②+③得：3x+4y=18⑤④×2得：10x+4y=32⑥⑥-⑤得：10x-3x=32-18解得：x=2把x=2代入④得：5×2+2y=16解得：y=3把x=2，y=3代入③得：2+3+z=6解得：z=1∴原方程组的解为【解析】（1）用代入消元法解方程；（2）用加减消元法解方程；（3）先去括号、去分母整理方程组，再观察用什么消元法解方程较简便；（4）观察到三个方程里z的系数都是1或-1，故先用加减消元法消去z，再把含x、y的方程联立方程组来解．本题考查了二（三）元一次方程组的解法，适当选择代入消元法和加减消元法是便捷、准确计算的前提．16.【答案】解：设经过x分钟后两人第一次相遇，可列方程：105x-25x=400解得x=5答：经过5分钟，两人第一次相遇．【解析】设经过x分钟后两人第一次相遇．根据题意在环形跑道上同向而行是追及问题，第一次相遇时甲比乙要多跑一圈，即：105x-25x=400，解方程即可．本题考查的是一元一次方程的应用，注意在环形跑道中的相遇与追及问题的意义，根据条件列17.【答案】解：由题目分析：设票价为X元则行李超重部分应付费为15×1.5%X元则有题目可得方程：X+15×1.5%X=1323解得：X=1080元所以飞机的票价为1080元答：飞机的票价为1080元．【解析】由题目分析可知，每人可以免费携带20千克的行李，只有超过20千克的行李才需要付钱．而且每千克按飞机票价的15%收费，题目中旅客携带了35千克的行李，则需收费部分为15千克，可设票价为X元，则行李超重部分应付费为15×1.5%X元．本题主要考查了一元一次方程，在实际生活中的应用，解题的关键在于读懂题目所给的信息，找出合适的等量关系来列出方程．18.【答案】解：（1）原式去括号得：4x+3=2x-1移项并合并同类项得，2x=-4系数化为1得，x=-2（2）原式去分母得，4（3x+7）=28-21x去括号得，12x+28=28-21x移项合并同类项得，33x=0系数化为1得，x=0（3）原式去括号得，x-4=2移项得，x=6（4）原式去分母得，18x-3（2-18x）=2x+36去括号得，18x-6+54x=2x+36移项合并同类项得，70x=42系数化为1得，x=【解析】（1）先去括号，移项并合并同类项，再把系数化为1即可（2）可以先左右两边乘以14，去分母再去括号，移项并合并同类项，将系数化为1即可（3）先去括号，合并同类项，将系数化为1即可（4）可左右两边同时乘以18，去分母后，移项并合并同类项，将系数化为1即可此题考查的是解一元一次方程，掌握解一元一次方程的步骤是解答此题的关键．解一元一次方程的步骤是：1．去分母：在方程两边都乘以各分母的最小公倍数； 2．去括号：先去小括号，再去中括号，最后去大括号； 3．移项：把含有未知数的项都移到方程的一边，其他项都移到方程的另一边（注意移项要改变运算的符号）； 4．合并同类项：把方程化成ax=b（a≠0）的形式； 5．系数化成1：在方程两边都除以未知数的系数a，得到方程的解．19.【答案】解：被污染的条件为：同样的空调每台优惠400元．根据题意，得解得答：“五一”前同样的电视每台2500元，空调每台3000元．【解析】被污染的条件为：同样的空调每台优惠400元，设“五一”前同样的电视每台x元，空调每台y元，根据题意列出方程组，求出方程组的解即可得到结果．此题考查了二元一次方程组的应用，弄清题中的等量关系是解本题的关键．20.【答案】解：（1）换电表前：0.52×（50+20）=36.4（元），换电表后：0.55×50+0.30×20=27.5+6=33.5（元），33.5-36.4=-2.9（元）．答：若上月初换表，则相对于换表前小张家的电费是节省了2.9元；（2）设小张家这个月使用“峰时”电是x度，则“谷时”电是（95-x）度，根据题意得0.55x+0.30（95-x）=0.52×95-5.9，解之，得x=60，95-x=95-60=35．答：小张家这个月使用“峰时”用电60度，谷时用电35度．【解析】（1）分别求出换表前后的电费情况，再进行比较计算即可．（2）可设小张家这个月使用“峰时”电是x度，则“谷时”电是（95-x）度，根据题意列出方程解答即可．本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．21.【答案】解：（1）∵一个人操作该采棉机的采摘效率为35公斤/时，大约是一个人手工采摘的3.5倍，∴一个人手工采摘棉花的效率为：35÷3.5=10（公斤/时），∵雇工每天工作8小时，∴一个雇工手工采摘棉花，一天能采摘棉花：10×8=80（公斤）；（2）由题意，得80×7.5a=900，解得a=；∴雇工工钱的标准为：每采摘1公斤棉花元；（3）设张家雇佣x人采摘棉花，则王家雇佣2x人采摘棉花，其中王家所雇的人中有的人自带采棉机采摘，的人手工采摘．∵张家雇佣的x人全部手工采摘棉花，且采摘完毕后，张家付给雇工工钱总额为14400元，∴采摘的天数为：，即：，∴王家这次采摘棉花的总重量是：（35×8×+80×）×=51200（公斤）．【解析】（1）先根据一个人操作采棉机的采摘效率为35公斤/时，大约是一个人手工采摘的3.5倍，求出一个人手工采摘棉花的效率，再乘以工作时间8小时，即可求解；（2）根据一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机，列出关于a的方程，解方程即可；（3）设张家雇佣x人采摘棉花，则王家雇佣2x人采摘棉花，先根据张家付给雇工工钱总额14400元，求出采摘的天数为：，然后由王家所雇的人中有的人自带采棉机采摘，的人手工采摘，两家采摘完毕，采摘的天数刚好一样，即可得出王家这次采摘棉花的总重量．本题考查了一元一次方程及列代数式在实际生产与生活中的应用，抓住关键语句，找出等量关系是解题的关键，本题难度适中．。
吉林省长春市东北师大附中(明珠校区)2018-2019学年七年级下期中考试数学试题(解析版)
(1) (用含 代数式表示)；
(2)求 的取值范围.
【答案】（1）1-5m，3-m；（2）-5＜m＜ ．
【解析】
【分析】
（1）将方程组两方程相减可得x-y，两式相加可得x+y；
（2）把x-y、x+y代入不等式组可得关于m的不等式组，求解可得．
【详解】（1）在方程组 中，
【详解】当x=2时，第1次运算结果为2×2+1=5，第2次运算结果为5×2+1=11，
∴当x=2时，输出结果=11，
若运算进行了2次才停止，则有 ，
解得： ＜x≤4.5．
∴x可以取的所有值是2或3或4，
故答案为：11，2或3或4．
【点睛】本题考查了一元一次不等式组的应用以及有理数的混合运算，根据运算程序找出关于x的一元一次不等式组是解题的关键．
所以这个方程组的解是 ．
【点睛】本题考查了二元一次方程组，此题难度不大，计算时认真审题、弄清题意是关键．
17.解下列不等式组,并把它们的解集在数轴上表示出来.
(1) ；(2)
【答案】（1）不等式组的解集为x>3；（2）不等式组的解集为-1≤x＜3
【解析】
【分析】
（1）先求出每个不等式的解集，再求出不等式组的解集，最后在数轴上表示出来即可；
B．a＞b，不等式两边同时乘以-1得：-a＜-b，即B项成立；
C．a＞b，若a和b同为负数，则a2＜b2，即C项不一定成立；
D．a＞b，不等式两边同时乘以 得： ，即D项成立，
故选：C．
【点睛】本题考查了不等式的性质，正确掌握不等式的性质是解题的关键．
6.一件进价为200元的商品，先按进价提高20%作为标价，但因销量不好，又决定按标价降价20%出售，那么这次生意的盈亏情况是每件（）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（下）期末数学试卷一、选择题（本大题共有8道小题．每小题3分，共24分）1．（3分）下面四幅作品分别代表二十四节气中的“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是（）A．B．C．D．2．（3分）如图，将△ABC沿BC方向平移1cm得到△DEF，若△ABC的周长为8cm，则四边形ABFD的周长为（）A．8cm B．9cm C．10cm D．11cm3．（3分）如图，∠ACD＝105°．∠A＝70°，则∠B的大小是（）A．25°B．35°C．45°D．65°4．（3分）小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，瓷砖形状不可以是（）A．正三角形B．正四边形C．正五边形D．正六边形5．（3分）如图，将△ABC就点C按逆时针方向旋转75°后得到△A′B′C，若∠ACB＝25°，则∠BCA′的度数为（）A．50°B．40°C．25°D．60°6．（3分）如果一个三角形的两边长分别为2和5，则第三边长可能是（）A．2B．3C．5D．87．（3分）如图，已知AB＝DE，∠B＝∠DEF，下列条件中不能判定△ABC≌△DEF的是（）A．∠A＝∠D B．AC∥DF C．BE＝CF D．AC＝DF8．（3分）如图，在△ABC中，∠B＝45°，AC的垂直平分线交AC于点D．交BC于点E，且∠BAE与∠EAC的比为4：1，则∠C的度数为（）A．20°B．22.5°C．25°D．30°二、填空题（本大题共有6道小题，每小题3分，共18分）9．（3分）在△ABC中，∠A：∠B：∠C＝4：3：2．则∠A＝度．10．（3分）东北师大附中校团委组织了职业微体验活动，初一（3）班52名学生分别去科技细和图书馆参观，去科技馆的人数比去图书馆人数的2倍少5人，去图书馆的人数为x人，则可列方程：11．（3分）如图所示，五角星的顶点是一个正五边形的五个顶点．这个五角星绕中心O至少旋转度能和自身重合．12．（3分）已知等腰三角形的周长为29，一边长为7，则此等腰三角形的腰长为．13．（3分）若不等式组恰有两个整数解，则m的取值范围是．14．（3分）如图，在△ABC中，BF⊥AC于F，AD⊥BC于D，BF与AD相交于E．若AD＝BD，BC＝8cm，DC ＝3cm，则AE＝cm．三、解答题（共10小题，满分78分）15．（8分）解下列方程（组）；（1）；（2）；16．（8分）解下列不等式（组）；（1）3（x﹣1）＞5x+1；（2）；17．（6分）如图，点F是△ABC的边BC的延长线上一点，FD⊥AB于点D．∠A＝30°，∠F＝40°，求∠ACB 的度数．18．（6分）五月份的第二个星期天是母亲节．如图，母亲节那天，很多同学给妈妈准备了鲜花和礼盒，根据图中提供信息，求每束鲜花和每个礼的价格．19．（6分）如图，在正方形网格中，△ABC的三个顶点都在格点上，点O也在格点上．（1）画A′B′C′．使△A′B′C′与△ABC关于直线OP成轴对称．（2）画△A''B''C''，使△A''B''C''与△A′B′C′关于点O成中心对称．20．（6分）如图，点B，F，C，E在同一直线上，AB＝DE，BF＝CE，AB∥DE，求证，AC＝DF．21．（8分）如图，△ABC是等边三角形，点D，E分别在AB，AC边上，且AE＝BD．（1）求证：△ABE≌BCD．（2）求∠EFC的度数．22．（8分）小明到某服装商场进行社会调查，了解到该商场为了激励营业员的工作积极性，实行“月总收入＝基本工资+计件奖金”的方法，并获得如下信息：营业员A：月销售件数100件，月总收入2400元；营业员B：月销售件数150件，月总收入2700元；假设营业员的月基本工资为x元，销售每件服装奖励y元．（1）求x、y的值；（2）若某营业员的月总收入不低于3000元，则她当月至少要卖出服装多少件？23．（10分）直角三角形ABC中．∠ACB＝90°，直线l过点C（1）当AC＝BC时，如图①，分别过点A、B作AD⊥l于点E．求证：△ACD≌△CBE．（2）当AC＝8，AC＝6时，如图②，点B与点F关于直线l对称，连接BF，CF．动点M从点A出发，以每秒1个单位长度的速度沿AC边向终点C运动．同时动点N从点F出发．以每秒3个单位的速度沿F→C→B→C→F向终点F运动．点M、N到达相应的终点时停止运动，过点M作MD⊥l于点D，过点N作l于点E，设运动时间为t秒．①用含t的代数式表示CN．②直接写出当△MDC与△CEN全等时t的值．24．（12分）已知△ABC和△ADE都是等腰三角形，AB＝AC，AD＝AE．∠DAE＝∠BAC．【初步感知】（1）特殊情形：如图①．若点D，E分别在边AB，AC上，则DB EC．（填“＞”、“＜”或“＝”）（2）发现证明：如图②，将图①中的△ADE绕点A旋转，当点D在△ABC外部，点E在△ABC内部时，求证：DB＝EC．【深入探究】（1）如图③，△ABC和△ADE都是等边三角形，点C，E，D在同一条直线上，则∠CDB的度数为线段CE，BD之间的数量关系为；（2）如图④，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，点C、D、E在同一直线上，AM 为△ADE中DE边上的高．则∠CDB的度数为；线段AM．BD，CD之间的数量关系为；【拓展提升】如图⑤，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，将△ADE绕点A逆时针旋转，连结BE、CD．当AB＝5．AD＝2时，在旋转过程中，△ABE与△ADC的面积和的最大值为．2018-2019学年吉林省长春市南关区东北师大附中明珠学校七年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共有8道小题．每小题3分，共24分）1．【解答】解：A、不是轴对称图形，本选项错误；B、不是轴对称图形，本选项错误；C、不是轴对称图形，本选项错误；D、是轴对称图形，本选项正确．故选：D．2．【解答】解：∵△ABC沿BC方向平移1cm得到△DEF，∴AD＝CF＝1，AC＝DF，∴四边形ABFD的周长＝AB+（BC+CF）+DF+AD＝AB+BC+AC+AD+CF，∵△ABC的周长＝8，∴AB+BC+AC＝8，∴四边形ABFD的周长＝8+1+1＝10cm．故选：C．3．【解答】解：∵∠ACD＝∠B+∠A，∠ACD＝105°，∠A＝70°，∴∠B＝105°﹣70°＝35°，故选：B．4．【解答】解：∵用一种正多边形镶嵌，只有正三角形，正四边形，正六边形三种正多边形能镶嵌成一个平面图案，∴小王到瓷砖店购买一种正多边形瓷砖铺设无缝地板，他购买的瓷砖形状不可以是正五边形．故选：C．5．【解答】解：根据旋转的定义可知旋转角∠ACA′＝75°，∴∠BCA′＝∠ACA′﹣∠ACB＝75°﹣25°＝50°．故选：A．6．【解答】解：设第三边长为x，则由三角形三边关系定理得5﹣2＜x＜5+2，即3＜x＜7．故选：C．7．【解答】解：A、根据ASA判定两个三角形全等；B、根据AAS可以判定两个三角形全等；C、BE＝CF则BC＝FE，根据SAS即可判定两个三角形全等；D、SSA，不能判定三角形全等．故选：D．8．【解答】解：∵ED是AC的垂直平分线，∴AE＝CE，∴∠C＝∠EAC，∵∠B＝45°，∴∠BAC+∠C＝135°，∵∠BAE与∠EAC的比为4：1，∴∠C+∠C+4∠C＝135°，∴∠C＝22.5°，故选：B．二、填空题（本大题共有6道小题，每小题3分，共18分）9．【解答】解：∵∠A：∠B：∠C＝4：3：2，∴可以假设∠A＝4x，∠B＝3x，∠C＝2x，∵∠A+∠B+∠C＝180°，∴4x+3x+2x＝180°，∴x＝20°，∴∠A＝80°，故答案为8010．【解答】解：已知去图书馆人数x人，则去科技馆人数为（2x﹣5）人，根据总人数为52人，可列方程x+（2x﹣5）＝52．故答案为x+（2x﹣5）＝52．11．【解答】解：根据题意，五角星的顶点是一个正五边形的五个顶点，这个五角星可以由一个基本图形（图中的阴影部分）绕中心O至少经过4次旋转而得到，每次旋转的度数为360°除以5，为72度．故答案为：7212．【解答】解：若腰长为7，则底边＝29﹣2×7＝15，∵7+7＜15∴不能组成三角形若底边为7，则腰长＝（29﹣7）÷2＝11故答案为1113．【解答】解：∵不等式组，∴该不等式组的解集为m≤x＜2，∵不等式组恰有两个整数解，∴﹣1＜m≤0，故答案为：﹣1＜m≤0．14．【解答】解：∵BF⊥AC于F，AD⊥BC于D，∴∠CAD+∠C＝90°，∠CBF+∠C＝90°，∴∠CAD＝∠CBF，∵在△ACD和△BED中，，∴△ACD≌△BED，（ASA）∴DE＝CD，∴AE＝AD﹣DE＝BD﹣CD＝BC﹣CD﹣CD＝2；故答案为2．三、解答题（共10小题，满分78分）15．【解答】解：（1）去分母得：2x+1＝3x﹣6，解得：x＝7；（2），①×3+②得：7x＝14，解得：x＝2，把x＝2代入①得：y＝3，则方程组的解为．16．【解答】解：（1）3x﹣3＞5x+1，3x﹣5x＞1+3，﹣2x＞4，x＜﹣2；（2）解不等式x+1≥0，得：x≥﹣1，解不等式5x﹣2＜3（x+2），得：x＜4，则不等式组的解集为﹣1≤x＜4．17．【解答】解：在△DFB中，∵FD⊥AB，∴∠FDB＝90°，∵∠F＝40°，∠F+∠B＝90°，∴∠B＝90°﹣40°＝50°．在△ABC中，∵∠A＝30°，∠B＝50°，∴∠ACB＝180°﹣∠A﹣∠B＝180°﹣30°﹣50°＝100°．18．【解答】解：设每束鲜花x元，每个礼盒y元，根据题意得：，解得：．答：每束鲜花12元，每个礼盒20元．19．【解答】解：（1）如图△A′B′C′即为所求．（2）如图△A''B''C''即为所求．20．【解答】证明：∵AB∥DE，∴∠B＝∠E．∵BF＝CE，∴BF+FC＝CE+FC，即BC＝EF．又AB＝DE，∴△ABC≌△DEF（SAS）．∴AC＝DF．21．【解答】证明：（1）∵△ABC是等边三角形，∴AB＝AC，∠A＝∠DBC＝60°，AE＝BD．∴△ABE≌△BCD（SAS）；（2）∵△ABE≌△BCD，∴∠ABE＝∠BCD．∴∠EFC＝∠FBC+∠FCB＝∠FBC+∠ABE＝∠ABC＝60°．22．【解答】解：（1）由题意，得，解得即x的值为1800，y的值为6；（2）设某营业员当月卖服装m件，由题意得，1800+6m≥3000，解得，m≥200，∵m只能为正整数，∴m最小为200，即某营业员当月至少要卖200件．23．【解答】（1）证明：△ACD与△CBE全等．理由如下：∵AD⊥直线l，∴∠DAC+∠ACD＝90°，∵∠ACB＝90°，∴∠BCE+∠ACD＝90°，∴∠DAC＝∠ECB，在△ACD和△CBE中，，∴△ACD≌△CBE（AAS）；（2）解：①由题意得，AM＝t，FN＝3t，则CM＝8﹣t，由折叠的性质可知，CF＝CB＝6，∴CN＝6﹣3t；②由折叠的性质可知，∠BCE＝∠FCE，∵∠MCD+∠CMD＝90°，∠MCD+∠BCE＝90°，∴∠NCE＝∠CMD，∴当CM＝CN时，△MDC与△CEN全等，当点F沿F→C路径运动时，8﹣t＝6﹣3t，解得，t＝﹣1（不合题意），当点F沿C→B路径运动时，8﹣t═3t﹣6，解得，t＝3.5，当点F沿B→C路径运动时，由题意得，8﹣t＝18﹣3t，解得，t＝5，当点F沿C→F路径运动时，由题意得，8﹣t＝3t﹣18，解得，t＝6.5，综上所述，当t＝3.5秒或5秒或6.5秒时，△MDC与△CEN全等．24．【解答】解：【初步感知】（1）∵DE∥BC，∴＝，∵AB＝AC，∴DB＝EC，故答案为：＝，（2）成立．理由：由旋转性质可知∠DAB＝∠EAC，在△DAB和△EAC中，∴△DAB≌△EAC（SAS），∴DB＝CE；【深入探究】（1）如图③，设AB，CD交于O，∵△ABC和△ADE都是等边三角形，∴AD＝AE，AB＝AC，∠DAE＝∠BAC＝60°，∴∠DAB＝∠EAC，在△DABDAB和△EAC中，∴△DAB≌△EAC（SAS），∴DB＝CE，∠ABD＝∠ACE，∵∠BOD＝∠AOC，∴∠BDC＝∠BAC＝60°；（2）∵△DAE是等腰直角三角形，∴∠AED＝45°，∴∠AEC＝135°，在△DAB和△EAC中，∴△DAB≌△EAC（SAS），∴∠ADB＝∠AEC＝135°，BD＝CE，∵∠ADE＝45°，∴∠BDC＝∠ADB﹣∠ADE＝90°，∵△ADE都是等腰直角三角形，AM为△ADE中DE边上的高，∴AM＝EM＝MD，∴AM+BD＝CM；故答案为：90°，AM+BD＝CM；【拓展提升】如图，由旋转可知，在旋转的过程中△ADE的面积始终保持不变，∴△ABE与△ADC面积的和达到的最大，∴△ADC面积最大，∵在旋转的过程中，AC始终保持不变，∴要△ADC面积最大，∴点D到AC的距离最大，∴DA⊥AC，∴△ABE与△ADC面积的和达到的最大为2××AC×AD＝5×2＝10，故答案为10．。