因式分解(公式法-完全平方公式)
14.3.3因式分解(公式法-完全平方公式)
2
的多项式称为完全平方式.
完全平方公式
a b
2
a 2ab b
2
2
a 2ab b ；
2 2
a 2ab b
2
2
完全平方式的特点：
1．有三部分组成． 2．其中有两部分分别是某两个数（或式）的平方， 另一部分是上述两数（或式） 且这两部分同号．
的乘积的2倍，符号可正可负．
一天,小明在纸上写了一个算式为
4x2 +8x+11,并对小刚说:“无论x取何值,这个
代数式的值都是正值,你不信试一试?”
4x 2 8x 11 2x 2 2x 2 22 7
2
2x 2 7 4 x 1 7
2 2
分解因式：
(1) 9x2+24x+16;
2 2
分解因式:
2x y
2
62x y 9
分解因式： (a b) 10(a b) 25．
2
因式分解：
(1)-a3b3+2a2b3-ab3 (2)9 - 12(a-b) + 4 (a-b)2
(3)16x4-8x2＋1
因式分解：
(4)(y2 + x2 )2 - 4x2y2 (5)(a+b)2＋2(a+b)(a-b)＋(a-b)2
2 2
(3) x 2 xy y ； 是
2 2
(4) x 2 xy y ； 不是
2 2
(5) x 2 xy y ． 是
2 2
a2 2ab b2 (a b)2 ; a2 2ab b2 (a b)2
1．判别下列各式是不是完全平方式，若是说出 相应的 a、 b 各表示什么？ (1) x 2 6 x 9；是 a表示x，b表示3.
因式分解公式一览表,因式分解的全部公式法
因式分解公式一览表，因式分解的全部公式法沪教版因式分解经常会用到公式1、平方差公式，a²-b²=(a+b)(a-b)2、完全平方和公式：a²+2ab+b²=(a+b)²3、完全平方差公式：a²-2ab+b²=(a-b)²4、二次项系数为1的二次三项式的十字相乘法：x方+（a+b）x+ab=（x+a）（x+b）5、二次三项式的求根公式法ax方+bx+c=a（x-x1）（x-x2）（a≠0）这当中，x1、x2为方程ax方+bx+c=0的两根。
因式分解的方式经常会用到的还有提取公因式法，分组分解法，十字相乘法，配方式，换元法，添项拆项法等。
答:因式分解又叫分解因式。
它贯穿了初等数学和高等数学的整个运算过程。
因式分解的方式不少在这里简述公式法。
1，平方差公:α方一b方=(α+b)(α一b)。
2，完全平方公式:α方±2αb+b方=(α±b)方。
3，立方和公式:α立方+b立方=(α+b)(α方一αb+b方)。
4，立方差公式:α立方一b立方=(α一b)(α方+αb+b 方)。
5，完全立和公式:α立方+3α方b十3αb方十b立方=(α+b)立。
6，α立方一3α方b+3αb方一b立方=(α一b)立方。
7求根公式法。
因式分解公式：平方差公式：(a+b)(a-b)=a²-b²完全平方公式：(a±b)²=a²±2ab+b²把式子倒过来：(a+b)(a-b)=a²-b²a²±2ab+b²= (a±b)²就变成了因式分解，因为这个原因，我们把用利用平方差公式和完全平方公式进行因式分解的方式称之为公式法。
例子：1、25-16x²=5²-(4x)²=(5+4x)(5-4x)2、p4-1=(p²+1)(p²-1)=(p²+1)(p+1)(p-1)3、x²+14x+49=x²+2·7·x+7²=(x+7)²4、(m-2n)²-2(2n-m)(m+n)+(m+n)²=(m-2n)²+2(m-2n)²(m+n)+(m+n)²=[(m-2n)+(m+n)]²=(2m-n)²因式分解经常会用到公式1、平方差公式：a²-b²=(a+b)(a-b)。
因式分解的公式大全,因式分解万能公式法的应用
因式分解的公式大全，因式分解万能公式法的应用因式分解的公式大全？因式分解公式：平方差公式：(a+b)(a-b)=a²-b²完全平方公式：(a±b)²=a²±2ab+b²把式子倒过来： (a+b)(a-b)=a²-b² a²±2ab+b²= (a±b)²就变成了因式分解，因为这个原因，我们把用利用平方差公式和完全平方公式进行因式分解的方式称之为公式法。
例子：1、25-16x²=5²-(4x)²=(5+4x)(5-4x)2、p4-1 =(p²+1)(p²-1) =(p²+1)(p+1)(p-1)3、x²+14x+49 =x²+2·7·x+7² =(x+7)²4、(m-2n)²-2(2n-m)(m+n)+(m+n)² =(m-2n)²+2(m-2n)²(m+n)+(m+n)² =[(m-2n)+(m+n)]² =(2m-n)²因式分解万能公式法？1、平方差公式：a²-b²=(a+b)(a-b)。
2、完全平方公式：a²+2ab+b²=(a+b)²。
3、立方和公式：a³+b³=(a+b)(a²-ab+b²)。
4、立方差公式：a³-b³=(a-b)(a²+ab+b²)。
5、完全立方和公式：a³+3a²b+3ab²+b³=(a+b)³。
6、完全立方差公式：a³-3a²b+3ab²-b³=(a-b)³。
分解因式公式法---完全平方公式
12(a+b)+36 就是一个完全平方式。即
(a+b)2-12(a+b)+36=(a+b)2-2×(a+b)×6+62 m2 - 2 ×6 +62 解： (a+b)2-12(a+b)+36 ×m = (a+b)2-2×(a+b)×6+62 =(a+b-6)2
现在回头来看看我们上课时提出的问题，
快速口算
完全平方式 a2 2ab b2 (a b)2
左边：① 项数：共三项，即a、b两数的平方项
，a、b两数积的2倍。
② 次数：左边每一项的次数都是二次。
③ 符号：左边a、b两数的平方项必须同号。
右边：是a、b两数和（或差）的平方。
当a、b同号时，a2+2ab+b2=(a+b)2
当a、b异号时，a2-2ab+b2=(a-b)2
∴ 2a2+4b-3=2×(-1)2+4×2-3
=7
考考你
(2)已知a、b、c是△ABC的三边的长，且满 足 a2+2b2+c2-2b(a+c)=0，试判断△ABC的 形状。 温馨提示：将条件a2+2b2+c2-2b(a+c)=0变形 为a2+2b2+c2-2ab-2bc=0，左边与完全平方式 十分相似。可将其奏成两个完全平方式的和， 然后利用非负数性质就能解决问题了。
3、深刻理解
下列各式是不是完全平方式，为什么？ 是 （1） x2-4x+4______________ 不是，缺乘积项 （2） x2+16 _________________ 不是，缺乘积项的2倍 （3 ） 9m2+3mn+n2_____________________ 不是，平方项异号 （4）-y2-12xy+36x2 是 __________________ 不是，只有一个平方项 2 （5） -m +10mn-25n2______________ （6 ）
14.3.2《因式分解--公式法--完全平方公式》教案
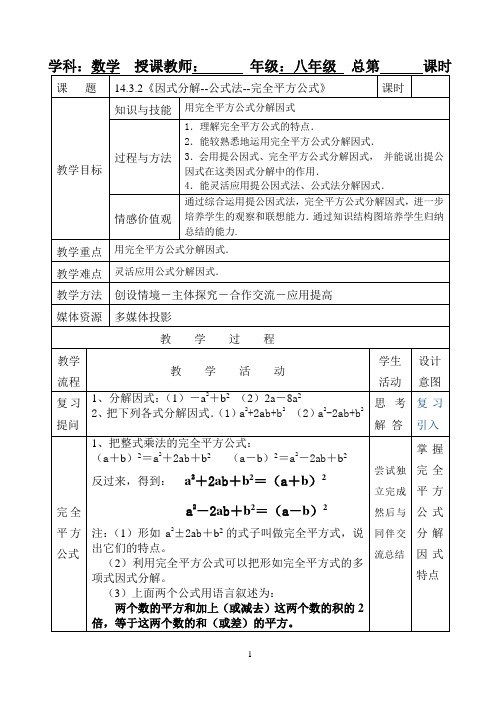
学科：数学授课教师：年级：八年级总第课时课题14.3.2《因式分解--公式法--完全平方公式》课时教学目标知识与技能用完全平方公式分解因式过程与方法1．理解完全平方公式的特点．2．能较熟悉地运用完全平方公式分解因式．3．会用提公因式、完全平方公式分解因式，•并能说出提公因式在这类因式分解中的作用．4．能灵活应用提公因式法、公式法分解因式．情感价值观通过综合运用提公因式法，完全平方公式分解因式，进一步培养学生的观察和联想能力．通过知识结构图培养学生归纳总结的能力.教学重点用完全平方公式分解因式．教学难点灵活应用公式分解因式．教学方法创设情境－主体探究－合作交流－应用提高媒体资源多媒体投影教学过程教学流程教学活动学生活动设计意图复习提问1、分解因式：（1）－a2＋b2（2）2a－8a22、把下列各式分解因式．（1）a2+2ab+b2 （2）a2-2ab+b2思考解答复习引入完全平方公式1、把整式乘法的完全平方公式：（a＋b）2＝a2＋2a b＋b2（a－b）2＝a2－2a b＋b2反过来，得到：a2＋2a b＋b2＝（a＋b）2a2－2a b＋b2＝（a－b）2注：（1）形如a2±2a b＋b2的式子叫做完全平方式，说出它们的特点。
（2）利用完全平方公式可以把形如完全平方式的多项式因式分解。
（3）上面两个公式用语言叙述为：两个数的平方和加上（或减去）这两个数的积的2倍，等于这两个数的和（或差）的平方。
尝试独立完成然后与同伴交流总结掌握完全平方公式分解因式特点例题练习1、分解因式：（1）16x2+24x+9 （2）-x2+4xy-4y22、练习：P119页：练习：1、2：（1）--（4）3、分解因式：（1）3ax2+6axy+3ay2（2）（a+b）2-12（a+b）+364、练习：P119页：练习：2：（5）（6）5下列多项式是不是完全平方式？为什么？（1）a2－2a＋1 （2）a2－4a＋4 （3）a2＋2ab－b 2（4）a2＋ab＋b2（5）9a2－6a＋1 （6）a2＋a＋1/4 思考动手板演归纳总结巩固知识因式分解的一般步骤1、把下列多项式分解因式，从中你能发现因式分解的一般步骤吗？（1）44yx-；（2）33abba-；（3）22363ayaxyax++；（4）22)()(qxpx+-+；（5）4x2+20（x-x2）+25（1-x）22、分解因式的一般步骤：（1）先提公因式（有的话）；（2）利用公式（可以的话）；（3）分解因式时要分解到每个多项式因式不能再分解为止．3、练一练：把下列多项式分解因式：（1）6a-a2-9；（2）-8ab-16a2-b2；（3）2a2-a3-a；课堂小结1、完全平方公式：两个数的平方和加上（或减去）这两个数的积的2倍，等于这两个数的和（或差）的平方。
因式分解-完全平方公式
因式分解 $$(x + 5)^2$$ $$(3x - 2)^2$$ $$(2x + 3)^2$$
结论
通过学习和运用完全平方公式，您将能够轻松因式分解二次方程，并更好地 理解和分析数学问题。继续锻炼和实践，您的因式分解技巧将日益提高。
完全平方公式的形式
完全平方公式的形式为：$$(a + b)^2 = a^2 + 2ab + b^2$$，其中a和b是实数。
解决问题的步骤
1. 将二次方程按照一般形式表示：$$ax^2 + bx + c$$ 2. 识别出平方项的系数a和常数项c 3. 计算平方项系数的一半，即$$\frac{b}{2a}$$ 4. 使用完全平方公式，进行平方项和常数项的加法和乘法操作 5. 将结果写成两个平方项相加的形式
完全平方公式的实例
例子1
假设有一个二次方程：$$x^2 + 6x + 9$$，我们可以使用完全平方公式将其因式分解为：$$(x + 3)^2$$。
例子2
另一个例子是二次方程：$$4x^2 - 12x + 9$$，使用完全平方公式进行因式分解，得到：$$(2x - 3)^2$$。
练习题目和答案
二次方程 $$x^2 + 10x + 25$$ $$9x^2 - 12x + 4$$ $$4x^2 + 12x + 9$$
因式分解-完全平方公式
本演讲将为您介绍因式分解的重要内容——完全平方公式，从定义到实例， 让您轻松学会并享受因式分解的乐趣。
完全平方公式的定义
完全平方公式是一种用于因式分解的数学技巧，适用于一元二次方程。它能够将一个二次方程转化为两个平方 项的乘积，并且是唯一的。
公式法因式分解
2 a2 6a 9 原式 x 32
3 4a2 4a 1 原式 2a 12
4 9m2 6mn n2 原式 3m n2
5 x2 1 x
4
原式
x
1 2
2
6 4a2 12ab 9b2 原式 2a 3b2
1. 因式分解 (1)9-a2-4ab-4b2 (2) 1+a2b2-a2-b2 (3) x2-4xy+4y2-5x+10y
（3）-3a+6a2-3a3 （4）4(a-b)3-9(a-b)
2.计算 （1）13×9.98+5.6×99.8+310×0.998
（2）9992-9982 （3）172+26×17+132
2.计算：542 462 2 54 46
3.已知 x y 2, xy ，2 求
x2 y2 6xy 的值。
(2)25m2 80m 64
(3)a2 1 a
(4) 24xy x2 y2
(5)(a b)2 18(a b) 81
[例3]分解因式： (1)(x+4)2+2x(x+4)+x2
(2)a4-2a2b2+b4
(3)（x2+3x）2-（x-1）2 （4）-2an+1+2an- 1 an-1
2
练习. 2.分解因式：
(1)x2 y 4 y
(2) 3x3 12x2 y 12xy2 (3)3ax2 6axy 3ay2 (4)a4 8a2 16
(5)x3 4x2 4x
3、计算：8002-1600×798+7982
应用提高、拓展创新
1.把下列多项式分解因式，从中你能发现 因式分解的一般步骤吗？
14.3.2公式法_因式分解(完全平方公式)
a 2ab b a 2ab b
2 2
2
2
完全平方式的特点： 1、必须是三项式 2、有两个“项”的平方 3、有这两“项”的2倍或-2倍
2 2 首 2首尾 尾
判别下列各式是不是完全平方式
1x 2 xy y 2 2 2A 2 AB B 2 2 3甲 2 甲乙 乙 2 2 4 2
a 2ab b a b
2 2
2
a 2ab b a b
2 2
2
这两个多项式有什么特征?
2 2 2 2 a +2ab+b 与a -2ab+b
这两个多项式是两个数的平方和加上(或 减去)这两个数的积的2倍，这恰是两个 数和或差的平方。
我们把 2 2 和 2 2 a +2ab+b a -2ab+b 这样的式子叫做完全平方式。
1. 因式分解：9x2－y2－4y－4＝_____． 2 2 【解析】9x －y －4y－4
= 9x2－(y2+4y+4） = 答案： 2. 分解因式：2a2–4a+2 2 【解析】 2a – 4a+2 = 2(a 2 – 2a +1) = 2(a – 1) 2
需要我们掌握： 1：如何用符号表示完全平方公式？
(1) (2) 1 6 a 4 + 2 4 a 2 b 2 + 9 b 4 2 2 解:（1）x － 12xy+36y 2 2 = x －2· x· 6y+ （ 6y ） = （ x － 6y ） 2 （ 2 ） 16a 4 +24a 2 b 2 +9b 4
2. 因式分解.
2 2 x － 12xy+36y
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2. 模仿例题完成P170练习1和2。
完全平方和--公式
完全平方差--公式
a 2ab b a b 2 2 2 a 2ab b a b
2 2 2
因式分解的完全平方公式—需要满足的条件： 从项数看： 都是有3项 从每一项看： 都有两项可化为两个数(或整式)的平方,
(2x y 3)
2
(1)已知9x2+mx+16是完全平方式,
则m= ±24 ____; (2)已知4x2-12xy+m是完全平方式,
9y2 则m=____.
(3) a3-8a2+16a
a(a-4)2
(4) 4x2(b-c) +y2(c-b) (b-c)(2x+y)(2x-y)
(5)-a2-10a -25
a b a2 + 2 · · + b2
解:(1)16x2+24x+9
=(4x)2+2· 3+32 4x·
=(4x+3)2.
例.分解因式： 分解因式的步骤：
2+4xy–4y2.(1)有公因式的先提取公因式; –x
（1）
(2) 观察剩下的因式能否套用公式法 即：–(x2-4xy+4y2) (二项式:平方差公式、 三项式:完全平方公式) 再次分解。
因式分解：
(1)-a3b3+2a2b3-ab3 (2)9 - 12(a-b) + 4 (a-b)2 (3)16x4-8x2＋1 (4)(y2 + x2 )2 - 4x2y2 (5)(a+b)2＋2(a+b)(a-b)＋(a-b)2
分解因式：
(1) 9x2+24x+16;
(2) –y2-4xy–4x2. (3) 4mnx2-8mnxy+4mny2; (4) (a-b)2- (a-b)+0.25.
1 2 ab 4 a _______ b 4 4 2 2 4 y 5 x 2 x y ______
2
分解因式：16x2+24x+9
分析：16x2=(4x)2,9=32,24x=2· 3, 4x· 所以16x2+24x+9是一个完全平方式， 即16x2+24x+9= (4x)2+ 2· 3 +32 4x·
[x 2 x (2y) (2y) ]
2 2
( x 2 y) 2
(3) 3ax2＋6axy＋3ay2
原式 3a( x 2 2xy y 2 ) 解：
3a(x y)2
(4) (2 x y) 6(2 x y) 9
2
原式 (2x y)2 2 (2x y) 3 32 解：
另一项为这两个数(或整式)的乘积的2倍.
填一填:
多项式
x 6x 9
2
是否是 完全平方式
a、b 各表示什么 a表示x， b表示3
表示（a+b）2 或（a－b）2
是
( x 3)2
(2 y 1) 2
4 y2 4 y 1
1 4a 2
1 1 x x 2 4
2
是
a表示2y，y+3ay2;
(3) (a+b)2-12(a+b)+36.
(1)
4a 12ab 9b
2
2
2
2
解： 原式 (2a) 2 (2a) (3b) (3b)
(2a 3b) 2
(2) -x2-4y2＋4xy 解：原式 ( x 2 - 4xy 4y 2 )
否
否
x 4x 4 y
2
2
2
2
否
是
a表示2y， 2 ( 2 y 3 x) b表示3x a表示(a+b)， 2 (a b 1) b表示1
4 y 12xy 9x
(a b)2 2(a b) 1
是
按照完全平方式填空:
2 2
2xy 1 x _______ y 2 2 12ab 2 4a 9b _______ 2 2 4xy 3 x ______ 4 y