2014年新苏科版八年级下10.1分式的概念课件
合集下载
苏科版八年级数学下册10.1 分式 (共18张PPT)

a 买练习本 本. b-1
10.1 分式
a-3 的值. 问题2 求当a=1时,分式 a+2
如果a=3呢?
请你选择一个喜欢的数a来计算这个分式的值.
2 a=- 呢? 5
当a=-2时呢? 分式的分母不能为0,如果分式中的字母所 取的值使分母为0,那么分式无意义。
10.1 分式
问题3
x-2 当x取什么值时,分式 有意义? 2 x-3
3、当x取何值时,下列分式的值为零?
2 x 1 x
x 2 4 3x
3x 2 3 5x 4
| x | 3 4 x3 归纳:对于分式,当 时分式有意义; 当 分式无意义; 当 时分式值为零。
x 2 64 5 x8
10.1 分式
做一做
2.填表: x -3 -2 -1
12 x
小时.
(2)班学生组成后队, 速度比(1)班每小时快 12 2千米,则(2)班到达目的地需要 x+2 小时.
10.1 分式
情境4 有两块棉田,一块面积为a ha,产棉花m kg; 另一块面积为b ha,产棉花n kg. 这两块棉田平均 每公顷产棉花
m+n a+b
kg.
a ha
b ha
10.1 分式
2
分式: 整式: __________________________(填写序号)
10.1 分式
问题1 小明a元钱去购买练习本,原价每本b
元,如果每本降价 1 元,那么现在可以购
a 分式 还可以表示什么? b-1
如果a表示长方形的面积, b表示长方形的宽, a 那么 b 1 表示宽减少1个单位长度后,面积仍 为a的长方形的长。
什么时候有意义?
3 解:由分母2x-3=0 ,得 x= , 2
苏科版八年级数学下册第十章《101 分式的概念》优课件(共16张PPT)

zxxkw
zxxkw
热身练习:(根据文字列代数式)
1. x除以x与8的和所的商; 2. a与c的差的一半; 3. 3m加上n和的倒数; 4. 甲乙相距180千米,一辆汽车行驶n小
时从甲地到达乙地,则汽车的速度是 多少?
分式的定义
A
¬ 两个整式A、B相除时,可以表示为 B
的形式。如果 分母 中含有 字母 ,那么 A
叫做 分式 。
B
zxxkw
例1:下列代数式,哪些是整式?哪些是分式?
5 x 1 , 2 x y , 1 2 , a , 1 x y , 4
2 3 a 33
x
整式 和 分式 统称有理式。
例用2:分式表示下列各式:
1. (x+2) ÷y
2. 2x : (y+1) 3. -x : (y³-1) 4. (2x-1) ÷[- (x²+1)]
谢谢观赏
You made my day!
我们,还在路上……
zxxkw
分式的意义
❖分式中分母的值不能为 零A
❖分式 B ห้องสมุดไป่ตู้B≠0
例3 :
当x取什么值时,分式 x 1 有意义? 4x 1
解:使得 x 1 有意义
4x 1
∴4x-1≠0
4x ≠1
x ≠1/4
x1
答:当x ≠1/4时,分式 4 x 1 有意义。
思考:
当x取什么值时,下列分式有意义?
1) 1 xa
的值是多少? ∴当x = 3时,此分式值为0。
小结:
分式的定义 分式的意义 分式的值为0
整式A、B相除可
写为
A B
的形式,
若分母中含有字
母,那么 A 叫做 分式。 B
zxxkw
热身练习:(根据文字列代数式)
1. x除以x与8的和所的商; 2. a与c的差的一半; 3. 3m加上n和的倒数; 4. 甲乙相距180千米,一辆汽车行驶n小
时从甲地到达乙地,则汽车的速度是 多少?
分式的定义
A
¬ 两个整式A、B相除时,可以表示为 B
的形式。如果 分母 中含有 字母 ,那么 A
叫做 分式 。
B
zxxkw
例1:下列代数式,哪些是整式?哪些是分式?
5 x 1 , 2 x y , 1 2 , a , 1 x y , 4
2 3 a 33
x
整式 和 分式 统称有理式。
例用2:分式表示下列各式:
1. (x+2) ÷y
2. 2x : (y+1) 3. -x : (y³-1) 4. (2x-1) ÷[- (x²+1)]
谢谢观赏
You made my day!
我们,还在路上……
zxxkw
分式的意义
❖分式中分母的值不能为 零A
❖分式 B ห้องสมุดไป่ตู้B≠0
例3 :
当x取什么值时,分式 x 1 有意义? 4x 1
解:使得 x 1 有意义
4x 1
∴4x-1≠0
4x ≠1
x ≠1/4
x1
答:当x ≠1/4时,分式 4 x 1 有意义。
思考:
当x取什么值时,下列分式有意义?
1) 1 xa
的值是多少? ∴当x = 3时,此分式值为0。
小结:
分式的定义 分式的意义 分式的值为0
整式A、B相除可
写为
A B
的形式,
若分母中含有字
母,那么 A 叫做 分式。 B
苏科版八年级数学下册第十章《10.1分式》优课件

把下列各式写成分式,并 试着赋予它们实际意义:
1、1÷a 2、(v1t1+v2t2)÷(t1+t2)
小结
1、谈一谈:你这一节课有什么收获? 2、课堂评价(评价表见附表)
内容
能把自己的想法与他人分享
自我评价
优 良好 需加油
能认真倾听他人的想法见解
会正确区分整式与分式
会识别分式有无意义
能用分式表示数量关系
B叫做分式的分母。
探索交流
(1)议一议:你们所发现的这一类新代数
式:
s t
,
a
n -
x,……它
们有
什么共同特
征?它们与整式有什么不同?
(2)类比分数,概括分式的概念及表达形式。
(3)小组内互举例子,判定是否分式
辨析
注意:30S0
与
S
t
的本质区别
强调:BA 中,B中一定要有字母
自主探究
填表:
a … -2 -1 0 1
知识储备 本节内容 后续学习
承
分数
上
整式
因式分解
分式概念 分式意义 模型思想
启
下 分式性质
分式运算
分式方程
分式概念
识别 描述
分式有无意义 数量关系
知识技能目标:掌握分式概念,学会判别分式 何时有意义,能用分式表示数量关系。
过程方法目标:经历分式概念的自我建构过程 及用分式描述数量关系的过程,学会与人合作 并获得代数学习的一些方法。
谢谢观赏
You made my day!
我们,还在路上……
本节课你的独特见解
本节课你还有疑惑的问题
你对老师的评价和建议
小组评价
苏科版八年级数学下册第十章《 分式》课课件

10.1 分式
10.1 分式
【学习目标】: 1.了解分式的概念,会判断一个代数式是
否是分式。 2.能用分式表示简单问题中数量之间的关系, 能解释简单分式的实际背景或几何意义。 3.能分析出一个简单分式有、无意义的条件。 4.会根据已知条件求分式的值。
时间1分钟
自学指导 认真看课本P98至P99结束,注意: 1、会背分式的定义,理解分式与分数、 整式之间的联系与区别。 2、学习例1会求分式的值。(注意解题格 式与步骤)。 3、研读例2,分析出一个简单分式有、无 意义的条件 五分钟后同桌互查,然后老师抽查。
x -3 -2 -1 0 1
x
3- x -
1 2
-2 -1
5
4
01 2
2
3
2 无意义
3.一个分式,分子为(x-5),并且这个 分式在x≠1时有意义.你能写出一个符
合上面条件的分式吗?
当堂训练
必做题:书 P100: 练习 伴你学P54随堂练习
选做题: 伴你学P54迁移应用
有古
一人
个云
在:
路“
上读
1、判断下列代数式哪些是分式?哪些是整式?
5 , 2, 3y
x y, 2
x 1, 2
2 , x1
(1)
(2)
(3)
(4)
x1, 40 a
2x y , 3
3x2 , (x 1)(x 1)
(5)
x 2 xy , x
(6)
(7)
(8)
(9)
2、一块长方形玻璃的面积为2 m2,
2
如果长是3 m,那么宽是 3 m.
。万
”卷
从书
古,
至行
今万
10.1 分式
【学习目标】: 1.了解分式的概念,会判断一个代数式是
否是分式。 2.能用分式表示简单问题中数量之间的关系, 能解释简单分式的实际背景或几何意义。 3.能分析出一个简单分式有、无意义的条件。 4.会根据已知条件求分式的值。
时间1分钟
自学指导 认真看课本P98至P99结束,注意: 1、会背分式的定义,理解分式与分数、 整式之间的联系与区别。 2、学习例1会求分式的值。(注意解题格 式与步骤)。 3、研读例2,分析出一个简单分式有、无 意义的条件 五分钟后同桌互查,然后老师抽查。
x -3 -2 -1 0 1
x
3- x -
1 2
-2 -1
5
4
01 2
2
3
2 无意义
3.一个分式,分子为(x-5),并且这个 分式在x≠1时有意义.你能写出一个符
合上面条件的分式吗?
当堂训练
必做题:书 P100: 练习 伴你学P54随堂练习
选做题: 伴你学P54迁移应用
有古
一人
个云
在:
路“
上读
1、判断下列代数式哪些是分式?哪些是整式?
5 , 2, 3y
x y, 2
x 1, 2
2 , x1
(1)
(2)
(3)
(4)
x1, 40 a
2x y , 3
3x2 , (x 1)(x 1)
(5)
x 2 xy , x
(6)
(7)
(8)
(9)
2、一块长方形玻璃的面积为2 m2,
2
如果长是3 m,那么宽是 3 m.
。万
”卷
从书
古,
至行
今万
苏科版八年级数学下册课件:10.1分式 (共12张PPT)
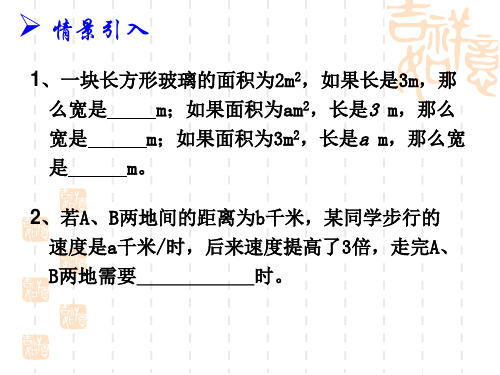
a3 例1:求分式 的值。 a2
(1) a = 1 ( 2) a = 3
(3) a= - 2
例题教学
x2 例2、当x取什么值时,分式 2x 3 (1)没有意义?(2)有意义?(3)值为零。
x2 4 拓展:当x是什么数时,分式 的值是0? x2
10.1 分式
1
x
1- x
-3
将其中2张卡片分别放在分子、分母上, 可以组成哪些代数式,其中哪些是分式?
A 字母 ,那么代数式 叫做分式,其中A是分式的分 B
子,B是分式的分母。
一般地,如果A、B表示两个整式,并且B中含有
分式
A B
B中含有字母
试一试
请同学们自己举出几个分式的例子。
试一试
请判断下列各式是否为分式?若不是, 请说明理由。
××√ × √ √
(1 )
5 , 3
b , 2
2 x 1 , , 2a+b, 4x b
情景引入
1、一块长方形玻璃的面积为2m2,如果长是3m,那
么宽是
宽是 是 m。
m;如果面积为am2,长是3 m,那么
m;如果面积为3m2,长是a m,那么宽
2、若A、B两地间的距离为b千米,某同学步行的 速度是a千米/时,后来速度提高了3倍,走完A、 B两地需要 时。
情景引入
3、小丽用b元钱买3袋同样的瓜子,后来又增 加了a袋,那么每袋瓜子的价格是 元。
(4) (5)
a b
(2) (3)
(6)
交流探讨
a a 试解释分式 b 、b 1 所表示的实际意义
例如: 如果a(元)表示购买笔记本的钱数,b(元) a 表示每本笔记本的售价,那么 表示买到笔 b a 记本的数量; 表示 每本笔记降价1元后, b 1 用a元可购得笔记本的本数;例题教学Βιβλιοθήκη 这些分式,它什么时候有意义?
八年级数学下册第10章分式:分式方程pptx课件新版苏科版

知识点 3 分式方程的增根
知3-讲
1. 增根 在解分式方程的过程中,为了化分式方程为整式方
程,需要在分式方程的两边同乘各分式的最简公分母, 若所得的解恰好使最简公分母的值为零,则这个解就是 增根 .
知3-讲
2. 分式方程无解有两种可能 (1)将分式方程转化成整式方程后,整式方程是
ax=b(a=0,b ≠ 0)的形式,即整式方程无解; (2)整式方程求得的根,使得原分式方程的最简公
知4-讲
(3)列:即列方程,根据相等关系列出分式方程; (4)解:即解所列的分式方程,求出未知数的值; (5)验:即验根,既要检验所求的未知数的值是否适合 分式方程,还要检验此解是否符合实际意义; (6)答:即写出答案,注意单位和答案要完整 .
知4-讲
2. 分式方程的实际问题主要涉及的类型 (1)行程问题:速度 ×时间 = 路程; (2)利润问题:利润 = 售价-进价;利润率 = 利润÷
知识点 2 分式方程的解法
知2-讲
1. 解分式方程的基本思路 去分母,把分式方程转化为整
式方程 .
2. 解分式方程的一般步骤
3. 检验方程根的方法
知2-讲
一般地,解分式方程时,去分母后所得整式方程的
解有可能使原分式方程中分母为 0,因此应做如下检验:
(1)将整式方程的解代入最简公分母,若最简公分母
知1-练
特别提醒 例1中(1)(5)是整式方程;例 1中(3)是分式方程,不
能约分变形.判断分式方程只看形式,如果分母含有未知 数,那么这个方程就是分式方程;分式方程可以转化为 整式方程 .
知1-练
解:(1)不是分式方程,因为分母中不含未知数; (2)是分式方程,因为分母中含有未知数; (3)是分式方程,因为分母中含有未知数; (4)是分式方程,因为分母中含有未知数; (5)不是分式方程,因为分母虽然是字母a,但a为非零常数, 不是未知数 .
苏科版八年级数学下_10.1分 式
感悟新知
知识点 2 分式有意义和无意义的条件
知2-讲
1. 分式有意义的条件 分式的分母表示除数,由于除数不能
为0,所以分式的分母不能为0,即当B
≠
0
时,分式
A B
才有意义.
2. 分式无意义的条件 分式的分母为0,即当B=0 时,分式
A B
无意义.
感悟新知
例4 x 满足什么条件时下列分式有意义? (1) 25xx+ -13;(2) |m|2-1; (3) xx2++13;(4) (x-x2-)(x2+4);
知3-讲
解题秘方:分式值为0 的条件:分子为0,分母不 为0.
感悟新知
教你一招 : 求分式值为0时字母值的方法:
知3-讲
1.解题时可以先求出使分子为0的字母的值,再检验
这个值是否使分母的值为0. 当分母的值不为0时,这
个值就是所要求的字母的值.切记使分母为0的值必须
舍去.
2. 若 有 多 个 值 使 分 式 的 值 为 0 , 则 这 几 个 值 之 间 用
知1-讲
m4 ,-2x2,5+3 y,25,x2+6 y2,pp2,14(3x-y),2x3+x 3,
3a2+π b,a3+a+b+bc.
解题秘方:利用分式的“三要素”判断即可.
感悟新知
解:分式有m4 ,5+3 y,pp2,a3+a+b+bc; 整式有-2x2,25,x2+6 y2,14(3x-y),3a2+π b.
即:对于分式 A ,当A=0 且B ≠ 0 时,A =0.
B
B
感悟新知
2. 常见的几种特殊分式值情况讨论
(1)若
Байду номын сангаас
A的值为正数,则 B
【数学课件】分式的概念课件
谈一谈这一节课你的收获和体会 。 分式的概念
①分子分母都是整式 ②分母中必含有字母
分母中字母的取值不能使分母 值为零,否则分式无意义.
当分子为零且分母不为零时, 分式值为零.
下课
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭
好好学习,天天向上。 2、教育人就是要形成人的性格。——欧文
,0 ,
a 3
,
ab 2
+
1 c
,
x 2
+y
1 5
(x+y)
,
0
,
a 3
,
x 2
+y
整式
x1 ² ,
3 x
,
ab + 2
1 c
分式
在分式中,分母的值不能是零。如果分 母的值是零,则分式没有意义。
例如:在分式
s a
中,a≠0;
在分式
9 m-n
中,m
-
n
≠ 0,即m≠n.
例2
当x取什么值时,下列分式有意义?
(6)当x_<__0_时,分式
x-1 |x|-x
有意义.
3、在下列各分式中,当x等于什么时,分 式的值是零?当x等于什么数时,分式没有 意义?
(1)
2x-1 2-x
(当x=
1 2
时,分式的值是零;
当x=2时,分式没有意义.)
(2)
x²-1 1+x
(当x=1时,分式的值是零; 当x=-1时,分式没有意义.)
(1)
x x-1
分析
(2)
x-2 2x+3
1 (3) x2 9
要使分式有意义,必须且只须分母不等于零.
解 (1)由x-1≠0,得x ≠ 1.
苏科版八年级数学下册10.1 分式 课件 (共23张PPT)
分 式
1.什么是分式,分式与分数有什么不同? 2.什么是分式的值,如何求分式的值? 3.分式的讨论,当字母取什么值时分式有 意义或无意义?
问题1
1÷2 -5÷4
a÷b
分母不能等于0!
1 2 -5 4 a b
如果用字母 a、b分别表示 分数的分子和 分母。如何?
⑴两个数相除可以把它们的商表示成分数的形式
5.x为何值时,分式 x 2 x 1 的值为负数?
2
x2
1 x 6.当x________时,分式 无意义,; 2x 5
当x________时,此分式的值为1;
7.当x________时,分式
x 2 x 1
2
的值为负
xb 8.已知:x=-2时,分式 无意义; xa
X=4时,此分式值为0,求
3 7
a 4 当a取什么数时,分式 a2
2
的值为0?
x5 当X =-5 时,分式 4 x
2x 6 呢? x3
的值为0。
的值为0。
x2 x 1
2
当X =2
时,分式
当X =-1 时,分式
x 5
x2 1 的值为0。 x1
当x取何值时, x 2 4x 5
分式的值为零?
1)当a=-1 时, 解: 3 a 3( - -1) =4 -12 a2 3 a 3 3 2)当a=3时, =0 3 2 a2
17 3) 8
练习三:对于分式
2 x 3 x 2
分母为0,则 分式无意义 分母不为0, 则分式有意义
⑴当x取什么值时,分式有意义? 解:由分母x-2≠0,得x≠2 ∴ 当x≠2时,分式有意义。 ⑵当x取什么值时,分式无意义?
讨论:字母a、b可以表示任何实数吗?
1.什么是分式,分式与分数有什么不同? 2.什么是分式的值,如何求分式的值? 3.分式的讨论,当字母取什么值时分式有 意义或无意义?
问题1
1÷2 -5÷4
a÷b
分母不能等于0!
1 2 -5 4 a b
如果用字母 a、b分别表示 分数的分子和 分母。如何?
⑴两个数相除可以把它们的商表示成分数的形式
5.x为何值时,分式 x 2 x 1 的值为负数?
2
x2
1 x 6.当x________时,分式 无意义,; 2x 5
当x________时,此分式的值为1;
7.当x________时,分式
x 2 x 1
2
的值为负
xb 8.已知:x=-2时,分式 无意义; xa
X=4时,此分式值为0,求
3 7
a 4 当a取什么数时,分式 a2
2
的值为0?
x5 当X =-5 时,分式 4 x
2x 6 呢? x3
的值为0。
的值为0。
x2 x 1
2
当X =2
时,分式
当X =-1 时,分式
x 5
x2 1 的值为0。 x1
当x取何值时, x 2 4x 5
分式的值为零?
1)当a=-1 时, 解: 3 a 3( - -1) =4 -12 a2 3 a 3 3 2)当a=3时, =0 3 2 a2
17 3) 8
练习三:对于分式
2 x 3 x 2
分母为0,则 分式无意义 分母不为0, 则分式有意义
⑴当x取什么值时,分式有意义? 解:由分母x-2≠0,得x≠2 ∴ 当x≠2时,分式有意义。 ⑵当x取什么值时,分式无意义?
讨论:字母a、b可以表示任何实数吗?
苏科版八年级下册数学:101 分式
10.1 分 式
想一想
1、一块长方形玻璃板的面积为2m2 , 如果宽是 3a m,那么这块玻璃板的 长是__m。
2、两块面积分别为3a 公顷、4b 公顷的 棉地,分别产棉花 30m00kg、n50k0g0kg , 这两块棉田平均每公顷产棉花____ kg。
分式的定义
一般地,如果A、B表示两个整式,并且B中 含有字母 ,那么代数式 A 叫做分式,其
a7
x 1 8
2.已知分式 x 3 ,当 x=2 时,分式无意义,则 a=
;
x2 a
3.填表:
a
1
2
3
-20
a a 20
4.请写出一个分式_________,使得当 a=2 时,分式无意义; 5. 请写出一个分式_________,使它的值永远不等于 1;
• 1. 2个 • 2. 4
11 3
a2 1
3
b4
(2)若 a 2 无意义, b2 1 的值为
0,那么 a b
b
你能合理解释分式 a 1 所表示的实际
情境吗?
设计一个情境,解释分式
a (a 0)的值随 a 变化的情况.
a 20
课堂评价
1.下列各式: 3 , a b ,5, 1 , x 中,分式有__________个;
1、当a=4时,整式a-1的值为_3__;
整式a+1的值为_5__;
2、当a=4时,你会求分式 a 1 的
值吗?
a 1
例1:当x取什么值时,分式 x 2
2x 3
(1)无意义 (2)有意义
当 x 取何值时,下列分式有意义?
x
1. 4 3x
x 2 2. x 2
讨论:(1)当a 为何值时,分式 a 1 的值为零?
想一想
1、一块长方形玻璃板的面积为2m2 , 如果宽是 3a m,那么这块玻璃板的 长是__m。
2、两块面积分别为3a 公顷、4b 公顷的 棉地,分别产棉花 30m00kg、n50k0g0kg , 这两块棉田平均每公顷产棉花____ kg。
分式的定义
一般地,如果A、B表示两个整式,并且B中 含有字母 ,那么代数式 A 叫做分式,其
a7
x 1 8
2.已知分式 x 3 ,当 x=2 时,分式无意义,则 a=
;
x2 a
3.填表:
a
1
2
3
-20
a a 20
4.请写出一个分式_________,使得当 a=2 时,分式无意义; 5. 请写出一个分式_________,使它的值永远不等于 1;
• 1. 2个 • 2. 4
11 3
a2 1
3
b4
(2)若 a 2 无意义, b2 1 的值为
0,那么 a b
b
你能合理解释分式 a 1 所表示的实际
情境吗?
设计一个情境,解释分式
a (a 0)的值随 a 变化的情况.
a 20
课堂评价
1.下列各式: 3 , a b ,5, 1 , x 中,分式有__________个;
1、当a=4时,整式a-1的值为_3__;
整式a+1的值为_5__;
2、当a=4时,你会求分式 a 1 的
值吗?
a 1
例1:当x取什么值时,分式 x 2
2x 3
(1)无意义 (2)有意义
当 x 取何值时,下列分式有意义?
x
1. 4 3x
x 2 2. x 2
讨论:(1)当a 为何值时,分式 a 1 的值为零?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分式的概念
①分子分母都是整式 ②分母中必含有字母
分母中字母的取值不能使分母 值为零,否则分式无意义. 当分子为零且分母不为零时, 分式值为零.
下
课
x x 4
的值是零?
解:由分子 |x| -4=0,得x=±4
所以当x=±4时,分式 x x 4 的值是零.
x 4
例
a 3 求分式 的值 a2
(1)a 3
2 ( 2) a 5
拓展创新
1、一个分子为x-5的分式,且知它在x≠1时
有意义。 你能写出一个符合上面条件的分式
上面的问题出现了代数式
S P , a mn
这些代数式与整式有什么不同?这些 代数式有什么共同特征? 分母中含有字母.
什么叫分式?
形如 A(A、B是整式,且B中含有字母,B≠0) B 的式子,叫做分式.
其中A叫做分式的分子,B叫做分式的分母.
整式和分式统称有理式,即 有理式 整式
分式 分母含字母
2、填空
a+ 1 (1)当 a_____ =0 时 ,分式 2a 无意义; a + 1 ≠0 时 ,分式 2a 有意义. (2)当a ____ a+ 1 =-1 时,则分式 2-a 的值为零. (3)当a_____ 8 (4)当x_____ =1 时,则分式 x-1 无意义. 1 = ± 3 (5)当x______时,则分式 无意义. x² -9 x- 1 <0 时,分式 |x|-x 有意义. (6)当x____
例1、下列各有理式中,哪些是整式?哪些是分式?
2 xy 2x y 1 x (1) ; (2) ; (3) ; (4) . x 2 x y 3
解:属于整式的有(2)、(4) 属于分式的有(1)、(3)
为什么(2)、(4)不是分 式?判断的关键是什么?
分母含有字母是分式,
分母不含字?
ab + 1 c 2
分式
在分式中,分母的值不能是零。如果分 母的值是零,则分式没有意义。
s 例如:在分式 a 中,a≠0; 9 在分式 m-n 中,m - n ≠ 0,即m≠n.
例2 当x取什么值时,下列分式有意义? x 1 (1) x-1 (2) x-2 2x+3 (3) x 2 9 分析
(1)5x-7
4 ( 4) 5b c
3 b 3 ( 5) ( 6) x 2 a 1 y 2 2 m( n p ) x xy y ( 7) ( 8) 7 2 x 1
x ( 2) 2
(3)3x2-1
2、把下列各有理式分别填入相应的圈内。
1 , 1 (x + y ) , 3 x² 5 x 1 (x + y ) , , 0 5 a x , + y 3 2 整式 , 0 , a , ab + 1 , x +y c 2 3 2 1 , 3 , x² x
1 ( 2) 2 x 9
2、当x为任意实数时,下列分式一定有意义 的是( )
(A)
2 x 2 1
1 (B) 2 x 2
(C)
1 x2
(D)
1 1 x
例题变形 1.当x取什么值时,下列分式无意义?
x (1) ; x 1 x2 ( 2) . 2x 3
2.当x取什么值时,下列分式的值为零?
3 、在下列各分式中,当 x 等于什么时,分 式的值是零?当x等于什么数时,分式没有 意义? 1 (当x= 2 时,分式的值是零; 2 x - 1 (1) 2-x 当x=2时,分式没有意义.)
-1 (2) x² 1+ x (当x=1时,分式的值是零;
当x=-1时,分式没有意义.)
谈一谈这一节课你的收获和体会 。
苏科版数学教材八年级下
§10.1 分式的概念
(1)面积为2平方米的长方形一边长3米,则它的另 2 一边长为________ 米; 3 (2)面积为s平方米的长方形一边长a米,则它的另 s 一边长为________ 米; a (3)一箱苹果售价p元,总重m千克,箱重n千克.则 p 每千克苹果的售价是_______ m-n 元. 两个整数相除,不能整除时结果可用分数表示. 当两个整式不能整除时,它们的商应该怎么表 示呢?
吗?试试看。 2、把甲、乙两种饮料按质量比x:y混合在一
起,可以调制成一种混合饮料。调制1千克这 种混合饮料需多少甲种饮料?
1、填空:(用分式表示)
(1)若某梨园m平方米产梨p千克,则平均每 p 平方米产梨___ m 千克; (2)小明t小时走了s千米的路,则他走这段路的 s 平均速度是____ t 千米/时; (3)一货车送货上山,上山的速度为x千米/时, 下山的速度为y千米/时,则该货车的平均速度 2 2xy 1 1 千米/时. 是________ + x + y x y
x (1) ; x 1 x2 (2) ; 2x 3 x2 4 (3) . x2
小结:分式有意义 分母不等于零
分式无意义 分母等于零 分式值为零 分子等于零且分母不等于零
阅读下面一题的解答过程,试判断是否正确, 如果不正确,请加以改正。
当x是什么数时,分式
x 4
要使分式有意义,必须且只须分母不等于零.
解 (1)由x-1≠0,得x ≠ 1.
x 所以,当x ≠ 1时,分式 x-1 有意义. 3 (2)由2x+3 ≠0,得x ≠- . 2 x- 2 3 所以,当x ≠- 时,分式 2x+3 有意义. 2
1、当x取什么值时,下列分式有意义?
8 ( 1) x 1
①分子分母都是整式 ②分母中必含有字母
分母中字母的取值不能使分母 值为零,否则分式无意义. 当分子为零且分母不为零时, 分式值为零.
下
课
x x 4
的值是零?
解:由分子 |x| -4=0,得x=±4
所以当x=±4时,分式 x x 4 的值是零.
x 4
例
a 3 求分式 的值 a2
(1)a 3
2 ( 2) a 5
拓展创新
1、一个分子为x-5的分式,且知它在x≠1时
有意义。 你能写出一个符合上面条件的分式
上面的问题出现了代数式
S P , a mn
这些代数式与整式有什么不同?这些 代数式有什么共同特征? 分母中含有字母.
什么叫分式?
形如 A(A、B是整式,且B中含有字母,B≠0) B 的式子,叫做分式.
其中A叫做分式的分子,B叫做分式的分母.
整式和分式统称有理式,即 有理式 整式
分式 分母含字母
2、填空
a+ 1 (1)当 a_____ =0 时 ,分式 2a 无意义; a + 1 ≠0 时 ,分式 2a 有意义. (2)当a ____ a+ 1 =-1 时,则分式 2-a 的值为零. (3)当a_____ 8 (4)当x_____ =1 时,则分式 x-1 无意义. 1 = ± 3 (5)当x______时,则分式 无意义. x² -9 x- 1 <0 时,分式 |x|-x 有意义. (6)当x____
例1、下列各有理式中,哪些是整式?哪些是分式?
2 xy 2x y 1 x (1) ; (2) ; (3) ; (4) . x 2 x y 3
解:属于整式的有(2)、(4) 属于分式的有(1)、(3)
为什么(2)、(4)不是分 式?判断的关键是什么?
分母含有字母是分式,
分母不含字?
ab + 1 c 2
分式
在分式中,分母的值不能是零。如果分 母的值是零,则分式没有意义。
s 例如:在分式 a 中,a≠0; 9 在分式 m-n 中,m - n ≠ 0,即m≠n.
例2 当x取什么值时,下列分式有意义? x 1 (1) x-1 (2) x-2 2x+3 (3) x 2 9 分析
(1)5x-7
4 ( 4) 5b c
3 b 3 ( 5) ( 6) x 2 a 1 y 2 2 m( n p ) x xy y ( 7) ( 8) 7 2 x 1
x ( 2) 2
(3)3x2-1
2、把下列各有理式分别填入相应的圈内。
1 , 1 (x + y ) , 3 x² 5 x 1 (x + y ) , , 0 5 a x , + y 3 2 整式 , 0 , a , ab + 1 , x +y c 2 3 2 1 , 3 , x² x
1 ( 2) 2 x 9
2、当x为任意实数时,下列分式一定有意义 的是( )
(A)
2 x 2 1
1 (B) 2 x 2
(C)
1 x2
(D)
1 1 x
例题变形 1.当x取什么值时,下列分式无意义?
x (1) ; x 1 x2 ( 2) . 2x 3
2.当x取什么值时,下列分式的值为零?
3 、在下列各分式中,当 x 等于什么时,分 式的值是零?当x等于什么数时,分式没有 意义? 1 (当x= 2 时,分式的值是零; 2 x - 1 (1) 2-x 当x=2时,分式没有意义.)
-1 (2) x² 1+ x (当x=1时,分式的值是零;
当x=-1时,分式没有意义.)
谈一谈这一节课你的收获和体会 。
苏科版数学教材八年级下
§10.1 分式的概念
(1)面积为2平方米的长方形一边长3米,则它的另 2 一边长为________ 米; 3 (2)面积为s平方米的长方形一边长a米,则它的另 s 一边长为________ 米; a (3)一箱苹果售价p元,总重m千克,箱重n千克.则 p 每千克苹果的售价是_______ m-n 元. 两个整数相除,不能整除时结果可用分数表示. 当两个整式不能整除时,它们的商应该怎么表 示呢?
吗?试试看。 2、把甲、乙两种饮料按质量比x:y混合在一
起,可以调制成一种混合饮料。调制1千克这 种混合饮料需多少甲种饮料?
1、填空:(用分式表示)
(1)若某梨园m平方米产梨p千克,则平均每 p 平方米产梨___ m 千克; (2)小明t小时走了s千米的路,则他走这段路的 s 平均速度是____ t 千米/时; (3)一货车送货上山,上山的速度为x千米/时, 下山的速度为y千米/时,则该货车的平均速度 2 2xy 1 1 千米/时. 是________ + x + y x y
x (1) ; x 1 x2 (2) ; 2x 3 x2 4 (3) . x2
小结:分式有意义 分母不等于零
分式无意义 分母等于零 分式值为零 分子等于零且分母不等于零
阅读下面一题的解答过程,试判断是否正确, 如果不正确,请加以改正。
当x是什么数时,分式
x 4
要使分式有意义,必须且只须分母不等于零.
解 (1)由x-1≠0,得x ≠ 1.
x 所以,当x ≠ 1时,分式 x-1 有意义. 3 (2)由2x+3 ≠0,得x ≠- . 2 x- 2 3 所以,当x ≠- 时,分式 2x+3 有意义. 2
1、当x取什么值时,下列分式有意义?
8 ( 1) x 1
