管理统计学多元线性回归分析,案例应用步骤解析及EXCEL操作详解共41页文档
Excel在线性回归方程中数据处理的方法和应用

Excel在线性回归方程中数据处理的方法和应用Excel在线性回归方程中数据处理的方法和应用宋爱萍等:Excel在线性回}羟方程中数据处理的方法和应用 Excel在线性回归方程中数据处理的方法和应用TheMethodandApplicationofExcelintheDataProcessingofLinearRegressionEquation 宋爱萍郑欢(江西东华计量测试研究所,江西南昌330029) 摘要:本文介绍了如何利用Excel来完成线性回归方程中数据处理,文中给出了计算的公式及电子表格的设计方法,只需输入活塞面积,指示器值P 和三次检测数据R,就可以自动生成所需要的回归方程,内插误差,负载效率等数据结果,主要例举了千斤顶和量力环数据的处理方法. 关键词:Excel;线性回归方程;千斤顶;量力环1线性回归方程的应用在检定与测试过程中,有大量的数据要进行分析处理,经常用到线性回归方程来计算测量结果,并需求得线性回归方程P:A+B×F 中系数A和B及数据组P和F 的相关性,此时可以利用Excel来自动生成对测量结果的线性回归方程的计算.下面通过千斤顶和量力环--+实例来说明Excel在线性回归方程中数据处理的应用.在千斤顶检测中,根据规程需要给出校准方程,也就是线性回归方程,以力值为自变量F,压力P为应变量的方程P=A+B×F,及负载效率内插误差等数据结果,并用于判断千斤顶是否合格,利用Excel可以节省大量的手动数据计算过程.线性方程为:P=A+B×F根据表1的测量数据,利用电子表格进行线性回归求出工作曲线的截距A,斜率B和相关系数尺值:A=0.010739B=0.019836R:0.999973 根据所求得的R值,可看出F和P成线性关系,其回归直线方程为:P=0.010739+0.019836xF 2Excel表格设计和函数公式的应用上述各值的计算均由表1的Excel电子表格来完成,根椐千斤顶规程设计好的电子表格见表1,下面将该表的主要设计方法作一介绍:(1)在A3中输入活塞的面积大小,B1,D1合并表格中输入方程式,B2,D2中输入各列的表示符号,将各列设置为居中,如表1所示.(2)在A4,A5-J4,J5表格中输入如表1的文字信息和符号,也将各列设置为居中.(3)在A6,Al6中输入压力P的各个检定点系列值. (4)在t36--B16中输入检测千斤顶时在标准测力仪上的各个检定点第一次的测量值.同样,在C6-C16中输入第二次的测量值.在D6--D16中输人第三次的测量值. (5)在B3单元格中输入":INTERCEPT(A6:A16, E6:El6)",在C3单元格中输入":SL0PE(A6:A16,E6: El6)",在D3单元格中输入"=CORREL(A6:A16,E6: El6)".可分别获得工作曲线的截距A,斜率B和相关系数尺值.(6)在E6中输入"=AVERAGE(B6,C6,I36)",在E7中输入"=AVERAGE(B7,C7,D7)",同理一直输入到B16,也可用复制方法以,把E6的内容复制到E7, El6单元格中,函数中的参数会自动和行数一致.(7)在F6中输入"=100*(MAX(136,C6,I36)一MIN(B6,C6,136))/E6",在F7中输入"=100*(MAX(B7,C7,D7),MIN(B7,,D7))/E7",同理一直输入到B16,也可用复制方法以,把F6的内容复制到F7,F16单元格中,函数中的参数会自动和行数一致.表1括l面积拉准方程式F=A~BxFiI.{^fBR!f'00532400.0107390.0199360.399373Ij 蝎;册;力值/kMf?捆6拮费载效率内插误差"算l^一一…i250.2251.050.8ro.i?66.20.04,25l50.315251.210507.35093『5085508.40.4,532.50.955038I-0915751.2752.I751.4.751.6'01}7087094'/5570.5,…20…L1002.7二0037l001.91002.80.21065.00.941007Tj0.525{1263926Z3264_-2_l25l__0.2,…j1331.一09312':99I-0330}15040506.31506102159709415il『043517763777.i1777.417769J0.i19637o.951739一-or402ol8.3:1018.2j2019.i…2019i00,?21299o?95208oI-o.1t5f2262.1f:1261I,2260.42261.2ro.123962o.94:2281io3502512?3{2515-02516?52514?7{02'266240?29zoio-28512775.02774.II2778.72778.1;0229288i095{27722【-01只斋镇^活塞面积,拍示嚣示值和对应三次的柱捌力值即可自动生成所嚣要的数据结果.注意单位一致(8)在G6中输入"=A6*A3*1000",即千斤顶的理论输出力值(F=P×S,S为活塞面积),同理在G7中输入"=A7*A3*1000",直至G16.(9)在H6中输入"=E6/G6",即各检定点的测量平均值除千斤顶理论输出力值.也可以用复制方法,把H6 的内容复制到哪,H16单元格中,函数中的参数会自动和行数一致.10)在16--116中是根据校准方程已算出来的系数计 (算出来的力值,即F=(P—A)/B,所以在I6中输入"=(A6 《计量与渤试技4C)2009年第36卷第5期一)/C3",I7中输入"=(A7一~)/C3",直至I16中. (1l1)在J6中是内插误差,按规程等于计算值减平均值再除平均值的百分数,在J6中输入"=100*(I6一 E6)/E6"同理复制一直到J16.表2菇鞭慧,鬻IA,?鬻》l糟;饕瓣B茹簸黧量力环}寰I试i羹数1载荷百分表示值2(kN)(m)30.0003.00040.1003.17050.2003.34060.3003.51270.4003.69080.5003.86290.6004.036100.7004.208110.8004.379120.9004.56113i.0004.740141.2005.09115量力环率定系数(N/O01m)5.73831617线性相关系数0999975关于该电子表格中的数据的对齐方式,数字的显示位数及显示形式的设置在此不再说明.表中有11个检测点,对于小于11个检测点的,后面的行空着就行,多于11个点可以再添加进去,到此,表格制作完成,只需输入活塞面积,指示器示值和对应三次的检测力值即可自动生成所需要的数据结果,大大减少数据处理的时间和错误. 3Excel在量力环数据处理的应用量力环是利用弹性体(钢环)的弹性形变,用百分表指示其形变进程来复现力值大小的,现多用于土工和地质勘察中,检定时要给出检定力值,线性度和率定系数等值.如表2制定电子表格,在A3,A14输入是检定点的负载值,在B3,B14输入是各点对应的百分表进程值, 在A16中输入":SLOPE(A3:A14,B3:B14)*10",即得到其率定系数(N/0.01mm),也就是百分表每走一格对应输出力值大小.在B17中输入":COr~REL(A3:A14,B3:B14)",即可得到此量力环的线性度.4结束语对于类似的测量数据处理只要对电子表格略作修改,可以求得所需要的数据处理结果,对回归方程的计算大大减少了用手工计算的重复和繁琐工作,可以自动生成所需的数据,减少人为计算过程中的偶然错误,若检定点数据多或少了则可以插入或删去即可,再将相关单元格中的公式进行复制或修改,十分方便快捷.这种利用工程软件来处理大量数据计算的方法,可以在计量检测中有更大的推广应用,如标准测力仪,负荷传感器,压力传感器以及不确定度评定的计算中都可应用. 参考文献[1]张迎新着.Excel2003函数应用完全手册.2004. [2]液压千斤顶检定规程(VerificationRegulationofHydraulicJack)JJ(21—2005.全国力值硬度计量技术委员会. 作者简介:宋爱萍,男,工程师.工作单位:江西东华计量测试研究所.通讯地址:330029江西省南昌市南池路35号. 郑欢,江西东华计量测试研究所(南昌330029). 收稿时间:2008—12—11(上接第44页)(u.2)V==^,jj4.66×10—V(4)标准电阻器引起的不确定度分量:标准电阻器标称值为100fl,0.01级,其最大允许误差(MPE):?0.01n,半宽为0.01Q,属均匀分布,包含因子k=?3,由标准电阻器引起的不确定度z'(R):=5.77x10—3Qj3.4合成标准不确定度"(A)=~/f}"()4-c2u()4-c2u(2)4-c2u(尺)=6.78×10—3mA3.5扩展不确定度取包含因子k:2,则:k?=2×6.78×10一.mA=1.4X10一mA测量点10mA的相对扩展不确定度:==×100%=0-14%3.6剩余电流动作特性检测仪剩余电流示值误差测量结果的相对扩展不确定度报告Urd=0.14%k=24结束语用校准仪器串联人剩余电流动作特性检测仪内部对剩余电流示值进行校准的方法,测量结果的不确定度较小,尽管该校准方法没有考虑外部线路及磁场对校准结果的影响,但计量检测部门利用现有仪器比较容易实现. 作者简介:刘四林,男,助理工程师.工作单位:广东省汕头市质量计量监督检测所.通讯地址:515041广东省汕头市东厦北路155号. 吴俊生,广东省汕头市质量计量监督检测所(汕头515041). 收稿时间:2009一Ol一13。
EXCEL在多元线性回归分析中的应用
EXCEL 在多元线性回归分析中的应用高 平/文在一元线性回归分析中,重点放在了用模型中的一个自变量X 来估计因变量Y 。
实际上,由于客观事物的联系错综复杂,一个因变量的变化往往受到两个或多个自变量的影响。
为了全面揭示这种复杂的依存关系,准确地测定它们的数量变动,提高预测和控制的精确度,就要考虑更多的自变量,建立多元回归模型。
多元回归分析的原理和方法同一元线性回归分析基本相同,但有两个不同点:1.不能用散点图来表示变量之间的关系。
2.多元回归的计算难度要远大于简单线性回归,且变量越多,计算越复杂。
但应用EXCEL 来完成计算将变得简单和轻松。
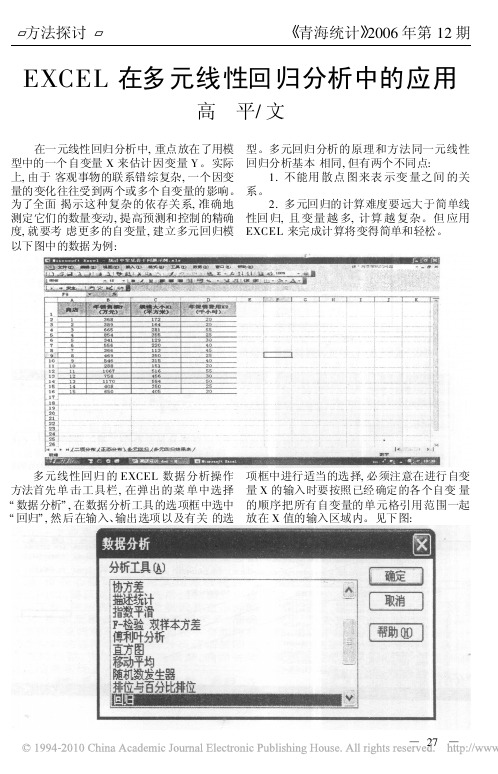
以下图中的数据为例: 多元线性回归的EXCEL 数据分析操作方法首先单击工具栏,在弹出的菜单中选择数据分析 ,在数据分析工具的选项框中选中 回归 ,然后在输入、输出选项以及有关的选项框中进行适当的选择,必须注意在进行自变量X 的输入时要按照已经确定的各个自变量的顺序把所有自变量的单元格引用范围一起放在X 值的输入区域内。
见下图:!27!点击 确定按钮,即可得到线性回归分析的结果。
见下图:!!28根据上图中的显示结果,可直接写出二元线性回归方程:Y i=b0+b1X1i+b2X2i=-51.3127+1. 4053x1i+6.3823x2ib1表示在促销费用固定时,商店的规模大小每增加1平方米,年销售额平均增加1.4053万元;b2表示在商店的规模大小固定时,促销费用每增加1万元,年销售额平均增加6.3823万元。
这里b1即商店的规模大小的回归系数比一元线性回归方程中的回归系数b= 1.6246小,是因为一元线性回归方程只考虑了商店的规模大小对年销售额的影响,忽略了促销费用这一很重要的因素,在商店的规模大小的影响中渗入了促销费用的影响。
这里的截距b0=-51.3127万元,与一元线性回归方程中的截距+99.01万元有很大的不同,因为X1=0和X2 =0都不在X1、X2的样本取值范围之内,因而对截距项的解释要非常谨慎。
多元统计分析及Excel应用

多元统计分析方法概述目录引言………………………………………………………………第四页多元线性回归方法原理简介……………………………………第四页多元线性回归案例叙述分析……………………………………第四页多元线性回归分析方法在社会的应用…………………………第八页聚类分析方法原理简介…………………………………………第八页聚类分析案例叙述分析…………………………………………第八页聚类分析方法在社会的应用……………………………………第十页主成份分析方法原理简介………………………………………第十页主成份分析案例叙述分析……………………………………第十一页主成份分析方法在社会的应用………………………………第十四页因子分析方法原理简述………………………………………第十四页因子分析案例叙述分析………………………………………第十四页因子分析方法在社会的应用…………………………………第十七页偏最小二乘回归分析方法原理简介…………………………第十八页偏最小二乘回归分析案例叙述分析…………………………第十九页偏最小二乘回归分析方法在社会的应用…………………第二十一页总结…………………………………………………………第二十一页参考文献……………………………………………………第二十二页谢辞…………………………………………………………第二十三页摘要本文主要概述了多元统计分析的各个方法,然后在后面介绍了多元统计分析方法在社会生活等方面的实际案例以及分析。
并由案例分析找出各个统计分析方法的对应使用领域。
关键词多元统计分方法回归分析聚类分析因子分析主成份分析偏最小二乘回归分析因素股市模型财务SummaryThe Chemometrics includes chemical experimental design and optimization (such as orthogonal design, simplex method and variance analysis), chemical pattern recognition (such as clusters, PCA, k-nearest neighbour analysis, SIMCA and ANN), multi-variance calibration (such as MLR, CLS, PCR and PLS) and spectrum analysis (Such as ITTFA, EFA and FSWEFA), signal processing (such as filtering, smoothing, derivation and convolution).keywordmultivariate statistical analysis method regression analysis cluster analysis factor analysis principal component analysis linear least squares estimate complication equity market model finance一、引言多元统计分析的基本方法。
用EXCEL做线性回归的方法

用EXCEL做线性回归的方法在Excel中进行线性回归分析是一种常见的统计方法,可以用来建立和评估两个变量之间的线性关系。
以下是在Excel中进行线性回归的步骤:2. 打开Excel并导入数据:在Excel中创建一个新的工作簿并将数据导入其中。
确保每个变量处于独立的列中,并将列标题放在第一行。
3.绘制散点图:选择包含两个变量的数据范围,然后通过选择“插入”选项卡上的“散点图”图标绘制散点图。
确保选择一个表示线性趋势的散点图类型(例如,线性散点图)。
4.添加趋势线:右键单击散点图上的任何一个数据点,然后选择“添加趋势线”选项。
在弹出的对话框中,选择“线性”作为趋势线类型。
还可以选择“显示方程式”和“显示R方值”,以显示方程式和决定系数。
5. 进行线性回归分析:在Excel中进行线性回归分析有两种常见的方法。
一种是使用“利用工具”功能进行线性回归,另一种是使用“数据分析”工具。
-利用工具:选择工作表中的一个空单元格,然后选择“数据”选项卡上的“数据分析”功能。
在弹出的对话框中,选择“回归”然后点击“确定”。
在输入区域中选择两个变量的列,并勾选“置信区间”和“残差”,然后点击“确定”进行分析。
- 数据分析工具:如果Excel中没有“数据分析”选项,则需要先启用。
选择“文件”选项卡上的“选项”,然后选择“添加-加载项”。
在弹出的对话框中,选择“Excel加载项”,并勾选“数据分析工具”,然后点击“确定”。
在“数据”选项卡上就会出现“数据分析”选项,然后执行和利用工具方法相同的步骤。
6. 解读结果:分析完成后,Excel将在单元格区域中输出回归方程式和其他相关统计信息。
主要关注回归方程式中的系数,这些系数表示参与线性回归的变量之间的关系。
还可以评估决定系数(R²)的值以确定回归模型的拟合程度。
7.绘制拟合曲线:使用回归方程式中的系数,可以在散点图中绘制拟合曲线。
选择散点图上的一个空白区域,然后选择“插入”选项卡上的“散点图”功能。
Excel数据分析工具进行多元回归分析

E x c e l数据分析工具进行多元回归分析TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-使用Excel数据分析工具进行多元回归分析使用Excel数据分析工具进行多元回归分析与简单的回归估算分析方法基本相同。
但是由于有些电脑在安装办公软件时并未加载数据分析工具,所以从加载开始说起(以Excel2010版为例,其余版本都可以在相应界面找到)。
点击“文件”,如下图:在弹出的菜单中选择“选项”,如下图所示:在弹出的“选项”菜单中选择“加载项”,在“加载项”多行文本框中使用滚动条找到并选中“分析工具库”,然后点击最下方的“转到”,如下图所示:在弹出的“加载宏”菜单中选择“分析工具库”,然后点击“确定”,如下图所示:加载完毕,在“数据”工具栏中就出现“数据分析”工具库,如下图所示:给出原始数据,自变量的值在A2:I21单元格区间中,因变量的值在J2:J21中,如下图所示:假设回归估算表达式为:试使用Excel数据分析工具库中的回归分析工具对其回归系数进行估算并进行回归分析:点击“数据”工具栏中中的“数据分析”工具库,如下图所示:在弹出的“数据分析”-“分析工具”多行文本框中选择“回归”,然后点击“确定”,如下图所示:弹出“回归”对话框并作如下图的选择:上述选择的具体方法是:在“Y值输入区域”,点击右侧折叠按钮,选取函数Y数据所在单元格区域J2:J21,选完后再单击折叠按钮返回;这过程也可以直接在“Y值输入区域”文本框中输入J2:J21;在“X值输入区域”,点击右侧折叠按钮,选取自变量数据所在单元格区域A2:I21,选完后再单击折叠按钮返回;这过程也可以直接在“X值输入区域”文本框中输入A2:I21;置信度可选默认的95%。
在“输出区域”如选“新工作表”,就将统计分析结果输出到在新表内。
为了比较对照,我选本表内的空白区域,左上角起始单元格为K10.点击确定后,输出结果如下:第一张表是“回归统计表”(K12:L17):其中:Multiple R:(复相关系数R)R2的平方根,又称相关系数,用来衡量自变量x 与y之间的相关程度的大小。
EXCEL多元回归分析PPT(共46张PPT)

用Excel计算描述统计量 用Excel进行相关分析 用Excel进行回归分析
用Excel计算描述统计量
用函数计算描述统计量 描述统计菜单项的使用
一、用函数计算描述统计量
常用的描述统计量有众数、中位数 、算术平均数、调和平均数、几何 平均数、极差、四分位差、标准差 、方差、标准差系数等。下面介绍 如何用函数来计算描述统计量。
单击任一空白单元格, 回车后得几何平均数为14.
产量与需水量之间的关系:抛物线 用Excel进行回归分析 ②R Square(复测定系数R2):用来说明自变量解释因变量变差的程度,以测定因变量y的拟合效果。 (1)手工输入函数名称及参数
输入“=STDEV(B2:B11)/AVERAGE( 6313,表示二者之间的关系是正相关。
用Excel进行回归分析
第二步:单击“确定”按钮,弹出“回归”对话框,在“Y值输入区域”输入 $B$1:$B$11;在“X值输入区域”输入$C$1:$C$11,在“输出选项”选 择“$E$1”,如下图所示。
多元回归分析
用Excel进行回归分析
第三步:单击确定按钮,得回归分析结果如下图所示。
回车后得偏度系数为-0. 回车后得调和平均数为1. 第二步:在array1中输入B3:B10,在array2中输入C3:C10,即可在对话框下方显示出计算结果为0. 用Excel进行回归分析 Excel回归分析工具的输出结果包括3个部分: (1)手工输入函数名称及参数 (1)手工输入函数名称及参数 输入“=HARMEAN(B2:B11)”, 方差分析表的主要作用是通过F检验来判断回归模型的回归效果。 用Excel进行回归分析 用Excel进行回归分析 ②R Square(复测定系数R2):用来说明自变量解释因变量变差的程度,以测定因变量y的拟合效果。 Excel进行回归分析同样分函数和回归分析宏两种形式,其提供了9个函数用于建立回归模型和预测,这9个函数分别是: 项,在“数据分析”项中选择“相关系数”,弹出 第一步:单击“工具”菜单,选择“数据分析” 如果按2/10,即从30个数据中去掉最大的一个值和最小的一个值,再求平均数。 函数的一般导入过程为:点菜单“插入”; 6.TREND计算线性回归线的趋势值 用Excel计算描述统计量 回车后得峰度系数为0.
利用Excel进行线性回归分析

利用Excel进行线性回归分析————————————————————————————————作者: ————————————————————————————————日期:ﻩ文档内容1.利用Excel进行一元线性回归分析2. 利用Excel进行多元线性回归分析1.利用Excel进行一元线性回归分析第一步,录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1第二步,作散点图如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)”。
图表向导的图标为。
选中数据后,数据变为蓝色(图2)。
图2点击“图表向导”以后,弹出如下对话框(图3):图3在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图4第三步,回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:1. 首先,打开“工具”下拉菜单,可见数据分析选项(见图5):图5用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):图62.然后,选择“回归”,确定,弹出如下选项表(图7):图7进行如下选择:X 、Y 值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图(图8-1)。
或者:X 、Y 值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图(图8-2)。
注意:选中数据“标志”和不选“标志”,X 、Y 值的输入区域是不一样的:前者包括数据标志:最大积雪深度x (米) 灌溉面积y (千亩)后者不包括。
这一点务请注意(图8)。
图8-1包括数据“标志”图8-2不包括数据“标志”3.再后,确定,取得回归结果(图9)。
用EXCEL进行生产函数的多元线性回归分析

用EXCEL进行生产函数的多元线性回归分析一、相关函数EXCEL电子制表系统中函数的语法分为函数名和参数两部分,参数用圆括号括起来,之间以逗号隔开。
参数可以为单元格区域、数组、函数、常数(逻辑型、数值型等)。
进行回归分析时,主要采用线性回归函数LINEST,辅以使用索引取值INDEX与四舍五入ROUND函数。
1、线性回归函数LINEST。
使用最小二乘法对已知数据进行最佳直线拟合,并返回描述此直线的数组。
因为此函数返回数值数组,所以必须以数组公式的形式输入。
该函数的功能为:运算结果返回一线性回归方程的参数,即当已知一组混合成本为Y 因变量序列值、N组Xi有关自变量因素的数量序列值时,函数返回回归方程的系数bi(i=1,2…n单位变动成本)和常数a(固定成本或费用)。
多元回归方程模型则为:y=b1x1+b2X2……+bnXn+a语法LINEST(known_y's,known_x's,const,stats)Known_y's 是关系表达式 y = mx + b 中已知的 y 值集合。
∙如果数组 known_y's 在单独一列中,则 known_x's 的每一列被视为一个独立的变量。
∙如果数组 known-y's 在单独一行中,则 known-x's 的每一行被视为一个独立的变量。
Known_x's 是关系表达式 y = mx + b 中已知的可选 x 值集合。
∙数组 known_x's 可以包含一组或多组变量。
如果只用到一个变量,只要 known_y's 和 known_x's 维数相同,它们可以是任何形状的区域。
如果用到多个变量,则known_y's 必须为向量(即必须为一行或一列)。
∙如果省略 known_x's,则假设该数组为 {1,2,3,...},其大小与 known_y's 相同。
