《相似多边形》PPT课件
合集下载
1.1相似多边形 课件 青岛版数学九年级上册

(3)求∠D′的大小. 解:由题意知,∠D′=∠D.∵AD∥BC,∠C=60°, ∴∠ D=180°-∠ C=120°. ∴∠ D′=12 0°.
感悟新知
知3-练
4-1. 已知四边形HGFE相似于四边形LMNK,如图所示. (1)求四边形HGFE与四边形LMNK 的相似比;
解:相似比为EKHL =140=25.
2. 表示方法 相似用符号“∽”表示,读作“相似于”,如: 四边形ABCD ∽四边形EFGH,读作“四边形ABCD 相 似于四边形EFGH”.
感悟新知
知2-讲
特别解读:(1)相似多边形的定义可用来判断两个多边 形是否相似.(2)用符号“∽”表示两个图形相似时,要把 表示对应顶点的字母写在对应的位置上.
感悟新知
(1)求梯形ABCD 与梯形A′B′C′D′的相似比k; 解:相似比k =AA′DD =46=23.
知3-练
感悟新知
பைடு நூலகம்
知3-练
(2)求A′B′和BC 的长;
解:∵梯形ABCD 与梯形A′B′C′D′相似,且由(1)知 相似比k =23,∴AA′BB=23, BB′CC= 23.
感悟新知
知3-练
感悟新知
知3-练
解题秘方:根据相似多边形的对应边成比例求解. 解:∵矩形ABCD ∽矩形BFEA, ∴ AB∶BF=AD∶BA.∴ AD·BF=AB·BA.
易知BF=12AD,∴ 12AD2=AB2 .∴AADB= 12= 22.
感悟新知
知3-练
3-1. 如图, 把矩形ABCD 对折, 折痕为EF, 若矩形 ABCD ∽矩形EABF,AB=2.求矩形ABCD 与矩形 EABF 的相似比.
感悟新知
知2-练
4.3《相似多边形》课件
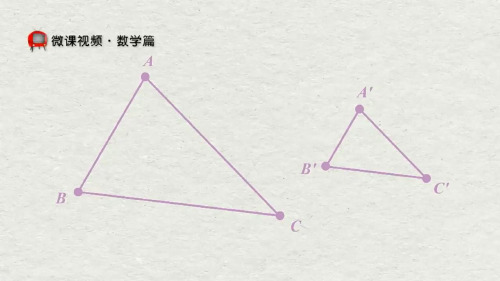
A 21 D
18
β
78° 83°
B
C
所以它们的对应边成比例,由此可得
x
H
E
EH EF ,即 x 24 .
AD AB
21 18
118° 24
α
解得 x=28.
F
G
23
1.相似多边形及其相关概念 各角分别相等、各边成比例的两个多边形叫做 相似多边形. 相似用符号“∽”表示,读作“相似于”. 相似多边形对应边的比叫做相似比.
7
想一想 下图中的两个多边形分别是计算机显示
屏上的多边形ABCDEF和投射到银幕上的多边形
A1B1C1D1E1F1,它们的形状相同吗? (1)在这两个多边形中,是否有
A F
B C
ED
对应相等的内角?设法验证你的猜想.
A1
B1
(2)在这两个多边形中,夹相等 F1
C1
内角的两边是否成比例?
E1
D1
8
不规则四边形
例如,五边形ABCDE∽五边形A1B1C1D1E1,对应
边的比 AB BC CD DE EA 4 ,因此五边形
A1B1 B1C1 C1D1 D1E1 E1 A1 5
ABCDE与五边形A1B1C1D1E1的相似比为
k1
4 5
,五边
形A1B1C1D1E1与五边形ABCDE的相似比为
k2
5 4
.
(3)
(4)
很明显,上面两组中的两个图形也不是全等图形,但每
组中的两个图形的形状相同,满足这种关系的两个图形是什么
关系呢?可以用什么名词来表达呢?与全等图形有怎样的联系
?
6
2.生活中同学们还会看到这样的图片.
相似多边形ppt课件四
相似多边形的对应角相等, 对应边成比例.
这个结论在今后学习的过程中 作用很大,你可要注意噢!
看一看,议一议
(1)、观察下面两组图形,图4-12(1)中 的两个图形相似吗?为什么?图4-12(2)中 的两个图形呢?与同桌交流.
10
10
12
12 (1)
10 图4-12
10
8
(2) 12
(2)、如果两个多边形不相似,那么它们 的各角可能对应相等吗?它们的各边可能对 应成比例吗?
AB 1 BC 1 CD 1 , , A' B ' 2 B ' C ' 2 C ' D ' 2 DE 1 EF 1 FA 1 , , D ' E ' 2 E ' F ' 2 F ' A' 2
对应角
对应边
结论: 六边形ABCDEF与六边形 A1B1C1D1E1F1是形状相同的图形; 它们的六个角都分别相等,称为 对应角;六条边的比都相等,称 为对应边.
F
(2)正方形ABCD与正方形EFGH.
解:(2)由于正方形每个角都是直角,所 以∠A=∠E= 900, ∠B=∠F= 900, ∠C=∠G= 900, ∠D=∠H= 900;
由于正方形四边相等,所以
E A B H
AB BC CD DA . EF FG GH HE
D
C F (2) G
• 形状相同的图形,它们的对应角有怎样的关 系?对应边呢?
150 A= —— B= 120 —— C= 105 —— D= 135 —— 120 E= ——
90 F= ——
90 F’= ——
《相似多边形》相似图形4精品 课件

•
九、没有人不想和你同坐一辆豪华轿车 ,但你 需要的 ,却是 轿车坏 了还会 和你一 起搭巴 士的人 。
•
十、我喜欢你的意思就是:从现在起, 你已经 具备伤 害我的 能力, 以及不 好意思 我看谁 都像情 敌。
•
十一、不相信下辈子,只想善待你今生 。因为 我不知 道,下 一辈子 是否还 能遇见 你,所 以我今 生才会 那么努 力把最 好的给 你。
人生如逆水行舟,不进则退。
•
优胜劣汰的世界里,你必须不断提升 自己的 价值。 一、放下大概就是这样,即使我们没在 一起, 我也会 好好的 ,谢谢 时间惊 艳了那 段有你 的记忆 ,也谢 谢现在 更努力 变好的 自己。
•
二、抱歉啊,不能为你金戈铁马,也不 能许你 一世繁 华,不 过我能 给你一 个小家 ,里面 温了杯 暖茶。
E
C 22 30 48
D
自主练习 书 P129
2.在下面的图形中,有两个相似三
角形,试确定 y、m、n的值。
△ABC∽△DEF A
D
n°
3a
10
y 2a 50°
B
45°
85° C 45°m°F
E
尝试解决 例1:有一块呈三角形形
状的草坪,其中一边的长是 20m,在这个草坪的图纸上,这条 边长 5cm,其他两边的长度都是3.5cm。 求该草坪其他两边的实际长度。
毕业八年的她被迫重返人才市场,但 彼时的 她与毕 业时相 比毫无 长进, 面试屡 屡碰壁 。
李尚龙曾说:
真正的安稳是历经世事后的淡薄,你 还没有 见过世 界,就 想隐退 山林, 到头来 只会是 井底之 蛙。”
人生如逆水行舟,不进则退。
•
优胜劣汰的世界里,你必须不断提升 自己的 价值。 一、放下大概就是这样,即使我们没在 一起, 我也会 好好的 ,谢谢 时间惊 艳了那 段有你 的记忆 ,也谢 谢现在 更努力 变好的 自己。
相似多边形PPT课件(冀教版)

知3-讲
例3 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩
形ABCD类似,已知AB=4.
(1) 求AD的长;
(2)求矩形DMNC与矩形ABCD的类似比.
导引:类似多边形的对应边的比相等,
A
M
D
其比值就是类似比.
B
E
C
知3-讲
解: (1)设AD=x,则 DM x . 2
∵矩形DMNC与矩形ABCD类似, ∴ AD CD .
∠C1,∠D=∠D1,
AB A1 B1
BC B1C1
CD C1 D1
DA D1 A1
.
因此四边形ABCD和四边形A1B1C1D1类似.
A
BA
B
CD
C
D
归纳
知2-导
类似多边形的性质:类似多边形的对应边的比相等, 对应角相等.
作用:常用来求类似多边形中未知的边的长度和角 的度数.
知2-讲
例 2 如图,五边形ABCDE∽五边形A1B1C1D1E1,求C1D1的 长和∠A的度数.
解: ∵五边形ABCDE∽五边
形A1B1C1D1E1,
∴ AB CD , A1B1 C1D1 ∠E=∠E1=145°.
∴AB=15, A1B1=10, CD=21,
15 21
∴
.
10 C1D1
解得C1D1=14.
知2-讲
又∵∠B=130°,∠C=∠D=90°, ∵∠A=(5-2)×180°-130°-145°-2×90°
知1-讲
解:类似图形有:图(1)和图(9),图(2)和图(4), 图(3)和图(10),图(5)和图(7).
总结
知1-讲
判断两个图形是否是类似图形的方法:看两个图 形的形状是否相同,即看其中一个图形是否是由另一 个图形放大或缩小得到的,如果是,那么它们是类似 图形,否则就不是类似图形.
《相似多边形》优秀课件doc资料

对应角相等
对应边成比例
AB
F
C
ED (1)
A1
B1பைடு நூலகம்
F1
C1
E1 D (2) 1
• 例 下列每组图形形状相同,它们的对应 角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF;
解:(1)由于正三角形每个角都等于
600,所以∠A=∠D= 600,∠B=∠E=
600, ∠C=∠F= 600;
D
相似多边形
想一想
还记得什么是全等图形吗? 全等图形有何特征?
图1
A
图2
B
C
A B C
请观察下边 图形
篮球巨星姚明同一张底片冲洗出来的2寸 照片和4寸照片中,人物的形状改变了吗?大 小呢?
符合国家标准的两面中国国 旗的形状相同吗?大小呢?
综合以上各组图形我们体会到: 两个图形的形状_完__全_相__同__,但图形的 大小_不一_定__相__等_,
相似多边形的对应角有什么 关系?对应边呢?
若两个多边形相似,那么他 们的对应角相等,对应边成比 例.
注意判断两个多边形相似的条件: 1. 对应角相等 2. 对应边成比例
两个条件缺一不可哟!
题型1 判断两个多边形相似
1. 判断下列每组图形是否相似,为什么?
5
6
5 正方形 6 菱形
(1)
题型1 判断两个多边形相似
11mm
E10 10mm D1
(2)
在上图中,六边形ABCDEF和六边形A1B1C1D1E1F1是形状相 同的图形.其中∠A与∠A1,∠B与∠B1,∠C与∠C1,∠D与 ∠D1,∠E与∠E1,∠F与∠F1分别对应相等;称为对应角, AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,FE与E1F1, FA与F1A1的比都相等.称为对应边,
《相似多边形》课件

工程测量
工程师使用相似多 边形来确定难以到 达的物体或地形的 尺寸。
解题技巧
绘制图形
首先绘制出相似多边形,标明对应边和角边形的未知 量。
确定比例尺
使用对应边的长度比例计算相似多边形的比 例尺。
检验结果
检查计算结果是否与已知信息和比例尺相 符。
总结
1
相似多边形概念
相似多边形是指形状相同、大小不同的多边形。
2
相似多边形特征
相似多边形的对应角度相等,对应边成比例。
3
相似多边形的用途
相似多边形可用于建筑设计、地图制作、影视特效等。
相似多边形
什么是相似多边形?学习相似多边形概念和基本特征,探索相似多边形的性 质和应用。
基本特征
1 定义
2 比例尺
相似多边形是指形状相同、大小不同的多 边形。它们的对应角度相等,对应边成比 例。
相似多边形的边长比例称为比例尺。
3 相似判定
4 尺形相似
两个多边形相似,必须满足一个条件:对 应角度相等。
比例判定
如果两个多边形的对应边成比 例,则它们相似。
旋转判定
如果一个多边形围绕另一个多 边形的一个定点旋转,可以重 合,则它们相似。
应用场景
建筑物
设计师使用相似多 边形来确定建筑物 的比例和尺寸。
地图
地图使用相似多边 形来表示现实世界 中的物体和地形。
影视特效
影视特效使用相似 多边形来制作逼真 的计算机图形。
两个多边形相似,不一定尺寸相同。但如 果它们的尺寸相同,则称为尺形相似。
性质
✔️ 对应角度相等 ✔️ 对应边成比例 ✔️ 相似图形面积比等于边长比的平方 ✔️ 多边形的比例尺相等,则这些多边形相似
《相似多边形》图形的相似PPT课件教学课件

4 J
5I
解:(1)相似比=CD : HI=3 : 5 (2)∵五边形ABCDE相似于五边形FGHIJ ∴ ∠F =∠A=120o, ∠C= ∠H=90o, ∴AB : FG = BC : GH = CD : HI = DE : IJ = EA : JF 即2 : FG = BC : 6 = 3/5 = 2.2 : IJ = AE :4 解得FG =10/3 cm, BC =18/5cm, IJ=11/3cm,AE=12/5cm
C´D´=__4
3A B 1°18 E
C 2 D B´
A´
6
E´
80°
五边形A´B´C´D´E´与五边形 . ABCDE的相似比为_2:_1
C´
D´
E
2、如图:下面的两个菱形相似吗?为什么? 满足什么条件的两个菱形一定相似?
6°0
A H
F
D
1°20 B
C
G
随堂练习
判断:
(1)任意两个矩形都是相似图形( ) (2)任意两个圆形是相似图形( )
对应角相等
AB = BC = AC ,A1B1 = B1C1 = A1C1
AB : A1B1 = BC : B1C1 = CD : C1D1 对应边成比例
对应角有什么关系?
A 150° B
F 正正八八边边形形 放放大大 B1
E
A1 150°
F1 E1
C
D
C1
∠A =∠A1, ∠B =∠B1, ∠C =∠C1 ∠D =∠D1, ∠E =∠E1, ∠F =∠F1
2、在记两个多边形相似时,要把表示对应角顶点的字母写 在对应的位置上。
A F
E
B C
D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15.如图所示,点E是菱形ABCD对角线CA的延长线上任 意一点,以线段AE为边作一个菱形 AEFG,且菱形 AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD.
证明:∵菱形AEFG∽菱形ABCD, ∴∠EAG=∠BAD, ∴∠EAG+∠GAB=∠BAD+∠GAB, ∴∠EAB=∠GAD. 又∵AE=AG,AB=AD, ∴△AEB≌△AGD,∴EB=GD.
同学们下课啦
授课老师:xxx
此页为防盗标记页(下载后可删)
教师课堂用语在学科专业方面重在进行“引”与“导”,通过点拨、搭桥等方式让学生豁然开朗,得出结论,而不是和盘托 出,灌输告知。一般可分为:启发类、赏识类、表扬类、提醒类、劝诫类、鼓励类、反思类。
一、启发类
1. 集体力量是强大的,你们小组合作了吗?你能将这个原理应用于生活吗?你的探究目标制定好了吗? 2. 自学结束,请带着疑问与同伴交流。 3. 学习要善于观察,你从这道题中获取了哪些信息? 4. 请把你的想法与同伴交流一下,好吗? 5. 你说的办法很好,还有其他办法吗?看谁想出的解法多? 二、赏识类
BS版九年级上
第四章 图形的相似
3 相似多边形
提示:点击 进入习题
1D 2A 3D 4B
5C 6C 7B 8C
答案显示
提示:点击 进入习题
9C
10 B
11 A 12 D
答案显示
13 见习题 14 见习题 15 见习题 16 见习题
1.下列说法中正确的是( D ) A.对应角相等的多边形一定是相似多边形 B.对应边的比相等的多边形是相似多边形 C.边数相同的多边形是相似多边形 D.对应角相等、对应边成比例的多边形是相似多边形
1. 说得太好了,老师佩服你,为你感到骄傲! 2. 你的设计(方案、观点)富有想象力,极具创造性。 3. 我非常欣赏你的想法,请说具体点,好吗? 4. 某某同学的解题方法非常新颖,连老师都没想到,真厉害! 5. 让我们一起为某某喝彩!同学们在学习过程中,也要敢于猜想,善于猜想,这样才能有所发现,有所创造! 三、表扬类
【点拨】把一个图形按一定比例扩大或缩小,各边都相应 地扩大或缩小,各角不变. 【答案】D
13 . 如 图 , 四 边 形 ABCD∽ 四 边 形 EFGH , ∠ A = 62° , ∠B=70°,∠H=140°,AD=18,EF=15,FG= 14,EH=12,求∠G的度数及AB,BC的长.
解:∵四边形 ABCD∽四边形 EFGH, ∴∠E=∠A=62°,∠F=∠B=70°. 又∵∠H=140°,∠E+∠F+∠G+∠H=360°,∴∠G=88°. ∵四边形 ABCD∽四边形 EFGH, ∴EAHD=AEBF=FBGC.又∵AD=18,EF=15,FG=14,EH=12, ∴AB=22.5,BC=21.
(2)如果多边形ABCDEF和多边形A1B1C1D1E1F1的相似比 是1:1.5,且CD=15 cm,求C1D1的长度.
解 : ∵ 多 边 形 ABCDEF 和 多 边 形 A1B1C1D1E1F1 的 相 似 比 是 1∶1.5 , 且 CD = 15 cm , ∴ C1D1 = 15×1.5 = 22.5(cm).
此页为防盗标记页(下载后可删)
1、谢谢大家听得这么专心。 2、大家对这些内容这么感兴趣,真让我高兴。 3、你们专注听讲的表情,使我快乐,给我鼓励。 4、我从你们的姿态上感觉到,你们听明白了。 5、我不知道我这样说是否合适。 6、不知我说清了没有,说明白了没有。 7、我的解释不知是否令你们满意,课后让我们大家再去找有关的书来读读。 8、你们的眼神告诉我,你们还是没有明白,想不想让我再讲一遍? 9、会“听”也是会学习的表现。我希望大家认真听好我下面要说的一段话。 10、从听课的情况反映出,我们是一个素质良好的集体。 1、谢谢你,你说的很正确,很清楚。 2、虽然你说的不完全正确,但我还是要感谢你的勇气。 3、你很有创见,这非常可贵。请再响亮地说一遍。 4、××说得还不完全,请哪一位再补充。 5、老师知道你心里已经明白,但是嘴上说不出,我把你的意思转述出来,然后再请你学说一遍。 6、说,是用嘴来写,无论是一句话,还是一段话,首先要说清楚,想好了再说,把自己要说的话在心里整理一下就能说清楚。 7、对!说得很好,我很高兴你有这样的认识,很高兴你能说得这么好! 8、我们今天的讨论很热烈,参与的人数也多,说得很有质量,我为你们感到骄傲。 9、说话,是把自己心里的想法表达出来,与别人交流。说时要想想,别人听得明白吗? 10、说话,是与别人交流,所以要注意仪态,身要正,不扭动,眼要正视对方。对!就是这样!人在小时候容易纠正不良习惯,经常 注意哦。
(2)若∠DAB=60°,AB=2,AG= 3,求 GD 的长. 解:如图所示,连接 BD 交 AC 于点 P,则 BP⊥AC. ∵∠DAB=60°,∴∠PAB=30°,∴BP=12AB=1, ∴AP= AB2-BP2= 3,又∵AE=AG= 3, ∴EP=2 3,∴EB= EP2+BP2= 12+1= 13, ∴GD=EB= 13.
5 . 若 多 边 形 ABCDEF∽ 多 边 形 A′B′C′D′E′F′ , 且 ∠ A = 68°,则∠A′等于( C )
A.22° B.112° C.68° D.54° 【点拨】本题考查的是相似多边形的性质,即相似多 边形的对应角相等,对应边成比例. 【解析】∵多边形ABCDEF∽多边形A′B′C′D′E′F′, ∴∠A与∠A′是对应角.∵∠A=68°, ∴∠A′=∠A=68°.
2 cm,那么它们的相似比是( C )
A.34
B.65
C.32
D.94
10.六边形 ABCDEF 与六边形 A′B′C′D′E′F′相似,若对 应边 AB 与 A′B′的长分别为 50 cm 和 40 cm,则六边 形 A′B′C′D′E′F′与六边形 ABCDEF 的相似比是( B ) A.5:4 B.4:5 C.5:2 D.2: 5
【答案】C
*7.如图,已知矩形 ABCD 中,AB=2,在 BC 上取一点 E,
沿 AE 将△ ABE 向上折叠,使 B 点落在 AD 边上的 F
点处,若四边形 EFDC 与矩形 ABCD 相似,则 AD 等
于( )
A. 5
B. 5+1
C.4
D.2 3
【点拨】设 AD=x,易知 FD=x-2,FE=2. ∵四边形 EFDC 与矩形 ABCD 相似, ∴FEDF=AADB,即x-2 2=x2. 解得 x1=1+ 5,x2=1- 5(不合题意,舍去),故选 B. 【答案】B
14.如图,多边形ABCDEF与多边形A1B1C1D1E1F1相似, 其中A,B,C,D,E,F的对应点分别为A1,B1,C1, D1,E1,F1,∠A=∠D1=135°,∠B=∠E1=120°, ∠C1=95°.
(1)求∠F的度数;
解 : ∵ 多 边 形 ABCDEF 和 多 边 形 A1B1C1D1E1F1 相 似 , 且 ∠C和∠C1,∠D和∠D1,∠E和∠E1是对应角, ∴∠C=95°,∠D=135°,∠E=120°. 由多边形内角和定理,知六边形的内角和为720°, ∴∠F=720°-(135°+120°+95°+135°+120°)= 115°.
*8.【2018·重庆】制作一块3 m×2 m长方形广告牌的成本 是120元,在每平方米制作成本相同的情况下,若将此 广告牌的四边都扩大为原来的3倍,那么扩大后长方形 广告牌的成本是( C )
A.360元 B.720元 C.1 080元 D.2 160元
【点拨】边长扩大3倍,面积扩大9倍.
9.如果两个相似多边形的一组对应边长分别为 3 cm 和
11.如图是用火柴棒摆出的两个正五边形的图案,它们的 相似比为( A ) A.1:2 B.2:3 C.1:3 D.2:5
12.把一个多边形按 1:3 的比例尺缩小,则下列说法正确 的是( ) A.各边都扩大到原来的 3 倍 B.各边和各角都缩小到原来的13 C.各边和各角都扩大到原来的 3 倍 D.各边都缩小到原来的13,各角不变
(2)如果相对着的两条小路的宽度均相等,宽度分别为x m, y m,如图②,试问x与y的比值为多少时,能使小路四周 所围成的矩形A′B′C′D′和矩形ABCD相似?请说明理由.
解:当20+202x=303+02y时,小路四周所围成的矩形 A′B′C′D′ 和矩形 ABCD 相似,化简20+202x=303+02y,得xy=23. ∴x 与 y 的比值为23时,能使小路四周所围成的矩形 A′B′C′D′ 和矩形 ABCD 相似.
6.如图,四边形 ABCD∽四边形 A1B1C1D1,AB=12, CD=15,A1B1=9,则 C1D1 的长是( ) A.10 B.12 C.445 D.356
【点拨】∵四边形 ABCD 与四边形 A1B1C1D1 相似, ∴AA1BB1=CC1DD1.又∵AB=12,CD=15,A1B1=9, ∴C1D1=9×1215=445.故选 C.
16.在AB=20 m,AD=30 m的矩形花坛四周修筑小路. (1)如果四周的小路的宽度均相等,都是a m,如图①, 那 么 小 路 四 周 所 围 成 的 矩 形 A′B′C′D′ 和 矩 形 ABCD 相 似吗?请说明理由.
解:如果四周的小路的宽度均相等,那么小路四周所围成 的矩形 A′B′C′D′和矩形 ABCD 不相似.理由如下: ∵30+ 302a=151+5 a,20+ 202a=101+0 a,∴30+ 302a≠20+ 202a, ∴小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 不相似.
1. 你真让人感动,老师喜欢你的敢想、敢说、敢问和敢辩,希望你继续保持下去。 2. 这么难的题你能回答得很完整,真是了不起!你是我们班的小爱因斯坦。 3. 你预习的可真全面,自主学习的能力很强,课下把你的学习方法介绍给同学们,好不好? 4. 哎呀. 通过你的发言,老师觉得你不仅认真听,而且积极动脑思考了,加油哇! 四、提醒类
