专题05 等值线图的阅读解析版
高考地理专项练习:等值线图(解析版)

高考地理专项练习:等值线图(解析版)一、选择题1.图为〝中纬度某地某日河流、风向、等压线、等高线、等温线、昏线的组合图〞,据此回答下题。
〔1〕该地域〔〕A. 位于南半球B. 该日昼长夜短C. 图中河段无凌汛现象D. 典型植被为亚热带常绿阔叶林〔2〕此时以下发作的现象中,能够的是〔〕A. 长江河口表层海水盐度到达一年中的最小值B. 青岛的海滨浴场人满为患C. 巴西利亚左近的草原一片翠绿D. 中国长城站出现极昼现象2.以下图是〝地球自转等线速度表示图〞,R、T在同一纬线上。
据此回答下面小题。
〔1〕该区域所在的半球位置和纬度位置是〔〕A. 南半球、低纬度B. 北半球、中纬度C. 南半球、中纬度D. 北半球、高纬度〔2〕R点地形最有能够是〔〕A. 山地B. 丘陵C. 高原D. 盆地3.以下图为我国西北沿海某城市功用分区表示图,图中字母代表的是不同的功用区,一条河流穿过该郊区〔图中没有画出河流,需依据等高线判别大致流向〕。
完成以下各题。
〔1〕假定在该河开发漂流旅游项目,那么漂流的动身地应设在〔〕A. a区B. d区C. e区D. g区〔2〕假定该市包括以下功用区且规划合理,那么g区最有能够是〔〕A. 住宅区B. 文明区C. 工业区D. 中央商务区4.〝雨舌〞是指丰沛降水区域呈〝舌头〞状向某中央向延伸的现象。
读西藏年等降水量线(单位:mm)和〝雨舌〞位置图,完成以下效果。
〔1〕影响〝雨舌〞区域的主要降水要素是〔〕A. 洋流B. 地形C. 植被D. 纬度〔2〕位于〝舌尖〞上的波密县,拥有共同的自然景观是〔〕A. 喀斯特别貌广布B. 冰川与森林相连C. 水网密布,水流湍急D. 土壤深沉,无机质多5.以下图中等值线为房价〔元/平方米〕,A处房价高于周围,其缘由不能够是〔〕A. 左近公路支线交汇,车辆过多B. 接近初等院校,文明气氛浓郁C. 临近景色区,环境优美D. 地势平整,工厂林立,失业方便6.四幅等降水量线图中,画法正确的选项是〔〕A. ①②B. ①③④C. ①④D. ①②③④7.气温、降水量和日照时数过高或过低都会给柑橘的生长发育带来风险,气候风险度越大,柑橘增产的能够性也越大。
中考数学常见几何模型专题05 一线三等角(K型图)模型(从全等到相似)(解析版)
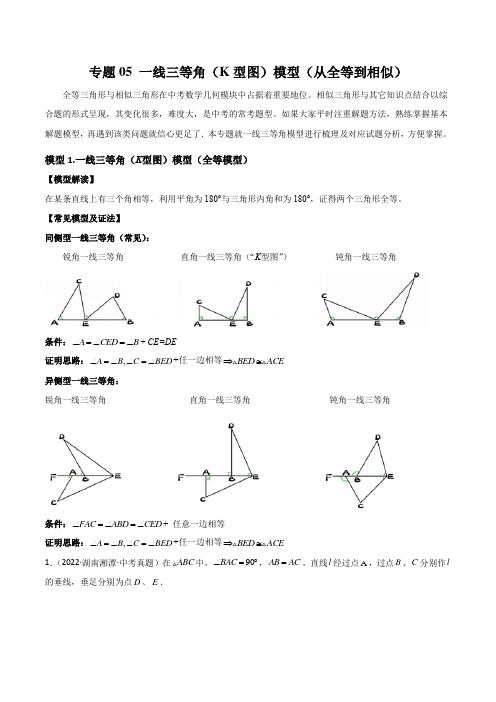
专题05 一线三等角(K 型图)模型(从全等到相似)全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K 型图)模型(全等模型)【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角(常见):锐角一线三等角 直角一线三等角(“K 型图”) 钝角一线三等角条件:A CED B ∠=∠=∠+ CE=DE证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅异侧型一线三等角:锐角一线三等角 直角一线三等角 钝角一线三等角条件:FAC ABD CED ∠=∠=∠+ 任意一边相等证明思路:,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅1.(2022·湖南湘潭·中考真题)在ABC 中,90BAC ∠=︒,AB AC =,直线l 经过点A ,过点B 、C 分别作l 的垂线,垂足分别为点D 、E .(1)特例体验:如图①,若直线l BC ∥,AB AC ==BD 、CE 和DE 的长;(2)规律探究:①如图②,若直线l 从图①状态开始绕点A 旋转()045αα<<︒,请探究线段BD 、CE 和DE 的数量关系并说明理由;②如图③,若直线l 从图①状态开始绕点A 顺时针旋转()4590αα︒<<︒,与线段BC 相交于点H ,请再探线段BD 、CE 和DE 的数量关系并说明理由;(3)尝试应用:在图③中,延长线段BD 交线段AC 于点F ,若3CE =,1DE =,求BFC S △.【答案】(1)BD =1;CE =1;DE =2(2)①DE =CE +BD ;理由见解析;②BD =CE +DE ;理由见解析 (3)258BFC S ∆=【分析】(1)先根据得出90452ABC ACB ︒∠=∠==︒,根据l BC ∥,得出45DAB ABC ∠=∠=︒,45EAC ACE ∠=∠=︒,再根据90BDA CEA ∠=∠=︒,求出45ABD ∠=︒,45ACE ∠=︒,即可得出45DAB ABD EAC ACE ∠=∠=∠=∠=︒,最后根据三角函数得出1AD BD ==,1AE CE ==,即可求出2DE AD AE =+=;(2)①DE =CE +BD ;根据题意,利用“AAS”证明ABD CAE ∆∆≌,得出AD =CE ,BD =AE ,即可得出结论; ②BD =CE +DE ;根据题意,利用“AAS”证明ABD CAE ∆∆≌,得出AD =CE ,BD =AE ,即可得出结论;(3)在Rt△AEC 中,根据勾股定理求出5AC =,根据DF CE ∥,得出AD AF AE CF=,代入数据求出AF ,根据AC =5,算出CF ,即可求出三角形的面积.(1)解:△90BAC ∠=︒,AB AC =,△90452ABC ACB ︒∠=∠==︒, △l BC ∥,△45DAB ABC ∠=∠=︒,45EAC ACE ∠=∠=︒,△BD △AE ,CE △DE ,△90BDA CEA ∠=∠=︒,△904545ABD ∠=︒-︒=︒,904545ACE ∠=-=︒︒︒,△45DAB ABD EAC ACE ∠=∠=∠=∠=︒,△sin 1AD BD AB DAB ==⨯∠==,sin 1AE CE AC EAC ==⨯∠=,△2DE AD AE =+=.(2)①DE =CE +BD ;理由如下:△BD △AE ,CE △DE ,△90BDA CEA ∠=∠=︒,△90DAB DBA ∠+∠=︒,△90BAC ∠=︒,△90DAB CAE ∠+∠=︒,△DBA CAE ∠=∠,△AB =AC ,△ABD CAE ∆∆≌,△AD =CE ,BD =AE ,△DE =AD +AE =CE +BD ,即DE =CE +BD ;②BD =CE +DE ,理由如下:△BD △AE ,CE △DE ,△90BDA CEA ∠=∠=︒,△90DAB DBA ∠+∠=︒,△90BAC ∠=︒,△90DAB CAE ∠+∠=︒,△DBA CAE ∠=∠,△AB =AC ,△ABD CAE ∆∆≌,△AD =CE ,BD =AE ,△BD =AE =AD +DE =CE +DE ,即BD =CE +DE .(3)根据解析(2)可知,AD =CE=3,△314AE AD DE =+=+=,在Rt△AEC 中,根据勾股定理可得:5AC =,△BD △AE ,CE △AE ,△DF CE ∥,△AD AF AE CF =,即345AF =,解得:154=AF , △155544CF AC AF =-=-=,△AB =AC =5,△1152552248BFC S CF AB ∆=⨯=⨯⨯=. 【点睛】本题主要考查了三角形全等的判定和性质,等腰三角形的判定和性质,勾股定理,平行线的性质,解直角三角形,根据题意证明ABD CAE ∆∆≌,是解题的关键.2.(2022·黑龙江·九年级期末)(1)如图(1),已知:在△ABC 中,△BAC =90°,AB =AC ,直线m 经过点A ,BD △直线m , CE △直线m ,垂足分别为点D 、E .证明△DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有△BDA =△AEC =△BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为△BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形,连接BD 、CE ,若△BDA =△AEC =△BAC ,试判断△DEF 的形状.【答案】(1)见解析(2)成立,证明见解析(3)△DEF为等边三角形,证明见解析【分析】(1)因为DE=DA+AE,故由全等三角形的判定AAS证△ADB△△CEA,得出DA=EC,AE=BD,从而证得DE=BD+CE;(2)成立,仍然通过证明△ADB△△CEA,得出BD=AE,AD=CE,所以DE=DA+AE=EC+BD;(3)由△ADB△△CEA得BD=AE,△DBA =△CAE,由△ABF和△ACF均等边三角形,得△ABF=△CAF=60°,FB=F A,所以△DBA+△ABF=△CAE+△CAF,即△DBF=△F AE,所以△DBF△△EAF,所以FD=FE,△BFD=△AFE,再根据△DFE=△DF A+△AFE=△DF A+△BFD=600得到△DEF是等边三角形.【详解】解:(1)证明:△BD△直线m,CE△直线m,△△BDA=△CEA=90°.△△BAC=90°,△△BAD+△CAE=90°.△△BAD+△ABD=90°,△△CAE=△ABD.又AB=AC,△△ADB△△CEA(AAS).△AE=BD,AD=CE.△DE=AE+AD=BD+CE;(2)成立.证明如下:△△BDA =△BAC=α,△△DBA+△BAD=△BAD +△CAE=180°-α.△△DBA=△CAE.△△BDA=△AEC=α,AB=AC,△△ADB△△CEA(AAS).△AE=BD,AD=CE.△DE=AE+AD=BD+CE;(3)△DEF为等边三角形.理由如下:由(2)知,△ADB△△CEA,BD=AE,△DBA =△CAE,△△ABF和△ACF均为等边三角形,△△ABF=△CAF=60°.△△DBA+△ABF=△CAE+△CAF.△△DBF=△F AE.△BF=AF,△△DBF△△EAF(SAS).△DF=EF,△BFD=△AFE.△△DFE=△DF A+△AFE=△DF A+△BFD=60°.△△DEF为等边三角形.【点睛】此题考查了全等三角形的性质和判定、等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定,等边三角形的性质和判定.3.(2022·江苏·九年级专题练习)【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.【模型应用】(2)如图4,将正方形OABC 放在平面直角坐标系中,点O 为原点,点A 的坐标为(,则点C 的坐标为________. 【模型变式】(3)如图5所示,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥于E ,AD △CE 于D ,4cm DE =,6cm AD =,求BE 的长.A BADE BFDAE BD∠=∠⎧⎪∠=∠⎨⎪=⎩△△AED△△BDF(AAS) 答案为:△BDF;②△△ABC是等边三角形△△B=△C=60゜△△BDE+△BED=180゜−△B=120゜△△EDF=60゜△△BDE+△CDF=180゜−△EDF=120゜△△BED=△CDF在△BDE和△CFD中B CBED CDFBD CF∠=∠⎧⎪∠=∠⎨⎪=⎩△△BDE△△CFD(AAS)故答案为:△CFD;③△四边形ABCD是正方形△△ABC=90゜,AB=BC△△ABE+△CBF=180゜−△ABC=90゜△AE△l,CF△l△△AEB=△CFB =90゜△△ABE+△EAB=90゜△△EAB=△CBF在△ABE和△BCF中AEB CFBEAB CBFAB BC∠=∠⎧⎪∠=∠⎨⎪=⎩△△ABE△△BCF(AAS)△AE=BF=1,BE=CF=2△EF=BE+BF=2+1=3 故答案为:3;(2)分别过A、C作x轴的垂线,垂足分别为点D、E,如图所示△四边形OABC是正方形△△AOC=90゜,AO=OC△△COE+△AOD=180゜−△ACO=90゜△AD△x轴,CE△x轴△△CEO=△ADO =90゜△△ECO+△COE=90゜△△ECO=△AOD模型2.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1.(2022·四川·一模)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:(1)如图1,已知:在△ABC中,AB AC=,D、A、E三点都在直线m上,并且有BDA AEC BACα∠=∠=∠=.试猜想DE、BD、CE有怎样的数量关系,请证明你的结论;(2)老师鼓励学习小组继续探索相似的情形.于是,学习小组又研究以下问题:如图2,△ABC中,(060)B Cαα∠=∠=<<︒.将一把三角尺中30°角顶点P放在BC边上,当P在BC边上移动时,三角尺中30°角的一条边始终过点A ,另一条边交AC 边于点Q ,P 、Q 不与三角形顶点重合.设CPQ β∠=.当β在许可范围内变化时,α取何值总有△ABP △△PCQ ?当α在许可范围内变化时,β取何值总有△ABP △△QCP ? (3)试探索有无可能使△ABP 、△QPC 、△ABC 两两相似?若可能,写出所有α、β的值(不写过程);若不可能,请说明理由.【答案】(1)DE AE AD BD CE =+=+;证明见解析;(2)30α=︒;75β=︒;(3)可能;30α=︒,30β=︒或52.5α=︒,75β=︒.【分析】(1)证明△ADB △△CEA (AAS ),由全等三角形的性质得出AE =BD ,AD =CE ,则可得出结论;(2)由β=△2或△1=△CQP ,即△2=30°+β-α=β,解得α=30°,即可求解;由β=△1或△2=△CQP ,同理可得:β=75°,即可求解;(3)①当α=30°,β=30°时,则△2=△B =α=30°,即可求解;②当β=75°,α=52.5°时,同理可解.【详解】解:(1)如图1,△BDA BAC α∠=∠=,△180DBA BAD BAD CAE ∠∠∠∠α+=+=︒-,△DBA CAE ∠=∠,在△ADB 和△CEA 中,DBA EAC BDA AEC BA AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,△△ADB △△CEA (AAS ),△AE BD =,AD CE =, △DE AE AD BD CE =+=+;(2)在△ABP 中,2230APC B αβ∠=∠+∠=+∠=︒+,△1150β∠=︒-,同理可得:230βα∠=︒+-;由2β=∠或1CQP ∠=∠,即230βαβ∠=︒+-=,解得30α=︒,则△ABP △△PCQ ;△当β在许可范围内变化时,30α=︒时,总有△ABP △△PCQ ;由1β=∠或2CQP ∠=∠,同理可得:75β=︒.△当α在许可范围内变化时,75β=︒总有△ABP △△QCP ;(3)可能.①当30α=︒,30β=︒时,则230B α∠=∠==︒,则△ABP △△PCQ △△BCA ;②当75β=︒,52.5α=︒时,同理可得:115075ββ∠=︒-=︒=,23052.5βαα∠=︒+-=︒=,△△ABP △△CQP △△BCA .【点睛】本题是相似形综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,熟练掌握相似三角形的性质是解本题的关键.2.(2022·河南新乡·二模)如图,△ABC 和△ADE 是有公共顶点A 的两个等腰直角三角形,△DAE =△BAC =90°,AD =AE ,AB =AC =6,D 在线段BC 上,从B 到C 运动,点M 和点N 分别是边BC ,DE 的中点.(1)【问题发现】若点D 是BC 边的中点时,BD MN= ,直线BD 与MN 相交所成的锐角的度数为 (请直接写出结果)(2)【解决问题]若点D 是BC 边上任意一点时,上述结论是否成立,请说明理由.(3)【拓展探究】在整个运动过程中,请直接写出N 点运动的路径长,及CN 的最小值.3.(2022·山东菏泽·三模)(1)问题:如图1,在四边形ABCD 中,点P 为AB 上一点,当90DPC A B ∠=∠=∠=︒时,求证:AD BC AP BP ⋅=⋅.(2)探究:若将90°角改为锐角或钝角(如图2),其他条件不变,上述结论还成立吗?说明理由.(3)应用:如图3,在ABC 中,AB =45B ∠=︒,以点A 为直角顶点作等腰Rt ADE △.点D 在BC上,点E 在AC 上,点F 在BC 上,且45EFD ∠=︒,若CE =CD 的长.)结论仍然成立,理由如下,BPD ∠=又BPD ∠=DPC BPC +∠DPC ∠=ADP ∴∽△(3)∠ABD DFE ∴∽,AB DF ∴ADE 是等腰直角三角形,,2AB =4DF =,45EFD ∠=135DEC =︒,EFC DEC ∴∽,FC EC CD∴=5EC =,()45FC CD FC FC ⋅=⋅+=,1FC ∴=【点睛】本题考查相似三角形的综合题,三角形的相似;能够通过构造45°角将问题转化为一线三角是解题的关键.模型3.一线三直角模型(相似模型)【模型解读与图示】“一线三直角”模型的图形,实则是“一线三等角”型的图形的特例,因为这种图形在正方形和矩形中出现的比较多,对它做一专门研究,这样的图形,因为有三个角是直角,就有两个角相等,再根据“等角的余角相等”可以得到另外一对角相等,从而判定两个三角形相似.1.(2022·湖南郴州·中考真题)如图1,在矩形ABCD 中,4AB =,6BC =.点E 是线段AD 上的动点(点E 不与点A ,D 重合),连接CE ,过点E 作EF CE ⊥,交AB 于点F .(1)求证:AEF DCE ∽;(2)如图2,连接CF ,过点B 作BG CF ⊥,垂足为G ,连接AG .点M 是线段BC 的中点,连接GM .①求AG GM +的最小值;②当AG GM +取最小值时,求线段DE 的长.【答案】(1)见解析(2)①5;②3DE =3DE =【分析】(1)证明出DCE AEF ∠=∠即可求解;(2)①连接AM .先证明132BM CM GM BC ====.确定出点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM 中利用勾股定理即可求出AM ,则问题得解.②先求出AF ,求AF 的第一种方法:过点M 作∥MN AB 交FC 于点N ,即有CMN CBF ∽△△,进而有12MN CM BF CB ==.设AF x =,则4BF x =-,()142MN x =-.再根据∥MN AB ,得到AFG MNG ∽△△,得到AF AG MN GM =,则有()21342x x =-,解方程即可求出AF ;求AF 的第二种方法:过点G 作GH AB ∥交BC 于点H .即有MHG MBA ∽△△.则有GM GH MH AM AB MB==,根据5AM =,可得3543GH MH ==,进而求出125GH =,95MH =.由GH AB ∥得CHG CBF ∽△△,即可求出AF .求出AF 之后,由(1)的结论可得AF AE DE DC.设DE y =,则6AE y =-,即有164y y -=,解得解方程即可求出DE . (1)证明:如图1,△四边形ABCD 是矩形,△90A D ∠=∠=︒,△90CED DCE ∠+∠=︒.△EF CE ⊥,△90CED AEF ∠+∠=︒,△DCE AEF ∠=∠,△AEF DCE ∽;(2)①解:如图2-1,连接AM .△BG CF ⊥,△BGC 是直角二角形.△132BM CM GM BC ====. △点G 在以点M 为圆心,3为半径的圆上.当A ,G ,M 三点不共线时,由三角形两边之和大于箒三边得:AG GM AM +>,当A ,G ,M 三点共线时,AG GM AM +=.此时,AG GM +取最小值.在Rt ABM中,5AM ==.△AG GM +的最小值为5. ②(求AF 的方法一)如图2-2,过点M 作∥MN AB 交FC于点N ,△CMN CBF ∽△△.△12MN CM BF CB ==. 设AF x =,则4BF x =-,△()11422MN BF x ==-. △∥MN AB ,△AFG MNG ∽△△,△AF AG MN GM=, 由①知AG GM +的最小值为5、即5AM =,又△3GM =,△2AG =.△()21342xx =-,解得1x =,即1AF =.(求AF 的方法二)如图2-3,过点G 作GH AB ∥交BC 于点H .△MHG MBA ∽△△.△GM GH MH AM AB MB==, 由①知AG GM +的最小值为5,即5AM =,又△3GM =,△3543GH MH ==.△125GH =,95MH =. 由GH AB ∥得CHG CBF ∽△△,△GH CH FB CB =,即1293556FB +=,解得3FB =. △1AF AB FB =-=.由(1)的结论可得AF AE DE DC . 设DE y =,则6AE y =-,△164y y -=,解得3y =3△036<<,036<,△3DE =或3DE =【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识,掌握相似三角形的判定与性质是解答本题的关键.2.(2022·山东济宁·二模)情境观察:将含45°角的三角板的直角顶点R 放在直线l 上,分别过两锐角的顶点M ,N 作l 的垂线,垂足分别为P , Q ,(1)如图1.观察图1可知:与NQ 相等的线段是______________,与NRQ ∠相等的角是_____ (2)问题探究直角ABC 中,90B ∠=︒,在AB 边上任取一点D ,连接CD ,分别以AC,DC为边作正方形ACEF和正方形CDGH ,如图2,过E ,H 分别作BC 所在直线的垂线,垂足分别为K ,L .试探究EK 与HL 之间的数量关系,并证明你的结论.(3)拓展延伸:直角ABC 中,90B ∠=︒,在AB 边上任取一点D ,连接CD ,分别以AC ,DC 为边作矩形ACEF 和矩形CDGH ,连接EH 交BC 所在的直线于点T ,如图3.如果AC kCE =,CD kCH =,试探究TE 与TH 之间的数量关系,并证明你的结论.【答案】(1)PR ,PMR ∠,(2)EK LH =,证明见解析;(3)ET HT =,证明见解析.【分析】(1)根据等腰直角三角形的性质得到,=MR RN ,90MRN ∠=︒,根据余角性质得到PMR NRQ ∠=∠,再证明MPR NRQ ≌△△,即可得到QN PR =,NRQ PMR ∠=∠;(2)证明ABC CEK ≌△△,得到EK BC =,再证明DCB CHL ≌△△,得到BC HL =,可得到EK LH =; (3)证明ACB ECM ∽△△,得到BC kEM =,证明BCD NHC ∽△△,得到BC kHN =,得到EM HN =,证明NHT EMT ≌△△即可得到ET HT =. (1)解:△MRN △是等腰直角三角形,△=MR RN ,90MRN ∠=︒,△MP PQ ⊥,NQ PQ ⊥,△90MPR NQR ∠=∠=︒,△90PMR MRP MRP NRQ ∠+∠=∠+∠=︒,△PMR NRQ ∠=∠,在MPR △和NRQ △中,PMR NRQ MPR NRQ MR NR ∠=∠⎧⎪∠=∠⎨⎪=⎩△MPR NRQ ≌△△,△QN PR =,NRQ PMR ∠=∠,故答案为:PR ,PMR ∠;(2)解:△四边形ACEF 是正方形,△AC CE =,90ACE ∠=︒,△EK BK ⊥△90B EKC ∠=∠=︒,△90BAC ACB ACB ECK ∠+∠=∠+∠=︒,△BAC ECK ∠=∠,在ABC 和CEK △中,BAC KCE B EKCAC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩△ABC CEK ≌△△,△EK BC =,在DCB和△3)解:过3.(2022·浙江·嘉兴一中一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①:在△ABC中,△ACB=90°,AC=BC,分别过A、B向经过点C直线作垂线,垂足分别为D、E,我们很容易发现结论:△ADC△△CEB.(1)探究问题:如果AC≠BC,其他条件不变,如图②,可得到结论;△ADC△△CEB.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线y=12x与直线CD交于点M(2,1),且两直线夹角为α,且tanα=32,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,AB=4,BC=5,点E为BC边上一个动点,连接AE,将线段AE 绕点E顺时针旋转90°,点A落在点P处,当点P在矩形ABCD外部时,连接PC,PD.若△DPC为直角三角形时,请你探究并直接写出BE的长.由(1)可得:△NFO△△OEM,△NF OF NOOE ME MO==,△点M(2,1),△OE=2,ME=1,ON33NF OF33课后专项训练:1.(2022·贵州铜仁·三模)(1)探索发现:如图1,已知Rt ABC 中,90ACB ∠=︒,AC BC =,直线l 过点C ,过点A 作AD l ⊥,过点B 作BE l ⊥,垂足分别为D 、E .求证:CD BE =.(2)迁移应用:如图2,将一块等腰直角的三角板MON 放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O 重合,另两个顶点均落在第一象限内,已知点N 的坐标为()4,2,求点M 的坐标.(3)拓展应用:如图3,在平面直角坐标系内,已知直线44y x =-+与y 轴交于点P ,与x 轴交于点Q ,将直线PQ 绕P 点沿逆时针方向旋转45︒后,所得的直线交x 轴于点R .求点R 的坐标.=35x+4.【点睛】本题是一次函数综合题,主要考查了待定系数法,全等三角形的判定和性质,构造出全等三角形2.(2022·广东·汕头市潮阳区教师发展中心教学研究室一模)(1)模型建立,如图1,等腰直角三角形ABC 中,△ACB=90°,CB=CA,直线ED经过点C,过A作AD△ED于D,过B作BE△ED于E.求证:△BEC△△CDA;(2)模型应用:①已知直线AB与y轴交于A点,与x轴交于B点,sin△ABO=35,OB=4,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x-5上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.和CDA中⎧⎪⎨⎪⎩①如图,过点中sin△ABO,AB=5m,)可证得CDB∆3.(2022·黑龙江·桦南县九年级期中)如图1,在ABC中,90ACB∠=︒,AC BC=,直线MN经过点C,且AD MN⊥于D,BE MN⊥于E.(1)由图1,证明:DE AD BE=+;(2)当直线MN绕点C旋转到图2的位置时,请猜想出DE,AD,BE的等量关系并说明理由;(3)当直线MN绕点C旋转到图3的位置时,试问DE,AD,BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).【答案】(1)证明见解析;(2)DE AD BE =-,证明过程见解析;(3)DE BE AD =-,证明过程见解析【分析】(1)先证明△ADC △△CEB ,得到AD=CE ,DC=BE ,进而得到DE=CE+DC=AD+BE 即可;(2)同(1)中思路,证明△ADC △△CEB ,进而得到DE=CE -DC=AD -BE 即可;(3)同(1)中思路,证明△ADC △△CEB ,进而得到DE=DC -CE=BE -AD 即可.【详解】解:(1)证明:在ABC 中,△90ACB ∠=︒,△90ACD BCE ∠+∠=︒,△AD MN ⊥,△90ACD CAD ∠+∠=︒,△BCE =∠∠CAD ,又△AC BC =,90ADC CEB ∠=∠=,△()≌ADC CEB AAS ,△AD CE =,DC BE =,△直线MN 经过点C ,△DE CE DC AD BE =+=+;(2)DE ,AD ,BE 的等量关系为:DE AD BE =-,理由如下:△AD MN ⊥于D ,BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒,△90CAD ACD ∠+∠=︒,90ACD BCE ∠+∠=︒,△CAD BCE ∠=∠,在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩,△()ADC CEB AAS △≌△△CE AD =,CD BE =,△DE CE CD AD BE =-=-;(3)当MN 旋转到图3的位置时,DE 、AD 、BE 所满足的等量关系是DE BE AD =-,理由如下: △AD MN ⊥于D ,BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒,△90CAD ACD ∠+∠=︒,90ACD BCE ∠+∠=︒,△CAD BCE ∠=∠,在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩,△()ADC CEB AAS △≌△△CE AD =,CD BE =,△DE CD CE BE AD =-=-.【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点,熟练掌握三角形全等的判定方法是求解的关键.4.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,90ACB ∠=︒,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D ,E , 2.5cm AD =, 1.7cm DE =.求BE 的长”,请直接写出此题答案:BE 的长为________. (2)探索证明:如图②,点B ,C 在MAN ∠的边AM 、AN 上,AB AC =,点E ,F 在MAN ∠内部的射线AD 上,且BED CFD BAC ∠=∠=∠.求证:ABE CAF ∆∆≌.(3)拓展应用:如图③,在ABC ∆中,AB AC =,AB BC >.点D 在边BC 上,2CD BD =,点E 、F 在线段AD 上,BED CFD BAC ∠=∠=∠.若ABC ∆的面积为15,则ACF ∆与BDE ∆的面积之和为________.(直接填写结果,不需要写解答过程)【答案】(1)0.8cm ;(2)见解析(3)5【分析】(1)利用AAS 定理证明△CEB △△ADC ,根据全等三角形的性质解答即可;(2)由条件可得△BEA =△AFC ,△4=△ABE ,根据AAS 可证明△ABE △△CAF ;(3)先证明△ABE △△CAF ,得到ACF ∆与BDE ∆的面积之和为△ABD 的面积,再根据2CD BD =故可求解.【详解】解:(1)△BE △CE ,AD △CE ,△△E =△ADC =90°,△△EBC +△BCE =90°.△△BCE +△ACD =90°,△△EBC =△DCA .在△CEB 和△ADC 中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CEB △△ADC (AAS ),△BE =DC ,CE =AD =2.5cm .△DC =CE −DE ,DE =1.7cm ,△DC =2.5−1.7=0.8cm ,△BE =0.8cm 故答案为:0.8cm ;(2)证明:△△1=△2,△△BEA =△AFC .△△1=△ABE +△3,△3+△4=△BAC ,△1=△BAC ,△△BAC =△ABE +△3,△△4=△ABE .△△AEB =△AFC ,△ABE =△4,AB =AC ,△△ABE △△CAF (AAS ).(3)△BED CFD BAC ∠=∠=∠△△ABE +△BAE =△F AC +△BAE =△F AC +△ACF△△ABE =△CAF ,△BAE =△ACF又AB AC =△△ABE △△CAF ,△ABE CAF S S =△ACF ∆与BDE ∆的面积之和等于ABE ∆与BDE ∆的面积之和,即为△ABD 的面积,△2CD BD =,△ABD 与△ACD 的高相同则13ABD ABC S S =△△=5 故ACF ∆与BDE ∆的面积之和为5故答案为:5.【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理,掌握全等三角形的判定定理和性质定理是解题的关键.5.(2022·无锡市九年级月考)(1)如图1,直线m 经过等腰直角△ABC 的直角顶点A ,过点B 、C 分别作BD ⊥m ,CE ⊥m ,垂足分别是D 、E .求证:BD +CE =DE ;(2)如图2,直线m 经过△ABC 的顶点A ,AB =AC ,在直线m 上取两点 D 、E ,使∠ADB =∠AEC =α, 补充∠BAC = (用α表示),线段BD 、CE 与DE 之间满足BD +CE =DE ,补充条件后并证明; (3)在(2)的条件中,将直线m 绕着点A 逆时针方向旋转一个角度到如图3的位置,并改变条件∠ADB =∠AEC = (用α表示).通过观察或测量,猜想线段BD 、CE 与DE 之间满足的数量关系,并予以证明.【答案】(1)证明见详解,(2)∠BAC=α,证法见详解,(3)180º-α,DE=EC-BD,证明见详解.【分析】(1)根据已知首先证明∠DAB=∠ECA,再利用AAS即可得出△ADB≌△CEA;(2)补充∠BAC=α.利用△ADB≌△CAE,即可得出三角形对应边之间的关系,即可得出答案;(3)180º-α,DE=CE-BD,根据已知首先证明∠DAB=∠ECA,再利用AAS即可得出△ADB≌△CEA,即可得出三角形对应边之间的关系,即可得出答案.【详解】证明:(1)∵BD⊥m,CE⊥m,∠ABC=90°,AC=BC,∴△ADB和△AEC都是直角三角形,∴∠DBA+∠DAB=90°,∴∠ECA+∠EAC=90°,∵∠BAC=90°,∠DAB+∠EAC=90º,∴∠DAB=∠ECA,又∵∠ADB=∠CEA=90°,AB=BC,所以△ADB≌△CEA(AAS),BD=AE,DA=EC,DE=DA+AE=EC+BD,BD+CE=DE.(2)∵等腰△ABC中,AC=CB,∠ADB=∠BAC=∠CEA=α,∴∠DAB+∠EAC=180°-α,∠ECA+∠CAE=180º-α,∴∠DAB=∠ECA,∵∠ADB=∠CEA=α,AC=CB,∴△ADB≌△CEA(AAS),∴CE=AD,BD=AE,∴AD+BE=CE+CD,所以BD+CE=DE.(3)180º-α,数量关系为DE=CE-BD,∵∠ADB=∠AEC=180º-α,∠BAC=α,∴∠ABD+∠BAD=α,∠BAD+∠EAC=α,∴∠ABD=∠CAE,∵AB=AC,∴△BAD≌△ACE(AAS),∴AD=CE,BD=AE,∴DE=AD-AE=EC-BD.【点睛】点评:此题主要考查了三角形全等的证明,根据已知得出∠DAB=∠ECA,再利用全等三角形的判定方法得出是解决问题的关键.6.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,△BAC=90°,ABAC=k,直线l经过点A,BD△直线I,CE上直线l,垂足分别为D、E.求证:BDAE=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,ABAC=k,D、A、E三点都在直线l上,并且有△BDA=△AEC=△BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,ABAE=ACAG=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.【答案】(1)见解析(2)结论还成立,证明见解析(3)①见解析②BC=AI【分析】(1)由条件可证明△ABD△△CAE,可得BDAE=ABAC=k;(2)由条件可知△BAD+△CAE=180°−α,且△DBA+△BAD=180°−α,可得△DBA=△CAE,结合条件可证明△ABD△△CAE,同(1)可得出结论;(3)①过点G作GM∥AE交AI的延长线于点M,连接EM,证明△ABC△△GMA,再得到四边形AGME是平行四边形,故可求解;②由①得到BC=12AM,再根据四边形AGME是平行四边形得到BC=AI,故可求解.【详解】(1)如图1,△BD△直线l,CE△直线l,△△BDA=△CEA=90°,△△BAC=90°,△△BAD+△CAE=90°△△BAD+△ABD=90°,△△CAE=△ABD△△ABD=△CAE,△BDA=△CEA,△△ADB△△CEA,△BDAE =ABAC=k;(2)成立,证明如下:如图2,△△BDA=△BAC=α,△△DBA+△BAD=△BAD+△CAE=180°−α,△△DBA=△CAE,△△ABD=△CAE,△BDA=△CEA△△ADB△△CEA,△BDAE =ABAC=k;(3)①过点G作GM∥AE交AI的延长线于点M,连接EM7.(2022·湖北武汉·模拟预测)[问题背景](1)如图1,ABC 是等腰直角三角形,AC BC =,直线l 过点C ,AM l ⊥,BN l ⊥,垂足分别为M ,N .求证:AMC CNB △≌△;[尝试应用](2)如图2,AC BC =,90ACB ∠=︒,N ,B ,E 三点共线,CN NE ⊥,45E ∠=︒,1CN =,2BN =.求AE 的长;[拓展创新](3)如图3,在DCE 中,45CDE ∠=︒,点A ,B 分别在DE ,CE 上,AC BC =,90ACB ∠=︒,若1tan 2DCA ∠=,直接写出AE AD 的值为 .在AMC和△△()AMC CNB AAS≌2)如图2AM NH⊥于M,)可知:AMC BNC≌,45DAM DFN=∠=∠=a,△32AF a=,8.(2022·黑龙江齐齐哈尔·三模)数学实践课堂上,张老师带领学生们从一道题入手,开始研究,并对此题做适当变式,尝试举一反三,开阔学生思维.(1)原型题:如图1,AB BD ⊥于点B ,CD BD ⊥于点D ,P 是BD 上一点,AP PC =,AP PC ⊥,则ABP △≌△________,请你说明理由.(2)利用结论,直接应用:①如图2,四边形ABCD 、EFGH 、NHMC 都是正方形,边长分别为a 、b 、c ,A 、B 、N 、E ,F 五点在同一条直线上,则CBN △≌△________,c =________(用含a 、b 的式子表示).②如图3,四边形ABCD 中,AB DC ,AB BC ⊥,2AB =,4CD =,以BC 上一点O 为圆心的圆经过A 、D 两点,且90AOD ∠=︒,则圆心O 到弦AD 的距离为________.(3)弱化条件,变化引申:如图4,M 为线段AB 的中点,AE 与BD 交于点C ,45DME A B ∠=∠=∠=︒,且DM交AC 于点F ,ME 交BC 于点G ,连接FG ,则AMF 与BGM 的关系为:________,若AB =3AF =,则FG =________.∽AMF BGM,即可求出长度,即可求出FG(1)解:ABP PDC△≌△△中在ABP△和PDC Array在AOB和△Rt AOB 中,AOD △中,12OE ⨯⨯=10=△圆心解:AMF 与BGM 的关系为:相似,45︒△AMD AFM +∠∠B =∠△∽AMF BGM △AM BG 45B ∠=︒△90ACB ∠=︒△AC 84433=-=△FG FC =【点睛】本题考查了全等三角形的判定和性质、正方形的性质、同角的余角相等、勾股定理、相似三角形9.(2022•郑州一模)如图,在平面直角坐标系xOy 中.边长为4的等边△OAB 的边OA 在x 轴上,C 、D 、E 分别是AB 、OB 、OA 上的动点,且满足BD =2AC ,DE ∥AB ,连接CD 、CE ,当点E 坐标为 时,△CDE 与△ACE 相似.【分析】因为DE ∥AB 得到∠DEC =∠ACE ,所以△CDE 与△ACE 相似分两种情况分类讨论.【解答】解:∵DE ∥AB ,∴∠DEC =∠ACE ,△ODE ∽△OBA ,∴△ODE 也是等边三角形,则OD =OE =DE ,设E (a ,0),则OE =OD =DE =a ,BD =AE =4﹣a .∵△CDE 与△ACE 相似,分两种情况讨论:①当△CDE ∽△EAC 时,则∠DCE =∠CEA ,∴CD ∥AE ,∴四边形AEDC 是平行四边形,∴AC =a ,, ∵BD =2AC ,∴4﹣a =2a ,∴a =.∴E ;②当△CDE ∽△AEC 时,∠DCE =∠EAC =60°=∠B ,∴∠BCD +∠ECA =180°﹣60°=120°, 又∵∠BDC +∠BCD =180°﹣∠B =120°,∴∠BCD +∠ECA =∠BDC +∠BCD ,∴∠ECA =∠BDC ,∴△BDC ∽△ACE ,∴,∴BC =2AE =2(4﹣a )=8﹣2a , ∴8﹣2a +2=4,∴a =.∴.综上所述,点E 的坐标为或.【点评】本题主要考查相似三角形,考虑分类讨论是本题的关键.10.(2022•广东中考模拟)(1)模型探究:如图1,D 、E 、F 分别为ABC ∆三边BC 、AB 、AC 上的点,且B C EDF α∠=∠=∠=,BDE ∆与CFD ∆相似吗?请说明理由.(2)模型应用:ABC ∆为等边三角形,其边长为8,E 为边AB 上一点,F 为射线AC 上一点,将AEF ∆沿EF 翻折,使点A 落在射线CB 上的点D 处,且2BD =.①如图2,当点D 在线段BC 上时,求AE AF 的值; ②如图3,当点D 落在线段CB 的延长线上时,求BDE ∆与CFD ∆的周长之比.【答案】(1)~∆∆BDE CFD ,见解析;(2)①57AE AF =;②BDE ∆与CFD ∆的周长之比为13. 【分析】 (1)根据三角形的内角和得到BED CDF ∠=∠,即可证明;(2)①设AE x =,AF y =,根据等边三角形的性质与折叠可知DE AE x ==,DF AF y ==,60EDF A ∠=∠=,根据三角形的内角和定理得BED CDF ∠=∠,即可证明~∆∆BDE CFD ,故BD BE DE CF CD FD ==,再根据比例关系求出AE AF的值; ②同理可证~∆∆BDE CFD ,得BD BE DE CF CD FD==,得28810x x y y -==-,再得到13x y =,再根据相似三角形的性质即可求解. 【详解】解(1)~∆∆BDE CFD ,理由:B C EDF α∠=∠=∠=,在BDE ∆中,180B BDE BED ∠+∠+∠=,180180BDE BED B α∴∠+∠=-∠=-,180BDE EDF CDF ∠+∠+∠=,180180BDE CDF EDF α∴∠+∠=-∠=-,BED CDF ∴∠=∠,B C ∠=∠,~BDE CFD ∴∆∆; (2)①设AE x =,AF y =,ABC ∆是等边三角形,60A B C ∴∠=∠=∠=,8AB BC AC ===, 由折叠知,DE AE x ==,DF AF y ==,60EDF A ∠=∠=,在BDE ∆中,180B BDE BED ∠+∠+∠=,180120BDE BED B ∴∠+∠=-∠=,180120BDE BED B ∠+∠=-∠=,180BDE EDF CDF ∠+∠+∠=,180120BDE CDF EDF ∴∠+∠=-∠=,BED CDF ∴∠=∠,60B C ∠=∠=,~BDE CFD ∴∆∆,BD BE DE CF CD FD∴==, 8BE AB AE x =-=-,8CF AC AF y =-=-,6CD BC BD =-=2886x x y y -∴==-,()()2868y x y x y x ⎧=-⎪∴⎨=-⎪⎩,105147x y ∴==,57AE AF ∴=; ②设AE x =,AF y =,ABC ∆是等边三角形, 60A ABC ACB ∴∠=∠=∠=,8AB BC AC ===, 由折叠知,DE AE x ==,DF AF y ==,60EDF A ∠=∠=,在BDE ∆中,180ABC BDE BED ∠+∠+∠=,180120BDE BED ABC ∴∠+∠=-∠=,180BDE EDF CDF ∠+∠+∠=,180120BDE CDF EDF ∴∠+∠=-∠=,BED CDF ∴∠=∠,60ABC ACB ∠=∠=,120DBE DCF ∴∠=∠=,~BDE CFD ∴∆∆,BD BE DE CF CD FD∴== 8BE AB AE x =-=-,8CF AF AC y =-=-,10CD BC BD =+=,28810x x y y -∴==-,2(8)10(8)y x y x y x =-⎧∴⎨=-⎩,13x y ∴=. ~BDE CFD ∆∆.BDE ∴∆与CFD ∆的周长之比为13DE x DF y ==. 【点睛】此题主要考查相似三角形的判定与性质,解题的关键是熟知等边三角形的性质及相似三角形的判定与性质.11.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在ABC 中,90ACB ∠=︒,AC BC =,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:ADC CEB △≌△.(1)探究问题:如果AC BC ≠,其他条件不变,如图②,可得到结论;ADC CEB △∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x =与直线CD 交于点()2,1M ,且两直线夹角为α,且3tan2α=,请你求出直线CD的解析式.(3)拓展应用:如图④,在矩形ABCD中,3AB=,5BC=,点E为BC边上—个动点,连接AE,将线段AE绕点E顺时针旋转90︒,点A落在点P处,当点P在矩形ABCD 外部时,连接PC,PD.若DPC△为直角三角形时,请你探究并直接写出BE的长.NF OF NO90△△ABE△△EFP 12.(2022·山东青岛·九年级期中)【模型引入】我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形,可以使得我们在观察新问题的时候很迅速地联想,从而借助已有经验,迅速解决问题.【模型探究】如图,正方形ABCD中,E是对角线BD上一点,连接AE,过点E作EF△AE,交直线CB于点F.(1)如图1,若点F在线段BC上,写出EA与EF的数量关系并加以证明;(2)如图2,若点F在线段CB的延长线上,请直接写出线段BC,BE和BF的数量关系.【模型应用】(3)如图3,正方形ABCD中,AB=4,E为CD上一动点,连接AE交BD于F,过F作FH△AE 于F,过H作HG△BD于G.则下列结论:①AF=FH;②△HAE=45°;③BD=2FG;④△CEH的周长为。
中考地理总复习知识清单与精练 专题05 中国的气候+等值线(练习)(解析版)

专题05 中国的气候+等值线(练习)中考地理总复习知识清单与精练一、选择题1.西北地区深居内陆,远离海洋,降水量自东向西逐渐减少,主要原因是A.夏季风的强弱关系B.冬季分的强弱关系C.距海远近的不同D.热力性质差异的大小【答案】C【解析】西北地区是我国跨经度最广的区域,各地距海远近不同,加之山脉的阻挡,年降水量表现出由东向西(或由沿海到内陆)逐渐减少的态势。
故选C。
【点睛】本题主要考查了我国西北地区降水量不同的原因。
2.不属于秦岭—淮河的意义的是A.湿润地区和干旱地区的分界线B.亚热带与暖温带地区的分界线C.800毫米等降水量线通过的地方D.我国北方地区和南方地区的分界线【答案】A【解析】秦岭—淮河的意义:一月0℃的等温线;800mm年等降水量线;暧温带与亚热带的分界线;湿润与半湿润地区的分界线;南方地区与北方地区的分界线等,故A错误。
故选:A。
【点睛】识记秦岭—淮河一线的意义。
3.我国冬季最冷的地方是A.漠河B.拉萨C.托克逊D.火烧寮【答案】A【解析】我国冬季南北温差大,纬度位置是其决定性因素,纬度越高,气温越低,漠河纬度位置最高,故其气温最低,本题选择A。
【点睛】本题考查冬季气温的分布特征。
4.2019年12月底应邀到银川参加“地理学综合学术年会”的代表中,身感天气特别寒冷的代表最有可能来自A.海口B.黑龙江C.北京D.乌鲁木齐【答案】A【解析】我国疆域辽阔,南北跨纬度大,冬季南北温差,黑龙江、北京、乌鲁木齐、银川都在北方地区,冬季气候寒冷,海口位于北回归线以南地区,位于热带,全年高温,所以到银川会感到特别寒冷。
故选A。
【点睛】该题考查我国冬季气温分布特点,分析解答即可。
5.我国南北气温差别最大的季节是A.春季B.夏季C.秋季D.冬季【答案】D【解析】我国冬季时,由于太阳直射在南半球,北半球各地纬度越高,正午太阳高度越小,白昼时间越短,气温很低,而南方地区正午太阳高度大,白昼时间长,气温高,南北气温差异是一年中最大的,主要是由于南北跨纬度大,故选D.【点睛】本题考查我国气温的有关知识.6.读“气温曲线与降水量柱状图”,判断哪一种是表示我国南方地区气候的A.B.C.D.【答案】A【解析】读图可知:A的气候特征是夏季高温多雨,冬季温和湿润,属于亚热带季风气候,亚热带气候为我国南方地区的气候,故选A。
专题05 地球上的水-2024年高考真题和模拟题地理分类汇编(教师卷)

专题05地球上的水(2024·黑龙江/吉林/辽宁)水体性质、运动和库区环境等因素影响水库浮游动物生物量及其分布。
恰甫其海是位于新疆伊犁谷地特克斯河上的水库,周边植被以草原为主。
水库消落区主要分布在南岸。
如图为2019年6月和9月恰甫其海表层浮游动物生物量等值线图。
据此完成下面小题。
1.(海水性质及其对生物的影响)影响6月恰甫其海表层浮游动物生物量分布的主要因素是()A.透明度B.流量C.营养盐D.流向2.(影响海水性质的因素)9月恰甫其海南岸丰富的碎屑食物吸引浮游动物聚集,这些碎屑食物主要来源于()A.底泥扰动上浮B.水位涨落携带C.表层水流汇集D.河川径流输入【答案】1.A2.B【解析】1.由材料可知,6月为丰水期,因为丰水期为水库蓄水期,上游冰雪融水形成的洪水经库尾进入水库后流速减缓,水体的物理状态发生改变,如泥沙沉降、冲刷力降低,水体透明度升高,此时气温较高,有利于光合作用的进行,浮游生物繁殖较快,数量较多,因此,6月恰甫其海表层浮游动物生物量较为丰富,A正确;与流量、营养盐、流向的关系不大,BCD错误。
故选A。
2.由材料可知,水库消落区主要分布在南岸。
9月是丰水期过后的平水期,恰甫其海南岸丰富的碎屑食物吸引浮游动物聚集,这些碎屑食物主要来源于水位涨落携带,且消落区为草原分布,有机质含量较多,B正确;9月份入库水量较少,不会引起大规模的底泥扰动上浮,A错误;9月份平水期,不会有大规模的表层水流汇集,C错误;9月份是平水期,河川径流输入较少,D错误。
故选B。
(2024·山东)海洋浮游植物密度的空间分布与海水性质、营养盐等环境因子密切相关。
远岸海域浮游植物密度受陆地影响较小。
如图示意孟加拉湾及其周边区域。
据此完成下面小题。
3.(季风洋流)下列月份中,M区域浮游植物密度最高的是()A.1月B.4月C.7月D.10月4.(海水盐度的影响因素)与7—8月相比,12月至次年1月N区域海水盐度较高的主要影响因素是()A.蒸发B.降水C.径流D.洋流【答案】3.C4.D【解析】3.根据图示信息可知,M区域位于北印度洋海域,夏季该地盛行西南季风,该海域为离岸风,形成离岸流,底层营养盐类上泛,有利于浮游生物的繁殖,浮游生物密度较高,7月为北半球夏季,M区域浮游植物密度最高,C正确;1月、4月、10月该海域上升流不强,营养物质较少,浮游生物密度较小,ABD 错误。
2023年北京各区(海淀朝阳丰台东西城等)高考地理一模专题汇编5 整体性与差异性含详解

专题05 整体性与差异性一、单选题1.(2023·北京西城·统考一模)内蒙古腰坝绿洲东依贺兰山,西邻腾格里沙漠,是阿拉善左旗重要的粮食产地。
图为该地区表层土壤含盐量等值线图。
读图,根据土壤含盐量可推测该地区()A.地处贺兰山迎风坡,降水多B.地势丙地高,甲地、乙地低C.传统灌溉方式是滴灌、喷灌D.丙地、丁地地下水超采严重(2023·北京朝阳·统考一模)下图为我国某山脉东段垂直地域分异示意图。
读图,回答下面小题。
2.该山脉是()A.阴山山脉B.天山山脉C.横断山脉D.祁连山脉3.该山脉东段下列植被类型分布区中,表层土壤水分含量较高的是()A.山地草原B.高寒草原C.高山灌丛草甸D.山地荒漠(2023·北京东城·统考一模)南迦巴瓦峰为喜马拉雅山脉东端的最高峰,其南坡是中国山地森林垂直带谱分布最完整的地区之一,如左图所示。
右图是南迦巴瓦峰植物多样性垂直分布图。
读图,回答下面小题。
4.南迦巴瓦峰植物多样性最丰富的区域出现在()A.半常绿雨林带B.常绿阔叶林带C.常绿落叶阔叶混交林带D.高山灌丛草甸带5.与同纬度山地相比,南迦巴瓦峰垂直带谱完整的主要原因有()①基带海拔高②山地南北跨度大③受暖湿气流影响大④山高谷深高差大A.①②B.②③C.①④D.③④(2023·北京房山·统考一模)下图为45°N附近某区域的遥感影像,其中深色部分为植被覆盖区,浅色部分为高原荒漠区;终年冰雪覆盖的山峰海拔3424米,距海约180千米。
读图,完成下面小题。
6.导致图中高原荒漠区与植被覆盖区年平均降水量差异的最主要因素是()A.纬度位置B.大气环流C.海陆位置D.地形7.该区域中山脉西坡山麓的自然植被属于()A.常绿阔叶林B.常绿硬叶林C.针阔叶混交林D.草原(2023·北京延庆·统考一模)丹霞地貌主要由砾岩和砂岩组成,多为宝塔状、柱状、峰林状地形,崖壁相对高度一般不超过200米,形成特殊的植被分布现象。
等值线图的判读与分析ppt 人教课标版优质课件

③根据等高线判读高度(绝对和相对高度)和 气温
④根据等高线判别地形地势,又由山谷的分布, 判断河流的位置及流向。
地理总复习 等值线图
例7:河流ab段的流 向为 ( ) A.自西北向东南 B.自东南向西北 C.自东北向西南 D.自西南向东北
地理总复习 等值线图
等高线判读
风向风速的判读
等压面弯曲判读
等压线季节判读
等压线天气判读
A
B
C
地理总复习 等值线图
等压线判读
季节判读
气压系统的判读
根据下图等压图判断其季节。
风向风速的判读
等压面弯曲判读
等压线季节判读
等压线天气判读
地理总复习 等值线图
等压线判读
天气状况判读
气压系统的判读
根据高、低气压中心判断天气状况。
风向风速的判读
①根据数值大小判读地形类型及地形部位
②根据疏密程度判读坡度的陡缓
③根据等高线判读高度(绝对和相对高度)和 气温
④根据等高线判别地形地势,又由山谷的分布, 判断河流的位置及流向。
⑤ 判别两点间可否通视,可通过绘制地形剖 面图判断
⑤ 判别两点间可否通视,可通过绘制地形剖 面图判断
某山区的一所学校,拟组织 学生对附近公路的交通流量 进行调查。读图4判断在E、 F、C三个地点中,能目测到 公路上经过H处车辆的 是。F NhomakorabeaE
H
H
地理总复习 等值线图
等高线判读
①根据数值大小判读地形类 型及地形部位
②根据疏密程度判读坡度的 陡缓
③根据等高线判读高度(绝 对和相对高度)和气温
④根据等高线判别地形地势, 判断河流的位置及流向。
等值线的阅读 PPT课件 人教版

•
13、认识到我们的所见所闻都是假象,认识到此生都是虚幻,我们才能真正认识到佛法的真相。钱多了会压死你,你承受得了吗?带,带不走,放,放不下。时时刻刻发悲心,饶益众生为他人。
•
14、梦想总是跑在我的前面。努力追寻它们,为了那一瞬间的同步,这就是动人的生命奇迹。
•
15、懒惰不会让你一下子跌倒,但会在不知不觉中减少你的收获;勤奋也不会让你一夜成功,但会在不知不觉中积累你的成果。人生需要挑战,更需要坚持和勤奋!
判断气压系统
高气压、低气压
判断风向
气压梯度力、地 球自转水平偏向 力
判断风力
密集处风力大、 稀疏处小
例1:读南半球等压线分布示意图,请判断图 中风向正确的是:
C
单位:百帕 A
1002 D
1004
1006
1008 B
1010
等高线图的阅读
判断坡度
稀疏处缓;密集处陡; 相交处为陡崖
判断地形
•
16、成功的秘诀在于永不改变既定的目标。若不给自己设限,则人生中就没有限制你发挥的藩篱。幸福不会遗漏任何人,迟早有一天它会找到你。
•
17、一个人只要强烈地坚持不懈地追求,他就能达到目的。你在希望中享受到的乐趣,比将来实际享受的乐趣要大得多。
•
18、无论是对事还是对人,我们只需要做好自己的本分,不与过多人建立亲密的关系,也不要因为关系亲密便掏心掏肺,切莫交浅言深,应适可而止。
铁路线(单虚线表示分水线,双虚线表示待选铁路线)。
分水线:
待选铁路线:
例3:下图是河北省山区某地示意图,读图并回答: (1)A处是 地形,B处是 地形。 (2)B处夏、冬气候特征各如何?并分析原因。
2022高考地理专题:等值线图的判读(真题展示+方法指导+提升训练)

2022高考地理专题:等值线图的判读(真题展示+方法指导+提升训练)【真题展示】读“某地等高线地形图和景观示意图”,回答(1)~(2)题:(1)图中M处地形部位的名称是()A.山峰B.山谷C.陡崖D.鞍部(2)符合图中信息的是()A.图中最高山峰南坡比北坡陡B.两座山峰的相对高度是200米C.EF段河流的流向是自东北向西南D.两座山峰的实际距离是150米【方法指导】(1)图中M位于两个山峰之间的低地,应该是鞍部。
(2)图示最高山峰海拔为720米,该山峰南坡等高线较北坡稠密,则南坡坡度大于北坡,故A正确;通过计算可知,两座山峰的相对高度是210米,故B错误;图中河流EF段的流向为自西北向东南,故C错误;两座山峰不在同一水平面上,则实际距离要大于图上比例尺反映的距离,故D错误。
答案:(1)D (2)A【建立模板】常见等值线主要有等高(深)线、等温线、等压线、等降水量线等,其中等高线是等值线的基础,其他等值线都是由其演化来的。
1.共同特征(1)同线等值:同一条等值线上各点的数值相等。
(2)全图等距:相邻两线相差一个等值距或数值相等。
(3)等值线是封闭的曲线,但在图幅有限范围内不一定全部闭合。
(4)两条等值线不能相交(等高线图中的陡崖处除外)。
(5)等值线疏密反映表达要素数值变化的快慢。
(6)局部闭合:两等值线间的局部闭合等值线,其数值“大于大的,小于小的”。
2.判读方法内容判读要领数值同线等值,全图等距(等值距):相邻两线相差一个等值距或数值相等;极大值、极小值及其位置;看数值的递变规律延伸方向等值线的延伸方向表明等值线数值变化的大致趋势及其影响因素,如等高线走向受地形、地势影响,等温线走向受太阳辐射、大气环流、海陆位置、地形地势、洋流等因素影响弯曲状况凸高为低——等值线向高值一侧凸,数值小;凸低为高——等值线向低值一侧凸,数值大。
可添加辅助线(垂线法、切线法)判断等值线弯曲处数值的大小。
平直——影响因素相对简单;弯曲——影响因素相对复杂疏密程度线密差值大,线疏差值小局部闭合介于两等值线间的异常区域,其数值“大于大的,小于小的”,即如果闭合等值线与相邻两线中的较小数值相等,则闭合区域低于较小数值;闭合等值线与相邻两线中的较大数值相等,则闭合区域高于较大数值分析成因等值线的延伸、弯曲、疏密、闭合受多种因素的影响,要根据等值线表达要素的特点,调用相关原理分析其成因3.等值线弯曲处数值大小的判读值线中心点高于两侧点,向数值小的方向凸出中心点低于两侧点,向数值大的方向凸出等压线脊线(高压脊) 槽线(低压槽)等高线山脊(分水线) 山谷(汇水线)等温线气温比两侧高,可能位于山谷处气温比两侧低,可能位于山脊处等降降水比附近地区多降水比附近地区少水量线等水温暖流流经寒流流经线等盐度比附近海域盐度高比附近海域盐度低线【提升训练】如图为我国某区域1月和7月等温线分布图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章地球与地图第5专题等值线图的阅读(解析版)【重难突破】一、等值线的共性特征(1) 同一条等值线上各点的数值相等。
(2) 相邻两条等值线值可以相等(如河谷两侧相邻的等高线),也可以按周边地区趋势依次递减或递增;同一幅图中相邻两条等值线的间隔相等。
(3) 同一幅图上任意两条等值线一般不会相交、不会重叠(等高线的陡崖除外)。
(4) 等值线一般应是闭合曲线,在局部图中受图幅所限不一定全部闭合,但一定在相邻的多张拼接图中闭合。
(5) 等值线弯曲度越大,其弯曲处的两侧变化越大。
二、等值线图的判读步骤②切线法:在等值线弯曲最大处作某条等值线的切线值大小。
若切点数值小于其他点的数值,数值,则该处为高值区(如图):如果两条数值不同的等值线中间有闭合的等值线规律确定其数值。
如图中有两条等值线小于b在等温线图中可判断半球位置、【典型题型】例1。
(2019。
石家庄二中)《中国国家地理》杂志社策划了“三纵一横”四条路线寻访秋天的活动,线路分布如图所示。
图中标注的日期为各地入秋时间(我国气象部门规定的“入秋日”是指日均温连续5天≤22 ℃时的第一天)。
读图,回答(1)~(2)题。
(1) 我国各地入秋时间的序列是( )A. 路线①的秋色是从南往北演进B. 路线②的秋色是从北往南演进C. 路线③的秋色是从中部往南、北演进D. 路线④的秋色是从东往西演进(2) 影响路线③的入秋时间序列的原因是( )A. 纬度与大气环流B. 地形与大气环流C. 纬度与地形D. 人类活动【析图建模】【解析】(1)读图可知路线①②的秋色均是由北往南演进;路线③的秋色是从南、北向中部演进;路线④的秋色是从西往东演进。
(2) 路线③中海拔较高的高山、高原地区入秋时间比周边地区早,可以推测是受地形影响的结果;纬度较低的塔里木盆地入秋时间较纬度高的准格尔盆地晚,可以推测影响因素是纬度。
【答案】(1)B (2) C例2. (2019·山东济宁期末)藏北高原南部高寒草原地带某湖泊,湖水清澈透明,水生生物少,只在湖体局部浅水区有茂密的水草和藻类生长。
下面左图为该湖等深线分布图,右图为一游客7月某日在湖边拍摄的日落照片。
读图,回答(1)~(3)题。
(1). 推测该湖泊面积最大的月份为( )A. 1月B. 4月C. 7月D. 10月(2). 某游客到该湖旅游,准备在湖边垂钓,最有可能选择的垂钓地点是 ( )A. ①B. ②C. ③D. ④(3). 照片中游客所在的位置最可能位于左图中 ( )A. 甲处B. 乙处C. 丙处D. 丁处【解析】(1)该湖泊位于藏北高原南部,海拔较高,高原降水较少,所以该湖泊的补给主要为高山冰雪融水,四个选项中,7月份气温最高,融水补给量大,所以湖泊面积最大的月份为7月。
(2)由材料“湖体局部浅水区有茂密的水草和藻类生长”得出浅水区有丰富的饵料,所以鱼类应分布在该湖泊的浅水区。
读图可知,②③两处等深线密集,湖水较深;①处有河流流入,河水带来丰富的营养物质,河流入湖口处湖水较浅,饵料丰富,与④相比较,①处鱼类更多。
故选A。
(3)7月份,该地日落方向为西北。
根据照片可知,游客和日落分别位于湖泊的两岸,故游客应位于湖泊的东岸。
丙、丁两处位于湖泊的西岸,C、D错误;甲处位于东南湖岸,游客向西北方向看日落,游客左侧为湖泊,与照片不符,A错误;游客在乙处向西北方向穿过湖泊可看到对岸的日落,与照片相符,B正确。
【答案】(1) C (2)A (3) B【过关检测】一、单项选择题(2019·辽宁东北育才中学)下图是我国东南地区某地1月份等潜水位线和等高线(单位:m)图。
读图,回答1~2题。
1. 图中地下水流速最大点和流向分别是 ( )A. 甲东北流向西南B. 甲正北流向正南C. 乙正西流向正东D. 丙西北流向东南【答案】1. B【解析】图中虚线表示等潜水位线,水流方向垂直于等潜水位线,指向低处。
潜水位线越密集,水流速度越快。
图中甲处等值线最密集,地下水流速最大点是甲,流向是向正南,B正确。
2. 下列有关图中信息的叙述,正确的是( )A. 若在乙点打井,井深110 m以上才能开采到地下水B. 该地区属季风气候区,冬季谷地河流干涸C. 丁点终年有地表水D. 该地河流自东南流向西北【答案】2. C【解析】根据图中等高线、等潜水位线可知,乙点海拔120 m,潜水位115 m,若在乙点打井,井深5 m以上便能开采到地下水,A错误;该地位于我国东南地区,属于亚热带季风气候区,降水较多,河流不存在干涸现象,B 错误;丁点潜水位高于谷地海拔,终年有地表水,C正确;河流流向与等高线凸向相反,该河流应自西北流向东南,D错误。
(2018·山西孝义一模)负积温是某时段内日平均气温小于0 ℃的累加,是农业生产的参考数据之一。
一个地区的负积温,影响着当地农作物的越冬安全,影响农业病虫害的发展和农药使用量。
下图示意1961-2008年我国北方局部地区负积温空间分布。
据此回答3~4题。
3. 影响图示地区负积温值东西差异的主导因素是 ( )A. 纬度位置B. 地形地势C. 距海远近D. 大气环流【答案】3. B【解析】读图分析可知,同纬度西部负积温等值线南凸,说明其数值大于东部,即西部较东部冷,主要是由于东部华北平原地形平坦,地势低,西部黄土高原,地势高,起伏较大,故选B。
4. 甲地负积温等值线明显弯曲可能给当地带来的影响 ( )A. 缩短农作物生长周期B. 减少农药使用量C. 利于果树的安全越冬D. 改变耕作制度【答案】4. B【解析】甲处负积温等值线向高值凸出,说明该处负积温值较同纬度偏低,积温低,会导致农作物生长周期延长,A错误;因气温低,病虫害少,农药使用量减少,B正确;积温低,农作物和果树容易遭受冻害,不利于安全越冬,C错误;不会改变耕作制度,D错误。
故选B。
(2019·云南玉溪一中)下图为某区域外流河等温线分布图。
读图,回答5~6题。
5. 对a、b、c、d四地温度大小关系的判断,正确的是 ( )A. a>bB. b=cC. a>cD. c=d【答案】5. A【解析】根据等值线递变规律,按某一递增或递减顺序变化。
图中相邻等值线温差是2 ℃,a、b、c、d四地温度,a温度为12~14 ℃,结合河流流向,b地海拔较高,温度小于12 ℃, a>b,A正确;c比a的地势低,温度呈升高趋势,环绕c的等温线是14 ℃,c的温度应大于14 ℃,b<c,B错误;a﹤c ,C错误;d温度小于12 ℃,c>d,D错误。
6. 下列符合图中河流干流流量随流程变化的是( )A BC D【答案】6. C【解析】图中河流干流由上游到下游,流量不断增大,每次支流汇入,干流流量就明显增大。
符合图中河流干流流量随流程变化的是图C,C正确;图A、图B不能体现支流汇入的影响,A、B错误;图D不符合支流汇入特点,D错误。
(2019·安徽合肥一模)洮河是黄河上游地区重要的支流。
下图示意洮河流域地理要素分布。
据此回答7~9题。
7. 岷县与海甸峡之间河流流向大致是( )A. 自西北向东南B. 自东南向西北C. 自东北向西南D. 自西南向东北【答案】7. B【解析】洮河在岷县与海甸峡之间汇入黄河。
根据图示可知,黄河在海甸峡与临洮之间由南向北流,故洮河在该河段的流向为自东南向西北。
8. 图中落差最大的河段是 ( )A. 碌曲—下巴沟B. 下巴沟—岷县C. 岷县—海甸峡D. 海甸峡—临洮【答案】8. B【解析】图中显示,四河段中,下巴沟—岷县的年均温差最大,地势落差最大,则该河段的落差最大。
9. 图中洮河自然状态下冬季不结冰的原因有 ( )①河流流速快②河流以地下水补给为主③气温高于0 ℃④河流水量大A. ①②B. ②③C. ①④D. ③④【答案】9. A【解析】洮河河段处于黄河上游,河流水量不大。
但洮河流域处在青藏高原和黄土高原的过渡地带,地势崎岖不平,相对高差较大,河流流速快,河流以地下水补给为主,因此冬季不结冰。
图中显示该流域年平均气温高于0 ℃,无法确定冬季的气温也高于0 ℃。
(2019·陕西二模)深圳湾地处深圳特区的西南面,属于慢淤积的浅水海湾,潮流(潮汐引起的水流)动力是维持深圳湾水深的主要动力,而维持这种动力的主要因素是深圳湾海水容量。
下图为1970—1999年深圳湾海岸线变化图。
据此回答10~12题。
10. 0 m等深线位置的变化反映了深圳湾( )A. 水深加大B. 水质变差C. 水量增大D. 面积缩小【答案】10. D【解析】0 m等深线即为海平面。
据图可知,其位置1970—1999年整体向深圳湾推进,说明深圳湾的面积不断缩小。
11. 导致深圳湾0 m等深线位置变化的主要人为因素是( )A. 深圳湾潮流动力减弱B. 深圳河泥沙量增多C. 深圳湾沿海工程建设D. 深圳湾水污染严重【答案】11. C【解析】根据题干可知,影响深圳湾0 m等深线位置变化的主要是人为因素,A、B属于自然因素,排除A、B;深圳经济发达,城市化进程快,深圳湾沿海工程建设以及填海造陆等人为因素导致其面积萎缩,C正确,D错误。
12. 减缓深圳湾海岸线变化的主要措施是( )A. 控制填海造陆规模B. 修复滨海红树林生态环境C. 改善海湾环境质量D. 加强对生态系统的监测【答案】12. A【解析】根据上题分析可知,其海岸线的变化主要是沿海工程建设和填海造陆导致的,因此减缓其海岸线变化的主要措施应控制填海造陆的速度和规模。
(2018·福建华安一中)气候倾向率反应气候要素的变化趋势,包括气温倾向率(℃/10年)和降水量倾向率(㎜/10年)。
下图示意1965—2005年某区域气候倾向率。
读图,回答13~14题。
13. 图中四地气温、降水量倾向率最大的分别是( )A. 红卫鸭绿河B. 勤得利胜利C. 红卫胜利D. 勤得利鸭绿河【答案】13. A【解析】读图,根据等值线的变化规律,总是按某一递增或递减的顺序变化。
根据图中数值可以判断,气温倾向率最大的地点是红卫,降水倾向率最大的地点是鸭绿河。
14. 据图可推测该区域( )A. 地表侵蚀增强B. 活动积温增加C. 土壤趋于干旱D. 粮食产量降低【答案】14. B【解析】根据表中数值,该地降水倾向率有负值区,说明有降水减少区域,地表侵蚀可能减弱,A错误;图中气温倾向率都为正值,说明活动积温增加,B正确;降水倾向率有减少区域,不能表示土壤趋于干旱,C错误;积温增加,粮食产量可能呈增加趋势,D错误。
(2018·湖南师大附中)下图为我国季节性冻土标准冻深线图(冻深是冬季时自地面以下冻结的深度,单位:cm)。
读下图,回答15~17题。
15. 关于我国季节性冻土深度分布规律的说法,正确的是( )A. 西浅东深B. 高原浅平原深C. 沿海浅内陆深D. 北浅南深【答案】15. C【解析】根据图中等值线可知,我国季节性冻土深度分布规律是南浅北深,A、D错误;高原深平原浅,B错误;图中季节性冻土等冻深线,在内陆地区向较低纬度弯曲,说明内陆冻土深度较大,沿海浅内陆深,C正确。
