课后作业(第七章 第八章 (带答案)
林崇德《发展心理学》笔记和课后习题(含考研真题)详解-第七章至第八章【圣才出品】

第7章小学儿童的心理发展【本章重点】1.学生学习的一般特点及其作用;2.学习障碍的特点、症状、原因;3.小学儿童的思维发展特点;4.儿童概念的发展;5.儿童推理能力的发展;6.儿童思维品质的发展特点;7.儿童自我意识的发展;8.儿童的社会性认知;9.小学儿童的人际关系;10.小学儿童品德发展的基本特点。
7.1复习笔记一、小学儿童的学习6、7岁到12、13岁是儿童开始进入小学学习的时期。
这是儿童心理发展的一个重要转折时期,被称之为前青春发育期。
在教育的影响下,小学儿童的认知能力、个性特点都在不断地发展变化,其发展过程表现出明显的协调性和过渡性的特点。
儿童进入学校以后,学习活动逐步取代游戏活动而成为儿童主要的活动形式。
(一)小学儿童的学习及其作用学习有广义和狭义之分:广义的学习,是指动物和人的经验的获得及行为变化的过程,人类的广义学习是在生活中进行的;狭义的学习,是指学生在教师指导下有目的、有计划、有系统地掌握知识技能和行为规范的活动,这是一种社会义务。
1.学生学习的一般特点学生的学习过程是一种认识或认知过程,学生在学习过程中认识世界,丰富自己,发展自己。
学习有下列几个基本特点:(1)在学习过程中,学生的认知或认识活动要越过直接经验的阶段。
学生以学习间接经验为主,不受时间空间的限制,越过直接经验,较迅速而直接地把最基本的东西学到手。
这是学生的学习过程区别于人类一般认识活动或认识过程的特殊本质。
(2)学生的学习是一种在教师指导下的认知或认识活动。
学生的学习是通过教学活动来实现的。
教与学是一种双边活动,教是为了学,学则需要教,二者互为条件,互相依存。
在学习过程中,学生的认知或认识活动受教师教授活动的制约。
(3)学生的学习过程是一种运用学习策略的活动。
学生最主要的学习是学会学习,最有效的知识是自我控制的知识。
要学会学习,就有学习策略的问题。
学习策略是指在学习活动中,为达到一定的学习目标而学会学习的规则、方法和技巧,是一种在学习活动中思考问题的操作过程,是认识(或认知)策略在学生学习中的一种表现形式。
人教版八年级物理下册第七章、第八章作图练习题(含答案)
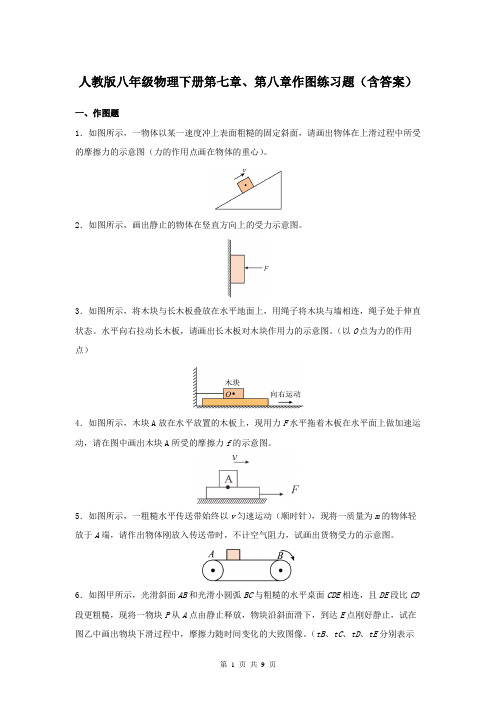
人教版八年级物理下册第七章、第八章作图练习题(含答案)一、作图题1.如图所示,一物体以某一速度冲上表面粗糙的固定斜面,请画出物体在上滑过程中所受的摩擦力的示意图(力的作用点画在物体的重心)。
2.如图所示,画出静止的物体在竖直方向上的受力示意图。
3.如图所示,将木块与长木板叠放在水平地面上,用绳子将木块与墙相连,绳子处于伸直状态。
水平向右拉动长木板,请画出长木板对木块作用力的示意图。
(以O点为力的作用点)4.如图所示,木块A放在水平放置的木板上,现用力F水平拖着木板在水平面上做加速运动,请在图中画出木块A所受的摩擦力f的示意图。
5.如图所示,一粗糙水平传送带始终以v匀速运动(顺时针),现将一质量为m的物体轻放于A端,请作出物体刚放入传送带时,不计空气阻力,试画出货物受力的示意图。
6.如图甲所示,光滑斜面AB和光滑小圆弧BC与粗糙的水平桌面CDE相连,且DE段比CD 段更粗糙,现将一物块P从A点由静止释放,物块沿斜面滑下,到达E点刚好静止,试在图乙中画出物块下滑过程中,摩擦力随时间变化的大致图像。
(tB、tC、tD、tE分别表示物块经过B、C、D、E点的时刻)7.如图所示是运动员骑自行车比赛时的情景,请画出地面对自行车后轮作用力的示意图(O点是力的作用点)。
8.如图两块完全相同的木板之间夹着重10N的木块C,木板对木块的压力恒定不变,木板保持竖直状态,木块C刚好匀速向下运动,如果用一个力F拉着木块C,使木块C刚好匀速竖直上升,请画出木块在竖直方向受到的力并标明大小。
9.如图所示,A、B两个物体叠放在粗糙的水平地面上,在拉力F的作用下物体A、B一起向右做匀速直线运动,请作出物体B受到地面的摩擦力f1和物体A对它的摩擦力f2的示意图。
(图中黑点为物体B的重心)10.一人用两个竖直的夹板将三块砖如图甲所示夹起保持静止,每块砖重为20N,将“2”号砖看成一个有质量的点,如图乙所示。
请在图乙中画出“2”号砖所受的摩擦力合力f的示意图,并标明大小。
人教版物理八年级下册课后习题参考答案

八年级下册课后练习及答案《第七章力》《7.1力》1.请举例说明:(1)力能使物体发生形变;(2)力能改变物体的运动状态;(3)力的作用效果与力的大小、方向、作用点有关。
(1)用力拉皮筋皮筋变长;大风将树吹弯了;用力压气球,气球被压扁。
(2)用头顶足球,会使足球变向;足球守门员将飞来的足球接住;汽车关闭发动机后,会慢慢停下来;用力蹬自行车,自行车会加速前进(3)推一个半开的门,你用力小了门是不动的,大了就动了,你推得方向不同门可能会打开或关闭,作用点是如果你在里门轴远的地方推,很容易推动,距离门轴近的地方很难推动2.用线将吊灯悬挂在天花板上,线对灯的拉力F=4N。
请在图中画出拉力F的示意图。
3.一位同学沿水平方向用75N的力推箱子,请在图中画出这个力的示意图。
4.如图,人坐在小船上,用力推另一艘小船,能够把另一艘小船推开而自己坐的小船不动吗?为什么?不能。
因为力的作用是相互的,当人用力推另一艘船时,另一只船也会给他一个反作用力,故两船都会运动,且运动方向相反.《7.2弹力》1.在“橡皮泥上留下漂亮的指印”“跳板被跳水运动员压弯(如图)”两个现象中,发生的是不是弹性形变?说说你的理由。
橡皮泥发生的不是弹性形变;跳板发生的是弹性形变。
因为撤去对橡皮泥施加的力后,橡皮泥不能自动恢复原状,所以橡皮泥发生的不是弹性形变。
而当跳水运动员离开跳板后跳板能够恢复原状,所以跳板发生的是弹性形变。
2.小强用弹簧拉力器锻炼身体,刚拉开时没有感到太费力,可是两手拉开的距离越大,就感到越费力。
这是什么原因?弹簧产生的弹力的大小与弹簧发生弹性形变的程度有关,弹性形变程度越大,产生的弹力越大。
3.试分析一个旧弹簧测力计不能准确测量的原因。
弹簧会因使用时间长了而失去原有的弹性,弹簧的变形系数k 就变了,即L F ∆发生了变化,无法与原来的刻度相搭配,测出来的力自然不再准确。
4.请读出图中两个弹簧测力计的示数。
圆筒测力计每个小格表示0.1N 。
机械原理第二版课后答案

机械原理第二版课后答案第一章结构分析作业1.2 解:F = 3n-2PL-PH = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2PL-PH = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2PL-PH = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2PL-PH = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2PL-PH = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取作机构位置mmmm l /5=μ图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s rad l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取作机构位置mmmm l /1=μ图如下图a 所示。
1. 求B2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B3点的速度V B3V B3 = V B2 + V B3B2 大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC取作速度多边mms mm v /10=μ形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ ,smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3srad l V BC B /2.212327033===ω5. 求nB a 222212/30003010s mm l a ABn B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + aB3B2k + aB3B2τ大小 ω32LBC ? ω12LAB 2ω3VB3B2 ? 方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BCn B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取作速度多边mms mm a 2/50=μ形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度aD 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即BE eb CEeCBb 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mm e 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
习题及答案(第七、八章)

7-1 已知物体的主、俯、左视图,画出物体的其他三个基本视图。
班 级姓 名学 号审 阅457-1 已知物体的主、俯、左视图,画出物体的其他三个基本视图。
45审 阅学 号姓 名班 级7-5 改正剖视图中的错误(将缺的线补上,在多余的线上打"×")。
(1)(2)(3)(4)(6)(5)(7)(8)班 级姓 名学 号审 阅47(5)(6)(7)(8)(4)(3)(2)(1)7-5 改正剖视图中的错误(将缺的线补上,在多余的线上打"×")。
47审 阅学 号姓 名班 级7-6 将机件的主视图改画成全剖视图。
(1)(2)班 级姓 名学 号审 阅487-6 将机件的主视图改画成全剖视图。
(1)(2)48班 级学 号审 阅姓 名7-7 求作主视图。
7-8 完成主视图(取半剖视),并求作左视图(取全剖视)。
(1)(2)姓 名学 号审 阅49班 级(2)(1)7-7 求作主视图。
49审 阅学 号姓 名班 级7-8 完成主视图(取半剖视),并求作左视图(取全剖视)。
7-9 求主视图改成半剖视图。
(1)(2)班 级姓 名学 号审 阅50(2)(1)7-9 求主视图改成半剖视图。
50审 阅学 号姓 名班 级7-9 求主视图改成半剖视图。
(3)班 级姓 名学 号审 阅51(3)7-9 求主视图改成半剖视图。
51审 阅学 号姓 名班 级7-10 对照立体图,在主视图上作全剖视,在俯、左视图上作半剖视。
班 级姓 名学 号审 阅527-10 对照立体图,在主视图上作全剖视,在俯、左视图上作半剖视。
52审 阅学 号姓 名班 级班 级姓 名学 号审 阅53第七章 机件的表达方法7-11 指出下列局部剖视图中的错误,并将(1)、(2)题在右面画出正确图形。
(1)(2)(4)(3)(3)(4)(2)(1)7-11 指出下列局部剖视图中的错误,并将(1)、(2)题在右面画出正确图形。
人教版高中数学必修二《第七章 复数》课后作业及答案解析

人教版高中数学必修二《第七章 复数》课后作业《7.1.1 数系的扩充和复数的概念》课后作业基础巩固1.复数2i -的虚部为( ) A .2B .1C .-1D .-i2.适合2()x i x y i -=+的实数x ,y 的值为( ) A .0x =,2y = B .0x =,2y =- C .2x =,2y =D .2x =,0y =3.设i 是虚数单位,如果复数()()17a a i ++-+的实部与虚部相等,那么实数a 的值为( )A .4B .3C .2D .14.若2(1)z a a i =+-,a R ∈(i 为虚数单位)为实数,则a 的值为( ) A .0B .1C .1-D .1或1-5.下列命题中,正确命题的个数是( )①若x ,y ∈C ,则x +yi =1+i 的充要条件是x =y =1; ②若a ,b ∈R 且a >b ,则a +i >b +i ; ③若x 2+y 2=0,则x =y =0. A .0 B .1 C .2 D .36.以复数3i 3-的实部为虚部的复数是________. 7.若x 是实数,y 是纯虚数,且()212i x y -+=,则x ,y 的值为______. 8.(1)已知21(2)0x y y i -++-=,其中i 为虚数单位,求实数x ,y 的值; (2)已知()(1)(23)(21)x y y i x y y i ++-=+++,其中i 为虚数单位,求实数x 、y 的值.能力提升9.若复数()234sin 12cos z i θθ=-++为纯虚数,()0,θπ∈,则θ=( )A .6π B .3π C .23π D .3π或23π 10.若不等式()2222i 9i m m m m m---<+成立,则实数m 的值为______. 11.已知复数()()2123i z m m m m =-++-,当实数m 取什么值时,(1)复数z 是零; (2)复数z 是实数; (3)复数z 是纯虚数.素养达成12.已知复数()2227656 ()1a a z a a i a R a -+=+--∈-,实数a 取什么值时,z 是:①实数?②虚数?③纯虚数?《7.1.1 数系的扩充和复数的概念》课后作业答案解析基础巩固1.复数2i -的虚部为( ) A .2 B .1C .-1D .-i【答案】C【解析】复数2i -的虚部为-1,故选C .2.适合2()x i x y i -=+的实数x ,y 的值为( ) A .0x =,2y = B .0x =,2y =- C .2x =,2y = D .2x =,0y =【答案】B【解析】由题意得:02x x y =⎧⎨+=-⎩,解得:02x y =⎧⎨=-⎩故选:B3.设i 是虚数单位,如果复数()()17a a i ++-+的实部与虚部相等,那么实数a 的值为( )A .4B .3C .2D .1【答案】B【解析】由题意得17,3a a a +=-=,选B.4.若2(1)z a a i =+-,a R ∈(i 为虚数单位)为实数,则a 的值为( )A .0B .1C .1-D .1或1-【答案】D【解析】若()21z a a i =+-,a R ∈(i 为虚数单位)为实数,则210, 1.a a -=∴=±本题选择D 选项.5.下列命题中,正确命题的个数是( ) ①若,,则的充要条件是;②若,且,则;③若,则.A .B .C .D . 【答案】A【解析】对①,由于x ,y ∈C ,所以x ,y 不一定是x +yi 的实部和虚部,故①是假命题;对②,由于两个虚数不能比较大小,故②是假命题;③是假命题,如12+i 2=0,但1≠0,i≠0.6.以复数32i 32i -的实部为虚部的复数是________. 【答案】33i -. 【解析】32i -的虚部为3,32i -的实部为3- ∴所求复数为33i -故答案为:33i -7.若x 是实数,y 是纯虚数,且()212i x y -+=,则x ,y 的值为______.【答案】12x =,2i y = 【解析】由()212i x y -+=,得210,2i ,x y -=⎧⎨=⎩解得12x =,2i y =.故答案为:12x =,2i y =. 8.(1)已知21(2)0x y y i -++-=,其中i 为虚数单位,求实数x ,y 的值; (2)已知()(1)(23)(21)x y y i x y y i ++-=+++,其中i 为虚数单位,求实数x 、y 的值.【答案】(1)122x y ⎧=⎪⎨⎪=⎩;(2)42x y =⎧⎨=-⎩ 【解析】(1)()2120x y y i -++-= 21020x y y -+=⎧∴⎨-=⎩,解得:122x y ⎧=⎪⎨⎪=⎩(2)由()()()()12321x y y i x y y i ++-=+++得:23121x y x y y y +=+⎧⎨-=+⎩,解得:42x y =⎧⎨=-⎩能力提升9.若复数()234sin 12cos z i θθ=-++为纯虚数,()0,θπ∈,则θ=( )A .6πB .3π C .23π D .3π或23π 【答案】B【解析】若复数()23412z sin cos i θθ=-++为纯虚数,则:234sin 012cos 0θθ⎧-=⎨+≠⎩,即:23sin 41cos 2θθ⎧=⎪⎪⎨⎪≠-⎪⎩, 结合()0,θπ∈,可知:sin 21cos 2θθ⎧=⎪⎪⎨⎪=⎪⎩,故3πθ=.10.若不等式()2222i 9i m m m m m---<+成立,则实数m 的值为______. 【答案】2【解析】依题意可得2220209m m m m m ⎧-=⎪-⎪=⎨⎪<⎪⎩,即0? 22033m m m m =⎧⎪=≠⎨⎪-<<⎩或且,解得2m =.故答案为:2. 11.已知复数()()2123i z m m m m =-++-,当实数m 取什么值时,(1)复数z 是零; (2)复数z 是实数; (3)复数z 是纯虚数.【答案】(1)1m =(2)1m =或3m =-(3)0m = 【解析】(1)若复数z 是零,则()210230m m m m ⎧-=⎨+-=⎩,解得1m =,即当1m =时,复数z 是零.(2)若复数z 是实数,则2230m m +-=,解得1m =或3m =-, 即当1m =或3m =-时,复数z 是实数. (3)若复数z 是纯虚数,则()210230m m m m ⎧-=⎨+-≠⎩,解得0m =,即当0m =时,复数z 是纯虚数.素养达成12.已知复数()2227656 ()1a a z a a i a R a -+=+--∈-,实数a 取什么值时,z 是:①实数?②虚数?③纯虚数?【答案】①6a =;②1a ≠±且6a ≠;③无解.【解析】()2227656 ()1a a z a a i a R a -+=+--∈- ①若复数z 是实数,则22560,10,a a a ⎧--=⎨-≠⎩即16,1,a a a =-=⎧⎨≠±⎩或即6a =.②若复数z 是虚数,则22560,10,a a a ⎧--≠⎨-≠⎩即16,1,a a a ≠-≠⎧⎨≠±⎩且即1a ≠±且6a ≠.③若复数z 是纯虚数,则222560,760,10,a a a a a ⎧--≠⎪-+=⎨⎪-≠⎩即16161a a a a a ≠-≠⎧⎪==⎨⎪≠±⎩且,且,,此时无解.《7.1.2 复数的几何意义》课后作业基础巩固1.在复平面内,复数-2+3i 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限2.设O 是原点,向量OA →,OB →对应的复数分别为2-3i ,-3+2i ,那么向量BA →对应的复数是( )A .-5+5iB .-5-5iC .5+5iD .5-5i3.如果z 是34i +的共轭复数,则z 对应的向量OA 的模是( ) A .1BCD .54.在复平面内,复数6+5i ,-2+3i 对应的点分别为A ,B ,若C 为线段AB 的中点,则点C 对应的复数是( )A .4+8iB .8+2iC .2+4iD .4+i5.已知0<a <2,复数z =a +i(i 是虚数单位),则|z |的取值范围是( ) A .(1,3) B .(1,5) C .(1,3)D .(1,5)6.已知复数z 1=a +i ,z 2=2-i ,且|z 1|=|z 2|,则实数a =________.7.复数3-5i,1-i 和-2+a i 在复平面上对应的点在同一条直线上,则实数a 的值为________.8.若复数z =(m 2+m -2)+(4m 2-8m +3)i(m ∈R)的共轭复数z 对应的点在第一象限,求实数m 的集合.能力提升9.已知复数z 的模为2,则|z -i|的最大值为( ) A .1 B .2 C. 5D .310.若复数z =(m 2-9)+(m 2+2m -3)i 是纯虚数,其中m ∈R ,则|z |=________. 11.已知复数z 1=3+i ,z 2=-12+32i.(1)求|z 1|及|z 2|并比较大小;(2)设z ∈C ,满足条件|z 2|≤|z |≤|z 1|的点Z 的轨迹是什么图形?素养达成12.设复数z =log 2(m 2-3m -3)+ilog 2(m -2),m ∈R 对应的向量为OZ →. (1)若OZ →的终点Z 在虚轴上,求实数m 的值及|OZ →|; (2)若OZ →的终点Z 在第二象限内,求m 的取值范围.《7.1.2 复数的几何意义》课后作业答案解析基础巩固1.在复平面内,复数-2+3i 对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限【答案】B【解析】复数-2+3i 在复平面内对应的点为(-2,3),故复数-2+3i 对应的点位于第二象限.2.设O 是原点,向量OA →,OB →对应的复数分别为2-3i ,-3+2i ,那么向量BA →对应的复数是( )A .-5+5iB .-5-5iC .5+5iD .5-5i【答案】D【解析】 由复数的几何意义,得OA →=(2,-3),OB →=(-3,2),BA →=OA →-OB →=(2,-3)-(-3,2)=(5,-5).所以BA →对应的复数是5-5i.3.如果z 是34i +的共轭复数,则z 对应的向量OA 的模是( )A .1BCD .5【答案】D【解析】由题意,34z i =-,∴z 对应的向量OA 的坐标为()3,4-5=.故选:D .4.在复平面内,复数6+5i ,-2+3i 对应的点分别为A ,B ,若C 为线段AB 的中点,则点C 对应的复数是( )A .4+8iB .8+2iC .2+4iD .4+i【答案】C【解析】 复数6+5i 对应的点为A (6,5),复数-2+3i 对应的点为B (-2,3).利用中点坐标公式得线段AB 的中点C (2,4),故点C 对应的复数为2+4i.5.已知0<a <2,复数z =a +i(i 是虚数单位),则|z |的取值范围是( ) A .(1,3) B .(1,5) C .(1,3) D .(1,5)【答案】B【解析】 |z |=a 2+1,∵0<a <2,∴1<a 2+1<5,∴|z |∈(1,5). 6.已知复数z 1=a +i ,z 2=2-i ,且|z 1|=|z 2|,则实数a =________. 【答案】±2【解析】依题意,a 2+1=4+1,∴a =±2.7.复数3-5i,1-i 和-2+a i 在复平面上对应的点在同一条直线上,则实数a 的值为________.【答案】5【解析】由点(3,-5),(1,-1),(-2,a )共线可知a =5.8.若复数z =(m 2+m -2)+(4m 2-8m +3)i(m ∈R)的共轭复数z 对应的点在第一象限,求实数m 的集合.【答案】m 的集合为⎩⎨⎧m ⎪⎪⎪⎭⎬⎫1<m <32.【解析】由题意得z =(m 2+m -2)-(4m 2-8m +3)i ,z 对应的点位于第一象限,所以有⎩⎪⎨⎪⎧m 2+m -2>0,-(4m 2-8m +3)>0,所以⎩⎪⎨⎪⎧m 2+m -2>0,4m 2-8m +3<0,所以⎩⎪⎨⎪⎧m <-2或m >1,12<m <32,即1<m <32,故所求m 的集合为⎩⎨⎧m ⎪⎪⎪⎭⎬⎫1<m <32.能力提升9.已知复数z 的模为2,则|z -i|的最大值为( ) A .1 B .2 C. 5 D .3【答案】D【解析】 ∵|z |=2,∴复数z 对应的轨迹是以原点为圆心,2为半径的圆,而|z -i|表示圆上一点到点(0,1)的距离,∴|z -i|的最大值为圆上点(0,-2)到点(0,1)的距离,易知此距离为3,故选D.10.若复数z =(m 2-9)+(m 2+2m -3)i 是纯虚数,其中m ∈R ,则|z |=________. 【答案】12【解析】由条件知⎩⎪⎨⎪⎧m 2+2m -3≠0,m 2-9=0,∴m =3,∴z =12i ,∴|z |=12.11.已知复数z 1=3+i ,z 2=-12+32i.(1)求|z 1|及|z 2|并比较大小;(2)设z ∈C ,满足条件|z 2|≤|z |≤|z 1|的点Z 的轨迹是什么图形? 【答案】(1)|z 1|>|z 2|. (2)见解析 【解析】(1)|z 1|= (3)2+12=2,|z 2|=⎝ ⎛⎭⎪⎫-122+322=1,∴|z 1|>|z 2|. (2)由|z 2|≤|z |≤|z 1|及(1)知1≤|z |≤2.因为|z |的几何意义就是复数z 对应的点到原点的距离,所以|z |≥1表示|z |=1所表示的圆外部所有点组成的集合,|z |≤2表示|z |=2所表示的圆内部所有点组成的集合,故符合题设条件点的集合是以O 为圆心,以1和2为半径的两圆之间的圆环(包含圆周),如图所示.素养达成12.设复数z =log 2(m 2-3m -3)+ilog 2(m -2),m ∈R 对应的向量为OZ →. (1)若OZ →的终点Z 在虚轴上,求实数m 的值及|OZ →|; (2)若OZ →的终点Z 在第二象限内,求m 的取值范围.【答案】(1)m =4,|OZ →|=1. (2)m ∈⎝ ⎛⎭⎪⎫3+212,4.【解析】(1)log 2(m 2-3m -3)=0,所以m 2-3m -3=1. 所以m =4或m =-1;因为⎩⎪⎨⎪⎧m 2-3m -3>0,m -2>0,所以m =4,此时z =i ,OZ →=(0,1),|OZ →|=1.(2)⎩⎪⎨⎪⎧log 2(m 2-3m -3)<0,log 2(m -2)>0,m 2-3m -3>0,m -2>0,所以m ∈⎝ ⎛⎭⎪⎫3+212,4.《7.2.1 复数的加、减法运算及其几何意义》课后作业基础巩固1.计算(3)(2)i i +-+的结果为( ) A .52i +B .i -C .1D .1- i2.若5634z i i +-=+,则复数z 的值为( ) A .210i -+B .15i -+C .410i -+D .110i -+3.34i z =-,则复数()1i z z -+-在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限4.在平行四边形ABCD 中,对角线AC 与BD 相交于点O,若向量OA ,OB 对应的复数分别是3+i,-1+3i,则CD 对应的复数是 ( )A .2+4iB .-2+4iC .-4+2iD .4-2i5.已知i 为虚数单位,实数x ,y 满足1z y xi =+,2z yi x =-,且122z z -=,则xy 的值是( )A .1B .2C .2-D .1-6.复平面内122,3z i z i =+=-两个复数122,3z i z i =+=-对应的两点之间的距离为_______.7.复数65i +与34i -+分别表示向量OA 与OB ,则表示向量BA 的复数为_________. 8.已知i 为虚数单位,计算: (1)(12)(34)(56)i i i ++--+;(2)5[(34)(13)]i i i -+--+; (3)()(23)3(,)a bi a bi i a b R +---∈.能力提升9.设f(z)=|z|,z 1=3+4i,z 2=-2-i,则f(z 1-z 2)= ( )A B .CD .10.已知复数12z ai =+,()2z a i a R =+∈,且复数12z z -在复平面内对应的点位于第二象限,则a 的取值范围是________.11.如图所示,平行四边形OABC ,顶点O ,A ,C 分别表示0,3+2i ,-2+4i ,试求:(1) ,AO BC 所表示的复数; (2)对角线CA 所表示的复数; (3)B 点对应的复数.素养达成12.已知平行四边形OABC 的三个顶点O A C ,,对应的复数为032i -24i ++,,. (1)求点B 所对应的复数0z ;(2)若01z z -=,求复数z 所对应的点的轨迹.《7.2.1 复数的加、减法运算及其几何意义》课后作业答案解析基础巩固1.计算(3)(2)i i +-+的结果为( ) A .52i + B .i -C .1D .1- i【答案】C【解析】由题得()()32i i +-+=3+i-2-i=1.故选C 2.若5634z i i +-=+,则复数z 的值为( ) A .210i -+ B .15i -+C .410i -+D .110i -+【答案】A【解析】∵5634z i i +-=+,∴()3456210z i i i =+--=-+,故选:A 3.34i z =-,则复数()1i z z -+-在复平面内对应的点在( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】C 【解析】34i z =-,5z ∴=,∴()1i 34i 51i 15i z z -+-=--+-=--,∴复数()1i z z -+-在复平面内对应的点为()1,5--,在第三象限.故选:C.4.在平行四边形ABCD 中,对角线AC 与BD 相交于点O,若向量OA ,OB 对应的复数分别是3+i,-1+3i,则CD 对应的复数是 ( )A .2+4iB .-2+4iC .-4+2iD .4-2i【答案】D【解析】 由题意可得,在平行四边形中CD BA OA OB ==-, 则(3)(13)42i i i +--+=-,所以CD 对应的复数为42i -,故选D .5.已知i 为虚数单位,实数x ,y 满足1z y xi =+,2z yi x =-,且122z z -=,则xy 的值是( )A .1B .2C .2-D .1-【答案】A【解析】12()()i 2z z y x x y -=++-=,即2,0,x y x y +=⎧⎨-=⎩1x y ∴==,1xy ∴=.故选:A6.复平面内122,3z i z i =+=-两个复数122,3z i z i =+=-对应的两点之间的距离为_______.【解析】21|12|d z z i =-=-==7.复数65i +与34i -+分别表示向量OA 与OB ,则表示向量BA 的复数为_________. 【答案】9i + 【解析】BA OA OB =-,所以,表示向量BA 的复数为()()65349i i i +--+=+.故答案为:9i +.8.已知i 为虚数单位,计算: (1)(12)(34)(56)i i i ++--+; (2)5[(34)(13)]i i i -+--+; (3)()(23)3(,)a bi a bi i a b R +---∈.【答案】(1)18i --;(2)44i -+;(3)(43)a b i -+-【解析】(1)(12)(34)(56)(42i)(56)18i i i i i ++--+=--+=--. (2)5[(34)(13)]5(4)44i i i i i i -+--+=-+=-+.(3)()(23)3(2)[(3)3](43)a bi a bi i a a b b i a b i +---=-+---=-+-能力提升9.设f(z)=|z|,z 1=3+4i,z 2=-2-i,则f(z 1-z 2)= ( )A B .C D .【答案】D【解析】 由题意得1255z z i -=+,所以12()(55)55f z z f i i -=+=+==故选D .10.已知复数12z ai =+,()2z a i a R =+∈,且复数12z z -在复平面内对应的点位于第二象限,则a 的取值范围是________.【答案】(2,)+∞【解析】由题得12z z -=(2-a )+(a-1)i ,因为复数12z z -在复平面内对应的点位于第二象限,所以20,210a a a -<⎧∴>⎨->⎩.故答案为(2,)+∞ 11.如图所示,平行四边形OABC ,顶点O ,A ,C 分别表示0,3+2i ,-2+4i ,试求:(1) ,AO BC 所表示的复数; (2)对角线CA 所表示的复数; (3)B 点对应的复数.【答案】(1) -3-2i (2) 5-2i (3) 1+6i【解析】(1) AO OA =-,所以AO 所表示的复数为-3-2i . 因为BC AO =,所以BC 所表示的复数为-3-2i .(2) CA OA OC =-,所以CA 所表示的复数为(3+2i )-(-2+4i )=5-2i . (3) OB OA OC =+,所以OB 所表示的复数为(3+2i )+(-2+4i )=1+6i , 即B 点对应的复数为1+6i .素养达成12.已知平行四边形OABC 的三个顶点O A C ,,对应的复数为032i -24i ++,,. (1)求点B 所对应的复数0z ;(2)若01z z -=,求复数z 所对应的点的轨迹.【答案】(1)016z i =+;(2)复数z 对应点的轨迹为以1,6B ()为圆心,1为半径的圆【解析】(1)由已知得(3,2),(2,4)OA OC ==-, ∴(1,6)OB OA OC =+=, ∴点B 对应的复数016z i =+. (2)设复数z 所对应的点Z , ∵01z z -=,∴点Z 到点()1,6B 的距离为1,∴复数z 所对应的点Z 的轨迹为以()1,6B 为圆心,1为半径的圆, 且其方程为()()22161x y -+-=.《7.2.2 复数的乘除运算》课后作业基础巩固1.已知复数z =2+i ,则z z ⋅=( )AB C .3D .52.设复数z 满足(1+i)z =2i ,则|z |=( )A .12B .2C D .23.若复数12az i i=+-(i 为虚数单位,a R ∈)的实部与虚部互为相反数,则a =( ) A .53-B .13- C .1- D .5-4.在复平面内,复数11i-的共轭复数对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限5.若为a 实数,且2i3i 1ia +=++,则a =( ) A .4-B .3-C .3D .46.已知复数(2i)(1i)a ++的实部为0,其中i 为虚数单位,则实数a 的值是_____. 7.设复数z 满足(23)64z i i -=+(其中i 为虚数单位),则z 的模为______. 8.计算:(1)(4)(62)(7)(43)i i i i -+--+; (2)32322323i ii i+-+-+; (3)(2)(1)(1)(1)i i i i i--+-+.能力提升9.设i 是虚数单位,复数1a ii-+为纯虚数,则实数a 的值为( ) A .1 B .1- C .12D .2-10.在复平面内,复数z 与52i-对应的点关于实轴对称,则z =______.11.在复数范围内解下列一元二次方程: (1)290x +=;(2)210x x -+=.素养达成12.古代以六十年为一个甲子用十天干和十二地支相配六十年轮一遍,周而复始。
毛概2013版课后作业答案

课后作业第一章马克思主义中国化两大理论成果1、马克思主义中国化的科学内涵和重要意义?P4科学内涵:第一,马克思主义中国化就是运用马克思主义解决中国革命、建设和改革的实际问题。
第二,马克思主义中国化就是把中国革命建设和改革的实践经验和历史经验提升为理论。
第三,马克思主义中国化就是把马克思主义植根于中国的优秀文化之中。
重要意义:第一,马克思主义中国化的理论成果指引着党和人民的伟大事业不断取得胜利。
第二,马克思主义中国化的理论成果提供了凝聚全党和全国各族人民的强大精神支柱。
第三,马克思主义中国化倡导和体现了对待马克思主义的科学态度和优良学风,不断开拓着马克思主义在中国发展的新境界。
2、如何理解马克思主义中国化两大理论成果的关系?P5-63、怎样把握毛泽东思想的主要内容和历史地位?P9-154、怎样把握中国特色社会主义理论体系的主要内容和历史地位?P18-235、如何理解马克思主义中国化两大理论成果的精髓?P29-30第二章新民主主义理论1、什么是新民主主义革命的总路线?P38;如何理解新民主主义革命的领导权问题? P41(2必然性,3条实现途径)2、新民主主义基本纲领的主要内容是什么?P44-463、如何认识中国革命走农村包围城市、武装夺取政权道路的必要性及重大意义?P48-494、如何理解新民主主义革命的三大法宝及其相互关系?统一战线:结成统一战线的2个必然性原因和3种可能性原因。
P49—50统一战线的内容(2个联盟)P50我党领导统一战线的经验P50武装斗争:武装斗争的必然性、依靠谁?谁领导?为了谁?怎样进行武装斗争?P51党的建设:P51-52三大法宝的相互关系:P53第三章社会主义改造理论1、为什么说新民主主义社会是一个过渡性的社会?P57,第二段2、怎样理解党在过渡时期的总路线?P58,最后一段3、我国社会主义改造的基本经验有哪些?P66-67,3条4、中国确立社会主义基本制度有着怎样的重大意义?P71—73,5条第四章社会主义建设道路初步探索的理论成果1、党在中国社会主义建设道路的初步探索中取得了哪些重要理论成果?P75-84调动一切积极因素为社会主义事业服务的思想正确认识和处理人民内部矛盾的思想走中国工业化道路的思想初步探索的其他成果:关于社会主义发展阶段;关于社会主义现代化的战略目标和步骤;关于经济建设方针;关于所有制结构;关于经制济体制和运行机制改革;关于社会主义民主政治建设;关于科学和教育;关于知识分子工作。
工程热力学课后作业答案(第七章)第五版

7-1当水的温度t=80℃,压力分别为0.01、0.05、0.1、0.5及1MPa时,各处于什么状态并求出该状态下的焓值。
解:查表知道t=80℃时饱和压力为0.047359MPa。
因此在0.01、0.05、0.1、0.5及1MPa时状态分别为过热、未饱和、未饱和,未饱和、未饱和。
焓值分别为2649.3kJ/kg,334.9 kJ/kg,335 kJ/kg,335.3 kJ/kg,335.7 kJ/kg。
7-2已知湿蒸汽的压力p=1MPa干度x=0.9。
试分别用水蒸气表和h-s图求出hx,vx,ux,sx。
解:查表得:h``=2777kJ/kg h`=762.6 kJ/kgv``=0.1943m3/kg v`=0.0011274 m3/kgu``= h``-pv``=2582.7 kJ/kg u`=h`-pv`=761.47 kJ/kgs``=6.5847 kJ/(kg.K)s`=2.1382 kJ/(kg.K)hx=xh``+(1-x)h`=2575.6 kJ/kgvx=xv``+(1-x)v`=0.1749 m3/kgux=xu``+(1-x)u`=2400 kJ/kgsx=xs``+(1-x)s`=6.14 kJ/(kg.K)7-3在V=60L的容器中装有湿饱和蒸汽,经测定其温度t=210℃,干饱和蒸汽的含量mv=0.57kg,试求此湿蒸汽的干度、比容及焓值。
解:t=210℃的饱和汽和饱和水的比容分别为:v``=0.10422m3/kg v`=0.0011726 m3/kgh``=2796.4kJ/kg h`=897.8 kJ/kg湿饱和蒸汽的质量:解之得:x=0.53比容:vx=xv``+(1-x)v`=0.0558 m3/kg焓:hx=xh``+(1-x)h`=1904kJ/kg7-4将2kg水盛于容积为0.2m3的抽空了的密闭刚性容器中,然后加热至200℃试求容器中(1)压力;(2)焓;(3)蒸汽的质量和体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《心理学》课后作业活页
学院专业班级
姓名学号成绩
第七章品德的发展与教育
第八章心理健康与教育
一、单项选择题。
1.张梅能用规则来约束自己的行为,认为规则是绝对的,是不可变更的,并表现出对规则的服从。
根据皮亚杰的道德认知发展理论,张梅的道德发展水平处于。
( B )
A.自我中心阶段
B.权威阶段
C.可逆阶段
D.公正阶段
2.晓旭认为,服从听话的孩子就是好孩子,对老师和家长绝对遵从,希望得到他们的赞许,根据科尔伯格的道德发展理论,他的道德发展处于。
( C )
A.社会契约阶段
B.相对功利阶段
C.寻求认可阶段
D.遵守法规阶段
3.某中学在“每月一星”的活动中,将表现好、进步快的学生照片贴在“明星墙”上以示奖励,并号召大家向他们学习。
这种做法体现出的德育方法是。
( D)
A.有效的说服
B.群体约定
C.价值辨析
D.良好的榜样
4.上学路上,徐燕看到一位同学正艰难地推着一位坐轮椅的老人上斜坡路,她非常感动。
这种道德情感属于。
( B )
A.动作性道德情感体验
B.形象性道德情感体验
C.想象性道德情感体验
D.伦理性道德情感体验
5.一般来说,学生道德的心理结构的发展遵循一定的认识规律,即由个别到一般,由具体到。
