专题07 三角函数(单选 多选)-2022-2023学年高一上学期期末数学试题分类汇编
2023-2024学年高一上数学《三角函数》测试卷及答案解析

2023-2024学年高一数学《三角函数》一.选择题(共12小题)1.(2022•鼓楼区校级三模)若,且,则=()A.B.C.2D.−2 2.(2022•鼓楼区校级模拟)已知角θ的大小如图所示,则=()A.﹣5B.5C.D.3.(2022•福州模拟)某智能主动降噪耳机工作的原理是利用芯片生成与噪音的相位相反的声波,通过两者叠加完全抵消掉噪音(如图).已知噪音的声波曲线y=A sin(ax+p)(其中A>0,a>0,0≤φ<2π)的振幅为1,周期为π,初相为,则用来降噪的声波曲线的解析式为()A.y=sin2x B.y=cos2x C.y=﹣sin2x D.y=﹣cos2x 4.(2022春•福州期中)已知α为锐角,且sin(α﹣)=,则cos(﹣α)=()A.B.﹣C.D.﹣5.(2022•鼓楼区校级三模)已知函数的图象过点,现将y=f(x)的图象向左平移个单位长度得到的函数图象也过点P,则()A.ω的最小值为2B.ω的最小值为6C.ω的最大值为2D.ω的最大值为66.(2021秋•鼓楼区校级期末)已知角α的终边在射线y=﹣2x(x≥0)上,则2sinα+cosα的值为()A.B.C.﹣D.﹣7.(2021秋•鼓楼区校级期末)函数f(x)的部分图象如图所示,则f(x)可能是()A.B.C.D.8.(2021秋•福州期末)已知函数f(x)=sin(ωx﹣φ)的部分图象如图所示,则f(x)的单调递增区间为()A.B.C.D.9.(2021秋•仓山区校级期末)与﹣2022°终边相同的最小正角是()A.138°B.132°C.58°D.42°10.(2022春•马尾区校级月考)已知弧长为的弧所对的圆心角为,则该弧所在的扇形面积为()A.B.C.D.11.(2021秋•鼓楼区校级期末)已知,tanα=3,,则tan(α﹣β)=()A.B.C.2D.12.(2021秋•鼓楼区校级期末)下列函数中,周期为π的是()A.y=B.y=tan2xC.y=sin x cos x D.y=sin|x|二.填空题(共4小题)13.(2022•福州模拟)已知2sin(α﹣)=cosα,则tanα=.14.(2022春•福州期中)如图,半圆O的半径为1,A为直径所在直线上的一点,且OA=,B为半圆弧上的动点.将线段AB绕点A顺时针旋转得到线段AC,则线段OC 长度的最大值是.15.(2022春•仓山区校级期中)在平面直角坐标系中,O(0,0),P(8,6),将向量OP按顺时针方向旋转后,得向量,则点Q的坐标是.16.(2021秋•福州期末)函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图像如图所示,BC∥x轴,则ω=,φ=.三.解答题(共5小题)17.(2021秋•福州期末)已知角α的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边过点P(,).(1)求cos(α+π)的值;(2)若tanβ=﹣2,求tan(α﹣β)的值.18.(2021秋•鼓楼区校级期末)已知角α的顶点为坐标原点,始边为x轴的非负半轴,终边经过点P(1,﹣m﹣1),且cos.(1)求实数m的值;(2)若m>0,求的值.19.(2021秋•鼓楼区校级期末)设函数.(1)求f(x)的单调增区间;(2)求f(x)在[0,π]上的最大值与最小值.20.(2021秋•福州期末)已知函数f(x)=.(1)求f(x)的最小正周期;(2)将y=f(x)的图象上的各点______得到y=g(x)的图象,当x∈时,方程g(x)=m有解,求实数m的取值范围.在以下①、②中选择一个,补在(2)中的横线上,并加以解答,如果①、②都做,则按①给分.①向左平移个单位,再保持纵坐标不变,横坐标缩短到原来的一半.②纵坐标保持不变,横坐标伸长到原来的2倍,再向右平移个单位.21.(2021秋•仓山区校级期末)在①f(x)是偶函数;②(,0)是f(x)的图象在y轴右侧的第一个对称中心;③f(x)相邻两条对称轴之间距离为.这三个条件中任选两个,补充在下面问题的横线上,并解答.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),满足_____.(1)求函数f(x)的解析式;(2)将函数y=f(x)的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标变为原来的2倍后所得到的图象对应的函数记作y=g(x);若函数F(x)=f(x)+k•g(x)在(0,nπ)内恰有2021个零点,求实数k与正整数n的值.2023-2024学年高一数学《三角函数》参考答案与试题解析一.选择题(共12小题)1.(2022•鼓楼区校级三模)若,且,则=()A.B.C.2D.−2【考点】两角和与差的三角函数.【专题】计算题;方程思想;综合法;三角函数的求值;数学运算.【分析】由已知可得=﹣,可求tan=﹣3,进而可求值.【解答】解:,可得=﹣,所以=﹣,解得tan=﹣3或tan=﹣,又,∴∈(,),∴tan=﹣3,故==﹣2.故选:D.【点评】本题考查二倍角的正弦公式,属中档题.2.(2022•鼓楼区校级模拟)已知角θ的大小如图所示,则=()A.﹣5B.5C.D.【考点】二倍角的三角函数.【专题】函数思想;定义法;三角函数的求值;数学运算.【分析】由已知求得tan()=﹣5,得到,再由倍角公式及同角三角函数基本关系式化弦为切求解.【解答】解:∵θ+的终边过P(﹣1,5),∴tan()=﹣5,即,∴,∴====.故选:A.【点评】本题考查任意角的三角函数的定义,考查倍角公式及同角三角函数基本关系式的应用,是基础题.3.(2022•福州模拟)某智能主动降噪耳机工作的原理是利用芯片生成与噪音的相位相反的声波,通过两者叠加完全抵消掉噪音(如图).已知噪音的声波曲线y=A sin(ax+p)(其中A>0,a>0,0≤φ<2π)的振幅为1,周期为π,初相为,则用来降噪的声波曲线的解析式为()A.y=sin2x B.y=cos2x C.y=﹣sin2x D.y=﹣cos2x【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】数形结合;综合法;三角函数的图象与性质;数学运算.【分析】由已知可得A=1,T=π,p=,由此即可求出a的值,由此即可求解.【解答】解:由已知可得A=1,T=π,p=,则a=2,所以y=﹣sin(2x+)=﹣cos2x,故选:D.【点评】本题考查了三角函数的图象及其求解解析式问题,考查了学生的运算能力,属于基础题.4.(2022春•福州期中)已知α为锐角,且sin(α﹣)=,则cos(﹣α)=()A.B.﹣C.D.﹣【考点】两角和与差的三角函数.【专题】转化思想;综合法;三角函数的图象与性质;数学运算.【分析】由题意,利用同角三角函数的基本关系、诱导公式,求得cos(﹣α)的值.【解答】解:∵α为锐角,且sin(α﹣)=,∴α﹣为锐角,cos(α﹣)==,则cos(﹣α)=cos(α﹣)=,故选:C.【点评】本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.5.(2022•鼓楼区校级三模)已知函数的图象过点,现将y=f(x)的图象向左平移个单位长度得到的函数图象也过点P,则()A.ω的最小值为2B.ω的最小值为6C.ω的最大值为2D.ω的最大值为6【考点】函数y=Asin(ωx+φ)的图象变换.【专题】计算题;转化思想;综合法;三角函数的求值;三角函数的图象与性质;逻辑推理;数学运算.【分析】直接利用函数的图象的平移变换的应用求出结果.【解答】解:函数的图象过点,所以f(0)=sinφ=,故φ=;当函数f(x)的图象向左平移个单位,得到,由于函数的图象经过点(0,);所以,故ω的最小值为2.故选:A.【点评】本题考查的知识要点:三角函数关系式的变换,函数的图象的平移变换,主要考查学生的运算能力和数学思维能力,属于基础题.6.(2021秋•鼓楼区校级期末)已知角α的终边在射线y=﹣2x(x≥0)上,则2sinα+cosα的值为()A.B.C.﹣D.﹣【考点】任意角的三角函数的定义.【专题】函数思想;定义法;三角函数的求值;数学运算.【分析】由已知可得α为第四象限角,且,结合平方关系求解sinα与cosα的值,则答案可求.【解答】解:∵角α的终边在射线y=﹣2x(x≥0)上,∴α为第四象限角,由,解得sinα=,cosα=,∴2sinα+cosα=,故选:D.【点评】本题考查三角函数的化简求值,考查任意角的三角函数的定义,是基础题.7.(2021秋•鼓楼区校级期末)函数f(x)的部分图象如图所示,则f(x)可能是()A.B.C.D.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】数形结合;数形结合法;三角函数的图象与性质;数学抽象.【分析】根据函数f(x)=A sin(ωx+φ)的部分图象,求出A、T和ω、φ的值.【解答】解:设函数f(x)=A sin(ωx+φ),由f(x)的部分图象知,A=2,=﹣=,解得T=π,所以ω==2,又函数的图象过点(,2),即2×+φ=+2kπ,k∈Z,解得φ=﹣+2kπ,k∈Z,令k=0,得φ=﹣,所以f(x)=2sin(2x﹣).故选:A.【点评】本题考查了函数f(x)=A sin(ωx+φ)的图象与性质的应用问题,是基础题.8.(2021秋•福州期末)已知函数f(x)=sin(ωx﹣φ)的部分图象如图所示,则f(x)的单调递增区间为()A.B.C.D.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式;正弦函数的单调性.【专题】计算题;方程思想;综合法;三角函数的图象与性质;数学运算.【分析】由图可得T=2,可求ω,又函数过点(,1),可求φ,从而可求函数解析式,可求单调递增区间.【解答】解:由图形可知=﹣=1,所以T=2,所以=2,所以ω=π,所以f(x)=sin(πx﹣φ),又函数f(x)过点(,1),所以sin(﹣φ)=1,所以﹣φ=+2kπ,k∈Z,所以φ=﹣2kπ,所以f(x)=sin(πx﹣),由2kπ﹣≤πx﹣≤2kπ+,可得2k﹣≤x≤2k+,k∈Z,所以f(x)的单调递增区间为[2k﹣,2k+],k∈Z,故选:D.【点评】本题考查由函数图象求解析式,求单调递增区间,属基础题.9.(2021秋•仓山区校级期末)与﹣2022°终边相同的最小正角是()A.138°B.132°C.58°D.42°【考点】终边相同的角.【专题】计算题;转化思想;综合法;三角函数的求值;数学运算.【分析】利用终边相同的角的定义得到α=﹣2022°+k•360°,k∈Z,然后令﹣2022°+k•360°>0,求出k的值,代入求出此时的α即可.【解答】解:与﹣2022°终边相同的角为α=﹣2022°+k•360°,k∈Z,由题意﹣2022°+k•360°>0,解得k>5.61,k∈Z,所以k的最小值为6,此时α=﹣2022°+6×360°=138°,故与﹣2020°终边相同的最小正角是138°.故选:A.【点评】本题考查了终边相同的角的应用,解题的关键是掌握终边相同角的表示,属于基础题.10.(2022春•马尾区校级月考)已知弧长为的弧所对的圆心角为,则该弧所在的扇形面积为()A.B.C.D.【考点】扇形面积公式.【专题】计算题;对应思想;综合法;三角函数的求值;数学运算.【分析】由已知利用弧长公式先求出圆半径,由此能求出这条弧所在的扇形面积.【解答】解:∵弧长为的弧所对的圆心角为,∴圆半径r==2,∴这条弧所在的扇形面积为S=lr=×2=.故选:B.【点评】本题考查扇形面积的求法,考查弧长公式、扇形面积等基础知识,考查运算求解能力,是基础题.11.(2021秋•鼓楼区校级期末)已知,tanα=3,,则tan(α﹣β)=()A.B.C.2D.【考点】两角和与差的三角函数.【专题】函数思想;分析法;三角函数的求值;数学运算.【分析】运用三角函数的同角公式,可得sin(α+β)的值,结合正切函数的两角差公式,分别求得tanβ、tan(α﹣β)的值,即可求解.【解答】解:∵tanα>0,,∴,,∵,∴,由三角函数的同角公式可得,=,∴tan(α+β)=,∵=,∴=,故选:B.【点评】本题考查两角和与差的三角函数,考查计算能力,需要学生熟练掌握公式,属于基础题.12.(2021秋•鼓楼区校级期末)下列函数中,周期为π的是()A.y=B.y=tan2xC.y=sin x cos x D.y=sin|x|【考点】三角函数的周期性.【专题】函数思想;分析法;三角函数的图象与性质;数学运算.【分析】根据三角函数的周期公式,即可得到结论.【解答】解:函数的周期,选项A,ω=1,,故A选项错误,选项B,ω=2,,故B选项错误,选项C,y=sin x cos x=,即ω=2,,故C选项正确,选项D,当x>0时,y=sin x,当x<0时,y=sin(﹣x)=﹣sin x,函数不是周期函数,故D选项错误,故选:C.【点评】本题主要考查三角函数的图象和性质,比较基础,属于基础题.二.填空题(共4小题)13.(2022•福州模拟)已知2sin(α﹣)=cosα,则tanα=1+.【考点】两角和与差的三角函数;同角三角函数间的基本关系.【专题】计算题;转化思想;转化法;三角函数的求值;数学运算.【分析】由已知利用两角差的正弦公式,同角三角函数基本关系式即可求解.【解答】解:因为2sin(α﹣)=cosα,所以2(sinα﹣cosα)=sinα﹣cosα=cosα,可得sinα=(1+)cosα,则tanα==1+.故答案为:1+.【点评】本题主要考查了两角差的正弦公式,同角三角函数基本关系式在三角函数化简求值中的应用,属于基础题.14.(2022春•福州期中)如图,半圆O的半径为1,A为直径所在直线上的一点,且OA=,B为半圆弧上的动点.将线段AB绕点A顺时针旋转得到线段AC,则线段OC 长度的最大值是3.【考点】三角函数的恒等变换及化简求值.【专题】计算题;函数思想;综合法;三角函数的图象与性质;数学运算.【分析】以O点为坐标原点,建立如图所示平面直角坐标系,设∠AOB=θ,则B(cosθ,sinθ),即可表示出C点坐标,从而得到,再根据向量模的坐标计算、三角恒等变换公式及正弦函数的性质计算可得.【解答】解:如图以O点为坐标原点,建立平面直角坐标系,设∠AOB=θ,则,则,过点C、B分别作CD⊥x轴、BE⊥x轴,交x轴于点D、E,显然△CAD与△ABE全等,所以CD=AE,AD=BE,从而得到,即,所以=,所以当,即时,,故答案为:3.【点评】本题考查了三角函数的性质,属于中档题.15.(2022春•仓山区校级期中)在平面直角坐标系中,O(0,0),P(8,6),将向量OP按顺时针方向旋转后,得向量,则点Q的坐标是(−,﹣7).【考点】弧长公式.【专题】计算题;对应思想;向量法;平面向量及应用;数学运算.【分析】由题意可设=(10cosθ,10sinθ),其中cosθ=,sinθ=,将向量按逆时针旋转后,得向量,由三角函数的公式即可求得点Q坐标.【解答】解:∵点O(0,0),P(8,6),∴=(8,6),故可设=(10cosθ,10sinθ),其中cosθ=,sinθ=,∵将向量按逆时针旋转后,得向量,设Q(x,y),则x=10cos(θ﹣)=10(cosθcos+sinθsin)=﹣,y=10sin(θ﹣)=10(sinθcos﹣cosθsin)=﹣7,∴点Q坐标是(−,﹣7)故答案为:(−,﹣7).【点评】本题考查平面向量的坐标运算,涉及三角函数公式的应用,属中档题.16.(2021秋•福州期末)函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的部分图像如图所示,BC∥x轴,则ω=2,φ=.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】计算题;数形结合;数形结合法;三角函数的图象与性质;数学运算.【分析】由周期求出ω,由五点法作图求出φ的值,即可得解.【解答】解:因为BC∥x轴,所以f(x)的图象的一条对称轴方程为x=(+)=,﹣==×,所以ω=2.由2×+φ=π+kπ,k∈Z,且0<φ<π,得φ=.故答案为2,.【点评】本题考查了由y=A sin(ωx+φ)的部分图象确定其解析式,考查了数形结合思想,属于基础题.三.解答题(共5小题)17.(2021秋•福州期末)已知角α的顶点与坐标原点重合,始边与x轴的非负半轴重合,终边过点P(,).(1)求cos(α+π)的值;(2)若tanβ=﹣2,求tan(α﹣β)的值.【考点】两角和与差的三角函数.【专题】计算题;转化思想;综合法;三角函数的求值;数学运算.【分析】角α的终边过点P(,),可求cosα,tanα,可求(1)(2)的值.【解答】解:角α的终边过点P(,).∴cosα=,tanα==,(1)cos(α+π)=﹣cosα=﹣;(2)tan(α﹣β)===﹣2.【点评】本题考查三角函数的定义,以及三角恒等变换,属基础题.18.(2021秋•鼓楼区校级期末)已知角α的顶点为坐标原点,始边为x轴的非负半轴,终边经过点P(1,﹣m﹣1),且cos.(1)求实数m的值;(2)若m>0,求的值.【考点】任意角的三角函数的定义.【专题】函数思想;定义法;三角函数的求值;数学运算.【分析】(1)由已知借助于余弦函数的定义列式求解m值;(2)由(1)可得sinα,cosα的值,结合三角函数的诱导公式可得的值.【解答】解:(1)由题意可得,∴,整理得(m+1)2=4,解得m=1或m=﹣3;(2)∵m>0,∴由(1)可得m=1,则,∴.【点评】本题考查任意角的三角函数的定义,考查诱导公式的应用,是基础题.19.(2021秋•鼓楼区校级期末)设函数.(1)求f(x)的单调增区间;(2)求f(x)在[0,π]上的最大值与最小值.【考点】三角函数的最值.【专题】整体思想;转化法;三角函数的求值;数学运算.【分析】(1)利用三角函数的恒等变换化简函数的解析式,再利用正弦函数的单调性求出函数的递增区间即可;(2)根据x的范围,求出x+的范围,求出函数的最大值和最小值即可.【解答】解:(1)==,令,得,所以f(x)的单调增区间为;(2)由x∈[0,π],得,所以当,即时,f(x)取最大值2;当,即x=π时,f(x)取最小值.【点评】本题主要考查三角函数的恒等变换,正弦函数的单调性,最值问题,是基础题.20.(2021秋•福州期末)已知函数f(x)=.(1)求f(x)的最小正周期;(2)将y=f(x)的图象上的各点______得到y=g(x)的图象,当x∈时,方程g(x)=m有解,求实数m的取值范围.在以下①、②中选择一个,补在(2)中的横线上,并加以解答,如果①、②都做,则按①给分.①向左平移个单位,再保持纵坐标不变,横坐标缩短到原来的一半.②纵坐标保持不变,横坐标伸长到原来的2倍,再向右平移个单位.【考点】函数y=Asin(ωx+φ)的图象变换;三角函数中的恒等变换应用;三角函数的周期性.【专题】转化思想;综合法;三角函数的图象与性质;数学运算.【分析】(1)由题意利用三角恒等变换化简f(x)的解析式,再利用正弦函数的周期性,得出结论.(2)由题意利用函数y=A sin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用余弦函数的定义域和值域,求得g(x)的范围,可得m的范围.【解答】解:(1)∵函数f(x)=sin2x+2cos2x+2=sin2x+2•+2=sin2x+cos2x+3=2sin(2x+)+3,故函数的周期为=π.(2)将f(x)=2sin(2x+)+3的图象按照变换①:向左平移个单位,再保持纵坐标不变,可得y=2sin(2x++)+3=2cos2x+3的图象,再横坐标缩小为原来的一半可得g(x)=2cos4x+3的图象,当x∈[,]时,4x∈[﹣,π],cos4x∈[﹣1,1],g(x)∈[1,5],若方程g(x)=m有解,则m∈[1,5].将f(x)=2sin(2x+)+3的图象按照变换②:纵坐标保持不变,横坐标伸长到原来的2倍,可得y=2sin(x+)+3的图象,再向右平移个单位,可得g(x)=2sin x+3的图象.当x∈[,]时,sin x∈[﹣,],g(x)∈[2,+3].若方程g(x)=m有解,则m∈[2,+3].【点评】本题主要考查三角恒等变换,函数y=A sin(ωx+φ)的图象变换规律,正弦函数的周期性,余弦函数的定义域和值域,属于中档题.21.(2021秋•仓山区校级期末)在①f(x)是偶函数;②(,0)是f(x)的图象在y轴右侧的第一个对称中心;③f(x)相邻两条对称轴之间距离为.这三个条件中任选两个,补充在下面问题的横线上,并解答.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),满足_____.(1)求函数f(x)的解析式;(2)将函数y=f(x)的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标变为原来的2倍后所得到的图象对应的函数记作y=g(x);若函数F(x)=f(x)+k•g(x)在(0,nπ)内恰有2021个零点,求实数k与正整数n的值.【考点】函数y=Asin(ωx+φ)的图象变换;由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】分类讨论;转化法;三角函数的图象与性质;数学运算.【分析】(1)根据三角函数的图象和性质,求出ω和φ的值即可,(2)根据函数图象变换关系,求出g(x)以及F(x)的解析式,根据函数零点性质建立方程进行讨论求解即可.【解答】解:(1)①f(x)是偶函数;②(,0)是f(x)的图象在y轴右侧的第一个对称中心;③f(x)相邻两条对称轴之间距离为.若选择①②,由①f(x)=sin(ωx+φ)是偶函数,∴φ=.即f(x)=sin(ωx+)=cosωx,由②(,0)是f(x)的图象在y轴右侧的第一个对称中心;则ω=,得ω=2,即f(x)=cos2x.选择①③:由①f(x)=sin(ωx+φ)是偶函数,∴φ=.即f(x)=sin(ωx+)=cosωx,由③知:f(x)相邻两条对称轴之间距离为.∴,即T=π,则=π,则ω=2,则f(x)=cos2x.若选②③:③知:f(x)相邻两条对称轴之间距离为.∴,即T=π,则=π,则ω=2,则f(x)=sin(2x+φ),由②(,0)是f(x)的图象在y轴右侧的第一个对称中心;∴2×+φ=π,得φ=,则f(x)=sin(2x+)=cos2x,综上f(x)=cos2x.(2)依题意,将函数y=f(x)的图象向右平移个单位,得y=cos2(x﹣)=cos (2x﹣)=sin2x,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的2倍得到y=sin x,可得g(x)=sin x,所以F(x)=cos2x+k sin x=﹣2sin2x+k sin x+1,当k=0时,F(x)=cos2x,则F(x)在(0,nπ)内的零点个数为偶数个,F(x)在(0,nπ)内恰有2021个零点,为奇数个零点,故k≠0,令F(x)=0,可得2sin2x﹣k sin x﹣1=0,令t=sin x∈[﹣1,1],则2t2﹣kt﹣1=0,Δ=k2+8>0,则关于t的二次方程2t2﹣kt﹣1=0必有两个不等的实根,t1,t2,且t1t2=﹣,则t1,t2异号,(i)当0<|t1|<1,且0<|t2|<1时,则方程sin x=t1和sin x=t2在区间(0,nπ)(n∈N*)均有偶数个根,从而2sin2x﹣k sin x﹣1=0在区间(0,nπ)(n∈N*)有偶数个根,不符合题意;(ii)当0<|t1|<1,且|t2|>1时,则方程sin x=t1在区间(0,nπ)有偶数个根,sin x=t2无解,从而方程2sin2x﹣k sin x﹣1=0在(0,nπ)有偶数个根,不合题意.同理,当0<|t2|<1且|t1|>1时,从而方程2sin2x﹣k sin x﹣1=0在(0,nπ)有偶数个根,不合题意.(iii)当t1=1,t2=﹣<0,当x∈(0,2π)时,sin x=t1只有一根,sin x=t2有两根,所以关于x的方程2sin2x﹣k sin x﹣1=0在(0,2π)有三个根,由于2021=3×673+2,则方程2sin2x﹣k sin x﹣1=0在(1346π,1347π)只有一个根,在区间(1347π,1348π)上无实解,方程sin x=t2在区间(1346π,1347π)上无实解,在区间(1347π,1348π)上有两个根.所以关于x的方程2sin2x﹣k sin x﹣1=0在区间(0,1347π)上有2020个根.在区间(0,1348π)上有2022个根.不合题意.(iⅤ)当t1=﹣1时,则t2=,当x∈(0,2π)时,sin x=t1只有一根,sin x=t2有两根,所以关于x的方程2sin2x﹣k sin x﹣1=0在(0,2π)上有三个根,由于2021=3×673+2,则方程2sin2x﹣k sin x﹣1=0在(0,1347π)上有3×673=2019个根.由于方程sin x=t1在区间(1346π,1347π)上无实数根,在区间(1347π,1348π)上只有一个实数根.由于方程sin x=t2在区间(1346π,1347π)上有两个实数根,在区间(1347π,1348π)上只有一个实数根.因此关于x的方程2sin2x﹣k sin x﹣1=0在(0,1347π)上有2021个根,在区间(0,1348π)上有2022个根,因此2×(﹣1)2﹣k(﹣1)﹣1=1+k=0.所以解得k=﹣1.n=1347.【点评】本题主要考查三角函数关系式的变换,三角函数图象和性质的应用,函数的零点和函数的图象的关系,主要考查学生的运算能力和转换能力及思维能力,综合性较强,运算量较大,属于难题.。
2022-2023学年高一数学必修第一册第五章《三角函数》测试卷及答案解析

=sin(2x )
∴g(x)=sin(2x )
对于 A:令
2x
,解得
b
t
,∴在区间[ , ]上单调递增;则 A 正
确. 对于 B:当 x b 时,可得函数值 f(x)=1,所以图象关于直线 x b 对称;则 B 正确.
对于 C:令
2x
,解得
t ,∴在区间[ , ]上不是单调递减;
则 C 不正确.
对于 D:令 x ,可得函数值 f(x)=0,∴图象关于点( ,0)对称;则 D 正确;
第 5 页 共 16 页
22.已知函数 Sth ሻ 已mS t hSሻ> , > ,图 图< h的部分图象如图所示. (1)求 A,ω,φ的值; (2)先将函数 y=f(x)的图象向右平移 个单位长度后,得到函数 y=g(x)的图象, 若函数 h(x)=f(x)+g(x)在[0,m]上单调递增,求 m 的取值范围.
第 6 页 共 16 页
2022-2023 学年高一数学必修第一册第五章《三角函数》测试卷
参考答案与试题解析
一.单项选择题(共 8 小题,每小题 5 分,共 40 分) 1.若 imS th ,则 sin2x=( )
A.
B.
C.
D.
解:∵ imS th ,
imt ∴
imt
,整理可得 tanx=3,
对 B,由 2x
可得, t
,故 f(x)在区间[ , ]上单调递减,B 正确;
对 C,因为 f( )=0,得到函数图象的一个对称中心为S , h,C 正确.
对 D,因为 已mS t h
t
由 t由
S由 h,D 正确.
故选:BCD.
10.将函数 f(x)=sin(2x )的图象向右平移 个单位长度得到 g(x)图象,则下列判
2022-2023学年高一上学期数学人教A版必修一第五章《三角函数》试卷

新人教A 版 必修一 三角函数单元素养测评卷(原卷+答案)一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列各对角中,终边相同的是( )A .32 π和2k π-32 π(k ∈Z )B .-π5 和225π C .-79 π和119 π D .203 π和1229π 2.已知α是第二象限角,sin α=35,则cos α=( ) A .-35 B .-45 C .35 D .453.已知角α的终边上一点P (x 0,-2x 0)(x 0≠0),则sin αcos α=( )A .25B .±25C .-25D .以上答案都不对 4.圆的一条弦的长等于半径,则这条弦所对的圆周角的弧度数为( )A .1B .12C .π6 或5π6D .π3 或5π35.函数f (x )=cos ⎝⎛⎭⎫π2-x 是( )A .奇函数,在区间⎝⎛⎭⎫0,π2 上单调递增B .奇函数,在区间⎝⎛⎭⎫0,π2 上单调递减 C .偶函数,在区间⎝⎛⎭⎫0,π2 上单调递增 D .偶函数,在区间⎝⎛⎭⎫0,π2 上单调递减 6.若cos ⎝⎛⎭⎫α-π4 =35,sin 2α=( ) A .2425 B .-725 C .-2425 D .7257.在△ABC 中,若tan A +tan B +2 tan A ·tan B =2 ,则tan 2C =( )A .-2B .2C .-22D .228.函数f (x )=A sin (ωx +φ)(A >0,ω>0,0<φ<π)的部分图象如图所示,将y =f (x )的图象向左平移π6个单位长度得到函数y =g (x )的图象,则函数y =g (x )的解析式是( )A.g (x )=sin 2xB .g (x )=sin (2x +π3) C .g (x )=sin (2x -π3) D .g (x )=sin (2x +2π3) 二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.)9.已知角α的终边与单位圆相交于点P (45 ,-35),则( ) A .cos α=45 B .tan α=-34C .sin (α+π)=35D .cos (α-π2 )=3510.已知θ∈(0,π),sin θ+cos θ=15,则下列结论正确的是( ) A .sin θ-cos θ=-75 B .cos θ=-35C .tan θ=-34D .θ∈⎝⎛⎭⎫π2,π 11.[2022·广东佛山高一期末]已知cos ⎝⎛⎭⎫π6+α =13,则( ) A .sin ⎝⎛⎭⎫π6+α =223 B .cos ⎝⎛⎭⎫5π6-α =-13C .sin ⎝⎛⎭⎫π3-α =13D .角α可能是第二象限角12.函数f (x )=sin x -3 cos x ,把图象上各点的横坐标缩短到原来的12,得到函数g (x )的图象,则下列说法正确的是( )A .函数g (x )的最小正周期为πB .函数g (x )的图象关于直线x =k π2 +5π12,k ∈Z 对称 C .函数g (x )在区间⎝⎛⎭⎫0,π3 上单调递增D .若x ∈⎣⎡⎦⎤π4,π2 ,则g (x )的值域为⎣⎡⎦⎤12,32 三、填空题(本题共4小题,每小题5分,共20分.)13.若cos (2π-α)=13,则sin ⎝⎛⎭⎫3π2-α =________. 14.已知θ是第三象限角,且满足⎪⎪⎪⎪sin θ2 =sin θ2 ,则θ2的终边在第________象限. 15.梅州城区某公园有一座摩天轮,其旋转半径30米,最高点距离地面70米,匀速运行一周大约18分钟.某人在最低点的位置坐上摩天轮,则第12分钟时,他距地面大约为________米.16.已知一扇形的弧长为2π9 ,面积为2π9,则其半径r =________,圆心角为________. 四、解答题(本题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.)17.(本小题满分10分)已知sin α=55 ,α∈⎝⎛⎭⎫π2,π . (1)求tan α,sin 2α的值;(2)求cos ⎝⎛⎭⎫α-π3 的值.18.(本小题满分12分)[2022·山东烟台高一期末]在平面直角坐标系xOy 中,角α的顶点在坐标原点O ,始边与x 轴的非负半轴重合,角α的终边经过点A (a ,3),cos α=-45. (1)求a 和tan α的值; (2)求sin (-α)+2sin (π2+α)3sin (3π2+α)+sin (π-α) 的值.19.(本小题满分12分)已知tan ⎝⎛⎭⎫π4+α =2,tan β=12. (1)求tan α的值;(2)求sin (α+β)-2sin αcos β2sin αsin β+cos (α+β)的值.20.(本小题满分12分)[2022·广东茂名高一期末]已知函数f (x )=2cos ⎝⎛⎭⎫2x -π3 ,x ∈R , (1)求f (x )的最小正周期;(2)求f (x )的单调递减区间.21.(本小题满分12分)已知-π<α<0,且满足________.从①sin α=55 ;②cos α+sin α=-55 ;③tan α=-2.三个条件中选择合适的一个,补充在上面的问题中,然后作答补充完整的题目.(1)求cos α-sin α的值;(2)若角β的终边与角α的终边关于y 轴对称,求cos β+sin βcos β-sin β的值.22.(本小题满分12分)[2022·福建泉州高一期末]函数f (x )=A sin (ωx +φ)(A >0,ω>0,0<φ<π2)在一个周期内的图象如图所示,O 为坐标原点,M ,N 为图象上相邻的最高点与最低点,P ⎝⎛⎭⎫-12,0 也在该图象上,且|OM |=172,|MN |=25 . (1)求f (x )的解析式;(2)f (x )的图象向左平移1个单位后得到g (x )的图象,试求函数F (x )=f (x )·g (x )在⎣⎡⎦⎤14,53 上的最大值和最小值.。
浙江省宁波市2022-2023学年高一上学期数学期末试卷(含答案)

A. , 쳌
B. , 쳌
C. , 쳌
合, 쳌 D. , 쳌
3.已知 , 为非零实数,则“
”是“
A.充分不必要条件 C.充要条件
4.函数 集 tan ሼ 쳌的定义域是( )
”的( ) B.必要不充分条件 D.既不充分也不必要条件
A. ሼ ሼ
,
B. ሼ ሼ
,
C. ሼ ሼ
,
D. ሼ ሼ
5.已知定义在 上的奇函数 ሼ쳌满足 ሼ 쳌 集 ሼ쳌,则
A. ,
ห้องสมุดไป่ตู้
, 쳌,使
log ,则下列关系式可能正确的是( )
B. ,
, 쳌,使 集
C. ,
,
三、填空题
13.化简求值:log
쳌,有 log log 쳌 集
D. ,
, 쳌,有
.
14.已知函数 集 ሼ쳌的图象是一条连续不断的曲线,当 ሼ 合 , 时,值域为合 , ,且在合 , 上
有两个零点,请写出一个满足上述条件的 ሼ쳌 集
由 cosሼ 得 cosሼ
,所以 ሼ
,,
所以 ሼ쳌的定义域是 ሼ ሼ
,
, ሼ쳌的定义域关于原点对称,
ሼ쳌 集 cos ሼ쳌 集 cosሼ 集 ሼ쳌,所以 ሼ쳌是偶函数,B 选项正确.
ሼ
쳌 集 cos ሼ 쳌 集 cosሼ 集 ሼ쳌,所以 ሼ쳌是周期函数,C 选项正确.
8
当ሼ
,
时, cosሼ 恒成立,
从而 log log 集 log 故答案为:ABCD
log ,所以
.综上所述可得
,所以 D 符合题意.
【分析】利用已知条件结合函数的单调性和全称命题和特称命题真假性判断方法,进而找出关系式可能的关 系式。 13.【答案】
2020-2022北京重点校高一(上)期末数学汇编及解析:三角函数的性质与图像

2020-2022北京重点校高一(上)期末数学汇编三角函数的性质与图像一、单选题1.(2022·北京市第五中学高一期末)甲:“x 是第一象限的角”,乙:“sin x 是增函数”,则甲是乙的( ) A .充分但不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件2.(2022·北京·清华附中高一期末)已知函数1()sin()f x x ωφ=+(0,2ωφπ><)的部分图象如图所示,则,ωφ的值分别为A .2,3πB .2, 3π-C .1, 6πD .1, 6π-3.(2022·北京·清华附中高一期末)下列四个函数中,以π为最小正周期,且在区间(,)2ππ上为减函数的是A .2|sin |y x =B .cos y x =C .sin 2y x =D .|cos |y x =4.(2021·北京·清华附中高一期末)函数()sin 26f x x π⎛⎫=- ⎪⎝⎭的图象关于直线x t =对称,则t 的值可以为( ) A .12πB .3π C .512π D .2π 5.(2021·北京二中高一期末)已知函数()sin 0,02y x πωϕωϕ⎛⎫=+><≤ ⎪⎝⎭的部分图象如图所示,则点(),P ωϕ的坐标为( )A .2,3π⎛⎫ ⎪⎝⎭B .2,6π⎛⎫ ⎪⎝⎭C .1,23π⎛⎫ ⎪⎝⎭D .1,26π⎛⎫ ⎪⎝⎭6.(2021·北京·101中学高一期末)函数sin 2y x π⎛⎫=+ ⎪⎝⎭,5,36x ππ⎛⎤∈- ⎥⎝⎦的值域为( )A .312⎡⎫⎪⎢⎪⎣⎭B .3⎡⎤⎢⎥⎣⎦C .1,12⎡⎤-⎢⎥⎣⎦D .132⎡-⎢⎣⎭7.(2021·北京二中高一期末)已知函数f (x )=2x -1,()2cos 2,0?2,0a x x g x x a x +≥⎧=⎨+<⎩(a ∈R ),若对任意x 1∈[1,+∞),总存在x 2∈R ,使f (x 1)=g (x 2),则实数a 的取值范围是 A .1,2⎛⎫-∞ ⎪⎝⎭B .2,3⎛⎫+∞ ⎪⎝⎭C .[]1,1,22⎛⎫-∞ ⎪⎝⎭D .371,,224⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦8.(2020·北京·清华附中高一期末)下列函数在定义域内单调递增的是( ) A .2yxB .tan y x =C .0.5x y =D .lg y x =二、填空题9.(2022·北京·清华附中高一期末)已知函数()sin()cos 22f x x xπ=+,给出下列四个命题:∈函数()f x 是周期函数;∈函数()f x 的图象关于点(,0)π成中心对称; ∈函数()f x 的图象关于直线2x π=-成轴对称; ∈函数()f x 在区间3(,)2ππ上单调递增. 其中,所有正确命题的序号是___________.10.(2021·北京·清华附中高一期末)函数()2sin 2?3f x x π⎛⎫=+ ⎪⎝⎭在,3m π⎡⎤-⎢⎥⎣⎦上单调递增,则实数m 的最大值为____________.11.(2021·北京·清华附中高一期末)已知函数()sin 1f x a x bx =++,若()12f -=,则()1f =_____________.12.(2021·北京二中高一期末)若函数()()cos 0f x x ωω=>在区间()2,3ππ内既没有最大值1,也没有最小值1-,则ω的取值范围是___________.13.(2021·北京·清华附中高一期末)函数()cos(2)6f x x π=-的最小正周期为_____________.14.(2020·北京·清华附中高一期末)关于函数()sin f x x =与()cos g x x =有下面三个结论: ∈函数()f x 的图像可由函数()g x 的图像平移得到 ∈函数()f x 与函数()g x 在,2ππ⎛⎫⎪⎝⎭上均单调递减∈若直线x t =与这两个函数的图像分别交于不同的A ,B 两点,则1AB ≤ 其中全部正确结论的序号为____15.(2020·北京·清华附中高一期末)已知函数()()sin f x A x =+ωϕ(0A >,0ω>,π<ϕ)的部分图象如图,则函数()f x 的单调递增区间为______.三、双空题16.(2021·北京二中高一期末)函数tan 23y x π⎛⎫=+ ⎪⎝⎭的最小正周期是___________,定义域是___________.四、解答题17.(2022·北京市第五中学高一期末)已知函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的最小正周期为π,再从下列两个条件中选择一个作为已知条件:条件∈:()f x 的图象关于点(,0)3π对称;条件∈:()f x 的图象关于直线12x π对称.(1)请写出你选择的条件,并求()f x 的解析式; (2)在(1)的条件下,当[,]36x ππ∈-时,求()f x 的最大值和最小值,并指出相应的x 取值. 注;如果选择条件∈和条件∈分别解答,按第一个解答计分.18.(2022·北京·清华附中高一期末)已知函数()f x 的定义域为D ,若存在实数a ,使得对于任意1x D ∈都存在2x D ∈满足()122x f x a +=,则称函数()f x 为“自均值函数”,其中a 称为()f x 的“自均值数”. (1)判断函数()2x f x =是否为“自均值函数”,并说明理由:(2)若函数()sin()(0)6g x x πωω=+>,[0,1]x ∈为“自均值函数”,求ω的取值范围;(3)若函数2()23h x tx x =++,[0,2]x ∈有且仅有1个“自均值数”,求实数t 的值.19.(2020·北京·首都师范大学附属中学高一期末)已知函数f (x )=cosx (acosx ﹣sinx )3-a ∈R ),且f (3π)3=- (1)求a 的值;(2)求f (x )的单调递增区间; (3)求f (x )在区间[0,2]上的最小值及对应的x 的值.参考答案1.D【分析】由正弦函数的单调性结合充分必要条件的定义判定得解. 【详解】由x 是第一象限的角,不能得到sin x 是增函数; 反之,由sin x 是增函数,x 也不一定是第一象限角. 故甲是乙的既不充分又不必要条件. 故选D .【点睛】本题考查充分必要条件的判定,考查正弦函数的单调性,是基础题. 2.B【详解】由条件知道:27,36x x ππ== 均是函数的对称中心,故这两个值应该是原式子分母的根,故得到27sin()0,sin()036w w πφπφ+=+=,由图像知道周期是π ,故2w =,故47sin()0,sin()033πφπφ+=+=,再根据三角函数的对称中心得到4+=k 3πφπ ,故.3πφ=- 如果7433k πφπφπ+=⇒=- ,根据2πφ<,得到.3πφ=- 故答案为B .点睛:根据函数的图像求解析式,一般要考虑的是图像中的特殊点,代入原式子;再就是一些常见的规律,分式型的图像一般是有渐近线的,且渐近线是分母没有意义的点;还有常用的是函数的极限值等等方法. 3.A【详解】2sin y x =最小正周期π,且在区间,2ππ⎛⎫⎪⎝⎭上为减函数,适合;cos y x =最小正周期为2π,不适合;sin2y x =最小正周期为π,在区间,2ππ⎛⎫⎪⎝⎭上不单调,不适合;cos y x =最小正周期为π,在区间,2ππ⎛⎫⎪⎝⎭上为增函数,不适合. 故选A 4.B【分析】令2,62x k k Z πππ-=+∈,可求得对称轴方程,对k 赋值,即可得答案. 【详解】令2,62x k k Z πππ-=+∈,解得,23k x k Z ππ=+∈, 所以对称轴,23k t k Z ππ=+∈, 令0k =,得3t π=,无论k 取任何整数,t 无法取12π、512π、2π,故选:B 5.A【分析】利用给定图象列出周期和初相关系式即可作答.【详解】观察图象得:1252632ππππω=-=⋅,则2ω=, 而3x π=时,0y =,于是有2,3k k Z πϕπ⋅+=∈,又02πϕ<≤,则1,3k πϕ==,所以点P 的坐标为2,3π⎛⎫⎪⎝⎭.故选:A 6.B【解析】由诱导公式化简函数后,结合余弦函数性质求解.【详解】由已知sin cos 2y x x π⎛⎫=+= ⎪⎝⎭,又5,36x ππ⎛⎤∈- ⎥⎝⎦,∈31y ≤≤.故选:B 7.C【分析】对a 分a=0,a <0和a >0讨论,a >0时分两种情况讨论,比较两个函数的值域的关系,即得实数a 的取值范围.【详解】当a =0时,函数f (x )=2x-1的值域为[1,+∞),函数()g x 的值域为[0,++∞),满足题意.当a <0时,y =22(0)x a x +<的值域为(2a ,+∞), y =()cos 20a x x +≥的值域为[a +2,-a +2], 因为a +2-2a =2-a >0,所以a +2>2a , 所以此时函数g (x )的值域为(2a ,+∞), 由题得2a <1,即a <12,即a <0.当a >0时,y =22(0)x a x +<的值域为(2a ,+∞),y =()cos 20a x x +≥的值域为[-a +2,a +2],当a ≥23时,-a +2≤2a ,由题得21,1222a a a a -+≤⎧∴≤≤⎨+≥⎩. 当0<a <23时,-a +2>2a ,由题得2a <1,所以a <12.所以0<a <12. 综合得a 的范围为a <12或1≤a ≤2, 故选C .【点睛】本题主要考查函数的图象和性质,考查指数函数和三角函数的图象和性质,意在考查学生对这些知识的理解掌握水平和分析推理能力. 8.D【分析】根据题意,依次分析选项中函数的单调性,综合即可得答案. 【详解】解:根据题意,依次分析选项:对于A ,2y x ,是二次函数,在其定义域上不是单调函数,不符合题意;对于B ,tan y x =,是正切函数,在其定义域上不是单调函数,不符合题意; 对于C ,0.5x y =,是指数函数,在定义域内单调递减,不符合题意; 对于D ,lg y x =,是对数函数,在定义域内单调递增,符合题意; 故选:D . 9.∈∈∈【分析】利用诱导公式化简函数()f x ,借助周期函数的定义判断∈;利用函数图象对称的意义判断∈∈;取特值判断∈作答.【详解】依题意,()cos cos 2f x x x =,因4(4)cos(4)cos cos cos ()22x xf x x x f x πππ++=+==,()f x 是周期函数,4π是它的一个周期,∈正确;因()cos()coscos sin 22πx x f πx πx x +=+=+,()cos()cos 2f πx πx πx =---cos sin 2xx =-, 即()()f x f x ππ+=--,因此()f x 的图象关于点(,0)π成对称中心,∈正确; 因(2)cos(2)coscos cos 222πx f πx πx x x -+=-+=--+,(2)cos(2)cos cos cos 222πxf πx πx x x --=--=---, 即(2)(2)f πx f πx -+=--,因此()f x 的图象关于直线2x π=-成轴对称,∈正确; 因()cos cos 02f πππ==,4421()cos cos 3334f πππ==,333()cos cos 0224f πππ==,显然有4332πππ<<,而34()()()23f f f πππ=<,因此函数()f x 在区间3(,)2ππ上不单调递增,∈不正确,所以,所有正确命题的序号是∈∈∈. 故答案为:∈∈∈【点睛】结论点睛:函数()y f x =的定义域为D ,x D ∀∈,(1)存在常数a ,b 使得()(2)2()()2f x f a x b f a x f a x b +-=⇔++-=,则函数()y f x =图象关于点(,)a b 对称.(2)存在常数a 使得()(2)()()f x f a x f a x f a x =-⇔+=-,则函数()y f x =图象关于直线x a =对称. 10.12π【分析】令222,232k x k k Z πππππ-≤+≤+∈,可求得()f x 的单调增区间,根据()f x 在,3m π⎡⎤-⎢⎥⎣⎦上单调递增,分析计算,即可得答案. 【详解】令222,232k x k k Z πππππ-≤+≤+∈,解得5,1212k x k k Z ππππ-≤≤+∈, 令0k =,可得()f x 的一个增区间为5,1212ππ⎡⎤-⎢⎥⎣⎦因为()f x 在,3m π⎡⎤-⎢⎥⎣⎦上单调递增,且5,31212πππ⎡⎤-∈-⎢⎥⎣⎦,所以12m π≤,即m 的最大值为12π.故答案为:12π11.0【分析】利用正弦函数的奇偶性可以得到()()112f f +-=,进而得到结果.. 【详解】因为()1sin11f a b =++,()1sin11f a b -=--+,所以()()112f f +-=, 因为()12f -=则()1f =0, 故答案为:0. 12.{}1120,,1323⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦【分析】由()2,3x ππ∈可得出23x πωωπω<<,分析可知()()2,3,k k πωπωπππ⊆+,其中Z k ∈,可得出关于实数ω的不等式组,由此可解得实数ω的取值范围. 【详解】当()2,3x ππ∈且0ω>时,23x πωωπω<<,因为函数()f x 在区间()2,3ππ内既没有最大值1,也没有最小值1-, 则()()2,3,k k πωπωπππ⊆+,其中Z k ∈,所以,23k k πωππωππ≥⎧⎨≤+⎩,解得()123k k k Z ω+≤≤∈,由123k k +≤,可得2k ≤, 因为0ω>且Z k ∈,当0k =时,103ω<≤;当1k =时,1223ω≤≤;当2k =时,1ω=. 综上所述,实数ω的取值范围是{}1120,,1323⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦.故答案为:{}1120,,1323⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦.13.π【解析】由题意得2ω=,再代入复合三角函数的周期公式2||T πω=求解. 【详解】解:根据复合三角函数的周期公式2||T πω=得, 2|2|T ππ∴== 函数()cos(2)6f x x π=-的最小正周期是π,故答案为:π.【点睛】本题考查了三角函数的周期性,以及复合三角函数的周期公式2||T πω=应用,属于基础题. 14.∈∈##∈∈【分析】根据三角函数的平移法则和单调性知∈∈正确,取3π4t =代入计算得到∈错误,得到答案. 【详解】()sin f x x =向左平移π2个单位得到πsin cos 2y x x ⎛⎫=+= ⎪⎝⎭,∈正确;函数()f x 在π,π2⎛⎫ ⎪⎝⎭上单调递减,函数()g x 在π,π2⎛⎫⎪⎝⎭上单调递减,∈正确;取3π4t =,则3π24f ⎛⎫= ⎪⎝⎭3π24g ⎛⎫= ⎪⎝⎭,2AB =∈错误.故答案为:∈∈15.()372,244k k k ⎡⎤++∈⎢⎥⎣⎦Z【分析】由函数的图象得到函数的周期,同时根据图象的性质求得一个单调增区间,然后利用周期性即可写出所有的增区间.【详解】由图可知函数f(x)的最小正周期512244T ⎛⎫=-= ⎪⎝⎭.如图所示,一个周期内的最低点和最高点分别记作,A B , 分别作在x 轴上的射影,记作11,A B ,根据()()sin f x A x =+ωϕ的对称性可得11,A B 的横坐标分别为37,44,∈37,44⎡⎤⎢⎥⎣⎦是函数f(x)的一个单调增区间, ∈函数()f x 的单调增区间是()372,244k k k ⎡⎤+∈⎢⎥⎣⎦Z ,故答案为:()372,244k k k ⎡⎤++∈⎢⎥⎣⎦Z ,【点睛】本题关键在于掌握函数图象的对称性和周期性.一般往往先从函数的图象确定函数中的各个参数的值,再利用函数的解析式和正弦函数的性质求得单调区间,但是直接由图象得到函数的周期,并根据函数的图象的性质求得一个单调增区间,进而写出所有的增区间,更为简洁. 16.2π |,122k x x k ππ⎧⎫≠+∈⎨⎬⎩⎭Z【分析】根据正切函数的性质,由T πω=且232x k πππ+≠+即可得解.【详解】最小正周期为2ππT ω==, 232x k πππ+≠+, 可得,122k x k ππ≠+∈Z , 故答案为:π;|,122k x x k ππ⎧⎫≠+∈⎨⎬⎩⎭Z . 17.(1)()2sin(2)3f x x π=+;(2)3x π=-时,()f x 有最小值3-12x π=时,()f x 有最大值2.【分析】(1)若选∈,根据周期求出ω,然后由()2Z 3k k πϕπ⨯+=∈并结合ϕ的范围求出ϕ,最后求出答案;若选∈,根据周期求出ω,然后由()2Z 122k k ππϕπ⨯+=+∈并结合ϕ的范围求出ϕ,最后求出答案;(2)结合(1),先求出x ωϕ+的范围,然后结合正弦函数的性质求出答案.(1)若选∈,由题意,22ππωω=⇒=,因为函数的图象关于点(,0)3π对称,所以()()22Z Z 33k k k k πϕπϕππ⨯+=∈⇒=-+∈,而22ππϕ-<<,则3πϕ=,于是()2sin(2)3f x x π=+. 若选∈,由题意,22ππωω=⇒=,因为函数的图象关于直线12x π=对称,所以()()2Z Z 1223k k k k πππϕπϕπ⨯+=+∈⇒=+∈,而22ππϕ-<<,则3πϕ=,于是()2sin(2)3f x x π=+. (2)结合(1),因为[,]36x ππ∈-,所以22,333x πππ⎡⎤+∈-⎢⎥⎣⎦,则当2333x x πππ+=-⇒=-时,()f x 有最小值为()2sin()333f ππ-=-=-23212x x πππ+=⇒=时,()f x 有最大值为()2sin 2122f ππ==. 18.(1)不是,理由见解析; (2)5[,)6π+∞; (3)12-35--【分析】(1)假定函数()2x f x =是 “自均值函数”,由函数2()f x 的值域与函数12y a x =-的值域关系判断作答.(2)根据给定定义可得函数2()g x 在[0,1]上的值域包含函数12y a x =-在[0,1]上的值域,由此推理计算作答. (3)根据给定定义可得函数2()h x 在[0,2]上的值域包含函数12y a x =-在[0,2]上的值域,再借助a 值的唯一性即可推理计算作答.(1)假定函数()2x f x =是 “自均值函数”,显然()2xf x =定义域为R ,则存在R a ∈,对于1x ∀∈R ,存在2Rx ∈,有2122x x a+=,即2122x a x =-,依题意,函数22()2xf x =在R 上的值域应包含函数12y a x =-在R 上的值域,而当2R x ∈时,2()f x 值域是(0,)+∞,当1R x ∈时,12y a x =-的值域是R ,显然(0,)+∞不包含R , 所以函数()2x f x =不是 “自均值函数”.(2)依题意,存在R a ∈,对于1[0,1]x ∀∈,存在2[0,1]x ∈,有12()2x g x a +=,即21sin()26x a x πω+=-,当1[0,1]x ∈时,12y a x =-的值域是[21,2]a a -,因此22()sin()6g x x πω=+在2[0,1]x ∈的值域包含[21,2]a a -,当2[0,1]x ∈时,而0ω>,则2666x πππωω≤+≤+,若62ππω+≤,则2min 1()2g x =,2()1g x ≤,此时2()g x 值域的区间长度不超过12,而区间[21,2]a a -长度为1,不符合题意, 于是得62ππω+>,2max ()1g x =,要22()sin()6g x x πω=+在2[0,1]x ∈的值域包含[21,2]a a -, 则22()sin()6g x x πω=+在2[0,1]x ∈的最小值小于等于0,又23[,]622x πππω+∈时,2()g x 递减,且()0π=g ,从而有6πωπ+≥,解得56πω≥,此时,取12a =,12y a x =-的值域是[0,1]包含于2()g x 在2[0,1]x ∈的值域,所以ω的取值范围是5[,)6π+∞. (3)依题意,存在R a ∈,对于1[0,2]x ∀∈,存在2[0,2]x ∈,有12()2x h x a +=,即2221232tx x a x ++=-,当1[0,2]x ∈时,12y a x =-的值域是[22,2]a a -,因此2222()23h x tx x =++在2[0,2]x ∈的值域包含[22,2]a a -,并且有唯一的a 值,当0t ≥时,2()h x 在[0,2]单调递增,2()h x 在2[0,2]x ∈的值域是[3,47]t +,由[22,2][3,47]a a t -⊆+得223247a a t -≥⎧⎨≤+⎩,解得57222a t ≤≤+,此时a 的值不唯一,不符合要求,当0t <时,函数2222()23h x tx x =++的对称轴为21x t=-,当12t -≥,即102t -≤<时,2()h x 在[0,2]单调递增,2()h x 在2[0,2]x ∈的值域是[3,47]t +,由[22,2][3,47]a a t -⊆+得223247a a t -≥⎧⎨≤+⎩,解得57222a t ≤≤+,要a 的值唯一,当且仅当57222t =+,即15,22t a =-=,则12t =-,当102t <-<,即21t <-时,2max 11()()3h x h t t =-=-,2min ()min{(0),(2)}h x h h =,(0)3h =,(2)47h t =+,由1[22,2][3,3]a a t -⊆-且112t -≤<-得:531222a t≤≤-,此时a 的值不唯一,不符合要求,由1[22,2][47,3]a a t t -⊆+-且1t <-得,9312222t a t +≤≤-,要a 的值唯一,当且仅当9312222t t +=-,解得35t --=65a -= 综上得:12t =-或35t --=,所以函数2()23h x tx x =++,[0,2]x ∈有且仅有1个“自均值数”,实数t 的值是12-35-- 【点睛】结论点睛:若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x =,则()f x 的值域是()g x 值域的子集. 19.(1)3a =(2)511,,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(3)512x π=时,取得最小值31- 【解析】(1)代入数据计算得到答案.(2)化简得到()3cos 26f x x π⎛⎫=+ ⎪⎝⎭2222,6k x k k πππππ+≤+≤+∈Z 得到答案.(3)计算2x 6π+∈[6π,76π],再计算最值得到答案. 【详解】(1)∈f (x )=cosx (acosx ﹣sinx )3-a ∈R ),且f (3π)3= ∈f (3π)12=(132a -33-=解得a 3=(2)由(1)可得f (x )=cosx 3﹣sinx )33=2x ﹣sinxcosx 1213322cos x +--sin 2x 3-=cos (2x 6π+)3令2k π+π≤2x 6π+≤2k π+2π,k ∈Z ,解得:k π512π+≤x ≤k π1112π+,k ∈Z ,可得f (x )的单调递增区间为:[k π512π+,k π1112π+],k ∈Z , (3)∈x ∈[0,2π],可得:2x 6π+∈[6π,76π],∈当2x 6π+=π,即x 512π=时,f (x )=cos (2x 6π+)3取得最小值为﹣13.【点睛】本题考查了三角函数的求值,单调性和值域,意在考查学生对于三角函数知识的综合应用.。
2022-2023学年全国高中高一上数学人教A版(2019)期末试卷(含解析)

2022-2023学年全国高一上数学期末试卷考试总分:141 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 7 小题 ,每题 5 分 ,共计35分 )1. 函数(其中)的图象如图所示,则函数的大致图象是( ) A. B. C. D.2. 已知:=,则=( )A.B.C.D.f(x)=(x −a)(x −b)a >b g(x)=+b a x sin(+θ)+3cos(π−θ)π2sin(−θ)sin θcos θ+θcos 215255–√535a =0.4logb =3log ()3. 设,,则 A.且B.且C.且D.且4. 已知=在=处取得最小值,则=( )A.B.C.D.5. 函数=的图象恒过点,若点在直线=上,其中,则的最小值为( )A.B.C.D.6. 函数=的图象大致为( )A.a =0.4log 3b =3log 2()ab >0a +b >0ab <0a +b >0ab >0a +b <0ab <0a +b <0f(x)ax +(x >0)8x x 4a 42112y (x +3)−1(a >0,a ≠1)log a A A mx +ny +10mn >0+1m 8n 16182022f(x)B. C. D.7. 扇形的周长为,面积是,则扇形的圆心角的弧度数是( )A.B.C.或D.或二、 多选题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )8. 在棱长为的正方体中,点在棱上,则下列结论正确的是( )A.直线与平面平行B.平面截正方体所得的截面为三角形C.异面直线与所成的角为D.的最小值为9. 下列函数中,既是偶函数,又在区间上单调递减的函数是( )A.6cm 2cm 21414241ABCD −A 1B 1C 1D 1M CC 1BM ADD 1A 1BMD 1AD 1A 1C 1π3|MB |+|M |D 15–√(−∞,0)y =x 2−−√3=(1x|B.C.D.=10. 如图是二次函数图象的一部分,图象过点,对称轴为.给出下面结论,其中正确的是( )A.B. C.D.11. 函数=,的所有零点之和为( )A.B.C.D.卷II (非选择题)三、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )12. 方程在上有解,则的取值范围是________.13. 已知函数 是定义在上的偶函数. ,且 ,都有,则不等式 的解集为________.14. 将函数=图象上各点横坐标变为原来的倍,再向左平移个单位,得到函数y =(12)|x|y =log 121|x |y sin xy =a +bx +c x 2A(−3,0)x =−1>4acb 22a −b =1a −b +c =05a <bf(x)2sin(πx)−11−xx ∈[−2,4]2468x −2cos x −a =0cos 2x ∈R a f (x +1)R ∀x,∈[1,+∞)x 2≠x 1x 2(−)[f ()−f ()]<0x 1x 2x 2x 1f (−+1)<f (5)2x+1y sin x f(x)f(x)[0,2π]的图象.已知在上有且只有个零点.在下列命题中:①的图象关于点对称;②在内恰有个极值点;③在区间内单调递减;④的取值范围是.所有真命题的序号是________.15. 函数,其中()的部分图象如图所示,则函数的解析式是________.四、 解答题 (本题共计 6 小题 ,每题 11 分 ,共计66分 ) 16. 求下列各式的值(1);(2)已知,求值. 17. 画出函数在长度为一个周期的闭区间上的图象.并求出当等于多少时,函数有最大值.18. 已知二次函数满足,图象的顶点在直线上,并且图象经过点,求:二次函数的解析式;使恒成立的实数的取值范围.19. 如图所示,在平面四边形中,,,求的值;求的长.f(x)f(x)[0,2π]5f(x)f(x)(0,2π)5f(x)ωf(x)=A sin(ωx +φ)A >0,ω>0,|φ|<π2f(x)−3++(2)14−12[](1−)2–√212log (2+)3√(−2)3√23–√2+2log 3+=3a 12a −12+a 32a −32+a 2a −2y =3sin(x +)12π12x y =f (x)f (2−x)=f (2+x)y =x −1(−1,−8)(1)y =f (x)(2)(m −2)f (x)+m >0m ABCD DA ⊥AB CD =AE =2ED =2,∠ADC =,∠BEC =2π3π3∠CED =α.(1)sin α(2)BE20. 已知函数=.(1)若不等式恒成立,求实数的取值范围;(2)在(1)的条件下,若、、为正实数,且三数之和为的最大值,求证:. 21. 某校为创建“绿色校园”,在校园内种植树木,有、、三种树木可供选择,已知这三种树木年内的生长规律如下:树木:种植前树木高米,第一年能长高米,以后每年比上一年多长高米;树木:种植前树木高米,第一年能长高米,以后每年生长的高度是上一年生长高度的倍:树木:树木的高度(单位:米)与生长年限(单位:年,)满足如下函数:表示种植前树木的高度,取.(1)若要求年内树木的高度超过米,你会选择哪种树木?为什么?(2)若选树木,从种植起的年内,第几年内生长最快?f(x)|x +2|+2|x −3|f(x)≥m m a b c m ++≥a 2b 2c 2A B C 6A 0.840.10.2B 0.840.042C f(t)t t ∈N f(t)=(f(0)71+e −0.5t+2e ≈2.7)65C 6参考答案与试题解析2022-2023学年全国高一上数学期末试卷一、 选择题 (本题共计 7 小题 ,每题 5 分 ,共计35分 )1.【答案】A【考点】指数函数的图象【解析】由的图象确定,的取值范围,结合指数函数的图象进行判断即可.【解答】解:由的图象可知,,则函数为减函数,且,故选:2.【答案】D【考点】三角函数的恒等变换及化简求值运用诱导公式化简求值【解析】由条件利用诱导公式求得 =,再利用同角三角函数的基本关系求得 的值.【解答】∵====,∴=,则,3.【答案】f(x)a b f(x)0<a <1b <−1g(x)g(0)=1+b <0A tan θ2sin θcos θ+θcos 2sin(+θ)+3cos(π−θ)π2cos θ−3cos θ−2cos θsin(−θ)−sin θtan θ2sin θcos θ+θ===cos 2sin θcos θθ+cos 2θθsin 2+cos 2tan θ+1θ+1tan 235B【考点】对数值大小的比较【解析】【解答】解:∵,,∴且故选.4.【答案】D【考点】基本不等式及其应用【解析】容易看出不符合题意,从而看出,从而得出在取得最小值,从而得出,解出即可.【解答】时,在上是减函数,无最小值,不符合题意,∴,∴在取得最小值,又在=处取得最小值,∴,解得.5.【答案】B【考点】基本不等式及其应用a =− 2.5∈(−1,0)log 3b >1ab <0a +b >0.B a ≤0a >0f(x)=a(x +)8a x x =8a −−√=48a −−√a a ≤0f(x)(0,+∞)a >0f(x)=a(x +)8a x x =8a −−√f(x)x 4=48a −−√a =12【解析】由题意可得定点,=,把要求的式子乘进行变形,然后结合基本不等式即可求解.【解答】∵函数=,且的图象恒过定点,令=,求得=,=,可得.∵点在直线=上,∴=,即=.则=,当且仅当且=即,时取等号,6.【答案】C【考点】函数的图象与图象的变换【解析】根据函数奇偶性的概念判断为奇函数,排除选项和;再对比余下两个选项,不妨比较与的大小关系.【解答】取=,则=,排除选项,故选:.7.【答案】C【考点】扇形面积公式【解析】设出扇形的圆心角为,半径为,根据扇形的周长为 ,面积是 ,列出方程组,求出扇形的圆心角的弧度数.【解答】解:设扇形的圆心角为,半径为,A(−2,−1)2m +n 11y (x +3)−1(a >0log a a ≠1)A x +31x −2y −1A(−2,−1)A mx +ny +10−2m −n +102m +n 1+=(+)(2m +n)1m 8n 1m 8n 10++×2≥10+2=18n m 8m n ⋅n m 16m n −−−−−−−−√=n m 16m n 2m +n 1m =16m =23f(x)B D f(1)0x 1f(1)A C αrad Rcm 6cm 2cm 2αrad Rcm则,解得或.选.二、 多选题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )8.【答案】A,C,D【考点】命题的真假判断与应用异面直线及其所成的角空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系【解析】此题暂无解析【解答】解:由题画图:延长至使,对于,∵面面,平面,∴可判定直线与平面平行,故正确;对于,如图,在上取点,使得,此时即为截正方体所得的截面,故错误;对于,异面直线与所成的角为,即可判定异面直线与所成的角为,故正确;对于,∵由图知:,当共线时,取到最小值,即为线段的长度,,故正确.故选.9.【答案】 2R +α⋅R =6⋅α=212R 2α=1α=4C DC B ′C =BC B ′A AD //D 1A 1BCC 1B 1BM ⊂BCC 1B 1BM ADD 1A 1B AA 1N M =AN C 1BM N D 1BMD 1C AD 1A 1C 1∠B A 1C 1AD 1A 1C 1π3D MB +M =D 1M +M B ′D 1,M,D 1B ′M +M B ′D 1D 1B ′==D 1B ′+1222−−−−−−√5–√ACDA,C【考点】奇偶性与单调性的综合【解析】结合奇偶性及单调性的定义,再结合指数与对数函数,幂函数及余弦函数的性质即可判断.【解答】解;结合幂函数的性质可知为偶函数且在上单调递减,符合题意;结合指数函数的性质可知,=在上单调递增,不符合题意;结合对数函数的性质可知,=上单调递减且为偶函数,符合题意;结合正弦函数的性质可知=为奇函数,不符合题意.10.【答案】A,D【考点】二次函数的性质【解析】此题暂无解析【解答】解:∵图象与轴有交点,对称轴为,与轴的交点在轴的正半轴上,又∵二次函数的图象是抛物线,∴与轴有两个交点,∴,即,故正确;∵对称轴为,∴,即,故错误;∵时,,由图象可知,故错误;由图象可知,图象与轴的另一交点为,图象与轴的交点在轴上方,则,把,代入解析式可得,,两式相加得:,整理可得,即,故正确.故选.11.【答案】【考点】函数的零点与方程根的关系y =x 2−−√3(−∞,0)y (12)|x|(−∞,0)y log (−∞,0)121|x |y sin x A x x =−=−1b 2a y y x −4ac >0b 2>4ac b 2A B x =−=−1b 2a 2a =b 2a −b =0B C x =−1y =a −b +c y ≠0C D x x =1y x c >0x =1x =−3a +b +c =09a −3b +c =010a −2b +2c =05a −b =−c <05a <b D AD【解析】作出=与的函数图象,根据图象的交点个数和对称性得出答案.【解答】令=得,作出=与的函数图象,如图所示:由图象可知两图象在上共有个交点,∴共有个零点,又两图象都关于点对称,∴个交点两两关于点对称,∴个零点之和为=.故选:.三、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )12.【答案】【考点】余弦函数的单调性二次函数的性质函数零点的判定定理【解析】方程在上有解,可转化为的值域问题,即可求得结论.【解答】解:∵y 2sin πx y =11−x f(x)02sin(πx)=11−xy 2sin πx y =11−x [−2,4]8f(x)8(1,0)8(1,0)84×28D −1≤a ≤3x −2cos x −a =0cos 2x ∈R a =x −2cos x cos 2x −2cos x −a =0cos 2a =x −2cos x =(cos x −1−12)2∴∵,∴函数在上单调递减∴故答案为:.13.【答案】【考点】奇偶性与单调性的综合【解析】未提供解析.【解答】解:函数是定义在上的偶函数,函数的图象关于对称,∵,且,都有,函数在上单调递增,在上单调递减,∵,∴,∴,解得.所以不等式的解集为.故答案为:.14.【答案】①④【考点】命题的真假判断与应用函数y=Asin (ωx+φ)的图象变换【解析】先作出函数=的图象,然后结合图象可判定①,根据在上有且只有个零点可求出的范围可判断四,在内可能有个或个或个极值点,且在区间内的单调性无法判断,从而可判定②③.【解答】a =x −2cos x =(cos x −1−1cos 2)2−1≤cos x ≤1[−1,1]−1≤a ≤3−1≤a ≤3(−∞,1)∵f (x +1)R ∴f (x)x =1∀,∈[1,+∞)x 1x 2≠x 1x 2(−)[f ()−f ()]<0x 1x 2x 2x 1∴f (x)[1,+∞)(−∞,1)−+1<1,f (−+1)<f (5),f (5)=f (−3)2x+12x+1f (−+1)<f (−3)2x+1−+1>−32x+1x <1f (−+1)<f (5)2x+1(−∞,1)(−∞,1)f(x)f(x)[0,2π]5ωf(x)(1,2π)567f(x)由题意可知,函数=,如图,对于①,由图象可知的图象关于点(-,对称,故①正确;对于②、③、④,由题意可知,,解得,④正确.∵令,解得.又∵,∴在内可能有个或个或个极值点,且在区间内的单调性无法判断,故②③不正确.15.【答案】【考点】由y=Asin (ωx+φ)的部分图象确定其解析式【解析】此题暂无解析【解答】解:根据函数的图象:,得,,解得,所以,进一步利用,得,所以函数的解析式为:,故答案为:.四、 解答题 (本题共计 6 小题 ,每题 11 分 ,共计66分 )16.f(x)f(x)0)f(x)(1,2π)567f(x)y =2sin(2x +)π6A (,2),B (,0)π611π12T =−3411π12π6T =πω=2A (,2)π6φ=π6y =2sin(2x +)π6y =2sin(2x +)π6【答案】解:根据指数幂与对数的运算,化简可得解:因为两边同时平方可得所以由立方和公式及完全平方公式化简可得【考点】有理数指数幂的运算性质及化简求值对数的运算性质有理数指数幂【解析】()由指数幂及对数的运算,化简即可求解()根据完全平方公式及立方和公式,化简即可求值.【解答】此题暂无解答17.【答案】解:的最小正周期为周期列表如下−3++(2)14−12[](1−)2–√212log (2+)3√(−2)3√23–√2+2log 3=−3++[]()322−12[(−1)]2–√2×12log (2+)3√(−2)3√23–√9+2log 3log 3=−3(−1)+2+232–√log (2+)3√12+3–√3(9×2)12log 3=−3+3−2+3232–√2–√=53+=3a 12a −12a ++2=9a −1a +=7a −1+a 32a −32+a 2a −2=(+)(a −1+)a 12a −12a −1−2(a +)a −12==3×(7−1)−2(7)2184712(1)f(x)T =4πx −π65π611π617π623π6x +12π120π2π3π22π描点连线,如图示即为函数在一个周期的闭区间上的图象.由图可知,的最大值为,此时【考点】五点法作函数y=Asin (ωx+φ)的图象【解析】利用周期公式可求周期,利用五点法,可得函数的图象;利用函数的图象,可得的最大值及其对应的取值集合.【解答】解:的最小正周期为周期列表如下 描点连线,如图示即为函数在一个周期的闭区间上的图象.由图可知,的最大值为,此时18.【答案】解:∵,∴二次函数的对称轴为,∵二次函数的顶点在直线上,∴顶点坐标为.设,∵图像经过点,即,∴,∴,即.若恒成立,则恒成立,y 030−30y =3sin(x +)12π12(2)f(x)3x =4kπ+(k ∈Z)5π6f(x)x (1)f(x)T =4πx −π65π611π617π623π6x +12π120π2π3π22πy 030−30y =3sin(x +)12π12(2)f(x)3x =4kπ+(k ∈Z)5π6(1)f(2−x)=f(2+x)f(x)x =2y =x −1(2,1)y =f(x)=a(x −2+1)2(−1,−8)−8=a(−1−2+1)2a =−1y =f(x)=−(x −2+1)2y =f(x)=−+4x −3x 2(2)(m −2)f(x)+m >0(m −2)(−+4x −3)+m >0x 2(m −2)−4(m −2)x +2m −6<02∴.①当,即时,成立;②当,则∴解得.综上所述,.【考点】函数解析式的求解及常用方法二次函数的性质函数恒成立问题【解析】此题暂无解析【解答】解:∵,∴二次函数的对称轴为,∵二次函数的顶点在直线上,∴顶点坐标为.设,∵图像经过点,即,∴,∴,即.若恒成立,则恒成立,∴.①当,即时,成立;②当,则∴解得.综上所述,.19.【答案】解:在中,由余弦定理,得中,由正弦定理,得.(m −2)−4(m −2)x +2m −6<0x 2m −2=0m =2−2<0m −2≠0{m −2<0,Δ=+3m +2<0,m 2{m <2,1<m <2,1<m <21<m ≤2(1)f(2−x)=f(2+x)f(x)x =2y =x −1(2,1)y =f(x)=a(x −2+1)2(−1,−8)−8=a(−1−2+1)2a =−1y =f(x)=−(x −2+1)2y =f(x)=−+4x −3x 2(2)(m −2)f(x)+m >0(m −2)(−+4x −3)+m >0x 2(m −2)−4(m −2)x +2m −6<0x 2m −2=0m =2−2<0m −2≠0{m −2<0,Δ=+3m +2<0,m 2{m <2,1<m <2,1<m <21<m ≤2(1)△CDE E =C +D −2CD ⋅ED ⋅cos ∠EDC =7,C 2D 2E 2△CDE =EC sin ∠EDCCD sin αD ⋅sin 2π于是.由题设知,,于是由知,,则,,在中,.【考点】解三角形余弦定理正弦定理【解析】此题暂无解析【解答】解:在中,由余弦定理,得中,由正弦定理,得.于是.由题设知,,于是由知,,sin α=CD ⋅sin2π3EC ==2×3–√27–√21−−√7(2)0<α<π3(1)cos α===1−αsin 2−−−−−−−−√1−2149−−−−−−√27–√7∠AEB =−α2π3cos ∠AEB =cos(−α)2π3=cos cos α+sin sin α2π32π3=7–√14Rt △EAB BE ===4AE cos ∠AEB 27–√147–√(1)△CDE E =C +D −2CD ⋅ED ⋅cos ∠EDC =7,C 2D 2E 2△CDE =EC sin ∠EDC CD sin αsin α=CD ⋅sin 2π3EC ==2×3–√27–√21−−√7(2)0<α<π3(1)cos α===1−αsin 2−−−−−−−−√1−2149−−−−−−√27–√7AEB =−α2π则,,在中,.20.【答案】(2)由(1)可知=,证明:因为,,,所以,所以==,所以.当且仅当==时取等号.【考点】不等式恒成立的问题【解析】此题暂无解析【解答】此题暂无解答21.【答案】设为第年内树木生长的高度,则=,,.设=,则,.令,因为在区间上是减函数,在区间上是增函数,所以当=时,取得最小值,从而取得最大值,此时=,解得=,因为,,故的可能值为或,又,,即∠AEB =−α2π3cos ∠AEB =cos(−α)2π3=cos cos α+sin sin α2π32π3=7–√14Rt △EAB BE ===4AE cos ∠AEB 27–√147–√a +b +c 5+≥2ab a 2b 6+≥2bc b 2c 6+≥2ac a 2c 52(++)≥5ab +2bc +2ac a 3b 2c 27(++)≥+++2ab +2bc +6ac a 2b 2c 5a 2b 2c 4(a +b +c)225++≥a 2b 2c 2a b c g(t)t +1g(t)f(t +1)−f(t)=−=71+e −0.5t+1.571+e −0.5t+27(−1)e −0.5t+1.5e 0.5(1+)(1+)e −0.5t+2e −0.5t+1.5t ∈N 0≤t ≤5u e −0.5t+1.5g(t)==7u(−1)e 0.5(1+u)(1+u)e 0.57(−1)e 0.5u +(1+)+e 0.5e 0.51u u ∈[,]e −1e 1.5φ(u)=u +e 0.51u φ(u)[,]e −1e −0.25[,]e −0.25e 1.5u e −0.25φ(u)g(t)e −0.5t+1.5e −0.25t 3.5t ∈N 0≤t ≤5t 34g(3)=−7271+e 0.5g(4)=−7271+e 0.5g g(1)=.因此,种植后第或第年内该树木生长最快【考点】根据实际问题选择函数类型【解析】(1)分别计算三种树木在年内的高度得出结论;(2)构造树木的生长高度关于年限的函数,利用换元法求出函数最大值即可得出结论.【解答】树木的高度为(米)树木的高度为(米),g(1)456t B 0.84+=3.360.04×(1−)261−2C f(6)==≈5.171+e −0.5×6+27e e +1。
2022-2023学年全国高中高一上数学人教A版期末试卷(含解析)

2022-2023学年全国高一上数学期末试卷考试总分:146 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息; 2.请将答案正确填写在答题卡上;卷I (选择题)一、 选择题 (本题共计 8 小题 ,每题 5 分 ,共计40分 )1. 已知集合=,=,则=( )A.,]B.(,C.,)D.(,2. 已知四个命题:;;;.以下命题中假命题是( )A.B.C.D.3. 已知,则( )A.B.C.A {x |1<x ≤2}B {x |y =ln(−6+13x −5)}x 2A ∩B [12](12):∃∈R ,sin −cos ≥p 1x 0x 0x 02–√:∀x ∈R ,tan x =p 2sin xcos x:∃∈R,++1≤0p 3x 0x 20x 0:∀x >0,x +≥2p 41x∨p 1p 4∨p 2p 4∨p 1p 3∨p 2p 3tan(α+)π12=−2tan(α+)π3=−1313−3D.4. 若,,点在直线=上,则的最小值为( )A.B.C.D.5. 若=,则在,,…,中,值为零的个数是( )A.B.C.D.6. 已知角的终边上有一点 ,则 A.B.C.D.7. 定义在上的函数满足,且当时,若方程有个不同的实根,则正实数的取值范围是 A.B.C.3a >0b >0P(3,2)l :ax +by 4+2a 3b923+23–√4+3–√6S n sin+sin +⋯+sin (n ∈)π72π7nπ7N +S 1S 2S 2017143144287288αP (3,4)tan α=()43−43−3434R f(x)f(x +4)=f(x)−1≤x ≤3f(x)={ −+1,−1≤x ≤1,x 2−|x −2|+1,1<x ≤3.f(x)=mx 9m ()(,)11018(,16−6)1107–√(,16+6)1107–√(0,16−6)–√D.8. 函数的单调增区间是( )A.B.C.D.二、 多选题 (本题共计 4 小题 ,每题 5 分 ,共计20分 ) 9. 下列关于平面向量的说法中正确的是( )A.已知,均为非零向量,若,则存在唯一实数,使得B.在中,若,则点为边的中点C.已知,均为非零向量,若,则D.若且,则10. 下列几个说法,其中正确的有A.已知函数的定义域是,则的定义域是B.若函数有两个零点,则实数的取值范围是C.函数与的图象交点个数是个D.若函数在区间上的最大值与最小值分别为和,则11. 下列函数中,最小值为的是( )A.B.C.,D.(0,16−6)7–√y =sin(−2x)π4[kπ−,kπ+](k ∈z)3π83π8[kπ+,kπ+](k ∈z)π85π8[kπ−,kπ+](k ∈z)π83π8[kπ+,kπ+](k ∈z)3π87π8a →b →//a →b →λ=λa →b→△ABC =+AD −→−12AB −→−12AC −→−D BC a →b →|+|=|−|a →b →a →b →⊥a →b→⋅=⋅a →c →b →c →≠c →0→=a →b→( )f (x)(,8]12f ()2x (−1,3]f (x)=|−2|−b 2x b 0<b <2y =2x y =x 22f (x)=4+lnx 21+x 1−x [−,]1212M m M +m =82y =+2x +3x 2y =+e x e −xy =sin x +1sin x x ∈(0,)π2y =+23x12. 已知函数,则下列命题中正确的是( )A.函数是奇函数,且在上是减函数B.函数()是奇函数,且在上是增函数C.函数是偶函数,且在上是减函数D.函数()是偶函数,且在上是增函数卷II (非选择题)三、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )13. 若,,则的值域是________.(请用区间表示)14. 在中,内角,,所对的边分别为,,.若,则的值为________.15. 已知两点、满足,,,则=________16. 用表示,中的较小者,则的最大值是________.四、 解答题 (本题共计 6 小题 ,每题 11 分 ,共计66分 )17. 已知全集=,集合=,=.(1)若=,求实数的值;(2)若=,求实数的取值范围. 18. 求值:(1);(2).f(x)=x |x |f(sin x)(−,)1212sin f(x)(−,)1212f(cos x)(0,1)cos f(x)(−1,0)f(x)=2x −5x +3x ∈[1,4)f (x)△ABC A B C a b c tan(+A)=2π4sin 2A sin 2A +A cos 2A(2,1)B(1,1+)3–√=(sin α,cos β)12AB →αβ∈(−,)π2π2α+βmin{a,b}a b f (x)=min {x,}(x >0)log 28xU R A {x |<≤8}2x B {x |x <m −2或x >m +2}A ∩B ∁U m A ∪B B m sin sin −sin cos 25∘215∘245∘35∘tan(−)+tan 3π47π121−tan 7π12=sin(ωx −)π19. 函数的周期为,且,为正整数.(1)求的值;(2)设是的最小值,用“五点法”作出函数在一个周期内的图象. 20. 已知幂函数的图象过点(1)求函数的解析式.(2)求函数的定义域与值域.(3)判断函数单调性,并证明你的结论.21. 解不等式:,其中且.22. 已知=是奇函数(为自然对数的底数).(1)求实数的值;(2)求函数=在上的值域;(3)令=,求不等式的解集.y =sin(ωx −)π4T 2<T <4ωωω1ωy =sin(x −)ω1π4y =f(x)(2,)2–√>(a 2x−11a )x−2a >0a ≠1f(x)−e x ae x e a y +−2λf(x)e 2x e −2x x ∈[0,+∞)g(x)f(x)+x g(x)+g(21o x −3)≥0log 22g 2参考答案与试题解析2022-2023学年全国高一上数学期末试卷一、 选择题 (本题共计 8 小题 ,每题 5 分 ,共计40分 )1.【答案】C【考点】交集及其运算【解析】可求出集合,然后进行交集的运算即可.【解答】∵=,==,∴.2.【答案】D【考点】命题的真假判断与应用【解析】此题暂无解析【解答】此题暂无解答3.【答案】A【考点】B A {x |1<x ≤2}B {x |−6+13x −5>0}x 2两角和与差的三角函数【解析】由题意利用两角差的和的正切公式,求得=的值.【解答】解:∵,则.故选.4.【答案】D【考点】基本不等式及其应用【解析】利用“乘法”与基本不等式的性质即可得出.【解答】由题意可得,=即,则=,当且仅当且=即=,时取等号,故最小值,5.【答案】D【考点】函数的零点与方程根的关系【解析】由于,,…,,=,,…,tan(α+)π3tan[(α+)+]π12π4tan(α+)π12=−2tan(α+)π3=tan[(α+)+]π12π4===−tan(α+)+tan π12π41−tan(α+)⋅tan π12π4−2+11−(−2)⋅113A 13a +2b 4+=13a 4b 2+=(+)(+)2a 3b 2a3b 3a 4b 23++≥3+2=6b a 9a 4b ⋅b a 9a 4b −−−−−−√=b a 9a 4b 3a +2b 4b 1a =236sin >0π7sin >02π7sin >067sin π0sin =−<08π7π7=−<013π6π=014π,,可得到,…,,=,而=,从而可得到周期性的规律,从而得到答案.【解答】由于,,…,,=,,…,,,可得到,…,,=,而=,=,∴,,…,中,值为零的个数是=.6.【答案】A【考点】任意角的三角函数【解析】此题暂无解析【解答】解:因为角的终边上有一点 ,所以 .故选7.【答案】B【考点】函数的零点与方程根的关系【解析】此题暂无解析【解答】解:由题意可得函数是以为周期的周期函数,做出函数与函数的图象,如图所示,sin=−<013π76π7sin =014π7>0S 1>0S 12S 130S 140sin>0π7sin >02π7sin >067sin π0sin =−<08π7π7sin =−<013π76π7sin =014π7>0S 1>0S 12S 130S 140201714×144+1S 1S 2S 2017144×2288αP (3,4)tan α=43A.f(x)4y=f(x)y=mx由图象可得方程 即 在上有个实数根,由解得 .再由方程 在内无解可得,.综上可得 .故选.8.【答案】D【考点】正弦函数的单调性【解析】求三角函数的单调区间,一般要将自变量的系数变为正数,再由三角函数的单调性得出自变量所满足的不等式,求解即可得出所要的单调递增区间.【解答】解:令,解得,函数的递增区间是故选.二、 多选题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )9.【答案】A,B,Cy=−(x −8+1)2=mx +(m −16)x +63x 2=0(7,9)2Δ=(m −16−252>0,)249+7(m −16)+63>0,81+9(m −16)+63>0,7<<9,16−m 2−2<m <16−67–√f(x)=mx (9,10)10m >1m >110<m <16−61107–√B y =sin(−2x)=−sin(2x −)π4π42kπ+<2x −<2kπ+π2π43π2k ∈Z kπ+<x <kπ+3π87π8k ∈Z[kπ+,kπ+](k ∈Z)3π87π8D【考点】平面向量数量积的运算命题的真假判断与应用数量积判断两个平面向量的垂直关系向量的三角形法则平行向量的性质【解析】根据平行向量的性质可判断,由平行四边形法则,可判断,根据平面向量的线性运算可判断;根据反例可判断.【解答】解:由平行向量的基本定理可知,选项是正确的;由平行四边形法则可得,在中,若,则点为边的中点,故正确;因为 ,,又,所以,则,故正确;当,时,满足但,大小方向都不一定相同,故错误.故选.10.【答案】A,B,D【考点】函数的定义域及其求法函数的零点与方程根的关系函数奇偶性的性质【解析】【解答】A B C D A △ABC =+AD −→−12AB −→−12AC −→−D BC B |+=+2⋅++a →b →|2a →2a →b →b →b →2|−=−2⋅++a →b →|2a →2a →b →b →b →2|+|=|−|a →b →a →b →⋅=0a →b →⊥a →b →C ⊥a →c →⊥b →c →⋅=⋅a →c →b →c →a →b →D ABC ≤81解:对于,由题设得,解得,所以的定义域为,故正确;对于,由题设得方程有两个实根,所以函数与有两个交点,可得,故正确;对于,根据与的增减性可知,两函数的图象有个交点,故错误;对于,令,,则,所以为上的奇函数,所以,所以,故正确.故选.11.【答案】A,B【考点】基本不等式在最值问题中的应用【解析】结合二次函数的性质可判断选项;结合指数函数与正弦函数的性质及基本不等式的条件可判断,,直接利用指数函数的性质可判断【解答】解:对,,当且仅当时取等号,故正确;对,,当且仅当时取等号,故正确;对,,等且仅当时取等号,又,故不可能成立,故错误;对,因为,故,故错误.故选.12.【答案】B,C,D【考点】函数单调性的性质与判断复合函数的单调性A <≤8122x −1<x ≤3f ()2x (−1,3]B |−2|=b 2x y =|−2|2x y =b 0<b <2C y =2x y =x 23D g(x)=ln x 21+x 1−x x ∈[−,]1212g(−x)=ln (−x)21−x 1+x =ln =−g(x)x 2()1+x 1−x −1g(x)[−,]1212g +g =0(x)max (x)min M +m =4+g +4+g =8(x)max (x)min ABD A B C D/A y =+2x +3=+2≥2x 2(x +1)2x =−1A B y =+≥2=2e x e −x ⋅e x e −x −−−−−−√x =0B C y =sin x +≥2=21sin x sin x ⋅1sin x −−−−−−−−−√sin x =1sin x x ∈(0,)π2C D y =>03x y =+2>23x D AB函数奇偶性的性质与判断【解析】根据题意,由的解析式分析的奇偶性和单调性,由此依次分析选项中函数的奇偶性和单调性,综合可得答案.【解答】解:,∴是奇函数,是奇函数,是偶函数,∴和是奇函数,和是偶函数,∴在上是增函数,∴在上是增函数,在上是减函数,∴在上是增函数,在上是减函数,故错误;正确;当时,,.在( 上单调速增,∴在( )上单调递增,故正确;当时,,在上单调递增,∴在上单调递增,故正确.故选.三、 填空题 (本题共计 4 小题 ,每题 5 分 ,共计20分 )13.【答案】【考点】函数的值域及其求法【解析】利用分离参数法即可求解.【解答】解:若,,f(x)f(x)f (−x)=−x|−x|=−x|x|=−f (x)f (x)y =sin x y =cos x f (sin x)sin(f (x))f (cos x)cos(f (x))f (x)=x|x|={,x ≥0,x 2−,x <0,x 2f (x)R y =sin x (−,)1212y =cos x (0,1)f (sin x)(−,)1212f (cos x)(0,1)A C x ∈(−,)1212f (x)∈(−,)1414y =sin x −,)1414sin(f (x))−,1212B x ∈(−1,0)f (x)∈(−1,0)y =cos x (−1,0)cos(f (x))(−1,0)D BCD [−,)3437f(x)=2x −5x +3x ∈[1,4)(x)==2−2(x +3)−11可得,∵,∴,∴.故答案为:.14.【答案】【考点】两角和与差的三角函数【解析】利用两角和的正切公式,求出的值,再利用同角三角函数的基本关系,求得要求式子的值.【解答】在中,若,∴,则,15.【答案】或.【考点】两角和与差的三角函数【解析】运用向量的加减运算和特殊角的三角函数值,可得所求和.【解答】两点、满足,可得==,f (x)==2−2(x +3)−11x +311x +3x ∈[1,4)<≤11711x +3114f(x)∈[−,)3437[−,)343725tan A △ABC tan(+A)=2=π41+tan A 1−tan Atan A =13====sin 2A sin 2A +A cos 22sin A cos A 2sin A cos A A +cos 22tan A 2tan A +123+123250−π3A(2,1)B(1,1+)3–√=(sin α,cos β)12AB →(−1,)123–√(−,)123–√2(sin α,cos β)β=–√即为,,,,可得,=,则=或.16.【答案】【考点】函数的最值及其几何意义【解析】此题暂无解析【解答】解:作出和的图象,根据表示,中的较小者,可得的图象如图所示,结合图象,可得最大值为.故答案为:.四、 解答题 (本题共计 6 小题 ,每题 11 分 ,共计66分 )17.【答案】由已知得=,=,∵=,∴,∴=.∵=,∴⊑.sin α=−12cos β=3–√2αβ∈(−,)π2π2α=−π6β±π6α+β0−π32y =x log 2y =8xmin{a,b}a b f (x)f(x)22A {x |−1<x ≤3}B ∁U {x |m −8≤x ≤m +2}A ∩B ∁U {x |≤x ≤3}m A ∪B B A B∴或,∴或.即实数的取值范围为.【考点】交、并、补集的混合运算【解析】此题暂无解析【解答】此题暂无解答18.【答案】原式===.原式.【考点】两角和与差的三角函数【解析】(1)直接利用诱导公式的应用和特殊角三角函数的值的应用求出结果.(2)利用三角函数关系式的恒等变换和诱导公式的应用及和角公式的运用求出结果.【解答】原式===.原式.19.【答案】解:(1)函数的周期,∵,∴,即,m −4>3m +2≤−3m >5m ≤−3m {m |m >6或m ≤−3}sin sin(+)−sin(−)cos 25∘180∘35∘270∘25∘35∘sin (−sin )−(−cos )cos 25∘35∘25∘35∘cos cos −sin sin 25∘35∘25∘35∘cos(+)=cos 60=25∘35∘12==tan(+)=tan =tan(π−)=−tan =−tan +tan π47π121−tan tanπ47π12π47π125π6π6π63–√3sin sin(+)−sin(−)cos 25∘180∘35∘270∘25∘35∘sin (−sin )−(−cos )cos 25∘35∘25∘35∘cos cos −sin sin 25∘35∘25∘35∘cos(+)=cos 60=25∘35∘12==tan(+)=tan =tan(π−)=−tan =−tan +tan π47π121−tan tanπ47π12π47π125π6π6π63–√3T =2πω2<T <42<<42πω<<112ωπω<ππ则,∵为正整数,∴或;(2)∵是的最小值,∴,则,列表:则对应的图象如图:【考点】五点法作函数y=Asin (ωx+φ)的图象【解析】(1)利用三角函数的周期公式即可得结论;(2)用“五点法”列表,即可作出函数在一个周期(闭区间)上的简图;【解答】解:(1)函数的周期,∵,∴,即,则,∵为正整数,∴或;(2)∵是的最小值,∴,则,列表:<ω<ππ2ωω=2ω=3ω1ω=2ω1y =sin(x −)=sin(2x −)ω1π4π4x π83π85π87π89π82x −π40π2π3π22πsin(2x−)010−1T =2πω2<T <42<<42πω<<112ωπ<ω<ππ2ωω=2ω=3ω1ω=2ω1y =sin(x −)=sin(2x −)ω1π4π4x π83π85π87π89π82x −π40π2π3π22πsin(2x−)010−1则对应的图象如图:20.【答案】解:(1)由题意可设,又函数图象过定点,∴,∴,∴,(2)由函数可知定义域为,值域为,(3)为增函数,理由如下设,,且,则,∴为增函数.【考点】幂函数的性质幂函数的概念、解析式、定义域、值域【解析】(1)先设出幂函数的解析式,由于过定点,从而可解得函数的解析式,(2)由解析式直接求出定义域和值域,(3)利用函数的单调性的定义证明即可.【解答】解:(1)由题意可设,又函数图象过定点,∴,∴,∴,(2)由函数可知定义域为,值域为,(3)为增函数,理由如下设,,且,则,∴为增函数.21.【答案】解:当时,由,得,即,解得;当时,由,得,即,解得.f(x)=x α(2,)2–√=2α2–√α=12f(x)=x −√f(x)=x −√[0,+∞)[0,+∞)f(x)x 1∈[0,+∞)x 2<x 1x 2f()−f()=−=<0x 1x 2x 1−−√x 2−−√−x 1x 2+x 1−−√x 2−−√f(x)f(x)=x α(2,)2–√=2α2–√α=12f(x)=x −√f(x)=x −√[0,+∞)[0,+∞)f(x)x 1∈[0,+∞)x 2<x 1x 2f()−f()=−=<0x 1x 2x 1−−√x 2−−√−x 1x 2+x 1−−√x 2−−√f(x)a >1>(a 2x−11a)x−2>a 2x−1a 2−x 2x −1>2−x x >10<a <1>(a 2x−11a)x−2>a 2x−1a 2−x 2x −1<2−x x <1(1,+∞)∴当时,原不等式的解集为;当时,原不等式的解集为.【考点】指、对数不等式的解法【解析】分和,由指数函数的性质化指数不等式为一次不等式求得解集.【解答】解:当时,由,得,即,解得;当时,由,得,即,解得.∴当时,原不等式的解集为;当时,原不等式的解集为.22.【答案】的定义域为,因为为奇函数,所以=,故=,即=.由检验知满足题目要求;设,所以\,设===,,①当时,,,所以值域为;②当时,,,所以值域为;的定义域为,因为为奇函数,所以====,故为奇函数.下面判断的单调性设,则,因为,故,所以,故在上单调递增,所以由,得,又为奇函数,即,所以,∴,解得或,故原不等式的解集为.【考点】奇偶性与单调性的综合函数奇偶性的性质与判断a >1(1,+∞)0<a <1(−∞,1)a >10<a <1a >1>(a 2x−11a)x−2>a 2x−1a 2−x 2x −1>2−x x >10<a <1>(a 2x−11a)x−2>a 2x−1a 2−x 2x −1<2−x x <1a >1(1,+∞)0<a <1(−∞,1)f(x)R f(x)f(0)01−a 0a 1−=t(t ≥0)e x 1e x +=+2e 2x 1e 2xt 2y h(t)−2λt +2t 2(t −λ+2−)2λ2t ≥0λ≤0h(t)∈[h(0)+∞)[2,+∞)λ>0h(t)∈[h(λ)+∞)[2−,+∞)λ2g(x)R f(x)g(−x)f(−x)−x −f(x)−x −[f(x)+x]−g(x)g(x)g(x)<x 1x 2g()−g()=(−)−(−)+(−)=(−)(1+)+−x 1x 2e x 1e x 21e x 11e x 2x 1x 2e x 1e x 21e +x 1x 2x 1x 2<x 1x 2(−)(1+)<0,−<0e x 1e x 21e +x 1x 2x 1x 2g()<g()x 1x 2g(x)R g(x)+g(21o x −3)≥0log 22g 2g(lo x)≥−g(21o x −3)g 22g 2g(x)g(lo x)≥g(−21o x +3)g 22g 2lo x ≥−21o x +3g 22g 2lo x +21o x −3≥0g 22g 2x ≥20<x ≤18(0,]∪[2,+∞)18【解析】(1)由奇函数的性质容易求得=,注意需要验证;(2)换元后,分类讨论即可得解;(3)先判断函数的奇偶性及单调性,进而将原不等式转化为,由此得解.【解答】的定义域为,因为为奇函数,所以=,故=,即=.由检验知满足题目要求;设,所以\,设===,,①当时,,,所以值域为;②当时,,,所以值域为;的定义域为,因为为奇函数,所以====,故为奇函数.下面判断的单调性设,则,因为,故,所以,故在上单调递增,所以由,得,又为奇函数,即,所以,∴,解得或,故原不等式的解集为.a 1g(x)lo x +21o x −3≥0g 22g 2f(x)R f(x)f(0)01−a 0a 1−=t(t ≥0)e x 1e x +=+2e 2x 1e 2xt 2y h(t)−2λt +2t 2(t −λ+2−)2λ2t ≥0λ≤0h(t)∈[h(0)+∞)[2,+∞)λ>0h(t)∈[h(λ)+∞)[2−,+∞)λ2g(x)R f(x)g(−x)f(−x)−x −f(x)−x −[f(x)+x]−g(x)g(x)g(x)<x 1x 2g()−g()=(−)−(−)+(−)=(−)(1+)+−x 1x 2e x 1e x 21e x 11e x 2x 1x 2e x 1e x 21e +x 1x 2x 1x 2<x 1x 2(−)(1+)<0,−<0e x 1e x 21e +x 1x 2x 1x 2g()<g()x 1x 2g(x)R g(x)+g(21o x −3)≥0log 22g 2g(lo x)≥−g(21o x −3)g 22g 2g(x)g(lo x)≥g(−21o x +3)g 22g 2lo x ≥−21o x +3g 22g 2lo x +21o x −3≥0g 22g 2x ≥20<x ≤18(0,]∪[2,+∞)18。
第07讲:第四章 三角函数(测)(基础卷)(含答案解析)
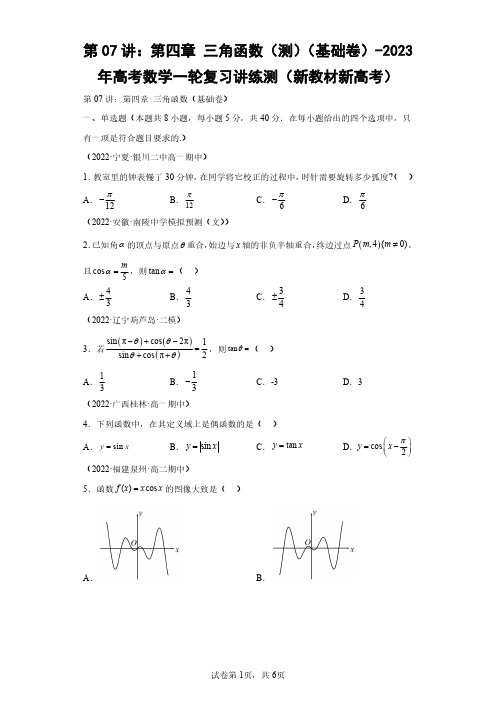
第07讲:第四章三角函数(测)(基础卷)-2023年高考数学一轮复习讲练测(新教材新高考)第07讲:第四章三角函数(基础卷)一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)(2022·宁夏·银川二中高一期中)1.教室里的钟表慢了30分钟,在同学将它校正的过程中,时针需要旋转多少弧度?()A .12π-B .12πC .6π-D .6π(2022·安徽·南陵中学模拟预测(文))2.已知角α的顶点与原点θ重合,始边与x 轴的非负半轴重合,终边过点()(),40P m m ≠,且cos 5mα=,则tan α=()A .43±B .43C .34±D .34(2022·辽宁葫芦岛·二模)3.若()()()sin πcos 2π1sin cos π2θθθθ-+-=++,则tan θ=()A .13B .13-C .-3D .3(2022·广西桂林·高一期中)4.下列函数中,在其定义域上是偶函数的是()A .sin y x=B .sin y x=C .tan y x=D .cos 2y x π⎛⎫=- ⎪⎝⎭(2022·福建泉州·高二期中)5.函数()cos f x x x =的图像大致是()A .B .C .D .(2022·四川省资中县第二中学高一阶段练习(理))6.已知,αβ都是锐角,()35sin ,cos 513ααβ=+=-,则cos β=()A .5665-B .1665-C .1665D .5665(2022·贵州六盘水·高一期中)7.我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”现有一类似问题,不确定大小的圆柱形木材,部分埋在墙壁中,其截面如图所示.用锯去锯这木材,若锯口深2CD =2AB =,则图中 ACB与弦AB 围成的弓形的面积为()A .22π-B .23πC .32π-D .33π-(2022·湖南·长沙市南雅中学高二阶段练习)8.已知()2cos 2cos f x wx wx wx =+,(0w >),若函数在区间,2ππ⎛⎫ ⎪⎝⎭内不存在对称轴,则w 的范围为()A .1130,,634⎛⎤⎡⎤ ⎥⎢⎝⎦⎣⎦B .1230,,334⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦ C .1120,,633⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦D .1250,336⎛⎤⎡⎤ ⎥⎢⎥⎝⎦⎣⎦二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)(2022·广西河池·高一期末)9.在360360-︒︒ 范围内,与410-︒角终边相同的角是()A .50-︒B .40-︒C .310︒D .320︒(2022·辽宁·沈阳市奉天高级中学高一期中)10.为了得到函数π()sin 36f x x ⎛⎫=- ⎪⎝⎭的图象,只需将函数()sin g x x =的图象()A .所有点的横坐标缩短到原来的13,纵坐标不变,再将所得图象向右平移π18个单位长度B .所有点的横坐标伸长到原来的3倍,纵坐标不变,再将所得图象向右平移π18个单位长度C .向右平移π6个单位长度,再将所得图象所有点的横坐标缩短到原来的13,纵坐标不变D .向右平移π18个单位长度,再将所得图象所有点的横坐标缩短到原来的13,纵坐标不变(2022·广东·佛山市顺德区容山中学高一期中)11.给出下列命题中,正确的是()A .存在实数α,使sin cos 1αα=B .存在实数α,使sin cos αα+=C .函数3sin 2y x π⎛⎫=+ ⎪⎝⎭是偶函数D .若α,β是第一象限的角,且αβ>,则sinαsinβ>(2022·黑龙江大庆·高三阶段练习(文))12.若tan tan6tan6αααα-=+,则α的值可能为()A .15π-B .215πC .415πD .1415π三、填空题:(本题共4小题,每小题5分,共20分,其中第16题第一空2分,第二空3分.)(2022·江西·高一阶段练习)13.已知()()2sin 32f x x ϕ=+是奇函数,则ϕ=__________.(写出一个值即可)(2022·全国·高三专题练习)14.函数()sin ,()(|),0,|f x A x A ωϕωϕπ=+><的部分图象如图,则4f π⎛⎫= ⎪⎝⎭___________.(2022·江苏·徐州市王杰中学高一阶段练习)15.已知()4cos 5αβ+=,()4cos 5αβ-=-,则cos cos αβ的值为________.(2022·北京育才学校模拟预测)16.已知函数()()sin 06f x x πωω⎛⎫=-> ⎪⎝⎭在[]0,π有且仅有3个零点,则函数()f x 在[]0,π上存在_____个极小值点,请写出一个符合要求的正整数ω的值______.四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分,解答应写出文字说明、证明过程或演算步骤.)(2022·辽宁省康平县高级中学高一阶段练习)17.已知()()()sin 3sin 232cos cos 2f παπααπαπα⎛⎫+-+ ⎪⎝⎭=⎛⎫--- ⎪⎝⎭.(1)化简()f α.(2)已知tan 3α=,求()f α的值.(2022·北京市第一六一中学高三阶段练习)18.已知3π是函数2()2sin cos 2cos 1f x a x x x =++的一个零点.(1)求实数a 的值;(2)求()f x 单调递减区间.(2022·江苏省阜宁中学高一阶段练习)19.如图,现要在一块半径为1m ,圆心角为π3的扇形白铁片AOB 上剪出一个平行四边形MNPQ ,使点P 在圆弧AB 上,点Q 在OA 上,点,M N 在OB 上,设BOP θ∠=,平行四边形MNPQ 的面积为S .(1)求S 关于θ的函数关系式;(2)求S 的最大值及相应的θ角.(2022·浙江·杭州市余杭高级中学高二学业考试)20.已知函数()()2sin cos f x a x x x x =-∈R ,若__________.条件①:0a >,且()f x 在x ∈R 时的最大值为1条件②:62f π⎛⎫= ⎪⎝⎭.请写出你选择的条件,并求函数()f x 在区间,43ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.注:如果选择条件①和条件②分别解答,按第一个解答计分.(2022·河南省嵩县第一高级中学高一阶段练习)21.已知函数π()2sin 23f x x ⎛⎫=- ⎪⎝⎭.(1)利用“五点法”完成下面的表格,并画出()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象;π23x -x()f x(2)解不等式()1f x ≥.(2022·江苏省镇江中学高一阶段练习)22.已知函数()sin()0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的部分图象如图所示.(1)求函数()f x 的解析式;(2)先将函数()f x 的图象向右平移3π个单位长度,再将所得图象上各点的纵坐标不变,横坐标变为原来的2倍,得到()g x 的图象.(i )若0m >,当[0,]x m ∈时,()g x 的值域为[2],求实数m 的取值范围;(ii )若不等式2()(21)()10g x t g x t -+--≤对任意的,32x ππ⎡⎤∈⎢⎥⎣⎦恒成立,求实数t 的取值范围.参考答案:1.A【分析】先由条件确定时针旋转的度数,再由弧度与角度的关系求对应的弧度数.【详解】将钟表校正的过程中,需要顺时针旋转时针15 ,其大小为15- ,故时针需要旋转12π-弧度,故选:A.2.A【分析】根据任意角的三角函数值的定义,即可求解.【详解】解:cos 5m α=,解得:3m =±,故44tan 3m α==±,故选:A 3.C【分析】利用诱导公式,弦化切进行计算.【详解】()()()sin πcos 2πsin cos 1sin cos πsin cos 2θθθθθθθθ-+-+==++-,分子分母同除以cos θ,tan 11tan 12θθ+=-,解得:tan 3θ=-故选:C 4.B【分析】根据奇偶性定义,结合三角函数的奇偶性可直接得到结果.【详解】对于A ,sin y x = 定义域为R ,()sin sin x x -=-,sin y x ∴=为奇函数,A 错误;对于B ,sin y x = 定义域为R ,()sin sin sin x x x -=-=,sin y x ∴=为偶函数,B 正确;对于C ,tan y x = 定义域为(),22k k k ππππ⎛⎫-+∈ ⎪⎝⎭Z ,即定义域关于原点对称,()tan tan x x -=-,tan y x ∴=为奇函数,C 错误;对于D ,cos sin 2y x x π⎛⎫=-= ⎪⎝⎭ 定义域为R ,()sin sin x x -=-,cos 2y x π⎛⎫∴=- ⎪⎝⎭为奇函数,D 错误.故选:B.5.A【分析】先根据函数奇偶性的概念可知()()f x f x -=-,即函数()f x 为奇函数,排除选项D ;再利用三角函数的性质排除BC 即得.【详解】()cos()cos ()f x x x x x f x -=--=-=- ,∴函数()f x 为奇函数,排除选项D ;当(0,2x π∈时,0x >,0cos 1x <<,0()f x x ∴<<,排除选项BC .故选:A .6.C【分析】由[]cos cos ()βαβα=+-,利用两角差的余弦公式求解.【详解】因为,αβ都是锐角,所以0αβ<+<π,又3sin 5α=,5cos()13αβ+=-,所以4cos 5α=,12sin()13αβ+=,所以[]cos cos ()βαβα=+-,cos()cos sin()sin αβααβα=+++,541231613513565=-⨯+⨯=,故选:C.7.B【分析】设圆的半径为r ,利用勾股定理求出r ,再根据扇形的面积及三角形面积公式计算可得;【详解】解:设圆的半径为r ,则(2OD r CD r =-=--,112AD AB ==,由勾股定理可得222OD AD OA +=,即(2221r r ⎡⎤-+=⎣⎦,解得2r =,所以2OA OB ==,2AB =,所以3AOB π∠=,因此221222233MBB AOB S S S ππ=-=⨯⨯= 弓形扇形.故选:B 8.C【分析】先通过三角恒等变换将()f x 化简成正弦型函数,再结合正弦函数性质求解即可.【详解】函数化简得()2cos 212sin 216f x wx wx wx π⎛⎫=++=++ ⎪⎝⎭,由()262wx k k πππ+=+∈Z ,可得函数的对称轴为()32k x k wππ+=∈Z ,由题意知,322k w πππ+≤且()132k w πππ++≥,即13436k k w ++≤≤,k ∈Z ,若使该不等式组有解,则需满足13436k k ++≤,即23k ≤,又0w >,故3406k +≤,即43k >-,所以4233k -<≤,又k ∈Z ,所以0k =或1k =,所以1120,,633w ⎛⎤⎡⎤∈ ⎥⎢⎥⎝⎦⎣⎦.9.AC【分析】利用终边相同的角的定义求解.【详解】因为50410360︒︒-=-+︒,3104102360=-+⨯︒︒︒,所以与410-︒角终边相同的角是50-︒和310︒,故选:AC .10.AC【分析】根据三角函数的图象变换规律逐个分析可得答案.【详解】将函数()sin g x x =的图象所有点的横坐标缩短到原来的13,纵坐标不变,再将所得图象向右平移π18个单位长度,可以得到函数π()sin 36f x x ⎛⎫=- ⎪⎝⎭的图象,A 正确.将函数()sin g x x =的图象所有点的横坐标伸长到原来的3倍,纵坐标不变,再将所得图象向右平移π18个单位长度,可以得到函数1π()si 4n 53f x x ⎛⎫=- ⎪⎝⎭的图象,B 不正确.将函数()sin g x x =的图象向右平移6π个单位长度,再将所得图象所有点的横坐标缩短到原来的13,纵坐标不变,可以得到函数π()sin 36f x x ⎛⎫=- ⎪⎝⎭的图象,C 正确.将函数()sin g x x =的图象向右平移π18个单位长度,再将所得图象所有点的横坐标缩短到原来的13,纵坐标不变,可以得到函数π()s 18in 3f x x ⎛⎫=- ⎪⎝⎭,D 不正确.故选:AC 11.BC【分析】A 由正弦的倍角公式直接判断;B 由辅助角公式进行判断即可;C 通过诱导公式及余弦函数的性质即可判断;D 直接取特殊值判断即可.【详解】对于A ,由sin cos 1αα=,得sin22α=,矛盾,错误;对于B ,由sin cos αα+=4πα⎛⎫+= ⎪⎝⎭4πα=即成立,正确;对于C ,3sin cos 2y x x π⎛⎫=+=- ⎪⎝⎭,显然是偶函数,正确;对于D ,取136απ=,3πβ=,α,β是第一象限的角,且αβ>,但sin sin αβ<,错误.故选:BC .12.ABD【分析】由题意易知10α≠,再根据两角差的正切公式,可知tan tan 63παα⎛⎫-= ⎪⎝⎭,进而求得6()3k k πααπ=-+∈Z ,由此即可得到()155k k ππα=-+∈Z ,对k 取值,逐项判断即可得到结果.【详解】由tan tan 6tan 6αααα=,可知()tan 1tan 6ααα=+,当10α=,即tan 3α=-时,即,()6k k παπ=-+∈Z 时,tan ,tan 6tan 604αααα-+=,显然tan tan6tan6αααα=+不成立,故1tan 0α≠;tan 6α=,则tan tan 63παα⎛⎫-= ⎪⎝⎭,所以6()3k k πααπ=-+∈Z ,即,()155k k ππα=-+∈Z ,当0k =时,15απ=-,当1k =时,215πα=,当5k =时,1415πα=,令411555k πππ-+=,得53k =∉Z ,故α的值不可能为415π.故选:ABD.13.2π(答案不唯一)【分析】根据正弦函数的性质计算可得;【详解】解:因为()()2sin 32f x x ϕ=+是奇函数,所以2k ϕπ=,Z k ∈,解得2k πϕ=,Z k ∈.故答案为:2π(答案不唯一)14.【分析】由三角函数的图象与性质求出解析式后求解【详解】由图可知2A =,427(33242T πππ=-=,故24Tπω==,将7(,2)24π-代入解析式得7sin()16πϕ+=-,又||ϕπ<,得3πϕ=,故()()2sin 43f x x π=+,4f π⎛⎫= ⎪⎝⎭故答案为:15.0【分析】根据两角和与差的余弦公式展开,联立方程即可解得.【详解】()4cos cos cos sin sin 5αβαβαβ+=-= ……(1)()4cos cos cos sin sin 5αβαβαβ-=+=-……(2)由(1)+(2)得:442cos cos 055αβ⎛⎫=+-= ⎪⎝⎭cos cos 0αβ∴=故答案为:016.13【分析】首先求6x πω-的范围,根据正弦函数的图象,确定极小值点个数,以及根据端点值,列不等式求ω的范围.【详解】[]0,x π∈ ,,666t x πππωωπ⎡⎤∴=---⎢⎥⎣⎦,由条件可知sin y t =在区间,66ωππ⎡⎤-π-⎢⎥⎣⎦有3个零点,∴由函数图象可知:有1个极小值点,两个极大值点,且236ωππ≤π-<π,解得:131966ω≤<,其中满足条件的一个正整数是3.故答案为:1;317.(1)cos 3sin 2sin cos αααα+-+;(2)2-.【分析】(1)由诱导公式进行化简,即可求得()f α;(2)由sin tan cos ααα=,代入即可求值.(1)()()()sin 3sin cos 3sin 232sin cos 2cos cos 2f παπααααπαααπα⎛⎫+-+ ⎪+⎝⎭==-+⎛⎫--- ⎪⎝⎭;(2)∵tan 3α=,∴cos 3sin 13tan 133()22sin cos 12tan 123f ααααααα+++⨯====--+--⨯.18.(1)(2),,63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z【分析】(1)利用函数的零点的定义,求得实数a 的值.(2)利用三角恒等变化化简函数的解析式,再利用余弦函数的单调性求得()f x 的单调递减区间.【详解】(1)解:因为2()2sin cos 2cos 1f x a x x x =++,所以()sin 2cos 22f x a x x =++由题意可知03f π⎛⎫= ⎪⎝⎭,即22sin cos 20333f a πππ⎛⎫⎪⎭= +⎝+=,即12032f π⎛⎫⎭- ⎪+⎝==,解得a =(2)解:由(1)可得()cos 2222cos 223f x x x x π=-+=⎛⎫ ⎪⎝⎭++,函数cos y x =的递减区间为[]2,2,k k k Z πππ+∈.令222,3k x k k ππππ<+<+∈Z ,得,63k x k k ππππ-<<+∈Z ,所以()f x 的单调递减区间为,,63k k k ππππ⎡⎤-+∈⎢⎥⎣⎦Z .19.(1)1πsin 22,(0,)263S θθθ=+∈(2)S 2,此时6πθ=【分析】(1)分别过,P Q 作PD OB ⊥于D ,QE OB ⊥于E ,则四边形QEDP 为矩形,则MN QP ED ==,直接利用平行四边形的面积公式求解即可.(2)利用辅助角公式恒等变形求其最值即可.【详解】(1)分别过,P Q 作PD OB ⊥于D ,QE OB ⊥于E ,则四边形QEDP 为矩形.由扇形半径为1m ,得sin PD θ=,cos OD θ=.在Rt △OEQ 中,33OE ==,cos 3MN QP ED OD OE θθ===-=-,2(cos )sin sin cos sin 33S MN PD θθθθθθ=⋅=-=-1sin 222θθ=,π(0,)3θ∈.(2)由(1)得1πsin 22)26S θθθ=+∵π(0,)3θ∈,∴ππ5π2(,)666θ+∈,∴π1sin(2(,1]62θ+∈当π6θ=时,2max m 6S =.20.选①或选②结论相同,最大值为0;最小值为12--.【分析】(1)根据二倍角的正弦、余弦公式和辅助角公式可得()()2f x x ϕ=--(其中tan ϕ=),选条件①或②都算出1a =,结合正弦函数的单调性即可求出结果.【详解】()2sin cos f x a x x x=-1cos2sin222a x x +=-sin22a x x =()22x ϕ=--,其中tan a ϕ=,122=-,解得1a =,得3πϕ=,所以()sin 232f x x π⎛⎫=-- ⎪⎝⎭,由,43x ππ⎡⎤∈-⎢⎥⎣⎦,得52,363x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,min 1()f x =--当233x ππ-=时,max (0)f x =;若选②,131624f a a π⎛⎫=⋅== ⎪⎝⎭,得3πϕ=,所以()sin 23f x x π⎛⎫=-- ⎪⎝⎭,由,43x ππ⎡⎤∈-⎢⎥⎣⎦,得52,363x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,min 1()f x =--当233x ππ-=时,max (0)f x =.21.(1)答案见解析(2)π7π,π()412k k k π⎡⎤++∈⎢⎥⎣⎦Z 【分析】(1)根据正弦函数的五点作图法可完成表格,利用五点作图法可得图象;(2)根据函数图象列式可求出结果.(1)完成表格如下:π23x -0π2π3π22πx6π5π122π311π127π6()f x 0202-0()f x 在区间π7π,66⎡⎤⎢⎥⎣⎦上的图象如图所示:(2)不等式()1f x ≥,即1sin 232x π⎛⎫-≥ ⎪⎝⎭.由ππ5π2π22π,636k x k k +≤-≤+∈Z ,解得π7πππ,412k x k k +≤≤+∈Z .故不等式()1f x ≥的解集为π7ππ,π()412k k k ⎡⎤++∈⎢⎥⎣⎦Z .22.(1)()2sin(2)3f x x π=+(2)55,63m ππ⎡⎤∈⎢⎥⎣⎦;1,3⎡⎫-+∞⎪⎢⎣⎭【分析】(1)由图象的最小值求得A ,函数的最小正周期求得ω,再求得ϕ,即可求出函数的解析式;(2)(i )利用三角函数的平移和伸缩变换,先求出()2sin 3g x x π⎛⎫=- ⎪⎝⎭,再由[0,]x m ∈,求出3x π-的范围,即可得出()g x 的值域为[2],m 的取值范围;(ii )利用恒成立将不等式转化为2(21)10n t n t -+--≤对任意的[]0,1n ∈恒成立,设()[]2(21)1,0,1n t n t n h n -+--∈=,对其对称轴进行讨论即可得出答案.【详解】(1)根据函数()sin()0,0,02f x A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的部分图象可得:2A =,332732441264T ππππωω⎛⎫=⋅=--=⇒= ⎪⎝⎭,又因为732122ππϕ⋅+=,所以3πϕ=,所以()2sin(2)3f x x π=+.(2)由(1)知,()2sin(2)3f x x π=+,先将函数()f x 的图象向右平移3π个单位长度,可得:2sin(2)3y x π=-,再将所得图象上各点的纵坐标不变,横坐标变为原来的2倍,得到()2sin 3g x x π⎛⎫=- ⎪⎝⎭.(i )[0,]x m ∈,[,333x m πππ-∈--,2sin 232π⎛⎫-=-= ⎪⎝⎭4,323m πππ⎡⎤-∈⎢⎥⎣⎦,所以55,63m ππ⎡⎤∈⎢⎥⎣⎦.(ii )不等式2()(21)()10g x t g x t -+--≤对任意的,32x ππ⎡⎤∈⎢⎥⎣⎦恒成立,令()[]2sin ,2sin ,,0,,3260,1333n g x x x x x ππππππ⎡⎤⎡⎤∈⎢⎢⎥⎛⎫⎛⎫==--∈-∈ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦,所以[]0,1n ∈,所以上式:不等式2(21)10n t n t -+--≤对任意的[]0,1n ∈恒成立,令()[]2(21)1,0,1n t n t n h n -+--∈=,对称轴为12n t =+,①11022t t +≤⇒≤,()()()max 112110h n h t t ==-+--≤,则13t ≥-,所以103-≤≤t .②11022t t +>⇒>,()()max 010h n h t ==--≤,则1t ≥-,所以0t >.故实数t 的取值范围为:1,3⎡⎫-+∞⎪⎢⎣⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2022-2023学年高一数学上学期期末分类汇总专题07 三角函数 (单选+多选)一、单选题1.函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,则512f π⎛⎫⎪⎝⎭的值为( )A .6B .3C .2D .1- 2.已知3cos 45πα⎛⎫-= ⎪⎝⎭,512sin 413πβ⎛⎫+=- ⎪⎝⎭,3,44ππα⎛⎫∈ ⎪⎝⎭,0,4πβ⎛⎫∈ ⎪⎝⎭,则()sin αβ+的值为( ) A .1665- B .5665 C .6365- D .33653.中国折扇有着深厚的文化底蕴.如图所示,在半径为20cm 的半圆O 中作出两个扇形OAB 和OCD ,用扇环形ABDC (图中阴影部分)制作折扇的扇面.记扇环形ABDC 的面积为1S ,扇形OAB 的面积为2S ,当1251S S -OCD 的半径为( )A .()1051cmB .(1035cmC .()551cmD .(35cm4.32tan 3π⎛⎫-⎪⎝⎭的值是( ) A 3B 3C .3-D .35.已知角θ为第四象限角,则点()sin ,tan P θθ位于( ) A .第一象限B .第二象限C .第三象限D .第四象限6.若α是三角形的一个内角,且1sin cos 5αα+=,则三角形的形状为( )A .钝角三角形B .锐角三角形C .直角三角形D .无法确定 7.与390-︒角的终边相同的最小正角是( )A .30-︒B .30︒C .60︒D .330︒8.“06x π<<”是“1sin 2x <”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分又不必要条件 9.若角α的终边过点(4,3)P -,则2sin cos αα+的值为( ) A .25-B .25C .25-或25D .110.为了得到函数sin 26y x π⎛⎫=- ⎪⎝⎭的图象,可以将函数sin 2y x =的图象( )A .向左平移6π个单位 B .向右平移6π个单位 C .向左平移12π个单位 D .向右平移12π个单位11.在直角坐标系中,已知圆C 的圆心在原点,半径等于1 ,点P 从初始位置()0,1开始,在圆C 上按逆时针方向,以角速度2rad /s 9π均速旋转3s 后到达P '点,则P '的坐标为( )A .1,2⎛ ⎝⎭B .21⎫-⎪⎪⎝⎭C .1,2⎛- ⎝⎭D .12⎛⎫- ⎪ ⎪⎝⎭12.已知ln3a =,23πsin 3b =,233c -=,则a ,b ,c 的大小关系是( ). A .a b c >>B .a c b >>C .c b a >>D .c a b >>13.电影《长津湖》中,炮兵雷公牺牲的一幕看哭全网,他的原型是济南英雄孔庆三.因为前沿观察所距敌方阵地较远,需要派出侦察兵利用观测仪器标定目标,再经过测量和计算指挥火炮实施射击.为了提高测量和计算的精度,军事上通常使用密位制来度量角度,将一个圆周分为6000等份,每一等份的弧所对的圆心角叫做1密位.已知我方迫击炮连在占领阵地后,测得敌人两地堡之间的距离是54米,两地堡到我方迫击炮阵地的距离均是1800米,则我炮兵战士在摧毁敌方一个地堡后,为了快速准确地摧毁敌方另一个地堡,需要立即将迫击炮转动的角度α=( ).注:(ⅰ)当扇形的圆心角小于200密位时,扇形的弦长和弧长近似相等;(ⅱ)取π等于3进行计算. A .30密位B .60密位C .90密位D .180密位14.正割()secant 及余割()cosecant 这两个概念是由伊朗数学家阿布尔⋅威发首先引入的.定义正割1sec cos αα=,余割1csc sin αα=.已知m 为正实数,且22csc tan 15m x x ⋅+≥对任意的实数π,2k x x k ⎛⎫≠∈ ⎪⎝⎭Z 均成立,则m 的最小值为( ) A .1B .4C .8D .915.sin390°的值是( )A .12 B C . D .12-16.已知1sin 63πα⎛⎫+= ⎪⎝⎭,且,3παπ⎛⎫∈ ⎪⎝⎭,则5cos 6πα⎛⎫- ⎪⎝⎭的值为( )A .13B .13-C 22D .2217.若sin 0θ>,tan 0θ<,则θ是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角18.已知角α的终边上有一点P 的坐标是()3,4,则cos 2πα⎛⎫- ⎪⎝⎭的值为( )A .45-B .35C .35D .4519.要得到cos(2)3y x π=-的图像,只需将函数sin 2y x =的图像( )A .向左平移12π个单位 B .向右平移12π个单位 C .向左平移6π个单位 D .向右平移6π个单位 20.已知幂函数()y f x =的图象过点()4,2A ,1sin ,2B m ⎛⎫ ⎪⎝⎭,()sin1,C n ,则m 与n 的大小关系为( )A .m n >B .m n <C .m n =D .不等确定21.已知函数()()sin tan 2R f x x k x k =-+∈,若()13f π=-,则()3f π-=( )A .5B .3C .1D .022.若θ为第二象限角,且()1tan 2θπ-=-1cos 1cos 31sin()1sin()22θθππθθ+---+- )A .4B .-4C .14D .14-23.sin 210=( ) A .12-B .12C .3D 324.水车是一种利用水流的动力进行灌溉的工具,其工作示意图如图所示.设水车的直径为8m ,其中心O 到水面的距离为2m ,水车逆时针匀速旋转,旋转一周的时间是120s .当水车上的一个水筒A 从水中(0A 处)浮现时开始计时,经过t (单位:s )后水筒A 距离水面的高度为()f t (在水面下高度为负数),则(140)f =A .3mB .4mC .5mD .6m25.设,a b R ∈,定义运算,,a a ba b b a b ≥⎧⊗=⎨<⎩,则函数()sin cos f x x x =⊗的最小值为( )A .1-B .C .12-D .026.一个扇形的弧长与面积的数值都是4,则该扇形圆心角(正角)的弧度数为( ) A .4B .3C .2D .127.若()tan 2πα+=,则()()2sin 4sin cos 2παπαα⎛⎫----= ⎪⎝⎭( )A .95-B .75- C .75 D .9528.已知扇形的圆心角为23π,面积为3π,则该扇形的弧长为( ) A .πB .2πC .3D .629.角θ为第一或第四象限角的充要条件是( ) A .sin tan 0θθ< B .cos tan 0θθ< C .sin 0tan θθ> D .sin cos 0>θθ二、多选题30.函数()()sin 2cos2,f x a x b x a b R =+∈,下列结论正确的有( ) A .当0a =,1b =时,()f x 为偶函数;B .当1a =,0b =时,()2f x 在区间0,4π⎛⎫⎪⎝⎭上是单调函数;C .当a =1b时,2xf ⎛⎫⎪⎝⎭在区间()2,2ππ-上恰有4个零点;D .当a =1b =时,设()f x 在区间0,4⎡⎤⎢⎥⎣⎦π上的最大值为M ,最小值为m ,则1M m +.31.已知函数()()()sin ,sin cos cos ,cos sin x x x f x x x x ⎧≥⎪=⎨>⎪⎩,则下列结论正确的是( )A .()f x 的最小正周期为2πB .()f x 是偶函数C .()f x 在区间54ππ⎛⎫⎪⎝⎭,上单调递增 D .()f x 的对称轴方程为()Z 4x k k ππ=+∈32.已知函数()()sin f x x ωϕ=+(其中0,2πωϕ><),()30,88f f x f ππ⎛⎫⎛⎫-=≤ ⎪ ⎪⎝⎭⎝⎭恒成立,且()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调,则( ) A .()f x 是偶函数 B .()304f f π⎛⎫=⎪⎝⎭C .ω是奇数D .ω的最大值为3 33.已知θ为第一象限角,下述正确的是( )A .02πθ<<B .2θ为第一或第三象限角C .sin tan θθ<D .()1cos sin 2θ>34.已知函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭,下述正确的是( )A .函数12y f x π⎛⎫=- ⎪⎝⎭为偶函数 B .函数()y f x =的最小正周期为πC .函数()y f x = 在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值为1D .函数()y f x =的单调递增区间为()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦35221cos 1sin x x--的值可能为( ). A .0 B .1 C .2 D .336.设函数()()()cos 0,0πf x x ωϕωϕ=+><<是R 上的奇函数,若()f x 在区间ππ,43⎡⎤⎢⎥⎣⎦上单调递减,则ω的取值可能为( ). A .6B .4C .32D .1237.已知(0,)θπ∈,7sin cos 5θθ-=,则下列结论正确的是( ) A .(2πθ∈,)π B .3cos 5θ=- C .3tan 4θ=- D .2tan 121tan 25θθ=-+38.已知函数()sin f x x =,则下列说法正确的是( ) A .()f x 的图像关于直线2x π=对称 B .(),0π是()f x 图像的一个对称中心C .()f x 的周期为πD .()f x 在区间(,0)2π-单调递减39.设函数()sin()(0)5f x x ωωπ=+>,若()f x 在[]0,π有且仅有5个最值点,则( )A .()f x 在()0,π有且仅有3个最大值点B .()f x 在()0,π有且仅有4个零点C .ω 的取值范围是4353[,)1010 D .()f x 在(0,)20π上单调递增 40.已知()0,θπ∈,且满足12sin cos 25θθ⋅=-,sin cos θθ>,则下列说法正确的是( ) A .,2πθπ⎛⎫∈ ⎪⎝⎭B .4tan 3θ=-C .4tan 3θ= D .1sin cos 5θθ+=41.已知3cos 5α=,()12cos 13αβ+=-,则cos β的值可能为( ) A .5665-B .2065-C .1665- D .156542.对于函数()sin cos sin cos 2x x x xf x ++-=,下列结论正确的是( )A .()f x 是以2π为周期的函数B .()f x 的单调递减区间为()52,2Z 24k k k ππππ⎡⎤++∈⎢⎥⎣⎦C .()f x 的最小值为-1D .()f x ≥的解集是()32,2Z 44k k k ππππ⎡⎤-++∈⎢⎥⎣⎦ 43.已知α是第三象限角,则2α可能是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角44.下列说法正确的有( )A .函数1y x -=的图象不经过第四象限B .函数tan y x =在其定义域上为增函数C .函数2x y =与2x y -=的图象关于y 轴对称D .函数2x y =与2log y x =的图象关于直线y x =对称 45.已知函数()cos cos()f x x x π=+,则下列结论正确的有( )A .()f x 是偶函数B .2π是()f x 的一个周期C .()f x 的最大值为2D .()f x 的最小值为2- 46.设函数()f x 的定义域为D ,如果对任意的1x D ∈,存在2x D ∈,使得12()()2f x f x c +=(c 为常数),则称函数()y f x =在D 上的均值为c ,下列函数中在其定义域上的均值为1的有( )A .3y x =B .tan y x =C .2sin y x =D .y =47.已知函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,则下列说法正确的是( )A .()f x 的最小正周期是πB .()f x 在区间0,3π⎛⎫ ⎪⎝⎭上单调递增C .将函数2sin 2y x =的图象向左平移3π个单位长度,得到函数()f x 的图象D .若方程()f x m =在区间,02π⎡⎤-⎢⎥⎣⎦上有两个不相等的实数根,则实数m 的取值范围是(2,- 48.下列结论成立的是( )A .1617sincos 78ππ> B .sin470sin115︒>︒ C .cos226sin224︒>︒ D .tan 200tan345︒>︒ 49.已知函数()tan 26πf x x ⎛⎫=- ⎪⎝⎭,则( )A .()f x 的周期为2πB .()f x 的定义域为,Z 3x x k k ππ⎧⎫≠+∈⎨⎬⎩⎭C .43f f ππ⎛⎫⎛⎫>- ⎪ ⎪⎝⎭⎝⎭D .()f x 在,32ππ⎛⎫⎪⎝⎭上单调递增50.关于函数()sin ,024,2x x f x x x π⎧≤≤=⎨->⎩,下列说法正确的是( )A .()1()32f f >B .17()()34f f > C .不等式()1f x >的解集为()2,3D .若存在实数(),,,,a b c d e a b c d e <<<<满足()()()()()f a f b f c f d f e ====,则()()()()()af a bf b cf c df d ef e ++++的取值范围为()0,7专题07 三角函数 (单选+多选)参考答案:1.C【详解】解:由图可知2A 741234T πππ=-=,即T π=,所以22πωπ==, 所以()()22f x x ϕ+,因为函数()()22f x x ϕ+的图象过点,03π⎛⎫⎪⎝⎭,所以sin 203πϕ⎛⎫⨯+= ⎪⎝⎭,又2πϕ<,所以3πϕ=,所以()223f x x π⎛⎫=+ ⎪⎝⎭,所以5722123652212f ππππ⎛⎫⨯+== ⎪⎝⎭⎛⎫= ⎪⎝⎭2.B【详解】因为3,44ππα⎛⎫∈ ⎪⎝⎭,所以,042ππα⎛⎫⎛⎫-∈- ⎪ ⎪⎝⎭⎝⎭,又3cos 45πα⎛⎫-= ⎪⎝⎭,所以24sin 1cos 445ππαα⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭;因为0,4πβ⎛⎫∈ ⎪⎝⎭,所以,442πππβ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭,又512sin sin sin 44413πππβπββ⎛⎫⎛⎫⎛⎫+=++=-+=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以12sin 413πβ⎛⎫+= ⎪⎝⎭, 所以2cos 1si 4135n 4ππββ⎛⎫⎛⎫+=-+= ⎪ ⎪⎝⎭⎝⎭,又()44ππβααβ⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝=⎭+所以()sin sin 44παβπβα⎡⎤⎛⎫⎛⎫+-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣=⎦+cos cos sin s 4444in ππππβαβα⎛⎫⎛⎫⎛⎫⎛⎫+--+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎭⎝=⎝⎭123545613513565⎛⎫=⨯-⨯-= ⎪⎝⎭. 3.A【详解】解:设AOB θ∠=,半圆O 的半径为r ,扇形OCD 的半径为1r ,1251S S -=,∴221211512212r r rθθθ--=221251r r r -- ∴22123562551()r r ---,∴151r r -= 又20cm r =,110(51)cm r ∴=. 4.A【详解】3244tan tan 12tan tan tan 333333πππππππ⎛⎫⎛⎫⎛⎫-=-==+== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【详解】因为θ是第四象限角,所以sin 0θ<,tan 0θ<,则点(sin ,tan )θθ位于第三象限, 6.A【详解】解:∵()21sin cos 25αα+=,∴242sin cos 25αα=-, ∵α是三角形的一个内角,则sin 0α>,∴cos 0α<, ∴α为钝角,∴这个三角形为钝角三角形. 7.D【详解】与390︒-角终边相同角的集合为{|390360}k k Z αα︒︒=-+⋅∈,,当2k =时,取得最小正角为330︒. 8.A【详解】06x π<<时,1sin 2x成立,是充分的,但0x =时,1sin 02x =<,不满足6x π<<,必要性不满足,因此是充分不必要条件. 9.B【详解】角α的终边过点(4,3)P -,则34sin ,cos 55αα==-,则22sin cos 5αα+=10.D【详解】解:sin(2)sin 2()612y x x ππ=-=-,故将函数sin 2y x =的图象向右平移12π个单位,可得sin(2)6y x π=-的图象,11.D【详解】点P ()0,1为角2πα=的终边上一点,3s 后点P 按逆时针方向旋转到达P '点,点P '落在角273296πβππ=+⨯=的终边上,71cos cos cos 66βππ==-=,711sin sin sin 662βππ==-=-;故P '的坐标为12⎛⎫- ⎪ ⎪⎝⎭12.B【详解】函数ln y x =在(0,)+∞上单调递增,而3e >,则ln3lne 1a =>=,ππsin 8sin 033b π⎛⎫=-=-=< ⎪⎝⎭,函数3x y =在R 上单调递增,而203-<,则2030331-<<=,即01c <<,所以a c b >>. 13.A【详解】有题意得:1密位=2π160001000=,因为圆心角小于200密位,扇形的弦长和弧长近似相等,所以5431800100α==,因为31301001000÷=,所以迫击炮转动的角度为30密位.【详解】由已知可得22222sin csc tan 15sin cos m x m x x x x ⋅+=+≥,可得422sin 15sin cos x m x x≥-, 因为()Z 2x k k ππ≠+∈,则(]2cos 0,1x ∈,因为()()2242222221cos sin 115sin 151cos 1716cos cos cos cos x x x x x x x x -⎛⎫-=--=-+ ⎪⎝⎭2211716cos 9cos x x ≤-⋅, 当且仅当21cos 4x =时,等号成立,故9m ≥. 15.A【详解】解:根据题意,得()()1sin 390sin 30360sin 302︒=︒+︒=︒=16.C【详解】由51sin sin ()sin()6663πππαπαα⎛⎫⎛⎫-=-+=+= ⎪ ⎪⎝⎭⎝⎭,而,3παπ⎛⎫∈ ⎪⎝⎭,∴5(,)662πππα-∈-,∴25522cos 1sin 66παπα⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭17.B【详解】由sin 0θ>,可得θ的终边在第一象限或第二象限或与y 轴正半轴重合, 由tan 0θ<,可得θ的终边在第二象限或第四象限, 因为sin 0θ>,tan 0θ<同时成立,所以θ是第二象限角. 18.D【详解】依题有22345r =+,∴4sin 5α,∴4cos sin 25παα⎛⎫-== ⎪⎝⎭.19.A 【详解】cos 2sin 2sin 2sin 2332612y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,∴需将函数sin 2y x =的图象向左平移12π个单位.20.B【详解】依题意,设()f x x α=,由()42f =得:42α=,解得12α=,则有()f x x =()f x 在[0,)+∞上单调递增,又sin y x =在(0,)2π上单调递增,即10sin sin12<<1sin sin12m n <,B 正确.故选:B 21.A【详解】依题意,令()sin tan g x x k x =-,则()g x 是奇函数,()()2f x g x =+,于是得()()[()2][()2]()()44333333f f g g g g ππππππ+-=++-+=-+=,所以()4()533f f ππ-=-=.22.B【详解】由()1tan 2θπ-=-得:1tan 2θ=-,而θ为第二象限角,则有sin 0θ>,=1cos 1cos 2cos 24sin sin sin tan θθθθθθθ+-=-===- 23.A【详解】试题分析:由诱导公式()1sin 210sin 18030sin 302︒︒︒︒=+=-=-,故选A .24.B【详解】由题设,水车的角速度为2/s 12060ππ=,又水车的直径8m ,中心O 到水面的距离2m ,∴03HOA π∠=,故t (单位:s )后水筒A 距离水面的高度为()24cos()360tf t ππ=-+m , ∴140(140)24cos()4m 360f ππ=-+=. 25.B【详解】由题意可得sin sin cos ()sin cos cos cos sin x x xf x x x x x x ≥⎧=⊗=⎨>⎩当sin cos x x ≥时,即sin cos 04x x x π⎛⎫-=-≥ ⎪⎝⎭则22,4k x k k Z ππππ≤-≤+∈,即522,44k x k k Z ππππ+≤≤+∈ 此时当52,4x k k Z ππ=+∈时,sin x有最小值为 当cos sin x x >时,即sin cos 04x x x π⎛⎫-=-< ⎪⎝⎭则222,4k x k k Z πππππ+<-<+∈,即5922,44k x k k Z ππππ+<<+∈此时,2cos x >;所以()f x 的最小值为226.C【详解】因为一个扇形的弧长与面积的数值都是4, 即4,4S l == 所以22S r l ==,所以圆心角为2lr= 27.B【详解】因为()tan tan 2παα+==所以()()222222cos 4sin cos 14tan 7sin 4sin cos cos 4sin cos 2cos sin 1tan 5παααααπαααααααα--⎛⎫----=-===- ⎪++⎝⎭28.B【详解】设扇形的弧长为l ,半径为r ,根据已知的扇形的圆心角23πα=,面积3S π=, 由扇形的面积公式212S r α=,得2123π23r π=⨯⨯,解得3r =, 由弧长公式2323l r παπ==⨯=, 29.C【详解】若角θ为第一象限角,则sin 0,cos 0,tan 0θθθ>>>, 若角θ为第四象限角,则sin 0,cos 0,tan 0θθθ<><, 所以若角θ为第一或第四象限角,则sin 0tan θθ>; 若sin 0tan θθ>,则sin 0,tan 0θ<θ<或sin 0,tan 0θθ>>,所以角θ为第一或第四象限角. 30.AC【详解】选项A :当0a =,1b =时, ()cos2f x x =,定义域为R ,()()cos(2)cos2f x x x f x -=-==,则()f x 为偶函数.判断正确;选项B :当1a =,0b =时,()2sin 4f x x =.()2sin 4f x x =在0,8π⎛⎫⎪⎝⎭单调递增,在,84ππ⎛⎫ ⎪⎝⎭单调递减. 选项B判断错误;选项C :当3a =1b时,3cos 2sin()26x f x x x π⎛⎫-=- ⎪⎝⎭由2sin()06x π-=,可得,Z 6x k k ππ=+∈,当0k =时,6x π=或6x π=-;当1k =时,76x π=或76x π=-即2x f ⎛⎫⎪⎝⎭在区间()2,2ππ-上恰有4个零点. 判断正确;选项D :a =1b =时,()2cos 22sin(2)6f x x x x π=+=+由04x π≤≤,得22663x πππ≤+≤,则12sin(2)26x π≤+≤ 即()f x 在区间0,4⎡⎤⎢⎥⎣⎦π上的最大值2M =,最小值1m =,则3M m +=.选项D 判断错误.31.ACD【详解】显然(2)()f x f x π+=,A.正确.画出函数()f x 在π3,22π⎡⎤-⎢⎥⎣⎦的图象,如图所示:22f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭,B 错. 在区间54ππ⎛⎫⎪⎝⎭,上sin cos x x >,()sin sin f x x x ==-为增函数,C 正确.由图可知()f x 的对称轴方程为()Z 4x k k ππ=+∈,D 正确.32.BCD【详解】∵08f π⎛⎫-= ⎪⎝⎭,3()8f x f π⎛⎫≤ ⎪⎝⎭,∴3188242k T πππ⎛⎫⎛⎫--==+ ⎪ ⎪⎝⎭⎝⎭,k ∈N , 故221T k π=+,21k ω=+,k ∈N , 由08f π⎛⎫-= ⎪⎝⎭,则()s n 08i f x πωϕ⎛⎫=+= ⎪⎭-⎝,故8k πωϕπ+=-,8k ϕπωπ=+,Z k ∈,当,1224x ππ⎛⎫∈- ⎪⎝⎭时,,246x k k ωπωπωϕππ⎛⎫+∈++⎪⎝⎭,Z k ∈, ∵()f x 在区间,1224ππ⎛⎫- ⎪⎝⎭上单调,故241282Tπππ⎛⎫--=≤ ⎪⎝⎭,故4T π≥,即8ω≤, 0243ωππ<≤,故62ωππ≤,故3ω≤,综上所述:1ω=或3ω=,故CD 正确;1ω=或3ω=,故8k ϕππ=+或38k ϕππ=+,Z k ∈,()f x 不可能为偶函数,A 错误; 由题可知38x π=是函数的一条对称轴,故3(0)4f f π⎛⎫= ⎪⎝⎭成立,B 正确. 33.BCD【详解】解:因为θ为第一象限角,所以22,Z 2k k k ππθπ<<+∈,故A 错误;,Z 24k k k θπππ<<+∈,当0k =时,024θπ<<,为第一象限角,当1k =时,524θππ<<,为第三象限角, 所以2θ为第一或第三象限角,故B 正确;0sin 1,0cos 1θθ<<<<,所以sin tan sin cos θθθθ=>,故C 正确; ()1cos sin cos1cos32πθ>>=,故D 正确. 34.ACD【详解】解:因为()2sin 23f x x π⎛⎫=- ⎪⎝⎭,所以对于A ,2sin 22cos 212231x x y f x πππ⎡⎤⎛⎫--=- ⎪⎛⎫=-= ⎪⎝⎭⎭⎢⎥⎝⎣⎦,又()cos 2cos2x x -=,所以函数12y f x π⎛⎫=- ⎪⎝⎭为偶函数,故A 正确;对于B ,函数()2sin 23f x x π⎛⎫=- ⎪⎝⎭的最小正周期为22ππ=,所以函数()y f x =的最小正周期为2π,故B 不正确;对于C ,当,44x ππ⎡⎤∈-⎢⎥⎣⎦时,52,366x πππ⎡⎤-∈-⎢⎥⎣⎦,所以1sin 21,32x π⎛⎫⎡⎤-∈- ⎪⎢⎥⎝⎭⎣⎦,所以[]2sin 22,13x π⎛⎫-∈- ⎪⎝⎭,所以函数()y f x = 在区间,44ππ⎡⎤-⎢⎥⎣⎦上的最大值为1,故C 正确;对于D ,令+22+2232k x k πππππ-≤-≤,解得51212+k x +k ππ-π≤≤π,所以函数()y f x =的单调递增区间为()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦,故D 正确, 35.BD【详解】令222sin cos ()|sin ||cos |1cos 1sin x xf x x x xx==+--,当x 为第一象限角时,sin 0,cos 0x x >>,则()3f x =, 当x 为第二象限角时,sin 0,cos 0x x ><,则()1f x =, 当x 为第三象限角时,sin 0,cos 0x x <<,则()3f x =-, 当x 为第四象限角时,sin 0,cos 0x x <>,则()1f x =-. 36.ACD【详解】∵函数()()()cos 0,0πf x x ωϕωϕ=+><<是R 上的奇函数, ∴()0cos =0f ϕ=,∴=2πϕ,∴()sin f x x ω=-,令(),sin z x f x z ω==-.当6ω=时,ππ3π,,,2432x z x ωπ⎡⎤⎡⎤∈∴=∈⎢⎥⎢⎥⎣⎦⎣⎦,在3π,22π⎡⎤⎢⎥⎣⎦上sin y z =单调递增,∴()f x 单调递减,符合题意,故A 正确;当4ω=时,ππ4,,,433x z x πωπ⎡⎤⎡⎤∈∴=∈⎢⎥⎢⎥⎣⎦⎣⎦,在4,3ππ⎡⎤⎢⎥⎣⎦上sin y z =单调递减,∴()f x 单调递增,不符合题意,故B 错误; 当32ω=时,ππ3π,,,4382x z x πω⎡⎤⎡⎤∈∴=∈⎢⎥⎢⎥⎣⎦⎣⎦,在3π,82π⎡⎤⎢⎥⎣⎦上sin y z =单调递增,∴()f x 单调递减,符合题意,故C 正确; 当12ω=时,πππ,,,4386x z x πω⎡⎤⎡⎤∈∴=∈⎢⎥⎢⎥⎣⎦⎣⎦,在π,86π⎡⎤⎢⎥⎣⎦上sin y z =单调递增,∴()f x 单调递减,符合题意,故D 正确; 37.AD【详解】由(0,)θπ∈,7sin cos 15θθ-=>,得sin 0θ>,cos 0θ<,则(2πθ∈,)π,故A 正确;由7sin cos 5θθ-=,两边平方得:4912sin cos 25θθ-=,则242sin cos 25θθ=-.∵(2πθ∈,)π,则3(,)444πππθ-∈,∴sin cos )4πθθθ-=-∈,又1sin cos 5θθ+==±, 当1sin cos 5θθ+=时,联立1sin cos 57sin cos 5θθθθ⎧+=⎪⎪⎨⎪-=⎪⎩,解得4sin 5θ=,3cos 5θ=-,∴sin 4tan cos 3θθθ==-,24tan 123161tan 2519θθ-==-++;当1sin cos 5θθ+=-时,联立1sin cos 57sin cos 5θθθθ⎧+=-⎪⎪⎨⎪-=⎪⎩,解得3sin 5θ=,4cos 5θ=-,∴sin 3tan cos 4θθθ==-,23tan 12491tan 25116θθ-==-++. 故B 、C 错误,D 正确. 38.ACD【详解】由()|sin()||cos |22f x x x ππ+=+=,()|sin()||cos |22f x x x ππ-=-=,即有()()22f x f x ππ+=-,所以()f x 的图象关于直线2x π=对称,故A 正确;由()()()()sin sin sin sin 2sin 0f x f x x x x x x ππππ++-=++-=+=≠, 故()f x 的图象不关于(,0)π对称,故B 错误.由()|sin()||sin ||sin |()f x x x x f x ππ+=+=-==,可得()f x 的周期为π,故C 正确; 当(,0)2x π∈-时,sin y x =,单调递增且sin 0y x =<;所以()|sin |f x x =在区间[,0]2π-单调递减,故D 正确. 39.ACD【详解】[]0,π,0x ω∈>,0x ωπω∴≤≤,555x πππωπω∴≤+≤+,令5t x πω=+,55t πππω∴≤≤+,画出sin y t =图像进行分析:对于A 选项:由图像可知:()f x 在[]0,π上有且仅有135,,x x x 这3个最大值点,故A 选项正确; 对于B 选项:当9525πππωπ≤+<,即4324105ω≤<时,()f x 在()0,π有且仅有4个零点; 当11552ππππω≤+<,即2453510ω≤<时,()f x 在()0,π有且仅有5个零点,故B 选项不正确;对于C 选项:()f x 在[]0,π有且仅有5个最值点,911252ππππω∴≤+<,43531010ω∴≤<, ω∴的取值范围是4353[,)1010,故C 选项正确;对于D 选项:π0,,020x ω⎛⎫∈> ⎪⎝⎭,π020x ωω∴<<,π55205x πππωω∴<+<+,由C 选项可知43531010ω∴≤<,83ππ93π200205200πω∴≤+<, 932002ππ<,()f x 在π0,20⎛⎫⎪⎝⎭上单调递增,故D 选项正确. 40.ABD【详解】因为()0,θπ∈,且满足12sin cos 025θθ⋅=-<,可得,2πθπ⎛⎫∈ ⎪⎝⎭,所以A 正确, 因为22sin cos 1θθ+=,所以22241sin cos 2sin cos 12525θθθθ++=-=, 222449sin cos 2sin cos 12525θθθθ+-=+=, 所以()21sin cos 25θθ+=,()249sin cos 25θθ-=, 因为sin cos θθ>,sin 0,cos 0θθ><,所以1sin cos 5θθ+=,7sin cos 5θθ-=,所以D 正确, 所以解得43sin ,cos 55θθ==-,所以sin 4tan cos 3θθθ==-,所以B 正确,C 错误,41.AC【详解】因3cos 5α=,则4sin 5α==±,又()12cos 13αβ+=-,则5sin()13αβ+=±, ()12336cos cos 13565αβα+=-⨯=-,而cos cos[()]cos()cos sin()sin βαβααβααβα=+-=+++, sin α与sin()αβ+同号,即20sin()sin 65αβα+=,则16cos 65β=-, sin α与sin()αβ+异号,即20sin()sin 65αβα+=-,则56cos 65β=-, 所以cos β的值可能为5665-或1665-. 42.AD【详解】依题意,()sin(2)cos(2)sin(2)cos(2)2()2x x x x f x f x πππππ+++++-++==,()f x 是以2π为周期的函数,A 正确;5sin ,2244()(Z)3cos ,2244x k x k f x k x k x k ππππππππ⎧+≤≤+⎪⎪=∈⎨⎪-<<+⎪⎩,函数sin y x =在5[2,2]24k k ππππ++()k ∈Z 上单调递减,函数cos y x =在[2,2]4k k πππ+()k ∈Z 上单调递减,B 不正确;函数cos y x =在3[2,2]4k k πππ-()k ∈Z 上单调递增,因此,324x k ππ=-()k ∈Z 时,min 2()f x =C 不正确;由()2f x ≥得522(Z)442sin k x k k x ππππ⎧+≤≤+∈⎪⎪⎨⎪≥⎪⎩或322(Z)442cos k x k k x ππππ⎧-<<+∈⎪⎪⎨⎪≥⎪⎩,解522(Z)442sin k x k k x ππππ⎧+≤≤+∈⎪⎪⎨⎪≥⎪⎩得322(Z)44k x k k ππππ+≤≤+∈, 解322(Z)442cos k x k k x ππππ⎧-<<+∈⎪⎪⎨⎪≥⎪⎩得22(Z)44k x k k ππππ-≤<+∈,综上得:322(Z)44k x k k ππππ-≤≤+∈,()2f x ≥3[2,2](Z)44k k k ππππ-+∈,D 正确. 43.BD【详解】因为α是第三象限角,所以3222k k πππαπ+<<+,Z k ∈,3224k k παπππ∴+<<+,Z k ∈, 当k 为偶数时,2α是第二象限角;当k 为奇数时,2α是第四象限角, 44.ACD【详解】对于A :函数1y x -= 的图像经过第一、三象限,故A 正确;对于B :函数tan y x = 的定义域为2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭, , 单调递增区间为()22k k k Z ππππ⎛⎫-++∈ ⎪⎝⎭,,,故B 错误; 对于C :若()x y , 在2xy = 的图象上,则()x y -, 在2xy -= 的图象上,所以图象关于y 轴对称,故C 正确;对于D :由于2xy = 与2log y x=互为反函数,所以图象关于y x = 对称,故D 正确.45.AC【详解】A :()cos()cos()cos cos()()f x x x x x f x ππ-=-+-=+=且定义域为R ,故()f x 是偶函数,正确; B :2(2)cos(2)cos[(2)]cos cos(2)()f x x x x x f x ππππππ+=+++=++≠,故2π不是()f x 的周期,错误; C :由()cos cos()112f x x x π=+≤+=,且当12x k π=,1k Z ∈时cos 1x =,当22x k =,2k Z ∈时cos 1x π=,故1222k k π=,即120k k ==时等号成立,则当0x =有max ()2f x =.D :同C 分析,()cos cos()112f x x x π=+≥--=-,且当1(21)x k π=+,1k Z ∈时cos 1x =-,当221x k =+,2k Z ∈时cos 1x π=-,故12(21)21k k π+=+,即212121k k π+=+时等号成立,显然π为无理数,212121k k ++为有理数,不可能相等,则()f x 的最小值不为2-. 46.ABD【详解】由题意可得1c =,则12()()12f x f x +=,即12()()2f x f x +=,将问题转化为关于2x 的方程是否存在有解问题,对于A ,3y x =的定义域为R ,则对于任意1R x ∈,关于2x 的方程为33122x x +=,则33212x x =-,2x ,方程一定有解,所以A 正确,对于B ,tan y x =的定义域为,2D x x k k Z ππ⎧⎫=≠+∈⎨⎬⎩⎭,值域为R ,则对于任意1x D ∈,总存在2x D ∈,使得12tan tan 2x x +=,所以B 正确,对于C ,2sin y x =的定义域为R ,值域为[2,2]-,当12x π=-时,1()2f x =-,此时不存在2x R ∈,使12()()2f x f x +=,所以C 错误,对于D,y ={}22D x x =-≤≤,值域为[0,2],则对于任意1x D ∈,关于2x的方程为2,整理得(22242x =-,则总存在2x D ∈满足上式,所以D 正确,47.AD【详解】因为函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,所以()f x 的最小正周期是22ππ=,故A 正确; 当0,3x π⎛⎫∈ ⎪⎝⎭时,2,33x πππ⎛⎫+∈ ⎪⎝⎭,所以()f x 在区间0,3π⎛⎫⎪⎝⎭上不单调递增,故B 错误;将函数2sin 2y x =的图象向左平移3π个单位长度,得到函数22sin 23y x π⎛⎫=+ ⎪⎝⎭的图象,故C 错误;当,02x π⎡⎤∈-⎢⎥⎣⎦时,22,333x πππ⎡⎤+∈-⎢⎥⎣⎦ 所以若方程()f x m =在区间,02π⎡⎤-⎢⎥⎣⎦上有两个不相等的实数根,则实数m的取值范围是(2,-,故D 正确 48.BD【详解】对于A ,162sinsin 77ππ=,173cos cos sin 888πππ==,230782πππ<<<, 函数sin y x =在π0,2⎛⎫⎪⎝⎭上单调递增,则23sin sin 78ππ<,A 不正确; 对于B ,sin 470sin 70=,sin115sin 65=,而0657090<<<, 函数sin y x =在π0,2⎛⎫⎪⎝⎭上单调递增,则sin 70sin 65>,B 正确;对于C ,cos 226sin 44=-,sin 224sin 44=-,则cos226sin224︒=︒,C 不正确; 对于D ,tan 200tan 200=>,tan345tan150=-<,即tan 200tan345︒>︒,D 正确. 49.ACD【详解】函数()tan(2)6f x x π=-的最小正周期为2T π=,故A 正确;由262x k k Z πππ-≠+∈,,得23k x k Z ππ≠+∈,, 所以函数()f x 的定义域为23k x x k Z ππ⎧⎫≠+∈⎨⎬⎩⎭,,故B 错误; ()tan(2)tan 34463f ππππ=⨯-==53tan 2tan 3366f ππππ⎛⎫⎛⎫⎛⎫-=-⨯-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以()4f π>()3f π-,故C 正确;()32x ππ∈,时,52()626x πππ-∈,,所以()f x 在()32ππ,上单调递增,故D 正确.50.BCD【详解】因函数()sin ,024,2x x f x x x π⎧≤≤=⎨->⎩,则1()|sin |122f π==,(3)431f =-=,A 不正确;13()|sin |33f π==,772()|sin |44f π==,B 正确; 当02x ≤≤时,()01f x ≤≤,则不等式()1f x >化为241x x >⎧⎨->⎩,解得23x <<,()1f x >的解集为()2,3,C正确;因存在实数(),,,,a b c d e a b c d e <<<<满足()()()()()f a f b f c f d f e ====,令()f a t =, 则方程()f x t =有4个互异实根,,,,a b c d e ,即函数()y f x =的图象与直线y t =有4个公共点, 作出函数()y f x =的图象与直线y t =,如图,因当02x ≤≤时,()01f x ≤≤,则01t <<,又()|sin |f x x π=在[0,1]上的图象关于直线12x =对称, 在[1,2]上的图象关于直线32x =对称,因此有:1,3,4a b c d e t +=+==-, 则()()()()()(8)af a bf b cf c df d ef e t t ++++=-,而函数28t t -+在(0,1)上递增,则有0(8)7t t <-<, 所以()()()()()af a bf b cf c df d ef e ++++的取值范围为()0,7,D 正确.。
