小学数学最难的13种题型
小学数学重难点突破:“鸡兔同笼”13种解题方法,学霸看了都私藏

⼩学数学重难点突破:“鸡兔同笼”13种解题⽅法,学霸看了都私藏
爱因斯坦曾经说过:“数学之所以⽐⼀切其它科学受到尊重,⼀个原因是因为他的命题绝对可靠
和⽆可争辩的。
另⼀个原由则是数学使⾃然科学实现定理化,给予⾃然科学某种程度的可靠
性。
”更深层的含义是,数学是⼀门极其理性的学科,学好数学能让孩⼦的逻辑思维更清晰,更
能开发孩⼦的⼤脑。
但在⼩学阶段的数学学习中,并不是⼀帆风顺的,对于孩⼦们⽽⾔,最头痛、丢分最多的,则
是应⽤题型。
考试中,应⽤题的分值占了三分之⼀,⽽⼤部分同学丢分都是在应⽤题型上掉了
链⼦,以致数学成绩不理想。
其实⼩数数学应⽤题,题⽬相对简单,结构也不复杂,题型就那
⼏种,答题模式也⼤都相似,同学们如果能够把这⼏类都学好,学习成绩⾃然能够提升。
就拿“鸡兔同笼”应⽤题来说,相信⼤⼈孩⼦都不陌⽣。
“鸡兔同笼”是历年数学考试都会出现的考
题(可以说是必考题)。
很多孩⼦在这类题中,失分⽐较严重。
鸡兔同笼应⽤题问题虽然复
杂,但解题⽅法却不⽌⼀种,学会了之后更能灵活变应。
下⾯,⽼师⽤⼀个例题,学习鸡兔同
笼问题的11种解答⽅法,相信能为孩⼦们做应⽤题这块打开思路。
小学数学最难的13种题型
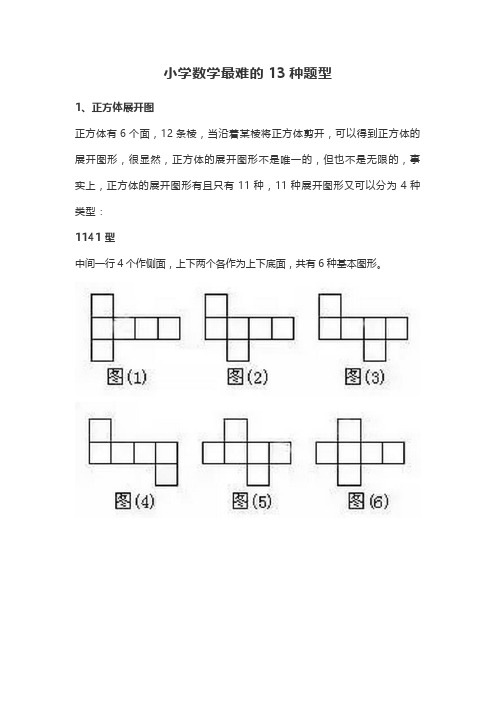
小学数学最难的13种题型1、正方体展开图正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:1141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
231型中间一行3个作侧面,共3种基本图形。
222型中间两个面,只有1种基本图形。
33型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
已知两数的和与差,求这两个数。
【口诀】和加上差,越加越大;除以2,便是大的;和减去差,越减越小;除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
3、鸡兔同笼问题【口诀】假设全是鸡,假设全是兔。
多了几只脚,少了几只足?除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24求鸡时,假设全是兔,则鸡数=(4X36-120)/(4-2)=12(1)加水稀释【口诀】加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)(1)相遇问题【口诀】相遇那一刻,路程全走过。
小学1-6年级奥数难点解析,附34个必考公式

现在,越来越多的家长希望孩子学习奥数。
奥数对青少年的脑力锻炼有着一定的作用,可以通过奥数对思维和逻辑进行锻炼,对学生起到的并不仅仅是数学方面的作用,通常比普通数学要深奥些。
今天,搜集整理了1-6年级奥数学习重点和部分例题,相信一定可以帮到各位家长。
一年级奥数一年级的孩子刚刚踏入小学。
不论是学习习惯还是学习方法,都需要全面的培养和正确的引导,这就需要家长对整个六年的小学学习有一个全面的规划。
学习重点难点解析:巧算与速算的基本知识:对于一年级的学生来说,计算是学生学习时遇到的第一个问题。
如果能够在看似无序的算式中寻找到一定的规律,化繁为简,那么学生一定能够增强学习数学的信心,提高学习数学的兴趣。
另外,计算与速算是各种后续问题学习的基础。
学好数学,首先就要过计算这关。
认识并学会数各种基本图形:正方形、长方体、圆和立方体等是小学学习中最常见的图形。
通过系统的指导,使一年级的学生能够计算出各种基本图形的个数;使学生建立起有序思维,为建立思维模式打下基础。
学习简单的枚举法:枚举法对于一年级的学生来说的确是有一定的困难。
在华数课本中,介绍这一难题时采用数数这种更为直观的方式,将复杂抽象的问题形象化,便于孩子们理解。
枚举法训练的重点在于有序的思维方式,学习之初将抽象问题形象化,能够更好地引导学生去主动思考,建立起自己的思维方式。
数字的奇与偶、不等与相等等关于数论的基础知识:数论问题是后续学习中的一个重点,而这学期将要学到的:数字的奇与偶、不等与相等等无疑将会是今后学习的基础,在这里我们把数论问题分解为各种类型逐一讲解,使华数学习更加系统。
二年级奥数二年级是开发孩子智力、形成良好思维习惯的最佳时期,学习奥数不仅能够极大地锻炼孩子的思维能力,也能为孩子之后的学习打下坚实的基础。
对于二年级的学生家长来说,激发孩子对华数的兴趣是最主要的。
学习重点难点解析:计算要过关:对于二年级学生的奥数学习来说,最先碰到的问题就是计算问题,计算问题是重点也是难点。
苏教版三年级下册数学重难点题型归类

易错题1⭐客车有45辆,小汽车开走17辆就和客车同样多,客车和小汽车一共有多少辆?【思路点拨】根据“小汽车开走17辆就和客车同样多”,可知小汽车比客车多17辆。
因此,小汽车有45+17=62(辆),客车和汽车一共有45+62=107(辆)。
【再练一题】客车有45辆,客车开走17辆就和小汽车同样多,客车和小汽车一共有多少辆?易错题2⭐判断:长方形甲里包含了10个正方形,长方形乙里包含了8个正方形,长方形甲的面积大于长方形乙的面积。
()【思路点拨】由于本题中没有说明两个图形中小正方形的大小是否相同,无法比较它们的面积。
因此,说法错误。
【再练一题】易错题3⭐丁丁沿着100米的直跑道跑了10个来回,共跑了()米。
【思路点拨】跑一个来回的路程是100×2=200(米),因此跑10个来回一共跑了200×10=2000(米)。
【再练一题】小军沿着100米的直跑道跑了5个来回,共跑了()米。
易错题4⭐⭐一块正方形手帕的周长是8分米,它的面积是多少平方分米?【思路点拨】根据这个正方形手帕的周长是8分米,可以先求出它的边长是8÷4=2(分米),它的面积是2×2=4(平方分米)。
【再练一题】一个正方形的周长是20分米,它的面积是多少平方分米?易错题5⭐⭐一架飞机上午9时从北京起飞,飞行了4小时20分,下午()时()分到达海口。
【思路点拨】问题中要填写的时间前面已经有时间词“下午”,因此括号中填写的时间必须用普通记时法表示。
应为1时20分。
【再练一题】判断:某学校下午16时20分放学。
()易错题6⭐⭐小明买了一支8.5元的钢笔和一块8角的橡皮。
小明一共用去多少元?【思路点拨】8.5元是以元作单位的,8角是以角作单位的,可以先统一单位再进行计算。
8角=0.8元,小明一共花去8.5+0.8=9.3(元)。
【再练一题】小青带了10元,买了一块9角的橡皮。
身上还剩多少元?易错题7⭐⭐判断:边长4厘米的正方形的周长和面积相等。
小学六年级数学上册重难点题型

【重点题一】长方体油箱长50厘米,宽35厘米,高20厘米。
做这个油箱至少需要铁皮多少平方分米?如果每升汽油重0.86千克,这个油箱最多能装多少千克汽油?(铁皮厚度忽略不计)【思路点睛】第1问是求长方体油箱的表面积,计算时要注意单位:(50×35+50×20+35×20)×2=6900(平方厘米),6900平方厘米=69平方分米。
第2问要先求出油箱的容积,再求能装多少汽油:50×35×20=35000立方厘米,35000立方厘米=35升,0.86×35=30.1(千克)。
第2问是易错题,有的同学在完成第1问后,直接用表面积与0.86相乘:69×0.86,这样做就错了。
【重点题二】一个泡沫包装盒厚3厘米,从外面量,长30厘米,宽26厘米,高21厘米,它的体积和容积各是多少立方厘米?能装下多少个棱长5厘米的正方体木块?【思路点睛】求体积用的是外尺寸:30×26×21=16380(立方厘米);求容积用的是内尺寸:长: 30-2×3=24cm,宽:26-2×3=20cm,高:21-2×3=15cm,容积是24×20×15=7200(立方厘米)。
第二问有些同学会错误地用“容积÷每个小立方体的体积”来算。
我们来算一算:沿着长只能放进4个木块,剩下的空间只好浪费了,沿着宽正好能放下4个木块,这样一层就放了16个木块,沿着高可放3层,一共能装下16×3=48(个)木块。
【重点题三】3个相同的长方体木块,长15厘米,宽8厘米,高4厘米,拼成一个大长方体,表面积最大是多少平方厘米?最小呢?【思路点睛】把3个相同的长方体拼成一个大长方体有3种拼法,但是同学们不必将3种拼法的表面积都算出来。
思考一下:要使表面积最大,应该把小长方体的什么面拼在一起?当然是把最小的面拼在一起(如上图)。
小学数学题型较难的试卷

1. 小明家养了5只鸡,每只鸡每天下2个鸡蛋,小明家每天可以收集到多少个鸡蛋?A. 10个B. 20个C. 25个D. 30个2. 下列哪个数是质数?A. 15B. 21C. 29D. 353. 小红有12个苹果,小明有18个苹果,他们两人共有多少个苹果?A. 30个B. 24个C. 36个D. 40个4. 小华用3个2分硬币和5个1分硬币买了一个玩具,这个玩具的价格是多少?A. 5分B. 6分C. 7分D. 8分5. 下列哪个数是偶数?A. 25B. 26C. 27D. 28二、填空题(每题5分,共25分)6. 2的平方等于______。
7. 下列数的立方根是2的有______。
8. 小明骑自行车去学校,每小时行驶12千米,他用了______小时才能到达学校。
9. 下列哪个数是正数?______。
10. 下列哪个数是负数?______。
三、解答题(每题10分,共30分)11. 小明从家里走到学校需要经过5个红绿灯,每个红绿灯前要等2分钟,小明走了10分钟到达学校,请问小明是否遇到了红灯?请说明理由。
12. 小红有30元,她要买一本书,这本书的价格是25元,小红还需要再找多少零钱?13. 小华的爸爸今年35岁,小华的弟弟今年5岁,小华和弟弟相差多少岁?四、应用题(每题15分,共30分)14. 小明在超市买了3个苹果,每个苹果重200克,他一共买了多少克苹果?15. 小丽家养了5只鸡,每只鸡每天下2个鸡蛋,小丽家一共养了多少只鸡?如果小丽家要收集100个鸡蛋,需要养多少只鸡?注意:本题难度较大,要求学生具备一定的数学基础和思维能力。
解答过程中,请注意逻辑清晰、步骤完整。
小学四年级数学上册重难点题型

【重点题一】甲、乙两个容器一共可盛900毫升水,已知乙容器的容量是甲容器的8倍,甲、乙两个容器的容量各是多少毫升?【分析与解】如果将甲容器的容量看作1份,乙容器的容量就有这样的8份,它们一共有1+8=9(份)。
容易求出甲容器的容量为900÷9=100(毫升),乙容器的容量为100×8=800(毫升)。
【重点题二】一个奶瓶的容量是250毫升,一个6个月大的婴儿每天要喝4瓶牛奶,这名婴儿每天摄入多少升牛奶?【分析与解】“6个月”在本题中是多余条件,解题时有些同学会受到它的影响。
要求这个婴儿每天要摄入多少升牛奶,只需求出4瓶牛奶的容量是多少升。
250×4=1000(毫升)1000毫升=1升答:婴儿每天要摄入1升牛奶。
【重点题三】如下图,小红从家到学校要13分钟,如果她用同样的速度从家到少年宫要走几分钟?【分析与解】要想求出小红从家到少年宫要走多少分钟,首先要求出小红每分钟走的路程。
通过看图可知小红家到学校的路程是845米,根据“小红从家到学校要13分钟”,可以先求出小红每分钟走的路程是845÷13=65(米),她从家到少年宫要走520÷65=8(分钟)。
【重点题四】明明在计算除法时,把除数23误写成了32,结果得到商18还余12。
你能算出正确的结果吗?【分析与解】这里我们可以用“将错就错”法来解题。
根据“把除数23误写成了32,结果得到商18还余12”可以求出被除数为18×32+12=588,正确的结果为588÷23=25 (13)【重点题五】一块边长18米的正方形草坪和一块长36米的长方形草坪面积相等。
长方形草坪的宽是多少米?【分析与解】正方形草坪的面积是18×18=324(平方米),因为本题中正方形和长方形的面积相等,所以长方形的面积也是324平方米。
再根据“宽=长方形的面积÷长”求出长方形的宽是324÷36=9(米)。
一年级数学十大重难点题型解析

小学一年级数学十大重难点题型解析重点题一(1)一共有()个水果。
(2)梨在香蕉的(左右)面。
[在合适的答案上打“√”](3)桃子的右面是()。
(4)()在梨的左面。
【指点迷津】在区分“左”和“右”的基础上,会用不同的表达方式说清物体间的位置关系。
如:梨在香蕉的(左)面,桃子的右面是(苹果等)。
重点题二(1)从右数起,是第()个,是第()个。
(2)把左起4个水果圈起来。
(3)在右起第4个水果上打"√"。
【指点迷津】分清从“左”数起还是从“右”数起,明确所问的是“几个”还是“第几个”。
“几个”一般是指物体的总个数,而“第几个”是指其中的“一个”。
重点题三(1)一共有()个物体。
长方体有()个,正方体有()个,圆柱有()个,球有()个。
(2)从左数起排在第()个。
(3)从右数起第()个、第()个是球。
【指点迷津】首先要能正确辨识长方体、正方体、圆柱和球,其次要能进行正确数数,再次还要能结合位置关系理清哪边起第几个物体是什么。
重点题四三只蚂蚁同时出发,速度一样。
哪只小蚂蚁第一个爬到终点?在它后面画【指点迷津】可以逐段逐段数一数,然后比较长短。
也可以先比横线段之和的长短,应该是一样长;接着比竖线段之和哪个最短,对应的那只蚂蚁先爬到终点。
显然,后一种方法比较灵活。
重点题五最重的画“√”,最轻的画“○”。
【指点迷津】先分别比较每个简易天平上水果的轻重。
再把重的与重的比,比出最重的;把轻的与轻的比,比出最轻的。
重点题六把上面的图形按照不同的标准分进下面3个框里。
【指点迷津】可按不同标准来分类。
一是按图形的形状,可分为圆形、正方形、三角形;二是按图形的颜色,可分为红色、绿色、黄色。
重点题七(1)3和8这两个数,()离0近一些。
(2)在上图中,比6小的数有()个。
(3)6在()的前面。
【指点迷津】能有序排列10以内的数,并正确比较出数的大小。
在比较3和8谁离0近一些时,可以通过数一数0与3之间相隔几个数,0与8之间相隔几个数来判定;当然也可以在直线上数0与3之间有几段,0与8之间有几段,从而作出判定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学最难的13种题型
1.和差问题
已知两数的和与差,求这两个数。
[例]已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)/2=6,小数=(10-2)/2=4。
2.鸡兔同笼问题
[例]鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)/(4-2)=24
求鸡时,假设全是兔,则鸡数 =(4X36-120)/(4-2)=12
3.余数问题
[例]如果时钟现在表示的时间是18点整,那么分针旋转1990圈后是几点钟?
分针旋转一圈是1小时,旋转24圈就是时针转1圈,也就是时针回到原位。
1980/24的余数是22,所以相当于分针向前旋转22个圈,分针向前旋转22个圈相当于时针向前走22个小时,时针向前走22小时,也相当于向后24-22=2个小时,即相当于时针向后拔了2小时。
即时针相当于是18-2=16(点)。
4.年龄问题
[例1]小军今年8 岁,爸爸今年34岁,几年后,爸爸的年龄的小军的3倍?岁差不会变,今年的岁数差点34-8=26,到几年后仍然不会变。
已知差与倍数,转化为差比问题。
26/(3-1)=13,几年后爸爸的年龄是13X3=39岁,小军的年龄是13X1=13岁,所以应该是5年后。
[例2]姐姐今年13岁,弟弟今年9岁,当姐弟俩岁数的和是40岁时,两人各应该是多少岁?岁差不会变,今年的岁数差13-9=4几年后也不改变。
几年后岁数和是40,岁数差是4,转化为和差题。
则几年后,姐姐的岁数:(40+4)/2=22,弟弟的岁数:(40-4)/2=18,所以答案是9年后。
5.牛吃草问题
[例]整个牧场上草长得一样密,一样快。
27头牛6天可以把草吃完;23头牛9天也可以把草吃完。
问21头多少天把草吃完。
每牛每天的吃草量假设是1,则27头牛6天的吃草量是27X6=162,23头牛9天的吃草量是23X9=207;大的减去小的,207-162=45;二者对应的天数的差值,是9-6=3(天)结果就是草的生长速率。
所以草的生长速率是45/3=15(牛/天);
原有的草量依此反推。
公式就是A头B天的吃草量减去B天乘以草的生长速率。
所以原有的草量=27X6-6X15=72(牛/天)。
将未知吃草量的牛分为两个部分:一小部分先吃新草,个数就是草的比率;这就是说将要求的21头牛分为两部分,一部分15头牛吃新生的草;剩下的21-15=6去吃原有的草,
所以所求的天数为:原有的草量/分配剩下的牛=72/6=12(天)
6.盈亏问题
[例1]小朋友分桃子,每人10个少9个;每人8个多7个。
求有多少小朋友多少桃子?
一盈一亏,则公式为:(9+7)/(10-8)=8(人),相应桃子为8X10-9=71(个)
[例2]士兵背子弹。
每人45发则多680发;每人50发则多200发,多少士兵多少子弹?
全盈问题。
大的减去小的,则公式为:(680-200)/(50-45)=96(人)则子弹为96X50+200=5000(发)。
[例3]学生发书。
每人10本则差90本;每人8 本则差8本,多少学生多少书?
全亏问题。
大的减去小的。
则公式为:(90-8)/(10-8)=41(人),相应书为41X10-90=320(本)7.工程问题
[例]一项工程,甲单独做4天完成,乙单独做6天完成。
甲乙同时做2天后,由乙单独做,几天完成?
[1-(1/6+1/4)X2]/(1/6)=1(天)
8.差比问题(差倍问题)
[例]甲数比乙数大12,甲:乙=7:4,求两数。
先求一倍的量,12/(7-4)=4,
所以甲数为:4X7=28,乙数为:4X4=16。
9.和比问题已知整体求部分。
[例]甲乙丙三数和为27,甲;乙:丙=2:3:4,求甲乙丙三数。
分母比数和,即分母为:2+3+4=9;分子自己的,则甲乙丙三数占和的比例分别为2/9,3/9,4/9。
和乘以比例,所以甲数为27X2/9=6,乙数为:27X3/9=9,丙数为:27X4/9=12。
10.追与问题
[例]姐弟二人从家里去镇上,姐姐步行速度为3千米/小时,先走2小时后,弟弟骑自行车出发速度6千米/小时,几时追上?先走的路程,为3X2=6(千米)速度的差,为6-3=3(千米/小时)。
所以追上的时间为:6/3=2(小时)。
11.相遇问题
[例]甲乙两人从相距120千米的两地相向而行,甲的速度为40千米/小时,乙的速度为20千米/小时,多少时间相遇?相遇那一刻,路程全走过。
即甲乙走过的路程和恰好是两地的距离120千米。
除以速度和,就把时间得。
即甲乙两人的总速度为两人的速度之和40+20=60(千米/小时),所以相遇的时间就为120/60=2(小时)
12.加糖浓化
例]有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X (1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17/(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)
13.加水稀释
[例]有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3/10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)。
