二分归并排序的时间复杂度以及递推式
数据结构第六-九章自测题及解答

一、概念题(每空0.5分,共45分)1.对于集合这逻辑结构来说,其中的数据元素之间也可以有各种各样的非逻辑关系,但任何一对数据元素之间没有________关系,即没有________关系。
2.查找表按其所包括的运算的不同分为________查找表和________查找表。
3.查找表中主关键字指的是________,次关键字指的是________。
4.静态查找表包括________、________、________三种基本运算。
5.动态查找表包括________、________、________、________、________五种基本运算。
6.假定key为主关键字,若顺序表中第n个元素的键值为K,则顺序查找算法的查找长度为1;若第1个元素的键值为K,则查找长度为________;若表中无键值等于K的元素,则查找长度为________。
7.二分查找在查找成功时的查找长度不超过________,其平均查找长度为________,当n较大时约等于________。
8.静态查找表的三种不同实现各有优缺点。
其中,________查找效率最低但限制最少。
________查找效率最高但限制最强。
而________查找则介于上述二者之间。
9.二叉搜索树是一种特殊的、增加了限制条件的二叉树,其限制条件是任一结点的键值________于其左孩子(及其子孙)的键值且________于其右孩子(及其子孙)的键值。
10. 在表示一棵二叉搜索树的二叉链表上,要找键值比某结点X的键值________的结点,只需通过结点X的左指针到它的左子树中去找。
11.中序遍历一棵二叉搜索树所得的结点访问序列是键值的________序列。
12.二叉搜索树上的查找长度不仅与________有关,也与二叉搜索树的________有关。
13.在随机情况下,含有n个结点的二叉搜索树的平均查找长度为________,其时间效率很高。
14.折半查找的查找效率与树的形态有关。
排序—时间复杂度为O(nlogn)的两种排序算法

(一)施工控制结构计算的一般原则
➢ 预应力混凝土连续梁桥、连续刚构桥的施工控制计算除了 必须满足与实际施工相符合的基本要求外,还要考虑诸多 相关的其他因素。
➢ 立0号段底模时,同时安装支座及防倾覆锚固装置。如图512所示。
0号块 1 2
3
0号块
1 2 3 4
1.底模架 2.支架 3.墩身
1.底模架 3.节点板
2.三角撑架 4.墩身
图5-12 支架搭设方式图
墩梁临时锚固
0号块
1 2 3 4
0号块
1 2 3
1.临时支座 3.临时支撑
2.永久支座 4.预应力钢绞线
(三)预应力混凝土连续梁的合拢施
工要点
1. 掌握合拢期间的气温预报情况,测试分析气温变化规律, 以确定合拢时间并为选择合拢锁定方式提供依据。
2. 根据结构情况及梁温的可能变化情况,选定适宜的合拢 方式并作力学建算。
3. 选择日气温较低、温度变化幅度较小时锁定合拢口并灌 注合拢段混凝土。
4. 合拢口的锁定,应迅速、对称地进行,先将外刚性支撑 一段与梁端预埋件焊接(或栓接),而后迅速将外刚性 支撑另一端与梁连接,临时预应力束也应随之快速张拉。 在合拢口锁定后,立即释放一侧的固结约束,使梁一端 在合拢口锁定的连接下能沿支座左右伸缩。
目的:桥梁施工控制的目的就是确保施工过程中结构
的可靠度和安全性,保证桥梁成桥桥面线 形及受力状态符合设计要求。
(二) 施工控制的内容
数据结构试卷带答案

数据结构试卷带答案问题说明部分题目或答案有问题,现将已经发现的公布如下,同学在作这些模拟题的时候应着重做题方法的理解,遇到问题以教材或课件为准,不确定的地方可找同学商量或问我(1)试卷1第一套填空题第1题,试卷1第2套选择题第3题关于循环队列队头指针和队尾指针的约定与教材不一致,以教材或课件为准,实际上front指向的是队头元素,rear指向当前尚未被占用的第一个队列空间,队慢或队空的判定条件及入队/出队等操作具体可参考课件或教材(2)试卷1第一套应用题第5题,不声明邻接点顺序时默认编号最小的邻接点为第一邻接点,该图的深度优先遍历序列为123465,答案错。
此外,当给定邻接表时则邻接点顺序按照邻接表中的前后顺序确定,如试卷1第二套填空题第8题(3)试卷1第五套应用题第4题,两种方法处理冲突的方法下所求ASL值相等都为7/6(4)试卷1第五套填空题第8题答案给出的是小顶堆需满足的条件,大顶堆满足ki>=k2i p->rlink->llink=p->llink;此外,注意课堂中讲的指针名和操作方法(12)第4套填空题第6题答案错,设哈夫曼树中共有99个结点,则该树中有____50_____个叶子结点;若采用二叉链表作为存储结构,则该树中有__100___个空指针域。
(13)第5套选择第8题答案应为A:设连通图G中的边集E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则从顶点a出发可以得到一种深度优先遍历的顶点序列为(A) abedfc(14)第5套应用题第3题题目未指明查找方法,没法作(15)第6套选择第5题应选B,实际是任意结点至多只有一个孩子:设二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树满足的条件是(B) 高度等于其结点数(16)第7套填空1题问题本身错,设指针变量p指向双向链表中的结点A,指针变量s指向被插入的结点X,则在结点A的后面插入结点X的操作序列为____s->left_____=p;s->right=p->right;___p->right_______=s;s->right->left=s;(设结点中的两个指针域分别为left和right)。
二路归并排序算法思想

二路归并排序算法思想
二路归并排序,又称为二路归并算法,是一种高效的排序算法。
它采用二分法的思想,将一组未排序的数据集合分为两个子集,先分别对每个子集进行排序,再将排序后的子集合归并在一起,得到一个完全有序的数据集合。
二路归并排序是一种“分而治之”的思想,三个步骤组成:分解、排序和合并。
首先,将数据集分解为两个规模较小的子数据集,然后分别对子集进行排序,最后将排序后的子集合归并在一起,得到一个完全有序的数据集合。
二路归并排序的时间复杂度和空间复杂度都比较低,其时间复杂度为O(nlogn),其空间复杂度为O(n)。
二路归并排序的优点在于:可以对非常大的数据集进行排序,非常稳定(相同的元素排序后仍然保持相同的排序),并且有效的利用计算机的内存空间。
总体来说,二路归并排序是一种低开销、高效率的排序算法,不但能够处理大数据集而且能保证排序的稳定性,使用场合很多。
分治算法知识点总结

分治算法知识点总结一、基本概念分治算法是一种递归的算法,其基本思想就是将原问题分解成多个相互独立的子问题,然后分别解决这些子问题,最后将子问题的解合并得到原问题的解。
分治算法的核心思想可以用一句话概括:分而治之,分即是将原问题分解成若干个规模较小的子问题,治即是解决这些子问题,然后将子问题的解合并起来得到原问题的解。
分治算法通常包括三个步骤:(1)分解:将原问题分解成若干个规模较小的子问题;(2)解决:递归地解决这些子问题;(3)合并:将子问题的解合并起来得到原问题的解。
分治算法的典型特征包括递归和合并。
递归指的是将原问题分解成若干个规模较小的子问题,然后递归地解决这些子问题;合并指的是将子问题的解合并得到原问题的解。
通常来说,分治算法的递归实现方式很容易编写,但有时可能会面临大量的重复计算,因此需要合并操作来避免这种情况。
二、原理分治算法的原理可以通过一个简单的例子来说明。
我们以计算数组中的最大值为例,具体的步骤如下:(1)分解:将数组分解成两个规模相等的子数组;(2)解决:递归地在这两个子数组中分别找到最大值;(3)合并:比较这两个子数组的最大值,得到原数组的最大值。
从这个例子可以看出,分治算法将原问题分解成两个子问题:分别在左边子数组和右边子数组中找到最大值,然后将这两个子问题的解合并起来得到原数组的最大值。
这种将问题分解成若干个规模较小的子问题,然后合并子问题的解得到原问题的解的方法正是分治算法的核心原理。
分治算法的优势在于它可以将原问题分解成多个规模较小的子问题,然后并行地解决这些子问题,最后合并子问题的解得到原问题的解。
这种并行的设计思路使得分治算法非常适合于并行计算,能够有效地提高计算效率。
三、应用分治算法在计算机科学领域有着广泛的应用,包括排序、搜索、图论、动态规划等多个方面。
下面我们将以排序算法和搜索算法为例,来介绍分治算法在实际应用中的具体情况。
1. 排序算法排序算法是计算机科学领域中一个重要的问题,分治算法在排序算法中有着广泛的应用。
算法分析基础——主定理

算法分析基础——主定理
对于形为T(n) = aT(n / b) + f(n)的递推⽅程,我们有如下结论:
主定理(MasterTheorem)设a≥1,b>1 为常数,f(n)为函数,n为⾮负整数,且 T(n) = aT(n / b) + f(n),则有以下结果:
1. 若存在ε>0,使得f(n) = O(n log b a-ε),则T(n) = Θ(n log b a)
2. 若f(n) = Θ(n log b a),则T(n) = Θ(n log b a logn)
3. 若存在ε>0,使得f(n) = Ω(n log b a+ε),并且对于某个常数c<1和所有充分⼤的n,有af(n / b)≤cf(n),则T(n) = Θ(f(n))
证明:详见教材(推导过程略复杂,不想写了qwq)。
由主定理可以直接得到下述推论:
推论1 依主定理条件,递推⽅程为T(n)= aT(n / b) + c,则
1. 当a≠1时,T(n) = Θ(n log b a)
2. 当a=1时,T(n) = Θ(logn)
推论2 依主定理条件,递推⽅程为T(n) = aT(n / b) + cn,则
1. 当a>b时,T(n) = Θ(n log b a)
2. 当a=b时,T(n) = Θ(nlogn)
3. 当a<b时,T(n) = Θ(n)
例根据主定理及其推论,我们可以直接得到⼆分检索算法的平均时间复杂度为Θ(logn),⽽⼆分归并排序的平均时间复杂度为Θ(nlogn)。
各种排序算法的时间复杂度和空间复杂度(阿里)
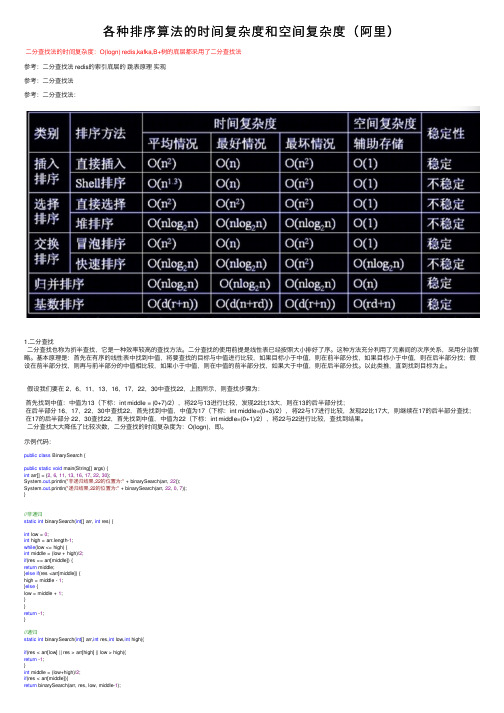
各种排序算法的时间复杂度和空间复杂度(阿⾥)⼆分查找法的时间复杂度:O(logn) redis,kafka,B+树的底层都采⽤了⼆分查找法参考:⼆分查找法 redis的索引底层的跳表原理实现参考:⼆分查找法参考:⼆分查找法:1.⼆分查找⼆分查找也称为折半查找,它是⼀种效率较⾼的查找⽅法。
⼆分查找的使⽤前提是线性表已经按照⼤⼩排好了序。
这种⽅法充分利⽤了元素间的次序关系,采⽤分治策略。
基本原理是:⾸先在有序的线性表中找到中值,将要查找的⽬标与中值进⾏⽐较,如果⽬标⼩于中值,则在前半部分找,如果⽬标⼩于中值,则在后半部分找;假设在前半部分找,则再与前半部分的中值相⽐较,如果⼩于中值,则在中值的前半部分找,如果⼤于中值,则在后半部分找。
以此类推,直到找到⽬标为⽌。
假设我们要在 2,6,11,13,16,17,22,30中查找22,上图所⽰,则查找步骤为:⾸先找到中值:中值为13(下标:int middle = (0+7)/2),将22与13进⾏⽐较,发现22⽐13⼤,则在13的后半部分找;在后半部分 16,17,22,30中查找22,⾸先找到中值,中值为17(下标:int middle=(0+3)/2),将22与17进⾏⽐较,发现22⽐17⼤,则继续在17的后半部分查找;在17的后半部分 22,30查找22,⾸先找到中值,中值为22(下标:int middle=(0+1)/2),将22与22进⾏⽐较,查找到结果。
⼆分查找⼤⼤降低了⽐较次数,⼆分查找的时间复杂度为:O(logn),即。
⽰例代码:public class BinarySearch {public static void main(String[] args) {int arr[] = {2, 6, 11, 13, 16, 17, 22, 30};System.out.println("⾮递归结果,22的位置为:" + binarySearch(arr, 22));System.out.println("递归结果,22的位置为:" + binarySearch(arr, 22, 0, 7));}//⾮递归static int binarySearch(int[] arr, int res) {int low = 0;int high = arr.length-1;while(low <= high) {int middle = (low + high)/2;if(res == arr[middle]) {return middle;}else if(res <arr[middle]) {high = middle - 1;}else {low = middle + 1;}}return -1;}//递归static int binarySearch(int[] arr,int res,int low,int high){if(res < arr[low] || res > arr[high] || low > high){return -1;}int middle = (low+high)/2;if(res < arr[middle]){return binarySearch(arr, res, low, middle-1);}else if(res > arr[middle]){return binarySearch(arr, res, middle+1, high);}else {return middle;}}}其中冒泡排序加个标志,所以最好情况下是o(n)直接选择排序:排序过程:1 、⾸先在所有数据中经过 n-1次⽐较选出最⼩的数,把它与第 1个数据交换,2、然后在其余的数据内选出排序码最⼩的数,与第 2个数据交换...... 依次类推,直到所有数据排完为⽌。
信息学奥赛基础测试题及答案

信息学奥赛基础测试题及答案1、计算机的基本硬件结构一直沿袭()设计的框架。
A.比尔•;盖茨B.冯•;诺依曼C.布尔D.图灵答案:B 2、下列无符号数中,最小的数是()A.(11011001)2B.(75)10C.(37)8D.(2A)16答案:C 3、在外部设备中,绘图仪属于()A.输入设备B.输出设备C.辅(外)存储器D.主(内)存储器答案:B 4、计算机主机是由CPU与()构成的A.控制器B.输入、输出设备C.运算器D.内存储器答案:D 5、计算机病毒的特点是()A.传播性、潜伏性、易读性与隐蔽性B.破坏性、传播性、潜伏性与安全性C.传播性、潜伏性、破坏性与隐蔽性D.传播性、潜伏性、破坏性与易读性答案:C 6、WINDOWS 9X是一种()操作系统A.单任务字符方式B.单任务图形方式C.多任务字符方式D.多任务图形方式答案:D 7、Internet的规范译名应为()A.英特尔网B.因特网C.万维网D.以太网答案:B 8、计算机网络是一个()系统A.管理信息系统B.管理数据系统C.编译系统D.在协议控制下的多机互连系统答案:D 9、计算机系统总线上传送的信号有()A.地址信号与控制信号B.数据信号、控制信号与地址信号C.控制信号与数据信号D.数据信号与地址信号答案:B 10、计算机的运算速度取决于给定的时间内,它的处理器所能处理的数据量。
处理器一次能处理的数据量叫字长。
已知64位的奔腾处理器一次能处理64个信息位,相当于()字节。
A.8个B.1个C.16个D.2个答案:A 11、某种计算机的内存容量是640K,这里的640K容量是指()个字节A.640B.640*1000C.640*1024D.640*1024*1024答案:C 12、下面哪些计算机网络不是按覆盖地域划分的()A.局域网B.都市网C.广域网D.星型网答案:D 13、在有N个叶子节点的哈夫曼树中,其节点总数为()A.不确定B.2N-1C.2N+1D.2N答案:B 14、已知数组中A中,每个元素A(I,J)在存贮时要占3个字节,设I从1变化到8,J从1变化到10,分配内存时是从地址SA开始连续按行存贮分配的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、简介
二分归并排序是一种常见的排序算法,它通过将问题分解为子问题,
并将子问题的解合并来解决原始问题。
该算法的时间复杂度非常重要,因为它直接影响算法的效率和性能。
在本文中,我们将深入探讨二分
归并排序的时间复杂度,并通过递推式来进一步分析算法的性能。
二、二分归并排序的时间复杂度
1. 分析
在二分归并排序中,时间复杂度可以通过以下三个步骤来分析:
- 分解:将原始数组分解为较小的子数组。
- 解决:通过递归调用来对子数组进行排序。
- 合并:将排好序的子数组合并为一个整体有序的数组。
2. 时间复杂度
在最坏情况下,二分归并排序的时间复杂度为O(nlogn)。
这是因为在每一层递归中,都需要将数组分解为两个规模近似相等的子数组,并
且在每一层递归的最后都需要将这两个子数组合并起来。
可以通过递
推式来进一步证明算法的时间复杂度。
3. 递推式分析
我们可以通过递推式来分析二分归并排序的时间复杂度。
假设对规模
为n的数组进行排序所需的时间为T(n),则可以得到以下递推式:
T(n) = 2T(n/2) +
其中,T(n/2)表示对规模为n/2的子数组进行排序所需的时间表示将
两个子数组合并所需的时间。
根据递推式的定义,我们可以得到二分
归并排序的时间复杂度为O(nlogn)。
三、结论与个人观点
通过以上分析,我们可以得出二分归并排序的时间复杂度为O(nlogn)。
这意味着该算法在最坏情况下也能保持较好的性能,适用于大规模数
据的排序。
我个人认为,二分归并排序作为一种经典的排序算法,其
时间复杂度的分析对于理解算法的工作原理和性能至关重要。
通过深
入研究递推式,可以更加直观地理解算法的性能表现,为进一步优化
算法提供了重要的参考依据。
四、总结
在本文中,我们探讨了二分归并排序的时间复杂度,通过分析和递推
式的方式深入理解了该算法的性能表现。
通过对时间复杂度的分析,
我们对算法的性能有了更深入的认识,并且能够更好地理解算法在实
际应用中的表现。
相信通过本文的阅读,读者能够对二分归并排序有
更全面、深刻和灵活的理解。
四、继续深入探讨二分归并排序的时间
复杂度
1. 时间复杂度的影响因素
在上一部分中,我们已经讨论了二分归并排序的时间复杂度为
O(nlogn),这是在最坏情况下的时间复杂度。
然而,实际情况中,算
法的性能受到多种因素的影响,可能会出现不同的时间复杂度。
下面
我们将进一步探讨这些影响因素。
影响时间复杂度的因素之一是初始数据的状态。
对于完全随机的数据,二分归并排序通常能够保持O(nlogn)的时间复杂度。
但是,在数据近乎有序或者完全逆序的情况下,算法的时间复杂度可能会有所不同。
具体来说,如果数据已经近乎有序,那么在进行合并操作时,算法的
时间复杂度可能会降低至O(n)级别;而在数据完全逆序的情况下,算
法的时间复杂度可能会接近O(nlogn)的最坏情况。
影响时间复杂度的因素之二是算法优化的策略。
在最基本的二分归并
排序中,每一次合并操作都是通过比较大小来完成的,这需要额外的
时间。
但是,在实际应用中,可以通过一些优化策略来降低合并操作的时间复杂度,从而提高整体排序的效率。
2. 实际应用中的时间复杂度
除了最坏情况下的时间复杂度之外,我们还需要关注二分归并排序在实际应用中的平均时间复杂度。
对于随机数据而言,该算法通常能够保持O(nlogn)的时间复杂度。
然而,在特定情况下,比如数据近乎有序或者完全逆序的情况下,算法的平均时间复杂度可能会有所不同。
在实际生产环境中,我们通常需要考虑算法的稳定性和鲁棒性。
虽然有些特定情况下可能会出现算法时间复杂度不稳定的情况,但是在大多数情况下,二分归并排序都能够保持较好的性能表现,适用于各种不同类型的数据。
3. 优化策略对时间复杂度的影响
除了理论上的时间复杂度分析之外,我们还需要关注算法优化对时间复杂度的影响。
在实际应用中,通过一些优化策略,我们可以进一步提高二分归并排序的性能表现。
可以通过迭代方式替代递归方式来实现排序操作,减少函数调用的开销;可以在合并操作中使用临时数组进行优化,减少比较次数和赋值
操作的开销;可以利用插入排序来优化小规模子问题的排序过程等等。
这些优化策略可以在一定程度上降低算法的时间复杂度,并提高算法
的效率和性能。
4. 总结
通过深入探讨二分归并排序的时间复杂度,我们可以更全面地理解算
法的性能表现。
除了最坏情况下的时间复杂度之外,我们还需要考虑
算法在实际应用中的平均时间复杂度、稳定性和鲁棒性。
算法优化对
时间复杂度的影响也是需要重点关注的方面。
通过不断优化算法,可
以提高算法的性能表现,更好地满足实际应用的需求。
在实际应用中,我们可以根据具体情况选择合适的排序算法,以及针
对具体问题进行算法优化,从而达到更好的排序效果。
二分归并排序
作为经典的排序算法之一,其时间复杂度分析对于理解算法的内在原
理和性能表现非常重要,希望通过本文的阐述能够对读者有所帮助。
