【圆周运动】3圆周运动中的相遇追及、周期性、多解性问题
高中物理圆周运动问题解题方法研究

高中物理圆周运动问题解题方法研究圆周运动是物理学中的重要概念,它在日常生活中有着广泛的应用。
高中物理课程中,圆周运动是一个常见的难点,学生常常对圆周运动问题感到困惑。
本文旨在研究高中物理圆周运动问题的解题方法,以帮助学生更好地理解和掌握这一概念。
我们需要清楚圆周运动的基本概念。
圆周运动是指物体在一个轨道上以一定的半径和速度进行运动的现象。
在解题时,需要明确物体的半径、速度、角速度、角加速度等基本参数,并且要建立合适的坐标系来描述运动。
接下来,我们来研究一些具体的解题方法。
常见的圆周运动问题有以下几类:1. 匀速圆周运动问题。
当物体在圆周轨道上以匀速运动时,可以使用简单的数学方法来解题。
已知物体的速度和半径,求解物体的周期、频率、角速度等。
在解题过程中,可以利用物体在一个周期内所通过的弧长和角度的关系进行计算。
3. 动力学问题。
除了静态问题外,还有一类问题是涉及到动力学的圆周运动问题。
已知物体的质量、半径、速度和角速度,求解物体的动能、动量、力矩等物理量。
在解题过程中,需要利用物体的机械能守恒和力矩平衡等原理进行计算。
在解题过程中,需要注意以下几点:1. 注意单位的转换。
在解题过程中,需将已知条件和所求结果的单位进行统一转换,以确保计算的准确性和一致性。
2. 综合运用不同物理知识。
圆周运动问题往往涉及到力学、运动学和动力学等多个方面的知识。
在解题时,需要灵活运用这些知识进行分析和计算,确保解题的准确性。
3. 注意符号的使用。
在解题过程中,需要正确地选择和使用符号,以避免混淆和错误。
特别是在使用向心力和离心力的计算中,需要注意力的方向和正负号的选择。
高中物理圆周运动问题的解题方法主要包括建立合适的坐标系、了解基本概念和参数、综合运用不同物理知识等。
通过对这些方法的研究和实践,可以帮助学生更好地理解和掌握圆周运动问题,提高解题能力。
进行大量的练习和例题分析也是非常重要的,只有不断地反复练习和思考,才能真正掌握圆周运动问题的解题方法。
圆周运动中的临界问题和周期性问题高中物理

圆周运动中的临界问题和周期性问题一、圆周运动问题的解题步骤:1、确定研究对象2、画出运动轨迹、找出圆心、求半径3、分析研究对象的受力情况,画受力图4、确定向心力的来源5、由牛顿第二定律r Tm r m r v m ma F n n 222)2(πω====……列方程求解 二、临界问题常见类型:1、按力的种类分类: (1)、与弹力有关的临界问题:接触面间的弹力:从有到无,或从无到有绳子的拉力:从无到有,从有到最大,或从有到无 (2)、与摩擦力有关的弹力问题:从静到动,从动到静,临界状态下静摩擦力达到最大静摩擦 2、按轨道所在平面分类: (1)、竖直面内的圆周运动 (2)、水平面内的圆周运动三、竖直面内的圆周运动的临界问题1、单向约束之绳、外轨道约束下的竖直面内圆周运动临界问题: 特点:绳对小球,轨道对小球只能产生指向圆心的弹力① 临界条件:绳子或轨道对小球没有力的作用:mg=mv 2/R →v 临界=Rg (可理解为恰好转过或恰好转不过的速度) 即此时小球所受重力全部提供向心力②能过最高点的条件:v ≥Rg ,当v >Rg 时,绳对球产生拉力,轨道对球产生压力. ③不能过最高点的条件:v <V 临界(实际上球还没到最高点时就脱离了轨道做斜抛运动) 例1、绳子系着装有水的木桶,在竖直面内做圆周运动,水的质量m=0.5kg ,绳子长度为l=60cm ,求:(g 取10m/s 2)A 、最高点水不留出的最小速度?B 、设水在最高点速度为V=3m/s ,求水对桶底的压力? 答案:(1)s m /6 (2)2.5N变式1、如图所示,一质量为m 的小球,用长为L 细绳系住,使其在竖直面内作圆周运动.(1)若过小球恰好能通过最高点,则小球在最高点和最低点的速度分别是多少?小球的受力情况分别如何?(2)若小球在最低点受到绳子的拉力为10mg ,则小球在最高点的速度及受到绳子的拉力是多少?2、单向约束之内轨道约束下(拱桥模型)的竖直面内圆周运动的临界问题:汽车过拱形桥时会有限速,是因为当汽车通过半圆弧顶部时的速度gr v =时,汽车对弧顶的压力FN=0,此时汽车将脱离桥面做平抛运动,因为桥面不能对汽车产生拉力.例2、半径为 R 的光滑半圆球固定在水平面上,顶部有一小物体, 如图所示。
相遇问题题型及解题方法和技巧(一)

相遇问题题型及解题方法和技巧(一)相遇问题题型及解题方法和技巧什么是相遇问题题型?相遇问题是指两个或多个运动的物体,会在某一时间点相遇的问题。
在数学和物理学中,相遇问题主要涉及距离、速度、时间等概念。
常见相遇问题题型1.直线相遇问题:两个物体沿着同一条直线运动,求它们相遇的时间和地点;2.圆周相遇问题:两个物体分别沿着两个圆周运动,求它们第一次相遇的时间和地点;3.绕圆相遇问题:一个物体沿着一个圆周运动,另一个物体以直线匀速运动绕着这个圆周运动,求它们相遇的时间和地点;4.追及问题:两个物体沿着不同的路径运动,一个物体从后面追击另一个物体,求它们相遇的时间和地点。
解题方法和技巧1.明确相遇点:对于直线相遇问题,我们可以通过相遇点求解相遇时间;对于圆周相遇问题,我们可以通过相遇点求解相遇时间和地点;2.使用公式:我们可以通过速度、时间、距离之间的关系,利用公式进行求解。
例如,对于直线相遇问题,我们可以使用“路程相等”公式;3.将条件转化:有些题目条件比较复杂,我们可以通过将条件进行转化,简化问题。
例如,对于绕圆相遇问题,我们可以将一个物体沿着一个圆周运动,看成另一个物体沿着一个直线匀速运动,从而使问题变得简单;4.画图辅助:画图可以帮助我们清楚地了解问题,找到问题的解法。
对于复杂的问题,我们可以把问题进行拆分,逐个进行分析。
总之,相遇问题需要我们灵活掌握不同的解题方法和技巧,并进行多方面的思考和尝试。
只有不断练习,才能掌握这一类问题解题的精髓。
例题分析题目描述:两架飞机从A 、B 两地同时起飞,相向而飞。
已知A 地与B 地的距离为1600千米。
两飞机飞行速度相等,相遇时速度之和为940千米/小时。
问:这两架飞机飞行的速度分别是多少?解题思路:1.画图,明确相遇点; 2.根据路程相等公式,列出方程; 3.解方程得到答案; 4. 反向验证,确认答案正确。
解题步骤:1. 假设两架飞机的速度分别为v1和v2;2. 明确相遇点为距A 点x 公里处,根据速度、时间、路程之间的关系,列出方程:x = v1 * t = (1600 - x) / 2 * v2 + v1 * t ,其中1600-x 表示距B 点的距离,除2是因为两飞机相向而行,会在一半的距离x/2处相遇;3. 整理方程,解出v1和v2。
匀速圆周运动相遇追及问题公式

匀速圆周运动相遇追及问题公式在解决匀速圆周运动相遇追及问题时,可以使用一些基本的公式来计算。
这些公式基于以下假设和定义:1.对于两个物体,它们都在一个平面上做匀速圆周运动。
我们假设物体之间的相对角速度是恒定的,即它们的运动速度相对于彼此是恒定的。
2.角度以弧度为单位。
圆周的长度可表示为它的半径乘以圆周的角度(弧度)。
圆周的角度与物体在一定时间内旋转的角度成正比。
3.运动物体的速度可以表示为速度大小与角度速度的乘积。
即v=rω,其中v是物体的线速度,r是半径,ω是角速度。
4.运动物体的位移可以用角度和半径的关系来表示。
即s=rθ,其中s是位移,r是半径,θ是角度。
在匀速圆周运动相遇追及问题中,我们想要找到两个物体相遇的时间。
我们可以将其中一个物体的位置视为原点,另一个物体的位置表示为x。
设第一个物体的半径为r1,角速度为ω1,第二个物体的半径为r2,角速度为ω2、假设它们相遇的时间为t,那么在相遇的时候,两个物体所在的角度分别是θ1和θ2对于第一个物体,它的位移可以表示为s1=r1θ1;对于第二个物体,它的位移可以表示为s2=r2θ2、相遇的条件是两个物体位移相等,即s1=s2根据以上的定义和假设,我们可以建立如下方程来解决这个问题:r1θ1=r2θ2另外,根据速度和位移的关系,我们可以得到:θ1=ω1t和θ2=ω2t将以上两个等式代入相遇条件的方程中,我们可以得到:r1(ω1t)=r2(ω2t)通过合并同类项,我们可以得到:(ω1r1-ω2r2)t=0为使上述方程成立,我们必须有(ω1r1-ω2r2)=0。
当(ω1r1-ω2r2)=0时,即两个物体的角速度和半径的乘积相等,它们将在同一时间相遇。
在此情况下,我们可以用任何一个物体的运动参数来计算相遇的时间t。
总结起来,匀速圆周运动相遇追及问题的公式是:(ω1r1-ω2r2)=0其中,ω1和r1是第一个物体的角速度和半径,ω2和r2是第二个物体的角速度和半径。
第 7 点 圆周运动的多解性

第 7 点 圆周运动的周期性造成多解匀速圆周运动的多解问题常涉及两个物体的两种不同的运动,其中一个做匀速圆周运动,另 一个做其他形式的运动 . 因匀速圆周运动具有周期性, 使得在一个周期中发生的事件在其他周 期同样可能发生,这就要求我们在解决此类问题时,必须考虑多解的可能性 . 一般处理这类 问题时,要把一个物体的运动时间 t ,与圆周运动的周期 T 建立起联系,才会较快地解决问题 .【对点例题1】如图所示,小球 Q 在竖直平面内绕 O 点做匀速圆周运动,当 Q 球转到图示位 置时,O 点正上方有另一小球 P 在距圆周最高点 h 处开始自由下落,要使两球在圆周最高点 相碰,则 Q 球的角速度 ω 应满足什么条件?解题指导:设P 球自由落体到圆周最高点的时间为t ,由自由落体可得:212h gt =求得 t =Q 球由图示位置转至最高点的时间也是t ,但做匀速圆周运动,周期为T ,有(41)4T t n =+ (n =0,1,2,3……)两式联立再由2T πω=,得 (41)2n πω+所以 ω =(42n π+ (n =0,1,2,3……) 【练习】1 如图所示,半径为R 的圆盘绕垂直于盘面的中心轴O 匀速转动,其正上方h 处有一个小球,B 为圆盘边缘上的一点,现将小球沿OB 方向水平抛出一小球,使球恰好只与圆盘边缘上的B相碰,则 (1)小球的初速度v 为多少?(2)圆盘转动的角速度ω为多少?解:(1)小球做平抛运动在竖直方向上:212h gt =则运动时间 t =又因为水平位移为R ,所以球的速度v =R t =(2)在时间t 内,盘转过的角度θ=n •2π,又因为θ=ωt ,则转盘角速度:ω=22n n t π=n =1,2,3…) 2 如图所示,B 物体放在光滑的水平地面上,在水平恒力F的作用下由静止开始向右运动,B 物体质量为m ,同时A 物体从图中位置开始在竖直面内由M 点开始逆时针做半径为r 、角速度为ω的匀速圆周运动.求力F 为多大时可使A 、B 两物体在某些时刻的速度相同 .解析 因为物体 B 在力 F 的作用下沿水平地面向右做匀加速直线运动,速度方向水平向右,要使A 与B 速度相同,则只有当A 运动到圆轨道的最低点时,才有可能 .设 A 、 B 运动时间 t 后两者速度相同 ( 大小相等,方向相同 ).对 A 物体有:332()44t T nT n πω=+=+ ( n = 0,1,2 … ) A v r ω= 对 B 物体有:B F F F ma a v at t m m==== 令 v B = v A , 得 32()4F n r m πωω+= 解得 22(43)mr F n ωπ=+ ( n = 0,1,2 … ).。
高中物理圆周运动知识点总结

高中物理圆周运动知识点总结圆周运动是高考必考的三大基础运动之一。
前两种基本运动是匀速直线运动和平抛运动。
先说圆周运动的基础知识,首先是对圆周运动基本物理量的理解。
我们都知道圆周运动的物理量,线速度,角速度,周期,向心加速度,向心力。
那我们就一个一个来了解吧!线速度 v 和角速度 \omega设一个物体做匀速圆周运动,在时间 t 内从A点运动到B 点,扫过的弧长为 l ,扫过的圆心角为θ,如下图所示。
则v=\frac{l}{t}, \omega=\frac{\theta}{t}当物体从A点出发运动一周回到A点,则 t=T , l=2\piR , \theta=2\pi :( T 为物体做匀速圆周运动的周期)v=\frac{l}{t}=\frac{2\pi R}{T},\omega=\frac{\theta}{t}=\frac{2\pi}{T}综合上面这两个式子,可得 v=\omega R 。
转速n:转速代表物体做圆周运动时1s内转过的圈数,而角速度\omega 代表1s内转过的弧度。
它们之间的关系是: \omega=2\pi\cdot n 。
向心加速度 a_向:a_向=\frac{v^2}{R}=\omega^2R=\frac{4\pi^2}{T^2}\cdot R=\omega v特点:方向永远指向圆心。
向心力 F_向:F_向=ma_向=m\frac{v^2}{R}=m\omega^2R=m\cdot\frac{4\pi^2}{T^2}\cd ot R向心力是按效果命名的力,不是某种性质的力,因此,向心力可以由某一个力提供,也可以由几个力的合力提供,要根据物体受力的实际情况判定.向心力公式:向心力公式是六个关键公式之一,可以说是六个关键公式中最简单的公式。
那么写向心力公式的基本步骤是什么呢?1.明确研究对象,确定位置(定点);2.受力分析;3.确定向心力方向;4.如果存在与向心力方向既不垂直也不平行的力,应正交分解;5.把所有与向心力方向垂直的力去掉;6.向心方向的力减去另一个方向的力得到向心力,列出向心力公式。
新教材 人教版高中物理必修第二册 第六章 圆周运动 知识点考点重点难点提炼汇总

第六章圆周运动6.1圆周运动 ........................................................................................................................... - 1 -6.2向心力 ............................................................................................................................... - 9 -6.3向心加速度 ..................................................................................................................... - 16 -6.4生活中的圆周运动 ......................................................................................................... - 21 -专题课向心力的应用和计算............................................................................................ - 32 - 专题课生活中的圆周运动................................................................................................ - 36 -6.1圆周运动一、圆周运动及线速度1.圆周运动的概念运动轨迹为圆周或一段圆弧的机械运动,称为圆周运动。
圆周运动的规律及其应用 知识点总结与典例(最新)
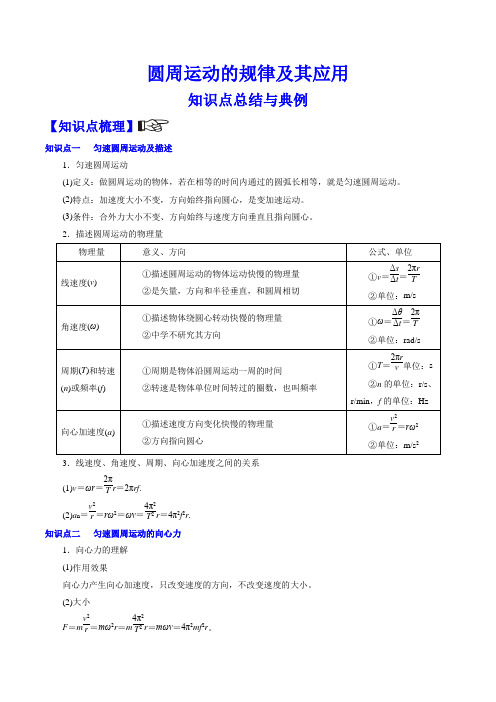
圆周运动的规律及其应用知识点总结与典例【知识点梳理】知识点一 匀速圆周运动及描述1.匀速圆周运动(1)定义:做圆周运动的物体,若在相等的时间内通过的圆弧长相等,就是匀速圆周运动。
(2)特点:加速度大小不变,方向始终指向圆心,是变加速运动。
(3)条件:合外力大小不变、方向始终与速度方向垂直且指向圆心。
2.描述圆周运动的物理量物理量 意义、方向公式、单位 线速度(v )①描述圆周运动的物体运动快慢的物理量 ②是矢量,方向和半径垂直,和圆周相切 ①v =Δs Δt =2πr T ②单位:m/s 角速度(ω)①描述物体绕圆心转动快慢的物理量 ②中学不研究其方向①ω=ΔθΔt =2πT ②单位:rad/s 周期(T )和转速(n )或频率(f )①周期是物体沿圆周运动一周的时间 ②转速是物体单位时间转过的圈数,也叫频率①T =2πrv 单位:s ②n 的单位:r/s 、r/min ,f 的单位:Hz向心加速度(a )①描述速度方向变化快慢的物理量 ②方向指向圆心①a =v 2r =rω2 ②单位:m/s 23.线速度、角速度、周期、向心加速度之间的关系 (1)v =ωr =2πT r =2πrf .(2)a n =v 2r =rω2=ωv =4π2T 2r =4π2f 2r . 知识点二 匀速圆周运动的向心力1.向心力的理解 (1)作用效果向心力产生向心加速度,只改变速度的方向,不改变速度的大小。
(2)大小F =m v 2r =mω2r =m 4π2T 2r =mωv =4π2mf 2r 。
(3)方向始终沿半径方向指向圆心,时刻在改变,即向心力是一个变力。
(4)来源向心力可以由一个力提供,也可以由几个力的合力提供,还可以由一个力的分力提供。
2.离心现象(1)现象做圆周运动的物体,在所受合外力突然消失或不足以提供圆周运动所需向心力的情况下,就做逐渐远离圆心的运动。
(2)受力特点①当F n=mω2r时,物体做匀速圆周运动。
